| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 5 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201424472 | |
| Published online | 09 December 2014 | |
Research Note
The surface signature of the tidal dissipation of the core in a two-layer planet
1 IMCCE, Observatoire de Paris – UMR
8028 du CNRS – Université Pierre et Marie Curie, 77 avenue Denfert-Rochereau, 75014
Paris,
France
e-mail: francoise.remus@obspm.fr, lainey@imcce.fr
2 LUTH, Observatoire de Paris – CNRS –
Université Paris Diderot, 5 place
Jules Janssen, 92195
Meudon Cedex,
France
e-mail: jean-paul.zahn@obspm.fr
3 Laboratoire AIM Paris-Saclay, CEA/DSM
– CNRS – Université Paris Diderot, IRFU/SAp Centre de Saclay, 91191
Gif-sur-Yvette,
France
e-mail: stephane.mathis@cea.fr
4 LESIA, Observatoire de Paris – CNRS –
Université Paris Diderot – Université Pierre et Marie Curie,
5 place Jules
Janssen, 92195
Meudon,
France
Received:
25
June
2014
Accepted:
30
September
2014
Context. Tidal dissipation, which is directly linked to internal structure, is one of the key physical mechanisms that drive the evolution of systems and govern their architecture. A robust evaluation of its amplitude is thus needed to predict the evolution time for spins and orbits and their final states.
Aims. The purpose of this paper is to refine a recent model of the anelastic tidal dissipation in the central dense region of giant planets, which are commonly assumed to retain a large amount of heavy elements, which constitute an important source of dissipation.
Methods. The previous paper evaluated the impact of the static fluid envelope on the tidal deformation of the core and on the associated anelastic tidal dissipation through the tidal quality factor Qc. We examine here its impact on the corresponding effective anelastic tidal dissipation through the effective tidal quality factor Qp.
Results. We show that the strength of this mechanism mainly depends on mass concentration. In the case of Jupiter- and Saturn-like planets, it can increase their effective tidal dissipation by, around, factors 2.4 and 2, respectively. In particular, the range of the rheologies compatible with the observations is enlarged compared to the results issued from previous formulations.
Conclusions. We derive here an improved expression of the tidal effective factor Qp in terms of the tidal dissipation factor of the core Qc, without assuming the commonly used assumptions. When applied to giant planets, the formulation obtained here allows a better match between the anelastic core’s tidal dissipation of a two-layer model and the observations.
Key words: planetary systems / planets and satellites: gaseous planets / planets and satellites: dynamical evolution and stability / planets and satellites: interiors / planets and satellites: general / planet-star interactions
© ESO, 2014
1. Introduction and motivations
In Remus et al. (2012, hereafter RMZL12), we have studied the tidal dissipation of the anelastic core of a two-layer planet. In that model, the core was assumed to be the main source of tidal dissipation. The envelope was considered as a non-viscous fluid, which was sensitive to the tidal deformation only through its action on shape deformation. The paper derived the tidal dissipation of the core, quantified by the ratio 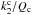 , where
, where 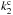 is the norm of the complex Love number of second-order at the mean surface of the core (
is the norm of the complex Love number of second-order at the mean surface of the core (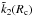 ), and Qc is its tidal quality factor. Nonetheless, the equations that describe the dynamical evolution of a given satellite are not directly expressed with
), and Qc is its tidal quality factor. Nonetheless, the equations that describe the dynamical evolution of a given satellite are not directly expressed with 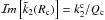 . According to Kaula (1962), for example, the evolution rate of the semi-major axis da/ dt is proportional to
. According to Kaula (1962), for example, the evolution rate of the semi-major axis da/ dt is proportional to 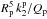 , where we use “p” sub- and superscripts that relate to the surface of the planet. Thus, the quantity that intervenes here is the global tidal dissipation, also called the effective tidal dissipation, i.e. the imaginary part of the complex Love number taken at the surface of the planet.
, where we use “p” sub- and superscripts that relate to the surface of the planet. Thus, the quantity that intervenes here is the global tidal dissipation, also called the effective tidal dissipation, i.e. the imaginary part of the complex Love number taken at the surface of the planet.
As mentioned in RMZL12, recent studies managed to extract the tidal dissipation of Jupiter (Lainey et al. 2009) and Saturn (Lainey et al. 2012) from astrometric data. This quantity corresponds to the ratio 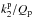 , assuming that Rp and the other parameters are known. Then, the question is which tidal dissipation in the core is able to account for the observed dissipation. In other words, if one considers, as in RMZL12, that the source of tidal dissipation is restricted to the core, it seems obvious that one has to relate the tidal dissipation in the core to the effective tidal dissipation of the planet, which can be directly compared to the observations. The purpose of this paper is to explicitly derive such a relation. In Sect. 2 we first discuss the limits of application of the standard formulation and its implicit consequences. Then, we show how to derive the effective tidal dissipation, knowing the tidal dissipation of the core, and taking both the overload and the gravitational attraction exerted by the envelope on the core into account. Finally, Sect. 3 evaluates the strength of this mechanism in giant gas planets.
, assuming that Rp and the other parameters are known. Then, the question is which tidal dissipation in the core is able to account for the observed dissipation. In other words, if one considers, as in RMZL12, that the source of tidal dissipation is restricted to the core, it seems obvious that one has to relate the tidal dissipation in the core to the effective tidal dissipation of the planet, which can be directly compared to the observations. The purpose of this paper is to explicitly derive such a relation. In Sect. 2 we first discuss the limits of application of the standard formulation and its implicit consequences. Then, we show how to derive the effective tidal dissipation, knowing the tidal dissipation of the core, and taking both the overload and the gravitational attraction exerted by the envelope on the core into account. Finally, Sect. 3 evaluates the strength of this mechanism in giant gas planets.
2. Effective tidal dissipation of a two-layer planet
As assumed in RMZL12, we consider a two-layer planet of radius Rp, that has homogeneous density ρc up to the radius Rc at which a density jump occurs down to ρo, then staying constant up to the surface of the planet.
2.1. The standard approach
Except for Dermott (1979) and recently RMZL12, none of the studies dealing with the anelastic tidal dissipation of planets or satellites have taken the role of an outer layer surrounding the anelastic region into account as a non-negligible factor that could enhance the tidal dissipation of the core. Thus, since the envelope had no influence on the core, it so far could be omitted. The problem could then be reduced to seeking the tidal dissipation of a homogeneous planet of radius Rc and density ρc, which would induce the same satellite migration as the supposed two-layer planet of radius Rp. In that case, such a quantity would obey, as commonly assumed, 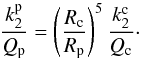 (1)Nevertheless, this formulation no longer holds if we consider both the gravitational attraction and the overload exerted by the tidally deformed envelope on the core.
(1)Nevertheless, this formulation no longer holds if we consider both the gravitational attraction and the overload exerted by the tidally deformed envelope on the core.
2.2. Retroaction of the static envelope
In this section, we show that considering these effects as in RMZL12, Eq. (1) is no longer valid. According to Eq. (6) of Dermott et al. (1988), 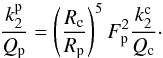 (2)In this paper, the authors referred to Dermott (1979) for the definition of the factor Fp, which “is a factor that allows for the enhancement of the tide in the core by the tide in the overlying ocean and for the effects of the density contrast between the core and the ocean”.
(2)In this paper, the authors referred to Dermott (1979) for the definition of the factor Fp, which “is a factor that allows for the enhancement of the tide in the core by the tide in the overlying ocean and for the effects of the density contrast between the core and the ocean”.
We derive here an explicit expression of the factor 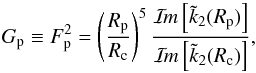 (3)thanks to RMZL12, where we discussed the weaknesses of Dermott’s formulation for the tidal dissipation of the core appearing in the 1979 paper.
(3)thanks to RMZL12, where we discussed the weaknesses of Dermott’s formulation for the tidal dissipation of the core appearing in the 1979 paper.
The complex Love number is given by 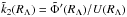 , where U designates the tidal potential,
, where U designates the tidal potential, 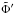 the perturbed gravitational potential, and the Λ subscripts stand either for c (for core surface quantities) or p (for planet surface quantities). At any point P(r,Θ), where r is the distance to the center of the planet, Θ the angle formed by the radial vector and the line of centers, the tidal potential has the form
the perturbed gravitational potential, and the Λ subscripts stand either for c (for core surface quantities) or p (for planet surface quantities). At any point P(r,Θ), where r is the distance to the center of the planet, Θ the angle formed by the radial vector and the line of centers, the tidal potential has the form 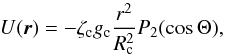 (4)where P2 the Legendre polynomial of second order, gc the gravity induced by the core at its surface, and
(4)where P2 the Legendre polynomial of second order, gc the gravity induced by the core at its surface, and 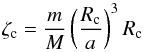 (5)is the tidal height at the surface of the core, with m the mass of the perturber and a the semi-major axis of its orbit.
(5)is the tidal height at the surface of the core, with m the mass of the perturber and a the semi-major axis of its orbit.
Let us denote the core and planet surfaces by ![\begin{eqnarray} \label{Eq:sc_sp_def} \mrm s_{\rm c} &=& R_{\rm c} \left[1 + S_2 P_2 (\cos\Theta) \right] , \\ \mrm s_{\rm p} &=& R_{\rm p} \left[1 + T_2 P_2 (\cos\Theta) \right] , \end{eqnarray}](/articles/aa/full_html/2015/01/aa24472-14/aa24472-14-eq34.png) respectively. Since there is no physical reason for the surfaces of the core and the envelope to suffer the same deformation, in general, T2 ≠ S2. The way these quantities are linked depends on the effective forces acting on the surface of the core. From here on, we denote by ε the ratio defined by
respectively. Since there is no physical reason for the surfaces of the core and the envelope to suffer the same deformation, in general, T2 ≠ S2. The way these quantities are linked depends on the effective forces acting on the surface of the core. From here on, we denote by ε the ratio defined by 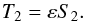 (8)We first consider a purely elastic core. The self-gravitational potential of the planet is the sum of the core and envelope contributions. In the envelope (where
(8)We first consider a purely elastic core. The self-gravitational potential of the planet is the sum of the core and envelope contributions. In the envelope (where 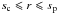 ), they are given by Eqs. (49), (50) of RMZL12:
), they are given by Eqs. (49), (50) of RMZL12: ![% subequation 947 0 \begin{eqnarray} \Phi_{\rm c} (r,\Theta) &=& - {g_{\rm c}}{R_{\rm c}} \left[\frac{R_{\rm c}}{r} + \frac{3}{5} \left( \frac{R_{\rm c}}{r} \right)^3 S_2 P_2 \right] \;, \\ \Phi_{\rm o} (r,\Theta) &=& - {g_{\rm c}}{R_{\rm c}} \frac{\rho_{\rm o}}{\rho_{\rm c}} \left[\frac{3 R_{\rm p}^2 - r^2}{2 R_{\rm c}^2} + \frac{3}{5} \left( \frac{r}{R_{\rm c}} \right)^2 T_2 P_2 \right. \nonumber \\ && \left. - \frac{R_{\rm c}}{r} - \frac{3}{5} \left( \frac{R_{\rm c}}{r} \right)^3 S_2 P_2 \right] . \end{eqnarray}](/articles/aa/full_html/2015/01/aa24472-14/aa24472-14-eq39.png) Thus, the effective deforming parts are
Thus, the effective deforming parts are 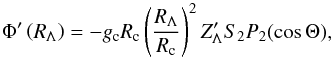 (10a)where
(10a)where ![% subequation 960 1 \begin{equation} Z'_\Lambda = \frac{3}{5} \left[\frac{\rho_{\rm o}}{\rho_{\rm c}} \varepsilon + \left( 1 - \frac{\rho_{\rm o}}{\rho_{\rm c}} \right) \left( \frac{R_\Lambda}{R_{\rm c}} \right)^5 \right] \cdot \end{equation}](/articles/aa/full_html/2015/01/aa24472-14/aa24472-14-eq41.png) (10b)Therefore,
(10b)Therefore, 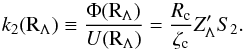 (11)The condition that the surface of the planet sc is an equipotential of the total field Φ + U leads to
(11)The condition that the surface of the planet sc is an equipotential of the total field Φ + U leads to 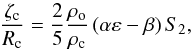 (12)where
(12)where 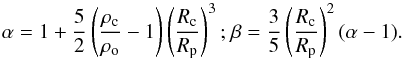 (13)We finally obtain the general form of the Love numbers, generalized to the case of a two-layer planet:
(13)We finally obtain the general form of the Love numbers, generalized to the case of a two-layer planet: 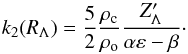 (14)All the unknown quantities require the expression of ε to be completely determined. As mentioned before, it depends on the forces acting on the surface of the core. According to RMZL12, the radial displacement at the surface of the core ξr(Rc) = RcS2P2(cosΘ) is linked to the total normal traction TN(Rc) = XP2(cosΘ) applied to it, following
(14)All the unknown quantities require the expression of ε to be completely determined. As mentioned before, it depends on the forces acting on the surface of the core. According to RMZL12, the radial displacement at the surface of the core ξr(Rc) = RcS2P2(cosΘ) is linked to the total normal traction TN(Rc) = XP2(cosΘ) applied to it, following 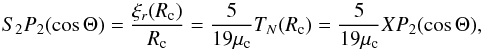 (15)where μc is the shear modulus of the core. This traction corresponds to the normal stress acting on the surface of the core, and it has to take both the gravitational forces and the solid and fluid loads into account. Therefore X is given by Eqs. (41) of RMZL12
(15)where μc is the shear modulus of the core. This traction corresponds to the normal stress acting on the surface of the core, and it has to take both the gravitational forces and the solid and fluid loads into account. Therefore X is given by Eqs. (41) of RMZL12![\begin{equation} \label{Eq:X_def} X = \frac{2 \rho_{\rm o} g_{\rm c} R_{\rm c}}{5} \left( 1-\frac{\rho_{\rm o}}{\rho_{\rm c}} \right) \left[\left( \alpha + \frac{3}{2} \right) \varepsilon - \beta - \frac{3}{2} - \frac{\rho_{\rm c}}{\rho_{\rm o}} \right] S_2 . \end{equation}](/articles/aa/full_html/2015/01/aa24472-14/aa24472-14-eq53.png) (16)From Eq. (15), we are now able to write
(16)From Eq. (15), we are now able to write 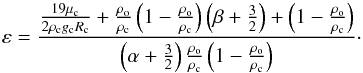 (17)To treat the anelastic case, we can apply the correspondence principle (Biot 1954), stipulating that all the developments made so far are still valid if we now consider complex quantities. We then denote the Fourier transform of a given quantity x by
(17)To treat the anelastic case, we can apply the correspondence principle (Biot 1954), stipulating that all the developments made so far are still valid if we now consider complex quantities. We then denote the Fourier transform of a given quantity x by 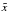 . The complex Love numbers at the core and planet surfaces can be expressed in terms of
. The complex Love numbers at the core and planet surfaces can be expressed in terms of 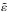 :
: 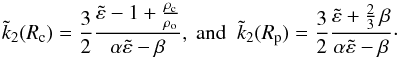 (18)Thanks to Eq. (18), we are now able to relate the tidal dissipation in the core to the effective tidal dissipation of the planet, given by the imaginary part of the corresponding Love numbers. We denote the real (resp. imaginary) part of
(18)Thanks to Eq. (18), we are now able to relate the tidal dissipation in the core to the effective tidal dissipation of the planet, given by the imaginary part of the corresponding Love numbers. We denote the real (resp. imaginary) part of 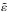 by ε1 (resp. ε2). The imaginary parts of the Love numbers
by ε1 (resp. ε2). The imaginary parts of the Love numbers 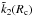 and
and 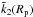 are
are ![% subequation 1082 0 \begin{eqnarray} \Imcro{\tilde{k}_2(R_{\rm c})} = - \frac{k_2^{\rm c}}{Q_{\rm c}} &= &\frac{3}{2} \frac{ \left[\left( 1 - \frac{\rho_{\rm c}}{\rho_{\rm o}} \right) \alpha - \beta \right] \varepsilon_2 } {\left( \alpha \varepsilon_1 - \beta \right)^2 + \left( \alpha \varepsilon_2 \right)^2 } , \\[2.5mm] \Imcro{\tilde{k}_2(R_{\rm p})} = - \frac{k_2^{\rm p}}{Q_{\rm p}} &= &- \frac{3}{2} \frac{ \left( 1 + \frac{2}{3} \alpha \right) \beta \varepsilon_2 } {\left( \alpha \varepsilon_1 - \beta \right)^2 + \left( \alpha \varepsilon_2 \right)^2 } \cdot \end{eqnarray}](/articles/aa/full_html/2015/01/aa24472-14/aa24472-14-eq62.png) Equation (2)linking these two quantities then becomes
Equation (2)linking these two quantities then becomes 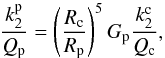 (20a)where Gp takes the form
(20a)where Gp takes the form 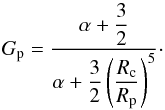 (20b)First, one may note that this quantity is not related to the factor F that accounts for the enhancement of the tidal deformation of the core due to the presence of the envelope (see Eq. (28) of RMZL12). That contradicts Dermott et al. (1988), in which, moreover, no derivation of the formula (given here in Eq. (2)) was detailed. Second, we note that Gp does not depend on ε, which links the amplitudes of the deformation of the core and planet surfaces, hence not on the shear modulus of the core μc. It only depends on the density contrast between the core and the envelope (through the ratio ρo/ρc) and the core size (through its normalized radius Rc/Rp). This result is coherent with our having considered a non-dissipative envelope. Therefore, factor Gp appears like a quantity that characterizes the transmission of the core’s tidal dissipation up to the surface of the planet. Last, Gp tends to the value 5/2 of the uniform asymptotic case when either Rc/Rp → 0 or ρo/ρc → 1.
(20b)First, one may note that this quantity is not related to the factor F that accounts for the enhancement of the tidal deformation of the core due to the presence of the envelope (see Eq. (28) of RMZL12). That contradicts Dermott et al. (1988), in which, moreover, no derivation of the formula (given here in Eq. (2)) was detailed. Second, we note that Gp does not depend on ε, which links the amplitudes of the deformation of the core and planet surfaces, hence not on the shear modulus of the core μc. It only depends on the density contrast between the core and the envelope (through the ratio ρo/ρc) and the core size (through its normalized radius Rc/Rp). This result is coherent with our having considered a non-dissipative envelope. Therefore, factor Gp appears like a quantity that characterizes the transmission of the core’s tidal dissipation up to the surface of the planet. Last, Gp tends to the value 5/2 of the uniform asymptotic case when either Rc/Rp → 0 or ρo/ρc → 1.
3. Application to Jupiter- and Saturn-like planets
In RMZL12, we used the standard formula (Eq. (1)) to quantify the effective tidal dissipation of Jupiter- and Saturn-like planets when modeled by a two-layer synthetic planet. In the present paper we show how using the refined formula (Eq. (20)) increases its predicted amplitude.
3.1. Internal structure parameters
As explained in RMZL12, we have poor constraints on the internal structure of the giant planets Jupiter and Saturn. Nonetheless, several models have been developed that give some insight into the plausible density profiles in such planets. Following RMZL12, we used the models of Guillot (1999) for Jupiter and Hubbard et al. (2009) for Saturn, from which we are able to build two-layer synthetic planetary models with a dense central icy/rocky core and a fluid envelope made of hydrogen and helium:
-
Jupiter-like:
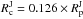 and
and 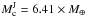 ,
, -
Saturn-like:
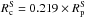 and
and 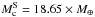 ,
,
where M⊕ stands for the mass of the Earth. The most unknown quantities concern the rheology of the predicted core of giant planets. Even so, one may consider some boundary values defining intervals in which the viscoelastic parameters, of the used Maxwell rheological model, are likely to take their values. In RMZL12, we estimated such ranges based on our present knowledge of the rheology of the Earth mantle and the icy satellites of Jupiter (Henning et al. 2009; Tobie 2003).
Recent studies of rocks viscosity at very high pressure (Karato 2011) were also considered. Thus, in RMZL12, the more realistic values of the viscoelastic parameters were assumed to lie in the ranges 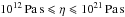 for the viscosity and
for the viscosity and 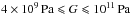 for the rigidity, for an unknown mixture of ice and silicates. We may also extrapolate the range of values taken by G at very high pressure and temperature by using a simple Steinberg-Cochran-Guinam law (Steinberg et al. 1980):
for the rigidity, for an unknown mixture of ice and silicates. We may also extrapolate the range of values taken by G at very high pressure and temperature by using a simple Steinberg-Cochran-Guinam law (Steinberg et al. 1980): 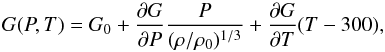 (21)where P, T, ρ, and ρ0 are the pressure, temperature, density, and density at the reference temperature T = 300 K, respectively. Assuming the values of G0 = 1.66 × 1011 Pa, ∂PG = 1.56, and ∂TG = −0.020 GPa K-1 given by Murakami et al. (2012) for the lower mantle of the Earth, and the rough approximation (ρ/ρ0)1/3 = 1, the rigidity of silicates at T = 12 300 K and P = 2000 GPa (as intermediate values at the upper boundary of the core of Jupiter and Saturn) reaches the value G = 3 ×1012 Pa. In the following, we thus assume, as the most likely values of the viscoelastic parameters,
(21)where P, T, ρ, and ρ0 are the pressure, temperature, density, and density at the reference temperature T = 300 K, respectively. Assuming the values of G0 = 1.66 × 1011 Pa, ∂PG = 1.56, and ∂TG = −0.020 GPa K-1 given by Murakami et al. (2012) for the lower mantle of the Earth, and the rough approximation (ρ/ρ0)1/3 = 1, the rigidity of silicates at T = 12 300 K and P = 2000 GPa (as intermediate values at the upper boundary of the core of Jupiter and Saturn) reaches the value G = 3 ×1012 Pa. In the following, we thus assume, as the most likely values of the viscoelastic parameters,
-
for the viscosity:
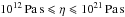 ,
, -
for the rigidity:
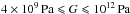 .
.
3.2. Impact of the envelope height
Our goal is to quantify the role of the fluid envelope in the effective tidal dissipation. According to Eq. (3), the strength of the associated mechanism is given by the factor Gp, represented in Fig. 1 as a function of the fluid envelope height, for gas giant planets. This figure shows that the effective tidal dissipation increases with the height of the envelope, by a factor of 1.95 to 2.43 for an envelope at least as high as for Jupiter and Saturn.
 |
Fig. 1 Factor Gp which quantifies the impact of the fluid envelope on the effective tidal dissipation factor Qp, as a function of the envelope height through the ratio Rc/Rp. |
3.3. Amplitude of the effective tidal dissipation
Using astrometric data, Lainey et al. (2009, 2012) determined the tidal dissipation in Jupiter (QJupiter = (3.56 ± 0.56) × 104) and Saturn (QSaturn = (1.682 ± 0.540) × 103), respectively. Figure 2 shows the amplitude of the effective tidal dissipation factor Qp, as given by Eq. (1) for Figs. 2a and c, and Eq. (20) for Figs. 2b and d, as a function of the viscoelastic parameters G and η of the Maxwell model, for the synthetic models of Jupiter and Saturn built in Sect. 3.1, and compares the results with the observed values.
 |
Fig. 2 Effective tidal dissipation factor Qp of synthetic models of Jupiter (a, c) and Saturn (b, d) as a function of the viscoelastic parameters G and η: (a, b) use Eq. (1)and (c, d) use Eq. (20). The red dashed lines give the values of Lainey et al. (2009, 2012). The blue lines bound the region of the most likely rheological values (see text). We assume: Rp = { 10.97,9.14 } R⊕ (R⊕ is the Earth radius); Mp = { 317.8,95.16 } M⊕. |
The contour plots of Qp from Eq. (20) (Figs. 2b and d) are slightly shifted to the bottom and expanded when compared to those resulting from Eq. (1) (Figs. 2a and c), as in Remus et al. (2012). If we only consider the more realistic values of the rheological parameters (as defined in Sect. 3.1), the observed values of tidal dissipation in Jupiter and Saturn are thus reached for sligthly enlarged ranges of values of G and η compared with previous results (Table 1).
Ranges of values of the rheological parameters G and η for which the effective tidal dissipation factor Qp of the two-layer model reaches the observed values.
4. Conclusions
In this work, we revisit the role of the fluid envelope of a two-layer giant planet where the dissipation is assumed to originate in the anelastic core. We derive an improved formulation of the effective tidal dissipation factor (Eq. (20)), which we express in terms of the tidal dissipation factor of the core obtained by RMZL12. It improves modeling of the role of the anelastic core of giant planets as an important source of tidal dissipation. When applied to the gas giants Jupiter and Saturn, the amplitude of their effective tidal dissipation is enhanced by about a factor of two, thus keeping the same order of magnitude (see Figs. 1 and 2). However, the model now takes all the physical mechanisms that act on the tidal dissipation of the core of giant planets into account. Finally, this new model has recently been used to compare the relative strength of the different tidal mechanisms that take place in gas giant planets, namely the anelastic tidal dissipation in the core (Remus et al. 2012) and the turbulent friction acting on tidal inertial waves in the convective envelope (Ogilvie & Lin 2004), showing that the former could slightly dominate the latter (Guenel et al. 2014).
Acknowledgments
This work was supported in part by the Programme National de Planétologie (CNRS/INSU), the EMERGENCE-UPMC project EME0911, the CNRS program Physique théorique et ses interfaces, the Campus Spatial Université Paris-Diderot, and the L’Oréal France-UNESCO foundation.
References
- Biot, M. A. 1954, J. Appl. Phys., 25, 1385 [NASA ADS] [CrossRef] [Google Scholar]
- Dermott, S. F. 1979, Icarus, 37, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Dermott, S. F., Malhotra, R., & Murray, C. D. 1988, Icarus, 76, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Guenel, M., Mathis, S., & Remus, F. 2014, A&A, 566, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T. 1999, Planet. Space Sci., 47, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, W. G., O’Connell, R. J., & Sasselov, D. D. 2009, ApJ, 707, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B., Dougherty, M. K., Gautier, D., & Jacobson, R. 2009, The Interior of Saturn, eds. M. K. Dougherty, L. W. Esposito, & S. M. Krimigis (Springer), 75 [Google Scholar]
- Karato, S.-I. 2011, Icarus, 212, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Kaula, W. M. 1962, AJ, 67, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V., Arlot, J.-E., Karatekin, Ö., & van Hoolst, T. 2009, Nature, 459, 957 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lainey, V., Karatekin, Ö., Desmars, J., et al. 2012, ApJ, 752, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Murakami, M., Ohishi, Y., Hirao, N., & Hirose, K. 2012, Nature, 485, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2004, ApJ, 610, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Remus, F., Mathis, S., Zahn, J.-P., & Lainey, V. 2012, A&A, 541, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinberg, D. J., Cochran, S. G., & Guinan, M. W. 1980, J. Appl. Phys., 51, 1498 [Google Scholar]
- Tobie, G. 2003, Ph.D. Thesis, Université Paris 7 – Denis Diderot, Paris, France [Google Scholar]
All Tables
Ranges of values of the rheological parameters G and η for which the effective tidal dissipation factor Qp of the two-layer model reaches the observed values.
All Figures
 |
Fig. 1 Factor Gp which quantifies the impact of the fluid envelope on the effective tidal dissipation factor Qp, as a function of the envelope height through the ratio Rc/Rp. |
| In the text | |
 |
Fig. 2 Effective tidal dissipation factor Qp of synthetic models of Jupiter (a, c) and Saturn (b, d) as a function of the viscoelastic parameters G and η: (a, b) use Eq. (1)and (c, d) use Eq. (20). The red dashed lines give the values of Lainey et al. (2009, 2012). The blue lines bound the region of the most likely rheological values (see text). We assume: Rp = { 10.97,9.14 } R⊕ (R⊕ is the Earth radius); Mp = { 317.8,95.16 } M⊕. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


