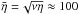| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201424060 | |
| Published online | 23 December 2014 | |
The angular momentum transport by unstable toroidal magnetic fields
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: gruediger@aip.de
Received: 24 April 2014
Accepted: 26 October 2014
We demonstrate with a nonlinear magnetohydrodynamic (MHD) code that angular momentum can be transported because of the magnetic instability of toroidal fields under the influence of differential rotation, and that the resulting effective viscosity may be high enough to explain the almost rigid-body rotation observed in radiative stellar cores. We only consider stationary, current-free fields, and only those combinations of rotation rates and magnetic field amplitudes which provide maximal numerical values of the viscosity. We find that the dimensionless ratio of the effective over molecular viscosity, νT/ν, linearly grows with the Reynolds number of the rotating fluid multiplied by the square-root of the magnetic Prandtl number, which is approximately unity for the considered red subgiant star KIC 7341231. For the interval of magnetic Reynolds numbers considered – which is restricted by numerical constraints of the nonlinear MHD code – the magnetic Prandtl number has a remarkable influence on the relative importance of the contributions of the Reynolds stress and the Maxwell stress to the total viscosity, which is magnetically dominated only for Pm ≳ 0.5. We also find that the magnetized plasma behaves as a non-Newtonian fluid, i.e., the resulting effective viscosity depends on the shear in the rotation law. The decay time of the differential rotation thus depends on its shear and becomes longer and longer during the spin-down of a stellar core.
Key words: instabilities / magnetic fields / diffusion / turbulence / magnetohydrodynamics (MHD)
© ESO, 2014
1. Introduction
Model calculations for the formation of red giants without turbulent or magnetic angular momentum transport lead to rather steep radial profiles of the angular velocity in the innermost core of the star. Ceillier et al. (2012) report a theoretical (quasi-Keplerian) profile Ω ∝ R− q with q ≃ 1.6 for the low-mass red giant KIC 7341231. Note that the exponent q = 1 would describe a quasi-galactic rotation profile with Uφ = const., while q = 2 represents the rotation law for uniform angular momentum ΩR2 ≈ const. The Kepler data, however, lead to much flatter rotation laws of the observed red giants: the cores of several subgiants and young red giants seem to rotate only (say) five times faster than the outer convection zone (Deheuvels et al. 2012; 2014). Eggenberger et al. (2012) argue that only an additional viscosity of 3 × 104 cm2/s may explain the unexpectedly flat internal rotation law of the more massive red giant KIC 8366239. The outward flux of angular momentum due to this enhanced viscosity, which exceeds the molecular value by a factor of νT/ν ≈ 500, suffices to produce the observed spin-down of the inner radiative core. Rüdiger & Kitchatinov (1996) needed just this viscosity value to produce by Maxwell stress the high degree of uniformity of the internal solar rotation, derived from helioseismologic measurements down to 0.15 R⊙.
Rotation laws with q< 2 are hydrodynamically stable. Under the presence of toroidal fields, however, they become unstable against nonaxisymmetric disturbances if the amplitude of the toroidal field is high enough, but such that the Alfvén frequency 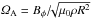 does not exceed the rotational frequency Ω, i.e., ΩA ≲ Ω. This nonaxisymmetric instability even exists for toroidal fields which are current-free in the considered domain. Because of this force-free character of the magnetic field, the instability has been called the azimuthal magnetorotational instability (AMRI). Within a cylindrical setup, AMRI has been studied in the linear approximation, but also with nonlinear simulations (Rüdiger et al. 2014). The consequences of both compressibility and heat transport (see Spruit 2002) cannot be studied with the present model. We know, however, that these influences become negligible for strong fields. It can also be shown that, with thermodynamics included, the radial components of flow and field are strongly damped, so that the resulting angular momentum transport should be reduced by the “negative buoyancy”. The viscosity values derived in the present paper are thus maximum values. If they are not high enough for νT/ν ≃ 500, then the concept of the instability of magnetic fields in the stellar interior is proven not to work.
does not exceed the rotational frequency Ω, i.e., ΩA ≲ Ω. This nonaxisymmetric instability even exists for toroidal fields which are current-free in the considered domain. Because of this force-free character of the magnetic field, the instability has been called the azimuthal magnetorotational instability (AMRI). Within a cylindrical setup, AMRI has been studied in the linear approximation, but also with nonlinear simulations (Rüdiger et al. 2014). The consequences of both compressibility and heat transport (see Spruit 2002) cannot be studied with the present model. We know, however, that these influences become negligible for strong fields. It can also be shown that, with thermodynamics included, the radial components of flow and field are strongly damped, so that the resulting angular momentum transport should be reduced by the “negative buoyancy”. The viscosity values derived in the present paper are thus maximum values. If they are not high enough for νT/ν ≃ 500, then the concept of the instability of magnetic fields in the stellar interior is proven not to work.
An important basis for realistic numerical simulations is the knowledge of the magnetic Prandtl number 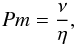 (1)where ν is the molecular viscosity of the fluid and η its magnetic diffusivity. So far, numerical nonlinear simulations are only possible for Pm exceeding (say) 0.01. The magnetic Prandtl number of the plasma inside main-sequence stars, however, is smaller (see Brandenburg & Subramanian 2005). We have thus first to probe the value of Pm in the radiative interiors of the considered Kepler subgiant stars.
(1)where ν is the molecular viscosity of the fluid and η its magnetic diffusivity. So far, numerical nonlinear simulations are only possible for Pm exceeding (say) 0.01. The magnetic Prandtl number of the plasma inside main-sequence stars, however, is smaller (see Brandenburg & Subramanian 2005). We have thus first to probe the value of Pm in the radiative interiors of the considered Kepler subgiant stars.
2. The stellar model of KIC 7341231
We constructed a model for the star KIC 7341231 using the Yale Rotational stellar Evolution Code (YREC) in its nonrotational configuration (Demarque et al. 2008). The code uses up-to-date input physics, such as OPAL 2005 equations of state (Rogers & Nayfonov 2002) and OPAL opacities (Iglesias & Rogers 1996). The treatment of the atmospheric boundary conditions is based on the Eddington gray T-τ relation; convection is described according to the mixing length theory (Böhm-Vitense 1958), with the mixing length parameter set to αMLT = 1.82, our solar-calibrated value. Our choice of the stellar parameters (e.g., M = 0.84 M⊙, [Fe/H] = −1.0, age ≈12 Gyr, etc.) is based on the best-fitting model of Deheuvels et al. (2012, see their Table 3). Our model of KIC 7341231 has effective temperature Teff = 5380 K, radius R = 2.66 R⊙, and a fractional radius at the bottom of the convective envelope of rbce = 0.34 at the age of 11.8 Gyr.
 |
Fig. 1 Stellar model of KIC 7341231 (blue) compared to a standard solar model (red). The vertical dashed line shows the outer boundary of the radiative stellar core of the red subgiant. |
The run of the viscosity ν and magnetic diffusivity η in the interior of this model, given by 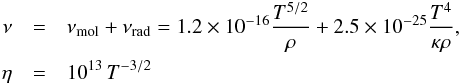 (2)(all in c.g.s. units), is shown in Fig. 2. The basic result is that a characteristic value for the microscopic magnetic diffusivity is 103 cm2/s, while the magnetic Prandtl number varies between 0.1 and 10. The microscopic magnetic diffusivity is thus close to that of the Sun, while the microscopic viscosity is much higher. Thus it makes sense to focus our attention on the results as a function of the magnetic Reynolds number, rather than of the ordinary Reynolds number. For different stellar models, therefore, the magnetic Reynolds number mainly encompasses the differences of the angular velocity of the inner rotation. The magnetic Reynolds number of the solar core is about 5 × 1012 and its magnetic Prandtl number is 5 × 10-3.
(2)(all in c.g.s. units), is shown in Fig. 2. The basic result is that a characteristic value for the microscopic magnetic diffusivity is 103 cm2/s, while the magnetic Prandtl number varies between 0.1 and 10. The microscopic magnetic diffusivity is thus close to that of the Sun, while the microscopic viscosity is much higher. Thus it makes sense to focus our attention on the results as a function of the magnetic Reynolds number, rather than of the ordinary Reynolds number. For different stellar models, therefore, the magnetic Reynolds number mainly encompasses the differences of the angular velocity of the inner rotation. The magnetic Reynolds number of the solar core is about 5 × 1012 and its magnetic Prandtl number is 5 × 10-3.
 |
Fig. 2 Diffusion coefficients from the stellar model of KIC 7341231. The vertical dashed line shows the outer boundary of the radiative stellar core. Note that the geometric average of the two diffusivities |
3. Numerical setup and the calculation of the effective viscosity
Following the above stellar structure calculations, it is thus reasonable to perform simulations with magnetic Prandtl numbers between 0.1 and unity. We should also mention that, as an additional approximation, the calculations focus on the angular momentum in the equatorial region. As a consequence of the Taylor-Proudman theorem for fast rotation, the angular velocity forms cylindrical isolines, Ω = Ω(R). To further simplify, the axial structure of the toroidal magnetic field belts is neglected, so that also Bφ = Bφ(R). The resulting viscosity values certainly overestimate the more realistic corresponding values for a spherical model.
We consider the same cylindrical setup used by Rüdiger et al. 2014; see this paper for more details). Cylindrical coordinates (R,z,φ) are adopted, with the z axis coincident with the axis of the bounding cylinders, of radii Rin and Rout. The cylinders are assumed as rotating with different frequencies so that differential rotation can easily be modeled.
An important detail of the calculations is the scaling of the instability for small magnetic Prandtl numbers. For rotation laws with q ≃ 2, the bifurcation map scales with the Reynolds number Re and the Hartmann number Ha,  (3)while, for flatter rotation laws, the corresponding parameters are the magnetic Reynolds number Rm = PmRe and the Lundquist number
(3)while, for flatter rotation laws, the corresponding parameters are the magnetic Reynolds number Rm = PmRe and the Lundquist number 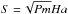 . The radial scale is
. The radial scale is 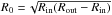 .
.
 |
Fig. 3 Curves of marginal instability for Ω ∝ 1 /R2 if rin = 0.5, i.e., μ = 0.25. For small magnetic Prandtl numbers, the curves scale with Re and Ha. For Pm = 1, the critical Reynolds number is (only) 100. The dotted lines mark the line of maximum growth rates. The dashed line represents, for Pm = 1, the lower limit of the condition (5). |
We imagine the formation of the toroidal field as due to the induction by the differential rotation from a fossil poloidal field Bp; hence Bφ ≲ RmBp, or what is the same, ΩA/Ω ≲ Spol, where Spol is the Lundquist number of the poloidal field: 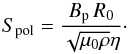 (4)Thus, with Spol close to unity, one always finds that:
(4)Thus, with Spol close to unity, one always finds that: 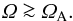 (5)Note also that Spol ≃ 1 is already fulfilled with rather weak poloidal fields, of the order of μG. For the rotation law at the Rayleigh limit (Ω ∝ 1 /R2) and the current-free magnetic background field Bφ ∝ 1 /R, the flow Uφ and the field Bφ have the same dependence on the radius. Chandrasekhar (1956) has demonstrated that all ideal MHD systems with U = B are stable. In contrast, Fig. 3 demonstrates that for non-ideal fluids an instability exists for ΩA = Ω. Moreover, if the Reynolds number of the fluid exceeds a critical value of (only) 100, then an extended area of instability exists above this line fulfilling just the condition (5).
(5)Note also that Spol ≃ 1 is already fulfilled with rather weak poloidal fields, of the order of μG. For the rotation law at the Rayleigh limit (Ω ∝ 1 /R2) and the current-free magnetic background field Bφ ∝ 1 /R, the flow Uφ and the field Bφ have the same dependence on the radius. Chandrasekhar (1956) has demonstrated that all ideal MHD systems with U = B are stable. In contrast, Fig. 3 demonstrates that for non-ideal fluids an instability exists for ΩA = Ω. Moreover, if the Reynolds number of the fluid exceeds a critical value of (only) 100, then an extended area of instability exists above this line fulfilling just the condition (5).
Tayler (1957, 1973) showed that toroidal fields with large enough amplitude become unstable against nonaxisymmetric disturbances in the absence of rotation. There is a local criterion for instability written in cylindrical coordinates, i.e., 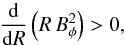 (6)which is fulfilled by the magnetic field generated by a homogeneous axial electric current, for which Bφ ∝ R. If an electric current flows unbounded in the axial direction, the critical Hartmann number
(6)which is fulfilled by the magnetic field generated by a homogeneous axial electric current, for which Bφ ∝ R. If an electric current flows unbounded in the axial direction, the critical Hartmann number 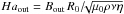 is about 20, which has indeed been realized in an experiment (Seilmayer et al. 2012; Rüdiger et al. 2012). Numerical simulations of this magnetic configuration showed, however, that the eddy viscosity resulting from this instability remains small compared with its microscopic value.
is about 20, which has indeed been realized in an experiment (Seilmayer et al. 2012; Rüdiger et al. 2012). Numerical simulations of this magnetic configuration showed, however, that the eddy viscosity resulting from this instability remains small compared with its microscopic value.
If the toroidal field is of the vacuum type, it runs as Bφ ~ 1 /R. Here the symmetry axis, R → 0, where the electric current flows, must be excluded from the domain of calculations. This field, alone, is stable according to the criterion (6). The field, however, destabilizes a differential rotation that would be stable in the hydrodynamical regime. The energy source of this instability is the differential rotation, which via AMRI drives a nonaxisymmetric magnetic instability pattern; the magnetic energy dominates the energy in the kinetic fluctuations. The basic saturation mechanism of the instability is the turbulence-induced decay of the rotation law. To this end, angular momentum must be transported into the direction of slow rotation, i.e., 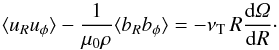 (7)Here u and b are the fluctuations of the velocity and magnetic field, their average values being U and B.
(7)Here u and b are the fluctuations of the velocity and magnetic field, their average values being U and B.
The calculation of the effective viscosity νT is thus possible by the calculation of the cross-correlations ⟨ uRuφ ⟩ and ⟨ bRbφ ⟩. Note that for a magnetic-dominated MHD turbulence the relation 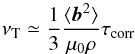 (8)holds (Vainshtein & Kichatinov 1983), which may be used as an estimation by replacing the unknown correlation time τcorr with the growth time 1 /ωgr, where ωgr is the maximal growth rate of the instability (see Spruit 2002). The maximum growth rates lead to the shortest timescale in the system. One can indeed show that for the magnetic instability there is a linear relation between the turnover frequency
(8)holds (Vainshtein & Kichatinov 1983), which may be used as an estimation by replacing the unknown correlation time τcorr with the growth time 1 /ωgr, where ωgr is the maximal growth rate of the instability (see Spruit 2002). The maximum growth rates lead to the shortest timescale in the system. One can indeed show that for the magnetic instability there is a linear relation between the turnover frequency 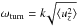 and the growth rate (Fig. 4). To the same level of approximation of the standard mixing length theory, we can set the turnover time equal to the correlation time. This is a useful result, as it allows us to express the saturated hydrodynamic energy by (the square of) the linear phase velocity.
and the growth rate (Fig. 4). To the same level of approximation of the standard mixing length theory, we can set the turnover time equal to the correlation time. This is a useful result, as it allows us to express the saturated hydrodynamic energy by (the square of) the linear phase velocity.
Rüdiger et al. (2014) have shown that, for Pm = 1, the growth rate of the unstable m = 1 modes scales as ωgr/Ωin ∝ Re. One also finds for the magnetic energy 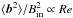 . Hence,
. Hence, 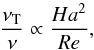 (9)which for the AMRI, where the maximal growth rates are located at a line with Ha ∝ Re (see Fig. 3), leads to the linear relation νT/ν ∝ Re. The question is how this relation is saturated by the magnetic feedback and whether this maximal effective viscosity is large enough to explain the above mentioned Kepler observations. The results of our numerical experiments indeed confirm that
(9)which for the AMRI, where the maximal growth rates are located at a line with Ha ∝ Re (see Fig. 3), leads to the linear relation νT/ν ∝ Re. The question is how this relation is saturated by the magnetic feedback and whether this maximal effective viscosity is large enough to explain the above mentioned Kepler observations. The results of our numerical experiments indeed confirm that 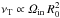 . The coefficient in this relation must be fixed with numerical calculations. With our numerical tools, however, we could not find the saturation effect so that the question on the maximum possible viscosity requires better numerical qualities. What we have nevertheless shown is that i) the Maxwell stress produced by the fluctuations of the AMRI forms the main contribution to the effective viscosity and ii) for slow rotation, the viscosity increases linearly with the magnetic Reynolds number.
. The coefficient in this relation must be fixed with numerical calculations. With our numerical tools, however, we could not find the saturation effect so that the question on the maximum possible viscosity requires better numerical qualities. What we have nevertheless shown is that i) the Maxwell stress produced by the fluctuations of the AMRI forms the main contribution to the effective viscosity and ii) for slow rotation, the viscosity increases linearly with the magnetic Reynolds number.
 |
Fig. 4 Linear relation between the turnover rate and the growth rate for various Pm and μ. The models possess the maximal growth rates as indicated in the instability domain of Fig. 3. |
We shall simulate two different rotation laws, i.e., the two limits Ω ∝ 1 /R2 and Ω ∝ 1 /R, bracketing the rotation law obtained in modeling subgiant stars without enhanced transport of angular momentum, i.e., Ω ∝ R-1.6 (Ceillier et al. 2012).
We start with the steep rotation law Ω ∝ 1 /R2, which is one of the two basic solutions for the stationary rotation law between two rotating cylinders, i.e., 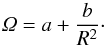 (10)With the definition μ = Ωout/Ωin and for rin = Rin/Rout = 0.5, one finds μ = 0.25. However, to avoid violating the Rayleigh criterion for hydrodynamical instability (μ< 0.25 in this notation), in our calculation we define the steep rotation as μ = 0.255. The instability map for the rotational profile with μ = 0.255 is given in Fig. 3 for Pm = 1 and, for comparison, for the extremely small value Pm = 10-6. We find that the dependence of the bifurcation map on the magnetic Prandtl number is very weak. The combination of (differential) rotation and toroidal field is unstable in the open cone between the lower and the upper branches of the nonmonotonic function Re = Re(Ha), where the growth rates vanish by definition. The dashed lines for Pm = 1 and Pm = 10-6 mark the locations of the maximal growth rate, which are strikingly close to the lower strong-field line of the instability cone. The eddy viscosities are numerically computed in this instability cone for fixed Reynolds number and various Hartmann numbers, with the general result that νT peaks at the location of the dashed line, i.e., for maximum growth rates.
(10)With the definition μ = Ωout/Ωin and for rin = Rin/Rout = 0.5, one finds μ = 0.25. However, to avoid violating the Rayleigh criterion for hydrodynamical instability (μ< 0.25 in this notation), in our calculation we define the steep rotation as μ = 0.255. The instability map for the rotational profile with μ = 0.255 is given in Fig. 3 for Pm = 1 and, for comparison, for the extremely small value Pm = 10-6. We find that the dependence of the bifurcation map on the magnetic Prandtl number is very weak. The combination of (differential) rotation and toroidal field is unstable in the open cone between the lower and the upper branches of the nonmonotonic function Re = Re(Ha), where the growth rates vanish by definition. The dashed lines for Pm = 1 and Pm = 10-6 mark the locations of the maximal growth rate, which are strikingly close to the lower strong-field line of the instability cone. The eddy viscosities are numerically computed in this instability cone for fixed Reynolds number and various Hartmann numbers, with the general result that νT peaks at the location of the dashed line, i.e., for maximum growth rates.
4. Nonlinear simulations
We know from Fig. 2 that the magnetic Prandtl number in the radiative core of the red giants varies between 0.1 and 10 so that it makes sense to focus the simulations on Pm ≲ 1. We first check the validity of the often used relation 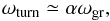 (11)see the discussion below Eq. (8). The factor α represents a characteristic Strouhal number formed with the growth rate instead of the characteristic spectrum frequency. The growth rates have been calculated from linear models for various Hartmann numbers along the line of maximal growth in the instability domain as indicated in Fig. 3. The applied rotation law varies between the steep rotation law with μ = 0.25 and the flat rotation law with μ = 0.5, an interval which certainly contains the internal stellar rotation. For the calculation of the turnover rates we need the nonlinear results for the (vertical) velocity and the cell size π/k.
(11)see the discussion below Eq. (8). The factor α represents a characteristic Strouhal number formed with the growth rate instead of the characteristic spectrum frequency. The growth rates have been calculated from linear models for various Hartmann numbers along the line of maximal growth in the instability domain as indicated in Fig. 3. The applied rotation law varies between the steep rotation law with μ = 0.25 and the flat rotation law with μ = 0.5, an interval which certainly contains the internal stellar rotation. For the calculation of the turnover rates we need the nonlinear results for the (vertical) velocity and the cell size π/k.
This procedure gives the results plotted in Fig. 4, which provides the linear relation (11) with α as a function of Pm and the shear. As expected, the maximum α (as a modified Strouhal number) is unity for steep rotation law and large magnetic Prandtl number. It becomes smaller both for decreasing Pm and for the flatter rotation rates. For known α, we thus have the surprising situation that the nonlinear turbulence intensity 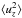 can be expressed by the characteristic quantities k and ωgr of the linear theory with the simple relation urms ≃ αωgr/k. This does not automatically mean, however, that the effective viscosity can be estimated just with these quantities, as the effect of the magnetic fluctuations cannot be neglected. It might be interesting to compare the traditional estimate νT ≃ α2ωgr/k2 with the nonlinear results. In any case, this relation suggests that the effective viscosity should decline for smaller magnetic Prandtl numbers and flatter rotation profiles. We assume, for the most optimistic case (Pm = 1 and μ = 0.25, from Rüdiger et al. 2014), that the maximal drift is 0.4 Ωin and the smallest wavenumber is about 3R0, so that the upper limit of the viscosity due to the hydrodynamic transport can be estimated as νT/ν ≃ 0.04 Re, which leads to νT/ν ≃ 4 for Re = 100. We shall see that the nonlinear values only exceed this value for much higher Reynolds numbers.
can be expressed by the characteristic quantities k and ωgr of the linear theory with the simple relation urms ≃ αωgr/k. This does not automatically mean, however, that the effective viscosity can be estimated just with these quantities, as the effect of the magnetic fluctuations cannot be neglected. It might be interesting to compare the traditional estimate νT ≃ α2ωgr/k2 with the nonlinear results. In any case, this relation suggests that the effective viscosity should decline for smaller magnetic Prandtl numbers and flatter rotation profiles. We assume, for the most optimistic case (Pm = 1 and μ = 0.25, from Rüdiger et al. 2014), that the maximal drift is 0.4 Ωin and the smallest wavenumber is about 3R0, so that the upper limit of the viscosity due to the hydrodynamic transport can be estimated as νT/ν ≃ 0.04 Re, which leads to νT/ν ≃ 4 for Re = 100. We shall see that the nonlinear values only exceed this value for much higher Reynolds numbers.
Now the effective viscosity is nonlinearly calculated by computing the RHS of the relation (7) within the instability domain in Fig. 3. For a given Reynolds number, the Hartmann number is varied until the maximum value of νT is found. Finally, the maximum viscosity between the inner and the outer cylinder is taken (see Fig. 5). The average procedure in (7) concerns only the azimuth and the vertical axis.
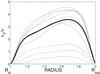 |
Fig. 5 Rotation law Ω ∝ 1 /R2: the fluctuating radial profiles between the inner and the outer radius of the effective viscosity in (7). The thick solid line gives the temporal average. Re = 850. |
For various magnetic Reynolds numbers, this procedure yields viscosities that linearly grow for growing Rm. This is true for all rotation laws between 1/R2 and 1/R, including Kepler rotation (Fig. 6). For the magnetic Reynolds numbers of the order of 103 (which our code is able to handle), we do not find any indication of a saturation. We also find that the resulting viscosity for Pm< 1 scales as: 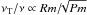 , which can also be written as
, which can also be written as 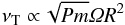 (12)or, which is the same,
(12)or, which is the same, 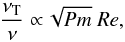 (13)with Re the Reynolds number of the fluid. The main result is the rather weak dependence of the viscosity on the magnetic Prandtl number Pm. Obviously, since Pm is proportional to the electric conductivity, it is the induction by the radial rotational shear that produces the strong correlations of the magnetic fluctuations given in (7), and this induction vanishes for Pm → 0.
(13)with Re the Reynolds number of the fluid. The main result is the rather weak dependence of the viscosity on the magnetic Prandtl number Pm. Obviously, since Pm is proportional to the electric conductivity, it is the induction by the radial rotational shear that produces the strong correlations of the magnetic fluctuations given in (7), and this induction vanishes for Pm → 0.
From Fig. 6 it follows that the missing numerical factor in relations (12) and (13) is of the order of 5 × 10-3. For the solar core, we thus find the rather high value of νT/ν ≃ 5 × 109. One must take into account, however, that i) our calculations always tend to find the maximal values of the viscosity, and ii) we have only verified that the linear relations (12) and (13) hold for Reynolds numbers up to 103, and cannot account for any saturation effect. We can only assume that the effective viscosity does not exceed the given value.
The dependence of the resulting eddy viscosity on the magnetic Prandtl number has consequences for stars with small Pm, like the solar radiative core. There, the eddy viscosity due to the instability of toroidal fields becomes rather small. This is not the case, however, for the radiative cores of red giants, with their magnetic Prandtl number close to unity. The magnetic-induced outward angular momentum transport will thus happen much faster for hot stars in comparison to solar-type stars.
 |
Fig. 6 Rotation law Ω ∝ 1 /R2 (top) and Ω ∝ 1 /R (bottom): the normalized viscosity grows with the magnetic Reynolds number Rm without indication of a saturation (Pm = 0.1...1, as indicated). |
Inserting characteristic stellar values for ΩR2, one obtains high viscosity values, of the order of 1012 cm2/s. However, in the present paper only upper limits for the viscosity are presented, to show that the resulting viscosities are not too small. Moreover, we could not find the saturation level resulting from the magnetic feedback onto the rotation laws.
The role of the Maxwell stress in comparison to the Reynolds stress is illustrated in Figs. 7 and 8. We find that the magnetic energy dominates the kinetic energy for large magnetic Prandtl numbers, while the energies are almost in equilibrium for small magnetic Prandtl numbers.
 |
Fig. 7 Magnetic and kinetic energy for Pm = 1 and Re = 800, normalizedto the diffusion velocity squared. The energies are in equilibrium for strong magnetic fields only (in this plot, μ = 0.255). |
For a fixed Reynolds number, the ratio ϵ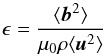 (14)reaches its maximum value for weak magnetic fields, and approaches unity for strong magnetic fields. The kinetic energy never exceeds the magnetic energy (Fig. 7). The dominance of the magnetic energy for Pm ≃ 1, however, is not too strong. It must remain open whether or not ϵ saturates for very large Rm. For numerical reasons, the calculations are limited to Reynolds numbers of order 103, where no saturation occurs. Within this interval the ratio ϵ increases slightly with growing Rm.
(14)reaches its maximum value for weak magnetic fields, and approaches unity for strong magnetic fields. The kinetic energy never exceeds the magnetic energy (Fig. 7). The dominance of the magnetic energy for Pm ≃ 1, however, is not too strong. It must remain open whether or not ϵ saturates for very large Rm. For numerical reasons, the calculations are limited to Reynolds numbers of order 103, where no saturation occurs. Within this interval the ratio ϵ increases slightly with growing Rm.
 |
Fig. 8 Top: magnetic to kinetic energy ϵ for various Pm, as indicated. The magnetic energy only dominates the kinetic energy for Pm ≳ 1. Bottom: the magnetic-induced part in units of the total viscosity (μ = 0.255 in this plot). |
On the other hand, for large magnetic Prandtl numbers the total viscosity is almost entirely due to the Maxwell stress (Fig. 8, bottom). For large Rm and for Pm ≳ 0.5, no visible differences exist between the total viscosity and the viscosity due to the Maxwell stress. The viscosity produced by the instability of current-free magnetic background fields is an almost purely magnetic phenomenon. The dominance of the corresponding Maxwell stress over the Reynolds stress turns out to be larger than the dominance of the magnetic energy over the kinetic energy. The reason for this is that, because of the induction by the radial differential rotation, an almost perfect correlation appears between the radial and the azimuthal magnetic field fluctuations. Nevertheless, as this induction becomes weaker for decreasing magnetic Prandtl number (Fig. 8, bottom, as well as for more shallow rotation profiles) a relation νT ∝ Pm becomes understandable (see Eq. (13)). For Pm → 0, the resulting eddy viscosity should approach the small values generated by the Reynolds stress.
For the special value of Pm = 1, the influence of the shear on the eddy viscosity is given in Fig. 9. There is a nonlinear influence of the shear on the stress tensor, which is often ignored in the Boussinesq formulation (7). As Fig. 9 clearly shows, the viscosity is reduced for shallower rotation laws. Obviously, the viscosity itself (and not only the total stress tensor) vanishes for rigid rotation. This leads to the important conclusion that the diffusive decay of differential rotation is decelerated in time and the decay time due to magnetic instabilities becomes longer and longer during the diffusion process. The outward transport of angular momentum is thus self-regulated: the original steep rotation law rapidly decays, producing a flatter rotation law, which then decays more slowly. If the viscosity itself depends on the shear, the considered fluid is called non-Newtonian. This phenomenon, known to exist for current-driven instabilities (e.g., Spruit 2002), also occurs for the current-free AMRI.
 |
Fig. 9 Normalized eddy viscosity for Pm = 1 and the rotation laws Ω ∝ 1 /R2 (μ = 0.25), Ω ∝ 1 /R3/2 (μ = 0.35), and Ω ∝ 1 /R (μ = 0.5). |
5. Discussion
In the sense of a proof of existence, nonaxisymmetric magnetic instabilities under the influence of differential rotation are shown to transport angular momentum in a direction orthogonal to the rotation axis. The toroidal background field is chosen as current-free (outside the axis), so that it cannot decay. The mass density is assumed as uniform, suppressing the influence of the buoyancy. The model is thus not applicable to solar-type stars on the main sequence, but only to the very hot radiative cores of subgiants. It is also shown, by use of a numerical stellar model, that the high temperatures in such cores result in microscopic magnetic Prandtl numbers varying between 0.1 and 10. This makes it possible to use a nonlinear MHD code, which only works for such Prandtl numbers. The code solves the nonlinear and nonaxisymmetric MHD differential equations in a cylindrical setup, and provides the R-φ-component of the complete stress tensor (Reynolds stress plus Maxwell stress), and averages the resulting number over the azimuth and the axial coordinate.
A spectral element code is used, based on the hydrodynamic code of Fournier et al. (2005). The solutions are expanded into Fourier modes in the azimuthal direction. The remaining meridional problems are solved with a Legendre spectral method.
If a linear code is used to find the classical eigenvalues for the onset of the marginal instability, then all solutions are optimized in the wave number k, yielding the smallest possible Reynolds numbers.
The boundary conditions at the cylinder walls are assumed to be no-slip and perfectly conducting. The resulting cross correlations thus vanish at the surfaces of the two cylinders, while they have a maximum near the center of the gap between the cylinders (Fig. 5). These maximum values are calculated and transformed into viscosity values by means of Eq. (7). The resulting viscosity values are compared for various Hartmann numbers in the instability cone but for the same Reynolds number (see Fig. 3). If the same procedure is done for various Reynolds numbers and various magnetic Prandtl numbers, one obtains the results presented in Fig. 6 for two different rotation laws. Note that the data for different Reynolds numbers do not belong to the same Hartmann number. The figures do not, therefore, contain evolutionary scenarios. As expected, the consequence of the results shown in Fig. 6 is that the viscosity for given shear linearly grows with the angular velocity. The most interesting result, however, is the dependence of the effective viscosity on the shear: the steeper the rotation law, the higher the viscosity value. Hence, the decay of a nonuniform stellar rotation law is a nonlinear process. The decay timescale does not remain constant in time, but it becomes larger and larger. The non-Newtonian behavior of the magnetized conducting fluid is basically connected with the mechanism of the azimuthal magnetorotational instability, which exists only in the presence of differential rotation. It thus leads automatically to saturation during stellar spin-down process, which is most violent at its beginning and becomes slower at later times.
As mentioned, the toroidal magnetic field with the current-free radial profile does not dissipate. As we therefore keep the magnetic field fixed for a given magnetic Prandtl number and consider the dependence of the effective viscosity on the angular velocity, the effective viscosity will grow, pass its maximum close to the line of maximum growth rate shown in Fig. 3, and again sink to zero at the lowest possible Reynolds number. Figure 6 demonstrates that, up to Reynolds numbers of the order of 103, along the line of maximum growth rate there is no saturation of the effective viscosities. The stronger the fields, the higher is the maximum viscosity that can be achieved.
While the instability domain is only slightly modified for Prandtl numbers smaller than unity, this is not true for the behavior of the second order correlations. The effective viscosity formed by Reynolds stress and Maxwell stress decreases for small Pm. It varies by one order of magnitude when Pm varies by two orders of magnitude. The ratio of magnetic energy to kinetic energy (taken for maximum viscosity) also decreases for small Pm (Fig. 8, top). Consequently, the Maxwell stress in relation to the Reynolds stress also sinks for small magnetic Prandtl numbers (Fig. 8, bottom). The effectiveness of the magnetic perturbations in transporting angular momentum is thus reduced for small Pm, i.e., at cooler temperatures.
Our results support the conclusion that magnetic instabilities of toroidal magnetic fields in the presence of differential rotation are a viable mechanism to explain angular momentum redistribution in stellar interiors, especially for subgiant and young red giant stars.
Acknowledgments
M. Gellert would like to acknowledge support by the Helmholtz alliance LIMTECH.
References
- Böhm Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ceillier, T., Eggenberger, T., et al. 2012, Astron. Nachr., 333, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1956, PNAS, 42, 273 [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demarque, P., Guenther, D. B., Li, L. H., Mazumdar, A., & Straka, C. W. 2008, Ap&SS, 316, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fournier, A., et al. 2005, J. Comput. Phys., 204, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Rüdiger, G., & Kitchatinov, L. L. 1996, ApJ, 466, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdiger, G., Gellert, M., Schultz, M., et al. 2012, ApJ, 755, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdiger, G., Rüdiger, G., Gellert, M., et al. 2014, MNRAS, 438, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Seilmayer, M., Stefani, F., Gundrum, T., et al. 2012, Phys. Rev. Lett., 108, 4501 [CrossRef] [PubMed] [Google Scholar]
- Spruit, H. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tayler, R. J. 1957, Proc. Phys. Soc. B, 70, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Tayler, R. J. 1973, MNRAS, 161, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Vainshtein, S. I., & Kichatinov, L. L. 1983, Geophys. Astrophys. Fluid Dyn., 24, 273 [Google Scholar]
All Figures
 |
Fig. 1 Stellar model of KIC 7341231 (blue) compared to a standard solar model (red). The vertical dashed line shows the outer boundary of the radiative stellar core of the red subgiant. |
| In the text | |
 |
Fig. 2 Diffusion coefficients from the stellar model of KIC 7341231. The vertical dashed line shows the outer boundary of the radiative stellar core. Note that the geometric average of the two diffusivities |
| In the text | |
 |
Fig. 3 Curves of marginal instability for Ω ∝ 1 /R2 if rin = 0.5, i.e., μ = 0.25. For small magnetic Prandtl numbers, the curves scale with Re and Ha. For Pm = 1, the critical Reynolds number is (only) 100. The dotted lines mark the line of maximum growth rates. The dashed line represents, for Pm = 1, the lower limit of the condition (5). |
| In the text | |
 |
Fig. 4 Linear relation between the turnover rate and the growth rate for various Pm and μ. The models possess the maximal growth rates as indicated in the instability domain of Fig. 3. |
| In the text | |
 |
Fig. 5 Rotation law Ω ∝ 1 /R2: the fluctuating radial profiles between the inner and the outer radius of the effective viscosity in (7). The thick solid line gives the temporal average. Re = 850. |
| In the text | |
 |
Fig. 6 Rotation law Ω ∝ 1 /R2 (top) and Ω ∝ 1 /R (bottom): the normalized viscosity grows with the magnetic Reynolds number Rm without indication of a saturation (Pm = 0.1...1, as indicated). |
| In the text | |
 |
Fig. 7 Magnetic and kinetic energy for Pm = 1 and Re = 800, normalizedto the diffusion velocity squared. The energies are in equilibrium for strong magnetic fields only (in this plot, μ = 0.255). |
| In the text | |
 |
Fig. 8 Top: magnetic to kinetic energy ϵ for various Pm, as indicated. The magnetic energy only dominates the kinetic energy for Pm ≳ 1. Bottom: the magnetic-induced part in units of the total viscosity (μ = 0.255 in this plot). |
| In the text | |
 |
Fig. 9 Normalized eddy viscosity for Pm = 1 and the rotation laws Ω ∝ 1 /R2 (μ = 0.25), Ω ∝ 1 /R3/2 (μ = 0.35), and Ω ∝ 1 /R (μ = 0.5). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.