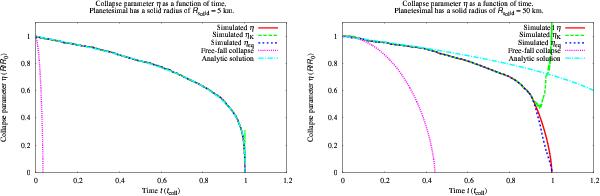
Total energy, parametrized through η ≡ R(t) /R₀, as a function of time for two clouds with, initially, cm-sized pebbles. Left panel: collapse of a cloud with R_solid = 5 km; right panel: cloud with R_solid = 50 km. The red lines show the actual size of the cloud, blue lines the equilibrium values (η_eq ≡ E₀/E), and green lines the kinetic energy (η_K ≡ T₀/T). The pink line shows the free-fall collapse of a cloud and the teal lines the analytic solution from Appendix A. We note that time is measured in units of the collapse time. Therefore the free-fall line is different for the two clouds. In the case of the low-mass cloud the collapse is slow and the only outcome of collisions is bouncing. Therefore it is in virial equilibrium until the very end of the collapse and follows the analytical solution (η = η_K = η_eq). The massive cloud, on the other hand, has initially higher collision speeds which lead to pebble fragmentation and rapid energy dissipation. At about η = 0.5 the energy dissipation becomes faster than free-fall, so the cloud does not get into virial equilibrium before the next pebble collision (the first term in Eq. (7)dominates over the second). This results in a transition to cold collapse (η is parallel to the free-fall curve) with subvirial speeds (η_K>η_eq).