| Issue |
A&A
Volume 569, September 2014
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 13 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201423442 | |
| Published online | 24 September 2014 | |
Proper use of Schwarzschild Ledoux criteria in stellar evolution computations
1
Institut d’Astrophysique et de Géophysique, Liège University
Allée du 6 Août, 17
4000
Liège
Belgium
e-mail: mgabriel@ulg.ac.be; Arlette.Noels@ulg.ac.be; j.montalban@ulg.ac.be
2
School of Physics and Astronomy, University of Birmingham,
Birmingham,
B15 2TT,
UK
e-mail:
miglioa@bison.ph.bham.ac.uk
Received:
16
January
2014
Accepted:
2
July
2014
The era of detailed asteroseismic analyses opened by space missions such as CoRoT and Kepler has highlighted the need for stellar models devoid of numerical inaccuracies, in order to be able to diagnose which physical aspects are being ignored or poorly treated in standard stellar modeling. We tackle here the important problem of fixing convective zone boundaries in the frame of the local mixing length theory. First we show that the only correct way to locate a convective zone boundary is to find, at each iteration step, through interpolations or extrapolations from points within the convective zone, the mass where the radiative luminosity is equal to the total luminosity. We then discuss two misuses of the boundary condition and the ways they affect stellar modeling and stellar evolution. The first consists in applying the neutrality condition for convective instability on the radiative side of the convective boundary. The second way of misusing the boundary condition comes from the process of fixing the convective boundary through the search for a change of sign of a possibly discontinuous function. We show that these misuses can lead to completely wrong estimates of convective core sizes with important consequences for the following evolutionary phases. We point out the advantages of using a double mesh point at each convective zone boundary. The specific problem of a convective shell is discussed and some remarks concerning overshooting are given.
Key words: convection / stars: interiors / stars: evolution / methods: numerical
© ESO, 2014
1. Introduction
It appears that there is a misunderstanding concerning which criterion should be used to fix the boundaries of convective zones and also concerning which numerical procedure should be used to find them. The numerous methods tested recently by Paxton et al. (2013) clearly show that stellar evolution results are very sensitive to the choice that is made. The answer to these questions cannot be found from comparing numerical results obtained with different assumptions in stellar evolution codes since other uncertainties affect stellar modeling.
Therefore we think it is useful to cite some very basic physical facts which allow us to discuss the problem correctly and to bring a theoretical answer to the questions presently discussed. The extent of convective cores in stars is crucial in order to fix the time frame of their evolution and is of particular importance for stellar and galactic evolution. Moreover, since models are often used to interpret seismic data, it is important that they be free from any numerical inaccuracy caused by an incorrect positioning of the convective zones boundaries so that any discrepancy between observation and theory may be attributed to inaccuracies in the physics.
It is interesting to point out that when comparing stellar models obtained with different codes, as was done in the frame of the CoRoT Evolution and Seismic Tools Activity1 of the Seismology Working Group of the CoRoT mission2, the main differences are found in the location of convective zone boundaries and in layers close to them (Lebreton et al. 2008). They are especially large in low mass stars models where the convective core mass increases during a large fraction of core hydrogen burning (see their Fig. 9).
For a long time the local mixing length theory (LMLT) was the only theory available for model computation, but progress has been made along two lines in recent decades. The first advance came with the progressive increase of computing power. However, numerical simulations will always be limited to domains of Rayleigh and Prandtl numbers very different from those encountered in stars, which sometimes makes the results difficult to extend to stellar conditions. So far, no general model replacing LMLT has been inferred from numerical simulations, but very interesting results have nevertheless been obtained, for instance concerning overshooting (see Sect. 8). The second one came from the development of more elaborate theories. This started in 1981 with the first work of Xiong who went on improving his theory, now with several collaborators (Xiong 1981, 1985, 1986, 1989; Xiong et al. 1997, 1998a,b, 2000). The Chinese group produced a few evolutionary sequences (see Sect. 8), but it is obvious that they have to solve a very unstable system with stiff equations and that model computation has become a much harder problem.
Canuto has been working on his own theory since 1992 (Canuto 1999b, 2000, 2011a−d and references therein), but so far no code has included his formalism. In order to progress it would be highly desirable that people developing evolution codes introduce some better theory than the LMLT; however, we have to note that this has not been done so far and worse, that some codes use a wrong numerical scheme to locate the boundaries of convective zones.
In this paper we use the term semi-convective to refer to layers where the temperature gradient is in between the Schwarzschild and the Ledoux gradients. This does not imply that we consider that they are necessarily partially mixed; on the contrary, we consider that practically all local treatments of the problem cannot be trusted. Canuto (1999b) has provided equations that, in principle, allow us to derive the non-local solution in each situation, but again no one has obtained a general non-local solution of Canuto’s equations. The problem of the semi-convective zone structure will not be discussed here. The purpose of this paper is more limited; we present here the correct condition at the boundaries of convective regions for single non-rotating stars in the frame of the LMLT, and what is the only correct way to implement it.
In Sect. 2 we present the physical aspects and the definition of a convection zone and a convective boundary as well as the only correct method to find the position of that boundary which was already given by Biermann (1932) in the frame of the LMLT. Section 3 discusses the consequence of the first misuse of the boundary condition, which is to apply the criterion fixing the neutrality condition on the radiative side of the boundary instead of its correct use on the convective side of the boundary. In Sect. 4 another way of computing incorrect extents of convective regions is presented. In Sect. 5, to illustrate the points discussed in the previous section, we have computed main sequence and core helium burning models with CLÉS (Code Liégeois d’Évolution Stellaire) (Scuflaire et al. 2008) with different implementation of the algorithm used to fix the convective zones boundaries. Section 6 discusses the advantages of introducing a double mesh point at convective zones boundaries. Section 7 raises the problems related to the occurrence of a convective shell in an otherwise radiative zone. A few remarks concerning overshooting are given in Sect. 8 and conclusions are drawn in Sect. 9.
2. Definition of a convective zone boundary and of the correct boundary condition
For any physical problem every basic mathematical equation must be the translation of a physical concept. Therefore, the definition of a convective zone boundary must be given out of a physical idea of what this boundary is. Only afterwards will it be possible to express it in terms of a mathematical formula.
A convection zone is a region where a fraction of the energy is carried by up and down motions of matter. Therefore, the natural way to define the surface of a convection zone is to say it is the surface where the radial component Vr of the velocity of the convective motions goes to zero. This definition was implicitly adopted from the very beginning; it was also given explicitly by Roxburgh (1978). This definition is completely general and using it, the convection zone includes what is called the overshooting region. It says nothing about the temperature gradient at that point; a condition such that the radiative temperature gradient is equal to the adiabatic value comes only from some convection theories and particularly from the local mixing length theory (LMLT).
In real stars this surface is very complex and therefore non-spherical and varying with time. However, in model computation, we have to assume that it is spherical and varying only on the timescale of stellar evolution. This means that we have to search for an approximate solution of the equations for convection, which leaves out some phenomena that may be important, such as wave generation. It is well known that convection generates modes responsible for the solar-like oscillations in low mass stars. Convection can also generate gravity waves in overshooting regions, which can carry energy and angular momentum. In model computation, we also have to assume that convective zones are chemically homogeneous. A way to escape this approximation could perhaps be found if a solution to the equations given in Canuto (1999b) could be obtained that filters out the short timescales and keeps only those comparable with that of stellar evolution. Theories such as those of Deng et al. (1996) or of Ventura et al. (1998), which contain enough parameters to allow a large variety of results, may not provide a satisfactory solution. Again, in particular when a convective boundary expands into the adjacent radiative one, this assumption is wrong in the outermost part of the overshooting region where convection becomes so weak that the mixing timescale becomes on the order of or larger than the evolution timescale. In these layers the chemical composition varies from that of the chemically homogeneous convective region to that of the radiative neighboring layers. This means that the density will then be continuous everywhere, as well as the opacity and the temperature gradient, and that most of the problems discussed in this paper will disappear (but a better theory than the LMLT is also required). According to Canuto (1999a) this layer is very narrow, so that a fine zoning is required to take it properly into account and also that the discontinuity introduced when assuming chemically homogeneous convective zones is a reasonably good approximation.
The basic equations for stationary convection of interest here (i.e., the Eulerian time
derivative of any variable cancels out) in absence of any other velocity field, give (see
Ledoux & Walraven 1958; Gabriel 1996; Grigahcene
et al. 2004) 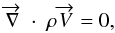 (1)where
(1)where
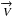 is the convection velocity. This equation implies
is the convection velocity. This equation implies 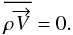 (2)The overbar indicates
the average over a spherical surface, which is large compared to the convective
characteristic lengths. Equation (2) simply
means that there is no net flux of matter through a large spherical surface. The equation of
thermal energy conservation is written
(2)The overbar indicates
the average over a spherical surface, which is large compared to the convective
characteristic lengths. Equation (2) simply
means that there is no net flux of matter through a large spherical surface. The equation of
thermal energy conservation is written 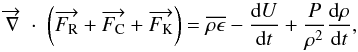 (3)where ϵ is the nuclear energy
generation rate and U is the internal energy per unit mass of the mixture
of gas and radiation. In Eq. (3)
(3)where ϵ is the nuclear energy
generation rate and U is the internal energy per unit mass of the mixture
of gas and radiation. In Eq. (3)
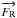 ,
,
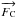 ,
and
,
and 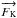 are, respectively, the radiative flux, the convective flux, and the flux of kinetic energy
of convection, with
are, respectively, the radiative flux, the convective flux, and the flux of kinetic energy
of convection, with 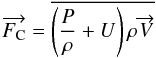 (4)and
(4)and
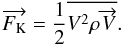 (5)These equations are very
basic ones and are independent of any theory of convection. The only approximation done in
Eq. (4) is to assume that the gas and the
radiation are in thermal equilibrium (more general equations are given in Gabriel 1996).
(5)These equations are very
basic ones and are independent of any theory of convection. The only approximation done in
Eq. (4) is to assume that the gas and the
radiation are in thermal equilibrium (more general equations are given in Gabriel 1996).
We shall now assume that the convective pressure fluctuations are much smaller than the
temperature and density fluctuations so that they can be neglected. This approximation is
almost always done in stellar convection theories and is valid as long as the convection
velocity is small compared to the sound speed. We also assume that the density and
temperature fluctuations are small enough so that we can neglect their powers larger than
one. It then follows that ![\begin{equation} \overrightarrow{F_{\rm C}} = \rho T \overline{\left [\Delta S \overrightarrow{V}\right ]} = C_{\rm P} \rho T \overline{\left [\frac{\Delta T}{T} \overrightarrow{V}\right ]} . \label{Fc2} \end{equation}](/articles/aa/full_html/2014/09/aa23442-14/aa23442-14-eq14.png) (6)The fluctuation of any
variable f is
Δf. In order
to obtain Eqs. (6) from (4) it is important to consider
(6)The fluctuation of any
variable f is
Δf. In order
to obtain Eqs. (6) from (4) it is important to consider
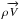 as a single variable in order to take Eq. (2)
properly into account. Equation (6) is the
relation usually used for the convective flux. The flux
as a single variable in order to take Eq. (2)
properly into account. Equation (6) is the
relation usually used for the convective flux. The flux
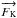 is nearly always neglected in stellar model computations because it cancels out in LMLT.
is nearly always neglected in stellar model computations because it cancels out in LMLT.
In spherically symmetric stars 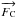 is a radial vector and from our definition of a convection zone boundary, Vr is equal to
zero everywhere on the spherical surface boundary. It follows from Eqs. (4) and (5), that the convective flux
is a radial vector and from our definition of a convection zone boundary, Vr is equal to
zero everywhere on the spherical surface boundary. It follows from Eqs. (4) and (5), that the convective flux 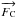 and the flux of mechanical energy of convection
and the flux of mechanical energy of convection 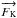 are equal to zero on that surface and also that the radiation carries out all the energy,
i.e.,
are equal to zero on that surface and also that the radiation carries out all the energy,
i.e., 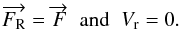 (7)In the frame of the
LMLT, it can be replaced by LR = L because
(7)In the frame of the
LMLT, it can be replaced by LR = L because
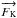 is neglected and consequently there is no point where
is neglected and consequently there is no point where
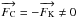 as in
more elaborate theories. Canuto (1999a, 2011d) has suggested to replace the boundary condition
(7) by the condition that the helium or
hydrogen concentration flux is equal to zero, i.e., that
as in
more elaborate theories. Canuto (1999a, 2011d) has suggested to replace the boundary condition
(7) by the condition that the helium or
hydrogen concentration flux is equal to zero, i.e., that
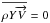 (as usual Y is the helium mass
abundance). This will indeed provide a more precise location of the boundary as convection
will be very inefficient in the outer overshooting zone so that
(as usual Y is the helium mass
abundance). This will indeed provide a more precise location of the boundary as convection
will be very inefficient in the outer overshooting zone so that
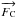 and
and 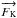 will be almost zero over an extended region while the chemical composition is expected to
vary quite rapidly near the surface. Unfortunately, with a simple theory such as LMLT, the
convective regions and the ad hoc added overshooting zones have to be chemically
homogeneous.
will be almost zero over an extended region while the chemical composition is expected to
vary quite rapidly near the surface. Unfortunately, with a simple theory such as LMLT, the
convective regions and the ad hoc added overshooting zones have to be chemically
homogeneous.
Condition (7) can also be obtained from the
following approach. The equation of radiative transfer holds everywhere in a star and the
only terms that can be discontinuous are the source function and the opacity coefficient. As
a result only the gradient of the radiative intensity can be discontinuous. It follows from
their definitions that the radiation energy per unit volume, the radiation flux, and the
radiation pressure are all continuous throughout a star (see, e.g., Schwarzschild 1958, p. 39). Obviously, the boundary condition
Vr =
0 or 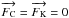 is meaningful only in a
convection zone and consequently condition (7) must be applied on the convective side of the boundary and not on the radiative
side.
is meaningful only in a
convection zone and consequently condition (7) must be applied on the convective side of the boundary and not on the radiative
side.
In stellar evolution the local Böhm-Vitense theory is commonly used to find the structure and to fix the position of the boundaries of a convection zone. Therefore, in this paper we shall only consider models computed in the frame of a local theory of convection, such as LMLT, and without overshooting since it is a non local phenomenon. So far no theory reliably predicts the properties of the overshooting region. Accordingly, its extent is just a free parameter often taken as a fraction of the local pressure scale height, while the assumed temperature gradient in this region differs from one code to the next. However, a brief discussion concerning overshooting will be given in Sect. 8.
Biermann (1932) showed that convective regions can
exist in the stellar interior and that the temperature gradient is adiabatic there. More
precisely, using LMLT, he showed that (∇ −
∇ad) is very small 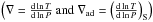 and also that
and also that 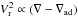 .
Therefore, at the boundaries of a convection zone the temperature gradient is adiabatic.
Since
.
Therefore, at the boundaries of a convection zone the temperature gradient is adiabatic.
Since 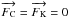 there, it follows from condition
(7) that
there, it follows from condition
(7) that 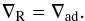 (8)Clearly this condition,
which is called the Schwarzschild criterion, must be satisfied on the convective side of the
boundary, just as the conditions
(8)Clearly this condition,
which is called the Schwarzschild criterion, must be satisfied on the convective side of the
boundary, just as the conditions 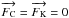 and
and
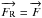 are. This is the conclusion already obtained by Biermann
(1932, see Eq. (30)). On the radiative side of the boundary, we must have
are. This is the conclusion already obtained by Biermann
(1932, see Eq. (30)). On the radiative side of the boundary, we must have
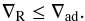 (9)The equality holds when
there is no discontinuity in the chemical composition since then all the variables
P,T,ρ, and
L are
continuous. The inequality holds when there is a discontinuity of the chemical composition
as then both the opacity and the density are discontinuous. Condition (8) gives the boundaries of a convective zone only
in the frame of local convection theories.
(9)The equality holds when
there is no discontinuity in the chemical composition since then all the variables
P,T,ρ, and
L are
continuous. The inequality holds when there is a discontinuity of the chemical composition
as then both the opacity and the density are discontinuous. Condition (8) gives the boundaries of a convective zone only
in the frame of local convection theories.
When convection takes place in superficial layers with low temperatures and densities, a
non-negligible departure of the temperature gradient from the adiabatic gradient is
required, but as long as a local theory such as Böhm-Vitense’s LMLT is used, it is found
that the condition Vr
= 0 or 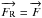 still leads to ∇R =
∇ad at the surface of the convective envelope. Consequently,
and since stellar models are usually computed with local convection theories, we shall use
in the forthcoming discussion the definition of a convective zone boundary given by LMLT,
i.e., Vr =
0,
still leads to ∇R =
∇ad at the surface of the convective envelope. Consequently,
and since stellar models are usually computed with local convection theories, we shall use
in the forthcoming discussion the definition of a convective zone boundary given by LMLT,
i.e., Vr =
0, 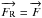 ,
or ∇R =
∇ad taken on the convective side of the boundary. This implies
that since during the iteration process of stellar modeling the assumed convection zone
boundaries are not the right ones, their position must be improved through extrapolations or
interpolations of LR from points in the convective zones in
order to find the mass where LR = L and
∇R =
∇ad. This is the way Henyey’s code worked (Henyey et al. 1964, bottom of p. 309)3.
,
or ∇R =
∇ad taken on the convective side of the boundary. This implies
that since during the iteration process of stellar modeling the assumed convection zone
boundaries are not the right ones, their position must be improved through extrapolations or
interpolations of LR from points in the convective zones in
order to find the mass where LR = L and
∇R =
∇ad. This is the way Henyey’s code worked (Henyey et al. 1964, bottom of p. 309)3.
It is also interesting to note that the boundary condition (8) was correctly applied at least up to 1958 when models were computed using the fitting technique. Most computed models were two-zone models with a discontinuity of molecular weight between the convective core and the radiative envelope. Such models were computed for instance by Ledoux (1947) and Oke & Schwarzschild (1952). Models with a μ-gradient region in between were first computed by Tayler (1954, 1956) and then by Kushwaha (1957). All these authors applied condition (8) on the convective side of the boundary, without justification since it was evident to them. We only find a detailed justification in Schwarzschild’s famous book (Schwarzschild 1958, pp. 167,168). He clearly explains why condition (8) must be applied on the convective side of the core boundary and not on the radiative one.
On the other hand, the Ledoux criterion was likely introduced in stellar modeling only after the discovery of main-sequence models with a semi-convective zone because it allows the computation of models showing up in these layers although ignoring what their real structure is. Instead, with the Schwarzschild criterion these layers are considered to be convective. This leads to convergence problems which disappear only when a theory that specifies the temperature gradient and the way to compute the chemical composition in these semi-convective regions is adopted.
Since the correct boundary condition must be obtained from points in the convective zone
only, any use of points in the radiative zone may lead to an incorrect positioning of the
convective zone boundary. When points located in the radiative zone are used, it is possible
to apply either the Schwarzschild criterion with y = ∇R − ∇ad or the Ledoux
criterion with y = ∇R
− ∇Ldx, where
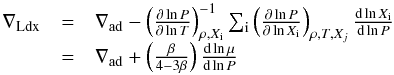 (10)and
the last equality holds for the simple equation of state P =
ℛρT/βμ with
β =
Pg/P.
(10)and
the last equality holds for the simple equation of state P =
ℛρT/βμ with
β =
Pg/P.
First, a question might be asked. Which of the criteria must be preferred, Schwarzschild’s or Ledoux’s? The question is of course physically meaningless since only points within the convective region should be used and both criteria are identical there. The use of points in the radiative zone raises problems when the function y is discontinuous at the convective zone boundary. With the Schwarzschild criterion this happens only when the chemical composition is discontinuous there. With the Ledoux criterion, y is discontinuous when the chemical composition is discontinuous at the convection boundary and also when there is only a μ-gradient in the adjacent radiative layers. Therefore, we can say that the Ledoux criterion more often leads to problems than the Schwarzschild criterion in model computation with the LMLT. However, this is only meaningful for numerical techniques but has no physical relevance and, as just said, the question is physically meaningless.
One might also wonder where these misuses of the boundary condition come from. Clearly they come from the use of Eq. (8) instead of the more fundamental one given by Eq. (7). Since in the radiative zone LR = L by definition, while in the convective zone LR<L, it is obvious that the only possible way to find the mass point of the convective region where radiation is finally able to carry out all the luminosity is through interpolation or extrapolation from points in the convective region, and that points in the radiative layers may be of no help for that purpose. When the Schwarzschild or the Ledoux criterion is used, the variable y defined above varies everywhere in the star and is nowhere constant, but one has to remember that it is just another way to write the original condition (7). When this is forgotten, one might be tempted to use points in the radiative zone. This works well when y is continuous at the interface between the two regions but, as will be shown below, when y is discontinuous there, the use of one or several radiative points will most often lead to an incorrect positioning of the boundary. This shows up very clearly when L − LR or ∇R − ∇ad is plotted. It is then seen that these quantities do not cancel on the convective side of the boundary.
Second, there are two ways of misusing the boundary condition. In the first one, the zero of y is obtained by interpolation or extrapolation from points in the radiative region; this is discussed in Sect. 3. In the second one a change of sign of y between two consecutive mesh points is searched for; these two points may both be radiative or both be convective or one may be radiative and the other convective, but y is then always interpolated between these two points. This is discussed in Sect. 4 and illustrated in Figs. 4, 6, and 8 in Sect. 5.
Taking into account that the temperature, the pressure, and the radius are continuous
functions throughout the stars, while the chemical composition may be discontinuous at some
points, and as a consequence the density, the opacity, and ∇ as well, the radiative transfer equation
taken on both sides of the boundary leads to 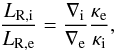 (11)where κ is the opacity coefficient
and the indices e and i refer, respectively, to the outer and inner sides of the convective
boundary. Any misuse of the boundary condition leads to the violation of either Eq. (7), LR,i =
L, or of the obvious one, LR,e =
L.
(11)where κ is the opacity coefficient
and the indices e and i refer, respectively, to the outer and inner sides of the convective
boundary. Any misuse of the boundary condition leads to the violation of either Eq. (7), LR,i =
L, or of the obvious one, LR,e =
L.
3. The first way to misuse the boundary condition
3.1. With the Ledoux criterion
One way is to use the Ledoux criterion for convective instability (∇R> ∇Ldx) and to require that it predict neutrality with ∇R − ∇Ldx = 0 on the radiative side of the boundary. We have to distinguish between several possibilities occurring at a convective zone boundary.
3.1.1. The chemical composition is discontinuous but there is no molecular weight gradient in the radiative zone
The Ledoux criterion is then identical to the Schwarzschild criterion. By hypothesis we take in this subsection ∇e = ∇R = ∇Ldx = ∇ad. Moreover, in a deep convective zone the temperature gradient is adiabatic and thus ∇i = ∇ad. We obviously have LR,e = L and Eq. (11) shows that, except in the unphysical situation where the opacity is independent of the chemical composition, we obtain LR,i ≠ L. We must consider two different cases:
-
1.
κe<κi Then LR,i<L and the convective luminosity must be positive, which implies a positive convective velocity. This means that convective motions will extend farther out than the assumed boundary, which is then not the right one since Vr ≠ 0. This situation was discussed by Schwarzschild (1958, pp. 167,168). He explicitly showed that the boundary condition must be applied on the convective side. On the contrary, if the condition ∇R = ∇ad (or LR,i = L) is applied on the convective side, a subadiabatic temperature gradient is sufficient for radiation to carry out all the luminosity in the radiative region.
-
2.
κe>κi Then LR,i>L which means that a subadiabatic temperature gradient is large enough to have radiation carry out all the luminosity. As a result, in the outer layers of the convection zone, FC< 0 and consequently ∇ < ∇ad. This means that they are stable and the assumed boundary must be moved inwards. If the condition ∇R = ∇ad is correctly applied on the convective side of the boundary, then LR,i = L>LR,e and layers located on the radiative side are convectively unstable. This is the difficulty met by Schwarzschild & Härm (1958) when they studied the evolution of massive main sequence stars where electron scattering is the main source of opacity. This led them to introduce semi-convection into models of these stars.
3.1.2. The chemical composition is continuous but the abundance gradients of some abundant elements are discontinuous
This situation is encountered at the surface of the convective core of intermediate
mass stars during core hydrogen burning phases. Since in all the situations encountered
in stellar evolution the chemical composition gradient terms in the Ledoux criterion
have a stabilizing influence, one has ∇e = ∇R = ∇Ldx>
∇ad on the radiative side. Relation 11 is now written with κe =
κi and thus ∇i = ∇ad<
∇R. Therefore
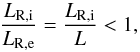 (12)which means that
(12)which means that
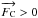 and Vr>
0 at the boundary of the convection zone. This implies that
convection will extend farther out than assumed.
and Vr>
0 at the boundary of the convection zone. This implies that
convection will extend farther out than assumed.
Had we applied the condition ∇R = ∇ad on the convective side of the boundary, then ∇e = ∇ad and the chemical composition gradient terms forces the Ledoux criterion to predict stability on the radiative side of the boundary in all known situations.
3.1.3. The chemical composition and its gradient are discontinuous
Here Eq. (11) gives 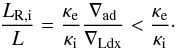 (13)Again we have
to distinguish between two possibilities:
(13)Again we have
to distinguish between two possibilities:
-
1.
κe<κi Then LR,i<L on the convective side which means that convective motions do not vanish there and that the convection zone must be extended.
-
2.
κe>κi Then one might find LR,i = L but only for a very special combination of κi/κe and of the gradient of molecular weight. In most cases it will be found that LR,i ≠ L and that the convective boundary must be moved in one direction or the other. This situation is met in MS low mass stars with a small growing convective core and nuclear reactions outside this convective core.
Had we used the correct boundary condition, we would have found that LR,i =
LR,e =
L and as the temperature gradient is adiabatic at
the boundary of the convective zone, ∇i = ∇ad, and we would have found from Eq.
(11) that ∇e =
∇adκe/κi.
Thus, the outer side of the boundary is stable provided that
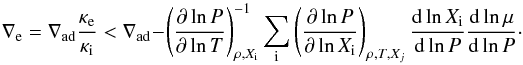 (14)If κe<κi
there is no problem. If κe>κi,
it is at first found that ∇i =
∇ad< ∇e =
∇R< ∇Ldx; such layers
are often considered to be semi-convective. However, when the ratio κe/κi
is large enough, we find that the radiative side of the boundary is convectively
unstable towards the Ledoux criterion leading again to a difficulty, but we do not know
of any case where such a situation is met.
(14)If κe<κi
there is no problem. If κe>κi,
it is at first found that ∇i =
∇ad< ∇e =
∇R< ∇Ldx; such layers
are often considered to be semi-convective. However, when the ratio κe/κi
is large enough, we find that the radiative side of the boundary is convectively
unstable towards the Ledoux criterion leading again to a difficulty, but we do not know
of any case where such a situation is met.
To our knowledge this method with the Ledoux criterion was never used in all cases discussed here in Sect. 3.1 because it leads to a convective core decrease that is much too fast as a result of the strong stabilizing influence of the μ-gradient term during core hydrogen burning. One can expect an even faster shrinking than that found in Paxton et al. (2013) in their Fig. 13 and a Hertzsprung-Russell track still less compatible with observations than what they found in their Fig. 14.
3.2. With the Schwarzschild criterion
Another way to misuse the boundary condition is to apply the Schwarzschild criterion (Eq. (8)) on the radiative side of a boundary. We have to distinguish between the same three cases as above:
-
1.
In the first case, Schwarzschild and Ledoux criteria are identicaland the same conclusions as above are reached.
-
2.
In the second case, the chemical composition is continuous and so are the opacity, the radiative luminosity, ∇R, and ∇ad. As a result the boundary condition leads to the same conclusion as the correct one.
-
3.
In the third case, the use of the Schwarzschild criterion leads to the same conclusions as in the first one.
This incorrect boundary was used by many researchers among these who, after 1960, wrote evolution codes using the finite difference method developed by Henyey et al. (1955a,b). During hydrogen burning the convective core generally shrinks, which means that there is no discontinuity in chemical composition there and this mistake has then no consequence.
However, later on when central helium burning was computed, it was found that the convective core expands and builds up a discontinuity in chemical composition. The mistake, which had important consequences on the models structure, was noticed and corrected by Castellani et al. (1971a,b) who rediscovered the justification given earlier by Schwarzschild (1958). The correction of that mistake also led them to discover that the mass of the convective core increases much more than with the incorrect boundary condition. When it becomes large enough, the physical situation discussed in Ledoux (1947) applied to the models they were considering. Following Ledoux, they introduced a semi-convective zone in some helium burning models. This example nicely illustrates the consequences of a mistake made perhaps consciously because it then had no consequences and was easier to implement than the correct one, but which led to incorrect results later on when an initially unexpected situation was encountered.
Summarizing, we repeat what was said at the beginning: the criterion fixing the
boundaries of convective regions must always be checked on the convective side of the
boundary and never on the radiative side. This criterion is Vr = 0 or
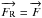 ,
which, in the local mixing length theory, is given by the neutrality of the Schwarzschild
criterion ∇R =
∇ad, equivalent to the Ledoux criterion there.
,
which, in the local mixing length theory, is given by the neutrality of the Schwarzschild
criterion ∇R =
∇ad, equivalent to the Ledoux criterion there.
On the other hand the Ledoux criterion must only and necessarily be used to answer the following question: in a region of varying mean molecular weight, given a layer supposedly in radiative equilibrium, when is the temperature gradient large enough for convective motions to start there?
4. The second way to misuse the boundary condition
Another way to misuse the convective zone boundary condition is found in many current codes. They scan the mesh points from the surface to the center (or the other way around) searching for a change of sign of either (∇R − ∇Ldx) or (∇R − ∇ad) and then they interpolate in order to find where it cancels. The procedure fails when the checked variable y is discontinuous at the boundary of the convective zone. It is always so with y = (∇R − ∇Ldx) (except for homogeneous models), and only when the chemical composition is discontinuous with y = (∇R − ∇ad). The reason is very simple. If, at one step during the iteration process, y changes sign between the two mesh points j and j + 1, then the convection zone boundary is assumed to be located between these two points. However, it is obviously not allowed to interpolate a function in an interval over which it has a discontinuity. This may have important consequences on the position of the convection zone boundary as we will now show.
We now consider the problem raised by a convective core, which is the most often encountered situation. The following discussion is also valid for the upper boundary of a convective shell and it is straightforward to transpose it for the bottom of a convective envelope or the lower boundary of a convective shell.
4.1. Overview of the problem
We first present the problems discussed in the following with a few very schematic figures. We consider a function y(m) where y is given either by y = ∇R − ∇ad or by y = ∇R − ∇Ldx and, as said above, we discuss here the problem of locating the mass at the convective core boundary, which is a priori unknown.
When y is continuous throughout the model, the location of the point y = 0 is unambiguous. Problems only arise when y is discontinuous at the location of the core boundary. First we consider the most commonly encountered situation: y is smaller on the radiative side of the discontinuity that on the convective one.
Since the transfer equation is not the same in convective and radiative zones, two different sets of differential equations are solved in these regions. As a result, it is possible to compute a relaxed model with, in our example, an arbitrary value for the convective core mass, that is to say a model such that r,P,T and L are continuous there and also such that the chemical composition varies according to the condition required by the sign of the time derivative of the convective core mass. However, among all these models, only one will also fulfill condition (7), LR = L or ∇R = ∇ad, on the convective side of the core boundary. In practice, we will deal with approximate models obtained after an iteration step and, in any reasoning done with them, we must hope that they are not too different from the relaxed one with the same core mass.
We assume that y =
Y1 for
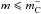 , i.e., in
the convective core, and that y = Y2 for
, i.e., in
the convective core, and that y = Y2 for
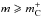 , i.e., in
the radiative zone, and also that Y1 and Y2 are two
continuous functions in the whole mass domain of interest. In the four cases illustrated
in the left panel of Fig. 1, the upper curve is
Y1 and the lower one is Y2 (they are
shown partly as dashed lines). In the right panel, the positions of Y1 and
Y2 are inverted. To simplify the problem,
we assume that Y1 and Y2 do not change
when the core mass varies.
, i.e., in
the radiative zone, and also that Y1 and Y2 are two
continuous functions in the whole mass domain of interest. In the four cases illustrated
in the left panel of Fig. 1, the upper curve is
Y1 and the lower one is Y2 (they are
shown partly as dashed lines). In the right panel, the positions of Y1 and
Y2 are inverted. To simplify the problem,
we assume that Y1 and Y2 do not change
when the core mass varies.
We consider that, as in Fig. 1 (left panel, case 1), such a model has been computed with a core boundary tentatively placed at point C. The solution representing the model is given by the solid line. If a new position of the core boundary is found through the extrapolation of the solution from the convective core and the new boundary is taken as the mass where Y1(m) = 0 (point A), then the model computed with that boundary is the correct one (see Sect. 2).
 |
Fig. 1 Left (right) panel: y is smaller (larger) on the radiative side of the convective core boundary. Cases 1 to 4 stand for different situations. Case 1 illustrates two possible ways of fixing the core boundary. Cases 2 to 4 show the different solutions found when the algorithm searches for a change of sign of y in the trial model. |
Another procedure, which similarly gives a unique solution, is to obtain the core boundary from an extrapolation of the solution from the radiative zone and locating the core boundary at point B. This procedure is incorrect, as was shown in Sect. 3. The position of the core boundary found by these two methods is independent of the initial estimated position of that boundary as can be seen in cases 2 to 4 where interpolations may indeed be used in some cases. It is also independent of the mesh points distribution.
The most often used procedure searches where y changes sign in the converged trial model (or in a given iteration). We consider briefly what happens next. First, we assume that the estimated core mass is too large, i.e., mC>mA (case 2). Again the full line represents the model and the interpolation of y(m), which is done in the convective core of the current model, gives y(mA) = 0, the correct location of the convective core boundary.
We now assume that the initial choice of the core mass is such that mC<mB (case 3); then the zero of y located along the solution is at point B, which is not the right location of the core boundary.
We finally consider the worst possibility, the initial core mass is such that mB<mC<mA (case 4). Then y changes sign at the location of the discontinuity. This means that any trial mass mC between mA and mB will appear to be the solution. This procedure must be banished as it finds different solutions when the initially estimated core mass varies.
More generally, if during the iteration procedure the core mass does not always remain larger than the correct value, then the solution found will be incorrect. Since there is a discontinuity of y at the core boundary, a double mesh point, i.e., two points with the same mass but different values of the density and/or of the chemical composition gradient, should be introduced there. Unfortunately, this is not generally the case and CESAM (Morel & Lebreton 2008) is the only code we know that puts a double mesh point at the boundary of a convective zone when the density is discontinuous there. In the other codes the discontinuity is replaced by a segment connecting the upper side of the discontinuity, which is point j, i.e., the last point in the convective core, to point j + 1, the first point in the radiative zone. It is readily seen that if interpolations are done between these two points they will just bring asymptotically the core boundary to point j + 1.
The right panel in Fig. 1 shows the same problem when y is larger on the radiative side than on the convective one of the discontinuity. The discussion of the different cases is the same as for the left figure and we will not repeat it. We note however, that point A still gives the correct position of the convective core boundary and also that now mA<mB. This situation will be further discussed at the end of Sect. 5.1.2.
4.2. Analysis of the possible situations
At some step of the iteration process, the estimated mass of the convective core mC is either too small (see Fig. 2, left panel) or too large (Fig. 2, right panel). The solid lines in Fig. 2 represent a schematic distribution of y as a function of the fractional mass for a model without discontinuity (case 1), for a model with a small discontinuity (case 2), and for a model with a large discontinuity (case 3) at the boundary of the convective core. The dashed lines show the extrapolations of y from the convective layers upwards and A, the point where it is equal to zero, gives the correct estimate of the convective boundary location. The dashed lines and the full lines in case 1 are only identical for homogeneous models. We note that since most codes do not add a double mesh point at the core boundary, they replace the discontinuity by a fast variation of y between j and j + 1, shown by the dotted lines in Fig. 2.
-
The estimated convective core is too large (Fig. 2, right panel).

Fig. 2 Left panel: illustration of a situation such that the assumed core mass of a model (not necessarily converged) is too small. In the right panel the assumed core mass is too large. The solid lines represent y in the model while the dashed ones are extrapolations. Case 1 stands for a model without discontinuity at the core boundary when the Schwarzschild criterion is used. Case 2 represents situations such that y has a small discontinuity. Case 3 stands for a larger discontinuity.
The zero of y is always in the convective core where y is continuous, the interpolation of y(m) is allowed and it leads to a significant improvement of the core boundary location since point A gives its correct position. It is always so when y is continuous (case 1), but in the two other cases, as soon as the location has been improved enough so that y changes sign between points j and j + 1, y is discontinuous in the interval and it is meaningless to try to improve its position through an interpolation of y between these two points. This is the situation illustrated by case 3 in the left panel of Fig. 2 (see discussion below) for which the correct convective boundary, given by point A, can fall outside the interval [ j,j + 1 ] depending on the value of y at point j (see also Sect. 2 and Schwarzschild 1958, pp. 167,168).
-
The estimated convective core is too small (Fig. 2, left panel). In cases 1 and 2, y is equal to 0 inside an interval where y is continuous and the interpolation will improve the location of the core boundary (which will be close to point A). The level of improvement nevertheless decreases as the discontinuity of y increases. In case 1 a new core mass larger than mA is found and at the next iteration we are back to the situation discussed previously (right panel). In case 2, if the discontinuity of y is very small (even smaller than the one displayed for case 2 in the left panel of Fig. 2), the interpolation along the solution in the radiative zone can predict a value of mB>mA and at the next iteration the core mass will be too large, which again will bring us back to the previous case (Fig. 2, right panel), but as the discontinuity becomes large enough compared to yj it will be found that mB<mA and the algorithm will become unable to increase the core mass up to its correct value, which is close to point A. When this core mass is adopted at the next iteration, y will be discontinuous at that point. As soon as the core boundary given by that algorithm has been located with the maximum accuracy it is able to achieve, i.e., when y changes sign between points j and j + 1 then case 2 evolves into case 3. In case 3, the discontinuity of y occurs at the location of the assumed core boundary, supposed to be at point j, and the interpolation is thus meaningless (since with a correct physics there is a discontinuity inside that interval) and moreover completely fails to improve the boundary location which will remain embedded in the layer [ j,j + 1 ], while the correct boundary, given by point A, can be located outside the interval [ j,j + 1 ] depending on the value of y at point j. If such a situation is encountered at the first iteration, the algorithm does not even allow any change in the core boundary location (see, e.g., Paxton et al. 2013, Fig. 15). This simply means that the algorithm does not work at all in case 3 and in case 2 as soon as the discontinuity in y is large enough. Moreover, the error made on the core mass may increase with the importance of the discontinuity since y may become large on the convective side of the discontinuity.
When the estimated convective core is too small, the algorithm discussed here will generally predict an incorrect convective boundary, while with a too large estimation the final boundary will be underestimated if an oscillation in the core mass occurs during the iteration process.
5. Examples with real stellar models
5.1. Core hydrogen burning
5.1.1. The convective core shrinks during MS
The method will converge toward the correct solution, provided the Schwarzschild criterion is used, since y is continuous at the core boundary and as long as there is no semi-convective zone on top of the convective core. Then, as already pointed out, convergence problems arise, which can only be properly solved after making some hypotheses on the structure of a semi-convective zone. These problems will be discussed in Sect. 5.1.2.
If the Ledoux criterion is used, then for the algorithm presented above to be valid in all three cases considered in Fig. 2, it is necessary to know beforehand the sign of the time derivative of the core mass and to always have an estimated core mass which is too large. Since in most MS stars the convective core mass decreases with time, a commonly used algorithm is to choose, for the zero order approximation core mass of the computed model, the same value as in the previous one. However, if during the iterations an estimated core mass is too small, the algorithm will predict an incorrect boundary and the extent of the convective core mass will be too small. As a result, its core hydrogen abundance decreases too quickly and this leads to a faster decrease of the core mass. This kind of problem with the estimated core mass during the iteration process is likely to occur several times during the main sequence phases, which, as a result, will be too short. This obviously has an important impact on the later stages of the star evolution.
 |
Fig. 3 Hydrogen profile as a function of time in a 16 M⊙ star with a convective core boundary correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel).The model displayed in Fig. 4 is drawn in solid line. |
Such a case is illustrated in Fig. 3 where the time evolution of the hydrogen profile is shown as a function of the fractional mass for a 16 M⊙ star computed with the Ledoux criterion. In the left panel the correct solution, obtained with an extrapolation of y from points in the convective core, is displayed while in the right panel the procedure discussed in Sects. 4.1 and 4.2 has been applied to fix the change of sign of y. One can see that, when reaching the end of core hydrogen burning, this star has a convective core that is too small by about 25% (right panel) with the method discussed in Sect. 4. Figure 4 shows the hydrogen profile (long dashed line), the radiative (solid line), adiabatic (dashed line), and Ledoux (dotted line) temperature gradients for the model drawn in full line in Fig. 3. In the deep internal layers of the models discussed in this section, the actual temperature gradient is the adiabatic one in convective zones and the radiative one elsewhere. The location of the convective core boundary (at the limit of the mixed region) is indeed obviously incorrect in the right panel since ∇R> ∇ad on the convective side of the boundary, which means LR<L(r) and LC> 0.
In addition, y must vary very quickly in the first radiative
shell above the core in order for it to cancel on the radiative side of its surface.
This is physically meaningless since this implies that there
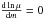 and
and
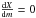 , but the derivative of X in the
radiative zone is given by
, but the derivative of X in the
radiative zone is given by ![\begin{equation} \frac{{\rm d}X}{{\rm d}m} = \left \{ \frac{{\rm d}X_{\rm C}}{{\rm d}t} \left [\frac{{\rm d}m_{\rm C}}{{\rm d}t} \right ]^{-1} \right \}_{t_{\rm C}} + \frac{{\rm d}}{{\rm d}m} \int_{t_{\rm C}}^t \frac{{\rm d}X(m)}{{\rm d}t} {\rm d}t, \label{dXdm} \end{equation}](/articles/aa/full_html/2014/09/aa23442-14/aa23442-14-eq118.png) (15)where
XC and mC are
respectively the hydrogen abundance in the core and its mass, while tC(m) gives the time
when mass m
stops belonging to the convective core. Obviously,
(15)where
XC and mC are
respectively the hydrogen abundance in the core and its mass, while tC(m) gives the time
when mass m
stops belonging to the convective core. Obviously,
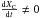 and
and
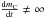 and
consequently
and
consequently 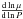 is discontinuous there. We note that in this situation, the discontinuity of
∇R −
∇Ldx increases very quickly since it is related to
is discontinuous there. We note that in this situation, the discontinuity of
∇R −
∇Ldx increases very quickly since it is related to
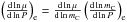 , and
, and
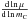 is large from the very beginning.
is large from the very beginning.
We also note that in both models ∇ad< ∇R< ∇Ldx in regions with a μ-gradient. Such layers are semi-convective and they are more extended in the incorrect model since ∇R − ∇ad is much larger. This is a direct consequence of the violation of the condition ∇R = ∇ad (or LR = L) on the convective side of the core boundary. In the correct model and within its accuracy, ∇R = ∇ad in the layers above the convective core (however their extent decreases as the mass increases and they have nearly disappeared in a 40 M⊙ star with the same central hydrogen abundance) and ∇R> ∇ad is found only in layers close to the homogeneous envelope.
 |
Fig. 4 Hydrogen profile (long dashed line), radiative (solid line), adiabatic (dashed line) and Ledoux (dotted line) temperature gradients for the MS model of 16 M⊙ displayed in solid line in Fig. 3, correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel), using in both cases the Ledoux criterion. |
In addition, a small shell with ∇R> ∇ad is found in the homogeneous region just on top of the ZAMS core and it should be handled as a convective shell. Its extent also grows with the mass of the star. This raises problems, however, because its bottom is not convectively neutral. It was shown by Gabriel (1970) that the overshooting at its bottom leads to mixing and to a downwards displacement of the shell able to form a semi-convective region with a chemical composition such that the Schwarzschild criterion is fulfilled everywhere. However, the end result is very sensitive to the ability of overshooting to produce mixing and Gabriel’s estimate was very likely overoptimistic. Later on, he made a less optimistic estimate and reached the same conclusion (Gabriel 1995). However, only numerical simulations of such situations seem able to provide a reliable answer. This has not yet been done.
However, we want to call attention to a point that is nearly always ignored: it is obvious that the occurrence of semi-convective regions in stellar models is directly related to the dependence of the opacity not only on the pressure and the temperature, but also on the chemical composition. Therefore this latter dependence must be taken into account in numerical simulations and in theoretical studies to be directly applicable to stellar models.
Figure 4 also shows that ∇Ldx is very different in the two panels. This means that the Brunt-Väisälä frequencies in the two models will significantly differ with all the consequences this may have for non-radial oscillations studies.
5.1.2. The convective core grows during MS
The problem is still worse when the convective core mass increases with time because most codes use the core mass of the last computed model as a starting estimate for the new one. As a result the algorithm will always provide a trial value of the core mass that is too small and it will quickly be unable to increase it up to its correct value. As soon as the discontinuity of y becomes large enough to meet case 3 (Fig. 2, left panel) at the first iteration, the boundary will stick to the initial estimate, making it impossible to obtain any further significant increase of the core mass.
At the beginning of the MS phases and whatever the stellar mass, the convective core mass increases up to its maximum extent. In stars massive enough, however, this maximum is reached very quickly before a significant change in μ (and so a discontinuity of y) can build up and the maximum extent of the core is very close to the correct one (see Fig. 3).
 |
Fig. 5 Hydrogen profile as a function of time in a 1.5 M⊙ star correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel). The model displayed in Fig. 6 is drawn in solid line. |
In low mass stars with a small convective core the situation is very different from that encountered in more massive ones since the convective core mass increases much more slowly. At the same time a μ-discontinuity builds up at the base of the radiative layers and a μ-gradient, resulting from nuclear reactions outside the convective core, slowly forms. Moreover, when the Ledoux criterion is used with the procedure discussed in Sect. 4 to fix the location of the convective core boundary, ∇Ldx − ∇ad soon becomes large enough to meet case 3 (Fig. 2). This prevents any further growth of the convective core mass long before it reaches its correct maximum value. Later on it goes on shrinking and rapidly vanishes.
This situation is illustrated in Figs. 5 and 6 for a 1.5 M⊙ star correctly computed through extrapolation from the convective core (left panels) and computed with the procedure discussed in Sect. 4 (right panels). Both evolutionary sequences were computed with the Ledoux criterion. The extent of the convective core (shown by the extent of the mixed region) is very different; the core even rapidly becomes very small when its boundary is incorrectly determined (also see, e.g., the results obtained by Silva Aguirre et al. 2011; Paxton et al. 2013, Fig. 13). It may also remain stuck at a maximum value reached before a significant μ-discontinuity has time to develop, although with ∇R> ∇ad at the convective boundary (as in the CESAM code, Y. Lebreton, priv. comm.).
From Fig. 6 showing the hydrogen profile (long dashed line), the radiative (solid line), adiabatic (dashed line), and Ledoux (dotted line) temperature gradients for the model drawn in full line in Fig. 5, it is obvious that the convective core boundary is incorrect in the right panel since ∇R is significantly larger than ∇ad at the boundary. The same problem shows up in Silva Aguirre et al. (2011, Fig. 1). As in more massive stars, discussed above with relation 15, the Ledoux gradient is very different in the radiative shell just above the core.
 |
Fig. 6 Hydrogen profile (long dashed line), radiative (solid line), adiabatic (dashed line) and Ledoux (dotted line) temperature gradients for the MS model of 1.5 M⊙ displayed in full line in Fig. 5, correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel), using in both cases the Ledoux criterion. |
We note that in these stars the opacity is larger just outside the core than just inside it because of the discontinuity of chemical composition. This does not affect our analysis since these models were computed with the Ledoux criterion and the stabilizing influence of the μ-gradient is much greater than the destabilizing one caused by the opacity increase. However, ∇ad< ∇R< ∇Ldx in some layers just above the convective core as can be seen in the left panel of Fig. 6 (they correspond to the layers between points A and B in the right panel of Fig. 1). Again this region is more extended in the right panel because in that model ∇R is much larger than ∇ad at the surface of the convective core. They are often considered as semi-convective and they disappear in the correct models when the convective core starts shrinking.
The same problem is encountered at the bottom of a red giant convective envelope as soon as a μ-discontinuity is present at the boundary; an incorrect use of the Ledoux criterion will quickly stop any further downwards extension of the envelope.
In low mass stars computed with the Schwarzschild criterion, we are in the situation considered in the right panel in Fig. 1. This is the only situation we know of where the Schwarzschild criterion leads to a positive discontinuity of y. With the correct method the core boundary is located at point A. A discontinuity of y is present at that point and the solution jumps from the lower curve to the upper one. As a result the model seems inconsistent since y> 0 in a non negligible region above point A extending up to point B. However, it is meaningless to check the stability with the Schwarzschild criterion there since a μ-gradient is present in that radiative region and is large enough to give ∇ad< ∇R< ∇Ldx.
If the core boundary is placed at the point where y = 0 in the radiative envelope, then it will be found at point B. The discontinuity of y is there and again, since it is positive, the solution jumps from the lower curve to the upper one when moving outwards. If the consistency of that model is checked it will be found to be inconsistent since y< 0 in the upper layers of the convective core and, since the core is chemically homogeneous, there is really a problem with such a model. This is the method followed in the ASTEC code (Christensen-Dalsgaard 2008). The layers between point A and B, although convectively stable are mixed with the convective core.
We now explore what happens when the method discussed in Sect. 4 is used. First, we assume that the initial core mass is larger than mB (right panel in Fig. 1, case 2). After the first iteration y changes sign in the convective core (close to point A) where it is continuous. The core boundary is now put close to its correct value for the second iteration. However, an interpolation never gives the perfect solution and, more importantly, during stellar model computations we are dealing with approximate solutions of the equations and not with relaxed models. As a result, the mass of the convective core obtained for the second iteration will turn out to be either too small or too large at the end of that iteration. If it is too large, there is at least one point in the core with y< 0 and we switch to case 4 (see below). It is nevertheless possible to find a new core mass close to point A for the next iteration and there is a chance that it leads to a relaxed model. However, that model has a convective shell. On the contrary, if it is too small, then y> 0 at the surface of the core, we are now in case 3 discussed below. As a result, at the third iteration, the core boundary will be moved close to point B.
In case 3, the initial core mass is smaller than mA. Then after the first iteration y changes sign close to point B and much too large a core mass is used for the second iteration, but again, since convergence will generally not be obtained at the end of the second iteration, what follows depends on the sign of y at the surface of the convective core. If y> 0 at the end of that iteration, we switch to case 4. It is nevertheless possible to find a new core mass close to point B for the next iteration and there is a chance that it leads to a converged model, but if y< 0 we are back to case 2 (discussed above) and at the next iteration the core boundary will be moved close to point A. We see that in both cases 2 and 3 the core boundary may oscillate between points A and B until, by chance, a converged model is found. Unfortunately, the final core mass could be close to either point A or B.
In case 4 the assumed core boundary is between points A and B. The function y changes sign three times in the initial estimated model. In the first iteration step, the model has a convective core which has about the right mass (close to point A), then a radiative shell followed by a convective one, and finally a radiative envelope. What follows after the end of that iteration depends again on the sign of y at the last point in the convective core. If y< 0, we remain in case 4 with about the same core mass and the model has a chance to converge (but it has an extended convective shell). If y> 0, we are back to case 3 and the core boundary will be moved close to point B at the next iteration (see above). Again, the core mass will oscillate between points A and B until by chance (or because of some trick used in the code) a converged model is found.
However, some codes choose to ignore convective shells. Then in case 4, what happens depends on the way the code searches for the zero of y, either starting from the center outwards or starting from the surface inwards. In the first hypothesis a core boundary close to point A will be found for the first iteration; with the second one it will be close to point B. With both methods, what happens next depends upon the sign of y at the core boundary after the next iteration and the same kind of discussion as above can be made. The final result will again be a model with a core boundary found by chance close to either point A or point B (Montalbán et al. 2007, Fig. 7).
 |
Fig. 7 Helium profile as a function of time in a core helium burning 8 M⊙ star correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel). The model displayed in Fig. 8 is drawn in solid line. |
 |
Fig. 8 Helium profile (dotted line), radiative (full line) and adiabatic (dashed line) temperature gradients for the core He-burning model of 8 M⊙ displayed in solid line in Fig. 7, correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel). |
The method used in ASTEC (see above; Christensen-Dalsgaard 2008), although leading to inconsistent models, prevents such oscillations of the convective core boundary. It leads to a convective core mass equal to the external envelope of the oscillating core mass just discussed here above (see the ASTEC curve in Fig. 9 in Lebreton et al. 2008).
5.2. Core helium burning
The convective core also expands during a large fraction of core He burning leading to a μ-discontinuity but not to a μ-gradient. Again, if the same core mass as in the previous model is taken as the initial estimate, the algorithm will quickly predict a core mass that is too small. As the discontinuity of y increases progressively with time, it will become large enough to meet case 3 at the first iteration. It will then be impossible to significantly increase the core mass any further (see, e.g., Fig. 15 in Paxton et al. 2013).
This is illustrated in Fig. 7 which shows the helium profile as a function of time in a 8 M⊙ core helium burning star computed with a correct location of the convective core (left panel) and with the method discussed in Sect. 4 (right panel). The extent of the convective core is significantly larger when a correct positioning is adopted. Figure 8 shows the mass distribution of helium, and of the radiative and adiabatic temperature gradients in the model drawn in solid line in Fig. 7. One can clearly see in the right panel that y> 0 or ∇R> ∇ad at the convective side of the core boundary, which means LR<L(r) and LC> 0. This is the problem encountered by Castellani et al. (1971b).
To summarize, the algorithm discussed here above may in some situations lead to solutions close to the right one, but in many others to completely incorrect ones.
6. Double mesh point at convective boundaries
The best way to deal more easily with the special properties of a convective zone boundary is to systematically introduce a double mesh point at each boundary. A discontinuity in chemical composition always leads to a discontinuity in density. If only one mesh point is present at such a discontinuity, the chemical composition and the density may not be clearly specified. Two mesh points, each with the same mass but with the chemical composition and density of each sides of the discontinuity, removes the ambiguity. Since the discontinuous variables appear in different places of the system of differential equations, their values must be properly known in order to correctly write the set of difference equations in the layers just above and just below the discontinuity. This is easily done when a double mesh point is introduced at the discontinuity.
A single mesh point or even an enlarged density of mesh points over some interval is unable to correctly stand for a discontinuity. For instance, the discontinuity in density is then replaced by a very steep μ-gradient in the shell adjacent to the convective zone. This leads in that shell to a stable stratification according to the Ledoux criterion while, when the discontinuity is properly taken care of, that term is much smaller. For instance, during the central helium burning phases there is practically no μ-gradient above the expanding convection core as it grows in practically pure helium layers. This is what is correctly found when a double mesh point is introduced at the surface of the core since there is no significant μ-gradient term in the Ledoux criterion above the core, while without a double mesh point there is a large μ-gradient in just the one shell that is on top of the convection core. As a result, the Ledoux criterion predicts a much stronger stability just in that shell with the consequence that the convection core quickly starts shrinking and finally disappears. This explains the difference in core mass found by Paxton et al. (2013) in their Fig. 15 when the Schwarzschild or the Ledoux criterion is used during core helium burning.
Moreover, as stars evolve, the displacement of these boundaries may in some cases leave behind a discontinuity in a radiative zone. This occurs for instance during the red giant phase after the first dredge-up. When the discontinuity is located in a radiative zone, a double mesh point is even more important, not only for the reason given above, but mainly to avoid destroying the discontinuity. Without a double mesh point the discontinuity is progressively smoothed out by the addition and retrieval of mesh points in a sort of numerical diffusion. This may completely change the chemical composition profile in an undue way indeed.
Even when the chemical composition is continuous at the boundary of a convective zone, a double mesh point is useful when there is a μ-gradient in the adjacent radiative layers since this μ-gradient is discontinuous at the convective zone boundary and therefore also the density gradient, as well as the Brunt-Väisälä frequency which is used for non-radial oscillations studies.
To our knowledge, the code developed by L. Henyey and his group is the only one to have introduced double mesh points in all the situations considered in this section. When there is a discontinuity in the chemical composition, the CESAM code developed by Morel also introduces a double mesh point at the boundary of a convective zone.
7. Problems raised when a convective shell sets in
We assume that in some parts of a region with a gradient in chemical composition, supposedly in radiative equilibrium, the Ledoux criterion predicts instability. These layers become convective and should be mixed. The problem is now to find the position of the boundaries which both verify the condition ∇R = ∇ad on the convective side. The end result will be a convective shell which has different boundaries than those initially found. This may not be an easy task for the code to find a solution, but assuming that such a solution does exist, it is still necessary to check its consistency.
 |
Fig. 9 Modification of the X profile when a convective shell AB sets in. |
At points A and B in Fig. 9, on the radiative side of
the discontinuity, we have 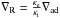 . In most cases
. In most cases
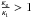 at one of the two boundaries.
For a coherent model to be found, the Ledoux criterion must predict stability on the
radiative sides of the discontinuities. Therefore, at one of the two boundaries the
temperature gradient is in between the Schwarzschild and Ledoux critical values. It is well
known that a semi-convection zone may develop in such a situation. It will not necessarily
be so, but the question needs to be studied each time it is encountered.
at one of the two boundaries.
For a coherent model to be found, the Ledoux criterion must predict stability on the
radiative sides of the discontinuities. Therefore, at one of the two boundaries the
temperature gradient is in between the Schwarzschild and Ledoux critical values. It is well
known that a semi-convection zone may develop in such a situation. It will not necessarily
be so, but the question needs to be studied each time it is encountered.
What is worse, however, is that it is not clear wether a static solution exists. In other
words, it might be impossible to fulfill the condition ∇R = ∇ad at both
boundaries of the convective shell. Inside a convection zone we have
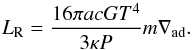 (16)Taking the
derivative, we end up with
(16)Taking the
derivative, we end up with ![\begin{equation} \frac{{\rm d}\ln \frac{L_{\rm R}}{L}}{{\rm d}\ln r} = U + \left [1 + \frac{\partial \ln \frac{\kappa}{\nabla_{\rm ad}}}{\partial \ln P} + \left ( \frac{\partial \ln \frac{\kappa}{\nabla_{\rm ad}}}{\partial \ln T} -4 \right ) \nabla_{\rm ad} \right ] V - \frac{{\rm d} \ln L}{{\rm d} \ln r}, \label{UV} \end{equation}](/articles/aa/full_html/2014/09/aa23442-14/aa23442-14-eq141.png) (17)where
U stands for
(
(17)where
U stands for
(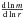 )
and V for (
)
and V for (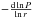 ).
The curve along which
).
The curve along which 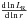 is equal to 0, assuming that the total luminosity is constant, is illustrated by the dotted
curve in Fig. 10. In most cases the derivatives of the
opacity, as well as of the adiabatic gradient and the luminosity, will change only slightly
over the extent of the shell.
is equal to 0, assuming that the total luminosity is constant, is illustrated by the dotted
curve in Fig. 10. In most cases the derivatives of the
opacity, as well as of the adiabatic gradient and the luminosity, will change only slightly
over the extent of the shell.
 |
Fig. 10 Schematic solutions for a convective core, a convective envelope, and a convective shell in the (U,V) plane. |
It is easily seen that 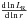 is positive below that curve and of course negative above it.
is positive below that curve and of course negative above it.
We will now consider the very often encountered case of a convective core large enough so
that there are no nuclear reactions in the vicinity of its surface. It is necessary that its
surface be reached when the solution is still below the critical line since if
LR<L
when its maximum value is reached, the condition LR = L will never be
fulfilled at its surface. In a convective envelope while progressing inwards,
LR
increases as long as the solution is above the critical line since there
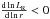 and its bottom must be reached
before the envelope solution crosses that critical line.
and its bottom must be reached
before the envelope solution crosses that critical line.
For a convective shell without nuclear reactions, its inner boundary must be above the critical line and its outer one below it, in order that the condition LR = L be fulfilled at both boundaries. At the bottom (j1) LR = L, then LR decreases until the critical curve is reached and afterwards it starts increasing to eventually reach LR = L at the top (j2). This requires a very special position of the shell and there is a priori no reason that any shell can satisfy this condition. In most cases LR will indeed be a monotonic function of the position within a convective shell.
There are, however, two cases where boundaries for a convective shell should be found
without any problem. The first one is when the convection zone is caused by an opacity bump,
related for instance to the ionization of a chemical element. The derivatives of the opacity
drastically change throughout that region and it is possible to have
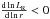 at the bottom and
>0 at the top. The second one is when the convection zone appears within
a shell where nuclear reactions significantly increase the luminosity. Then the term
at the bottom and
>0 at the top. The second one is when the convection zone appears within
a shell where nuclear reactions significantly increase the luminosity. Then the term
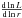 that we have neglected in our discussion becomes important and strongly varies with the
position in the shell.
that we have neglected in our discussion becomes important and strongly varies with the
position in the shell.
What happens when a static solution cannot be found? The convective velocity is then positive at one boundary of the shell and overshooting must take place, bringing in material with a different chemical composition. The result is a change in the chemical composition of the shell, which will move. This might be a way to produce a semi-convective zone, the same mechanism as that proposed by Gabriel (1970) for massive main sequence stars. However, the difficult and yet unsolved question is how to compute the speed of this shell motion.
8. A few remarks concerning overshooting
First, it must be realized that there are two kinds of overshooting problems. The first one is encountered when convective motions penetrate stable layers with the same chemical composition. In this situation, convective material is progressively slowed down and is eventually thermalized. It then has the same density as the surrounding material so that it has no natural tendency to move backwards. It also applies to a shrinking convective core provided that the mass on top of the overshooting zone also decreases and does not itself become convectively unstable. These problems have been discussed theoretically, but there are still too few numerical simulations and situations studied with the moment theory to allow us to find a rule to specify the depth of the overshooting (undershooting) layers and the run of the temperature gradient (see, e.g., Kupka & Montgomery 2002; Kupka et al. 2009; Montgomery & Kupka 2004; Zhang & Li 2012a,b; Zhang 2013 and, for numerical simulations, Freytag 1996; Freytag & Steffen 2004; Kochukhov et al. 2007; Rogers et al. 2006; Tian et al. 2009; Viallet et al. 2013).
When it is possible to use better theories, the usual boundary condition (8) becomes meaningless and the more fundamental condition (7), or its equivalent Vr = 0, has to be used. Of course they do not apply outside convective zones, but at the moment we can only introduce an overshooting (undershooting) region of arbitrary thickness, do, above (below) the point where ∇R = ∇ad. This point is now located in a chemically homogeneous region. It follows that ∇Ldx = ∇ad there and that the function y = ∇R − ∇ad has of course no discontinuity. As a result, the methods considered in Sects. 2 and 4 give the same result and there is no longer a problem. However, we have to realize that limdo → 0MC(XC,do) is equal to the function MC(XC) obtained with the exact method of Sect. 2 and not with that given by Sects. 3 and 4. As a result, when it comes to discussing the influence of overshooting on some observables, the methods discussed in Sects. 3 and 4 offer an incorrect zero point.
The second kind of overshooting problem occurs when material overshoots in layers with a different chemical composition. This occurs for instance when the core expands or also during the first dredge-up if undershooting occurs at the bottom of the convective envelope. Here we will discuss the problem for a convective core. Then in the overshooting layers, the raising material is immediately significantly heavier than its surrounding and it is quickly slowed down by buoyancy forces. Moreover, even if it advects some surrounding material, its molecular weight remains larger than that of the surrounding. Therefore, when it stops moving upwards, it comes naturally back downwards even if it manages to reach the same temperature as the surrounding material. We therefore expect a much smaller overshooting than when there is neither a gradient nor a discontinuity in molecular weight. Indeed Canuto (1998, 1999b) demonstrated that the extent of overshooting is smaller when it takes place in a region with a gradient in molecular weight. However, the author does not specify the amount of that decrease. Those who have to compute stellar models have thus two possible choices: either they solve the system of equations given by Canuto (unfortunately nobody does that), or they choose the value of the overshooting extent (the way out always adopted).
9. Conclusions
Following a growing uneasiness among stellar modelers as to what should be the correct implementation of a reliable algorithm to fix the boundaries of convection zones in stars, we have attempted to discuss and clarify some related important points. First, we have noted the physical aspects of a convective zone and its boundaries and we have given the only correct way to find them. While Eq. (7) must be satisfied by any theory, it reduces to LR = L or to ∇R = ∇ad (see Eq. (8)) in the frame of the LMLT. All these conditions must be verified on the convective side of the boundary. We have then shown that there are two possible ways of misusing the convective zone boundary condition and we have discussed the consequences for models computation. Our main conclusions are the following.
-
1.
The neutrality condition LR = L, or ∇R = ∇ad when LMLT is used, must be applied on the convective side of a boundary and during the iteration process the improvement of a boundary location must imperatively be done through extrapolations or interpolations from points in the convective zone only in order to find the point for which LR = L. This result obtained in Sect. 2 stands on a very firm basis and can hardly be put into question. It allows a very simple test to anyone computing stellar models: either L − LR or ∇R − ∇ad can be plotted throughout the models; if this does not cancel out at each boundary of convective zones (within the accuracy required for converged models), then there is a problem with the algorithm used to locate them.
-
2.
The neutrality condition which can then be chosen either as y = ∇R − ∇Ldx = 0 or y = ∇R − ∇ad = 0 should never be applied on the radiative side when the checked variable is discontinuous at the boundary. More precisely, during the iteration process the improvement of a boundary location should not be done through extrapolations or interpolations from points in the radiative zone in order to find the point for which either ∇R − ∇Ldx = 0 or ∇R − ∇ad = 0 (see Sect. 3).
-
3.
When the convective boundary is searched for through a change of sign of y (y = ∇R − ∇Ldx or y = ∇R − ∇ad) (see Sect. 4), we have more explicitly discussed the situation for a convective core. Two cases have to be considered separately:
-
(a)
At the core boundary y is larger on the convective side than on the radiative side of the discontinuity. Two possibilities arise at each step of the iteration process. If the estimated convective core is too small the algorithm will generally predict an incorrect boundary. If it is too large, its extent will be correct provided the estimated core mass always remains too large, but it will be underestimated if during the iterations an oscillation in the core mass around the correct value occurs.
-
(b)
At the core boundary y is smaller on the convective side than on the radiative side of the discontinuity. Then the position of the core boundary may, just by chance, be either close to the correct value or much larger.
-
(a)
-
4.
The best way to avoid inconsistencies in the definition of variables appearing at a convective boundary is to add a double mesh point at the exact location of the boundary with the neutrality condition satisfied on the convective side of the double mesh point. If there is a discontinuity in the chemical composition at the convection zone boundary, then the inner mesh point will have the same chemical composition as the convective zone and the upper mesh point that of the outer radiative region (see Sect. 6).
-
5.
Since the location of convective boundaries must be found from extrapolations from inside a convective zone (see points 1 and 2), the Ledoux criterion is only required to check the appearance of a convective layer in an otherwise radiative zone located in a μ-gradient region.
-
6.
If such a convective shell appears, it could be impossible to locate its boundaries in such a way that the neutrality condition is satisfied on the convective side of each of them and then it is possible that a semi-convective layer forms just above (or below) its upper (lower) boundary (see Sect. 7).
-
7.
The correct application of the problems addressed in this paper is an essential prerequisite to any attempts to introduce more sophisticated physics, and to any attempts or claims of testing stellar model/physics using observations, of which seismology is presently the most promising, but not the only one.
In 1968, while MG was in Berkeley on a postdoctoral position, Henyey gave us his code. Of course we made it evolve with time, but we always kept its main characteristics, i.e., the same variables, the same way of handling convective zone boundaries, and the introduction of double mesh points. We used it until 1999.
Acknowledgments
The authors wish to especially thank Pierre Morel for long and interesting discussions which helped improve significantly several of the arguments presented in this paper. They are also grateful to Richard Scuflaire and Marc-Antoine Dupret for their careful rereading of the manuscript and for their pertinent remarks. Many thanks to Yveline Lebreton who computed for us some MS low mass star models with CESAM.
References
- Biermann, L. 1932, Z. Astrophys., 5, 117 [NASA ADS] [Google Scholar]
- Canuto, V. M. 1998, ApJ, 508, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M. 1999a, ApJ, 518, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M. 1999b, ApJ, 524, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M. 2000, ApJ, 534, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M. 2011a, A&A, 528, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canuto, V. M. 2011b, A&A, 528, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canuto, V. M. 2011c, A&A, 528, A79 [Google Scholar]
- Canuto, V. M. 2011d, A&A, 528, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castellani, V., Giannone, P., & Renzini, A. 1971a, Ap&SS, 10, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, V., Giannone, P., & Renzini, A. 1971b, Ap&SS, 10, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2008, Ap&SS, 316, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Deng, L., Bressan, A., & Chiosi, C. 1996, A&A, 313, 145 [NASA ADS] [Google Scholar]
- Freytag, B. 1996, in M.A.S.S., Model Atmospheres and Spectrum Synthesis, eds. S. J. Adelman, F. Kupka, & W. W. Weiss, ASP Conf. Ser., 108, 93 [Google Scholar]
- Freytag, B., & Steffen, M. 2004, in The A-Star Puzzle, eds. J. Zverko, J. Ziznovsky, S. J. Adelman, & W. W. Weiss, IAU Symp., 224, 139 [Google Scholar]
- Gabriel, M. 1970, A&A, 6, 124 [NASA ADS] [Google Scholar]
- Gabriel, M. 1995, in Liège International Astrophysical Colloquia, 32, 95 [Google Scholar]
- Gabriel, M. 1996, Bull. Astron. Soc. India, 24, 233 [Google Scholar]
- Grigahcene, A., Dupret, M. A., Garrido, R., Gabriel, M., & Scuflaire, R. 2004, Commun. Asteroseismol., 145, 10 [Google Scholar]
- Henyey, L. G., Lelevier, R., & Levée, R. D. 1955a, PASP, 67, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Henyey, L. G., Lelevier, R., & Levée, R. D. 1955b, PASP, 67, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Henyey, L. G., Forbes, J. E., & Gould, N. L. 1964, ApJ, 139, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Kochukhov, O., Freytag, B., Piskunov, N., & Steffen, M. 2007, in IAU Symp. 239, eds. F. Kupka, I. Roxburgh, & K. L. Chan, 68 [Google Scholar]
- Kupka, F., & Montgomery, M. H. 2002, MNRAS, 330, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Ballot, J., & Muthsam, H. J. 2009, Commun. Asteroseismol, 160, 30 [Google Scholar]
- Kushwaha, R. S. 1957, ApJ, 125, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Lebreton, Y., Montalbán, J., Christensen-Dalsgaard, J., Roxburgh, I. W., & Weiss, A. 2008, Ap&SS, 316, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, P. 1947, ApJ, 105, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, P., & Walraven, T. 1958, Handbuch der Physik, 51, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Montalbán, J., Théado, S., & Lebreton, Y. 2007, in EAS Pub. Ser. 26, eds. C. W. Straka, Y. Lebreton, & M. J. P. F. G. Monteiro, 167 [Google Scholar]
- Montgomery, M. H., & Kupka, F. 2004, MNRAS, 350, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Oke, J. B., & Schwarzschild, M. 1952, ApJ, 116, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, T. M., Glatzmaier, G. A., & Jones, C. A. 2006, ApJ, 653, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W. 1978, A&A, 65, 281 [NASA ADS] [Google Scholar]
- Schwarzschild, M. 1958, Structure and evolution of the stars (Princeton University Press) [Google Scholar]
- Schwarzschild, M., & Härm, R. 1958, ApJ, 128, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Ap&SS, 316, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Silva Aguirre, V., Ballot, J., Serenelli, A. M., & Weiss, A. 2011, A&A, 529, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tayler, R. J. 1954, ApJ, 120, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Tayler, R. J. 1956, MNRAS, 116, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, C.-L., Deng, L.-C., & Chan, K.-L. 2009, MNRAS, 398, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Zeppieri, A., Mazzitelli, I., & D’Antona, F. 1998, A&A, 334, 953 [NASA ADS] [Google Scholar]
- Viallet, M., Meakin, C., Arnett, D., & Mocák, M. 2013, ApJ, 769, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Xiong, D. 1981, Scientia Sinica, 24, 1406 [Google Scholar]
- Xiong, D. R. 1985, A&A, 150, 133 [NASA ADS] [Google Scholar]
- Xiong, D.-R. 1986, A&A, 167, 239 [NASA ADS] [Google Scholar]
- Xiong, D.-R. 1989, A&A, 209, 126 [NASA ADS] [Google Scholar]
- Xiong, D. R., Cheng, Q. L., & Deng, L. 1997, ApJS, 108, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Xiong, D. R., Cheng, Q. L., & Deng, L. 1998a, ApJ, 500, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Xiong, D. R., Deng, L., & Cheng, Q. L. 1998b, ApJ, 499, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Xiong, D. R., Cheng, Q. L., & Deng, L. 2000, MNRAS, 319, 1079 [CrossRef] [Google Scholar]
- Zhang, Q. S. 2013, ApJS, 205, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q. S., & Li, Y. 2012a, ApJ, 746, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q. S., & Li, Y. 2012b, ApJ, 750, 11 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Left (right) panel: y is smaller (larger) on the radiative side of the convective core boundary. Cases 1 to 4 stand for different situations. Case 1 illustrates two possible ways of fixing the core boundary. Cases 2 to 4 show the different solutions found when the algorithm searches for a change of sign of y in the trial model. |
| In the text | |
 |
Fig. 2 Left panel: illustration of a situation such that the assumed core mass of a model (not necessarily converged) is too small. In the right panel the assumed core mass is too large. The solid lines represent y in the model while the dashed ones are extrapolations. Case 1 stands for a model without discontinuity at the core boundary when the Schwarzschild criterion is used. Case 2 represents situations such that y has a small discontinuity. Case 3 stands for a larger discontinuity. |
| In the text | |
 |
Fig. 3 Hydrogen profile as a function of time in a 16 M⊙ star with a convective core boundary correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel).The model displayed in Fig. 4 is drawn in solid line. |
| In the text | |
 |
Fig. 4 Hydrogen profile (long dashed line), radiative (solid line), adiabatic (dashed line) and Ledoux (dotted line) temperature gradients for the MS model of 16 M⊙ displayed in solid line in Fig. 3, correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel), using in both cases the Ledoux criterion. |
| In the text | |
 |
Fig. 5 Hydrogen profile as a function of time in a 1.5 M⊙ star correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel). The model displayed in Fig. 6 is drawn in solid line. |
| In the text | |
 |
Fig. 6 Hydrogen profile (long dashed line), radiative (solid line), adiabatic (dashed line) and Ledoux (dotted line) temperature gradients for the MS model of 1.5 M⊙ displayed in full line in Fig. 5, correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel), using in both cases the Ledoux criterion. |
| In the text | |
 |
Fig. 7 Helium profile as a function of time in a core helium burning 8 M⊙ star correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel). The model displayed in Fig. 8 is drawn in solid line. |
| In the text | |
 |
Fig. 8 Helium profile (dotted line), radiative (full line) and adiabatic (dashed line) temperature gradients for the core He-burning model of 8 M⊙ displayed in solid line in Fig. 7, correctly computed (left panel) and computed with the method discussed in Sect. 4 (right panel). |
| In the text | |
 |
Fig. 9 Modification of the X profile when a convective shell AB sets in. |
| In the text | |
 |
Fig. 10 Schematic solutions for a convective core, a convective envelope, and a convective shell in the (U,V) plane. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


