| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | L11 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201424439 | |
| Published online | 21 August 2014 | |
The Centaur 10199 Chariklo: investigation into rotational period, absolute magnitude, and cometary activity⋆
1 LESIA, Observatoire de Paris, CNRS, UPMC Univ. Paris 06, Univ. Paris-Diderot, 5 place J. Janssen, 92195 Meudon Cedex, France
e-mail: sonia.fornasier@obspm.fr
2 Univ. Paris Diderot, Sorbonne Paris Cité, 4 rue Elsa Morante, 75205 Paris Cedex 13, France
3 Observatório Nacional, COAA, rua Gal. José Cristino 77, 20921-400 Rio de Janeiro, Brazil
4 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig Weg 3, 37077 Göttingen, Germany
5 INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
6 Qatar Environment and Energy Research Institute, Qatar Foundation, Tornado Tower, Floor 19, PO Box 5825, Doha, Qatar
Received: 20 June 2014
Accepted: 13 July 2014
Context. Rings have recently been discovered around the Centaur 10199 Chariklo.
Aims. In this paper we present new photometric data, obtained at the 4.2 m SOAR Telescope, aiming to investigate Chariklo’s absolute magnitude and rotational period, which is still unknown, and to look for potential cometary activity.
Methods. The field background of the images was very crowded so several approaches were used for the extraction of Chariklo fluxes. The background sources were subtracted using difference image analysis and then aperture photometry was applied. A Fourier polynomial fit was used to determine the period.
Results. We find a synodic rotation period of 7.004±0.036 h. The visual absolute magnitude derived from the SOAR data is Hv = 7.03 ± 0.10. We model the rings’ contribution to the flux, and find that the derived Hv is consistent with the predicted ring system aspect angle. We also revised the Chariklo system albedo (4.2%) and effective radius (119 ± 5 km) from a re-analysis of Herschel and WISE thermal data obtained during 2010 with the correct Hv value. No coma is detected from the SOAR data, nor in previous VLT images acquired in 2007−2008, where the rings’ aspect angle was close to zero. The upper limit to the dust production rate is 2.5 kg/s.
Key words: Kuiper belt objects: individual: 10199 Chariklo / methods: observational / techniques: photometric
Figure 3 is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Centaurs are one of the most primordial populations in the solar system, and their study helps in constraining the composition of the primordial nebula and its thermal and dynamical evolution. Two rings were recently discovered around the largest Centaur, 10199 Chariklo (1997 CU26, Table 1) from stellar occultation observations (Braga-Ribas et al. 2014).
Chariklo shows a strong variation (0.8 mag) of the absolute magnitude value Hv over time and within a relatively small heliocentric distance range, from 13.8 AU to the perihelion distance of 13.1 AU (McBride et al. 1999; Jewitt & Luu 2001; Tegler & Romanishin 1998; Peixinho et al. 2001; Bauer et al. 2003; Dotto et al. 2003; DeMeo et al. 2009; Guilbert et al. 2009; Belskaya et al. 2010). Before the discovery of the ring system, these brightness variations were attributed to unexplained cometary activity variations during the orbit or to spin axis orientation effects, with possibly pole-on geometry in the 1999−2000 period, and an equatorial view in the 2007−2010 timeframe (Belskaya et al. 2010; Fornasier et al. 2013). Chariklo interestingly also shows spectral variability over time: deep absorption bands (up to 20% depth) due to amorphous water ice were detected just after its discovery in 1999−2000 (Brown & Koresko 1998; Dotto et al. 2003), but had completely disappeared in the spectra acquired during 2007−2008 (Guilbert et al. 2009). Its visible spectrum is mostly featureless (Barucci et al. 1999; Guilbert et al. 2009; Fornasier et al. 2009), although Alvarez-Candal et al. (2008) found a shallow band centred at 0.7 μm that might be due to aqueous alteration. Both brightness variations and spectral variability may be satisfactorily explained by the different aspects of the bright ring system over time.
Until now, Chariklo’s rotational period was unknown. The only rotational period estimation available was obtained by Peixinho et al. (2001), who found that the period should be long (15 h or 34 h), and that Chariklo’s absolute magnitude shows evidence of variations over a few months. In 2010 Chariklo was observed from the Herschel space observatory within the programme “TNOs are Cool: A survey of the trans-Neptunian region”. The Herschel observations were coupled with the Spitzer-MIPS and WISE ones and modelled with both near-Earth asteroid thermal model (NEATM) and thermophysical models. The derived diameter is 248±18 km (Fornasier et al. 2013), confirming that Chariklo is the largest Centaur, with a dark surface (albedo of 3.5±1.0% assuming Hv = 7.4 ± 0.2 at the time of the Herschel observations). The thermophysical model tested different spin-vector orientations, and it indicated that Chariklo was seen close to the equator-on viewing geometry during the Herschel observations in August 2010, with an estimated spin vector latitude of 66.6±30.0°. The equatorial viewing geometry in 2010 is in agreement with the rings’ aspect angle during these observations (~14°), assuming that the rings are in Chariklo’s equatorial plane.
The interpretation of these infrared data is nevertheless limited by the fact that Chariklo’s rotational period and spin axis were not known at that time. In that context, we asked for observing time at the SOAR Telescope – aiming to constrain Chariklo’s rotational period, and test if a faint coma is present at these large distances (14 AU). In this paper we present the results of this observing run, performed in June 2013, before the discovery of the ring system.
Orbital and physical characteristics of 10199 Chariklo.
2. Observations and data reduction
The observations were carried out during 10, 11, and 12 June 2013 at the SOAR Telescope (Cerro Pachón, Chile). We used the SOAR Optical Imager (SOI), whose detector is a mosaic of two E2V CCD-44-82, in a 1×1 binning providing a pixel scale of 0.0767 arcsec/pixel. Integration times varied from 20 s up to 40 s. Most of the observations were taken in the R filter (Kron-Cousin system). The last night of observations was photometric and standard stars from Landolt fields (Landolt 1992) were observed to obtain zero points, as well as extinction coefficients. Observations in the B and V filters were carried out on the nights of 10 and 11 June, that were not as good in terms of sky transparency and finally not photometric, so not useful for deriving Chariklo’s colours.
During these observations Chariklo appeared against a crowded stellar background, so conventional aperture photometry was impossible in many of the frames. Data reduction was made using IRAF and IDL with three different approaches.
-
1.
Aperture correction using curve of growth, based on thetechnique proposed by Stetson (1990). We selected severalbright isolated stars and measured the instrumental magnitudesin several apertures to compute the correction. Nevertheless, theresults were not satisfactory because the field is very crowded andthe seeing variable during the night, making the computedcorrection not as reliable as desired.
-
2.
Cleaning the stars in a circular area centred on Chariklo (radius = 100 pixels) using the CHEF mathematical bases (Jiménez-Teja & Benítez 2012) in order to successively perform traditional aperture photometry with the resulting models. A different basis is created for each star, according to its position and size, with no a priori assumption on the PSF. Then, the CHEF models are computed and removed from the original image. This approach was also not able to produce adequate results: some of the background stars were not identified as individual objects by SExtractor (Bertin & Arnouts 1996; Bertin 2011), thus remaining and contaminating the measurements.
-
3.
Subtraction of all background sources using difference image analysis (DIA). This method was the best at removing the background and the one finally used to derive Chariklo fluxes. The DIA analysis, developed primarily for variable star studies and used to search for microlensing signals in crowded galactic bulge fields, takes a single template image and then blurs it to match the seeing in each science image in a sequence. By subtracting the blurred template image from each image in the time-series, this efficiently removes all fixed and non-varying sources, revealing variable stars and moving objects. While this method has been a standard tool in stellar photometry for some years, its use in solar system observations has only recently been recognised (Snodgrass et al. 2013; Snodgrass & Bramich, in prep.). We used the DanDIA1 implementation of DIA (Bramich 2008) in IDL, which also provides basic reduction (bias subtraction, flat fielding) of the images. Although the data were taken at the native pixel scale of the SOI detector, they were binned 4×4 before processing to increase the signal-to-noise ratio (S/N) and the speed in computing the numerical convolution kernels. The DIA method returns difference images with all fixed sources removed, and also a list of photometric scale factors for each image (relative to the template). We then proceeded with aperture photometry on Chariklo in each image, using a circular aperture with radius equal to the FWHM of the seeing in each image, which gives the optimum S/N. Aperture corrections were applied to ensure that the total flux was included, scaling the flux within the narrow aperture using the PSF shape that is determined as part of the DanDIA process. The image-to-image scale factors from the subtraction process were then used to account for extinction variations between each frame, to give the final light curve. This was then calibrated on an absolute scale using the magnitudes of stars from the AAVSO Photometric All-Sky Survey (APASS) catalogue found in the reference frame.
3. Results
3.1. Rotational period
To compute Chariklo’s rotational period, we finally analysed 693 R images acquired on the 11 and 12 June 2013. Despite our efforts in data reduction, for the Chariklo images from 10 June the subtraction of the background sources was poor and the derived fluxes too variable, so we finally decided to discard these data in the analysis.
Chariklo was observed during nearly 9 h on the nights of 11 and 12 June and both datasets clearly show a complete double peaked light curve. These time-series were modelled with a 5th order Fourier polynomial (Harris et al. 1989), whose best-fit relation corresponded to a synodic rotation period (Psyn) of 7.004±0.036 h. The dispersion of the composite light curve and the error associated with the period are mostly due to the errors in the individual magnitudes, which are dominated by photon noise from the crowded background. The data folded with the best-fit period are shown in Fig. 1.
The light curve has asymmetric double peaks and an amplitude of 0.11 mag. It is reliably covered with data from the two nights, except around rotational phase 0.4−0.5. The estimated a/b ratio of the triaxial ellipsoid shape is >1.1, implying an elongation of at least 10%.
 |
Fig. 1 Composite light curve of 10199 Chariklo determined from the SOAR Telescope observations. The continuous line is the polynomial fit. |
3.2. Absolute magnitude and revised albedo
At the time of the observations Chariklo was at r = 14.548 AU, Δ = 13.580 AU, and α = 1.25 deg. The average reduced magnitude, measured on 12 June, is R(1, 1, α) = 6.622±0.077. Using a V − R colour index of 0.48 (Barucci et al. 2005) and a phase function of 0.06 mag/deg (Belskaya et al. 2010), we obtain an Hv value of 7.03±0.10. In Fig. 2 we report the Hv variation over time from the literature data (Belskaya et al. 2010), and from our measurement. To test if Hv variations are consistent with brightness variations associated with the changing aspect of the rings, we compute the ratio of the fluxes between the rings and Chariklo, 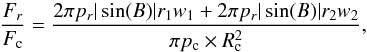 (1)where B is the aspect angle of the rings, r1 and r2 the radial distances of the rings to the main body, w1 and w2 their width, pr = 0.09 the visual albedo of the rings as determined by Braga-Ribas et al. (2014), and pc the Chariklo albedo.
(1)where B is the aspect angle of the rings, r1 and r2 the radial distances of the rings to the main body, w1 and w2 their width, pr = 0.09 the visual albedo of the rings as determined by Braga-Ribas et al. (2014), and pc the Chariklo albedo.
We then model the total absolute magnitude as 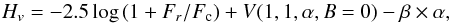 (2)where β is the phase coefficient (0.06 mag/deg), α the phase angle, and V(1, 1, α, B = 0) the absolute magnitude of Chariklo when the rings are not visible (B = 0). Figure 2 shows that the Hv model reproduces most of the observations, as is similary found also by Duffard et al. (2014). However, it must be noted that apparent surface area variations due to changing viewing geometry of the centaur may also contribute to the Hv variation over time.
(2)where β is the phase coefficient (0.06 mag/deg), α the phase angle, and V(1, 1, α, B = 0) the absolute magnitude of Chariklo when the rings are not visible (B = 0). Figure 2 shows that the Hv model reproduces most of the observations, as is similary found also by Duffard et al. (2014). However, it must be noted that apparent surface area variations due to changing viewing geometry of the centaur may also contribute to the Hv variation over time.
Fornasier et al. (2013) determined a value of 3.5±1.0% for Chariklo’s albedo, assuming Hv = 7.4 ± 0.25. Nevertheless, from Fig. 2 the Hv value must have been 7.2±0.1 during the Herschel observations. Considering this revised value of Hv, we ran the NEATM model on the Herschel-PACS and WISE data (see Tables 1−3 in Fornasier et al. 2013 for details on the observing conditions and flux values), that were both acquired during 2010 (6 months apart), so at similar rings’ aspects. During these observations the aspect angle of the rings was small, and their contribution to Chariklo’s thermal flux should be negligible. We find a radius of 119±5 km, an albedo of 4.2±0.5%, and a beaming factor η = 1.12 ± 0.14 during the 2010 observations. Uncertainties on the fitted parameters were obtained as described in Fornasier et al. (2013), using a Monte Carlo approach in which 1000 synthetic datasets were randomly generated using the uncertainties in the measured fluxes and in the Hv magnitude. The size determined via this method is very close to the one found directly during stellar occultation events (Req = 121 ± 1 km; Sicardy et al. 2014).
 |
Fig. 2 Absolute magnitude of 10199 Chariklo versus time. The heliocentric distance (in AU) is indicated at the top. The continuous line represents the predicted Chariklo absolute magnitude from Eq. (2), and the arrow indicates the date corresponding to the observations obtained with Herschel. |
4. Cometary activity investigation
We analyse the R images to look for cometary activity, which was proposed as one of the potential source of the rings (Braga-Ribas et al. 2014). In doing so, we stack together some images where Chariklo was far enough from background stars and we applied the ∑ Af function (Tozzi et al. 2007) to investigate the presence of a coma. This function is equal to 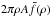 , where ρ is the projected nucleocentric distance, A is the dust geometrical albedo, assumed constant, and
, where ρ is the projected nucleocentric distance, A is the dust geometrical albedo, assumed constant, and 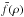 is the average filling factor at ρ. In the case of dust outflow with constant velocity and without dust fragmentation and sublimation, the function is constant and its value is simply π times that of Afρ, defined by A’Hearn et al. (1984), and used as a standard measure of dust production rates. The ∑ Af profile of Chariklo is shown in Fig. 3 together with that of a background star, normalised to the flux of Chariklo. In the inner part, for ρ< 20 000 km, we found the contribution of the Chariklo nucleus. No coma is detected by comparing this profile to that of a background star. However, the stacked images were still affected by the numerous background stars giving enormous errors in the Afρ estimation, which has a 1σ standard deviation of 300 cm. Assuming single-size grains, Afρ is related to Qdust through
is the average filling factor at ρ. In the case of dust outflow with constant velocity and without dust fragmentation and sublimation, the function is constant and its value is simply π times that of Afρ, defined by A’Hearn et al. (1984), and used as a standard measure of dust production rates. The ∑ Af profile of Chariklo is shown in Fig. 3 together with that of a background star, normalised to the flux of Chariklo. In the inner part, for ρ< 20 000 km, we found the contribution of the Chariklo nucleus. No coma is detected by comparing this profile to that of a background star. However, the stacked images were still affected by the numerous background stars giving enormous errors in the Afρ estimation, which has a 1σ standard deviation of 300 cm. Assuming single-size grains, Afρ is related to Qdust through 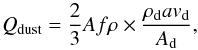 (3)where a is the grain radius, ρd is the dust density, and Ap is the geometric albedo of the dust (Jorda 1995). The derived upper limit in the Qdust is ~2.5 kg s-1, assuming the same dust parameters described in Fornasier et al. (2013), i.e. a = 1 μm, vd = 100 m s-1, ρd = 500 kg m-3, and Ad = 0.04.
(3)where a is the grain radius, ρd is the dust density, and Ap is the geometric albedo of the dust (Jorda 1995). The derived upper limit in the Qdust is ~2.5 kg s-1, assuming the same dust parameters described in Fornasier et al. (2013), i.e. a = 1 μm, vd = 100 m s-1, ρd = 500 kg m-3, and Ad = 0.04.
To investigate the possibility of cometary activity we re-analysed some Chariklo R-Bessel images (Texp = 60 s) obtained at the VLT telescope between 2007 and 2008 during a polarimetric study of this Centaur (Belskaya et al. 2010). Cometary activity was not detected, except for a potential 1.1σ detection during the June 2008 observations (Table 2). We conclude that the activity of Chariklo, if present, was below our detection limits. Moreover activity on Chariklo has never been reported since its discovery, but we cannot exclude that the rings may have been fed by cometary activity developed in the past, before its discovery.
We also used the ∑ Af function to compute the Chariklo cross section (SAtot), i.e. the illuminated surface (SA, surface × albedo) of the nucleus plus the rings, by integrating over the nucleus signature, after having subtracted the signal of the coma (in this case equal to 0). Because the Hv value varies over time, we first computed the Chariko albedo for the different runs using the aforementioned WISE and Herschel thermal data. We then applied the NEATM model to these data using as input value the Hv magnitude derived directly from the observations during the different runs (Belskaya et al. 2010; this paper). In doing so, we assume that the rings’ contribution to the thermal fluxes is negligible, and that the thermal fluxes measured in 2010 can be considered constant during the 2007−2013 period. The SAtot values, corrected for the phase angle, are reported in Table 2. The indicated errors are mainly due to the photometric calibration that are about 0.03 mag and 0.08 mag for the VLT and the SOAR data, respectively. The statistical error is about one order of magnitude smaller. The error associated with a possible presence of a coma is negligible.
Results of the cometary activity analysis.
We finally use the SAtot value to have an independent estimation of Chariklo’s size. The obtained equivalent radius is indicated in Table 2. The Stot values include the contribution of the nucleus and that of the rings, i.e. SAtot = SAnucleus + SAring. This is the reason why the Req derived from the SOAR data is bigger than that derived from the VLT data: the estimated surface of the rings times their albedo in June 2013 is 1219 km2, thus their contribution to the visual flux is important. From the median of Req values derived from the VLT data, where the rings’ contribution to the total flux is negligible, we derive a radius of 120±5 km, in agreement with the value estimated from the radiometric method, and with the size directly derived from stellar occultation events (Sicardy et al. 2014).
5. Conclusions
We present new photometric observations of the centaur Chariklo acquired at the SOAR Telescope before the discovery of its ring system. We also analyse some VLT images obtained during 2007−2008 to investigate if cometary activity was present, as cometary activity was claimed as one of the possible origins of the rings. These data allow us to
-
1.
obtain the first estimation of Chariklo’s rotational period, 7.004±0.036 h;
-
2.
determine an absolute visual magnitude of 7.03±0.10 in June 2013, implying that Chariklo was much brighter than in the previous 2007−2008 observations; this value is in agreement with the prediction of Hv variation over time due to the different ring system aspect angles;
-
3.
investigate potential cometary activity: no coma is found in the SOAR data, nor in the VLT images of 2007−2008, except for a potential 1.1 sigma detection in June 2008; the upper limit in the dust production rate is 2.5 kg/s;
-
4.
refine the size and albedo values from Herschel and WISE observations obtained during 2010 with the updated Hv value: we find Req = 119 ± 5 km, and an albedo of 4.2 ± 0.5%.
Online material
 |
Fig. 3 ∑ Af profile obtained from stacked SOAR images: Chariklo is represented with the continuous red line and a background star with the dashed line. The two profiles are overlapping, indicating that no coma is present. |
DanDIA is built from the DanIDL library of IDL routines available at http://www.danidl.co.uk
Acknowledgments
We thank B. Sicardy who kindly provided the predicted ring aspect angle versus time. Data used in the present paper were obtained under Programme ID: SO2013A-012. This project was supported by the French Planetology National Programme (INSU-PNP). C.S. received funding from the European Union Seventh Framework Programme (FP7/2007−2013) under grant agreement No. 268421. CNPq, FAPERJ and CAPES are acknowledged for diverse grants and fellowships to D.L., A.A.-C., J.M.C. and S.C.S., and Y.J.-T., in particular projects No. 402085/2012-4 and 305369/2009-1 (CNPq), E-26/102.967/2011 (FAPERJ), and A062/2013 (CAPES). D.M.B. was supported by NPRP grant X-019-1-006 from the Qatar National Research Fund.
References
- A’Hearn, M. F., Schleicher, D. G., Feldman, P. D., Millis, R. L., & Thompson, D. T. 1984, AJ, 89, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Alvarez-Candal, A., Fornasier, S., Barucci, M. A., de Bergh, C., & Merlin, F. 2008, A&A, 487, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barucci, M. A., Lazzarin, M., & Tozzi, G. P. 1999, AJ, 117, 1929 [NASA ADS] [CrossRef] [Google Scholar]
- Barucci, M. A., Belskaya, I. N., Fulchignoni, M., & Birlan, M. 2005, AJ, 130, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, J. M., Meech, K. J., Fernandez, Y. R., et al. 2003, Icarus, 166, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Belskaya, I., Bagnulo, S., Barucci., M. A., et al. 2010, Icarus, 210, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2011, ASP Conf. Ser., 442, 435 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braga-Ribas, F., Sicardy, B., Ortiz, J. L., et al. 2014, Nature, 508, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Bramich, D. M. 2008, MNRAS, 386, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E., & Koresko, C. 1998, ApJ, 505, L65 [NASA ADS] [CrossRef] [Google Scholar]
- DeMeo, F., Fornasier, S., Barucci, M. A., et al. 2009, A&A, 493, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dotto, E., Barucci, M. A., Leyrat, C., et al. 2003, Icarus, 164, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Duffard, R., Pinilla-Alonso, N., Ortiz, J. L., et al. 2014, A&A, 568, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fornasier, S., Barucci, M. A., de Bergh, C., et al. 2009, A&A, 508, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fornasier, S., Lellouch, E., Müller, T., et al. 2013, A&A, 555, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilbert, A., Barucci, M. A., Brunetto, R., et al. 2009, A&A, 501, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, A. W., Young, J. W., Bowell, E., et al. 1989, Icarus, 77, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C., & Luu, J. X. 2001, AJ, 122, 2099 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Teja, Y., & Benítez, N. 2012, ApJ, 745, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Jorda, L. 1995, Ph.D. Thesis, University of Paris 7 [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- McBride, N., Davies, J. K., Green, S. F., & Foster, M. J. 1999, MNRAS, 306, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Peixinho, N., Lacerda, P., & Ortiz, J. L. 2001, A&A, 371, 753 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sicardy, B., Braga-Ribas, F., Benedetti-Rossi, G., et al. 2014, ACM Conf., Finland [Google Scholar]
- Snodgrass, C., Tubiana, C., Bramich, D. M., et al.. 2013, A&A, 557, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stetson, P. B. 1990, PASP, 102, 932 [NASA ADS] [CrossRef] [Google Scholar]
- Tegler, S. C., & Romanishin, W. 1998, Nature, 392, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, G. P., Boehnhardt, H., Kolokolova, L., et al., 2007, A&A, 476, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Composite light curve of 10199 Chariklo determined from the SOAR Telescope observations. The continuous line is the polynomial fit. |
| In the text | |
 |
Fig. 2 Absolute magnitude of 10199 Chariklo versus time. The heliocentric distance (in AU) is indicated at the top. The continuous line represents the predicted Chariklo absolute magnitude from Eq. (2), and the arrow indicates the date corresponding to the observations obtained with Herschel. |
| In the text | |
 |
Fig. 3 ∑ Af profile obtained from stacked SOAR images: Chariklo is represented with the continuous red line and a background star with the dashed line. The two profiles are overlapping, indicating that no coma is present. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


