| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201424430 | |
| Published online | 19 August 2014 | |
The evolution of the self-lensing binary KOI-3278: evidence of extra energy sources during CE evolution
1
Instituto de Física y Astronomía, Universidad de Valparaíso,
Av. Gran Bretaña 1111, 5030,
Valparaíso
Chile
e-mail:
mzorotov@dfa.uv.cl
2
Millennium Nucleus “Protoplanetary Disks in ALMA Early Science”,
Universidad de Valparaíso, Casilla
36- D Santiago,
Chile
Received:
18
June
2014
Accepted:
21
July
2014
Post-common-envelope binaries (PCEBs) have been frequently used to observationally constrain models of close-compact-binary evolution, in particular common-envelope (CE) evolution. However, recent surveys have detected PCEBs consisting of a white dwarf (WD) exclusively with an M dwarf companion. Thus, we have been essentially blind with respect to PCEBs with more massive companions. Recently, the second PCEB consisting of a WD and a G-type companion, the spectacularly self-lensing binary KOI-3278, has been identified. This system is different from typical PCEBs not only because of the G-type companion, but also because of its long orbital period. Here we investigate whether the existence of KOI-3278 provides new observational constraints on theories of CE evolution. We reconstruct its evolutionary history and predict its future using BSE, clarifying the proper use of the binding energy parameter in this code. We find that a small amount of recombination energy, or any other source of extra energy, is required to reconstruct the evolutionary history of KOI-3278. Using BSE we derive progenitor system parameters of M1,i = 2.450 M⊙, M2,i = 1.034 M⊙, and Porb,i ~ 1300 d. We also find that in ~9 Gyr the system will go through a second CE phase leaving behind a double WD, consisting of a C/O WD and a He WD with masses of 0.636 M⊙ and 0.332 M⊙, respectively. After IK Peg, KOI-3278 is the second PCEB that clearly requires an extra source of energy, beyond that of orbital energy, to contribute to the CE ejection. Both systems are special in that they have long orbital periods and massive secondaries. This may also indicate that the CE efficiency increases with secondary mass.
Key words: binaries: close / white dwarfs / stars: evolution
© ESO, 2014
1. Introduction
Post-common-envelope binaries (PCEBs) consisting of a white dwarf (WD) and a main-sequence (MS) companion are close-binary stars with orbital periods typically shorter than a day. Their discovery (Kraft 1958) immediately raised the question of their origin, because the progenitor of the WD must have been much bigger than the separation of the two stars in the currently observed system. Based on the pioneering works of Paczyński (1976) and Webbink (1984) the puzzle now seems to be solved. If the initially more massive star fills its Roche lobe as a giant and if the mass ratio q = Mdonor/Mgainer exceeds a critical value qcrit1, dynamically unstable mass transfer is generated. This leads to the formation of a common envelope (CE) engulfing both the core of the primary (the future WD) and the secondary star. The CE is expelled at the expense of orbital energy and angular momentum leaving behind a short period PCEB consisting of the compact core of the primary and the secondary star.
Despite significant recent progress (Ricker & Taam 2012), numerical calculations still fail to simultaneously cover the large range of time and spatial scales involved in CE evolution and to make detailed predictions for the parameters of the emerging PCEB. Therefore, a simple energy equation relating the binding energy of the envelope to the change in orbital energy parametrized with the so-called CE efficiency (αCE) is normally used to predict the outcome of CE evolution. Such an approach requires observational constraints on the efficiency parameter.
Recent surveys of PCEBs have established large samples of close binaries containing a WD and an M-dwarf companion (e.g., Nebot Gómez-Morán et al. 2011; Parsons et al. 2013). These samples have been proved useful to understand several aspects of close-compact-binary evolution (e.g., Zorotovic et al. 2010); however, they only contain low-mass secondary stars. The predicted significant population of PCEBs containing a WD plus a massive (≳1 M⊙) secondary star (see, e.g., Zorotovic et al. 2014) has not yet been identified. This is because such a massive MS star completely outshines the WD at all wavelengths longer than UV. Finding and analyzing the evolutionary history of these PCEBs is crucial not only because the CE efficiency may depend on the mass of the secondary, as speculated by e.g., Politano & Weiler (2007), but also because these systems may hold the key to understanding one of the oldest problems in astrophysics: the progenitor problem for supernovae Type Ia (SN Ia, see, e.g., Wang & Han 2012, for a recent review). PCEBs with a massive MS secondary star are the progenitors of the two most popular channels proposed towards SN Ia. In the single-degenerate channel (Whelan & Iben 1973) these PCEBs start thermal-timescale mass transfer which allows the WD mass to grow until it eventually explodes as a SN Ia. In the double-degenerate channel (Webbink 1984) a WD with a close and massive companion (either a PCEB or a close binary emerging from stable mass transfer) evolves into a CE phase which leaves behind a double-degenerate system that may finally merge and, in the case of two C/O WDs with a total mass exceeding the Chandrasekhar limit, produce a SN Ia explosion.
Recently, the second WD with a close and massive companion star has been identified (after IK Peg). This system, KOI-3278, identified using data from the Kepler spacecraft (Kruse & Agol 2014), is remarkable not only for its long orbital period (88.18 days), but also because it is eclipsing. This combination of long period and high inclination results in a spectacular five-hour pulse once every orbit, caused by the 0.634 M⊙ C/O WD acting as a gravitational lens as it passes in front of its 1.042 M⊙ MS companion.
Given the small separation and the masses of the two stars, KOI-3278 must have evolved through a CE. Assuming that stable mass transfer occurred in KOI-3278 would require a large critical mass ratio (q ~ 1.5) and strong wind mass loss of the WD progenitor on the AGB. While this configuration cannot be completely excluded, the resulting stable mass transfer could not have reduced the binary orbital period to the measured 88.18 days. Thus, KOI-3278 is the second PCEB containing a massive companion star.
Here we reconstruct the evolutionary history of KOI-3278 to derive constraints on the CE efficiency and predict its future to evaluate whether it might be the first progenitor of a double WD that will be formed through two CE phases.
2. Constraints on CE evolution from KOI-3278
In its simplest form, the energy equation describing CE evolution can be expressed as
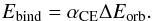 (1)The most basic assumption
is to approximate the binding energy only by the gravitational energy of the envelope,
(1)The most basic assumption
is to approximate the binding energy only by the gravitational energy of the envelope,
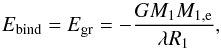 (2)where M1,
M1,e, and R1 are the total
mass, envelope mass, and radius of the primary star, and λ is a binding energy
parameter that depends on the structure of the primary star. Simulations of PCEBs (e.g.,
de Kool & Ritter 1993; Willems & Kolb 2004; Politano
& Weiler 2006) have been performed assuming different values of
αCE and assuming λ = 0.5 or 1.0. However, keeping λ constant is not a very
realistic assumption for all types of possible primaries as was pointed out by e.g., Dewi & Tauris (2000). Very loosely bound envelopes
in more evolved stars can reach much higher values, especially if the recombination energy
Urec available within the envelope supports
the ejection process. Therefore, a more realistic form for the binding energy equation is
(2)where M1,
M1,e, and R1 are the total
mass, envelope mass, and radius of the primary star, and λ is a binding energy
parameter that depends on the structure of the primary star. Simulations of PCEBs (e.g.,
de Kool & Ritter 1993; Willems & Kolb 2004; Politano
& Weiler 2006) have been performed assuming different values of
αCE and assuming λ = 0.5 or 1.0. However, keeping λ constant is not a very
realistic assumption for all types of possible primaries as was pointed out by e.g., Dewi & Tauris (2000). Very loosely bound envelopes
in more evolved stars can reach much higher values, especially if the recombination energy
Urec available within the envelope supports
the ejection process. Therefore, a more realistic form for the binding energy equation is
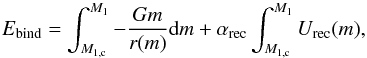 (3)where αrec is the
efficiency of using recombination energy, i.e., the fraction of recombination energy that
contributes to the ejection process. The effects of the extra energy source can be included
in the λ
parameter by equating Eqs. (2) and (3).
(3)where αrec is the
efficiency of using recombination energy, i.e., the fraction of recombination energy that
contributes to the ejection process. The effects of the extra energy source can be included
in the λ
parameter by equating Eqs. (2) and (3).
2.1. Previous observational constraints on CE efficiencies
While the above straightforward energy equation accurately describes the basic idea of CE evolution, it requires observational constraints to estimate the efficiencies. Several attempts to provide such constraints have been made using PCEBs consisting of a WD and a late-type (M dwarf) companion. In Zorotovic et al. (2010) we have shown that the evolutionary history of the identified PCEBs can be reconstructed assuming that both efficiencies are in the range of 0.2−0.3. The case for such relatively small efficiencies has recently been strengthened by Toonen & Nelemans (2013) and Camacho et al. (2014) who performed binary population models of PCEBs taking into account selection effects affecting the observed samples. While the relative contributions of recombination and orbital energy remain unclear (e.g., Rebassa-Mansergas et al. 2012), the small values of the CE efficiencies are also in agreement with first tentative results obtained from numerical simulations of the CE phase (Ricker & Taam 2012).
However, we have no information whether these values hold for larger secondary masses. While the decrease of αCE with increasing secondary masses proposed by de Marco et al. (2011) seems unlikely (Zorotovic et al. 2011b), the efficiencies may perhaps increase with secondary mass. The parameters of the only previously known PCEB with a G-type secondary, i.e., IK Peg (Porb = 21.722 d, MWD = 1.19 M⊙, Msec = 1.7 M⊙), indicate that we can probably not simply apply the constraints for PCEBs with M-dwarfs to larger secondary masses. As shown by e.g., Davis et al. (2010) and Zorotovic et al. (2010), IK Peg is the only PCEB that requires additional energy sources to be at work during CE evolution. Despite the potential importance of IK Peg for our understanding of CE evolution, we cannot develop evolutionary theories based on just one system. Every new PCEB with a massive secondary therefore needs to be carefully analyzed.
 |
Fig. 1 Right: orbital period, secondary mass, and WD mass for the known PCEBs. The gray surfaces represent the maximum period of PCEBs if orbital energy is the only energy source for expelling the envelope during the CE phase. This maximum period is a function of Msec and MWD. It increases with core mass for progenitors that fill their Roche lobe on the the first giant branch (i.e., for MWD ≲ 0.47 M⊙, gray surface in the back) and is generally long for AGB progenitors (MWD ≳ 0.51 M⊙, gray surface in the front). KOI-3278 (red cross) and IK Peg (red point) are the only known PCEBs with solar-type secondary stars, and both systems are located above this limit. All WD+M-dwarf PCEBs (blue points) are well below the critical value. Left: 2D projections of the right hand plot. The three black lines in the upper panel represent the maximum period for a fixed mass of the secondary star. The solid line is for 0.3 M⊙ (typical for the WD+M-dwarf PCEBs), the dashed line for 1.042 M⊙ (the companion in KOI-3278), and the dotted line for 1.7 M⊙ (the companion in IK Peg). |
2.2. A note of caution for BSE users
In their discovery paper, Kruse & Agol (2014) used the binary star evolution (BSE) code from Hurley et al. (2002) and found a possible evolutionary path for KOI-3278 assuming αCE = 0.3 and λ = 0.2. However, if we run BSE with the initial parameters obtained by Kruse & Agol (2014) with these values, the binary system does not survive the CE phase. This discrepancy is easily explained by taking a closer look at the evolution of BSE. In its original version, the code requested a fixed value for λ as an input parameter. However, the code was frequently updated over the years and a function to compute the value of λ was included2. This change is not described in the README file and is not commented in the main code (bse.f). However, digging into the code it becomes clear that in the current version the input parameter called “lambda” represents the fraction of the recombination (ionization) energy that is included to compute the real value of λ, i.e., αrec. If the user still wants to use a fixed value for λ, the input value must be negative (e.g., if one wants to use λ = 0.2, the input parameter should be − 0.2).
The result obtained by Kruse & Agol (2014) thus only shows that the evolutionary history of KOI-3278 can be understood if recombination energy significantly contributes to expelling the envelope. Given the long orbital period of KOI-3278, however, the crucial question is if it represents the second system after IK Peg that requires additional energy sources to contribute during CE evolution.
2.3. Reconstructing KOI-3278
Given the importance of understanding the evolution of PCEBs with massive secondaries, we here properly reconstruct the evolution of KOI-3278. We use the BSE code from Hurley et al. (2002) to identify possible progenitors of KOI-3278 and investigate whether additional energy sources are required to understand its evolutionary history. Our reconstruction algorithm is described in detail in Zorotovic et al. (2011a).
We first try to reconstruct the CE phase allowing the stellar parameters to vary within the 1σ uncertainties of the measured stellar parameters (as given by Kruse & Agol 2014) but without considering additional energy sources. Interestingly, as in the case of IK Peg, we do not find possible progenitors for KOI-3278 without violating energy conservation, i.e., for any possible progenitor of the WD, the CE could not have been expelled by the use of orbital energy alone. This represents an important result as KOI-3278 is only the second PCEB with a massive secondary star and, in contrast to all PCEBs with low-mass secondary stars, both these systems require αrec> 0. Figure 1 illustrates our finding. It shows the maximum orbital period that a system can have if the only energy source used to expel the envelope is the orbital energy (αrec = 0 and αCE = 1) as a function of secondary mass, orbital period, and WD mass. The two systems with massive companions, KOI-3278 and IK Peg, are the only two that require extra energy sources. If a fraction of the recombination energy is assumed to contribute to expelling the envelope, the evolutionary history of both systems can be reconstructed. Assuming αCE = αrec = 0.25 (Zorotovic et al. 2010) we derive initial masses of M1,i = 2.450 M⊙ and M2,i = 1.034 M⊙ and an initial orbital period of Porb,i ~ 1300 d for the progenitor of KOI-3278, which is similar to the values obtained by Kruse & Agol (2014) for αCE = 0.3 and αrec = 0.2.
3. Predicting the future of KOI-3278
While reconstructing the evolution of KOI-3278 provides new information about the efficiencies of CE evolution, the future of close binaries consisting of WDs and massive companions is equally important as these systems may either enter a second CE phase, which may lead to a double WD (DWD), or start thermal-timescale mass transfer. These configurations represent the two classical channels towards SN Ia, i.e. the double- and single-degenerate channel. Which of the two channels is taken by a given system depends on the timescale of nuclear evolution of the secondary and the timescale of orbital angular momentum loss until the secondary fills its Roche lobe.
If the PCEB has a relatively long orbital period, the secondary is likely to evolve off the MS and fill its Roche lobe as a giant. This configuration leads to dynamically unstable mass transfer if q > qcrit ~ 1−1.5. It depends then on the CE efficiencies and the orbital period at the onset of CE evolution if the system survives the CE phase or if the two stars merge. In the first case, a DWD is formed. The two WDs lose angular momentum because of gravitational radiation and if this DWD has a total mass exceeding the Chandrasekhar limit it may produce a SN Ia.
If, on the other hand, the PCEB has a short orbital period, angular momentum loss due to magnetic braking and gravitational radiation can cause the secondary to fill its Roche lobe while it is still on the MS. This will lead to thermal-timescale mass transfer (for q ≳ 1) and the systems appear as a super-soft X-ray source, i.e., the mass-transfer rate is high enough to generate stable hydrogen burning on the surface of the WD, allowing the WD mass to grow. It may explode as SN Ia if it reaches the Chandrasekhar limit.
We predict the future of KOI-3278 using BSE and the current system parameters as derived in Kruse & Agol (2014). Given the age of the system and the mass of the secondary, the latter will evolve off the MS and fill its Roche lobe during the first giant branch, in ~9 Gyr. At that moment the orbital period will still be ~80 d, the secondary will have a total mass of 1.009 M⊙ with a core-mass of 0.332 M⊙. Given the mass ratio of the system, mass transfer will be dynamically unstable and lead to CE evolution. KOI-3278 will survive this second CE phase and form a DWD, a C/O WD plus a He WD, for almost any value of the efficiencies (even if αrec = 0, αCE needs to be only larger than 0.0433 to avoid a merger). This makes KOI-3278 the first known progenitor of a DWD formed by two CEs.
 |
Fig. 2 Orbital period versus mass of the brighter WD (usually the younger one) for the DWDs found by the SPY survey (filled circles) and by the ELM survey (open circles). The cross marks the position KOI-3278 will take in ~9 Gyr. The error bar has been calculated taking into account all possible values of the efficiencies during the second CE. |
In Fig. 2 we relate the future DWD parameters of
KOI-3278 to the currently known sample of DWDs. The two surveys that have identified most of
the currently known DWDs are the SPY survey (Napiwotzki
et al. 2003) and the ELM survey (Kilic et al.
2010). We compiled the DWDs from both surveys using the tables provided in Nelemans et al. (2005) and Brown et al. (2012, 2013). With an orbital
period of 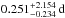 and a
mass of 0.332
M⊙ for the WD that will form during the
second CE phase, KOI-3278 will become a very typical DWD that will evolve towards shorter
orbital periods driven by orbital angular momentum loss due to gravitational radiation.
Given the mass ratio, and depending on the strength of spin-orbit coupling, the binary may
either become an AM CVn system or, more probably, merge (see Marsh et al. 2004, their Fig. 1).
and a
mass of 0.332
M⊙ for the WD that will form during the
second CE phase, KOI-3278 will become a very typical DWD that will evolve towards shorter
orbital periods driven by orbital angular momentum loss due to gravitational radiation.
Given the mass ratio, and depending on the strength of spin-orbit coupling, the binary may
either become an AM CVn system or, more probably, merge (see Marsh et al. 2004, their Fig. 1).
4. Conclusion
Understanding the evolution of the two known PCEBs containing a G-type secondary star requires additional sources of energy, such as recombination energy, to contribute during CE evolution. This may indicate that a larger fraction of the total available energy is used to expel the envelope. In other words, at least one of the efficiencies may increase with secondary mass. If this can be confirmed, the population of PCEBs with F- and
G-type secondaries will be dominated by long orbital period systems (Porb ~ 2−100 d) and most secondaries will evolve into giants before the second phase of mass transfer and may, such as KOI-3278, survive a second CE. This, finally, may imply that the double-degenerate channel towards SN Ia is more likely to occur than the single-degenerate channel.
Early calculations led to qcrit ~ 1 (Webbink 1988) while more recent works do not exclude values as high as qcrit = 1.5 (Passy et al. 2012; Woods & Ivanova 2011).
The function called celamf can be found in the file called zfuncs.f and it was recently published in Claeys et al. (2014).
Acknowledgments
We thank Fondecyt for their support under the grants 3130559 (MZ), 1141269 (MRS), and 3140585 (SGP).
References
- Brown, W. R., Kilic, M., Allen de Prieto, C., & Kenyon, S. J. 2012, ApJ, 744, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Kilic, M., Allen de Prieto, C., Gianninas, A., & Kenyon, S. J. 2013, ApJ, 769, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Camacho, J., Torres, S., García-Berro, E., et al. 2014, A&A, 566, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claeys, J. S. W., Pols, O. R., Izzard, R. G., Vink, J., & Verbunt, F. W. M. 2014, A&A, 563, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, P. J., Kolb, U., & Willems, B. 2010, MNRAS, 403, 179 [NASA ADS] [CrossRef] [Google Scholar]
- de Kool, M., & Ritter, H. 1993, A&A, 267, 397 [NASA ADS] [Google Scholar]
- de Marco, O., Passy, J., Moe, M., et al. 2011, MNRAS, 411, 2277 [NASA ADS] [CrossRef] [Google Scholar]
- Dewi, J. D. M., & Tauris, T. M. 2000, A&A, 360, 1043 [NASA ADS] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Brown, W. R., & McLeod, B. 2010, ApJ, 708, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P. 1958, ApJ, 127, 625 [Google Scholar]
- Kruse, E., & Agol, E. 2014, Science, 344, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, T. R., Nelemans, G., & Steeghs, D. 2004, MNRAS, 350, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Napiwotzki, R., Christlieb, N., Drechsel, H., et al. 2003, The Messenger, 112, 25 [NASA ADS] [Google Scholar]
- Nebot Gómez-Morán, A., Gänsicke, B. T., Schreiber, M. R., et al. 2011, A&A, 536, A43 [CrossRef] [Google Scholar]
- Nelemans, G., Napiwotzki, R., Karl, C., et al. 2005, A&A, 440, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paczyński, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan (D. Reidel Publishing Co), IAU Symp., 73, 75 [Google Scholar]
- Parsons, S. G., Gänsicke, B. T., Marsh, T. R., et al. 2013, MNRAS, 429, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Passy, J.-C., Herwig, F., & Paxton, B. 2012, ApJ, 760, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Politano, M., & Weiler, K. P. 2006, ApJ, 641, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Politano, M., & Weiler, K. P. 2007, ApJ, 665, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Rebassa-Mansergas, A., Zorotovic, M., Schreiber, M. R., et al. 2012, MNRAS, 423, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, P. M., & Taam, R. E. 2012, ApJ, 746, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Toonen, S., & Nelemans, G. 2013, A&A, 557, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, B., & Han, Z. 2012, New A Rev., 56, 122 [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1988, The Symbiotic Phenomenon, eds. J. Mikolajewska, M. Friedjung, S. J. Kenyon, & R. Viotti, IAU Colloq., 103, 311 [Google Scholar]
- Whelan, J., & Iben, Jr., I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Willems, B., & Kolb, U. 2004, A&A, 419, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woods, T. E., & Ivanova, N. 2011, ApJ, 739, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., & Gänsicke, B. T. 2011a, A&A, 536, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., et al. 2011b, A&A, 536, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., García-Berro, E., et al. 2014, A&A, in press, DOI: 10.1051/0004-6361/201323039 [Google Scholar]
All Figures
 |
Fig. 1 Right: orbital period, secondary mass, and WD mass for the known PCEBs. The gray surfaces represent the maximum period of PCEBs if orbital energy is the only energy source for expelling the envelope during the CE phase. This maximum period is a function of Msec and MWD. It increases with core mass for progenitors that fill their Roche lobe on the the first giant branch (i.e., for MWD ≲ 0.47 M⊙, gray surface in the back) and is generally long for AGB progenitors (MWD ≳ 0.51 M⊙, gray surface in the front). KOI-3278 (red cross) and IK Peg (red point) are the only known PCEBs with solar-type secondary stars, and both systems are located above this limit. All WD+M-dwarf PCEBs (blue points) are well below the critical value. Left: 2D projections of the right hand plot. The three black lines in the upper panel represent the maximum period for a fixed mass of the secondary star. The solid line is for 0.3 M⊙ (typical for the WD+M-dwarf PCEBs), the dashed line for 1.042 M⊙ (the companion in KOI-3278), and the dotted line for 1.7 M⊙ (the companion in IK Peg). |
| In the text | |
 |
Fig. 2 Orbital period versus mass of the brighter WD (usually the younger one) for the DWDs found by the SPY survey (filled circles) and by the ELM survey (open circles). The cross marks the position KOI-3278 will take in ~9 Gyr. The error bar has been calculated taking into account all possible values of the efficiencies during the second CE. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


