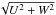| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201423817 | |
| Published online | 11 July 2014 | |
Investigating the possible connection between λ Bootis stars and intermediate Population II type stars
1 Department of Theoretical Physics and Astrophysics, Masaryk University, Kotlářská 2, 611 37 Brno, Czech Republic
e-mail: epaunzen@physics.muni.cz
2 Rozhen National Astronomical Observatory, Institute of Astronomy of the Bulgarian Academy of Sciences, PO Box 136, 4700 Smolyan, Bulgaria
3 Argelander-Institut für Astronomie der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
4 Institutionen för fysik och astronomi, Uppsala universitet, Box 516, 751 20 Uppsala, Sweden
5 Institute for Astrophysics, University of Vienna, Türkenschanzstr. 17, 1180 Vienna, Austria
Received: 16 March 2014
Accepted: 2 June 2014
Context. The λ Bootis stars are located at the upper main sequence of the Hertzsprung-Russell diagram and exhibit a peculiar abundance pattern. The light elements (C, N, O, and S) present solar abundances whereas all other elements are moderately to strongly underabundant. It has not yet been determined whether that abundance pattern is intrinsic, or is restricted to the stellar surface.
Aims. If we follow the hypothesis that the λ Bootis stars are intrinsically metal-weak, then there should be a connection with the intermediate Population II and F-weak objects. Such a possible affinity has not been previously investigated.
Methods. We present detailed elemental abundances, including those of the light elements carbon and oxygen, for 38 bright intermediate Population II and F-weak objects. In addition, we investigate the kinematic characteristics of the groups.
Results. From photometric, spectroscopic, and kinematic data, there is no distinction between the intermediate Population II and F-weak type stars. We therefore conclude that the two groups are identical. However, it is possible to distinguish the λ Bootis stars from the intermediate Population II stars on the basis of elemental abundances, though not in terms of their kinematics.
Conclusions. The λ Bootis stars seem to be distinct from the intermediate Population II group. Further asteroseismologic investigations and analyses of spectroscopic binary systems are needed to strengthen this conclusion.
Key words: stars: abundances / stars: chemically peculiar / stars: early-type / stars: Population II
© ESO, 2014
1. Introduction
The λ Bootis stars are a small group (only 2%) of late-B to early-F stars that show moderate to extreme surface underabundances (up to a factor of 100) of most Fe-peak elements, but solar abundances of lighter elements (C, N, O, and S). They stand out among the chemically peculiar stars of the upper main sequence because all other groups exhibit strong overabundances of elements, probably caused by magnetic fields, slow rotation or atmospheric diffusion (e.g. Netopil et al. 2008). Several members of the group exhibit a strong infrared excess and a disk (Paunzen et al. 2003; Booth et al. 2013).
To explain the λ Bootis phenomenon, Venn & Lambert (1990) suggested that the peculiar chemical abundance is caused by selective accretion of circumstellar material. One of the principal features of that hypothesis is that the observed abundance anomalies are restricted to the stellar surface. Members of the group are therefore true Population I type objects. Later, Kamp & Paunzen (2002) and Martinez-Galarza et al. (2009) developed models that describe the interaction of the star with its local interstellar and/or circumstellar environment, whereby different degrees of underabundance are produced by different amounts of accreted material relative to the photospheric mass. The fact that the fraction of λ Bootis stars on the main sequence is so small would then be a consequence of the low probability of a star-cloud interaction, and by the effects of meridional circulation which dissolves any accretion pattern a few million years after the accretion has stopped. The hot cut-off would be the limitation of significant stellar winds for stars with Teff > 12 000 K whereas the cool end, at about 6500 K, would be defined by convection which prevents the accreted material from appearing at the stellar surface.
Astrophysical and kinematic parameters for our target sample.
The important question as to whether or not λ Bootis stars are intrinsically metal-weak does not seem to have been raised very often in the literature. Recently, Casas et al. (2009) made a detailed asteroseismological analysis of the pulsational behaviour of 29 Cygni (HR 7736), which is one of the prototypes of the λ Bootis group and exhibits very strong underabundances of the Fe-peak elements compared to the Sun ([Fe / H] = −1.63 dex; Paunzen et al. 2002). From their best-fitting models they concluded that 29 Cyg is an intrinsic metal-weak main-sequence object. Unfortunately, there is only one other similar analysis in the literature: Breger et al. (2006) investigated the pulsational characteristics of HD 210111 (HR 8437) and found no differences from the behaviour of the classical δ Scuti star, FG Virginis, which has a similar evolutionary status. The star HD 210111 was later found to be a spectroscopic binary system with almost equal components (Paunzen et al. 2012). Although the components have [M/H] = −1.0 dex, the pulsational models of Breger et al. (2006) adopted solar abundances. It would be very interesting to re-analyse their observations with corresponding metal-weak models.
Incorporating unrepresentative metal abundances in the models has consequences not only for the theories already developed to explain the λ Bootis phenomenon, but also for the calibration of the astrophysical parameters. For example, in order to derive stellar ages one would need to use isochrones calculated for abundances that were intrinsically non-solar.
As a rider to that hypothesis, it would be difficult to describe the λ Boo stars as true Population I type objects. A first possible connection between these star groups was suggested by Gray (1989), who introduced a new classification scheme for the intermediate Population II (hereafter ip II) stars. In this paper we present a fresh detailed investigation of a possible connection between the F-weak objects and ip II ones, using detailed elemental abundances, photometric diagrams, and kinematic data.
2. Target selection, observations, and reductions
We chose 38 bright (V< 7.5 mag) F-weak and ip II stars from the samples by Jaschek et al. (1989) and Gray (1989); all have parallaxes measured by Hipparcos (van Leeuwen 2009). We expressly selected objects that overlap the λ Bootis stars in terms of effective temperature and surface gravity. The stars are listed in Table 1.
Observations of the sample were made between 2001–2002 with the coudé spectrograph of the 2 m Ritchey-Chrétien telescope of the Bulgarian National Astronomical Observatory, Rozhen, using the Photometrics AT200 camera with a SITe SI003AB 1024 × 1024 CCD chip. Typical seeing was 2−3″; the slit width was set to 300 μm, which corresponded to 0 8 on the sky. A Bausch & Lomb grating with 632 lines mm-1 was centred on two different spectral regions, 7120 Å (C-region) and 7770 Å (O-triplet), and provided a resolving power of about 30 000 and 22 000, respectively. A hollow-cathode ThAr lamp produced a reference spectrum of comparison lines with a FWHM of about 2 pixels. A tungsten projection lamp mounted in front of the entrance slit provided flat-fielding.
8 on the sky. A Bausch & Lomb grating with 632 lines mm-1 was centred on two different spectral regions, 7120 Å (C-region) and 7770 Å (O-triplet), and provided a resolving power of about 30 000 and 22 000, respectively. A hollow-cathode ThAr lamp produced a reference spectrum of comparison lines with a FWHM of about 2 pixels. A tungsten projection lamp mounted in front of the entrance slit provided flat-fielding.
Additional high signal-to-noise ratio spectra were also obtained during several observing runs in 2001 and 2002 with the Sandiford Cassegrain Echelle Spectrograph (McCarthy et al. 1993) on the 2.1-m telescope at McDonald Observatory, USA. Those spectra covered continuously a wavelength range from about 4800 to 7000 Å with a resolving power of about 60 000. Each night the spectrum of a broad-lined B star was obtained with a signal-to-noise ratio that exceeded those of the programme stars by a factor of several, to enable corrections for telluric lines where necessary.
By using IRAF1 we processed the CCD images, subtracted scattered light, extracted echelle orders, and performed wavelength calibrations and continuum normalization. Equivalent widths were measured from the normalized spectra by adopting a Gaussian approximation to the line profile.
Photometric data were taken from the General Catalogue of Photometric Data (GCPD2). Where possible, averaged and weighted mean values were used throughout. To derive the effective temperatures and surface gravities, we employed the following calibrations for the individual photometric systems:
-
Johnson UBV: Napiwotzkiet al. (1993);
-
Strömgren uvbyβ: Moon & Dworetsky (1985); Napiwotzki et al. (1993);
-
Geneva 7-colour: Kobi & North (1990); Künzli et al. (1999).
When parameters from several different systems and calibrations were derived, a simple average and standard deviation was calculated; these values are listed in Table 1. The average uncertainties were 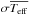 = 63(23) K and
= 63(23) K and 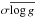 = 0.12(6) dex. No significant outliers were detected, so all the photometric measurements are intrinsically consistent.
= 0.12(6) dex. No significant outliers were detected, so all the photometric measurements are intrinsically consistent.
Element abundances for our sample of stars, relative to the solar values given by Grevesse et al. (1996).
To compute model atmospheres for the target stars, we employed the LLmodels stellar model-atmosphere code (Shulyak et al. 2004). Local thermodynamical equilibrium (LTE) and plane-parallel geometry were assumed for all the calculations. We used the Vald database (Piskunov et al. 1995; Kupka et al. 1999; Ryabchikova et al. 1999) as a source of atomic line parameters for the opacity calculations and abundance determinations. We also assumed a universal microturbulent velocity (υmic) of 2.0 km s-1 (Landstreet et al. 2009); this choice was confirmed by our analysis of Fe i lines for the few stars for which our spectra included enough lines that were both weak and strong and could thus support a reliable determination of υmic.
We derived the LTE abundances of the low-υsini stars (υsini ≤ 30 km s-1) by analysing measured equivalent widths with a modified version (Tsymbal 1996) of the Width9 code (Kurucz 1993). For the faster rotators we derived LTE abundances by fitting synthetic spectra that had been calculated with Synth3 (Kochukhov 2007). The tools and methodology adopted were the same as those described in Fossati et al. (2007). For solar abundances we used the values from Grevesse et al. (1996) in order to be compatible with the abundances published for the λ Bootis stars by Paunzen et al. (2002). The uncertainties in the abundances were typically ±0.2 dex.
The oxygen triplet at 7771-5 Å is known to be severely influenced by non-LTE (NLTE) effects (Paunzen et al. 1999). We therefore used the corrections given by Sitnova et al. (2013) for log g = 4.0 (see their Fig. 5) as they are valid for main-sequence stars. We applied the NLTE corrections according to the effective temperatures listed in Table 1. None of the other lines was significantly affected by NLTE. In the case of carbon, for instance, NLTE effects for the lines that we observed are below 0.1 dex (Paunzen et al. 1999). The abundances thus derived are listed in Table 2.
We checked our results against those from the Geneva-Copenhagen survey (Holmberg et al. 2009) and the PASTEL catalogue (Soubiran et al. 2010). The first includes kinematic data, effective temperature and absolute magnitudes, whereas the second includes effective temperature, surface gravity and [Fe/H]. The differences between the values are listed in Table 3. We found excellent agreement between all the parameters with those listed in the literature, thus strengthening confidence in our reduction, calibration and analysis methods.
The element abundances of superficially normal stars were taken from Adelman (1991), Adelman et al. (1991), Adelman (1994), Adelman (1996), Adelman et al. (1997), Caliskan & Adelman (1997), Hill & Landstreet (1993), Hill (1995), Takeda et al. (2009), Varenne & Monier (1999). The selected objects cover the complete range of Teff and log g in the other two samples. Values for the λ Bootis stars were taken from Paunzen et al. (2002, Table 1 therein). We checked the literature, but did not find reports of any additional light-element abundances for the stars listed there.
3. Discussion
There is considerable confusion in the literature over the definitions and origins of weak-lined F-type stars on the one hand and ip II stars on the other, and this question needs further discussion.
3.1. The weak-lined F-type stars and the ip II stars
We first summarize the results that have already been published, and then analyse the available photometric and kinematic data.
3.1.1. Historical facts
Baade’s original concept of a stellar “population” in the Milky Way was based on a disk (I) and a halo (II) population. The concept later evolved into a scheme with subdivisions. In one such subdivision, the old metal-weak Population II was divided into halo (extreme) and ip II objects. The latter was comprised of objects that had a velocity dispersion, a chemical composition, and a concentration towards the Galactic plane that was intermediate between those of the halo and the disk populations. The ip II population was later proposed in order to explain and fit both the global and the local Galactic kinematics. Robin & Crézé (1986) estimated that about 1.5% of all stars in the solar neighbourhood are ip II objects.
However, Strömgren (1964) and Blauuw (1965) had already pointed out that, owing to a steady transition between the populations and also to insufficient precision in their ages, no clear distinction between the groups could be made. Strömgren (1966) therefore proposed using the uvbyβ photometric system, as it would be more illuminating. The δm1 index, for instance, was used to distinguish solar from underabundant objects in the spectral-type domain between early F and mid G. Olsen (1979) listed the following boxes for cool ip II type stars (i.e. later than F4):  For the hotter stars (+0.043 < (b − y) < +0.270 and +0.045 < δm1) Strömgren found overlaps with “classical” λ Bootis stars and with field horizontal-branch stars which could then be separated easily by their c1 values.
For the hotter stars (+0.043 < (b − y) < +0.270 and +0.045 < δm1) Strömgren found overlaps with “classical” λ Bootis stars and with field horizontal-branch stars which could then be separated easily by their c1 values.
Differences between our derived values for the target sample and those in the Geneva-Copenhagen survey (GCS, Holmberg et al. 2009) and the PASTEL catalogue (Soubiran et al. 2010).
Gray (1989) obtained spectra at a classification dispersion (67 Å mm-1) of a sample of metal-weak stars that were selected according to the above criteria. He established metal-weak standards for that spectral range so as to extend the Yerkes MK system, and labelled his sample “intermediate Population II-type stars”.
Independently, Jaschek et al. (1989) conducted a survey of metal-weak F-type stars, and also used spectra with a classification dispersion (80 Å mm-1). Both Jaschek et al. and Gray employed the strengths of the Balmer lines, the G-band (CH), and metallic lines, but Jaschek et al. labelled their sample of metal-weak F-type stars simply “F-weak type stars”. Hauck et al. (1991) subsequently investigated the same sample as Jaschek et al. using the Geneva photometric system; the metallicity-sensitive indices that calibrate [Fe/H] are the same as those in the Strömgren system.
In this paper we have therefore adopted the expression ip II group/stars to describe stars listed in the literature as members of either the ip II or the F-weak group.
 |
Fig. 1 Photometric plots of the unreddened indices [m1], [c1], and β for λ Bootis (open circles), F-weak (red triangles), and ip II (black triangles) stars. |
3.1.2. Photometric and kinematic data
We employed the Strömgren uvbyβ system search for similarities between the two groups. Figure 1 plots unreddened indices [m1], [c1], and β for λ Bootis stars (Paunzen et al. 2002), F-weak (Jaschek et al. 1989) stars, and ip II stars (Gray 1989). To derive reddening-free parameters we used the definition originally introduced by Strömgren (1966): ![\begin{eqnarray} \left[{m_1}\right]&=&{m_1}+0.18\left(b-y\right), \\ \left[{c_1}\right]&=&{c_1}-0.20\left(b-y\right). \end{eqnarray}](/articles/aa/full_html/2014/07/aa23817-14/aa23817-14-eq36.png) In general, β is temperature sensitive, [m1] correlates with metallicity, and [c1] is correlated with surface gravity and thus with the age of a star for a given spectral type. As the figure indicates, there is no clear separation between the two groups.
In general, β is temperature sensitive, [m1] correlates with metallicity, and [c1] is correlated with surface gravity and thus with the age of a star for a given spectral type. As the figure indicates, there is no clear separation between the two groups.
 |
Fig. 2 Q = |
That result from the photometric data was supported by kinematical data which were computed from proper motions (from the Hipparcos catalogue) and mean radial velocities (from the literature) as described in Johnson & Soderblom (1987). A right-handed coordinate system for U, V, and W was used, so the velocities are positive in the directions of the Galactic centre, Galactic rotation and the North Galactic Pole. The standard solar motion in that system is in units of [km s-1] (+10.4, +14.8, +7.3) according to Mihalas & Routly (1968). For our analysis we adopted the V, and the quantity 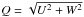 which is a measure of the kinematic energy other than that associated with rotation. Since all velocities are heliocentric, stars with V> − 40 km s-1 and Q< 65 km s-1 are probable disk members (Caloi et al. 1999). Figure 2 plots
which is a measure of the kinematic energy other than that associated with rotation. Since all velocities are heliocentric, stars with V> − 40 km s-1 and Q< 65 km s-1 are probable disk members (Caloi et al. 1999). Figure 2 plots 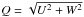 against V. There is no distinction between the two groups in that diagram.
against V. There is no distinction between the two groups in that diagram.
 |
Fig. 3 Different element abundances for the star groups investigated. The λ Bootis stars are clearly separated. |
The following conclusion can be drawn from this analysis:
-
There are no obvious differences between the sample chosen byGray (1989) and the one selected by Jascheket al. (1989). This means thatip II and F-weak type stars are simply names forthe same group of stars.
3.2. The groups of λ Bootis and ip II stars
One of the most important features that distinguishes λ Bootis from other stellar groups is their unusual abundance patterns. Although the light elements have solar abundances, the heavier elements are overabundant but nearly to the same extent. This means that, for example, silicon shows more or less the same amount of overabundance as iron. We therefore investigated these abundance characteristics shown by our selected sample. Figure 3 shows the results for three different combinations: [Fe/C] versus [Fe/H], [Fe/O] versus [Fe/H], and [Fe/H] versus [Ca/H]. In all three diagrams, the ip II stars are located among the normal non-peculiar objects, the λ Bootis stars are clearly separated from them, and the light elements are offset by −0.5 dex. The behaviour of the heavier elements was then examined for possible correlations between the samples in respect of [Fe/H] versus [Ca/H]. For the normal, ip II, and λ Bootis samples (see Fig. 3) we derived ![\begin{eqnarray} \left[\mathrm{Fe/H}\right]&=&-0.01\left(2\right)+0.32\left(9\right)\left[\mathrm{Ca/H}\right]\!,N=95, \\ \left[\mathrm{Fe/H}\right]&=&-0.25\left(4\right)+0.26\left(9\right)\left[\mathrm{Ca/H}\right]\!,N=26,\\ \left[\mathrm{Fe/H}\right]&=&-0.68\left(13\right)+0.40\left(11\right)\left[\mathrm{Ca/H}\right]\!,N=24, \\ \left[\mathrm{Fe/H}\right]&=&-0.32\left(11\right)+0.83\left(12\right)\left[\mathrm{Ca/H}\right]\!,N=23. \end{eqnarray}](/articles/aa/full_html/2014/07/aa23817-14/aa23817-14-eq42.png) here N denotes the number of available individual abundances for each star group.
here N denotes the number of available individual abundances for each star group.
The last correlation did not include the outlier (HD 91130) which has a calcium abundance of −3.0 dex. The first two samples show a slope of about 0.30 whereas the λ Bootis stars show almost no slope. The ip II sample overlaps the normal stars across a wide range of abundances.
 |
Fig. 4 Q = |
From this analysis, we define a λ Bootis star on the basis of elemental abundances if
-
1.
[C/H] < −0.50 – [Fe/C],
-
2.
[O/H] < −0.50 – [Fe/O],
-
3.
[Fe/H] < −0.50,
-
4.
Heavy elements scale with [Fe/H].
This definition separates the ip II stars from λ Bootis stars.
We also analysed the photometric and kinematic data of both groups. (see Sect. 3.1). Figure 1 plots the unreddened indices [m1], [c1], and β. The λ Bootis stars scarcely overlap at all with the ip II objects. That characteristic could become an additional criterion for distinguishing both groups.
Figure 4 shows the kinematic data for the λ Bootis stars and the ip II (Table 1) sample. The two outliers (HD 6870 and HD 84123) were already been discussed in Paunzen et al. (2002). Their U and W velocities qualify them as being Population I objects. In respect of our total sample, we can state that they all belong kinematically to the Galactic disk. We therefore conclude that there is no distinction between the vast majority of the members of either group on the basis of their kinematic data.
[Z] values for the λ Bootis stars (from Paunzen et al. 2002) using individual elemental abundances.
3.3. Evolutionary status and metallicity
In order to investigate the possibility of an intrinsic chemical peculiarity in the λ Bootis stars, we calculated individual [Z] values for 26 objects whose abundances are listed in Table 5 of Paunzen et al. (2002). The absolute mass fraction abundances (χ) were taken from Grevesse et al. (1996); [Z]⊙ = 0.017. Where light-element abundances were not known, the value for carbon was used; the value for iron was adopted as representative of Fe-peak elements. In total, we included all elements for which χ> 10-8. Table 4 lists our results for the sample. The light elements (C, N, O, and S) distribute the most, in absolute numbers, for [Z]. Therefore, two stars (HD 74873 and HD 106223) even have absolute overabundances with [Z] = 0.024, while all other objects have values as low as 0.006. As a next step, we examined the relationship between metallicity and ages by selecting isochrones from (from Bressan et al. 2012) for the corresponding metallicity values. Figure 5 plots the Hertzsprung-Russell diagram for the corresponding range of [Z]. Several stars lie beyond the terminal-age main sequence (luminosity class IV), but none close to the zero-age main-sequence. The complete metallicity range is compatible with the observed data, so (within the errors) no objects is located below the zero-age main sequence (which from an astrophysical standpoint would not be possible).
 |
Fig. 5 λ Boo stars in the Hertzsprung-Russell diagram, with isochrones from Bressan et al. (2012) for the whole range of [Z] values listed in Table 4. |
4. Conclusions and outlook
We investigated a possible connection between the λ Bootis stars and intermediate Population II, F-weak stars on the basis of elemental abundances and kinematic data. It tackled the important questions whether the λ Boo stars are intrinsically metal-weak, and thus belong to the intermediate Population II, or whether their ususual abundances are restricted to the outer layers of the atmosphere. Recent results from an asteroseismologic study suggest the former. If so, the λ Bootis stars become even more interesting, especially those in which accretion disks have been detected.
Our analysis of 38 ip II/F-weak stars was based on detailed element abundances, including the light elements carbon and oxygen, and kinematic data from the Hipparcos catalogue.
First we investigated whether the ip II and F-weak stars are separate groups or whether the names are merely synonyms for identical objects. From photometric, spectroscopic and kinematic data, we conclude that the two groups are indeed identical.
We then compared the elemental abundances of normal, λ Bootis, and ip II stars. The ip II group overlaps with the normal stars, but is completely separated from the λ Bootis objects. We, therefore, defined four constraints regarding the discrimination of both groups. From the kinematic data, no similar differentiation can be drawn.
Finally, we calculated the overall [Z] values for the λ Bootis stars and plotted them, along with corresponding isochrones, in the Hertzsprung-Russells diagram. Using metal-poor isochrones would shift several stars beyond the terminal-age main sequence.
As independent tests, we propose that asteroseismological studies (Casas et al. 2009) be made of pulsating members, and that spectroscopic binary systems (Iliev et al. 2002) containing λ Bootis-type components be investigated. One very interesting star in that respect is HD 210111, which is a δ Scuti pulsator in a spectroscopic binary system.
Another interesting stellar system is the eclipsing binary HR 854 (τ Persei). The primary is a late G-type giant, and the secondary could belong to the λ Bootis group (Griffin et al. 1992). Its K-line type is earlier than derived from the hydrogen lines (Ginestet & Carquillat 2002). Therefore, this system is an excellent test for fitting isochrones of different metallicities.
Acknowledgments
This project is financed by the SoMoPro II programme (3SGA5916). The research leading to these results has acquired a financial grant from the People Programme (Marie Curie action) of the Seventh Framework Programme of EU according to the REA Grant Agreement No. 291782. The research is further co-financed by the South-Moravian Region. It was also supported by the grant 7AMB14AT015, the financial contributions of the Austrian Agency for International Cooperation in Education and Research (BG-03/2013 and CZ-09/2014), NSF grant 01/7 − DNTS AT, and the Austrian Research Fund via the project FWF P22691-N16. We thank our referee, Elizabeth Griffin, for her efforts to significantly improve this paper. This work reflects only the author’s views and the European Union is not liable for any use that may be made of the information contained therein.
References
- Adelman, S. J. 1991, MNRAS, 252, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Adelman, S. J. 1994, MNRAS, 271, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Adelman, S. J. 1996, MNRAS, 280, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Adelman, S. J., Bolcal, C., Hill, G., & Kocer, D. 1991, MNRAS, 252, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Adelman, S. J., Caliskan, H., Kocer, D., & Bolcal, C. 1997, MNRAS, 288, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Blauuw, A. 1965, in Galactic Structure, eds. A. Blauuw, & M. Schmidt (Chicago: University of Chicago Press), 435 [Google Scholar]
- Booth, M., Kennedy, G., Sibthorpe, B., et al. 2013, MNRAS, 428, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M., Beck, P., Lenz, P., et al. 2006, A&A, 455, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Caliskan, H., & Adelman, S. J. 1997, MNRAS, 288, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Caloi, V., Cardini, D., D’Antona, F., et al. 1999, A&A, 351, 925 [NASA ADS] [Google Scholar]
- Casas, R., Moya, A., Suárez, J. C., et al. 2009, ApJ, 697, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Bagnulo, S., Monier, R., et al. 2007, A&A, 476, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginestet, N., & Carquillat, J. M. 2002, ApJS, 143, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, R. O. 1989, AJ, 98, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., Noels, A., & Sauval, A. J. 1996, in Cosmic Abundances, eds. S. S. Holt, & G. Sonneborn, ASP Conf. Ser., 99, 117 [Google Scholar]
- Griffin, R. E. M., Schroder, K. P., Misch, A., & Griffin, R. F. 1992, A&A, 254, 289 [NASA ADS] [Google Scholar]
- Hauck, B., Jaschek, C., Jaschek, M., & Andrillat, Y. 1991, A&A, 252, 260 [NASA ADS] [Google Scholar]
- Hill, G. M. 1995, A&A, 294, 536 [NASA ADS] [Google Scholar]
- Hill, G. M., & Landstreet, J. D. 1993, A&A, 276, 142 [NASA ADS] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iliev, I. Kh., Paunzen, E., Barzova, I. S., et al. 2002, A&A, 381, 914 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaschek, M., Andrillat, Y., & Jaschek, C. 1989, A&A, 218, 180 [NASA ADS] [Google Scholar]
- Johnson, D. R. H., & Soderblom, D. R. 1987, AJ, 93, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Kamp, I., & Paunzen, E. 2002, MNRAS, 335, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Kobi, D., & North, P. 1990, A&AS, 85, 999 [NASA ADS] [Google Scholar]
- Kochukhov, O. 2007, Spectrum synthesis for magnetic, chemically stratified stellar atmospheres, in Magnetic Stars 2006, eds I. I. Romanyuk, D. O. Kudryavtsev, O. M. Neizvestnaya, & V. M. Shapoval, 109, 118 [Google Scholar]
- Künzli, M., North, P., Kurucz, R. L., & Nicolet, B. 1997, A&AS, 122, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kurucz, R. 1993, ATLAS9: Stellar Atmosphere Programs and 2 km s-1 grid. Kurucz CD-ROM No. 13 (Cambridge: Smithsonian Astrophysical Observatory) [Google Scholar]
- Landstreet, J. D., Kupka, F., Ford, H. A., et al. 2009, A&A, 503, 973 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinez-Galarza, J. R., Kamp, I., Su, K. Y. L., et al. 2009, AJ, 694, 165 [Google Scholar]
- McCarthy, J. K., Sandiford, B. A., Boyd, D., & Booth, J. 1993, PASP, 105, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., & Routly, P. M. 1968, Galactic Astronomy, Freeman & Co., San Francisco, 101 [Google Scholar]
- Moon, T. T., & Dworetsky, M. M. 1985, MNRAS, 217, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Napiwotzki, R., Schoenberner, D., & Wenske, V. 1993, A&A, 268, 653 [NASA ADS] [Google Scholar]
- Netopil, M., Paunzen, E., Maitzen, H. M., North, P., & Hubrig, S. 2008, A&A, 491, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olsen, E. H. 1979, A&AS, 37, 367 [NASA ADS] [Google Scholar]
- Paunzen, E., Kamp, I., Iliev, I. Kh., et al. 1999, A&A, 345, 597 [NASA ADS] [Google Scholar]
- Paunzen, E., Iliev, I. Kh., Kamp, I., & Barzova, I. 2002, MNRAS, 336, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Paunzen, E., Kamp, I., Weiss, W. W., & Wiesemeyer, H. 2003, A&A, 404, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paunzen, E., Heiter, U., Fraga, L., & Pintado, O. 2012, MNRAS, 419, 3604 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Robin, A., & Crézé, M. 1986, A&A, 157, 71 [Google Scholar]
- Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., Kupka, F., & Weiss, W. W. 1999, Phis. Scr. T, 83, 162 [Google Scholar]
- Shulyak, D., Tsymbal, V., Ryabchikova, T., Stütz, Ch., & Weiss, W. W. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sitnova, T. M., Mashonkina, L. I., & Ryabchikova, T. A. 2013, Astron. Lett., 39, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Le Campion, J.-F., Cayrel de Strobel, G., & Caillo, A. 2010, A&A, 515, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strömgren, B. 1964, Astrophys. Norv., 9, 333 [Google Scholar]
- Strömgren, B. 1966, ARA&A, 4, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y., Kang, D.-I., Han, I., Lee, B.-C., & Kim, K.-M. 2009, PASJ, 61, 1165 [NASA ADS] [Google Scholar]
- Tsymbal, V. V. 1996, in Model Atmospheres and Spectral Synthesis, eds. S. J. Adelman, F. Kupka, & W. W., Weiss, ASP Conf. Ser., 108, 198 [Google Scholar]
- van Leeuwen, F. 2009, A&A, 497, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varenne, O., & Monier, R. 1999, A&A, 351, 247 [NASA ADS] [Google Scholar]
- Venn, K. A., & Lambert, D. L. 1990, ApJ, 363, 234 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Element abundances for our sample of stars, relative to the solar values given by Grevesse et al. (1996).
Differences between our derived values for the target sample and those in the Geneva-Copenhagen survey (GCS, Holmberg et al. 2009) and the PASTEL catalogue (Soubiran et al. 2010).
[Z] values for the λ Bootis stars (from Paunzen et al. 2002) using individual elemental abundances.
All Figures
 |
Fig. 1 Photometric plots of the unreddened indices [m1], [c1], and β for λ Bootis (open circles), F-weak (red triangles), and ip II (black triangles) stars. |
| In the text | |
 |
Fig. 2 Q = |
| In the text | |
 |
Fig. 3 Different element abundances for the star groups investigated. The λ Bootis stars are clearly separated. |
| In the text | |
 |
Fig. 4 Q = |
| In the text | |
 |
Fig. 5 λ Boo stars in the Hertzsprung-Russell diagram, with isochrones from Bressan et al. (2012) for the whole range of [Z] values listed in Table 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.