| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A126 | |
| Number of page(s) | 31 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201323263 | |
| Published online | 28 July 2014 | |
Warsaw Catalogue of cometary orbits: 119 near-parabolic comets⋆
Space Research Centre of the Polish Academy of Sciences, Bartycka 18A, 00-716 Warsaw, Poland
e-mail: mkr@cbk.waw.pl
Received: 17 December 2013
Accepted: 23 May 2014
Context. The dynamical evolution of near-parabolic comets strongly depends on the starting values of the orbital elements derived from the positional observations. In addition, when drawing conclusions about the origin of these objects, it is crucial to control the uncertainties of orbital elements at each stage of the dynamical evolution.
Aims. I apply a completely homogeneous approach to determine the cometary orbits and their uncertainties. The resulting catalogue is suitable for the investigation of the origin and future of near-parabolic comets.
Methods. First, osculating orbits were determined on the basis of positional data. Second, the dynamical calculations were performed backwards and forwards up to 250 au from the Sun to derive original and future barycentric orbits for each comet. In the present investigation of dynamical evolution, the numerical calculations for a given object start from the swarm of virtual comets constructed using the previously determined osculating (nominal) orbit. In this way, the uncertainties of orbital elements were derived at the end of numerical calculations.
Results. Homogeneous sets of orbital elements for osculating, original and future orbits are given. The catalogue of 119 cometary orbits constitutes about 70 per cent of all the first class so-called Oort spike comets discovered during the period 1801−2010 and about 90 per cent of those discovered in 1951−2010, for which observations were completed at the end of 2013. Non-gravitational (NG) orbits are derived for 45 comets, including asymmetric NG solution for six of them. Additionally, the new method for cometary orbit-quality assessment is applied for all these objects.
Key words: catalogs / comets: general / Oort Cloud
The catalogue is available at ssdp.cbk.waw.pl/LPCs and also at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/567/A126
© ESO, 2014
1. Introduction
This catalogue presents for the first time the osculating, original and future orbital elements of near-parabolic comets that were determined by myself and in their majority were further investigated in collaboration with Piotr A. Dybczyński from the Astronomical Observatory Institute at Poznań. In a series of papers, i.e. Królikowska & Dybczyński (2010, hereafter Paper 1), Dybczyński & Królikowska (2011, Paper 2), Królikowska et al. (2012, Paper 3) and Królikowska & Dybczyński (2013, Paper 4), we focused on the problem of the origin of near-parabolic comets with original inverse semi-major axes inside the so-called Oort spike. Investigating the dynamical orbital evolution of these observed Oort-spike comets to the previous perihelion passage, we showed that only part of them make their first visit into the planetary zone, that is, we found that barely 50 per cent of these comets have a previous perihelion distance below 15 au (Paper 2).
The catalogue presents a homogeneous set of osculating orbits of just such comets, the nongravitational effects were determined for more than 40 per cent of them. The full sample of 119 comets forming this catalogue constitutes almost 70 per cent of all first class so-called Oort spike comets (condition of 1 /aori< 150 × 10-6 au-1 was taken with a spare) discovered during the period of 1801–2010, ~90 per cent of those discovered in the years 1951−2010, for which observations were completed at the end of 2013. The completeness of all three subsamples of these comets is presented in more detail in Sect. 3. In the next years the catalogue will be supplemented by comets discovered a long time ago, and will be updated with newly discovered objects after 2010. In particular, the complete sample of comets discovered during the years 1901−1950 is under consideration as an independent project of the New Catalogue of One-Apparition Comets, the first part of which, that includes 38 comets with 1 /aori ≤ 0.000130 au-1 according to Marsden & Williams Catalogue (2008, hereafter MWC 08), is completed.
The paper is organized as follows: in the next section, I shortly describe the methods and model of motion applied to orbital determinations. In some cases the non-gravitational (hereafter NG) orbits were determinable, thus a brief description of the adopted model of NG acceleration is given in Sect. 2.1. Since the new method for evaluating the quality of osculating cometary orbits is used in the present catalogue, the accuracy of the cometary orbit is discussed in some detail in Sect. 2.2. The last part of Sect. 2 describes how the original and future orbits and their uncertainties were determined. Section 3 is divided into four parts that deal with tabular parts of the catalogue given in appendices. Thus, this section includes a general description of the observational material of the analysed comets (Part I of the catalogue), as well as osculating orbital elements (Part II), and original and future orbital elements (Parts III and IV). The article ends with concluding remarks on the accuracy of orbital solutions given in the catalogue and future plans (Sect. 4).
This publication is accompanied by an online catalogue also providing entries to full swarms of original and future virtual comets (hereafter VCs, see Sect. 2.3) that formed the basis for the detailed analysis of dynamical evolution presented in Papers 1–4. Thus, this catalogue also allows one to construct and analyse the observed distribution of Oort spike comets and to investigate the problem of cometary origin.
2. Methods and assumptions
For each comet from the catalogue, I determined the osculating nominal orbit (GR – pure gravitational or NG if possible; see next subsection) based on the astrometric data, selected and weighted according to the methods described in great detail in Paper 1. This allowed me to construct a homogeneous sample of cometary osculating orbits as well as homogeneous samples of original and future orbits.
The equations of a comet’s motion were integrated numerically using the recurrent power series method (Sitarski 1989, 2002), taking into account perturbations by all the planets (additionally, Pluto was taken into account to be consistent with DE405/WAW) and including the relativistic effects. All orbital calculations performed for this catalogue were based on the Warsaw numerical ephemeris DE405/WAW of the solar system (Sitarski 2002), consistent with a high accuracy with the JPL ephemeris DE405.
2.1. Nongravitational model of motion applied to orbit determination
To determine the NG cometary orbit the standard formalism proposed by Marsden et al. (1973, hereafter MSY) was used where the three orbital components of the NG acceleration acting on a comet are scaled with a function g(r) symmetric relative to perihelion:
![\begin{eqnarray} &&F_{i}=A_{i}\cdot g(r) ,\qquad A_i={\rm ~const.~~for}\quad{i}=1,2,3,\label{eq:g_r}\\ & & g(r) =\alpha\left(r/r_{0}\right)^{-2.15}\left[1+\left(r/r_{0}\right)^{5.093}\right]^{-4.614},\label{eq:ng_std} \end{eqnarray}](/articles/aa/full_html/2014/07/aa23263-13/aa23263-13-eq8.png) where F1,F2,F3 are the radial, transverse and normal components of the NG acceleration, respectively, and the radial acceleration is defined outward along the Sun-comet line. The normalization constant α = 0.1113 gives g(1 AU)= 1; the scale distance r0 = 2.808 AU. From orbital calculations, the NG parameters A1, A2, and A3 were derived together with six orbital elements within a given time interval (numerical details are described in Królikowska 2006). The standard NG model assumes that water sublimates from the whole surface of an isothermal cometary nucleus. The asymmetric model of NG acceleration is derived by using function g(r(t − τ)) instead of g(r(t)). Thus, this model introduces an additional NG parameter τ – the time displacement of the maximum of the g(r) relative to the moment of perihelion passage.
where F1,F2,F3 are the radial, transverse and normal components of the NG acceleration, respectively, and the radial acceleration is defined outward along the Sun-comet line. The normalization constant α = 0.1113 gives g(1 AU)= 1; the scale distance r0 = 2.808 AU. From orbital calculations, the NG parameters A1, A2, and A3 were derived together with six orbital elements within a given time interval (numerical details are described in Królikowska 2006). The standard NG model assumes that water sublimates from the whole surface of an isothermal cometary nucleus. The asymmetric model of NG acceleration is derived by using function g(r(t − τ)) instead of g(r(t)). Thus, this model introduces an additional NG parameter τ – the time displacement of the maximum of the g(r) relative to the moment of perihelion passage.
In the present catalogue, NG solutions were determined for 45 near-parabolic comets, including asymmetric NG solution for six of them (C/1959 Y1, C/1990 K1, C/1993 A1, C/2007 N3, C/2007 W1 and C/2008 A1). Moreover, 66 per cent of comets with small perihelion distance have NG orbits in the catalogue (33 of 50; see samples A1 and A2 in Sect. 3.1 and Table A.1).
NG parameters for all NG solutions given in this catalogue are presented in Table A.4 in Part II of this catalogue. One can see in Fig. 1 that NG accelerations at perihelion derived for near-parabolic comets are below the 10-3 of solar gravitational acceleration with a typical value of about 10-4·F⊙.
2.2. Accuracy of the cometary orbit
In 1978 Marsden et al. (1978, hereafter MSE) formulated the recipe to evaluate the accuracy of the osculating cometary orbits obtained from the positional data. They proposed to measure this accuracy by the quantity Q defined as 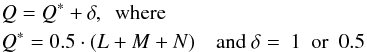 (3)to make Q an integer number, and L denotes a small integer number that depends on the mean error of the determination of the osculating 1 /a, M is a small integer number that depends on the time interval covered by the observations, and N is a small integer number that reflects the number of planets whose perturbation were taken into account.
(3)to make Q an integer number, and L denotes a small integer number that depends on the mean error of the determination of the osculating 1 /a, M is a small integer number that depends on the time interval covered by the observations, and N is a small integer number that reflects the number of planets whose perturbation were taken into account.
Values of L, M and N are obtained following the scheme presented in the original Table II given by MSE. The integer Q-value calculated from Eq. (3) should next be replaced with the orbit quality class as follows: a value of Q = 9,8 means orbit of orbital class 1A, Q = 7 of class 1B, Q = 6 of class 2A, Q = 5 of class 2B, and Q< 5 means lower than second-class orbit.
In Paper 4 we discussed three reasons for which we found that some modifications of the above recipe of orbital accuracy estimation should be done. Briefly, these are the following:
-
1.
In the modern orbit determination all solar system planets arealways taken into account, therefore we always have N = 3.
-
2.
Current cometary positional observations are generally of significantly higher precision than 30 years ago. Moreover, modern LPCs are often observed much longer in time than the four years predicted by MSE in their scheme. Thus, the possibility of arbitrarily low values of a mean error of 1 /aosc and an arbitrarily long time span of observations should be included to the original Table II given by MSE.
-
3.
Almost all orbits of currently discovered LPCs should be classified as quality class 1A using the MSE quality scheme. Therefore, a better diversification between orbit accuracy classes is necessary. We realized this postulate by new δ-definition and introducing three quality classes 1a+, 1a and 1b instead of the former 1A and 1B.
The final form of a new orbital quality scheme was constructed after an inspection of orbital uncertainties and data intervals in the sample of 22 comets discovered in the years 2006−2010 (Paper 4), and samples of near-parabolic comets from Papers 1−3. The new scheme proposed in Paper 4 is based on a slightly modified Eq. (3): 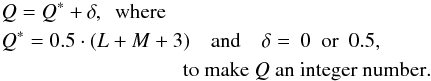 (4)To distinguish the proposed quality system from the MSE system, in Paper 4 we used the lower-case letters “a” and ‘b” in quality class descriptions instead of the original “A” and “B” in the following way: Q = 9 – class 1a+, Q = 8 – class 1a, Q = 7 – class 1b, Q = 6 – class 2a, Q = 5 – class 2b, Q = 4 – class 3a, Q = 3 – class 3b, and Q ≤ 2 – class 4, where Q is calculated according to Eq. (4). The quality classes 3a, 3b and 4 were not defined by MSE, but we adopted here the idea published by IAU Minor Planet Center Web Pages (2013) as “a logical extension to the MSE scheme”.
(4)To distinguish the proposed quality system from the MSE system, in Paper 4 we used the lower-case letters “a” and ‘b” in quality class descriptions instead of the original “A” and “B” in the following way: Q = 9 – class 1a+, Q = 8 – class 1a, Q = 7 – class 1b, Q = 6 – class 2a, Q = 5 – class 2b, Q = 4 – class 3a, Q = 3 – class 3b, and Q ≤ 2 – class 4, where Q is calculated according to Eq. (4). The quality classes 3a, 3b and 4 were not defined by MSE, but we adopted here the idea published by IAU Minor Planet Center Web Pages (2013) as “a logical extension to the MSE scheme”.
How to calculate the quantities L and M is described in Table 1, which is a simpler form of the original Table II given by MSE. We only introduced in this table the possibility of arbitrarily low values of a mean error of 1 /aosc and an arbitrarily long time span of observations, and, as mentioned before, we completely removed the redundant column describing the number of planets taken into account in the orbit determination process. Instead, we set N = 3 in Eq. (4). Thus, the mean error of 1 /aosc smaller than 1 unit (i.e. 1 × 10-6 au-1) now gives L = 7 and a time span of data longer than 48 months results in M = 8.
This new orbit quality scheme separates the orbits of very good quality in MSE system, 1A, into three quality classes in the new system, where the lowest of orbits in class 1A (Q∗ = 7) in the MSE system are classified as 1b in the new scheme.
Quantities for establishing accuracy of orbit.
2.3. Original and future orbits
To calculate the original and future orbital elements as well as their uncertainties (taken at 250 au from the Sun where planetary perturbations are negligible) the dynamical calculations for swarms of starting osculating orbits were performed for each catalogue comet. Each swarm was constructed according to the Monte Carlo method proposed by Sitarski (1998), where the entire swarm fulfil the Gaussian statistics of fitting to positional data used for a given osculating orbit determination (examples are in Paper 1). Each swarm consists of 5001 VCs including the nominal orbit; this number of orbital clones gives a sufficient sample to obtain reliable statistics at 250 au from the Sun. Values of uncertainties of original/future orbital elements were derived by fitting the distribution of a given orbital element of an original/future swarm of VCs to Gaussian distribution. All distributions of orbital elements including 1 /a distributions of analysed comets were still perfectly Gaussian at 250 au from the Sun.
3. The catalogue
3.1. Description and structure of tabular materials
To avoid very long tables with dozens of entries in each row it was convenient to divide the tabular material into four general parts.
-
Part I. Description of the observational material
Table A.1 describes the sets ofpositional observations taken for each orbit determination andgives the new quality assessment of derived osculating orbitsusing the scheme proposed in Paper 4. The presentation of considered comets is separated into threesamples.
-
Sample A1
This sample consists of28 near-parabolic comets ofqosc< 3.1 au and 1 /aori< 150 × 10-6 au-1 discovered before the year 2006. Sample A1 is very incomplete and includes 40 per cent of all discovered LPCs that fulfil the above conditions (see Table 2). Most comets from this sample (except for six objects, see Table A.1) have NG orbits, and these solutions are characterized by a clear decrease in root-mean-square error (rms) compared with the rms for GR orbits, only C/1974 F1 displays a slight decrease of rms for NG solution. Orbital solutions for most comets belonging to this sample were used for dynamical evolution discussed in Papers 1–3. However, three comets analysed in these papers (C/1913 Y1, C/1940 R2 and C/1946 U1) are not presented here because they are included in the independent project of the New Catalogue of One-Apparition Comets from the Years 1901–1950, Part I of which is just completed. In the present catalogue the new NG solutions are given for C/1990 K1, C/1993 A1, C/2002 T7 (POST type of data), C/2003 K4, and four new comets are added to the sample analysed previously (C/2001 B1, C/2002 Q5, C/2003 T3, C/2005 E2, Sect. 2.1 and Table A.1.
-
This is a complete sample of 22 comets of qosc< 3.1 au and 1 /aori< 150 × 10-6 au-1 discovered in the period 2006–2010 (Table 2). NG solutions are determined for eleven of them. These comets were examined in Paper 4.
-
This is an almost complete sample of 69 comets of qosc> 3.1 au and 1 /aori< 150 × 10-6 au-1 discovered in the period 1970−2010; the missing four comets (C/2008 S3, C/2009 F4, C/2010 S1, and C/2010 U3) were still observed at the end of 2013. Orbits of six comets of Sample B were redetermined using longer data intervals than those used in Papers 1–2 (C/1997 A1, C/1999 F1, C/1999 N4, C/1001 J4, C/2003 S3, and C/2005 K1, see notes 3–8 to Table A.1) and the sample was enriched with ten comets in comparison to previous analyses (C/2005 L3, C/2006 S3, C/2007 D1, C/2007 VO53, C/2008 FK75, C/2008 P1, C/2009 P2, C/2009 U5, C/2010 D3, and C/2010 R1). Twelve comets from this sample have NG orbits in the present catalogue.
-
Sample A1
-
Part II. Osculating orbital elements
Tables A.1−A.3 show heliocentric osculating orbital elements for all objects structured in accordance with Table A.1. Table A.4 gives the NG parameters for all comets with NG orbits in the catalogue.
-
Tables C.1−C.3 include the original barycentric orbits in the same order.
The entire catalogue, that is, all tables given in appendices, is made available also through the Strasbourg Astronomical Data Centre (CDS).
Completeness of the sample of comets in the present catalogue in comparison to MWC 08 as a function of the time distribution of cometary discovery (five periods given in Col. [1]) and the perihelion distance (qosc< 3.1 au or qosc ≥ 3.1 au, Cols. [2], [3] and [4], [5], respectively).
 |
Fig. 1 Maximum NG accelerations, FNG,perih, as a function of perihelion distance for all 45 near-parabolic comets with determinable NG effects. Three samples A1, A2 and B are shown by red, magenta and turquoise symbols, respectively. The dotted curves represent the 10-5, 10-4 and 10-3 of the solar gravitational acceleration F⊙, respectively. NG parameters taken for preparation of this plot are in Part II of this catalogue (Table A.4). |
3.2. Part I of the catalogue. Characteristics of the observational material
This part of the catalogue consists of one extensive table where the description of observational material is given for each comet including the new quality-class assessment proposed in Paper 4 and briefly described in Sect. 2.2.
The full list of catalogue comets is shown in Table A.1 and is available at ssdp.cbk.waw.pl/LPCs.
Table A.1 includes the detailed description of the observational data sets used for osculating orbit determination (Cols. (4 − 8)), type of the best possible model that can be determined using these data (Col. (9)) and then its quality assessment in the proposed new scheme (Col. (12)). The number of residuals used for orbit determination and resulting rms are given in Col. (13), and Col. (14) informs where this solution was used for dynamical studies.
Since Table A.1 is also focused upon the best/preferred orbit for investigating the dynamical origin of near-parabolic comets, the more dedicated models for this purpose are given whenever it is necessary, that is, when even the NG model based on entire data set not fully satisfies three criteria described in detail in Papers 1−4 (based on rms, O−C-diagram and O−C-distribution). This is indicated by subscript “un” in Col. (9) of Table A.1 (some additional details are given in the notes to this table). Thus, for the cases marked NGun in Col. (9), the better models based on some subsample of data are shown in the next rows for a given comet.
For an unsatisfactory solution based on an entire data set, it was found that the best method is to divide the data set into pre- and post- perihelion subsets to determine the pre-perihelion and post-perihelion osculating orbit for the purpose of past and future dynamical evolution, respectively (as for example for C/2007 W1), or to construct a dedicated subset of data taken at large heliocentric distances from the Sun (as for C/2001 Q4). Then the preferred models for the past/future dynamical evolution are given in the second/third row of a given object in almost all cases where orbital solution based on the entire data seems to be unsatisfactory (except for two comets, C/1990 K1 and C/1993 A1, where a more individual data treatment has not been taken yet; see also notes to Table A.1 for these comets). It is important to note that in these cases the quality assessment may change as, for example, for comet C/2007 W1 or C/2008 A1.
Therefore, the statistics of orbital classes also depends on types of osculating orbits taken into account. Table 3 shows this statistics for the sample of 119 near-parabolic comets for two sets of osculating orbits: the best osculating orbits determined on the basis of an entire interval of data (second column labelled as “standard”) and the most preferred orbits for the past dynamical investigation (third column labelled as “past evolution”).
Statistics of orbital quality classes for investigated comets (more details in the text).
The osculating orbits corresponding to all models described in Table A.1 as well as their original and future orbits are given in Parts II, III and IV, respectively.
3.2.1. Application of the new scheme of orbital quality assessment
The new quality estimates of the orbits of 119 LPCs are presented in Cols. (10)–(12) of Table A.1.
There is a higher diversification in orbital classes between investigated comets than was found using the original MSE recipe. This can easily be checked by taking the Q∗-values given in Col. (10) or (11) of Table A.1 and using Eq. (4).
In Papers 1–4, the orbit determination is based quite often on a larger data set (in most cases currently available at IAU Minor Planet Center Database 2013) than was used in MWC 08 or at IAU Minor Planet Center Database to obtain the orbital elements given there. Thus, our orbital quality assessment sometimes lists a better quality class than that shown in MWC 08, although our method of quality assessment is more restrictive (see numerous notes appended to Table A.1).
3.2.2. Sample A1. Near-parabolic comets of qosc< 3.1 au discovered before the year 2006
The modified method of orbital quality determination was applied to pure GR as well as to NG orbits of analysed small perihelion comets. All Oort spike comets were chosen from MWC 08 as objects with highest quality orbits (classes 1A or 1B) or with an NG orbit1.
Table A.1 shows that of the 28 comets of qosc< 3.1 au almost all have determinable NG orbits; C/1992 J1, C/2001 B1, C/2001 K3, C/2002 Q5, C/2003 T3, and C/2005 E2 are six exceptions. We found that six comets from this sample should be classified as second-quality orbit according to new, more restrictive method (see Table 4). Uncertainties of 1 /aosc are lower than 20 in units of 10-6 au-1 for five of them (Col. (3) of Table 4), which means that they are significantly poorer than for the remaining comets in this sample. All five have NG orbits, which is a natural consequence because more parameters were used for the orbit determination (six orbital elements plus NG parameters). For the sixth comet, C/2001 K3, only a pure GR orbit was determinable and its second-class quality of osculating orbit is mainly due to a very short time interval.
Additionally, from seven comets with an NG orbit in MWC 08 only three listed in Table 4 have second-quality orbits according to the modified method (applying the original MSE method to our orbit determinations – only two comets). Some comment is needed for C/1952 W1. In Paper 1, we determined an osculating orbit from 36 positional observations taken from the literature2. This is in fact the only comet, for which we had determined the orbit on the basis of fewer measurements than in the MWC 08; for more details see Paper 1. Thus, the MWC 08 describes an orbit of C/1952 W1 as 1B class (64 observations, the data interval is the same as ours), whereas using the MSE method for our orbit determination we obtain class 2A (Cols. 2 and 3 of Table 4).
According to the more restrictive orbital quality assessment in the sample of 28 comets we obtained 8 comets of class 1a+, 4 comets of class 1a, 10 of class 1b, 5 of class 2a, and 1 object of class 2b in this sample.
3.2.3. Sample A2. Near-parabolic comets of qosc< 3.1 discovered in the years 2006–2010
In Paper 4 we selected all near-parabolic comets discovered in the years 2006–2010 that have small perihelion distances, qosc< 3.1 au, and 1 /aori< 0.000150 au-1. According to the proposed method of orbital quality assessment we have in this sample a lower fraction of comets of the best orbital classes: 11 instead of 15 derived using the MSE quality system. Additionally, these 11 comets are now divided into five comets of class 1a+ and six comets of class 1a using the entire data sets shown in Table A.1 in the first row of a given object. Moreover, the orbit of one comet, C/2008 C1, is reclassified as a second-class orbit. For more details see Paper 4.
3.2.4. Sample B. Near-parabolic comets of qosc≥ 3.1 au discovered in the period 1970–2010
In the sample of comets with large perihelion distances, the lowest value of Q∗ (Eq. (4)) is 6.0 for two comets, C/2006 YC and C/2007 Y1 (Table 5). Therefore, orbits of these two comets should be classified as second quality (2a class), according to our more restrictive method. In MWC 08, both orbits were classified as class 2A probably because of the very short intervals of observations, two months for C/2006 YC and 2.5 months for C/2007 Y1 (Col. 2 of Table 5). The current orbits of these two comets are based on almost periods of data twice as long, 4 and 4.5 months, respectively, which resulted in improving the quality of orbits from second to first class when using the MSE method of quality assessment (Col. 3 of Table 5). For this reason, these two comets were also investigated by us in Paper 2.
Three comets with greatest 1 /aosc uncertainties in this sample, C/1978 G2 (37.9 × 10-6 au-1), C/1983 O1 (20.5 × 10-6 au-1) and C/1976 U1 (21.5 × 10-6 au-1), now have class 1b, 1a, 1b (1B, 1A and 1B in MWC 08), respectively, because of the relatively long time interval of data. C/1983 O1 stands out among them because of the longest data interval (7.5 years) and the closest perihelion distance of 3.3 au to the Sun, which allowed determining the NG orbit (Paper 2). The remaining two comets have qosc> 5.5 au, so any NG traces in the motion, and data intervals shorter than two years. In general, the NG orbit (if determinable) seems to be closer to the actual motion of a given comet than the pure GR orbit, but when the NG parameters are included in the orbit determinations this can result in significantly grater uncertainties of orbital elements than for the pure GR orbit. This is the case of C/1983 O1, where the uncertainty of 1 /a determination of NG orbit is one order of magnitude larger (20.5 × 10-6 au-1) than for GR orbit (1.5 × 10-6 au-1). When NG orbits, although they are more realistic than pure GR orbits, are characterized by significantly larger uncertainties of orbital elements than GR orbits, then the second parameter of orbital quality assessment, the time interval of data, plays an important role, as for C/1983 O1.
Comets of class 1A or 1B or NG orbits according to MWC 08 and with orbital quality poorer than first class according to the proposed, modified classification of orbit quality for 28 small-perihelion comets (qosc< 3.1 au).
According to our new orbital quality assessment, we obtained 24 comets of class 1a+, 36 comets of class 1a, 7 of class 1b, and 2 objects of class 2a in sample B.
3.3. Part II of the catalogue. Osculating orbital elements
This part of the catalogue consists of three tables (Tables A.1−A.3) including samples A1, A2 and B, respectively. Each of them contains the comet designation and its name (Col. (1)), epoch (osculation date, Col. (3)) and the six heliocentric orbital elements usually given for comets (Cols. (3)–(9)), that is, perihelion time (TT), perihelion distance (in astronomical units), eccentricity, argument of perihelion (in degrees, equinox 2000.0), longitude of ascending node (in degrees, equinox 2000.0), and inclination (in degrees, equinox 2000.0). Additionally, the inverse semi-major axis is presented in Col. (9).
The astrometric data sets used for each orbital solution determination are presented in Part I of the catalogue (Table A.1).
The NG parameters for all NG osculating orbits included in the catalogue (i.e. for 45 comets, see Table A.1) are shown in the separate Table A.4. Most comets from sample A1 have NG orbits (almost 80 per cent). These NG solutions are characterized by a clear decrease in rms compared with the rms for purely GR orbits, only for C/1974 F1 this decrease is infinitesimal. Sample A2 includes 11 osculating NG orbits, thus 50 per cent of comets discovered in the period of 2006−2010 with a small perihelion distance (qosc< 3.1 au) have determinable NG effects in their motion. On the other hand, only 12 of 69 comets of sample B have NG orbits. For some comets even NG orbits exhibit some trends in O−C time variations. In these peculiar cases the second and sometimes the third orbital solutions are presented. Additional orbits are based on some subsamples of data, as described in Table A.1 (see also Sect. 3.2). These dedicated solutions are more appropriate for studying the origin and/or future evolution of the cometary orbit.
3.4. Part III of the catalogue. Original orbital elements
Similarly as in Part II, three tables (Tables C.1, C.2, and C.3) corresponding to samples A1, A2, and B are presented here. Each of them contains the original barycentric orbits calculated at the distance of 250 au from the Sun. Tables have an analogous structure and entries to those in Part II.
 |
Fig. 2 Distribution of 1 /aori (upper panel), 1 /afut (lower panel) for 119 considered LPCs. The uncertainties of 1 /a determinations were incorporated into these 1 /a histograms by taking the full cloud of VCs for each comet. This means that both distributions are composed of 119 individual normalized 1/a distributions resulting from the dynamical calculations of 5001 VCs. |
To derive the original and future inverse semi-major axis, the dynamical calculations of a swarm of VCs of each individual objects were performed backwards and forwards in time until it reached 250 au from the Sun, that is, at a distance where the planetary perturbations are already completely negligible. Each individual swarm of starting osculating orbits consists of 5001 VCs including the nominal orbit and was constructed according to a Monte Carlo method proposed by Sitarski (1998), where the entire swarm fulfilled the Gaussian statistics of fitting to positional data used for a given osculating (nominal) orbit determination. This method allowed us to determine the uncertainties of original and future orbital elements, including the inverse semi-major axes by fitting each orbital element of original/future swarm of VCs to Gaussian distribution (see Tables C.1−D.3).
The distribution of 1 /aori based on the best solutions derived from past dynamical studies and incorporating the uncertainties of 1 /aori determinations is shown in Fig. 2. The only object from the sample of 119 comets seems to be a serious candidate to interstellar comet (C/2007 W1 Boattini, for more details see Paper 4). The left and negative wing of the main distribution is formed by a few comets with rather broad individual 1 /aori distributions (Gaussians), such as C/1978 G2 (see Table C.3) with a formally negative, but poorly known, inverse semi-major axis of − 22.4 ± 37.8 in units of 10-6 au-1, or by C/1984 W2 with 1 /aori = 36.1 ± 20.2 in the same units. The main peak of 1 /aori is broad and extends between 10 and 65 in units of 10-6 au-1 (aori: ~15 400−100 000 au). More precisely, the calculated 10 and 90 per cent deciles are 11.5 and 74.5 in units of 10-6 au-1, respectively. The median value of the 1 /aori distribution is 37.95 × 10-6 au-1 (aori ≃ 26 300 au). The main part of 1 /aori distribution seems to have a local minimum somewhere between 25−35 in units of 10-6 au-1, but the histogram based on twice wider bins gives a broad single maximum. This dip in broad Oort maximum is exclusively caused by large-perihelion comets. Thus, significantly richer statistics are needed to confirm or refute the double nature of this maximum.
3.5. Part IV of the catalogue. Future orbital elements
This part consists of Tables D.1−D.3 (samples A1, A2, B) giving future barycentric orbits calculated at a distance of 250 au from the Sun.
The 1 /afut distribution constructed from the future orbits presented in these tables are shown in the lower panel of Fig. 2. Fifteen comets (~13 per cent of the sample) have a future inverse semi-major axis within the same range of 0 < 1 /afut< 100 × 10-6 au-1 where the original 1/a distribution is placed, ~51 per cent of comets leave the solar system on hyperbolic orbits, and about 36 per cent of objects have evolved into more tightly bound orbits under the influence of planetary perturbations. The narrow peak in the range | 1 /afut | < 100 × 10-6 au-1 is evident and includes more than 30 per cent of the entire sample. This peak mostly consists of comets with large perihelion distances (qosc> 3.1 au), which means that these comets reproduced 78.5 per cent of the peak, whereas the entire sample of 118 objects taken for this statistics (comet C/2010 X1 Elenin disintegrated shortly after perihelion passage) includes only 69 large-perihelion comets (58 per cent of the sample).
4. Concluding remarks
4.1. About accuracy
 |
Fig. 3 Projection of the 6D space of 5 001 VCs of C/1988 B1 onto six chosen planes of osculating orbital elements. Vertical axes given in the right-hand panels are exactly the same as the vertical axes in the left-hand panels. Each grey point represents a single virtual orbit, while the large red point represents the nominal orbit solution given here and the green point is taken from MWC 08 (see also Table 6). Each plot is centred on the nominal values of the respective pair of osculating orbital elements denoted by the subscript “0”; see also Table 6. |
In this catalogue great care was taken to treat the data completely homogeneously together with an individual approach to determining NG effects wherever it seemed necessary. In Papers 1–2 it was shown that data treatment is crucial for an orbit determination of one-apparition comets and the applied methods of data selection and weighting are there discussed in details. An individual approach was applied when there were any doubts about the O−C time variation of residuals or the O−C distribution of residuals (for the standard model based on the all available data). Thus, sometimes two sets of osculating orbits are offered for a given comet, in particular, for some comets with determinable NG effects. In these cases, the first set always gives the overall model of NG motion derived using the entire set of data. The second set describes the orbit derived using a subset of data, e.g. using only the pre-perihelion data for ingoing leg of orbit, and post-perihelion data for outgoing leg of orbit, respectively (see for example the case of C/2007 T2 or C/2008 A1). This approach was necessary because of the simplicity of the NG model used for orbital calculations (usually three constant NG parameters, see Table A.4). In fact, it was the only possible model for the purpose of such a massive NG determination in the motion of LPCs. A detailed discussion of the different forms of NG accelerations is given in Paper 3 for the two small-perihelion comets C/2001 Q4 and C/2007 T2. In that paper, we showed that determining the exponents for the g(r)-like function is very difficult and, in practice, this was only possible for these two particular comets from the catalogue sample.
An additional note is needed for large-perihelion comets with NG orbits in the catalogue. The g(r)-form of NG accelerations used here describes the water ice sublimation. Thus, this relationship is very coarse for comets with large perihelion distances, where the percentage of the more volatile ices may be relatively high.
In the context of this discussion, we strongly emphasize that all the uncertainties of osculating orbital elements given in the catalogue tables (and hence the uncertainties of original and future orbits) represent the formal errors derived by fitting the assumed model of motion (GR or NG) to positional observations. If it were possible to explore the NG acceleration along the orbit of a given comet more precisely, the solution might be different. How different depends on the case in question. However, as was shown in Paper 3, the scatter of 1 /aori values for various NG models appears to be significantly smaller than the difference between the 1 /a-values between the pure GR and the standard NG model for the two comets examined there. Therefore, it seems that this relatively simple type of model of NG acceleration applied for the purpose of this catalogue gives orbits that are significantly closer to the actual past and future motion of analysed comets. When the various NG orbits are given in the catalogue, a more cautious approach to the formal errors is necessary. For this reason, in the case of comet C/2007 W1 Boattini, which is the best candidate for a comet on an original hyperbolic orbit, the various NG models were taken into account (see Paper 4) to be conclusive about the shape of its barycentric original orbits. We concluded in Paper 4 that all of them indicate that this comet moved on a barycentric hyperbolic orbit before entered the planetary zone. This makes this comet the best candidate to have an interstellar origin among the catalogue comets.
Generally, the GR orbits given in this catalogue differ from the solutions given in MWC 08 or IAU Minor Planet Center Database (2013) by no more than 3σ-error for each orbital element; typically by even less than a 2σ-error. Two representative examples are given in Table 6 for comets C/1988 B1 and C/2002 J4, which have 1a and 1a+ quality class orbit, respectively. Both solutions are based on the data span over long time intervals (more than 4 yr). In the last line for each comet in Table 6 the difference in each orbital element is expressed as combined errors and assuming the same orbital element uncertainties for the solution given in MWC 08 (IAU Minor Planet Center Database 2013) as derived here. Additionally, for C/1988 B1, the solution taken from MWC 08 is compared in Fig. 3 with the swarm of osculating VCs derived for the past and future evolutionary calculations. Orbit of C/1988 B1 given in MWC 08 was determined using 112 residuals (rms = 1.̋00), whereas the orbit presented here was obtained on the basis of 127 residuals (rms = 0.̋98, without weighting of the data).
An extensive discussion of possible differences of the NG solutions given in this catalogue from other published results is presented in Paper 4 for two comets with variable NG effects, C/2007 W1 and C/2008 A1.
For comets with two different NG solutions given in this catalogue, both orbits can be taken by the user to investigate a cometary activity within the observational interval. However, for long-time orbital calculations, the more dedicated orbit is recommended, for example to investigate the cometary origin, the orbit determined using the pre-perihelion data should be taken into account.
The web catalogue also offers the swarms of original and future VCs, that is, the barycentric orbital elements at the distances where planetary perturbations are negligible for all models from Table 2. Thus, the swarms of original and future NG orbits are also available in this catalogue for further investigation by the user.
4.2. Future plans
This catalogue will be supplemented in the future by the sample of one-apparition comets discovered in the first half of the twentieth century. Orbits of such old comets particularly need to be redetermined because they were originally obtained using very different numerical methods and assumptions on the model of the solar system, including the number of planets taken into account. The first part of this long-standing project describing the analysis of 38 comets from the Oort spike will soon be submitted for publication.
One of the issues awaiting for extensive numerical tests is whether the gravitational influence of the mass of the asteroid belt, Kuiper Belt, and Oort Cloud will have a strong effect in particular cases on the orbital elements of near-parabolic comets that general move on steeply inclined orbits to the ecliptic plane. Some test were made for the most massive bodies from the Main Belt (which seems to be the more important agent for the comets investigated here), and no important orbital changes were so far noticed for a few exercised comets. The uncertainties of orbital elements were more than two orders of magnitude greater than the differences in nominal orbit determined using the standard solar system model and that taking into account four massive asteroids from the Main Belt. However, without more scrupulous testing one cannot rule out the rare possibility that a particular comet will be sensitive to perturbations coming from one of the relatively massive bodies (due to close encounter). In the future it will be potentially interesting to incorporate the many massive minor planets into the dynamical model of the solar system and perform such tests for all comets with previously determined orbits. Additionally, it is not obvious how the global mass distribution of mentioned three populations of solar system minor bodies are gravitationally important for near-parabolic comets. These plans of comprehensive tests will be gradually put into practice.
At the IAU Minor Planet Center Database (2013) only six observations are available.
At JPL Small-Body Database Browser (2013) no orbital quality assessment is published, thus we calculated here orbital class using our new scheme.
Acknowledgments
I wish to thank the reviewer Luke Dones for many constructive suggestions that improved this paper. The orbital calculation was performed using the numerical orbital package developed by Professor Grzegorz Sitarski and the Solar System Dynamics and Planetology Group at SRC PAS.
References
- Dybczyński, P. A., & Królikowska, M. 2011, MNRAS, 416, 51 (Paper 2) [NASA ADS] [Google Scholar]
- IAU Minor Planet Center 2013, MPC Database Search, http://www.minorplanetcenter.net/db_search/ [Google Scholar]
- IAU Minor Planet Center 2013, Uncertainty Parameter U and Orbit Quality Codes,http://www.minorplanetcenter.net/iau/info/UValue.html [Google Scholar]
- JPL Small-Body Database Browser, 2013, JPL Database Search, http://ssd.jpl.nasa.gov/sbdb.cgi [Google Scholar]
- Królikowska, M. 2006, Acta Astron., 56, 385 [NASA ADS] [Google Scholar]
- Królikowska, M., & Dybczyński, P. A. 2010, MNRAS, 404, 1886 (Paper 1) [NASA ADS] [Google Scholar]
- Królikowska, M., & Dybczyński, P. A. 2013, MNRAS, 435, 440 (Paper 4) [NASA ADS] [CrossRef] [Google Scholar]
- Królikowska, M., Dybczyński, P. A., & Sitarski, G. 2012, A&A, 544, A119 (Paper 3) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsden, B. G., & Williams, G. V. 2008, Catalogue of Cometary Orbits, 17th edn. (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Marsden, B. G., Sekanina, Z., & Yeomans, D. K. 1973, AJ, 78, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, B. G., Sekanina, Z., & Everhart, E. 1978, AJ, 83, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Nakano, S. 2009a, Nakano Note 1731a, available at http://www.oaa.gr.jp/~oaacs/nk1731a.htm [Google Scholar]
- Nakano, S. 2009b, Nakano Note 1731b, available at http://www.oaa.gr.jp/~oaacs/nk1731b.htm [Google Scholar]
- Nakano, S. 2009c, Nakano Note 1807, available at http://www.oaa.gr.jp/~oaacs/nk1807.htm [Google Scholar]
- Sitarski, G. 1989, Acta Astron., 39, 345 [NASA ADS] [Google Scholar]
- Sitarski, G. 1998, Acta Astron., 48, 547 [NASA ADS] [Google Scholar]
- Sitarski, G. 2002, Acta Astron., 52, 471 [NASA ADS] [Google Scholar]
Appendix A: Part I. Description of observational material and orbital quality assessment
Characteristics of observational material and the new quality assessment for 119 near-parabolic comets investigated in Papers 1–4 (see references in the last col.).
Additional notes on some individual objects given in Table A.1
Comet C/1990 K1. MWC 08 gives an NG orbit based on significantly fewer observations (314) and the same time interval as in the table. In June 2013, 693 observations were available at the IAU Minor Planet Center Database (2013), but the osculating orbit was the same as in MWC 08. Since MWC 08 gives an NG orbit, orbital quality class is not given there. The pure GR osculating orbit (1a quality class3) given at the JPL Small-Body Database Browser (2013) is based on 553 observations. In Paper 1 the symmetric NG model based on full data interval was analysed, where some trends in O−C variations were reported. The present symmetric NG solution results in 1a quality class. The asymmetric model (function g(r(t − τ))) listed in this catalogue gives τ = 5.3 ± 1.7 day and orbit of class 1b. However, still some trends in O−C time variations are easily seen and a more dedicated treatment is necessary for this comet, maybe similar to that in Paper 3 for C/2001 Q4 and C/2002 T7.
Comet C/1993 A1. MWC 08 gives NG orbit based on a poorer data set (539 observations) and shorter time interval (2 January 1993 – 10 June 1994). In June 2013, 745 observations were available at the IAU Minor Planet Center Database (2013), but the osculating orbit was the same as in MWC 08. Since MWC 08 gives an NG orbit, an orbital quality class is not given there. In Paper 1 the symmetric NG model based on the full data interval was used (orbit of class 1a) and some trends in O−C variations were reported. The asymmetric model (function g(r(t − τ))) presented here gives τ = − 34.2 ± 3.2 day and slightly decreasing rms (orbit of class 1a) compared with the GR model, but still some trends in O−C time variations are easily recognizable. Probably a more dedicated treatment is necessary for this comet, maybe similar to that in Paper 3 for C/2001 Q4 and C/2002 T7.
Comet C/2001 Q4. MWC 08 gives an NG orbit based on significantly fewer observations (1106) and shorter arc (4 August 2001–11 June 2004). In June 2013, 2681 observations were available at the IAU Minor Planet Center Database (2013), but the osculating orbit was the same as in MWC 08. Since MWC 08 gives an NG orbit, the orbital quality class is not given there. The NG osculating orbit (quality class 1a+) given at the JPL Small-Body Database Browser (2013) is based on 2567 observations. Here, two models are listed: (1) an NG solution based on a full data interval and (2) the most recommended model for past and future dynamical evolution. The first model gives NG orbit of class 1a+ with evident trends in O−C time variations. The asymmetric model gives τ = 0.73 ± 0.45 day, and no decrease in rms, therefore the symmetric model is included in this catalogue. The second model is based on data taken at large distances and gives orbit of class 1a+ and O−C time variations with no trends in right ascension and declination. In Paper 3, we recommend this model for dynamical studies and investigation of the origin of this comet. For more details see model DIST2 in Paper 3.
Comet C/2002 T7. MWC 08 gives an NG orbit based on 3825 observations and a significantly shorter arc (12 October 2002–11 June 2004). In June 2013, 4517 observations were available at the IAU Minor Planet Center Database (2013), which span the same time interval as in this table. However, the osculating orbit was the same as in MWC 08. Since MWC 08 gives an NG orbit, the orbital quality class is not given there. The NG osculating orbit (quality class 1a+) given at the JPL Small-Body Database Browser (2013) is based on 4399 observations and a slightly shorter data interval (12 October 2002–07 March 2006). Here, two models are listed: (1) an NG solution based on full data interval and (2) the most recommended models for past and future dynamical evolution, respectively. The first model gives an NG orbit of class 1a+ with evident trends in O−C time variations. The asymmetric model gives τ = − 12.9 ± 0.6 day, | A1 | ≪ | A2 | and an infinitesimal decrease in rms, therefore the symmetric model is shown in this catalogue. The second (PRE) and third (POST) models are based on data taken before and after perihelion passage, respectively, and give orbits of class 1a and 1b as well as O−C time variations with no trends in right ascension and declination. In Paper 3, we recommend osculating orbits based on these two models to study the origin and future of this comet. For more details see model PRE in Paper 3.
Comet C/2003 K4. MWC 08 gives an GR orbit based on significantly fewer observations (2244) and shorter arc (28 May 2006 – 09 July 2004). In June 2013, 3712 observations were available at the IAU Minor Planet Center Database (2013) that span the same time interval as in this table, but the orbit was the same as in MWC 08. The NG osculating orbit (quality class 1a+) given at the JPL Small-Body Database Browser (2013) is based on 3606 observations. In Paper 1 the symmetric NG model based on a full data interval is given (orbit of class 1a+) and some trends in O−C variations are reported. The asymmetric model (function g(r(t − τ))) gives a very long time shift τ = − 89 ± 3 day and slightly decreasing rms (orbit of class 1a) compared with the symmetric NG solution, but still similar trends in O−C time variations are easily visible. Thus, two models are listed here: (1) the symmetric NG solution based on the full data interval (where observations are weighted slightly differently from the solutions investigated in Paper 1), and (2) the most recommended model for past and future dynamical evolution based on observations taken at large heliocentric distance from the Sun. In the second model no trends in O−C time variations are noted.
Comets C/2006 HW51, C/2006 L2 and C/2008 T2. In Paper 4, we decided to analyse the GR solutions since the NG solutions give a negative normal component of NG acceleration (parameter A1 < 0) for these comets which makes the NG solution rather uncertain. For more details see Paper 4.
Comet C/2006 VZ13. MWC 08 gives a GR orbit (class 1B) based on 356 observations and the time interval of 13 November 2006−27 June 2007. In June 2013, 1173 observations were available at the IAU Minor Planet Center Database (2013) span the same time interval as the first model for this comet in our table. However, the orbit given at the IAU Minor Planet Center Database (2013) was the same as in MWC 08. The GR osculating orbit (quality class 1b) given at JPL Small-Body Database Browser (2013) is based on 1037 observations and the time interval 13 November 2006−05 August 2007. Since observations have stopped soon after perihelion passage, a dedicated solution is only possible for pre-perihelion data. Here, two models are listed: (1) the NG solution based on the full data interval, and (2) the most recommended model for past dynamical evolution. In Paper 4, we recommend this second solution (of quality class 2b) for backward dynamical studies and a NG solution based on all data for forward extrapolation of motion (class 1b) with the remark that the future motion of this comet is additionally uncertain because of the lack of post-perihelion data. For more details see Paper 4.
Comet C/2007 N3. Evident trends in the O−C time variations for the NG solution (important normal component of NG acceleration) based on an entire data set were noticed. Therefore we list in this catalogue two types of models: (1) an asymmetric NG solution based on a full data interval, and (2) the most recommended two separate GR models based on pre-perihelion and post-perihelion data, for past and future dynamical evolution, respectively. Fore more details see Paper 4.
Comet C/2007 O1. According to the JPL Small-Body Database Browser (2013), this comet was also known as 2006 GA38, therefore eight positional observations of this object were also used for orbit determination. For more details see Paper 4.
Comet C/2007 Q1. In MWC 08 and the JPL Small-Body Database Browser (2013) only a parabolic orbit for this comet is given (assumed e = 1 thus unknown 1/a, no quality class). For more details see Paper 4.
Comet C/2007 Q3. At the IAU Minor Planet Center Database (2013) over ten times more observations are available than were used in MWC 08 for the orbit determination. In Paper 4, we noted visible trends in the O−C solution for an NG solution based on all positional data. Therefore we list two types of models: (1) a symmetric NG solution based on a full data interval; and (2) the most recommended two separate GR models based on pre-perihelion and post-perihelion data, for past and future dynamical evolution, respectively. For more details see Paper 4.
Comet C/2007 W1. MWC 08 includes only a pure GR orbit of a class 1B for this comet (based on 344 observations taken until 16 Mar 2008). Here, 1703 observations given at the IAU Minor Planet Center Database (2013) were taken. Some part of them were used at the IAU Minor Planet Center Database (2013) to recalculate an orbit of this comet using the NG model. The GR osculating orbit (quality class 1b) given at the JPL Small-Body Database Browser (2013) is based on 599 observations and the data interval of 20 November 2007−30 August 2008. A full asymmetric NG model gives orbit of class 1a, but very strong trends in O−C diagram were noted and NG effects seem to be variable in the motion of C/2007 W1. Therefore in Paper 4, similarly to Nakano (2009a,b), we determined two dedicated NG orbits for backward and forward dynamical studies. The orbit based on pre-perihelion data is of class 1b while the post-perihelion solution gives an orbit of quality class 2b. In this catalogue the asymmetric NG solution based on the entire data set is slightly different from that used in Paper 4 (observations were selected using a more restrictive criterion). A detailed discussion of this unique comet is given in Paper 4.
Appendix B: Part II. Osculating orbital elements (heliocentric)
Comet C/2008 A1. MWC 08 includes only a pure GR orbit of a class 1B for this comet (basing on 240 observations taken until 15 May 2008). Here, 937 observations given at the IAU Minor Planet Center Database (2013) were used. Some parts of them (until 1 May 2009) were used at the IAU Minor Planet Center Database (2013) to recalculate NG orbit of this comet. The GR osculating orbit (quality class 1a) given at JPL Small-Body Database Browser (2013) is based on 595 observations and the data interval of 10 January 2008−17 January 2010. See also Nakano (2009c). The full asymmetric NG model gives orbit of class 1a, but very strong trends in the O−C diagram were easily seen and NG effects seem to be variable in its motion. Because of the erratic behaviour of this comet we proposed in Paper 4 two different NG solutions (both class 1b) based on pre- and post-perihelion data (similarly to C/2007 W1). More details are given in Paper 4.
Comet C/2009 K5. In June 2013, 2544 observations were available at the IAU Minor Planet Center Database (2013), and the GR osculating orbit (class 1A) given there was based on 2307 observations, whereas the GR orbit (class 1a+) given at the JPL Small-Body Database Browser (2013) was based on 2487 observations. Some trends in O−C time variations in the pure GR model (class 1a+) based on an entire data set were noted. Therefore we recommend in Paper 4 two separate orbital solutions for the backward and forward dynamical orbital evolution of this comet, both are pure GR and give osculating orbits of class 1a. For more details see Paper 4.
Comet C/2010 X1. In June 2013, 2276 observations were available at the IAU Minor Planet Center Database (2013), the GR osculating orbit (class 1A) given there was based on 1896 observations and on the time interval of 10 December 2010−07 September 2011. The GR osculating orbit (quality class 1b) given at the JPL Small-Body Database Browser (2013) is based on 2209 observations taken within the data interval of 10 December 2010−1 August 2011. This comet was observed until 7 September, but started to disintegrating in August. Therefore the data for GR orbit determination were taken here until the end of July for the first model (as at JPL), and to the end of May for the second model. The first solution exhibits some trends in O−C time variation, the second model is much better and also gives orbit of class 1b. For more details see Paper 4.
Appendix C: Part III. Original barycentric orbital elements
Appendix D: Part IV. Future barycentric orbital elements
All Tables
Completeness of the sample of comets in the present catalogue in comparison to MWC 08 as a function of the time distribution of cometary discovery (five periods given in Col. [1]) and the perihelion distance (qosc< 3.1 au or qosc ≥ 3.1 au, Cols. [2], [3] and [4], [5], respectively).
Statistics of orbital quality classes for investigated comets (more details in the text).
Comets of class 1A or 1B or NG orbits according to MWC 08 and with orbital quality poorer than first class according to the proposed, modified classification of orbit quality for 28 small-perihelion comets (qosc< 3.1 au).
Characteristics of observational material and the new quality assessment for 119 near-parabolic comets investigated in Papers 1–4 (see references in the last col.).
All Figures
 |
Fig. 1 Maximum NG accelerations, FNG,perih, as a function of perihelion distance for all 45 near-parabolic comets with determinable NG effects. Three samples A1, A2 and B are shown by red, magenta and turquoise symbols, respectively. The dotted curves represent the 10-5, 10-4 and 10-3 of the solar gravitational acceleration F⊙, respectively. NG parameters taken for preparation of this plot are in Part II of this catalogue (Table A.4). |
| In the text | |
 |
Fig. 2 Distribution of 1 /aori (upper panel), 1 /afut (lower panel) for 119 considered LPCs. The uncertainties of 1 /a determinations were incorporated into these 1 /a histograms by taking the full cloud of VCs for each comet. This means that both distributions are composed of 119 individual normalized 1/a distributions resulting from the dynamical calculations of 5001 VCs. |
| In the text | |
 |
Fig. 3 Projection of the 6D space of 5 001 VCs of C/1988 B1 onto six chosen planes of osculating orbital elements. Vertical axes given in the right-hand panels are exactly the same as the vertical axes in the left-hand panels. Each grey point represents a single virtual orbit, while the large red point represents the nominal orbit solution given here and the green point is taken from MWC 08 (see also Table 6). Each plot is centred on the nominal values of the respective pair of osculating orbital elements denoted by the subscript “0”; see also Table 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


