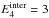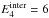| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 12 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201323141 | |
| Published online | 09 July 2014 | |
Absolute evaporation rates of non-rotating neutral polycyclic aromatic hydrocarbon clusters
1
Université de Toulouse, UPS-OMP, IRAP,
31028
Toulouse,
France
e-mail: julien@obs-besancon.fr
2
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
Received:
27
November
2013
Accepted:
17
March
2014
Context. Clusters of polycyclic aromatic hydrocarbons (PAHs) have been proposed as candidates for evaporating very small grains, which are thought to be precursors of free-flying PAHs. Evaporation rates have been calculated so far only for species containing up to a few 100-C atoms, whereas interstellar PAH clusters could contain up to ~1000 C atoms.
Aims. We present a method that generalises the calculation of the statistical evaporation rate of large PAH clusters and provides rates for species containing up to ~1000 C-atoms.
Methods. The evaporation of non-rotating neutral homo-molecular PAH clusters containing up to 12 molecules from a family of highly symmetric compact PAHs is studied. Statistical calculations were performed and completed with molecular dynamics simulations at high internal energies to provide absolute values for the evaporation rate and distributions of kinetic energy released. The calculations used explicit atom-atom Lennard-Jones potentials in the rigid molecule approximation. A new method is proposed to take both inter- and intra-molecular vibrations into account.
Results. Without any parameter adjustment, the calculated evaporation rates agree well with available experimental data. We find that the non-rotation assumption has a limited impact on the evaporation rates. The photostability of PAH clusters increases dramatically with the size of molecules in the clusters, and to a lesser extent with the number of molecules in the clusters. For values of the UV radiation field that are typical of the regions where evaporating very small grains are observed, the smallest clusters in this study (~50 C-atoms) are found to be quickly photo-evaporated, whereas the largest clusters (~1000 C-atoms) are photostable.
Conclusions. Our results support the idea that large PAH clusters are good candidates for evaporating very small grains.
Key words: astrochemistry / molecular processes / molecular data / dust, extinction / photon-dominated region (PDR) / ISM: molecules
© ESO, 2014
1. Introduction
Astronomical observations have revealed a set of emission bands in the mid-infrared range, the so-called infrared aromatic bands (AIBs), the most intense falling at 3.3, 6.2, 7.7, 8.6, 11.3, and 12.7 μm. Following the studies of Léger & Puget (1984) and Allamandola et al. (1985), this emission is generally attributed to polycyclic aromatic hydrocarbons (PAHs), and this proposal has motivated numerous studies on PAHs (see Joblin & Tielens 2011, for a recent compilation of works on this topic).
Rapacioli et al. (2005a) have analysed the spectral variations of the AIBs in photodissociation regions (PDRs) and suggest that free PAHs are produced by evaporation of very small grains (VSGs) containing at least ~400 carbon atoms. They propose that VSGs are made of PAH clusters that evaporate under UV irradiation. (Pilleri et al. 2012) confirm this mechanism over a wide range of physical conditions and propose to call these species evaporating very small grains (eVSG).
PAH clusters are also considered as key species in flames and circumstellar shells, where they could be involved in the transition from molecular growth to nucleation of soot particles (Frenklach 2002; Cherchneff 2011). The dimerisation of pyrene (C16H10) and sometimes of other PAHs has been invoked in numerous studies (Schuetz & Frenklach 2002, and references therein) as a critical step in soot formation models. However, the experimental results of Sabbah et al. (2010) contradict this proposal unless larger species than pyrene are involved.
The size distribution of PAH clusters in natural environments, such as flames, PDRs, or circumstellar shells, results from the balance between nucleation and evaporation processes. To our knowledge there is only one experimental study of the evaporation properties of large PAH clusters by Schmidt et al. (2006), while several theoretical studies address the questions of their structure and stability (Rapacioli et al. 2005b; Herdman & Miller 2008). In addition, Rapacioli et al. (2006) initiated a theoretical investigation on the formation and photo-evaporation in PDRs of neutral clusters containing up to ~300 C-atoms. They show that in regions where eVSGs are observed, these clusters are photo-evaporated much faster than they can be reformed by collisions. However, this study was based on coronene (C24H12), whereas we have recently shown that PAHs smaller than ~50–70 carbon atoms are strongly photo-dissociated, and therefore larger PAHs have to be considered (Montillaud et al. 2013).
In this study, we aim at providing absolute evaporation rates for neutral PAH clusters of large molecules. These rates are calculated as a function of the total excess energy in the clusters, defined as the sum of inter- and intra-molecular potential energy and of kinetic energy. To sample the parameter space of PAH cluster size, we focussed on three highly symmetric and compact species, namely coronene C24H12, circumcoronene C54H18, and circumcircumcoronene C96H24, forming clusters containing up to 12 molecules. For the sake of simplicity, we limit the study to non-rotating clusters. We show in Sect. 3.1.1 and Appendix A.4 that this assumption has no strong impact on the applicability of our results in the astrophysical context.
The calculations of absolute evaporation rates by Rapacioli et al. (2006) were based on the statistico-dynamical method (Weerasinghe & Amar 1993; Calvo & Parneix 2003). It consists in combining the assets of (i) the phase space theory (PST); which provides accurate relative data over broad energy ranges; and (ii) molecular dynamics (MD) simulations to get absolute data, but only for a limited range at high energies. When applied to the evaporation of large molecular clusters, the need for long MD trajectories usually makes it necessary to simplify the simulations by assuming that molecules are rigid. This approximation raises difficulties for taking both the intra- and inter-molecular vibrations into account when combining PST and MD results. We propose here a simple method for circumventing this difficulty while relaxing the rigid molecule approximation to some extent. To assess the reliability of this method and of obtained molecular data, we compare our results on coronene clusters with the experimental data by Schmidt et al. (2006).
The paper is structured as follows. The methods used to compute the structures, energetic properties, and evaporation rates of PAH clusters are presented in the next section. Further details on the methods can be found in the Appendix. In Sect. 3, we report our absolute evaporation rates and compare them with the available experimental results. The first astrophysical consequences of our new molecular data are discussed in Sect. 4. A summing-up of this work with perspectives on possible extensions of our method, the remaining open questions, and astrophysical modelling concludes the paper. Readers mostly interested in using the molecular data and in their astrophysical consequences may skip the following section dedicated to methods.
2. Methods
2.1. Structures and binding energies of neutral PAH clusters
Prior to investigating the dynamical behaviour of the evaporation process, the knowledge
of the static properties of the clusters, namely their ground state structure and binding
energy, is required. Rapacioli et al. (2005b)
determined these properties for several neutral PAH clusters ranging from pyrene to
circumcoronene clusters with 2 to 32 molecules. They assumed the molecules to be rigid and
to interact through an explicit atom-atom potential built on two contributions:
![\begin{eqnarray} \label{eq:Vinter} V = \sum_{i\,<\,j} \sum_{\alpha \in i} \sum_{\beta \in j} \left[ V_{\rm LJ}(r_{i_{\alpha},j_{\beta}}) + V_{\rm Q}(r_{i_{\alpha},j_{\beta}}) \right], \end{eqnarray}](/articles/aa/full_html/2014/07/aa23141-13/aa23141-13-eq7.png) (1)where
VLJ(riα,jβ)
denotes the dispersion-repulsion energy between the atom iα of the molecule
i and the
atom jβ of the molecule
j, and for
which the Lennard-Jones (LJ) form is used. Here, VQ(riα,jβ)
denotes the point charge electrostatic interaction between the partial charges carried by
the atoms of the molecules.
(1)where
VLJ(riα,jβ)
denotes the dispersion-repulsion energy between the atom iα of the molecule
i and the
atom jβ of the molecule
j, and for
which the Lennard-Jones (LJ) form is used. Here, VQ(riα,jβ)
denotes the point charge electrostatic interaction between the partial charges carried by
the atoms of the molecules.
For VLJ, we used the parameters proposed by van de Waal (1983). The electrostatic-potential-fitted (EPF) partial charges are used, because they exhibit good transferability from one PAH to another, according to Rapacioli et al. (2005b). In this work, for the coronene and circumcoronene molecules, we used the structure and EPF charges computed by Rapacioli et al. (2005b). The structure and EPF charges of the circumcircumcoronene molecule were derived from the B3LYP density functional theory (DFT) calculation of Bauschlicher et al. (2008).
Rapacioli et al. (2005b) performed the optimisation with two methods: the basin-hopping or Monte-Carlo + minimisation method for the smaller clusters, and parallel tempering Monte-Carlo for the larger ones. They show that for pyrene, coronene, and circumcoronene clusters, the lowest energies are obtained for single stacks in the case of small numbers of molecules and for several stacks above 7, 8, and 16 molecules for pyrene, coronene, and circumcoronene clusters, respectively. This strongly suggests that the one-stack geometry prevails for circumcircumcoronene clusters containing up to at least 16 molecules. Therefore, we used the structures of coronene clusters computed by Rapacioli et al. (2005b) as first guess structures for (C96H24)N (N = 2, 12). We then optimised these structures using classical molecular dynamics simulations in the rigid molecule approximation using the following method. We computed several trajectories with several initial kinetic energies between 0.01 and 2 eV in order to let the system explore the configurational space around the initial structure, and we recorded the potential energy minima on-the-fly. Quenching was performed for each recorded minimum, and we considered the structure corresponding to the deepest potential energy as optimised.
Starting with a modified one-stack structure, we checked on the example of coronene clusters that our procedure leads to the same geometries and energies as those determined by Rapacioli et al. (2005b). We found circumcircumcoronene clusters to have the same one-twisted-stack geometries as coronene clusters. The distance between two successive molecules is found to decrease from coronene (3.52 Å) to circumcoronene (3.49 Å) and to circumcircumcoronene clusters (3.47 Å). The same π/ 6 angle is found between two successive molecules. Herdman & Miller (2008) also studied the structures of neutral PAH dimers with a very similar approach differing essentially through the choice of the point charge description. Their results favoured parallel-displaced geometries as in graphite. However, Rapacioli et al. (2005b) show that the final structure is very sensitive to the point charge values, while the difference in energy between twisted and parallel-displaced stacks is lower than 0.02 eV for the dimer of coronene.
 |
Fig. 1 Binding energy per carbon atom in the cluster for some neutral homo-molecular PAH clusters. Red filled circles are for dimers, black open circles for larger clusters with 3 to 12 molecules. The binding energy per carbon atom increases with the size of monomers and with the number of molecules in the cluster. The blue curve is the empirical relation determined by Herdman & Miller (2008) and shows a maximum relative difference of 7% with our results. The structures of the three monomers considered in this study, coronene C24H12, circumcoronene C54H18, and circumcircumcoronene C96H24, are also shown. |
In terms of binding energy, our results agree within 7% with those of Herdman & Miller (2008) for the dimers. The binding energy increases faster than the number of carbon atoms in the monomers (see Fig. 1) because the repulsive part of the intermolecular potential is related to the Coulomb interaction of peripheral atoms, whose number decreases relative to the total number of carbon atoms when the size of the molecule increases. Because of long-range interactions, the binding energy per molecule increases with the number of molecules in the cluster. However, this effect is close to saturation for twelve molecules, giving an estimate of (i) the spatial extent of the intermolecular interactions; and (ii) a typical size for bulk properties to emerge.
2.2. Evaporative trajectories with molecular dynamics
A first evaluation of the absolute evaporation rates was performed using molecular dynamics (MD) simulations for non-rotating parent clusters. We considered molecules as rigid and assumed they are frozen in their optimal structure. This approximation prevents us from taking the coupling between intra- and inter-molecular vibrations into account. However, only the lowest frequency modes are expected to contribute significantly to this coupling, and full-dimensional calculations are beyond reach for the large systems we are considering here. Rapacioli et al. (2007) investigated the effect of the rigid molecule approximation on the frequencies of intermolecular modes in coronene clusters. They show that these frequencies are affected by less than 5% for one-stack clusters, but larger differences are found for two-stack structures. Therefore the results of our MD simulations should not be significantly affected by the coupling between inter- and intra-molecular vibrations except for (C24H12)12, which is the only two-stack cluster in this work.
The classical equations of motion were integrated using a leapfrog algorithm with quaternion coordinates, the forces between molecules being derived from the intermolecular potential presented in 2.1. The clusters were initially heated to a temperature ~10 K along 1000 integration steps to prepare random initial conditions and then suddenly heated to a given intermolecular energy. This was done by randomly distributing the excess energy in molecular velocities during a single time step. The total linear and angular momenta were set to zero since our study focusses on non-rotating clusters. The trajectories were propagated with time steps between 1 and 5 fs according to the size of the molecules to ensure an energy conservation better than 0.1% along the 106 steps (~10-9 s) of each trajectory. The simulation was stopped after 106 integration steps or when an evaporation event was observed, i.e. when the distance between one molecule and the mass centre exceeded five times the typical dimension of the cluster. The last step for which the velocity of the evaporating molecule pointed inwards was considered as the evaporation time. For each cluster, we computed enough trajectories to record 10 000 evaporation events. For high energies, each trajectory led to an evaporation, while for the lowest energies computed here, typically one evaporation was recorded every two or three trajectories. We never observed the simultaneous evaporation of several molecules. This is consistent with the dissociation energy being higher for such events than for single molecule evaporations. The number N(t) of trajectories that are not yet evaporated after time t is expected to follow a first-order kinetics law N(t) = N(0)exp(−kt), from which we extracted the evaporation rate k using a linear fit of the logarithmic variations in N(t).
Evaporation rates were found to increase drastically with the excess energy in the cluster, defined here as the sum of intermolecular potential energy and kinetic energy. The usual computational resources enable only high energy simulations for which the evaporation rates are greater than ~109 s-1. A statistical approach is needed to calculate evaporation rates at lower energies.
2.3. Statistical approach of evaporation
Phase space theory (PST) is a statistical theory that is well suited to describing molecular and cluster evaporation. It is presented in detail in several papers (see for instance Chesnavich & Bowers 1977; Weerasinghe & Amar 1993; Calvo & Parneix 2003). In this section, we are limited to the formalism needed to describe the evaporation of PAH clusters. We emphasise the difficulties raised by the use of the rigid molecule approximation and propose a simple method that enables these difficulties to be circumvented.
2.3.1. The phase space theory framework
PST was shown to provide an efficient framework for computing unimolecular reaction
rates (Weerasinghe & Amar 1993; Calvo & Parneix 2004; Calvo et al. 2010). As a statistical theory, it relates the
evaporation rate to the ratio of the densities of states (DOS) of the fragments over the
parent, with the specificity to take the conservation of both energy and angular
momentum into account. During the evaporation process, the initial angular momentum
J is
shared between the rotation of the fragments Jr and the orbital angular momentum
L.
Similarly, the initial excess energy EN of the parent is
shared between the kinetic energy released (KER) ϵtr, the
internal energy of the released molecule E1, the internal energy of the
fragment cluster EN − 1, and the
dissociation energy 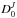 that
depends on J. Therefore, the total DOS of the fragments
results from the convolution of the vibrational densities of states (VDOS) of the two
fragments ΩN −
1 and Ω1 and of the rotational density of states (RDOS)
Γ(ϵtr,J).
that
depends on J. Therefore, the total DOS of the fragments
results from the convolution of the vibrational densities of states (VDOS) of the two
fragments ΩN −
1 and Ω1 and of the rotational density of states (RDOS)
Γ(ϵtr,J).
In the orbiting transition state version of PST (Chesnavich & Bowers 1977), the fragments separate with a certain
amount of translational-rotational energy ϵtr whose translational part
ϵr has to overcome the centrifugal
barrier ϵ†(L) that arises
from the centrifugal potential combined to the presence of a long range interaction
potential between the fragments. Therefore a minimum translational-rotational energy
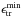 is
required to enable the evaporation. The RDOS of the fragments Γ(ϵtr,J) results from
the integration over the accessible volume of rotational states whose boundaries emerge
from the interplay between the conservation of energy and angular momentum and depend on
the geometry of the fragments. Detailed procedures for this calculation can be found in
the work by Chesnavich & Bowers (1977) and
Calvo & Parneix (2004). Finally, most of
the complexity related to the conservation of angular momentum is encapsulated in the
RDOS, and the evaporation rate kevap in the PST framework can be
summarised by the relation:
is
required to enable the evaporation. The RDOS of the fragments Γ(ϵtr,J) results from
the integration over the accessible volume of rotational states whose boundaries emerge
from the interplay between the conservation of energy and angular momentum and depend on
the geometry of the fragments. Detailed procedures for this calculation can be found in
the work by Chesnavich & Bowers (1977) and
Calvo & Parneix (2004). Finally, most of
the complexity related to the conservation of angular momentum is encapsulated in the
RDOS, and the evaporation rate kevap in the PST framework can be
summarised by the relation: 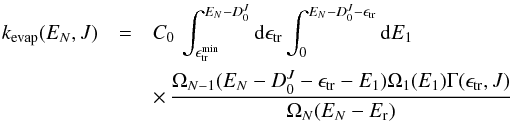 (2)where
C0 is a constant, Er the
rotational energy of the parent, E1 the energy of the released
molecule,
(2)where
C0 is a constant, Er the
rotational energy of the parent, E1 the energy of the released
molecule, 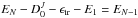 is
the energy of the larger fragment, and
is
the energy of the larger fragment, and 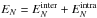 the
energy of the parent cluster, which is conserved during the evaporation process.
the
energy of the parent cluster, which is conserved during the evaporation process.
Evaluating C0 from theoretical considerations is
not straightforward. For this reason it is customary to use MD simulations at high
excess energy to calibrate C0. We used the results of the MD
simulations of Sect. 2.2 for this purpose. However,
MD calculations were performed using the rigid molecule approximation and therefore
provide rigid molecule evaporation rates 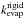 as a function
of the intermolecular energy Einter of the parent clusters. In
contrast, Eq. (2) provides evaporation
rates kevap considering all vibrational
degrees of freedom, as a function of the total excess energy EN of the parent
clusters. It is therefore necessary to find a relationship between kevap and
as a function
of the intermolecular energy Einter of the parent clusters. In
contrast, Eq. (2) provides evaporation
rates kevap considering all vibrational
degrees of freedom, as a function of the total excess energy EN of the parent
clusters. It is therefore necessary to find a relationship between kevap and
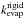 before an
estimate of C0 can be given.
before an
estimate of C0 can be given.
2.3.2. To the rigid molecule approximation and beyond
In previous work, Rapacioli et al. (2006) linked
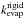 , expressed as
a function of the intermolecular energy Einter, and kevap,
expressed as a function of the total internal energy in the cluster, by computing the
mean intermolecular energy for each total energy and exchanging the variables. This
approach neglects that the values of the intermolecular energy follow a broad
distribution. We denote
, expressed as
a function of the intermolecular energy Einter, and kevap,
expressed as a function of the total internal energy in the cluster, by computing the
mean intermolecular energy for each total energy and exchanging the variables. This
approach neglects that the values of the intermolecular energy follow a broad
distribution. We denote 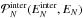 as the density of
probability for a cluster of N molecules bearing an total energy of
EN to have an
intermolecular energy
as the density of
probability for a cluster of N molecules bearing an total energy of
EN to have an
intermolecular energy 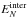 . This
quantity can be computed from the VDOS:
. This
quantity can be computed from the VDOS: 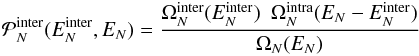 (3)where
(3)where
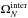 and
and
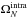 are the
VDOS of inter- and intra-molecular modes. Despite their rare occurrence, the highest
reachable values of
are the
VDOS of inter- and intra-molecular modes. Despite their rare occurrence, the highest
reachable values of 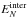 can
play a major role in the evaporation process, in particular for moderate values of the
total energy for which the corresponding mean intermolecular energy is less than the
dissociation energy. Such situations can severely affect the lifetime of these species
in interstellar environments.
can
play a major role in the evaporation process, in particular for moderate values of the
total energy for which the corresponding mean intermolecular energy is less than the
dissociation energy. Such situations can severely affect the lifetime of these species
in interstellar environments.
We show here how to adapt Eq. (2) to the
rigid molecule approximation, taking the distribution of intermolecular energy into
account. One needs to distinguish between inter- and intra-molecular modes. This can be
done by noticing that for a cluster with total energy E, the VDOS can be
expanded as 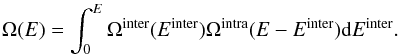 (4)We
apply this procedure simultaneously to ΩN and ΩN − 1 in Eq.
(2), in order to explicitly develop the
integration over
(4)We
apply this procedure simultaneously to ΩN and ΩN − 1 in Eq.
(2), in order to explicitly develop the
integration over 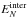 :
:
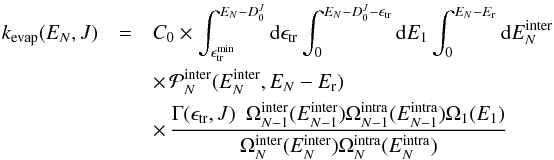 (5)where
the conservation of energy
(5)where
the conservation of energy 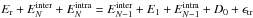 a priori prevents
us from separating the integrations over intra- and inter-molecular energies.
Nevertheless, in the framework of the rigid molecule approximation, only intermolecular
modes contribute to the dissociation process, and the conservation of energy applies to
inter- and intra-molecular energies independently, leading to
a priori prevents
us from separating the integrations over intra- and inter-molecular energies.
Nevertheless, in the framework of the rigid molecule approximation, only intermolecular
modes contribute to the dissociation process, and the conservation of energy applies to
inter- and intra-molecular energies independently, leading to
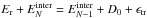 . Therefore, the
integrations over the intra- and inter-molecular energies can now be performed
separately. The integration over the intramolecular energy vanishes, while the rigid
molecule evaporation rate emerges from the integration over the KER distributions,
leading to
. Therefore, the
integrations over the intra- and inter-molecular energies can now be performed
separately. The integration over the intramolecular energy vanishes, while the rigid
molecule evaporation rate emerges from the integration over the KER distributions,
leading to 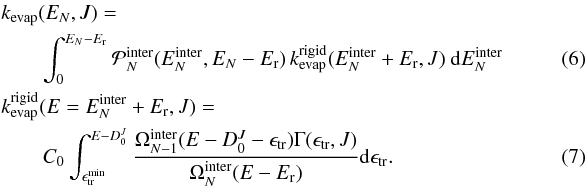 The
evaporation rate kevap(EN,J)
is therefore a simple statistical weighting of the rigid molecule evaporation rate, and
the calibration constant C0 is not modified through this
procedure. Our method enables taking advantage of the rigid molecule approximation and
recovering the major effects of intramolecular vibrations afterwards in terms of
statistical redistribution of the energy.
The
evaporation rate kevap(EN,J)
is therefore a simple statistical weighting of the rigid molecule evaporation rate, and
the calibration constant C0 is not modified through this
procedure. Our method enables taking advantage of the rigid molecule approximation and
recovering the major effects of intramolecular vibrations afterwards in terms of
statistical redistribution of the energy.
2.4. Vibrational densities of states
The accuracy of the calculated (microcanonical) evaporation rates depends on the accuracy of the vibrational densities of states. Computing anharmonic quantum VDOS for such large systems is beyond the scope of this work. We computed all other combinations of quantum + harmonic, classical + harmonic, and classical + anharmonic, and we specifically selected the most relevant for each term in Eq. (6). The details of the calculations are provided in the Appendix, along with the motivations for the chosen combinations. We summarise here which approximations were used for the VDOS involved in the calculations of the rates and distribution probabilities in the following.
In Eq. (7),
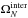 and
and
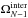 were
computed using the classical anharmonic approximation. This choice provides the best
possible description of the anharmonicity, which is important at the high energies of the
MD simulations (Sect. 2.2).
were
computed using the classical anharmonic approximation. This choice provides the best
possible description of the anharmonicity, which is important at the high energies of the
MD simulations (Sect. 2.2).
In Eq. (3), the whole range of energy is important. Because of the large number of vibrational degrees of freedom in PAH clusters, the average energy per vibrational mode is expected to be low in most cases, therefore quantum effects are important. Thus, in this equation, all VDOS were computed using the quantum harmonic approximation.
3. Results and discussion
In this paper, we focus on the absolute evaporation rates of a few non-rotating PAH clusters, namely (C24H12)N, (C54H18)N (N = 2,3,4,8,12), and (C96H24)N (N = 4,8). To test our method, the results for coronene clusters are compared with the experimental results of Schmidt et al. (2006).
3.1. Evaporation rates at fixed energy
In this section, we discuss the parameters used to compute RDOS. The RDOS are then
combined with (i) the classical anharmonic intermolecular VDOS presented in Sect. A.1 to provide the rigid molecule evaporation rates,
according to Eq. (7); (ii) the MD results
obtained in Sect. 2.2 to derive absolute values of
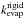 ; and (iii) the
probability distribution of the intermolecular energy, according to Eq. (6), to provide absolute evaporation rates as a
function of the total internal energy. The reliability of the method is assessed from the
comparison with MD data in Sect. 3.1.2, and the
absolute evaporation rates are presented in Sect. 3.1.3.
; and (iii) the
probability distribution of the intermolecular energy, according to Eq. (6), to provide absolute evaporation rates as a
function of the total internal energy. The reliability of the method is assessed from the
comparison with MD data in Sect. 3.1.2, and the
absolute evaporation rates are presented in Sect. 3.1.3.
3.1.1. PST input parameters
The typical evolution of the RDOS at low angular momenta is approximated well (Klots 1971; Calvo
& Parneix 2004) by 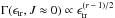 ,
with r = 6
being the number of rotational degrees of freedom of the fragments. For the large
species considered in this study, these variations are rather slow with respect to the
VDOS that scale with Es − 1 where
s is the
number of vibrational degrees of freedom. This leads to a low sensitivity of the
evaporation rates to rotational parameters. Therefore, limiting this study to
non-rotating clusters does not exclude applying its results to clusters with rotational
temperatures up to a few 100 K, as in interstellar conditions (Ysard & Verstraete 2010).
,
with r = 6
being the number of rotational degrees of freedom of the fragments. For the large
species considered in this study, these variations are rather slow with respect to the
VDOS that scale with Es − 1 where
s is the
number of vibrational degrees of freedom. This leads to a low sensitivity of the
evaporation rates to rotational parameters. Therefore, limiting this study to
non-rotating clusters does not exclude applying its results to clusters with rotational
temperatures up to a few 100 K, as in interstellar conditions (Ysard & Verstraete 2010).
The effects of the geometry of the fragments on the KER distribution were discussed in detail by Calvo and Parneix in a series of papers (Calvo & Parneix 2003, 2004; Parneix & Calvo 2003, 2004). Rapacioli et al. (2006) considered the accuracy of the description of the cluster geometry as a limitation to the study of neutral coronene clusters and limited their investigation to two clusters, (C24H12)4 and (C24H12)13, whose fragments are modelled well by a spherical cluster + oblate molecule geometry. However, we found no quantitative argument for such a limitation and noticed that large errors on the rotational constants of the fragments lead to very small variations in the KER distribution and the evaporation rate (see Appendix A.4). Therefore, in the following, the parent and fragment clusters are approximated by spheres. The rotational constants A, B, and C of each cluster were computed in the most stable geometry described in Sect. 2.1. Assuming that inertia momenta should be combined linearly, the rotation constant of the equivalent sphere was evaluated as the reduced value 3ABC/ (AB + AC + BC). The monomer fragment is considered as an oblate top molecule.
Calvo & Parneix (2003) show that the need for an accurate description of the attractive interaction potential between the fragments increases with the rotation of the parent cluster and that the simple parametrisation as − C6/r6 holds for non-rotating clusters. We found that for J = 0, the KER and evaporation rates are highly insensitive to the value of C6 (see Appendix A.4). For each cluster, therefore, we simply evaluated C6 by fitting the dissociation curve along the specific evaporation path for which the most external molecule leaves radially the cluster without rotating.
Finally, the errors resulting from the simple description of the geometry and the long-range interaction potential are found to be negligible with respect to the effect of varying the angular momentum (see Appendix A.4).
3.1.2. Assessment of the statistical method
Weerasinghe & Amar (1993) have shown the relevance of the KER distributions for assessing the accuracy of the statistical calculations. For each MD evaporative trajectory, the KER was recorded to build a histogram that was compared to the distribution predicted by PST. Figure 2 shows a typical KER for the example of (C96H24)4. Despite the crude approximations concerning the geometry and the long-range potential parameter of the clusters, MD and PST results exhibit a comparable level of agreement as reported by other authors for similar studies (Rapacioli et al. 2006; Calvo et al. 2010).
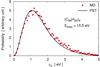 |
Fig. 2 Distribution of the kinetic energy released upon the evaporation of (C96H24)4 with an intermolecular energy equal to 15.5 eV prior to evaporation. The points represent the results from MD and the solid line the prediction based on PST. |
An alternative assessment comes from the relative evolution of evaporation rates
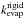 as derived
from MD simulations and PST. We tuned the coefficient C0 in Eq.
(7) to best fit the MD results. Most MD
points deviate by less than 15% from the calibrated PST rates, and the maximum deviation
is less than 60%. Compared with the orders of magnitude spanned by the evaporation
rates, these moderate differences reinforce the validity of this method.
as derived
from MD simulations and PST. We tuned the coefficient C0 in Eq.
(7) to best fit the MD results. Most MD
points deviate by less than 15% from the calibrated PST rates, and the maximum deviation
is less than 60%. Compared with the orders of magnitude spanned by the evaporation
rates, these moderate differences reinforce the validity of this method.
3.1.3. Absolute evaporation rates
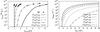 |
Fig. 3 Left: evaporation rates of some coronene clusters as a function of the internal energy in the rigid-molecule approximation from PST (lines) and MD (points) calculations. Right: corresponding evaporation rates as a function of the total energy taking the distribution of energy over the inter- and intra-molecular modes into account. |
As mentioned in the previous section, the relative rates
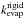 predicted by
PST were calibrated with the absolute results from MD simulations. The resulting
absolute evaporation rates
predicted by
PST were calibrated with the absolute results from MD simulations. The resulting
absolute evaporation rates 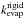 are
summarised in Fig. 3. The size of the molecules
affects the results essentially through the increase in the dissociation energy with the
number of carbon atoms and, similarly to the VDOS (Fig. A.1), the curves roughly overlap when plotted as a function of Einter/D0.
When increasing the number of molecules, the intermolecular energy is distributed
amongst more intermolecular modes, leading to less steep rates.
are
summarised in Fig. 3. The size of the molecules
affects the results essentially through the increase in the dissociation energy with the
number of carbon atoms and, similarly to the VDOS (Fig. A.1), the curves roughly overlap when plotted as a function of Einter/D0.
When increasing the number of molecules, the intermolecular energy is distributed
amongst more intermolecular modes, leading to less steep rates.
The absolute values of the evaporation rates kevap as a function of the total
energy were derived from Eq. (6). No
further calibration is needed for this procedure. The results are presented in Figs.
3 and 4. The
rates kevap increase much more slowly with
energy than 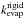 because they
also take the distribution of the energy over the intramolecular modes into account.
Their evolution with the total number of carbon atoms in the cluster is faster when
increasing the size of molecules than when increasing their number. This results from
the combination of two effects: the dissociation energy increases with the size of the
molecules, and for a given number of carbon atoms in the cluster, the fraction of
intermolecular modes decreases with the size of molecules.
because they
also take the distribution of the energy over the intramolecular modes into account.
Their evolution with the total number of carbon atoms in the cluster is faster when
increasing the size of molecules than when increasing their number. This results from
the combination of two effects: the dissociation energy increases with the size of the
molecules, and for a given number of carbon atoms in the cluster, the fraction of
intermolecular modes decreases with the size of molecules.
The simpler approach proposed by Rapacioli et al. (2006) provides very different rates at low energies since they only consider the most probable value of the intermolecular energy. The difference vanishes at high energies for which high values of Einter are statistically probable. Both results are compared to available experimental data in the next section.
 |
Fig. 4 Same as in the right panel of Fig. 3 for clusters of circumcoronene (dot-dashed lines) and circumcircumcoronene (dashed lines). |
3.2. Comparison with experimental results
The study of the evaporation of coronene clusters performed by Schmidt et al. (2006) provides the only available data for testing the robustness of our approach. Using an aggregation source, the authors generated a population of neutral coronene clusters that were thermalised in a helium thermal bath, irradiated by a 4 eV pulsed laser, and detected with a time-of-flight mass spectrometer. They observed ionised coronene clusters with a wide size distribution up to at least 26 units. The authors also provide experimental constraints on the evaporation of neutral coronene clusters that we can analyse here using the results presented in Sect. 3.1.3.
The time of 500 μs required for the neutral clusters to cross the thermalisation chamber enables thermal equilibrium with the helium bath to be reached. The clusters are then photoionised by the 4 eV pulsed laser and detected in the time-of-flight mass spectrometer. Varying the temperature of the thermal bath, the authors observed a full evaporation above 470 ± 50 K and no evaporation below.
We assume that the evaporation occurs in the thermal bath. The minimum evaporative rate a cluster needs to evaporate within 500 μs is typically 2000 s-1. According to our results, such rates occur at internal energies of 2.2, 2.8, 3.7, 6.5, and 13.8 eV for (C24H12)N with N = 2, 3, 4, 8, and 12, respectively. Using the caloric curves derived from the VDOS of each cluster, these energies correspond to temperatures of 494, 446, 439, 406, and 478 K, in good agreement with the experimental threshold temperature of 470 ± 50 K.
The same reasoning was applied using the evaporation rates derived by Rapacioli et al. (2006), leading to rather different threshold temperatures, with ~800 K for (C24H12)4 and ~600 K for (C24H12)13. This shows the importance of considering the distribution of internal energy over both the inter- and intra-molecular modes to derive the evaporation temperature, as implemented in our study.
4. Astrophysical implications
 |
Fig. 5 Comparison of the curves of kevap obtained from full statistico-dynamical calculations (red curves) or from the interpolation methods (black curves) for clusters made of the same molecules a) or for clusters with the same number of molecules b). |
To evaluate the lifetime of neutral PAH clusters in PDRs, we used the results presented in the previous section to model their evolution as a function of time in the physical conditions typical of such environments. In this section, we present the astrochemical model and its results, as well as some perspectives for future developments.
4.1. Modelling the evaporation of PAH clusters in photodissociation regions
To model the time evolution of PAH clusters in PDRs, we used the model presented in Montillaud et al. (2013) that we have developed to study the charge and hydrogenation states of PAHs in interstellar conditions. This model fully describes the time evolution of the abundance and the internal energy of the species, based on their evaporation and IR emission rates. It thereby naturally considers the building up of internal energy due to possible successive absorptions of several UV photons before the species have completely cooled down by IR emission (multi-photon events). Such events are expected to be crucial considering the low values of the evaporation rates of circumcoronene and circumcircumcoronene clusters at 13.6 eV, which corresponds to the maximum energy that can be absorbed via a single UV photon. In the following sections, we explain the hypotheses of the model, and show how we computed the complementary molecular data needed for the modelling.
4.1.1. General hypotheses of the astrochemical model
The numerical aspects of the astrochemical model are presented in detail in Montillaud et al. (2013). We assumed that the clusters can evolve according to the following processes:
-
gain of one or several molecules by collision with a PAH or anotherPAH cluster;
-
increase in the internal energy by absorption of UV photons;
-
decrease in the internal energy by emission of IR photons;
-
loss of one molecule by evaporation.
We modelled the clusters of coronene, circumcoronene, and circumcircumcoronene separately. We limited the number of molecules in PAH clusters to 12 molecules. Initially, the abundances of the clusters with N molecules were set to 1 for N = 12 and to 0 otherwise.
4.1.2. Formation of PAH clusters
Rapacioli et al. (2006) have shown that for temperatures below a few 1000 K the collision of coronene molecules (C24H12) always leads to the formation of a dimer. The situation is even more favourable for collisions between larger molecules, between a PAH molecule and a cluster, or between two clusters, because of the larger number of degrees of freedom available to distribute the collisional energy. Therefore, we assumed a sticking coefficient S = 1, and computed the collision rates using the average geometric cross-sections. We show in Sect. 4.2 that the results do not depend on this assumption.
4.1.3. Interpolation of kevap
In Sect. 3, we computed the evaporation rates for
a limited set of PAH clusters, containing 2, 3, 4, 8, and 12 molecules for coronene and
circumcoronene clusters, and only 4 and 8 molecules for circumcircumcoronene clusters.
The computed evaporation rates show very regular trends with the size and number of
molecules in the cluster. Figure 5a shows the
result of the logarithmic interpolation between the curves of evaporation rates of
(C54H18)4 and (C54H18)12 to evaluate the
evaporation rate of (C54H18)8. The result is in good
agreement with the rate obtained by the detailed calculation presented in Sect. 3. Therefore, we have built a full set of evaporation
rates for coronene, circumcoronene, and circumcircumcoronene clusters using the equation
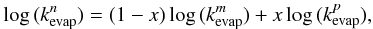 (8)where
x = (n −
m) / (p −
m), m and p are the numbers of molecules in the clusters
with known evaporation rates
(8)where
x = (n −
m) / (p −
m), m and p are the numbers of molecules in the clusters
with known evaporation rates 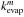 and
and
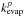 , and
n is the
number of molecules in the cluster for which the evaporation rate is interpolated.
, and
n is the
number of molecules in the cluster for which the evaporation rate is interpolated.
Interestingly, we find similar trends with the size of molecules in the clusters.
Figure 5b shows that one can derive a fair estimate
of the evaporation rate of (C54H18)4 from the interpolation
of the evaporation rates of (C24H12)4 and (C96H24)4
using the formula 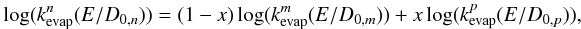 (9)where
D0,i (i = n,
m,
p) is the
dissociation energy of the species i.
(9)where
D0,i (i = n,
m,
p) is the
dissociation energy of the species i.
These regular trends stem from the very similar structures of the clusters. Indeed, for coronene clusters, we find that the interpolation provides poor estimates when one bases the interpolation on one cluster smaller than eight molecules and the other larger than eight molecules. This is related to the transition from the one-stack to two-stack geometry of this cluster. One should therefore use this interpolation method with caution, and only for clusters with similar geometries.
 |
Fig. 6 Left: evaporation timescales of a few PAH clusters as a function of the intensity of the UV radiation field, obtained with a model considering the growth of clusters by collisions with a sticking coefficient S = 1, a hydrogen nuclei density of nH = 1.5 × 103 cm-3, and a gas temperature of T = 100 K. The thin black lines show the slopes of –1, characteristic of single-photon evaporation, and of –6, indicative of highly multi-photon evaporations. Right: results of the model for a UV radiation field of G0 = 4 × 104 in units of Habing as a function of time for circumcoronene clusters when considering the growth of clusters by collisions with S = 1 (black dashed lines) or S = 0.01 (blue solid lines). |
4.1.4. IR emission rates
Using our astrochemical model requires computing the cooling rate for each cluster,
which is dominated by the emission of IR photons from intramolecular vibrational modes.
We follow Rapacioli et al. (2006) by considering
that the vibrational properties of the molecules involved in a cluster are weakly
perturbed by the other molecules of the clusters. Therefore, the IR emission rate
kIR of a cluster as a function of the
total intramolecular energy in the cluster Eintra is scaled from the
kIR of the monomer
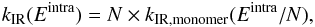 (10)where
N is the
number of molecules in the cluster. The intramolecular energy is assumed to be equally
distributed among the molecules. The error resulting from this approximation on
kIR(Eintra)
is expected to be small because this rate is mainly determined by the most probable
values of Eintra. Furthermore, the final results,
i.e. the time evolution of clusters in astrophysical conditions, are quite insensitive
to the exact value of kIR, as noticed on comparable systems
by Le Page et al. (2001) or Montillaud et al. (2013), among others. In contrast, it is necessary
to properly describe the distribution of the total energy Etot between
Eintra and Einter. We
computed the IR emission rate as a function of the total internal energy Etot
consistently with the method presented in Sect. 2.3.2 using
(10)where
N is the
number of molecules in the cluster. The intramolecular energy is assumed to be equally
distributed among the molecules. The error resulting from this approximation on
kIR(Eintra)
is expected to be small because this rate is mainly determined by the most probable
values of Eintra. Furthermore, the final results,
i.e. the time evolution of clusters in astrophysical conditions, are quite insensitive
to the exact value of kIR, as noticed on comparable systems
by Le Page et al. (2001) or Montillaud et al. (2013), among others. In contrast, it is necessary
to properly describe the distribution of the total energy Etot between
Eintra and Einter. We
computed the IR emission rate as a function of the total internal energy Etot
consistently with the method presented in Sect. 2.3.2 using 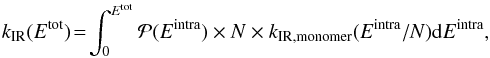 (11)where
(11)where
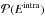 is the complementary probability of
is the complementary probability of 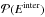 .
The resulting values of kIR increase slowly with
Etot in the 1–100 s-1 range.
.
The resulting values of kIR increase slowly with
Etot in the 1–100 s-1 range.
4.2. Results
We computed the time evolution of the three kinds of clusters for a hydrogen nuclei density of nH = 1.5 × 103 cm-3 and a gas temperature of T = 100 K. The UV radiation field was scaled from the interstellar radiation field of Mathis et al. (1983) to values ranging from G0 = 1 to 3 × 107 in Habing units (Habing 1968).
Figure 6 shows the variations in the timescale for photo-evaporation of a few clusters as a function of the intensity of the UV-visible radiation field. Different clusters exhibit very different behaviours. Coronene clusters are found to be quickly evaporated even in faint radiation fields. In contrast, circumcircumcoronene clusters require very intense radiation fields to evaporate. (C96H24)12 does not evaporate significantly on timescales of 108 years, longer than the typical lifetime of a molecular cloud. In between, circumcoronene clusters show an interesting range of timescales. Smaller clusters are resistant in faint radiation fields but are quickly evaporated for values higher than G0 ≈ 103 in Habing units. The larger circumcoronene clusters require rather intense radiation fields (G0 ≳ 104 in Habing units) to evaporate. Therefore, our results show that PAH clusters made of medium-sized PAH molecules (~50 C-atoms) have evaporation properties compatible with the evaporating very small grains observed in numerous photodissociation regions.
The evaporation timescales of coronene clusters vary as 1/G0, consistently with these clusters being evaporated by a single photon, because their threshold energy Eth (defined by kevap(Eth) = kIR(Eth)) is lower than the maximum energy carried by a single photon (13.6 eV). Conversely, evaporation timescales of circumcoronene and circumcircumcoronene clusters have steeper variations with G0, because multiphoton events are necessary to evaporate these clusters owing to their high threshold energies. Interestingly, Fig. 6 shows in the case of (C54H18)12 that for very intense radiation fields, the evaporation timescale presents a break and varies as 1/G0. This is because the mean time between the successive absorption of two UV photons becomes shorter than the cooling timescale, and there is no longer any difference between a single photon and a multi-photon event.
We checked whether our results depend on the value of the sticking coefficient by computing one model with a sticking coefficient of S = 0.01. Figure 6 shows on the example of circumcoronene clusters with G0 = 4 × 104 in Habing units that the abundance of dimers is divided by 100 compared to the case with S = 1, once steady state is reached. However, in these conditions, the abundance of the dimer is always dominated by at least five orders of magnitude by (C54H18)12 (on short timescales) or C54H18 (on long timescales), while the abundance and the timescales of the dominant species do not change significantly. Our results are thus robust against the assumptions for the growth of clusters by collisions, and this validates the approximation in Sect. 4.1.2, in typical PDR conditions.
4.3. Perspectives
The results presented in the previous sections show that PAH clusters are promising candidates for the population of astronomical eVSGs. Still, we only considered neutral homo-molecular clusters of highly symmetric compact PAHs, and natural mixtures are unlikely to be so simple. We examine here a few directions for future studies.
In Appendix A.1, we show that vibrational densities of states of clusters of large PAHs can be derived from a simple scaling procedure from clusters of smaller molecules. This could be useful to compute easily evaporation rates of other clusters.
The binding energies of a few heteroclusters have been evaluated by Rapacioli et al. (2005b). They find their energies to be intermediate between the binding energies of clusters made of only the largest or the smallest molecules. For example, (C24H12)4, (C24H12)2(C54H18)2, and (C54H18)4 have binding energies of -294.5, -572.8, and -802.0 kJ/mol, respectively. Similarly, less symmetric PAHs are likely to deviate from the trends that are found in this paper. Therefore, considering a whole family of interstellar PAHs with sizes ranging between 24 and 96 carbon atoms provides a wealth of clusters with properties that could fit the observational constraints.
Other processes may also occur before clusters photo-evaporate. Rapacioli & Spiegelman (2009) show that the ionization potential of coronene clusters decreases when the number of units in the cluster increases. The authors report a decrease from 7.6 eV for the monomer to 6.4 eV for the octomer. In addition, larger PAHs have a lower ionisation potential than smaller ones. For example, the ionization potential of C96H24 is estimated to be ~5.7 eV (Ruiterkamp et al. 2005). A description of the charge state of PAH clusters in PDRs is therefore necessary. In addition, because the binding energy of ionised PAH clusters containing a small number of molecules is significantly larger than in the corresponding neutral clusters (Rapacioli & Spiegelman 2009), ionisation is expected to affect the photo-stability of these species in PDRs.
PAHs in clusters may not be always saturated, for instance, because of interactions with cosmic rays. This could imply intra-cluster reactivity and the formation of chemical bonds between the PAH units within the cluster. This could represent a limitation to the applicability of our results, if such reactivity occurs on timescales shorter than the evaporation timescales. Adaptation of the framework used in the present paper to intra-cluster reactivity might be possible as long as the processes are statistical.
Only the largest clusters that survive evaporation in PDRs (if they exist) could be found in HII regions where they are submitted to EUV photons of ~20–30 eV. In PDRs, such energies can only be attained in rare events by sequential absorption of milder UV photons. We can therefore expect that the destruction of PAH clusters will be very efficient in HII regions. The absorption of EUV photons is likely to open other relaxation pathways, such as multiple-ionisation or intra-cluster reactivity, and therefore the description of the evolution of PAH clusters in HII regions is beyond the scope of the present study.
5. Conclusion
We have computed the absolute evaporation rates of non-rotating neutral PAH clusters of astrophysical interest, made of 2 to 12 molecules of coronene C24H12, circumcoronene C54H18, or circumcircumcoronene C96H24. We thereby provided essential data for testing the relevance of PAH clusters as models for the so-called eVSGs whose sizes span the range between ~100 to ~1000 C-atoms (Rapacioli et al. 2005a; Pilleri et al. 2012).
We performed the calculations using the statistico-dynamical approach proposed by Weerasinghe & Amar (1993), and further analysed and developed by Calvo & Parneix (2003). We proposed an extension of the method that enables taking the distribution of the excess energy into account amongst all the inter- and intra-molecular modes in a microcanonical framework, despite the use of the rigid molecule approximation. A successful comparison with the experimental results of Schmidt et al. (2006) on coronene clusters, without any fitting parameter, gives us confidence in the method.
The evaporation rates exhibit very regular trends that we found to be related to the structural similarities between the studied species. When considering clusters of molecules with different geometries, as well as heteroclusters, one should expect deviations from these trends that could be interesting to consider for studying natural mixtures, such as in astrophysical environments or in flames. The absolute values of the evaporation rates decrease strongly with the number of molecules in the cluster, and even more with the size of molecules, indicating that clusters of large PAHs are more likely to survive in PDRs. These results also indicate that large PAHs could play a significant role in the nucleation process of soot particles.
We evaluated the impact of most approximations that have been made, on our results. The sensitivity of evaporation rates to the accuracy of the geometric and the long-range interaction parameters used in PST should be considered of second order compared to the sensitivity to other approximations made in the calculations. Rather small errors result from the use of our rates to PAH clusters with rotational temperatures up to a few hundred K. For higher temperatures, the initial angular momentum of parent clusters should be considered, and a more accurate evaluation of the geometric and long-range interaction parameters could then be necessary (Calvo & Parneix 2004).
The anharmonicity of intramolecular vibrations was estimated to play a minor role thanks to the dispersion of energy among numerous intra-molecular modes. On the contrary, the anharmonicity of intermolecular modes is crucial for reproducing the variations in the evaporation rates with excess energy revealed by molecular dynamics. Only the anharmonicity resulting from the coupling between inter- and intra-molecular modes cannot be modelled with our method. A comparative study with full-atom methods could help quantify the effects of this coupling on the statistical and dynamical properties of molecular cluster evaporation.
We used our molecular data to study the evolution of PAH clusters in conditions typical of PDRs. We showed that the whole range of photostability properties, from very easily photo-evaporated to extremely photostable, is covered when considering clusters made of PAHs with sizes in the expected range for astrophysical PAHs. Our results therefore reinforce the idea that PAH clusters are good candidates for eVSGs, if the size of individual units is large enough (≳50 C-atoms).
This work provides most of the elements needed to investigate the survival of neutral PAH clusters in the interstellar medium. Nevertheless, numerous studies are needed to have a complete set of data that would enable modelling realistic interstellar PAH clusters, including the effects of the charge state, the blending of molecules, and the rotation of the clusters. Apart from the molecular data, valuable progress in our understanding of the nature of eVSGs now relies on a closer comparison of the results of modelling and astronomical observables.
Acknowledgments
The authors gratefully acknowledge A. Simon, who kindly provided the results of DFT calculations presented in this work, and thank F. Spiegelman, M. Rapacioli, and P. Parneix for stimulating discussions and helpful comments. J. Montillaud acknowledges the support of the French Agence Nationale de la Recherche (ANR), under grant GASPARIM “Gas-phase PAH research for the interstellar medium”, ANR-2010-BLANC-0501.
References
- Allamandola, L. J., Tielens, A. G. G. M., & Barker, J. R. 1985, ApJ, 290, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Basire, M., Parneix, P., & Calvo, F. 2008, J. Chem. Phys., 129, 1101 [CrossRef] [PubMed] [Google Scholar]
- Bauschlicher, C. W., Peeters, E., & Allamandola, L. J. 2008, ApJ, 678, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Calvo, F., & Labastie, P. 1995, Chem. Phys. Lett., 247, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Calvo, F., & Parneix, P. 2003, J. Chem. Phys., 119, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Calvo, F., & Parneix, P. 2004, J. Chem. Phys., 120, 2780 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Calvo, F., Douady, J., & Spiegelman, F. 2010, J. Chem. Phys., 132, 024305 [NASA ADS] [CrossRef] [Google Scholar]
- Cherchneff, I. 2011, in EAS Pub. Ser., 46, 177 [Google Scholar]
- Chesnavich, W. J., & Bowers, M. T. 1977, J. Chem. Phys., 66, 2306 [NASA ADS] [CrossRef] [Google Scholar]
- Frenklach, M. 2002, Phys. Chem. Chem. Phys., 4, 2028 [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Herdman, J. D., & Miller, J. H. 2008, J. Phys. Chem. A, 112, 6249 [CrossRef] [Google Scholar]
- Joblin, C., & Tielens, A. G. G. M. 2011, PAHs and the Universe, EAS Pub. Ser., 46 [Google Scholar]
- Joblin, C., D’Hendecourt, L., Leger, A., & Defourneau, D. 1994, A&A, 281, 923 [NASA ADS] [Google Scholar]
- Klots, C. 1971, J. Phys. Chem., 75, 1526 [Google Scholar]
- Labastie, P., & Whetten, R. 1990, Phys. Rev. Lett., 65, 1567 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2001, ApJS, 132, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., & Puget, J. L. 1984, A&A, 137, L5 [NASA ADS] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Montillaud, J., Toublanc, D., & Joblin, C. 2013, A&A, 552, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parneix, P., & Calvo, F. 2003, J. Chem. Phys., 119, 9469 [NASA ADS] [CrossRef] [Google Scholar]
- Parneix, P., & Calvo, F. 2004, J. Chem. Phys., 121, 11088 [NASA ADS] [CrossRef] [Google Scholar]
- Pilleri, P., Montillaud, J., Berné, O., & Joblin, C. 2012, A&A, 542, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rapacioli, M., & Spiegelman, F. 2009, Eur. Phys. J. D, 52, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rapacioli, M., Joblin, C., & Boissel, P. 2005a, A&A, 429, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rapacioli, M., Calvo, F., Spiegelman, F., Joblin, C., & Wales, D. J. 2005b, J. Phys. Chem. A, 109, 2487 [CrossRef] [PubMed] [Google Scholar]
- Rapacioli, M., Calvo, F., Joblin, C., et al. 2006, A&A, 460, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rapacioli, M., Calvo, F., Joblin, C., Parneix, P., & Spiegelman, F. 2007, J. Phys. Chem. A, 111, 2999 [CrossRef] [PubMed] [Google Scholar]
- Ruiterkamp, R., Cox, N. L. J., Spaans, M., et al. 2005, A&A, 432, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sabbah, H., Biennier, L., Klippenstein, S. J., Sims, I. R., & Rowe, B. R. 2010, J. Phys. Chem. Lett., 1, 2962 [CrossRef] [Google Scholar]
- Schmidt, M., Masson, A., & Bréchignac, C. 2006, Int. J. Mass Spectrom., 252, 173 [Google Scholar]
- Schuetz, C., & Frenklach, M. 2002, P. Combust. Inst., 29, 2307 [CrossRef] [Google Scholar]
- Stein, S. E., & Rabinovitch, B. S. 1973, J. Chem. Phys., 58, 2438 [NASA ADS] [CrossRef] [Google Scholar]
- van de Waal, B. W. 1983, J. Chem. Phys., 79, 3948 [NASA ADS] [CrossRef] [Google Scholar]
- Weerasinghe, S., & Amar, F. G. 1993, J. Chem. Phys., 98, 4967 [NASA ADS] [CrossRef] [Google Scholar]
- Ysard, N., & Verstraete, L. 2010, A&A, 509, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, Y., & Truhlar, D. G. 2008, Acc. Chem. Res., 41, 157 [CrossRef] [Google Scholar]
Appendix A: Calculations of vibrational densities of states
Appendix A.1: Classical anharmonic VDOS of intermolecular modes
When a cluster contains enough energy to evaporate, the system abundantly explores regions of the intermolecular potential surface that strongly deviate from the quadratic approximation and that is likely to experience isomerisation, especially for large numbers of molecules and for small molecules. Anharmonicity of the intermolecular modes is thus expected to play a significant role in the evaporation process.
Labastie & Whetten (1990) developed the multiple histogram method to compute VDOS on the basis of MD simulations. We adapted this method to our microcanonical systems following Calvo & Labastie (1995). For this purpose, we performed additional MD simulations using the code presented in Sect. 2.2. For each cluster, trajectories were integrated over 10-9 s for ~30 different initial energies up to the dissociation energy. When an evaporation event was detected, the last records were deleted until the velocity vector of the evaporating molecule was found to point towards the fragment cluster, and a new trajectory was started with new random initial velocities. The first 10 000 points were systematically discarded to ensure thermal equilibrium. The recorded potential energies were distributed among the 1000 bins of the histograms that we treated with a least square minimisation inspired from Weerasinghe & Amar (1993).
The anharmonicity is found to occur at rather high energies, typically greater than 50% of the binding energy, except for the two-stack clusters (C24H12)11 and (C24H12)12. These clusters exhibit strong anharmonicity as soon as Einter = 2 eV, suggesting that they are more prone to isomerisation than one-stack clusters. Interestingly, the intermolecular VDOS of different one-stack clusters with the same number of molecules almost overlap when scaled to the corresponding dissociation energy, as illustrated with the example of tetramers in Fig. A.1. This opens the possibility of building empirical laws parametrised with the number and size of PAH molecules in the cluster.
In the following, we use this method to compute 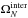 and
and
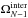 in Eq.
(7).
in Eq.
(7).
Appendix A.2: Quantum vibrational densities of states
The exact quantum harmonic vibrational densities of states are easily computed from the vibrational frequencies of the species using the Beyer-Swinehart algorithm as proposed in Stein & Rabinovitch (1973). Density functional theory (DFT) was used to compute vibrational frequencies. The functional M06-2X (Zhao & Truhlar 2008) was selected, because it is more appropriate to describe medium-range correlation energy, such as van der Waals attraction, than the popular B3LYP. It was associated to the basis 6-31G* to compute the quantum harmonic frequencies of C24H12, (C24H12)2, (C24H12)4, C54H18, and (C54H18)2 (A. Simon, priv. comm.). We applied correction factors of 0.948 to the C-H stretch mode frequencies and 0.974 for all other modes, which were determined using the experimental data of Joblin et al. (1994) for coronene in neon matrix at 4 K. The DFT frequencies of circumcircumcoronene C96H24 were taken from Bauschlicher et al. (2008).
Molecular dimers have six intermolecular modes. Only the three lowest frequency modes of both dimers were found to be purely intermolecular. All other modes showed some intramolecular character, so we qualitatively looked for the three modes with the largest intermolecular character. Following the analysis by Rapacioli et al. (2007), we considered modes to have a large intermolecular character when they involve large scale motions in the molecule, i.e. collective motions of many atoms. A good typical example is the antisymmetric bowl mode of the coronene dimer, as illustrated in the Fig. 1 of Rapacioli et al. (2007). In contrast, the C−H stretching mode in PAH molecules can be considered as an almost pure intramolecular mode. The three modes with large intermolecular components that we selected are the antisymmetric bowl mode and two antisymmetric butterfly-like modes. They fall in the typical frequency range of soft modes (~50–120 cm-1). Together with the three purely intermolecular modes, they constitute the set of six (approximately) intermolecular modes used for calculating intermolecular VDOS. Changing the chosen soft modes was found to affect the corresponding VDOS only by an overall factor for energies over a few 0.1 eV.
 |
Fig. A.1 Classical vibrational densities of states extracted from molecular dynamics simulations of the tetramers of coronene, circumcoronene, and circumcircumcoronene scaled to their dissociation energy D0. They exhibit very similar behaviour even for energies higher than 1.7D0, for which the anharmonic contribution cannot be neglected. |
For a cluster containing N coronene or circumcoronene molecules, a set of intermolecular modes was built by duplicating N − 1 times the intermolecular modes of the corresponding dimer, and a set of intramolecular modes by duplicating N times the intramolecular modes of the monomer. For circumcircumcoronene clusters, we used the same intermolecular modes as for circumcoronene.
We investigated the impact of this method by comparing the VDOS calculated using the DFT modes of the tetramer of coronene and the VDOS computed with duplicated modes as described above. As shown in Fig. A.2, the ratio of the two VDOS is constant for energies greater than ~2 eV and remains within a factor of 2 below 2 eV. These differences can be considered as small with respect to the numerous orders of magnitudes spanned by the VDOS. In addition, the main use of these results consists in a convolution product of inter- and intra-molecular VDOS (see Sect. A.3), which is notably insensitive to these errors.
 |
Fig. A.2 Inter- and intra-molecular vibrational densities of states of (C24H12)4 computed using either the full set of DFT frequencies of (C24H12)4 (solid lines) or duplicated modes (long dashed lines, see text for details). Their ratio is plotted on the right axis (short dashed lines). |
A first estimation of the factor to apply to the quantum harmonic VDOS to correct for anharmonic effects was empirically derived from the results of Basire et al. (2008). According to their Fig. 2, the ratio of the full coupled anharmonic VDOS to the harmonic VDOS of the monomer naphthalene molecule C10H8 is approximated well by exp(E/a) with a = 6 eV. We take the dilution of the energy into account amongst the N vibrational modes of the studied species by exp [ (48 /N) × E/a ], where 48 is the number of vibrational modes of naphthalene. This leads to a decreasing correction factor with increasing cluster size for a given energy. In the absence of a better estimate, we apply this correction in the next section for both the inter- and intra-molecular modes in order to get an estimate of the impact of anharmonicity on calculating the distribution of intermolecular energy. One should note, however, that Basire et al. (2008) did not consider intermolecular vibrations in their calculations.
Appendix A.3: Determining the statistical distribution of energy
The statistical distribution between inter- and intra-molecular energy is characterised
by the probability distribution of the intermolecular energy, computed following Eq.
(3). Figure A.3 uses the example of (C24H12)8 to show that
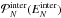 peaks at rather low energies,
where the anharmonicity of intermolecular modes is expected to play a minor role on the
peak position of
peaks at rather low energies,
where the anharmonicity of intermolecular modes is expected to play a minor role on the
peak position of 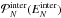 . We tested this idea by
approximating quantum anharmonic VDOS using the anharmonic corrections derived from the
work by Basire et al. (2008) as discussed in
previous section. Figure A.3 shows that
. We tested this idea by
approximating quantum anharmonic VDOS using the anharmonic corrections derived from the
work by Basire et al. (2008) as discussed in
previous section. Figure A.3 shows that
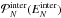 is marginally modified by the
anharmonic corrections. In contrast, the classical harmonic approximation leads to a
significant shift in the peak position. In addition, since the distribution
is marginally modified by the
anharmonic corrections. In contrast, the classical harmonic approximation leads to a
significant shift in the peak position. In addition, since the distribution
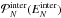 is the expression of the
balance between inter- and intra-molecular modes, it is convenient to keep the same
level of description for both kinds of modes. In this study we therefore use the
intermolecular energy distribution derived from the quantum harmonic VDOS for both
inter- and intra-molecular vibrations.
is the expression of the
balance between inter- and intra-molecular modes, it is convenient to keep the same
level of description for both kinds of modes. In this study we therefore use the
intermolecular energy distribution derived from the quantum harmonic VDOS for both
inter- and intra-molecular vibrations.
Appendix A.4: Sensitivity of results to PST input parameters and to assumptions
We performed a series of tests to assess how sensitive our evaporation rates are to the
various assumptions we made and to the accuracy of the parameters. We considered the
case of circumcoronene tetramer (C54H18)4 and used PST to compute
the KER distributions and evaporation rate for different models. Figure A.4 shows the rigid molecule evaporation rates
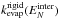 and the KER distributions at
and the KER distributions at
 and 6
eV, defined by
and 6
eV, defined by 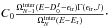 We
emphasise that the value of
We
emphasise that the value of 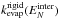 is therefore given by the
integration of the KER over ϵtr for a given
is therefore given by the
integration of the KER over ϵtr for a given
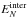 (see
Eq. (7)). For an easier comparison, we
normalised all the results (i.e. we chose the value of C0) to have
kevap =
1010 s-1 at Einter = 6 eV.
(see
Eq. (7)). For an easier comparison, we
normalised all the results (i.e. we chose the value of C0) to have
kevap =
1010 s-1 at Einter = 6 eV.
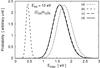 |
Fig. A.3 Probability distribution of the intermolecular energy of (C24H12)8, computed for several levels of description of the vibrational densities of states. For (a), we used different approximations for intermolecular modes (classical harmonic VDOS) and intramolecular modes (quantum harmonic VDOS), but not for the others: (b) classical harmonic; (c) approximated quantum anharmonic; (d) quantum harmonic. |
We investigated the influence of the geometry by doing the computation in the sphere-sphere approximation and in the sphere + oblate top approximation. In the latter case, we also did the computation for modified values of the rotational constants of the sphere or the oblate top with modification factors of 100 and 0.01. In one case we modified the ratio A/C by a factor 2 × 104. Figure A.4 shows that these major modifications of the geometry affect the KER and evaporation rates by factors of ≲3, while the values of the evaporation rates spans more than 14 decades for a total cluster energy between 3 eV and 6 eV. This very weak influence is permitted by the assumption J = 0, and higher sensitivity of the results to cluster geometry is be expected when considering rotating clusters (Calvo & Parneix 2004). Similar conclusions were reached when investigating the effect of the C6 parameter of the attractive term in the Lennard-Jones potential.
We estimated the impact of the non-rotation assumption (J = 0) by computing the KER and evaporation rate with J = 2000. We found a factor of a few tens in kevap with respect to the J = 0 case, which again should be compared to the 14 decades spanned by kevap between 3 eV and 6 eV of total energy. This appears to be the most critical assumption in our calculations.
Finally Fig. A.4 shows the results obtained when using harmonic VDOS instead of the anharmonic VDOS of Appendix A.1. The overall shape of kevap is greatly modified, illustrating that anharmonicity of intermolecular modes is crucial in this study.
 |
Fig. A.4 Evaporation rate (upper panel), and distribution of KER at
|
All Figures
 |
Fig. 1 Binding energy per carbon atom in the cluster for some neutral homo-molecular PAH clusters. Red filled circles are for dimers, black open circles for larger clusters with 3 to 12 molecules. The binding energy per carbon atom increases with the size of monomers and with the number of molecules in the cluster. The blue curve is the empirical relation determined by Herdman & Miller (2008) and shows a maximum relative difference of 7% with our results. The structures of the three monomers considered in this study, coronene C24H12, circumcoronene C54H18, and circumcircumcoronene C96H24, are also shown. |
| In the text | |
 |
Fig. 2 Distribution of the kinetic energy released upon the evaporation of (C96H24)4 with an intermolecular energy equal to 15.5 eV prior to evaporation. The points represent the results from MD and the solid line the prediction based on PST. |
| In the text | |
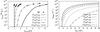 |
Fig. 3 Left: evaporation rates of some coronene clusters as a function of the internal energy in the rigid-molecule approximation from PST (lines) and MD (points) calculations. Right: corresponding evaporation rates as a function of the total energy taking the distribution of energy over the inter- and intra-molecular modes into account. |
| In the text | |
 |
Fig. 4 Same as in the right panel of Fig. 3 for clusters of circumcoronene (dot-dashed lines) and circumcircumcoronene (dashed lines). |
| In the text | |
 |
Fig. 5 Comparison of the curves of kevap obtained from full statistico-dynamical calculations (red curves) or from the interpolation methods (black curves) for clusters made of the same molecules a) or for clusters with the same number of molecules b). |
| In the text | |
 |
Fig. 6 Left: evaporation timescales of a few PAH clusters as a function of the intensity of the UV radiation field, obtained with a model considering the growth of clusters by collisions with a sticking coefficient S = 1, a hydrogen nuclei density of nH = 1.5 × 103 cm-3, and a gas temperature of T = 100 K. The thin black lines show the slopes of –1, characteristic of single-photon evaporation, and of –6, indicative of highly multi-photon evaporations. Right: results of the model for a UV radiation field of G0 = 4 × 104 in units of Habing as a function of time for circumcoronene clusters when considering the growth of clusters by collisions with S = 1 (black dashed lines) or S = 0.01 (blue solid lines). |
| In the text | |
 |
Fig. A.1 Classical vibrational densities of states extracted from molecular dynamics simulations of the tetramers of coronene, circumcoronene, and circumcircumcoronene scaled to their dissociation energy D0. They exhibit very similar behaviour even for energies higher than 1.7D0, for which the anharmonic contribution cannot be neglected. |
| In the text | |
 |
Fig. A.2 Inter- and intra-molecular vibrational densities of states of (C24H12)4 computed using either the full set of DFT frequencies of (C24H12)4 (solid lines) or duplicated modes (long dashed lines, see text for details). Their ratio is plotted on the right axis (short dashed lines). |
| In the text | |
 |
Fig. A.3 Probability distribution of the intermolecular energy of (C24H12)8, computed for several levels of description of the vibrational densities of states. For (a), we used different approximations for intermolecular modes (classical harmonic VDOS) and intramolecular modes (quantum harmonic VDOS), but not for the others: (b) classical harmonic; (c) approximated quantum anharmonic; (d) quantum harmonic. |
| In the text | |
 |
Fig. A.4 Evaporation rate (upper panel), and distribution of KER at
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.