| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 11 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201423864 | |
| Published online | 23 June 2014 | |
R-matrix electron-impact excitation data for the Be-like iso-electronic sequence ⋆
1
Department of PhysicsUniversity of Strathclyde,
Glasgow
G4 0NG, UK
e-mail: luis.fernandez-menchero@strath.ac.uk
2
Department of Applied Mathematics and Theoretical Physics,
University of Cambridge, Cambridge
CB3 0WA,
UK
Received: 21 March 2014
Accepted: 15 May 2014
Aims. Emission lines from ions in the Be-like isoelectronic sequence can be used for reliable diagnostics of temperature and density of astrophysical and fusion plasmas over a wide range of temperatures. Surprisingly, interpolated data is all that is available for a number of astrophysically important ions.
Methods. We have carried out intermediate coupling frame transformation R-matrix calculations which include a total of 238 fine-structure levels in both the configuration interaction target and close-coupling collision expansions. These arise from the configurations 1s2 2 {s, p} nl with n = 3−7, and l = 0−4 for n ≤ 5 and l = 0−2 for n = 6,7.
Results. We obtain ordinary collision strengths and Maxwell-averaged effective collision strengths for the electron-impact excitation of all the ions of the Be-like sequence, from B+ to Zn26+. We compare with previous R-matrix calculations and interpolated values for some benchmark ions. We find good agreement for transitions n = 2−2 with previous R-matrix calculations but some disagreements with interpolated values. We also find good agreement for the most intense transitions n = 2−3 which contribute via cascade to the (n = 2) diagnostic radiating levels.
Key words: atomic data / techniques: spectroscopic
These data are made available in the archives of APAP via http://www.apap-network.org and OPEN-ADAS via http://open.adas.ac.uk
© ESO, 2014
1. Introduction
Emission lines from beryllium-like ions are used in astrophysics to study a variety of emission sources. For example, solar corona ultraviolet spectra (Vernazza & Reeves 1978; Sandlin et al. 1986) or solar flares (Neupert et al. 1967). Emission lines have been recorded by several solar missions, such as Skylab (Dere 1978). In the recent years, high-resolution XUV spectroscopic observations by Chandra and XMM-Newton satellites, have also shown that a vast number of astrophysical sources produce emission lines from Be-like ions, such as Fe XXIII (Audard 2003).
Many emission lines from Be-like ions have temperature or density sensitivity, so they can be used for diagnostics of astrophysical plasmas. In particular, the intensity ratios of the resonance versus the intercombination transitions in the Be-like ions is an excellent temperature diagnostic. The ratio between the 2s 2p 1P1−2p21D2 and the intercombination transition is also a good diagnostic, considering that the lines always fall close in wavelength. Indeed, this ratio has provided one of very few direct measurements of electron temperatures in the solar corona from SOHO (see, e.g., Wilhelm et al. 1998). Be-like ion emission lines can be also used for diagnostics of fusion plasmas (Inoue et al. 2001; Summers et al. 1992).
Despite their importance, accurate electron impact excitation data for ions in this sequence are sparse. Coulomb-Born-plus-Exchange intermediate coupling (IC) calculations to n = 3 were carried out by Sampson et al. (1984) for seventeen ions between Ne6+ and W70+. R-matrix calculations were carried out by Berrington et al. (1985) for C2+, O4+, Ne6+, and Si10+ in LS-coupling followed by algebraic recoupling of the reactance matrices, only for transitions among the n = 2 levels (which give rise to ten fine-structure levels). The effective collision strengths of Berrington et al. (1985) were interpolated by Keenan et al. (1986) to provide data for N3+, F5+, Na7+, Mg8+, and Al9+. With the addition of data for Ca16+ from R-matrix calculations similar to Berrington et al. (1985) by Dufton et al. (1983), Keenan (1988) provided interpolated data for P11+, S12+, Cl13+, Ar14+, and K15+. These two sets of interpolated rates have been widely used in the literature, and have been included in early versions of the CHIANTI database (Dere et al. 1997).
However, the irregular contribution of resonances to effective collision strengths along an iso-electronic sequence (Witthoeft et al. 2007) places an unknown uncertainty on such interpolated data. For example, significant problems with the interpolated values were found by Del Zanna et al. (2008). Del Zanna et al. (2008) performed an explicit R-matrix calculation for Mg8+ and compared the intensities of the main lines with those obtained with the interpolated values. Significant differences (up to 50%) were found. There is therefore a need for explicit R-matrix calculations for all Be-like ions of astrophysical interest. This is the aim of the present work, which is part of a larger program of work to use the R-matrix method to calculate effective collision strengths for all ions, up to Zn, of all L-shell sequences as well as a start on the M-shell. The most recent sequence to-date is the B-like by Liang et al. (2012) and which contains references to earlier work on other sequences.
Some further LS-plus-algebraic recoupling R-matrix calculations were carried out by Ramsbottom and co-workers up to 2s3d (12 terms) for N3+ (Ramsbottom et al. 1994b) and up to 2p3d (26 terms) for Ne6+ (Ramsbottom et al. 1994a; Ramsbottom et al. 1995). Zhang & Sampson (1992) obtained fully-relativistic distorted wave collision strengths, for transitions within the n = 2 complex, for all of the Be-like ions from O4+ to U88+. More recent fully-relativistic work includes distorted wave data (up to 2p4d and 2s5d) for Si10+ by Bhatia & Landi (2007) and R-matrix results (up to n = 5) for S12+, obtained using the Dirac R-matrix code (DARC) by Li et al. (2013).
Because of their importance to astrophysics, extensive IC R-matrix calculations for Be-like iron and nickel were carried out by Chidichimo et al. (2005; 2003) within the Iron Project, following an early distorted wave study by Bhatia & Mason (1981). In Chidichimo et al. (2005), collision strengths and effective collision strength were obtained for Be-like Fe for the configurations n = 2,3,4, including a total of 98 fine-structure levels in the basis set. A quite fine mesh was used for the electron impact energies, so the resonances were well resolved. In Del Zanna & Mason (2005), these atomic data were benchmarked against observations, pointing out temperature and density diagnostics. Overall good agreement between predicted and observed intensities was found. We therefore adopt this work on Fe22+ as a benchmark of the whole sequence.
We also adopt the Del Zanna et al. (2008) results for Mg8+ as a benchmark. Del Zanna et al. (2008) adopted the same target as Chidichimo et al. (2005) to calculate the scattering data for Mg8+. They also benchmarked the atomic data against SOHO spectroscopic observations of the solar corona, finding excellent agreement, thus resolving long-standing discrepancies between observed and predicted line intensities. The use of R-matrix data resulted in significantly higher electron temperatures.
Finally, we also adopt as a benchmark the R-matrix results for C2+ by Berrington et al. (1985, n = 2) and Berrington et al. (1989, n = 3). In this latter case (n = 3) no algebraic recoupling of the LS-coupling reactance matrices was carried out. Rather, when these data were uploaded to the CHIANTI database, level resolved data were obtained by splitting the LS-coupling effective collision strengths according to statistical weights (see Dere et al. 1997).
We note also that Mitnik et al. (2003) carried out an R-matrix with pseudostates calculation for C2+, but only in LS-coupling. They found that inclusion of pseudostates reduced effective collision strengths for transitions n = 2−3 by typically 10% and those n = 2−4 by 20−30%. Furthermore, a similar R-matrix with pseudostates calculation by Badnell et al. (2003) found reductions of up to a factor of two in effective collision strengths for transitions to n = 4 in B+. The effect of coupling to the continuum diminishes rapidly with increasing charge state though and so we would expect only modest overestimates for our N3+ data.
In the present work we include states up to n = 7 in our configuration interaction (CI) expansion, for a total of 238 fine-structure levels. This basis set includes more bound states than any other previous non-pseudostate work and so levels up to n = 4 are better represented. In addition, cascading effects following collisional excitation up to the n = 7 shell can be examined with this basis set expansion. We use the same basis set and methods for the whole isoelectronic sequence, from B+ to Zn26+. The present data therefore includes significantly more transitions than the previous published works for ions in the same sequence.
Traditionally, astrophysics interest stops at Zn − for example, the Chianti and Cloudy modeling packages span H−Zn. This is because elemental abundance, e.g., solar, drops by over an order of magnitude at the next element onwards. However, we continue on up to Kr for magnetic fusion application. There-on, relativistic effects may need to be included in the wave functions themselves, e.g., via use of the Dirac R-matrix code. We leave no gaps because of the difficulty of deeming a priori those elements which will never be of interest to astrophysics or, especially, magnetic fusion. Any such would be small in number and so their omission not represent any significant saving of effort.
The paper is organised as follows. In Sect. 2 we give details of our description of the atomic structure and in Sect. 3 that of the R-matrix calculation. In Sect. 4 we show some representative results and compare them with the previous data of other R-matrix calculations or interpolated values. In Sect. 5 the main conclusions are discussed. Atomic units are used unless otherwise is specified.
2. Structure
To obtain the wave functions of the isolated target we used the autostructure program (Badnell 2011). autostructure calculates the wave functions by diagonalizing the Breit-Pauli Hamiltonian (Eissner et al. 1974), which includes the relativistic terms, mass-velocity, spin-orbit, and Darwin, as a perturbation. The electronic potential is included in terms of the Thomas-Fermi-Dirac-Amaldi model, adjusting the scaling parameters λ through a variational method, minimizing the equally-weighted sum of all LS term energies. We included a total of 21 atomic orbitals in the basis set: 1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f, 5s, 5p, 5d, 5f, 5g, 6s, 6p, 6d, 7s, 7p, 7d. In the configuration interaction we included all the configurations 1s2 2s2, 1s2 2s 2p, 1s2 2p2, 1s2 2s nl and 1s2 2p nl, with nl all the orbitals previously mentioned with n ≥ 3, for a total of 39 configurations. The minimized values of the scaling parameters are shown in Table 3 for all the ions in the sequence. As the atomic number increases, λ for the 1s orbital increases far away from unity. This is due to the Darwin term becoming more important as the charge of the nucleus increases. This does not affect the actual atomic structure nor the values of the level energies. The values of λ for orbitals with high angular momentum d, f and g are also much larger than the unity, which is necessary to influence the wave function for these eccentric orbits.
 |
Fig. 1 Comparative plot of oscillator strengths for C2+, Mg8+, and Fe22+. x-axis, present work; y-axis, refers to: C2+Tachiev & Fischer (1999), Mg8+Chidichimo et al. (2005), Fe22+Del Zanna et al. (2008); ° for n = 2 upper levels; □ for n = 3 upper levels; × for n = 4 upper levels. |
For such a configuration list we get a total of 130 LS terms, which are split into 238 IC levels. The calculated target energies for the IC levels up to n = 4 of the sample ions C2+, Mg8+, and Fe22+ are shown in Tables 4–6, respectively. They are compared with the observed ones, taken from the National Institute of Standards and Technology (NIST1) database (Moore 1993 for carbon, Martin & Zalubas 1980 for magnesium and Sugar & Corliss 1985 for iron) and previous theoretical works collected in the CHIANTI database (Berrington et al. 1985 for carbon n = 2, Berrington et al. 1989 for carbon n = 3, Del Zanna et al. 2008 for magnesium and Chidichimo et al. 2005 for iron). With a few exceptions in the lower excited singlet levels, the agreement with the observed values is within 1.5%. The deviation of the calculated energies respect the observed values is smaller in present work than in previous ones, only in the case of carbon it is larger than Berrington et al. (1985, 1989), this is due to their use of pseudo-orbitals. We prefer to use a spectroscopic orbitals so as to avoid having to deal with pseudo-resonances. In any case, our philosophy is to use the same approach to the structure along the entire sequence. The energy values for the rest of the levels and the other ions of the sequence not shown in Tables 4–6, can be found online. As with the previous sequences that we have considered, we use the calculated energies in the R-matrix calculation.
Comparison of gf values for some selected transitions of the ion Fe22+.
To check the quality of the calculated wave functions of the target we compare the oscillator strengths (gf values) for selected transitions in Table 1 for Fe22+ with data from Chidichimo et al. (2005), which can be found on line in the CHIANTI database. Very good agreement is found, with the exception of the very weak transition 1−62: 2s21S0−2p 4s 3P1.
Figure 1 shows a global comparison of oscillator strengths gf for all the transitions between the levels shown in Tables 4–6, with the upper level with a configuration 2lnl′ with n ≤ 4, for the benchmark ions. We plot in the x-axis the present results, and in the y-axis the results of Tachiev & Fischer (1999) for carbon, Del Zanna et al. (2008) for magnesium, and Chidichimo et al. (2005) for iron. We note that the CHIANTI data for magnesium and iron are actually the results of separate structure calculations, and not those employed for the scattering target.
Points lying on the diagonal x
= y in Fig. 1 mean
a full agreement between our calculation and previous ones. On the graph we display about
1200 gf values
and more than a 90% of them
deviate less than a 5% from the
diagonal. In carbon we appreciate four points far from the diagonal, they correspond to the
transitions 2s21S0−2s 3p
3P1, 2p21D2−2s 3p
3P1, 2s
3s 1S0−2s 3p 3P1 and
2p21S0−2s 3p
3P1 (off the scale of the graph). Tachiev & Fischer (1999) used a multiconfiguration
Hartree-Fock (MCHF) calculation followed by a configuration interaction (CI) calculation
using the Breit-Pauli Hamiltonian. These transitions are forbidden ones as they are
spin-changing, and the non-zero value of gf comes from state mixing, between the
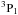 and the
and the
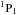 . Such E1-transitions are very sensitive to
the precise mixing. In carbon the nuclear charge is quite low, so the relativistic effects
which can mix singlets and triplets are quite small. Repeating the autostructure
calculation with different scaling parameters λ, we checked that the value
of the gf for
those transitions is very sensitive and it can vary up to six orders of magnitude,
nevertheless, the values of the level energies remain stable.
. Such E1-transitions are very sensitive to
the precise mixing. In carbon the nuclear charge is quite low, so the relativistic effects
which can mix singlets and triplets are quite small. Repeating the autostructure
calculation with different scaling parameters λ, we checked that the value
of the gf for
those transitions is very sensitive and it can vary up to six orders of magnitude,
nevertheless, the values of the level energies remain stable.
Such extreme sensitivity has little physical consequence. The radiative lifetime of the 2s 3p 3P1 is dominated the strong E1-transition to 2s 3s 3S1. The corresponding electron-impact excitation transitions are mediated by the two-body electrostatic exchange operator. As such, the effective collision strengths will behave for the most of the temperature range of interest as a forbiden transition, tending to zero. Only at high temperatures, above 106 K, will a dipole tail appear tending to a non zero value. Such temperatures are much above the ionization temperature of C2+. This sensitivity in such transition probabilities will also be reduced as the charge of the nucleus increases because the relativistic effects become larger and the state mixing fractions become more stable.
For iron and magnesium the agreement shown in Fig. 1 is very good, all the points for n = 2,3 lie on the diagonal (less than a 5% of deviation) and about 90% of the n = 4 too, only the ones which correspond to weak transitions have a larger deviation. The points which lie far from the diagonal correspond to transitions between levels with configurations 4d and 4f, the last orbitals included in the basis sets of Chidichimo et al. (2005) and Del Zanna et al. (2008). As our basis set includes more bound orbitals, up to 7d, the description of these excited levels can vary respect the previous works and that is the likely reason for the discrepancy in the gf values for those transitions.
3. Scattering
We use the R-matrix method (Hummer et al. 1993; Berrington et al. 1995) in combination with an intermediate coupling frame transformation (ICFT; Griffin et al. 1998; Badnell & Griffin 1999). The approach used is the same one as Chidichimo et al. (2005) and Del Zanna et al. (2008) for Be-like Fe and Mg, but with a larger close-coupling expansion.
In the R-matrix inner region, exchange effects were included for angular momentum up to 2J = 23, then extended using a non-exchange approximation for 2J up to 89, the contributions for higher J values were added using a top-up with the Burgess sum rule (Burgess 1974) for dipole transitions and a geometric series for the non-dipole transitions (Badnell & Griffin 2001). In the outer region we used two different meshes for the impact energy. A coarse mesh was applied for the non exchange calculation in the whole energy range and also for the exchange calculation for impact energies above the highest target level energy. This coarse mesh was around 10-4z2 Ry, with z the ion charge Z−4, being Z the atomic number.
The characteristic scattering energy increases as a factor z2 with the charge of the ion, nevertheless the width of the resonances remains constant. In order to maintain the resolution of the resonances over the sequence, we should use a constant fine energy step, thus increasing the number of grid points by a factor z2. This is computationally impractical for all but small calculations. In practice, we have found (Witthoeft et al. 2007) that increasing the number of grid points by a factor z samples and converges the resonance structure satisfactorily. Thus, we use a fine energy mesh step which varies continuously versus the ionic charge, from 6.4 × 10-5 for B+ up to 2.2 × 10-6 for Zn26+.
We convoluted the collision strengths Ω(i − j) with a Maxwellian
distribution for the energies of the plasma electrons to form integrated effective collision
strengths Υ(i −
j): 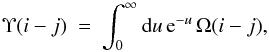 (1)where u =
E/kT and E is the energy of the
scattered electron, T the electron temperature and k the Boltzmann constant. We
calculated the effective collision strengths for a wide range of temperatures from
1.6 × 104 to
1.6 × 108 K, which
covers the whole range of interest for astrophysical and fusion plasmas.
(1)where u =
E/kT and E is the energy of the
scattered electron, T the electron temperature and k the Boltzmann constant. We
calculated the effective collision strengths for a wide range of temperatures from
1.6 × 104 to
1.6 × 108 K, which
covers the whole range of interest for astrophysical and fusion plasmas.
For this integration, the collision strengths were extended to high energies by interpolation using the appropriate infinite-energy limits in the Burgess & Tully (1992) scaled domain. The infinite-energy limits were calculated with autostructure depending on the transition type: for the dipole-allowed transitions the results are given by 4S/3, where S is the line strength, and for the non-dipole-allowed transitions by the Born approximation as described in Burgess et al. (1997). This infinite energy point can also be used to compare the present atomic structure with the previous ones. In Table 2 we show a comparison between the values of the collision strengths for infinite impact energy with the ones calculated by Chidichimo et al. (2005). Agreement below the 5% is found in most cases, with larger discrepancies present for the higher n = 4 levels.
Comparison of (scaled) infinite energy limit points for some dipole (4S/3) and allowed (Born) transitions in Fe22+.
Thomas-Fermi-Dirac-Amaldi potential scaling factors used in autostructure calculation.
C2+ target levels.
Mg8+ target levels.
Fe22+ target levels.
4. Results
We calculated the collision strengths Ω(i − j) and effective collision strengths Υ(i − j) for the electron impact excitation of ions in the Be-like isoelectronic sequence, from B+ to Zn26+, for all transitions between the first 238 fine structure levels. This results in a total of 28 203 transitions for each ion.
The effective collision strengths Υ(i − j) have been stored as an Atomic Data Format file adf04. These files also contain the full set of one-photon allowed transition A-values calculated with autostructure. These data can be used for diagnostic of temperature and density of astrophysical and fusion plasmas. Nevertheless, for non Maxwellian velocity distributions in plasma, these adf04 files can not be used and the collision strengths Ω should be used directly.
As a sample of the results, we show in Fig. 2 the collision strengths for some important transitions within the n = 2 complex (see Del Zanna et al. 2008) for the benchmark ions in the Be-like sequence. We show four different types of transitions: dipole-allowed (1 −5), dipole-allowed through spin-orbit mixing (1−3), a double-electron-jump Born transition (1−9), and a forbidden one (1−4). The collision strengths present the usual structure, a resonance region for the energies which correspond to transitions between the calculated levels, and a regular background. For dipole-allowed transitions, the collision strength diverges logarithmically as the energy tends to infinity, while for non dipole-allowed transitions it tends to a constant and for forbidden transitions the collision strength tends to zero as E-2 in the infinite energy limit.
Looking down the columns of Fig. 2 we can follow the isoelectronic trend, or lack thereof, of a transition. The resonance structure and background varies differently as the ion charge increases. The resonance widths remain constant while the impact energy increases as a factor z2. The height of the resonances increases as a factor z2 too, with respect to the background. The relative strength of the background can also increase with increasing charge due to increased spin-orbit mixing, for example, in singlet-triplet mixing. This effect is clearly seen in the transition 1−3. The spin-orbit mixing of 3P with 1P turns this transition into a dipole-allowed one for iron, with corresponding asymptotic behavior, while in carbon (with a much lower nuclear charge) it behaves as a forbidden transition still.
For the case of Fe22+, we show also in Fig. 2 a comparison with the distorted wave results of Bhatia & Mason (1981). While there is good agreement between the distorted wave collision strengths and the background R-matrix ones, the omission of resonances by the former method can give rise to significant differences in Maxwellian rate coefficients for some transitions. Chidichimo et al. (1999, 2005) compared their R-matrix results for ground-state transitions to levels of n = 2 and 3 with the distorted wave ones of Bhatia & Mason (1981) and found differences of up to a factor of two and ~30%, respectively, at 107 K.
Figure 3 shows our Maxwell integrated effective collision strengths for the same transitions as shown in Fig. 2. The figure also shows a comparison with the previous benchmark calculations: Berrington et al. (1985); Del Zanna et al. (2008); Chidichimo et al. (2005); Mitnik et al. (2003). The Mitnik et al. (2003) calculation included Laguerre pseudostates in the close-coupling expansion. It was performed in LS-coupling and a direct comparison without further recoupling can only be made for transitions which involve a singlet state (or an S-state), following a generalization of Burgess et al. (1970), Eq. (99) etc. For the singlet–triplet transitions, level resolution can be determined simply by multiplying the effective collision strength by the fractional statistical weight of the level. The inclusion of pseudostates gives a difference of less than 10% compared to calculations without them.
 |
Fig. 2 Electron-impact excitation collision strengths versus the impact energy for some selected transitions within the n = 2 complex for the benchmark ions. Full line: present R-matrix work; □: distorted wave results of Bhatia & Mason (1981). |
 |
Fig. 3 Electron-impact excitation effective collision strengths versus the electron temperature for some selected transitions and targets, as in Fig. 2. Full line: present work; dashed line: C2+Berrington et al. (1989), Mg8+Del Zanna et al. (2008), and Fe22+Chidichimo et al. (2005); dotted line: C2+Mitnik et al. (2003). |
For low temperatures, the center of the Maxwellian envelope lies on the resonance region, so such temperatures are quite sensitive to the good description of the resonances, if the impact energy mesh is fine enough. Thus, we have carried out a convergence study of the effective collision strengths at low temperature and we have checked that the fine mesh step used is sufficient for the ions under consideration. Overall, excellent agreement with previous calculations is found. This indicates that resonance excitation due to the extra configurations in our extended target does not produce significant enhancements for the n = 2 transitions. The transition (1−3) shows when the spin orbit gives an important contribution. For carbon and magnesium this transition behaves as forbidden for temperatures of physical interest, but for iron it shows dipole behavior.
The main population mechanism to states which radiate the important lines for plasma diagnosis (electric dipole 2p2−2s2p) is direct excitation from the ground state. A secondary population mechanism lies in the direct excitation from the ground state to n = 3 and n = 4 levels and afterwards cascade to these 2p2 levels. The most intense transitions to n = 3 calculated in the present work mainly agree with previous R-matrix calculations and also with the interpolated data, but some discrepancies were found in weaker transitions, double electron jumps or forbidden ones.
Effective collision strengths for weak transitions can have a considerable contribution from resonances at lower temperatures. The present close-coupling expansion is larger than those used in previous (non-pseudo-state) R-matrix works, especially those which only expanded up to n = 3. Consequently, we expect a larger resonance enhancement compared to those works, and we illustrate a case in Fig. 4. There we compare our effective collision strengths for the 2s21S0−2s3p 3P1 transition in Ne6+ with the LS-plus-algebraic recoupling R-matrix results of Ramsbottom et al. (1995). At low temperatures our results display a much larger resonance enhancement, compared to those of Ramsbottom et al. (1995), while at high temperatures we see the influence of spin-orbit mixing turning the high-energy/temperature tail from a forbidden to weak dipole-allowed one.
 |
Fig. 4 Electron-impact excitation effective collision strengths versus the electron temperature for transition 1−152s21S0−2s3p 3P1 of Ne6+. Full line: present work; dashed line: Data from Ramsbottom et al. (1995). |
Figure 5 shows the effective collision strengths for some selected transitions of P11+. Be-like P11+ has not been calculated before using the R-matrix method or a DW method, and the data currently used for diagnostic modeling within the CHIANTI database are interpolated ones from Keenan (1988). In this figure we show the same set of transitions as in Fig. 3. The double-electron-jump (1−9) shows differences between the R-matrix calculations and the interpolated data, and in the spin-changing transition (1−3) the discrepancy is quite large. Asymptotically, the transition 1−3 behaves as a dipole one through spin-orbit mixing, as discussed earlier. But, algebraic recoupling only of LS-coupling data does not include such mixing and it (1−3) behaves as a forbidden one still. Thus, neither the original data nor the interpolated data are valid for such transitions, at these energies.
We close this section with a note of caution: we have shown only a selection of transitions and when the totality of excitations plus-cascade are modeled then Del Zanna et al. (2008) has shown that significant problems can arise on using interpolated data.
5. Conclusions
We have presented a complete data set of ICFT R-Matrix calculations of electron-impact excitation of all ions in the Be-like isoelectronic sequence from B+ to Zn26+. We have shown a selected set of collision strengths and effective collision strengths for some important n = 2 transitions and ions, finding good agreement with previous similar calculations. The present work expands the previous ones Del Zanna et al. (2008); Chidichimo et al. (2003, 2005) for Be-like Mg, Fe and Ni, by significantly increasing the orbitals in the basis set.
The present data set constitutes a significant improvement over previous available data for many ions in the Be-like sequence, which was based upon interpolated data. With our basis set emission lines including from cascade effects from levels up to n = 7 can be predicted. With the present data, emission lines from Be-like ions can reliably be used for diagnostics of temperature and density of astrophysical and fusion plasmas. The atomic data are made available at our APAP network web page2. They will also be uploaded into the OPEN-ADAS3 and CHIANTI4 databases.
Work is in progress to expand the method to other isoelectronic sequences, in particular, the Mg-like, which is similar to this one in the sense that it consist of a closed n-shell plus two electrons.
 |
Fig. 5 Electron-impact excitation effective collision strengths versus the electron temperature for some selected transitions of P11+. Full line: present work; dashed line: interpolated data from Keenan (1988). |
Acknowledgments
The present work was funded by STFC (UK) through the University of Strathclyde UK APAP network grant ST/J000892/1 and the University of Cambridge DAMTP astrophysics grant.
References
- Audard, M. 2003, Adv. Space Res., 32, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2011, Comput. Phys. Commun., 182, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R., &Griffin, D. C. 1999, J. Phys. B, 32, 2267 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R., &Griffin, D. C. 2001, J. Phys. B, 34, 681 [Google Scholar]
- Badnell, N. R.,Griffin, D. C., & Mitnik, D. M. 2003, J. Phys. B At., Mol. Opt. Phys., 36, 1337 [NASA ADS] [CrossRef] [Google Scholar]
- Berrington, K. A., Burke, P. G., Dufton, P. L., &Kingston, A. E. 1985, Atom. Data Nucl. Data Tables, 33, 195 [Google Scholar]
- Berrington, K. A., Burke, V. M., Burke, P. G., &Scialla, S. 1989, J. Phys. B, Atomic, Molecular and Optical Physics, 22, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Berrington, K. A.,Eissner, W. B., & Norrington, P. H. 1995, Comput. Phys. Commun., 92, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Bhatia, A. K., &Landi, E. 2007, Atom. Data Nucl. Data Tables, 93, 275 [Google Scholar]
- Bhatia, A. K., &Mason, H. E. 1981, A&A, 103, 324 [NASA ADS] [Google Scholar]
- Burgess, A. 1974, J. Phys. B, At. Mol. Phys., 7, L364 [Google Scholar]
- Burgess, A., &Tully, J. A. 1992, A&A, 254, 436 [NASA ADS] [Google Scholar]
- Burgess, A., Hummer, D. G., &Tully, J. A. 1970, Philos. Trans. R. Soc. London, Ser. A, 266, 225 [Google Scholar]
- Burgess, A., Chidichimo, M. C., &Tully, J. A. 1997, J. Phys. B, 30, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Chidichimo, M. C., Zeman, V., Tully, J. A., &Berrington, K. A. 1999, A&AS, 137, 175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chidichimo, M. C.,Badnell, N. R., & Tully, J. A. 2003, A&A, 401, 1177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chidichimo, M. C., Del Zanna, G.,Mason, H. E., et al. 2005, A&A, 430, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DelZanna, G., &Mason, H. E. 2005, A&A, 432, 1137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Rozum, I., &Badnell, N. R. 2008, A&A, 487, 1203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P. 1978, ApJ, 221, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E.,Monsignori-Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dufton, P. L.,Kingston, A. E., & Scott, N. S. 1983, J. Phys. B., 16, 3053 [Google Scholar]
- Eissner, W. M., Jones, M., & H, N. 1974, Comput. Phys. Commun., 8, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, D. C.,Badnell, N. R., & Pindzola, M. S. 1998, J. Phys. B, 31, 3713 [Google Scholar]
- Hummer, D. G.,Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] [Google Scholar]
- Inoue, T., Nakai, M., Tanaka, A., et al. 2001, Plasma Phys. Control. Fusion, 43, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, F. P. 1988, Phys. Scr., 37, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, F. P.,Berrington, K. A., Burke, P. G., Dufton, P. L., & Kingston, A. E. 1986, Phys. Scr., 34, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Li, F., Liang, G. Y., Bari, M. A., &Zhao, G. 2013, A&A, 556, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, G. Y.,Badnell, N. R., & Zhao, G. 2012, A&A, 547, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, W. C. &Zalubas, R. 1980, J. Phys. Chem. Ref. Data, 9, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Mitnik, D. M.,Griffin, D. C.,Ballance, C. P., & Badnell, N. R. 2003, J. Phys. B, At. Mol. Opt. Phys., 36, 717 [Google Scholar]
- Moore, C. E. 1993, in Tables of Spectra of Hydrogen, Carbon, Nitrogen and Oxygen Atoms and Ions, ed. J. W. Gallacher, CRC Series in Evaluated Data in Atomic Physics (CRC Press) [Google Scholar]
- Neupert, W. M., Gates, W., Swartz, M., &Young, R. 1967, ApJ, 149, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsbottom, C. A.,Berrington, K. A., & Bell, K. L. 1994a, J. Phys. B, 27, L811 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsbottom, C. A.,Berrington, K. A., Hibbert, A., &Bell, K. L. 1994b, Phys. Scr., 50, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsbottom, C. A.,Berrington, K. A., & Bell, K. L. 1995, Atom. Data Nucl. Data Tables, 61, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Sampson, D. H., Goett, S. J., &Clark, R. E. H. 1984, Atom. Data Nucl. Data Tables, 30, 125 [Google Scholar]
- Sandlin, G. D., Bartoe, J.-D. F.,Tousey, R., & Van Hoosier, M. E. 1986, ApJS, 61, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Sugar, J., & Corliss, C. 1985, J. Phys. Chem. Ref. Data, 14, Suppl. 2, 1 [Google Scholar]
- Summers, H. P.,Dickson, W. J.,Boileau, A., et al. 1992, Plasma Physics and Controlled Fusion, 34, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Tachiev, G., &Fischer, C. F. 1999, J. Phys. B, 32, 5805 [Google Scholar]
- Vernazza, J. E., &Reeves, E. M. 1978, ApJS, 37, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Wilhelm, K., Marsch, E., Dwivedi, B. N., et al. 1998, ApJ, 500, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Witthoeft, M. C.,Whiteford, A. D., & Badnell, N. R. 2007, J. Phys. B, At. Mol. Opt. Phys., 40, 2969 [Google Scholar]
- Zhang, H. L., &Sampson, D. H. 1992, Atom. Data Nucl. Data Tables, 52, 143 [Google Scholar]
All Tables
Comparison of (scaled) infinite energy limit points for some dipole (4S/3) and allowed (Born) transitions in Fe22+.
Thomas-Fermi-Dirac-Amaldi potential scaling factors used in autostructure calculation.
All Figures
 |
Fig. 1 Comparative plot of oscillator strengths for C2+, Mg8+, and Fe22+. x-axis, present work; y-axis, refers to: C2+Tachiev & Fischer (1999), Mg8+Chidichimo et al. (2005), Fe22+Del Zanna et al. (2008); ° for n = 2 upper levels; □ for n = 3 upper levels; × for n = 4 upper levels. |
| In the text | |
 |
Fig. 2 Electron-impact excitation collision strengths versus the impact energy for some selected transitions within the n = 2 complex for the benchmark ions. Full line: present R-matrix work; □: distorted wave results of Bhatia & Mason (1981). |
| In the text | |
 |
Fig. 3 Electron-impact excitation effective collision strengths versus the electron temperature for some selected transitions and targets, as in Fig. 2. Full line: present work; dashed line: C2+Berrington et al. (1989), Mg8+Del Zanna et al. (2008), and Fe22+Chidichimo et al. (2005); dotted line: C2+Mitnik et al. (2003). |
| In the text | |
 |
Fig. 4 Electron-impact excitation effective collision strengths versus the electron temperature for transition 1−152s21S0−2s3p 3P1 of Ne6+. Full line: present work; dashed line: Data from Ramsbottom et al. (1995). |
| In the text | |
 |
Fig. 5 Electron-impact excitation effective collision strengths versus the electron temperature for some selected transitions of P11+. Full line: present work; dashed line: interpolated data from Keenan (1988). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


