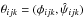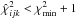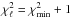| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 7 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201423661 | |
| Published online | 30 April 2014 | |
Frequentist confidence intervals for orbits⋆
Astrophysics Group, Blackett Laboratory, Imperial College London, Prince Consort Road London SW7 2AZ UK
e-mail: l.lucy@imperial.ac.uk
Received: 17 February 2014
Accepted: 25 March 2014
The problem of efficiently computing the orbital elements of a visual binary while still deriving confidence intervals with frequentist properties is treated. When formulated in terms of the Thiele-Innes elements, the known distribution of probability in Thiele-Innes space allows efficient grid-search plus Monte-Carlo-sampling schemes to be constructed for both the minimum-χ2 and the Bayesian approaches to parameter estimation. Numerical experiments with 104 independent realizations of an observed orbit confirm that the 1 − and 2σ confidence and credibility intervals have coverage fractions close to their frequentist values.
Key words: binaries: visual / stars: fundamental parameters / methods: statistical
Appendix is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
When error bars or confidence intervals are reported, the reader expects them to have their frequentist meaning. Thus, a 95% confidence interval is interpreted as implying a probability of 0.95 that the true result is enclosed by that interval. Similarly, the interval defined by ± 1σ error bars is expected to include the true answer with probability 0.683. However, this frequentist ideal is often not realized. This may be the result of observers misjudging the precision of their measurements or of large measurment errors occurring more frequently than expected for a normal distribution.
Such practical issues are absent when data analysis techniques are investigated with simulations, since precision can be exactly specified and measurement errors can be assigned with random Gaussian variates, so that one might then expect a rigorous recovery of the frequentist ideal. But approximations can still compromise statistical rigour. For example, if a grid is required, confidence intervals might be affected if the grid is too coarse. In such cases, with increased computational resources, the limit as the grid steps → 0 can be closely approached and accurate results obtained.
Of more concern are approximations that compromise confidence intervals independently of any such limit. Two examples in the recent literature occur in hybrid problems – i.e., non-linear problems with a subset of linear parameters. The first example is the code EXOFAST for analysing transit and radial velocity data for stars with orbiting planets (Eastman et al. 2013). These authors note that the convergence of their Markov chain Monte Carlo (MCMC) parameter search is much faster if the exact solution for the linear parameters is introduced. However, the resulting uncertainties in the linear parameters are as much as 10 times smaller than when fitted non-linearly. Pending further research, these authors sensibly choose the inefficient option of treating all parameters as non-linear.
A similar but less extreme example arises when Bayesian estimation is applied to visual binaries (Lucy 2014; L14). When formulated in terms of the Thiele-Innes elements, the problem becomes linear in four of the seven elements. But when this linearity is exploited, coverage fractions (L14, Sect. 5.5) indicate that the standard errors of the four linear elements are too small by factors of up to 2.1.
These examples pose a statistical challenge in the analysis of orbits: How can we benefit from partial linearity without losing the frequentist properties of confidence intervals? In this paper, this challenge is addressed in its visual binary context and for both frequentist and Bayesian procedures.
2. Synthetic orbits
The paper L14 is followed closely with regard both to notation and in the creation of synthetic data.
2.1. Orbital elements
The orbit of the secondary relative to its primary is conventionally parameterized by its Campbell elements P,e,T,a,i,ω,Ω. Here P is the period, e is the eccentricity, T is a time of periastron passage, i is the inclination, ω is the longitude of periastron, and Ω is the position angle of the ascending node. However, from the standpoint of computational economy, many investigators – references in L14 Sect. 2.1 – prefer the Thiele-Innes elements. Thus, the Campbell parameter vector θ = (φ,ϑ), where φ = (P,e,τ) and ϑ = (a,i,ω,Ω), is replaced by the Thiele-Innes vector (φ,ψ), where the components of the vector ψ are the Thiele-Innes constants A,B,F,G. (Note that in the φ vector, T has been replaced by τ = T/P which by definition ∈ (0,1).)
2.2. Model binary
As in L14, the adopted model binary has the following Campbell elements:
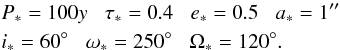 (1)An observing campaign for this binary is simulated by creating measured Cartesian sky coordinates
(1)An observing campaign for this binary is simulated by creating measured Cartesian sky coordinates 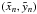 with weights wn at uniformly-spaced times tn for n = 1,...,N as described in L14 Sect. 3.2. The parameters defining a campaign are forb, the fraction of the orbit observed, N, the number of observations, and σ, the standard error for unit weight.
with weights wn at uniformly-spaced times tn for n = 1,...,N as described in L14 Sect. 3.2. The parameters defining a campaign are forb, the fraction of the orbit observed, N, the number of observations, and σ, the standard error for unit weight.
For given orbital elements, the predicted orbit (xn,yn) is computed as described in L14 Sect. A.1, and the quality of the fit is determined by 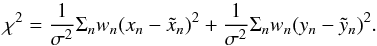 (2)
(2)
3. Minimum-χ2 estimation
The conventional (frequentist) approach to orbit-fitting is the method of least squares – i.e., finding the elements 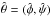 that minimize χ2. When the problem is non-linear, the search for the minimum typically involves successive differential corrections obtained from linearized equations, starting with an initial guess. However, in treating incomplete orbits and imprecise data, it is preferable to find
that minimize χ2. When the problem is non-linear, the search for the minimum typically involves successive differential corrections obtained from linearized equations, starting with an initial guess. However, in treating incomplete orbits and imprecise data, it is preferable to find 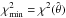 by means of a grid search (e.g., Hartkopf et al. 1989; Schaefer et al. 2006) and then to derive confidence intervals from constant χ2 “surfaces” in parameter space (e.g., Press et al. 1992, Chap. 15.6; James 2006, Chap. 9.1.2).
by means of a grid search (e.g., Hartkopf et al. 1989; Schaefer et al. 2006) and then to derive confidence intervals from constant χ2 “surfaces” in parameter space (e.g., Press et al. 1992, Chap. 15.6; James 2006, Chap. 9.1.2).
3.1. Grid search
In a brute force approach to finding 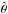 , values of χ2 would be computed throughout a 7D grid. Confidence intervals for the elements would then be derived from projections of the 7D volume
, values of χ2 would be computed throughout a 7D grid. Confidence intervals for the elements would then be derived from projections of the 7D volume 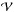 defined by the inequality
defined by the inequality 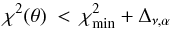 (3)where the constant Δν,α is detemined by ν, the number of degrees of freedom and α, the desired confidence level. With a typical 100 steps for each dimension, the brute force method requires χ2 to be evaluated at ~1014 grid points. However, if the linearity with respect to the Thiele-Innes elements can be exploited, χ2 is only required at ~106 grid points. This potential reduction by a factor of ~108 in the number of computed orbits is a powerful incentive to solve the challenge posed in Sect. 1.
(3)where the constant Δν,α is detemined by ν, the number of degrees of freedom and α, the desired confidence level. With a typical 100 steps for each dimension, the brute force method requires χ2 to be evaluated at ~1014 grid points. However, if the linearity with respect to the Thiele-Innes elements can be exploited, χ2 is only required at ~106 grid points. This potential reduction by a factor of ~108 in the number of computed orbits is a powerful incentive to solve the challenge posed in Sect. 1.
On the assumption that linearity can be exploited, grid searches in this paper are restricted to the φ-elements P,e,τ. The grid is defined by taking constant steps spanning the intervals (log PL,log PU),(eL,eU),(τL,τU). The grid cells are labelled (i,j,k) and the φ-elements at the mid-points are log Pi,ej,τk. With these values fixed, 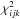 is a function of ψ = (A,B,F,G) and has its minimum value
is a function of ψ = (A,B,F,G) and has its minimum value 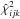 at the point
at the point 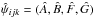 given by Eqs. (A.7) in L14.
given by Eqs. (A.7) in L14.
Because 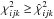 , it follows that nowhere in (φijk,ψ)-space is
, it follows that nowhere in (φijk,ψ)-space is 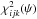 less than the minimum value found in the 3D search. Accordingly, in the limit of vanishingly small grid steps,
less than the minimum value found in the 3D search. Accordingly, in the limit of vanishingly small grid steps, 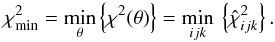 (4)Thus, as has long been understood (e.g, Hartkopf et al. 1989), the minimum-χ2 elements
(4)Thus, as has long been understood (e.g, Hartkopf et al. 1989), the minimum-χ2 elements 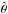 can be found with a grid search restricted to the non-linear elements.
can be found with a grid search restricted to the non-linear elements.
3.2. Approximate confidence intervals
With 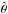 determined, the calculation of confidence intervals requires projections of
determined, the calculation of confidence intervals requires projections of 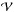 , the volume in θ-space defined by Eq. (3). In the absence of a 7D grid, a possible approach is to derive approximate confidence intervals from projections of the 3D grid points satisfying Eq. (3) – i.e., from projections of the domain
, the volume in θ-space defined by Eq. (3). In the absence of a 7D grid, a possible approach is to derive approximate confidence intervals from projections of the 3D grid points satisfying Eq. (3) – i.e., from projections of the domain 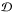 comprising grid points such that
comprising grid points such that 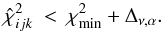 (5)This derivation of confidence intervals has exploited linearity since it relies on obtaining
(5)This derivation of confidence intervals has exploited linearity since it relies on obtaining 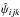 and therefore also
and therefore also 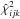 without iteration. However, every point
without iteration. However, every point 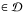 also satisfies Eq. (3), so that
also satisfies Eq. (3), so that 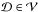 . Accordingly, these approximate intervals will always be enclosed within the true intervals and so may give a misleading impression of the elements’ precision.
. Accordingly, these approximate intervals will always be enclosed within the true intervals and so may give a misleading impression of the elements’ precision.
3.3. Accurate confidence intervals
An asymptotically rigorous calculation proceeds as follows: first, since 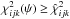 , the points (φijk,ψ) are all exterior to
, the points (φijk,ψ) are all exterior to 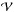 when
when 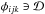 . Thus grid points
. Thus grid points 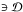 are no longer of interest.
are no longer of interest.
Now consider a point 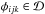 . A point in the ψ-space attached to φijk has a χ2 higher than the least squares value at φijk by the amount
. A point in the ψ-space attached to φijk has a χ2 higher than the least squares value at φijk by the amount 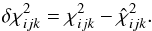 (6)This point is on the 6D surface
(6)This point is on the 6D surface 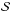 of the volume
of the volume 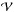 if
if 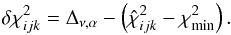 (7)The contribution to
(7)The contribution to 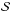 arising from the grid point (i,j,k) can therefore be obtained by randomly sampling the attached ψ-space subject to this constraint on
arising from the grid point (i,j,k) can therefore be obtained by randomly sampling the attached ψ-space subject to this constraint on 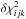 . The superposition of these contributions from all
. The superposition of these contributions from all 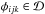 then maps out
then maps out 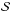 , and the projections of
, and the projections of 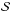 give the desired confidence intervals.
give the desired confidence intervals.
If 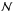 is the number of random points ψℓ on
is the number of random points ψℓ on 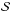 generated at each φijk, the ensemble of generated points (φijk,ψℓ) becomes an exact representation of
generated at each φijk, the ensemble of generated points (φijk,ψℓ) becomes an exact representation of 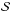 in the limits
in the limits 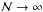 and grid steps → 0. In other words, in these limits no finite surface element
and grid steps → 0. In other words, in these limits no finite surface element 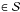 would be missed by the random sampling.
would be missed by the random sampling.
The merits of this procedure are the following: 1) The random sampling on 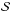 does not require further orbits to be calculated; 2) in contrast to acceptance-rejection methods common in Monte Carlo sampling, all points are accepted; and 3) in contrast to the brute force approach, no points are computed either interior or exterior to
does not require further orbits to be calculated; 2) in contrast to acceptance-rejection methods common in Monte Carlo sampling, all points are accepted; and 3) in contrast to the brute force approach, no points are computed either interior or exterior to 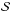 .
.
3.4. An example
To illustrate this calculation of confidence intervals, the model binary with elements given in Eq. (1) is observed in a campaign with parameters forb = 0.6,N = 15,σ = 0″05. The initial 3D search for 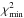 is on a coarse 1003 grid spanning the intervals (1,4),(0,1),(0,1) in log P,e,τ, respectively. Given the resulting initial estimate of
is on a coarse 1003 grid spanning the intervals (1,4),(0,1),(0,1) in log P,e,τ, respectively. Given the resulting initial estimate of 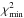 , the search boundaries are pruned in such a way that no point with
, the search boundaries are pruned in such a way that no point with  is excluded, and then a new 1003 grid is computed. The resulting
is excluded, and then a new 1003 grid is computed. The resulting 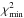 and its location are then slightly improved by making small random displacements and acceping those that reduce χ2.
and its location are then slightly improved by making small random displacements and acceping those that reduce χ2.
An investigator selects the confidence intervals of interest by specifying ν and α. Here we take α = 0.683, corresponding to ± 1σ limits, and ν = 1, thus computing confidence intervals for each element individually – i.e., independently of the other elements. With these choices, Δν,α = 1. For ± 2σ limits, α = 0.954 and Δν,α = 4.
With Δν,α = 1, the refined grid has 506 points satisfying Eq. (5). These define 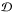 and, as described in Sect. 3.2, approximate confidence intervals are obtained from projections of
and, as described in Sect. 3.2, approximate confidence intervals are obtained from projections of 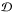 . The details are as follows: At each point
. The details are as follows: At each point 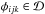 , the least squares values
, the least squares values 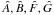 are available from the grid search. From these, the Campbell elements
are available from the grid search. From these, the Campbell elements 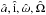 are calulated as described in Sect. A4 of L14. Thus the Campbell elements θijk are known at every point
are calulated as described in Sect. A4 of L14. Thus the Campbell elements θijk are known at every point 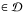 and the projections of this ensemble give the ± 1σ intervals. Figure 1 illustrates this procedure. The (log a,i)-projection of the θijk vectors
and the projections of this ensemble give the ± 1σ intervals. Figure 1 illustrates this procedure. The (log a,i)-projection of the θijk vectors 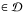 is plotted as are the resulting ± 1σ limits.
is plotted as are the resulting ± 1σ limits.
 |
Fig. 1 Approximate confidence intervals. The ensemble of orbit vectors |
Now, for the same observed orbit 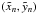 and with the same refined grid, accurate ± 1σ intervals are computed according to the procedure of Sect. 3.3. At each of the 506 grid points ∈
and with the same refined grid, accurate ± 1σ intervals are computed according to the procedure of Sect. 3.3. At each of the 506 grid points ∈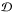 ,
, 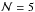 random points on
random points on 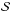 are calculated as described in Sect. A.5. These points ψℓ are such that
are calculated as described in Sect. A.5. These points ψℓ are such that 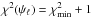 . For each ψℓ, the corresponding Campbell elements are then derived as described in Sect. A.4 of L14. The final result is 2530 vectors
. For each ψℓ, the corresponding Campbell elements are then derived as described in Sect. A.4 of L14. The final result is 2530 vectors 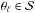 . The projections of
. The projections of 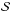 give the desired ± 1σ limits. Figure 2 illustrates this step by again projecting the cloud of points on to the (log a,i)-plane.
give the desired ± 1σ limits. Figure 2 illustrates this step by again projecting the cloud of points on to the (log a,i)-plane.
Because Figs. 1 and 2 refer to the same orbit and are plotted to the same scale, we see immediately that, as anticipated in Sect. 3.2, the approximate ± 1σ intervals are enclosed by the accurate intervals. The ratios accurate:approximate are 1.4 for log a and 1.9 for i.
A point to note from Figs. 1 and 2 is that with finite samples, the derived confidence limits will always be underestimates. In the above example, increasing 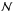 from 5 to 500 increases the confidence intervals for log a and i by additional factors of 1.045 and 1.055, respectively. Convergence experiments indicate that sufficient accuracy is achieved with
from 5 to 500 increases the confidence intervals for log a and i by additional factors of 1.045 and 1.055, respectively. Convergence experiments indicate that sufficient accuracy is achieved with 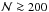 .
.
The error bars derived with these procedures for a quantity Q are in general not symmetric about its minimum-χ2 value. Accordingly, in testing these procedures, attention is focussed not on error bars but on confidence intervals (QL,QU).
 |
Fig. 2 Accurate confidence limits. The ensemble of orbit vectors |
3.5. Coverage fractions
Confidence intervals calculated as described in Sect. 3.3 are claimed to be asymptotically rigorous. This implies that, with a fine enough grid and a sufficiently large 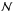 , coverage fractions will be close to their frequentist values. To test this, two experiments similar to those in Sect. 5.5 of L14 are now reported. In each experiment, the example of Sect. 3.4 is repeated 10 000 times with independent realizations
, coverage fractions will be close to their frequentist values. To test this, two experiments similar to those in Sect. 5.5 of L14 are now reported. In each experiment, the example of Sect. 3.4 is repeated 10 000 times with independent realizations 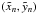 of the observed orbit. For each trial, confidence intervals are computed for various quantities Q, and an interval is counted as a success if QL<Qexact<QU. The quanties Q are the Campbell elements plus the mass estimator ℳ defined in Eq. (17) of L14.
of the observed orbit. For each trial, confidence intervals are computed for various quantities Q, and an interval is counted as a success if QL<Qexact<QU. The quanties Q are the Campbell elements plus the mass estimator ℳ defined in Eq. (17) of L14.
The approximate and accurate intervals of Sect. 3.2 and Sect. 3.3 – now with 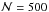 – are investigated in experiments i and ii, respectively. In each experiment, both ± 1σ and ± 2σ intervals are tested.
– are investigated in experiments i and ii, respectively. In each experiment, both ± 1σ and ± 2σ intervals are tested.
The results are reported in Table 1. From experiment i, we see that the approximate confidence intervals are too small by factors of up to 1.9 for the ± 1σ intervals and up to 1.4 for the ± 2σ intervals. In contrast, the results for experiment ii are close to ideal. Specifically, to within errors, the ± 2σ coverage fractions match the frequentist value. On the other hand, the ± 1σ coverage fractions fall short by the inconsequential factor of 1.016, indicating the need for a somewhat larger 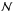 .
.
These results support the claim that the procedure developed in Sect. 3.3 is asymptotically rigorous. Moreover, the additional computational burden is negligible: experiment ii required a mere 11% more computer time than experiment i.
Coverage fractions f for confidence intervals from 104 trials.
4. Bayesian estimation
In this section, the Bayesian treatment of L14 is modified to eliminate its dependence on the profile likelihood – Eq. (3) in L14.
4.1. Posterior density
The posterior probability density function (PDF) at (φ,ψ) given data D is 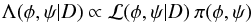 (8)where ℒ is the likelihood of (φ,ψ) given D, and π(φ,ψ) is a PDF that quantifies the investigator’s prior beliefs or knowledge about (φ,ψ). As in L14, we assume that π is the product of seven independent priors, one for each element. With the same choices as in L14, π can be omitted from Eq. (8) if the φ elements are now understood to be (log P,e,τ).
(8)where ℒ is the likelihood of (φ,ψ) given D, and π(φ,ψ) is a PDF that quantifies the investigator’s prior beliefs or knowledge about (φ,ψ). As in L14, we assume that π is the product of seven independent priors, one for each element. With the same choices as in L14, π can be omitted from Eq. (8) if the φ elements are now understood to be (log P,e,τ).
Since coefficients independent of (φ,ψ) can be ignored 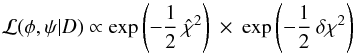 (9)where
(9)where 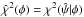 is the minimum value of χ2 at fixed φ, and δχ2(δψ | φ) is the positive increment in χ2 for the displacement
is the minimum value of χ2 at fixed φ, and δχ2(δψ | φ) is the positive increment in χ2 for the displacement 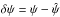 . The second factor in Eq. (9) can be eliminated using Eq. (A.9), so that
. The second factor in Eq. (9) can be eliminated using Eq. (A.9), so that 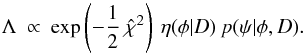 (10)If we now approximate p(ψ | φ,D) by a sum of δ functions as discussed in Sect. A.3, then
(10)If we now approximate p(ψ | φ,D) by a sum of δ functions as discussed in Sect. A.3, then 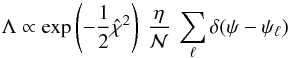 (11)where the ψℓ are
(11)where the ψℓ are 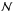 independent vectors that randomly sample the exact quadrivariate normal PDF.
independent vectors that randomly sample the exact quadrivariate normal PDF.
The PDF Λ is for the Thiele-Innes elements. The corresponding PDF Γ(θ | D) for the Campbell elements θ is 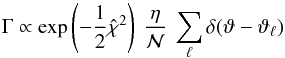 (12)where ϑℓ = ϑ(ψℓ).
(12)where ϑℓ = ϑ(ψℓ).
4.2. Credibility intervals
In terms of a 3D scan over φ-space, the PDF Γ(θ | D) is approximated by the ensemble of 7D vectors 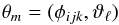 (13)with weights
(13)with weights 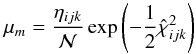 (14)Here m is an index that enumerates the random points ϑℓ across all grid points (i,j,k).
(14)Here m is an index that enumerates the random points ϑℓ across all grid points (i,j,k).
If Q(θ) is a quantity for which a credibility interval is required, the data from which this can be computed are the values Qm = Q(θm) with weights μm. From this data, an estimate of the PDF of Q is 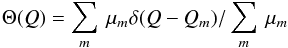 (15)with corresponding cumulative distribution function (CDF)
(15)with corresponding cumulative distribution function (CDF) 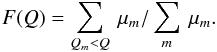 (16)The equal tail credibility interval (QL,QU) corresponding to ± 1σ is then obtained from the equations
(16)The equal tail credibility interval (QL,QU) corresponding to ± 1σ is then obtained from the equations  (17)so that the enclosed probability 0.6826.
(17)so that the enclosed probability 0.6826.
These credibility intervals are asymptotically rigorous – i.e., are exact in the limits 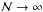 and grid steps → 0.
and grid steps → 0.
4.3. Calculation procedure
The basic steps required to derive credibility intervals are as follows:
-
1)
At every point (log Pi,ej,τk), the minimum-χ2 Thiele-Innes elements
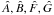 are obtained with Eqs. (A.7) of L14, and the corresponding
are obtained with Eqs. (A.7) of L14, and the corresponding 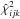 computed.
computed. -
2)
The variances and covariances defining the exact quadrivariate normal PDF p(ψ | φ,D) at φijk are computed with Eqs. (A.9), (A.10) of L14.
-
3)
Random points ψℓ sampling the exact PDF p(ψ | φijk,D) are computed as described in Sect. A.4.
-
4)
The Campbell elements ϑℓ corresponding to ψℓ are computed as described in Sect. A.4 of L14.
-
5)
The vectors θm are then (φijk,ϑℓ) with weights μm given by Eq. (14).
-
6)
Lastly, credibility intervals are derived from Qm with the approximate CDF given in Eq. (16).
4.4. An example
To illustrate this procedure, credibility intervals are computed for the orbit 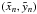 discussed in Sect. 3.4. A scatter diagram analogous to Figs. 1 and 2 is not readily constructed because the points θm are not of equal weight. Instead, the confidence intervals derived as in Fig. 2 (but now with
discussed in Sect. 3.4. A scatter diagram analogous to Figs. 1 and 2 is not readily constructed because the points θm are not of equal weight. Instead, the confidence intervals derived as in Fig. 2 (but now with 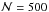 ) are compared with the credibility intervals derived from Eqs. (17).
) are compared with the credibility intervals derived from Eqs. (17).
The Δν,α = 1 confidence interval for log a is (− 0.020, 0.006), whereas the equal-tail 68.3% credibility interval is (− 0.019, 0.008). The corresponding intervals for i are 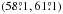 and
and 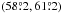 , respectively.
, respectively.
In these calculations, 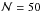 for
for 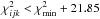 and =1 otherwise. The domain defined by this inequality corresponds to Δν,α with α = 0.9973 and ν = 7, thus ensuring an accurate treatment of the wings of the posterior PDF’s to beyond ± 2σ. Convergence experiments indicate that sufficient accuracy is achieved with
and =1 otherwise. The domain defined by this inequality corresponds to Δν,α with α = 0.9973 and ν = 7, thus ensuring an accurate treatment of the wings of the posterior PDF’s to beyond ± 2σ. Convergence experiments indicate that sufficient accuracy is achieved with 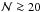 .
.
In contrast to confidence intervals derived from scatter plots such as Fig. 2, the credibility intervals calculated from Eqs. (17) are not biased. Convergence to the asymptote is therefore faster and sufficient accuracy is achieved with a smaller 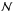 .
.
4.5. Coverage fractions
For comparison with Sect. 3.5 above and with Sect. 5.5 of L14, coverage fractions for credibility intervals are computed for 10 000 independent realizations of the observed orbit, and an interval is again counted as a success if QL<Qexact<QU. The results of this experiment (iii) are given in Table 2.
Because these are credibility not frequentist intervals, there is no rigorous asymptotic expectation that the frequentist fractions should be recovered. Nevertheless, these ideal fractions are closely matched and so the credibility intervals calculated according to Sect. 4.2 can be described as well-calibrated (Drawid 1982).
When Table 2 is compared to Table 1 in L14, we see that the previous low coverage fractions for the ψ-elements log a,i,ω,Ω and for the derived quantity log ℳ are now replaced by fractions close to their frequentist values. This confirms the conjecture in L14 that the shortfall was due to the profile likelihood.
As in Sect. 3.5, statistical rigour is achieved with only a modest increase in the computional burden. Experiment iii required 22% more computer time than experiment i.
When Bayesian estimates depend on informative priors, the PDF π(θ) may have a significant gradient at θ∗, the elements of a particular binary. A coverage experiment restricted to θ∗ will then (correctly) deviate from the frequentist expectation. In coverage tests for such cases, each independent orbit 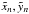 should also be for a random θ drawn from π(θ).
should also be for a random θ drawn from π(θ).
Coverage fractions for credibility intervals from 104 trials.
5. Comparison of estimates
The relative performance of minimum-χ2 and Bayesian estimation in experiments ii and iii is summarized in Table 3. The means ⟨ δQ ⟩ and standard deviations sδQ of the residuals δQ = Qest − Qexact are tabulated, where Qest is either the minimum-χ2 value of Q or its posterior mean, and Qexact is given in Eq. (1).
Table 2 shows that in this test the two estimation methodologies yield closely similiar results. This is to be expected for a non-informative prior π(θ) with negligible gradient at θ∗.
Comparison of residuals δQ.
6. Conclusion
This paper has addressed a technical issue in the statistical analysis of orbits: how to achieve statistical rigour while taking advantage of the linearity of a subset of the orbital elements. The coverage experiments reported in Sects. 3.5 and 4.5 demonstrate that statistical rigour is achieved for both minimum-χ2 and Bayesian estimation. Moreover, the reported timings show an inconsequential increase in the computational burden.
The key to this success is that at each grid point the distribution of probability in Thiele-Innes space is known. For minimum-χ2 estimation, this allows Monte Carlo sampling to be targeted (Sect. A.5) precisely on the constant χ2 surface defining the desired confidence level. For Bayesian estimation, the known PDF allows Monte Carlo sampling in Thiele-Innes space to be concentrated (Sect. A.4) on the high probability domain enclosing the least-squares points 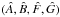 . Moreover, in each case, the random sampling does not require additional orbits to be computed.
. Moreover, in each case, the random sampling does not require additional orbits to be computed.
The approach developed here is not specific to visual binaries or to the Thiele-Innes elements. In principle, an analogous procedure can be constructed for any partially linear estimation problem.
Online material
Appendix A: Statistics in Thiele-Innes space
In Appendix A of L14, formulae are derived for 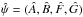 , the least squares Thiele-Innes constants at given φ = (log P,e,τ). The resulting value of χ2 then determines the profile likelihood ℒ† used in the approximation of posterior means – Eq. (7) of L14. Now we wish to sample points displaced from
, the least squares Thiele-Innes constants at given φ = (log P,e,τ). The resulting value of χ2 then determines the profile likelihood ℒ† used in the approximation of posterior means – Eq. (7) of L14. Now we wish to sample points displaced from 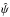 . Let such a displacement be δψ = (a,b,f,g).
. Let such a displacement be δψ = (a,b,f,g).
Appendix A.1: Probability density function p(ψ | φ, D)
In Sect. A.4 of L14, the PDF at δψ is shown to be the product of two independent PDF’s, each a bivariate normal distribution, one for (a,f), the other for (b,g). Formulae for the variances 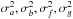 and the covariances cov(a,f),cov(b,g) that define these PDF’s are given in Eqs. (A.9) and (A.10) of L14.
and the covariances cov(a,f),cov(b,g) that define these PDF’s are given in Eqs. (A.9) and (A.10) of L14.
The PDF for (a,f) is 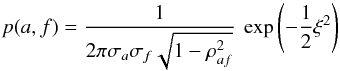 (A.1)where ρaf = cov(a,f)/(σaσf) and
(A.1)where ρaf = cov(a,f)/(σaσf) and ![\appendix \setcounter{section}{1} \begin{equation} \xi^{2} = \frac{1}{1-\rho_{af}^{2}} \left [\left(\frac{a}{\sigma_{a}}\right)^{2} + \left(\frac{f}{\sigma_{f}}\right)^{2} - 2 \rho_{af} \: \left(\frac{a}{\sigma_{a}}\right)\left(\frac{f}{\sigma_{f}}\right) \right] \end{equation}](/articles/aa/full_html/2014/05/aa23661-14/aa23661-14-eq251.png) (A.2)The point (0,0) corresponds to the minimum-
(A.2)The point (0,0) corresponds to the minimum-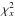 solution
solution 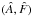 , where
, where 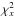 is the x-coordinate contribution to χ2 – see Eq. (2). The displacement (a,f) therefore results in a positive increment
is the x-coordinate contribution to χ2 – see Eq. (2). The displacement (a,f) therefore results in a positive increment 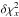 given by
given by ![\appendix \setcounter{section}{1} \begin{equation} \sigma^{2} \delta \chi^{2}_{x} = \Sigma_{n} w_{n} \left[(x_{n}-\tilde{x}_{n})^{2} - (\hat{x}_{n}-\tilde{x}_{n})^{2} \right]. \end{equation}](/articles/aa/full_html/2014/05/aa23661-14/aa23661-14-eq258.png) (A.3)Now, for displacement (a,f), the predicted
(A.3)Now, for displacement (a,f), the predicted 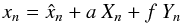 (A.4)where X,Y are given by Eqs. (A.3) in L14. Substitution in Eq. (A.3) then gives
(A.4)where X,Y are given by Eqs. (A.3) in L14. Substitution in Eq. (A.3) then gives 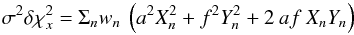 (A.5)where terms linear in a and f vanish because the minimum is at (0,0). The summations in Eq. (A.5) can be eliminated in favour of
(A.5)where terms linear in a and f vanish because the minimum is at (0,0). The summations in Eq. (A.5) can be eliminated in favour of 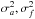 and cov(a,f) with the formulae given in Eqs. (A.6), (A.9) and (A.10) of L14. After lengthy algebra, we find that
and cov(a,f) with the formulae given in Eqs. (A.6), (A.9) and (A.10) of L14. After lengthy algebra, we find that ![\appendix \setcounter{section}{1} \begin{equation} \delta \chi^{2}_{x} = \frac{1}{1-\rho_{af}^{2}} \left [\left(\frac{a}{\sigma_{a}}\right)^{2} + \left(\frac{f}{\sigma_{f}}\right)^{2} - 2 \rho_{af} \: \left(\frac{a}{\sigma_{a}}\right)\left(\frac{f}{\sigma_{f}}\right) \right] \end{equation}](/articles/aa/full_html/2014/05/aa23661-14/aa23661-14-eq265.png) (A.6)and so
(A.6)and so 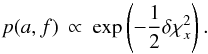 (A.7)Exactly the same analysis applies to the independent pair (b,g), so that
(A.7)Exactly the same analysis applies to the independent pair (b,g), so that 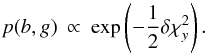 (A.8)Combining these formulae, we find that the PDF at
(A.8)Combining these formulae, we find that the PDF at 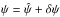 is
is 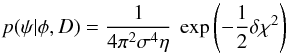 (A.9)where
(A.9)where 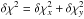 and η(φ | D) is given by
and η(φ | D) is given by 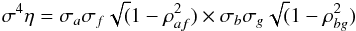 (A.10)
(A.10)
Appendix A.2: Modified Thiele-Innes constants
The familiar device of “completing the square” applied to Eq. (A.2) suggests new variables 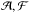 defined by
defined by 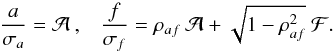 (A.11)Substitution in Eq. (A.6) then gives
(A.11)Substitution in Eq. (A.6) then gives 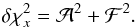 (A.12)The Jacobian of this transformation is
(A.12)The Jacobian of this transformation is 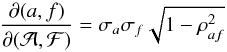 (A.13)so that, by conservation of probability, the PDF of
(A.13)so that, by conservation of probability, the PDF of 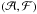 is
is ![\appendix \setcounter{section}{1} \begin{equation} \Psi({\cal A},{\cal F}) = \frac{1}{2 \pi} \: \exp \left[-\frac{1}{2} \left({\cal A}^{2} +{\cal F}^{2}\right) \right] . \end{equation}](/articles/aa/full_html/2014/05/aa23661-14/aa23661-14-eq278.png) (A.14)Now, exactly the same analysis applies to the independent pair (b,g). Thus, if we define new variables
(A.14)Now, exactly the same analysis applies to the independent pair (b,g). Thus, if we define new variables 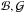 by the equations
by the equations 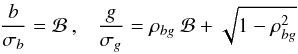 (A.15)then the PDF of
(A.15)then the PDF of 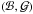 is
is 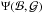 , and
, and 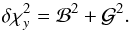 (A.16)If ζ denotes the vector
(A.16)If ζ denotes the vector 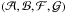 , then Π(ζ), the PDF in ζ-space, is
, then Π(ζ), the PDF in ζ-space, is 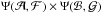 – i.e.,
– i.e., ![\appendix \setcounter{section}{1} \begin{equation} \Pi(\zeta) = \frac{1}{4 \pi^{2}} \: \exp \left[-\frac{1}{2} \left({\cal A}^{2} +{\cal B}^{2} + {\cal F}^{2} +{\cal G}^{2}\right) \right] . \end{equation}](/articles/aa/full_html/2014/05/aa23661-14/aa23661-14-eq288.png) (A.17)Accordingly, the distribution of probability in ζ-space is simply the product of four independent normal distributions, each with zero mean and unit variance.
(A.17)Accordingly, the distribution of probability in ζ-space is simply the product of four independent normal distributions, each with zero mean and unit variance.
The increment in χ2 is given by Eqs. (A.12) and (A.16) as 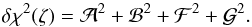 (A.18)
(A.18)
Appendix A.3: Approximate PDFs
A distribution of probability can be represented by a sum of δ functions in such a way that the probability attached to any finite element of space is approximated with arbitrary accuracy. Thus, the PDF giving the distribution of probability in ζ-space is given approximately by 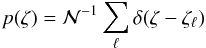 (A.19)where each ζℓ is an independent random vector sampling the PDF Π(ζ) given by Eq. (A.17). The integral of p(ζ) over a finite element in ζ-space converges to the exact value as
(A.19)where each ζℓ is an independent random vector sampling the PDF Π(ζ) given by Eq. (A.17). The integral of p(ζ) over a finite element in ζ-space converges to the exact value as 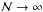 .
.
Equations (A.11) and (A.15) transform the point ζℓ into the displacement 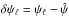 . The corresponding approximate PDF in ψ-space is therefore
. The corresponding approximate PDF in ψ-space is therefore 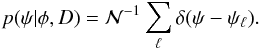 (A.20)Note that the Jacobian of this transformation from ζ- to ψ- space is implicit in the changes in number densities of the delta functions in the respective spaces.
(A.20)Note that the Jacobian of this transformation from ζ- to ψ- space is implicit in the changes in number densities of the delta functions in the respective spaces.
Similarly, the PDF for the Campbell elements ϑ corresponding to the Thiele-Innes elements ψ is 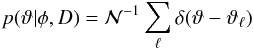 (A.21)where ϑℓ = ϑ(ψℓ) is derived as described in Sect. A.4 of L14.
(A.21)where ϑℓ = ϑ(ψℓ) is derived as described in Sect. A.4 of L14.
Appendix A.4: Random sampling in ψ-space
According to Eq. (A.17), a random point in ζ-space is (z1,z2,z3,z4), where the zi are independent random Gaussian variates drawn from 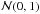 . This point corresponds to the displacement (a,b,f,g) given by Eqs. (A.11) and (A.15) and therefore to the point
. This point corresponds to the displacement (a,b,f,g) given by Eqs. (A.11) and (A.15) and therefore to the point 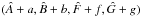 in ψ-space. Thus, a point randomly selected from the exact PDF p(ψ | φ,D) can be derived from four independent Gaussian variates, and the resulting increment in χ2 is given by Eq. (A.18) as
in ψ-space. Thus, a point randomly selected from the exact PDF p(ψ | φ,D) can be derived from four independent Gaussian variates, and the resulting increment in χ2 is given by Eq. (A.18) as 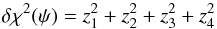 (A.22)
(A.22)
Appendix A.5: Random sampling at fixed δχ2
A random point in ψ-space subject to a constraint on δχ2 can be found by first selecting a random point on the 4D sphere in ζ-space defined by Eq. (A.18). This is achieved as follows: If zi again denotes a Gaussian variate from 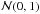 , then a random point on this hypersphere is (z1,z2,z3,z4) /Z, where
, then a random point on this hypersphere is (z1,z2,z3,z4) /Z, where 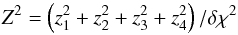 (A.23)(Muller 1979). The corresponding point (A,B,F,G) in ψ-space is then derived from Eqs. (A.11) and (A.15).
(A.23)(Muller 1979). The corresponding point (A,B,F,G) in ψ-space is then derived from Eqs. (A.11) and (A.15).
The random sampling procedures of Sects. A.4 and A.5 predict χ2 without the need to compute an orbit. This is achieved by exploiting the linearity of the ψ-elements and is the basis of the computational efficiency of the techniques of Sects. 3.3 and 4.1. However, during code development, this prediction should be tested by actually computing the orbit and independently evaluating χ2 from Eq. (2).
Acknowledgments
The issue of error underestimation in hybrid problems was raised by the referee of the previous paper (L14) and was the direct stimulus of this investigation. This same referee provided useful comments on this paper.
References
- Dawid, A. P. 1982, J. Am. Stat. Assoc., 77, 605 [CrossRef] [Google Scholar]
- Eastman, J., Gaudi, B., & Agol, E. 2013, PASP, 125, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Hartkopf, W. I., McAlister, H. A., & Franz, O. G. 1989, AJ, 98, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- James, F. 2006, Statistical Methods in Experimental Physics (Singapore: World Scientific Publishing Co.) [Google Scholar]
- Lucy, L. B. 2014, A&A, 563, 126 (L14) [Google Scholar]
- Muller, M. E. 1959, Comm. Assoc. Comp. Mach., 2, 19 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes, 2nd edn. (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Schaefer, G. H., Simon, M., Beck, T. L., Nelan, E., & Prato, L. 2006, AJ, 132, 2618 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Approximate confidence intervals. The ensemble of orbit vectors |
| In the text | |
 |
Fig. 2 Accurate confidence limits. The ensemble of orbit vectors |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.