| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 5 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201423578 | |
| Published online | 20 May 2014 | |
Non-radiative inelastic processes in lithium-helium ion-atom collisions
1 Department of Theoretical Physics and Astronomy, Herzen University, St. Petersburg 191186, Russia and Max-Planck Institute for Astrophysics, Postfach 1371, 85741 Garching, Germany
e-mail: andrey.k.belyaev@gmail.com
2 Charles University in Prague, Faculty of Mathematics and Physics, Department of Chemical Physics and Optics, Ke Karlovu 3, 12116 Prague 2, Czech Republic
3 Max-Planck Institute for Astrophysics, Postfach 1371, 85741 Garching, Germany
Received: 5 February 2014
Accepted: 12 March 2014
Aims. The aims are to estimate efficiencies of non-radiative inelastic processes in lithium-helium ion-atom collisions and to compare them to those for radiative processes.
Methods. Non-radiative inelastic cross-sections and rate coefficients for different lithium-helium ion-atom collisions are estimated by means of the recently proposed branching probability current method, which is based on the accurate ab initio adiabatic Born-Oppenheimer potentials that have been recently calculated for the low-lying 1,3Σ+ and 1,3Π states of the LiHe+ ion.
Results. It is shown that at low temperatures the radiative depopulation in Li+ + He and Li + He+ collisions dominates over the non-radiative processes, while in Li+ + He(2s 3S) collisions the non-radiative processes dominate over the radiative association at temperatures above 3000 K, which can be expected to have some influence on depopulations of metastable He in high temperature astrophysical environments.
Key words: atomic data / molecular data / scattering
© ESO, 2014
1. Introduction
Studies of non-adiabatic effects in the interactions between (Li+ + He) and (Li + He+) collisional complexes on different excitation levels can contribute to a better understanding of primordial and interstellar lithium chemistry, especially when the efficiencies of radiative and non-radiative processes at different temperatures are compared.
According to the Big Bang nucleosynthesis theory, lithium is the heaviest stable element produced in this event (Burles et al. 2001). After the initial period, when in the rapidly expanding Universe matter and radiation were in close thermal contact, the Universe became transparent and temperature was sufficiently lowered to allow the initially formed fully stripped atomic nuclei (H+, D+, He2+, Li3+) to recombine with electrons to form finally neutral atoms. In the case of lithium, the recombination process proceeded sequentially in the order of its ionization potentials: beginning with Li3+, ending with both Li atoms and remaining Li+ ions, which could not readily recombine due to a lack of free electrons by the end of the recombination era. Intensive studies were performed to investigate the primordial lithium chemistry (Stancil & Zygelman 1996; Stancil & Dalgarno 1997; Galli & Palla 1998, 2013) and to analyze the effect of neutral lithium on the cosmic microwave background anisotropies (Palla et al. 1995; Loeb 2001). At the time when the fractional abundances of Li and Li+ became comparable at a z ≈ 100 redshift (Stancil et al. 2002), the abundance of He+ ions dropped by several orders of magnitude (Stancil et al. 1998). At smaller redshifts, reactions of neutral Li atoms with He+ ions are therefore rather improbable. They are, however, included in this study because (Li + He+) collision pairs are obtained here via charge transfer processes in (Li+ + He) collisions. In addition, even if lithium is rather rare compared to the other primordial elements synthesized in the early Universe, inelastic collisional processes of neutral lithium with hydrogen and other atomic or ionic species are of high interest in modeling stellar atmospheres (Carlsson et al. 1994; Barklem et al. 2003; Belyaev & Barklem 2003).
Parameters of the non-adiabatic regions for LiHe+.
To get a first overview of the possible non-adiabatic effects in lithium-helium ion-atom interactions at different excitation levels, a model approach (Belyaev & Lebedev 2011; Belyaev 2013a) is applied here to estimate the cross-sections and rate coefficients in the corresponding non-radiative inelastic collisions.
2. Nonadiabatic nuclear dynamics
The theoretical treatment is performed within the standard adiabatic Born-Oppenheimer (BO) approach, which considers a collision problem in two steps: (i) electronic structure calculations and (ii) a study of the non-adiabatic nuclear dynamics.
Adiabatic BO potentials and electric dipole moment functions for several low-lying excited 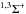 and 1,3Π states of the LiHe+ ion were recently determined on a high-accuracy level of ab initio theory (Soldán & Kraemer 2012). For the X
and 1,3Π states of the LiHe+ ion were recently determined on a high-accuracy level of ab initio theory (Soldán & Kraemer 2012). For the X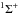 ground state, the calculated characteristic spectroscopic data were found to be in perfect agreement with the best obtained results available from the literature in the past (Senff & Burton 1986; Elford et al. 1999). For the ground state (X-state) and the first excited
ground state, the calculated characteristic spectroscopic data were found to be in perfect agreement with the best obtained results available from the literature in the past (Senff & Burton 1986; Elford et al. 1999). For the ground state (X-state) and the first excited 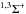 states (A- and a-states), radiative association processes were investigated in detail (Augustovičová et al. 2012; Bovino et al. 2011). In addition, depopulation of metastable He(23S) by radiative association processes was most recently studied (Augustovičová et al. 2014).
states (A- and a-states), radiative association processes were investigated in detail (Augustovičová et al. 2012; Bovino et al. 2011). In addition, depopulation of metastable He(23S) by radiative association processes was most recently studied (Augustovičová et al. 2014).
The excited-states adiabatic BO potentials calculated by Soldán & Kraemer (2012) are used here as a basis for the present model calculations.
In general, in order to study non-adiabatic nuclear dynamics entirely by means of quantum mechanical methods one needs to know not only adiabatic BO potentials, but also non-adiabatic couplings. On the other hand, non-adiabatic transition probabilities, inelastic cross-sections, and rate coefficients can be estimated within a model approach, especially when complete quantum-chemical information is not available. Such a model approach, the so-called branching probability current method, that requires information only about adiabatic potentials, has been recently proposed (Belyaev 2013a) and applied to inelastic aluminium-hydrogen collisions (Belyaev 2013a,b). The main assumption of the approach is that non-adiabatic transition probabilities can be estimated within the framework of the Landau-Zener (LZ) model (Landau 1932a,b; Zener 1932). The bottleneck of the LZ-model application is twofold: (i) the conventional LZ formula requires the knowledge of diabatic parameters though a diabatization procedure is not uniquely defined; and (ii) usually, there are several non-adiabatic regions that determine the non-adiabatic nuclear dynamics without a particular order. The branching probability current method handles the latter by branching all incoming and outgoing probability currents after each traverse of the non-adiabatic regions in any order they appear during a collision. The method is similar to the branching classical trajectory method (Belyaev & Lebedev 2011), which is based on classical trajectories and determines LZ parameters along each trajectory. The branching probability current method determines LZ parameters beforehand and then varies an internuclear distance R without calculating any classical trajectories (see Belyaev 2013a).
The key point of the branching probability current method is a novel formula for a non-adiabatic transition probability within the LZ model, the so-called adiabatic-potential-based formula (Belyaev & Lebedev 2011; Belyaev 2013a). Positions of non-adiabatic regions Rc are determined by minima of adiabatic splittings Zjk = | Uj − Uk | between adjacent adiabatic states with Uj,k(R) being adiabatic potentials. In these regions, the LZ parameters are determined by the following formula (Belyaev & Lebedev 2011; Belyaev 2013a): 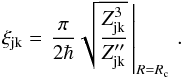 (1)Primed quantities are referred to derivatives with respect to the internuclear distance R. Equation (1) expresses the LZ parameter only in terms of the adiabatic splitting Zjk and its second distance derivative at Rc. Finally, a non-adiabatic transition probability
(1)Primed quantities are referred to derivatives with respect to the internuclear distance R. Equation (1) expresses the LZ parameter only in terms of the adiabatic splitting Zjk and its second distance derivative at Rc. Finally, a non-adiabatic transition probability 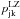 after a single traverse of a non-adiabatic region is written in the usual form,
after a single traverse of a non-adiabatic region is written in the usual form, 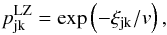 (2)where v is a radial velocity of colliding atoms. All values are evaluated at the centers of the non-adiabatic regions.
(2)where v is a radial velocity of colliding atoms. All values are evaluated at the centers of the non-adiabatic regions.
Thus, Eqs. (1) and (2) allow one to calculate non-adiabatic transition probabilities in each non-adiabatic region based on the information about adiabatic potentials only. Then branching of incoming and outgoing currents allows one to compute probabilities for transitions between a given initial state and a given final state, and finally inelastic cross-sections and rate coefficients.
3. Results of calculations
3.1. Nonadiabatic regions
In the present paper, we treat non-adiabatic transitions separately between the low-lying 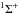 states, between the low-lying
states, between the low-lying 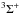 states, and between the pair of the lowest excited 3Π states. The adiabatic BO potentials for these symmetries are taken from Soldán & Kraemer (2012). For the lowest excited pair of 1Π states, the form and relative separation of their potentials (Soldán & Kraemer 2012) indicate that non-adiabatic coupling between them is negligible. It is therefore not considered here. Transitions between states of different symmetries are also not considered in the present estimates.
states, and between the pair of the lowest excited 3Π states. The adiabatic BO potentials for these symmetries are taken from Soldán & Kraemer (2012). For the lowest excited pair of 1Π states, the form and relative separation of their potentials (Soldán & Kraemer 2012) indicate that non-adiabatic coupling between them is negligible. It is therefore not considered here. Transitions between states of different symmetries are also not considered in the present estimates.
The parameters of the non-adiabatic regions for the 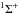 ,
, 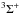 and 3Π symmetries of LiHe+ are collected in Table 1. The centers Rc of these regions are determined by the local minima of the corresponding adiabatic splittings Zjk. The LZ parameters ξjk are then calculated in each region by means of Eq. (1). There are five non-adiabatic regions within the
and 3Π symmetries of LiHe+ are collected in Table 1. The centers Rc of these regions are determined by the local minima of the corresponding adiabatic splittings Zjk. The LZ parameters ξjk are then calculated in each region by means of Eq. (1). There are five non-adiabatic regions within the 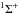 symmetry, six regions within the
symmetry, six regions within the 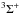 symmetry, and one region within the 3Π symmetry. Table 1 also shows that within the
symmetry, and one region within the 3Π symmetry. Table 1 also shows that within the 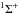 and
and 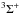 symmetries, several non-adiabatic regions can exist for certain pairs of adjacent potentials, which makes the non-adiabatic nuclear dynamics more complicated. Actually, the branching probability current method applied here takes this situation automatically into account. The calculated LZ parameters allow us to estimate inelastic cross-sections and rate coefficients.
symmetries, several non-adiabatic regions can exist for certain pairs of adjacent potentials, which makes the non-adiabatic nuclear dynamics more complicated. Actually, the branching probability current method applied here takes this situation automatically into account. The calculated LZ parameters allow us to estimate inelastic cross-sections and rate coefficients.
3.2. Inelastic cross-sections
According to the data for non-adiabatic transitions within the 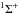 symmetry, that are listed in Table 1, a non-adiabatic region around Rc = 6.94 au is indicated by the present model calculations for the adiabatic potentials of the ground state (X
symmetry, that are listed in Table 1, a non-adiabatic region around Rc = 6.94 au is indicated by the present model calculations for the adiabatic potentials of the ground state (X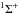 ) and the first excited state (A
) and the first excited state (A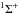 ). The energy gap, however, between these two potentials is very big (see Table 1 for the minimum of the adiabatic splitting Zjk), resulting in the large LZ parameter ξjk and making the probabilities for non-adiabatic transitions from and to the ground molecular state extremely small. Inelastic non-radiative collision processes involving the Li+ + He(1s21S) channel (both as the initial and as the final channels) have, thus, negligible inelastic cross-sections and rate coefficients and are therefore disregarded here.
). The energy gap, however, between these two potentials is very big (see Table 1 for the minimum of the adiabatic splitting Zjk), resulting in the large LZ parameter ξjk and making the probabilities for non-adiabatic transitions from and to the ground molecular state extremely small. Inelastic non-radiative collision processes involving the Li+ + He(1s21S) channel (both as the initial and as the final channels) have, thus, negligible inelastic cross-sections and rate coefficients and are therefore disregarded here.
 |
Fig. 1 Inelastic cross-sections within the |
The inelastic cross-sections for the other transitions within the 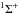 symmetry are shown in Fig. 1 as a function of the collision energy E. The initial collision channel is specified in the top of each panel, whereas the final collision channels, which are labeled by colors, are defined in the insets of panels (a) and (b). The definitions of the color labels are common for all figures in the present paper.
symmetry are shown in Fig. 1 as a function of the collision energy E. The initial collision channel is specified in the top of each panel, whereas the final collision channels, which are labeled by colors, are defined in the insets of panels (a) and (b). The definitions of the color labels are common for all figures in the present paper.
Figure 1 shows that practically all partial cross-sections have large energy thresholds, reaching from 3.4 eV up to about 28 eV. These large thresholds are due to the fact that most non-adiabatic regions within the 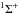 symmetry are located at short internuclear distances in the repulsive part of the adiabatic potentials with Rc< 3.5 au. For non-adiabatic transitions to occur, the collision system has therefore to have enough kinetic energy. For the charge transfer reaction Li(2s) + He+ ⇌ Li+ + He(2s 1S), however, there exists a second non-adiabatic region at large internuclear distance (Rc = 13.376 au). The LZ parameter here is relatively large and the non-adiabatic transition probabilities get remarkable values at rather high collision energies.
symmetry are located at short internuclear distances in the repulsive part of the adiabatic potentials with Rc< 3.5 au. For non-adiabatic transitions to occur, the collision system has therefore to have enough kinetic energy. For the charge transfer reaction Li(2s) + He+ ⇌ Li+ + He(2s 1S), however, there exists a second non-adiabatic region at large internuclear distance (Rc = 13.376 au). The LZ parameter here is relatively large and the non-adiabatic transition probabilities get remarkable values at rather high collision energies.
At low collision energies, most partial cross-sections have rather small values in Fig. 1. An exception here is the Li+ + He(2s 1S) ⇌ Li(2p) + He+ charge transfer into excited state processes. For this endothermic process, the cross-section increases rapidly right above the threshold and reaches its maximum value of 2.7 Å2 at a collision energy of E = 14 eV. Similar large cross-sections are obtained for other processes only at higher collision energies.
 |
Fig. 2 Inelastic cross-sections within the |
 |
Fig. 3 Inelastic rate coefficients within the |
The calculated partial inelastic cross-sections within the 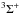 system and within the 3Π system are shown in Fig. 2 by solid and dotted lines, respectively. Initial and final collisional channels are specified here in the same way as in Fig. 1. Obviously many partial cross-sections have also relatively large energy thresholds for the same reasons discussed before for the
system and within the 3Π system are shown in Fig. 2 by solid and dotted lines, respectively. Initial and final collisional channels are specified here in the same way as in Fig. 1. Obviously many partial cross-sections have also relatively large energy thresholds for the same reasons discussed before for the 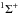 system. The cross-sections for the Li+ + He(2p 3P) ⇌ Li(2p) + He+ charge transfer into excited state processes, on the other hand, have a small energy threshold (actually, 0.08 eV for the endothermic process and practically no energy threshold for the exothermic process). This occurs because the second non-adiabatic region at large internuclear distance with Rc = 24.753 au is located between the c3Σ+ and d3Σ+ molecular states with the close-lying potentials in this region (Soldán & Kraemer 2012). For the 3Π system the non-adiabatic region also occurs at a long distance, Rc = 22.898 au. However, the LZ parameter obtained in this region appears to be large, given the effect that the non-adiabatic transitions with observable probabilities and larger inelastic cross-sections occur only at higher energies (indicated by the dotted lines in Fig. 2).
system. The cross-sections for the Li+ + He(2p 3P) ⇌ Li(2p) + He+ charge transfer into excited state processes, on the other hand, have a small energy threshold (actually, 0.08 eV for the endothermic process and practically no energy threshold for the exothermic process). This occurs because the second non-adiabatic region at large internuclear distance with Rc = 24.753 au is located between the c3Σ+ and d3Σ+ molecular states with the close-lying potentials in this region (Soldán & Kraemer 2012). For the 3Π system the non-adiabatic region also occurs at a long distance, Rc = 22.898 au. However, the LZ parameter obtained in this region appears to be large, given the effect that the non-adiabatic transitions with observable probabilities and larger inelastic cross-sections occur only at higher energies (indicated by the dotted lines in Fig. 2).
Cross-sections obtained here for the 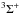 system have typically larger values compared to those for the
system have typically larger values compared to those for the 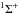 system. The values range from a few Å2 at low collision energies to 5–7 Å2 at E = 10 eV and up to 80 Å2 at high energies for the Li+ + He(2p 3P) ⇌ Li(2p) + He+ charge transfer processes. For these processes, the transitions mainly take place in the non-adiabatic region around R = 24.753 au, that is, at large internuclear distances. In addition, the excitation/de-excitation processes Li+ + He(2s 3S) ⇌ Li+ + He(2p 3P) also have large cross-section values reaching 1.2 Å2 as a maximum.
system. The values range from a few Å2 at low collision energies to 5–7 Å2 at E = 10 eV and up to 80 Å2 at high energies for the Li+ + He(2p 3P) ⇌ Li(2p) + He+ charge transfer processes. For these processes, the transitions mainly take place in the non-adiabatic region around R = 24.753 au, that is, at large internuclear distances. In addition, the excitation/de-excitation processes Li+ + He(2s 3S) ⇌ Li+ + He(2p 3P) also have large cross-section values reaching 1.2 Å2 as a maximum.
Apart from the processes discussed here, other partial processes can occur via non-adiabatic transitions within different molecular symmetries. The Li+ + He(2p 3P) ⇌ Li(2p) + He+ charge transfer processes, for example, involve transitions within the 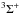 and 3Π systems and the Li(2s) + He+ ⇌ Li(2p) + He+ excitation/de-excitation processes are based on non-adiabatic transitions within the
and 3Π systems and the Li(2s) + He+ ⇌ Li(2p) + He+ excitation/de-excitation processes are based on non-adiabatic transitions within the 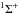 and
and 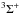 systems.
systems.
Finally, it should be emphasized that the LZ model might provide less accurate transition probabilities for non-adiabatic regions with large adiabatic splittings or for cases when other quantum effects, such as tunneling, are substantial. In those situations the model estimates have larger uncertainties for small transition probabilities and, hence, low cross-sections. A fully quantum-mechanical treatment of the tunneling effect at short internuclear distances in the repulsive part of the potentials, for instance, could increase some non-adiabatic transition probabilities and lower the energy threshold. This would eventually increase the rate coefficients, whereas the model provides smaller estimates. However, for cases with substantial transition probabilities, the model applied here has been found to provide reliable estimates of the dominant cross-sections and rate coefficients (Belyaev 2013a).
3.3. Rate coefficients
The calculated inelastic rate coefficients are presented in Fig. 3 as a function of the temperature T in the range between 103 to 106 K. The initial collision channels are again specified in the top of each panel and the same color labels are used for the final collision channels as in Figs. 1 and 2.
The gross behavior of the rate coefficients reflects the characteristics of the corresponding cross-sections. The rate coefficients increase from very low values at low temperatures up to roughly 6 × 10-8 cm3/ s at high temperatures. Low rate coefficients for the partial processes at low temperatures are partly due to the large energy thresholds for the partial cross-sections and partly to low values of the low-energy cross-sections, as discussed above. The high temperature increase of the rate coefficients corresponds to the increase of the cross-sections at high collision energies.
It is seen from Fig. 3 that depopulation of the Li(2s) + He+ channel is inefficient at low temperatures that are below 104 K. The partial rate coefficients are smaller than 4 × 10-22 cm3/ s, and all depopulation processes are endothermic, since the cross-section for the only exothermic channel, Li+ + He(1s21S), is negligible. At high temperatures, depopulation of the Li(2s) + He+ channel can occur due to several processes, which are mostly due to charge transfer and excitation. The rate coefficients can reach the values up to 5 × 10-10 cm3/ s, which are mainly due to transitions into the Li+ + He(2s 3S) final channel. Depopulation of the Li+ + He(2p 1P) channel is much less efficient than that for the Li(2s) + He+ channel. Actually it is the least efficient among the treated collision channels. Depopulation of the Li+ + He(2s 1S) channel is more efficient even at low temperatures mainly because of the Li+ + He(2s 1S) → Li(2p) + He+ charge transfer into excited state process. The corresponding rate coefficient is equal to 5.4 × 10-12 cm3/ s at T = 104 K and increases up to 1.4 × 10-9 cm3/ s at T = 106 K. The efficiency of decay of the Li+ + He(2s 3S) channel is comparable to that of the Li+ + He(2s 1S). The rate coefficient equals 7.5 × 10-12 cm3/ s for the Li+ + He(2s 3S) → Li+ + He(2p 3P) excitation process at T = 104 K and is 5.2 × 10-10 cm3/ s, 3.5 × 10-10 cm3/ s, and 2.6 × 10-10 cm3/ s for the Li(2s) + He+, the Li+ + He(2p 3P), and the Li(2p) + He+ final channels, respectively, at T = 106 K. The largest values for the rate coefficients correspond to the Li+ + He(2p 3P) ⇌ Li(2p) + He+ charge transfer processes. They are equal to 1.8 × 10-11 cm3/ s and 1.5 × 10-11 cm3/ s for the direct and the inverse processes, respectively, at T = 104 K, and to 5.8 × 10-8 cm3/ s and 4.4 × 10-8 cm3/ s for direct and inverse processes, respectively, at T = 106 K. The rate coefficients for these charge transfer processes in the 3Π symmetry also reach values at T = 106 K, which are almost exactly one order of magnitude smaller than those for the 3Σ system, as shown by the dotted curves in Fig. 3. At relatively low temperatures, the Li+ + He(2p 3P) → Li+ + He(2s 3S) de-excitation process also contributes noticeably into decay of He(2p 3P) in collisions with Li+: the corresponding rate coefficient equals 9.4 × 10-12 cm3/ s at T = 104 K.
All partial inelastic rate coefficients decrease rapidly with decreasing the temperature below 104 K. The only noticeable rate coefficient remaining at low temperatures is that for the exothermic charge transfer process Li(2p) + He+ → Li+ + He(2p 3P).
4. Discussion and conclusion
The non-radiative cross-sections and rate coefficients estimated in the present paper can be compared to the radiative association cross-sections and rate coefficients calculated by Augustovičová et al. (2012, 2014) for the same collision systems. The comparison shows that there are a couple of basic differences some of which are listed below.
First of all, the radiative association treatment provides noticeable cross-sections and rate coefficients from and to the ground molecular state LiHe+(X 1Σ+), for which the present model study estimates negligible non-radiative cross-sections and rate coefficients. The non-radiative processes, thus, do not change depopulation of the Li+ + He(1s21S) channel.
Second, the energy dependence of the cross-sections and the temperature dependence of the rate coefficients for radiative and non-radiative processes are totally different. The radiative cross-sections and rate coefficients generally decrease with increasing collision energy and temperature in the low-energy regime. In contrast to this, an increase of the cross-sections and rate coefficients with increasing energy and temperature is observed for non-radiative processes. A general conclusion from this controversial behavior would be that radiative processes are expected to be dominant over non-radiative ones at low energies. This finding actually agrees with the results of the treatment of radiative and non-radiative processes in He+ + H collisions (Zygelman et al. 1989), as well as in cold and ultra-cold Yb+ + Rb collisions (Sayfutyarova et al. 2013).
Third, depopulation of the Li(2s) + He+ collision system due to the radiative association into both the 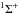 and the
and the 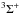 symmetries, i.e., depopulation of the A and a molecular states (see Table 1), was recently studied by Augustovičová et al. (2012). It is shown there that the dominant channel corresponds to the A → X transitions with a rate coefficient varying from 10-14 cm3/ s at 0.1 K down to 10-16 cm3/ s at 104 K. In this temperature range the present estimates show that the non-radiative depopulation of the same states has a maximum total rate coefficient of 4.4 × 10-22 cm3/ s at 104 K due to transitions a → c, b, d within
symmetries, i.e., depopulation of the A and a molecular states (see Table 1), was recently studied by Augustovičová et al. (2012). It is shown there that the dominant channel corresponds to the A → X transitions with a rate coefficient varying from 10-14 cm3/ s at 0.1 K down to 10-16 cm3/ s at 104 K. In this temperature range the present estimates show that the non-radiative depopulation of the same states has a maximum total rate coefficient of 4.4 × 10-22 cm3/ s at 104 K due to transitions a → c, b, d within 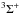 symmetry, whereas the rate coefficients for depopulation of the A state within the
symmetry, whereas the rate coefficients for depopulation of the A state within the 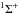 symmetry are much smaller than in the
symmetry are much smaller than in the 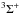 symmetry (see Fig. 3). This leads to the conclusion that the radiative depopulation of the Li(2s) + He+ collision system dominates over the non-radiative depopulation in the low-temperature range (below 104 K).
symmetry (see Fig. 3). This leads to the conclusion that the radiative depopulation of the Li(2s) + He+ collision system dominates over the non-radiative depopulation in the low-temperature range (below 104 K).
Fourth, most recently, depopulation of the Li+ + He(2s 3S) collision system due to radiative association in the 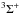 symmetry, i.e. depopulation of the b molecular state, was studied by Augustovičová et al. (2014). The dominant transition here is b → a with the corresponding rate coefficient of 4.54 × 10-15 cm3/ s at 104 K. For the same transition, the non-radiative rate coefficient is much smaller, 10-21 cm3/ s at 104 K. On the other hand, according to Fig. 3, the rate coefficients for depopulation of the b state into other channels are much larger: 7.5 × 10-12 cm3/ s at 104 K for the b → c transition (i.e., the Li+ + He(2s 3S) → Li+ + He(2p 3P) excitation process), and 5.6 × 10-14 cm3/ s at 104 K for the b → d transition (i.e., the Li+ + He(2s 3S) → Li(2p) + He+ charge transfer process). Comparison of the temperature dependence of the rate coefficients for the radiative and non-radiative depopulation shows that the non-radiative depopulation dominates over the radiative one for the Li+ + He(2s 3S) collision channel at T> 3000 K.
symmetry, i.e. depopulation of the b molecular state, was studied by Augustovičová et al. (2014). The dominant transition here is b → a with the corresponding rate coefficient of 4.54 × 10-15 cm3/ s at 104 K. For the same transition, the non-radiative rate coefficient is much smaller, 10-21 cm3/ s at 104 K. On the other hand, according to Fig. 3, the rate coefficients for depopulation of the b state into other channels are much larger: 7.5 × 10-12 cm3/ s at 104 K for the b → c transition (i.e., the Li+ + He(2s 3S) → Li+ + He(2p 3P) excitation process), and 5.6 × 10-14 cm3/ s at 104 K for the b → d transition (i.e., the Li+ + He(2s 3S) → Li(2p) + He+ charge transfer process). Comparison of the temperature dependence of the rate coefficients for the radiative and non-radiative depopulation shows that the non-radiative depopulation dominates over the radiative one for the Li+ + He(2s 3S) collision channel at T> 3000 K.
Based on these results, it can be concluded that at relatively high temperatures a non-radiative decay (due to non-adiabatic transitions) is expected to dominate over a radiative decay for higher-lying excited states. A critical temperature has to be determined in each particular case. More generally, it appears that radiative and non-radiative processes apply to different areas in interstellar environments when studying atomic or molecular astrophysical questions. For example, non-radiative collision processes can, therefore, be expected to be dominant in stellar atmospheres.
Acknowledgments
A.K.B. gratefully acknowledges support from the Russian Foundation for Basic Research (Grant No. 13-03-00163-a) and from the Max-Planck Institute for Astrophysics at Garching (Germany). L.A. acknowledges funding from the Grant Agency of the Charles University in Prague – GAUK (Grant No. 550112).
References
- Augustovičová, L., Špirko, V., Kraemer, W. P., & Soldán, P. 2012, Chem. Phys. Lett., 531, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Augustovičová, L., Kraemer, W. P., & Soldán, P. 2014, ApJ, 782, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Belyaev, A. K., & Asplund, M. 2003, A&A, 409, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belyaev, A. K. 2013a, Phys. Rev. A, 88, 2704 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, A. K. 2013b, A&A, 560, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belyaev, A. K., & Barklem, P. S. 2003, Phys. Rev. A, 68, 2703 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, A. K., & Lebedev, O. V. 2011, Phys. Rev. A, 84, 4701 [Google Scholar]
- Bovino, S., Tacconi, M., & Gianturco, F. A. 2011, ApJ, 740, 101, erratum 2012, ApJ, 748, 150 [Google Scholar]
- Burles, S., Nollett, K. M., & Turner, M. S. 2001, ApJ, 552, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., Rutten, R. J., Bruls, J. H. M. J., & Shchukina, N. G. 1994, A&A, 288, 860 [NASA ADS] [Google Scholar]
- Elford, M. T., Røeggen, I., & Skullerud, H. R. 1999, J. Phys. B At. Mol. Phys., 32, 1873 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, D., & Palla, F. 1998, A&A, 335, 403 [NASA ADS] [Google Scholar]
- Galli, D., & Palla, F. 2013, ARA&A, 51, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. D. 1932a, Phys. Z. Sowietunion, 1, 88 [Google Scholar]
- Landau, L. D. 1932b, Phys. Z. Sowietunion, 2, 46 [Google Scholar]
- Loeb, A. 2001, ApJ, 555, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., Galli, D., & Silk, J. 1995, ApJ, 451, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Sayfutyarova, E. R., Buchachenko, A. A., Yakovleva, S. A., & Belyaev, A. K. 2013, Phys. Rev. A, 87, 2717 [NASA ADS] [CrossRef] [Google Scholar]
- Senff, U. E., & Burton, P. G. 1986, Mol. Phys., 58, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Soldán, P., & Kraemer, W. P. 2012, Chem. Phys., 393, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Stancil, P. C., & Dalgarno, A. 1997, ApJ, 490, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Stancil, P. C., & Zygelman, B. 1996, ApJ, 472, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Stancil, P. C., Lepp, S., & Dalgarno, A. 1998, ApJ, 509, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Stancil, P. C., Loeb, A., Zaldarriaga, M., Dalgarno, A., & Lepp, S. 2002, ApJ, 580, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Zener, C. 1932, Proc. Roy. Soc. A, 137, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Zygelman, B., Dalgarno, A., Kimura, M., & Lane, N. F. 1989, Phys. Rev. A, 40, 2340 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Inelastic cross-sections within the |
| In the text | |
 |
Fig. 2 Inelastic cross-sections within the |
| In the text | |
 |
Fig. 3 Inelastic rate coefficients within the |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


