| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 7 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201323344 | |
| Published online | 15 May 2014 | |
A method to deconvolve stellar rotational velocities
1 Instituto de Física y Astronomía, Universidad de Valparaíso, 2340000 Valparaíso, Chile
e-mail: michel.cure@uv.cl
2 Departamento de Matemáticas, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, 428 Buenos Aires, Argentina
e-mail: drial@mate.uba.ar
3 Instituto de Estadística, Pontificia Universidad Católica de Valparaíso, 2362807 Valparaíso, Chile
e-mail: alejandra.christen@ucv.cl
4 Universidad Nacional de General Sarmiento, 1613 Los Polvorines, Buenos Aires, Argentina
e-mail: jcassett@ungs.edu.ar
Received: 27 December 2013
Accepted: 13 March 2014
Aims. Rotational speed is an important physical parameter of stars, and knowing the distribution of stellar rotational velocities is essential for understanding stellar evolution. However, rotational speed cannot be measured directly and is instead the convolution between the rotational speed and the sine of the inclination angle v sin i.
Methods. We developed a method to deconvolve this inverse problem and obtain the cumulative distribution function for stellar rotational velocities extending the work of Chandrasekhar & Münch (1950, ApJ, 111, 142)
Results. This method is applied: a) to theoretical synthetic data recovering the original velocity distribution with a very small error; and b) to a sample of about 12.000 field main-sequence stars, corroborating that the velocity distribution function is non-Maxwellian, but is better described by distributions based on the concept of maximum entropy, such as Tsallis or Kaniadakis distribution functions.
Conclusions. This is a very robust and novel method that deconvolves the rotational velocity cumulative distribution function from a sample of v sin i data in a single step without needing any convergence criteria.
Key words: methods: data analysis / methods: numerical / methods: statistical / stars: rotation / stars: fundamental parameters / methods: analytical
© ESO, 2014
1. Introduction
It is well known that all stars rotate and the understanding about how stars rotate is essential to describe and model their formation, internal structure and evolution, and how they interact with their companions, disks or planets. Unfortunately, it is not possible to measure the value of their rotational velocities from observations, and instead the projected value of v sin i is the measured quantity, where i is the inclination angle. The standard assumption to disentangle or deconvolve the rotational velocity distribution function is that the inclination angles are uniformly distributed over the sphere. Based on this assumption, Chandrasekhar & Münch (1950) studied the integral equations that describe the distribution of the true (v) and the apparent (v sin i) rotational velocities, finding that the formal solution is proportional to a derivative of Abel’s integral.
As Chandrasekhar & Münch (1950) pointed out, the differentiation in this formal solution can lead to misleading results due to an intrinsic numerical problem associated with the derivative of Abel’s integral, unless the sample is of high precision. This is the main reason why this method is not usually applied. An alternative and general method was introduced by Lucy (1974). Lucy’s method is a Bayesian iterative method for deconvolving a distribution function assuming a prescribed formula for the kernel of Eq. (1); e.g., for the case of rotational velocities, this kernel describes the projections of an uniform distribution of inclination angles i. Lucy’s method has the disadvantage that it poses no convergence criteria and the requested number of iterations is only justified a posteriori in view of the results. Nevertheless, Lucy’s method is widely used in the astronomical community to disentangle distribution functions from different samples of observations.
In this article, we are able to enhance the pioneer work of Chandrasekhar & Münch (1950), by integrating the probability distribution function (PDF) for the rotational velocities and obtain the cumulative distribution function (CDF) for the velocities. This CDF is attained in just one step, without the need for the convergence criteria usually necessary in iterative methods, giving robustness to our novel method.
This article is structured as follows. In Sect. 2, we present the mathematical description of the method. In Sect. 3, we apply it to a theoretical example of v sin i, and we show that v sin i is given by an χ distribution when the velocity distribution comes from a Maxwellian distribution (Deutsch 1970). Our method recovers the Maxwellian distribution with a very high degree of confidence. We also discuss in this section the relation between the length of the sample and the error in the CDF. Section 4 is dedicated to a real sample of circa 12 000 main-sequence field stars. We obtain for the first time the true CDF for the velocities of this sample. Furthermore, we recover the results of Carvahlo et al. (2009), demonstrating that the rotational velocity distribution function for this sample is non-Maxwellian, and instead is better described by Tsallis or Kaniadakis distribution functions. In the last section, we discuss our conclusions and future work.
2. The method
An important class of inverse problems in astronomy has the following form: 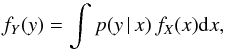 (1)which is known as Fredholm integral problem of the first kind (Lucy 1994), where fY is a function accessible to observation and fX is the function of interest. The kernel p of this integral is related to the remoteness of the measurement process. Different approaches are considered in the literature (see Lucy 1994, and references therein), almost all of them based on maximum likelihood, where the optimization is carried out using Bayesian-based iterative methods (see Richardson 1972).
(1)which is known as Fredholm integral problem of the first kind (Lucy 1994), where fY is a function accessible to observation and fX is the function of interest. The kernel p of this integral is related to the remoteness of the measurement process. Different approaches are considered in the literature (see Lucy 1994, and references therein), almost all of them based on maximum likelihood, where the optimization is carried out using Bayesian-based iterative methods (see Richardson 1972).
In many problems, the function of interest is the cumulative distribution FX of the random variable X, different approaches could be applied. For a special form of the kernel p related to a specific applications, we can invert the integral problem (1).
2.1. The basic problem
The problem that we wish to consider may be formulated in the following form: a positive continuous random variable X occurs with a probability given by a unknown density function fX. The probability density function fY of an observed variable Y is related to fX by Eq. (1), where p is the kernel or conditional probability density function, i.e.: 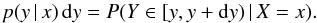 (2)This mathematical problem consists in obtaining fX from the theoretical function p and the observed distribution fY. We study the particular case where Y is a projection of X: p(y | x) = 0 if y>x or y< 0 and depends only on the ratio s = y/x. In this case, we can write p(y | x) dy = q(y/x) dy/x and then
(2)This mathematical problem consists in obtaining fX from the theoretical function p and the observed distribution fY. We study the particular case where Y is a projection of X: p(y | x) = 0 if y>x or y< 0 and depends only on the ratio s = y/x. In this case, we can write p(y | x) dy = q(y/x) dy/x and then 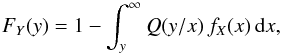 (3)where FY the cumulative distribution function.
(3)where FY the cumulative distribution function.
Chandrasekhar & Münch (1950) considered the integral equation governing the distribution of the true and apparent rotational velocities of stars, y = x sin i, where x = v and i is the inclination angle, assuming uniform distribution over the sphere (a detailed derivation of Q(y/x) is given in Appendix A). In this case, the integral equation reads as follows: 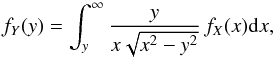 (4)They obtain the solution to this problem, based on the formal solution to Abel’s integral equation, namely:
(4)They obtain the solution to this problem, based on the formal solution to Abel’s integral equation, namely: 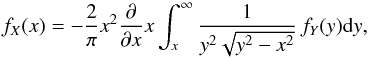 (5)which is not of much practical use, since it requires differentiation of a functional of the observed density function fY and it can lead to the wrong results (see Chandrasekhar & Münch 1950).
(5)which is not of much practical use, since it requires differentiation of a functional of the observed density function fY and it can lead to the wrong results (see Chandrasekhar & Münch 1950).
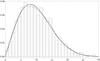 |
Fig. 1 Histogram of a synthetic sample of y = v sin i with n = 1000 from the PDF (Eq. (13)), with σ = 8. The solid black line plots the corresponding theoretical (Maxwellian) PDF. The dashed line shows the corresponding KDE of this sample calculated with a Gaussian kernel. |
From the definition of CDF of a random variable 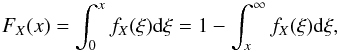 and using Eq. (5), we obtain:
and using Eq. (5), we obtain: 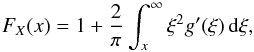 where
where 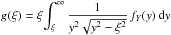 . After applying integration by parts, we get:
. After applying integration by parts, we get: 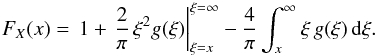 (6)Using the following inequality
(6)Using the following inequality 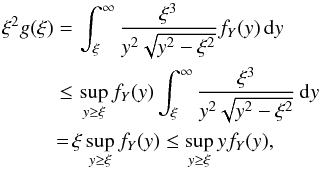 it holds that limξ → ∞ξ2g(ξ) = 0, provided limy → ∞yfY(y) = 0. The latter assumption is true for all of the known distribution functions. Therefore, rearranging Eq. (6), we get:
it holds that limξ → ∞ξ2g(ξ) = 0, provided limy → ∞yfY(y) = 0. The latter assumption is true for all of the known distribution functions. Therefore, rearranging Eq. (6), we get: 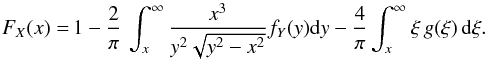 (7)By interchanging the order of integration, the last integral can be written as
(7)By interchanging the order of integration, the last integral can be written as 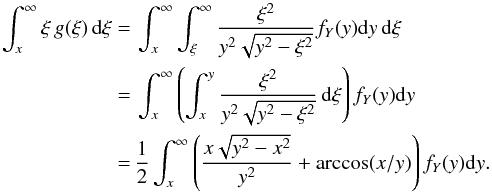 Finally, substituting into (7), we obtain:
Finally, substituting into (7), we obtain: 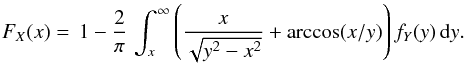 (8)This equation provides a numerically stable method for solving (1) in this particular case. Our purpose is to develop a novel algorithm for solving the general problem (1) that can serve as an alternative to the iterative method proposed by Lucy (1974), and to recover the original Chandrasekhar & Münch method, without introducing numerical instabilities due to the derivative (see Eq. (5)).
(8)This equation provides a numerically stable method for solving (1) in this particular case. Our purpose is to develop a novel algorithm for solving the general problem (1) that can serve as an alternative to the iterative method proposed by Lucy (1974), and to recover the original Chandrasekhar & Münch method, without introducing numerical instabilities due to the derivative (see Eq. (5)).
3. A theoretical test
In this section, we evaluate the proposed method in Sect. 2. We assume that the distribution of velocities is given by a Maxwellian distribution (as it is considered by Deutsch 1970) with dispersion σ, i.e., 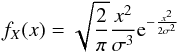 (9)where x> 0. The behavior of this distribution is shown as a solid line in Fig. 1.
(9)where x> 0. The behavior of this distribution is shown as a solid line in Fig. 1.
Therefore, Eq. (4) yields: 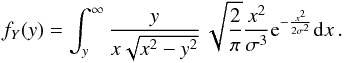 (10)This integral has an explicit analytic solution, which is:
(10)This integral has an explicit analytic solution, which is: 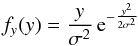 (11)for y> 0. Whereas the definition of the χ-distribution is:
(11)for y> 0. Whereas the definition of the χ-distribution is: 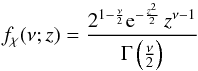 (12)where ν is a real positive parameter, z is any positive real number, and Γ is the Gamma function. Then, Eq. (11) corresponds to:
(12)where ν is a real positive parameter, z is any positive real number, and Γ is the Gamma function. Then, Eq. (11) corresponds to: 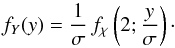 (13)To apply this method, we first create a sample of v sin i values using Eq. (13), i.e., generating n random values {Y1,Y2,··· ,Yn − 1,Yn}, then we obtain
(13)To apply this method, we first create a sample of v sin i values using Eq. (13), i.e., generating n random values {Y1,Y2,··· ,Yn − 1,Yn}, then we obtain 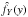 using a kernel density estimator method (KDE) for this sample and insert it in Eq. (8). The KDE is a nonparametric method to estimate the probability distribution of a random variable (in our case y = x sin i) from a random sample.
using a kernel density estimator method (KDE) for this sample and insert it in Eq. (8). The KDE is a nonparametric method to estimate the probability distribution of a random variable (in our case y = x sin i) from a random sample.
The KDE estimator is defined as follows:  (14)where K is the kernel function and h is the bandwidth. In this work, we use a Gaussian kernel,
(14)where K is the kernel function and h is the bandwidth. In this work, we use a Gaussian kernel, 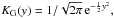 because this kernel smooths the distribution. The bandwidth is defined as:
because this kernel smooths the distribution. The bandwidth is defined as: 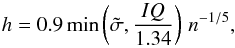 where
where 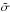 is the standard deviation of the random variable under study, Y, and IQ is the correspondent interquartile range (Silverman 1986). Figure 1 shows histogram of a synthetic sample of n = 1000, and the corresponding KDE function is shown as a dashed line.
is the standard deviation of the random variable under study, Y, and IQ is the correspondent interquartile range (Silverman 1986). Figure 1 shows histogram of a synthetic sample of n = 1000, and the corresponding KDE function is shown as a dashed line.
The steps of our algorithm to get the estimated CDF are the following: i) have a sample of v sin i; ii) obtain a KDE from this sample using a suitable kernel function; and iii) calculate the estimated CDF using Eq. (8) with KDE (from previous step) as the fY(y) function.
We point out, that exists an arbitrary choice in the number of values of x that can be obtained from Eq. (8). A reasonable restriction is to take a Δx not lower than the sample’s measurement error. For the sample we use in Sect. 4, the error is Δx = 1 km s-1, hence the value that we use in this theoretical example.
Figure 2 shows the estimated CDF in the interval 0 to 35 km s-1, with a step of 1 km s-1, for a synthetic sample of v sin i of size n = 1000 and parameter σ = 8. These data were obtained directly using the method described previously, without needing any convergence criteria. From this empirical CDF we can calculate the moments of the distribution (e.g., mean, variance), but moments analysis in Chandrasekhar & Münch (1950) is more straightforward. Nevertheless, with this new method we can calculate percentiles, intervals, and, in general, any probability associated with the velocity distribution.
Figure 2 also shows the theoretical CDF (solid line) of this Maxwellian distribution for the same parameter, i.e., 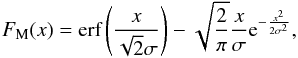 (15)where erf corresponds to the error function.
(15)where erf corresponds to the error function.
 |
Fig. 2 CDF values calculated from Eq. (8) with a step of 1 km s-1 (black dots). The theoretical Maxwellian distribution is shown as a solid black line. |
In order to get an estimation of our method’s error, we use the standard discrete integrated square error (ISE) defined as: 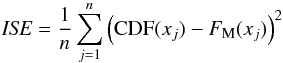 (16)and afterward we obtain the standard discrete mean integrated square error (MISE) by computing the mean of ISE for several samples of a given fixed size n. Therefore, we run a monte carlo (MC) simulation calculating ISE for a set of 500 samples of n = 1000 data and another set of 500 samples with n = 10 000 data. Figure 3 shows the ISE histogram for both sets of samples, and Table 1 shows the mean and median values of our simulations, where the mean value of each set represents the estimated MISE of our model. Clearly, we find the greater the data sample, the lower the error in the estimation of the CDF.
(16)and afterward we obtain the standard discrete mean integrated square error (MISE) by computing the mean of ISE for several samples of a given fixed size n. Therefore, we run a monte carlo (MC) simulation calculating ISE for a set of 500 samples of n = 1000 data and another set of 500 samples with n = 10 000 data. Figure 3 shows the ISE histogram for both sets of samples, and Table 1 shows the mean and median values of our simulations, where the mean value of each set represents the estimated MISE of our model. Clearly, we find the greater the data sample, the lower the error in the estimation of the CDF.
 |
Fig. 3 Histogram of the ISE for a set of 500 samples with 1000 data each, shown in light-gray and a set of 500 samples of 10 000 data each shown in dark-gray (see text for details). |
MISE.
The MISE depends mostly on the KDE of each sample used for computation of the CDF, when the KDE from the sample is improved, as does the estimation of CDF. We can conclude that our method recovers the Maxwellian distribution with very high precision.
4. Application to main-sequence field stars
In this section, we apply this method to a large sample of measured v sin i data. We use the sample from the Geneva-Copenhagen survey of the solar neighborhood (Nordström et al. 2004; Holmberg et al. 2007), which contains information about 16 500 F and G main-sequence field stars. In this catalog, 12 931 stars have values of v sin i. Furthermore, considering that the listed values of v sin i are rounded to the nearest km s-1 up to 30 km s-1, and upwards of that value the survey lists v sin i to the nearest 5 or 10 km s-1, and that about 91% of the sample have rotational speeds below 30 km s-1, we only select (following Carvalho et al. 2009) stars with v sin i ≤ 30 km s-1, obtaining a sample of 11 818 stars.
Applying our method, we obtained the estimated CDF from this sample, as shown as black dots in Fig. 4. To estimate the error of the estimated CDF, we create 1000 bootstrap samples of the original and calculate the corresponding 1000 bootstrap CDF. In Fig. 4, we also plotted all the bootstrap CDF in light-gray. Concerning the error’s estimator we add in each point of Fig. 4 an error bar which is the 95% confidence interval (see the zoomed plot in Fig. 4). Since the estimated bootstrap CDF from the original sample are functions, it is difficult to obtain the distribution of probability of the estimator. Therefore, to calculate the probability of the original estimated CDF, we used the approximated confidence interval with normal standard percentile Zα/ 2, namely: 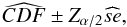 where
where 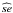 is the standard deviation of bootstrap samples, Zα/ 2 is the value in which the standard normal distribution accumulate 97.5% of the area under its PDF, and α = 0.05 (=1 − 0.95) is the complement of the confidence. This procedure is the simplest one for calculating confidence intervals from Bootstrap method proposed in Efron (1993).
is the standard deviation of bootstrap samples, Zα/ 2 is the value in which the standard normal distribution accumulate 97.5% of the area under its PDF, and α = 0.05 (=1 − 0.95) is the complement of the confidence. This procedure is the simplest one for calculating confidence intervals from Bootstrap method proposed in Efron (1993).
One of the advantages of getting the CDF is to provide information about the rotational velocity distribution. Observing the black dots from Fig. 4, we see that approximately 50% of the sample have a magnitude less than 7 km s-1 and 10% of the fastest rotational speeds are approximately between 24 km s-1 and 30 km s-1.
Deutsch (1970) proved, using methods of classical statistical mechanics, that the distribution of rotational speeds is given by a Maxwellian distribution (Eq. (9)), under the assumption that the angles are distributed uniformly over the sphere. Therefore, to describe the rotational velocity distribution function, we fit a Maxwellian CDF to our estimated CDF. The fitting method minimizes the least squares, i.e., 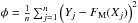 , where FM is the CDF for the Maxwellian distribution (Eq. (15)). For the minimization process, we use the Nelder-Mead simplex algorithm (Nelder & Mead 1965) .
, where FM is the CDF for the Maxwellian distribution (Eq. (15)). For the minimization process, we use the Nelder-Mead simplex algorithm (Nelder & Mead 1965) .
Figure 5 shows the estimated CDF and also shows the Maxwellian’s CDF (solid black line). The minimization gives a dispersion of σ = 5.64 that corresponds to the minimum value of φ = 0.0087. Clearly from this figure, a Maxwellian distribution cannot describe the proper distribution of the rotational speeds of this sample. Indeed, the estimated CDF has tails with higher positive probability than those of Maxwellian’s CDF, i.e., the distribution of rotational velocity has more dispersion than the CDF from a Maxwellian distribution.
 |
Fig. 4 Estimated CDF from the sample of 11 818 stars are shown as black dots, with an approximated confidence interval (error bar). All the bootstrap CDFs are also plotted in light-gray . The zoomed inset shows the error bar calculated using the methodology from Efron (1993). |
 |
Fig. 5 Empirical CDF from the sample, shown as black dots without error bar. The fitted CDF function from a Maxwellian distribution with σ = 5.64 is shown as a solid black line, fitted Tsallis distribution with σq = 3.46 and q = 1.41 is shown as a dashed line and fitted Kaniadakis distribution with σk = 4.64 and k = 0.45 is shown as a dotted line. |
This sample has been used by Carvalho et al. (2009), who performed a statistical study of it, showing that the empirical distribution function of this sample cannot be fitted using a Maxwellian distribution (Deutsch 1970). They obtained a much better fit when the assumption of Gibbs entropy in standard statistical mechanics is released and distribution functions from nonextensive statistical mechanics are applied to the sample. Specifically, they used the Tsallis distribution (Tsallis 1998) and the Kaniadakis power-law distribution (Kaniadakis 2002, 2005), both based on the concept of maximum entropy (Gell-Mann & Tsallis 2004).
These distributions are also plotted in Fig. 5. We can see that for the left tail, the estimated CDF (black dots) and both Tsallis and Kaniadakis distributions have velocity values below 8 km s-1, representing the 60% of the data, while for the Maxwellian distribution this percentage is reached of about 10 km s-1. Concerning the right tail, the Maxwellian distribution for the rotational velocity of less than 17 km s-1 has a probability of about 95%, while for the other two distributions this probability is reached for rotational speeds with values above 25 km s-1.
Having a known integral expression (given by Eq. (8)), our method allows us to fit any known distribution. In this case, we reach the same conclusion as Carvalho et al. (2009), but using a different algorithm, i.e., Tsallis or Kaniadakis distributions are in close agreement to the empirical CDF, although the two distributions show a slight discrepancy in their tails.
Non-linear model results.
5. Discussion and conclusions
In this work, we have obtained the cumulative distribution function of “de-projected” velocities. It is well known that from the estimated CDF we can obtain general aspects of the probabilities, e.g., the distributional moments, the probability of an interval, median, percentiles, and any other statistical feature of the sample.
This novel method we present is an extension of the pioneer work introduced by Chandrasekar & Münch (1950). Our method allows to obtain the CDF without numerical instability caused by the use of a derivative, which was the main disadvantage of the PDF of Chandrasekar & Münch (1950). Furthermore, this estimated CDF is obtained in just one step without needing any convergence criteria in comparison with the widely used iterative method of Lucy (1974).
Deutsch (1970) shows that if the direction of the rotational velocity is uniformly distributed and each Cartesian component is distributed independent of the other ones, then the magnitude of the velocity follows a Maxwellian distribution law. However, the independence assumption is not clear and we proved in the previous section that the Maxwellian distribution does not accurately fit the empirical CDF.
On the other hand, Carvalho et al. (2009) found a better agreement for two other probability distributions, namely: Tsallis and Kaniadakis. These distributions are based on the concept of maximum entropy. In our case, using the new method, we confirm their analysis but this time from the rotational velocity estimated CDF. These results open the question about the validity of the assumption of Maxwellian distribution.
Future work:we will extend the applicability of our model for samples that show bimodal velocity distributions, e.g., the data from VLT FLames Tarantula Survey (Ramírez-Agudelo et al. 2013).
There are samples that show few, if any, stars with very low rotational velocities (see, e.g., Yudin 2011; Ramírez-Agudelo et al. 2013). If the distribution of inclination angles is uniform, then independent of the rotational velocity distribution, there must be a nonnegligible portion of the sample with lower values of the projected rotational velocity due to low values of i. There are some studies of open clusters where this assumption no longer seems reasonable, see Silva et al. (2013) and Rees y Zijlstra (2013). We want to develop a “completeness” test for the uniform distribution of angles of a sample of v sin i.
Furthermore, we want to use a general function to describe an arbitrary orientation of rotational axes and to study the distribution of rotational velocities in a more general description. Finally, a very ambitious project will be to simultaneously obtain both distributions from a data sample.
Acknowledgments
This work has been partially supported by project CONICT-Redes 12-0007. M.C. thanks the support of FONDECYT project 1130173 and Centro de Astrofísica de Valparaíso. J.C. thanks the financial support from project: “Ecuaciones Diferenciales y Análisis Numérico” – Instituto de Ciencias, Instituto de Desarrollo Humano e Instituto de Industria – Universidad Nacional de General Sarmiento. D.R. acknowledges support from project PIP11420090100165, CONICET. A.C. thanks the support from Instituto de Estadística, Pontificia Universidad Católica de Valparaíso.
References
- Carvalho, J. C., do Nascimento Jr., J. D., Silva, R., & de Medeiros, J. R. 2009, ApJ, 696, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S., & Münch, G. 1950, ApJ, 111, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Deutsch, A. J. 1970, in Stellar Rotation, ed. A. Slettebak (Dordrecht: Reidel), Proc. IAU Colloq., 4, 207 [Google Scholar]
- Efrom, B., & Tibshirani, R. J. 1993, An Introduction to the Bootstrap (London: Chapman and Hall) [Google Scholar]
- Gell-Mann, M., & Tsallis, C. 2004, in Nonextensive Entropy – Interdisciplinary Applications (New York: Oxford Univ. Press) [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Kaniadakis, G. 2002, Phys. Rev. E, 66, 056125 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kaniadakis, G. 2005, Phys. Rev. E, 72, 036108 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Lucy, L. B. 1974, AJ, 79, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1994, Rev. Mod. Astron., 7, 31 [NASA ADS] [Google Scholar]
- Nelder, J., & Mead, R. 1965, Comput. J., 7, 308 [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez-Agudelo, O. H., Simón-Díaz, S., Sana, H., et al. 2013, A&A, 560, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rees, W. H., & Zijlstra, 2013, MNRAS, 435, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, W. H. 1972, J. Opt. Soc. Am., 62, 55 [Google Scholar]
- Silva, J. R. P., Nepomuceno, M. M. F., Soares, B. B., & de Freitas, D. B. 2013, ApJ, 777, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, B. W. 1986, Density estimation for statistics and data analysis, Monographs on Statistics and Applied Probability No. 26 (London: Chapman and Hall) [Google Scholar]
- Tsallis, C. 1988, J. Statist. Phys., 52, 479 [CrossRef] [Google Scholar]
- Yudin, R. V. 2001, A&A, 368, 912 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Distribution of projected angles
Let x be a random vector in 3D and y be the projection of x to the plane normal to the line of sight. If X = ∥x∥, Y = ∥y∥, i is the angle between x and the line of sight, and S = |sin(i)| = Y/X ∈ [0,1], the condition S ≤ s is equivalent to 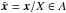 , where A is the polar region of the unit sphere corresponding to the inclination angle i ∈ [0, i0] ∪ [π − i0, π], azimuthal angle φ ∈ [0, 2π], and i0 = arcsin(s) (see Fig. B). Asume X,
, where A is the polar region of the unit sphere corresponding to the inclination angle i ∈ [0, i0] ∪ [π − i0, π], azimuthal angle φ ∈ [0, 2π], and i0 = arcsin(s) (see Fig. B). Asume X, 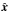 are independent and
are independent and 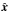 is uniformly distributed over the unit sphere, i.e.,
is uniformly distributed over the unit sphere, i.e., 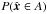 is proportional to the area of A. Therefore,
is proportional to the area of A. Therefore, 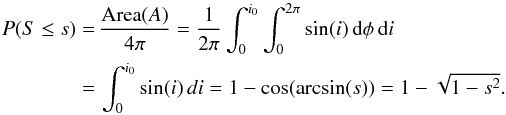 Since the PDF verifies fS(s) = d P(S ≤ s) /ds, we have
Since the PDF verifies fS(s) = d P(S ≤ s) /ds, we have 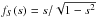 , and substituting into (1)we obtain:
, and substituting into (1)we obtain: 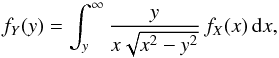 (A.1)which corresponds to Eq. (9) from Chandrasekhar & Münch (1950).
(A.1)which corresponds to Eq. (9) from Chandrasekhar & Münch (1950).
Appendix B: Tsallis & Kaniadakis distributions
 |
Fig. B.1 Distribution of sin i. |
A standard assumption of statistical mechanics, based on the Gibbs entropy is that quantities, such as energy are extensive variables, i.e., the total energy of the system is proportional to the system size; similarly, the entropy is also supposed to be extensive. Tsallis statistical mechanics is based on the concept of maximum entropy (see details in Gell-Mann & Tsallis 2004). From a mathematical point of view, the Tsallis PDF is defined as: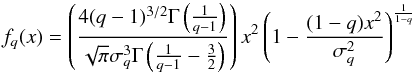 (B.1)where σq is the dispersion. When the q-parameter tends to 1 the standard Maxwellian distribution is attained. The CDF of this distribution is:
(B.1)where σq is the dispersion. When the q-parameter tends to 1 the standard Maxwellian distribution is attained. The CDF of this distribution is: ![\appendix \setcounter{section}{2} \begin{eqnarray} F_q(x)&=& \left( 2 \sqrt{\pi } \sqrt{q-1} \sigma_q ^3 \Gamma\left(\frac{1}{2}+\frac{1}{q-1}\right) \left((q-1) x^2+\sigma_q ^2\right)\right)^{-1} \,\nonumber \\ &&\quad\times\sigma_q ^{\frac{2}{q-1}} x^{\frac{q+3}{1-q}} \Gamma \left(\frac{1}{q-1}\right) \left(-q-\frac{\sigma_q ^2}{x^2}+1\right)^{\frac{1}{1-q}} \nonumber \\ && \quad\times \left[\sigma_q ^{-\frac{2}{q-1}} x^{-\frac{2}{q-1}} \left(\frac{(q-1) x^2}{\sigma_q ^2}+1\right)^{\frac{1}{1-q}} \left(\sigma_q ^2 x^{\frac{2}{q-1}}+(q-1) x^{\frac{2 q}{q-1}}\right)\nonumber\right. \\ && \quad\times \left(-q-\frac{\sigma_q ^2}{x^2}+1\right)^{-\frac{1}{1-q}} \left(2 \sigma_q ^2 x^{\frac{4}{q-1}} \left((q-1) x^2+\sigma_q ^2\right) \right. \,\nonumber \\ && \quad\times \left. _2F_1\left(1,\frac{1}{2}+\frac{1}{1-q};\frac{1}{2};-\frac{(q-1) x^2}{\sigma_q ^2}\right) \right.\nonumber \\ && \quad \left. \left. +\, (q-3) (3 q-5) x^{\frac{4 q}{q-1}}-\sigma_q ^2 x^{\frac{4}{q-1}} \left(4 (2 q-3) x^2+3 \sigma_q ^2\right)\right) \right. \nonumber \\ && \quad +\, {\rm e}^{\frac{i \pi }{q-1}} \left((9 q-17) \sigma_q ^4 x^{\frac{2 q}{q-1}}+x^{\frac{2}{q-1}} \left(-(q-3)^2 (q-1) x^6 \right.\right. \nonumber \\&&\quad\left.\left.\left. +\, (q (7 q-18)+7) \sigma_q ^2 x^4+\sigma_q^6\right) \right) \right] . \end{eqnarray}](/articles/aa/full_html/2014/05/aa23344-13/aa23344-13-eq128.png) (B.2)
(B.2)
Here 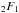 is the Gauss Hypergeometric function and Γ is the Gamma function.
is the Gauss Hypergeometric function and Γ is the Gamma function.
Kaniadakis (2002, 2005), based on the same concept of maximum entropy, developed a power-law statistics, where the distribution function is given by: 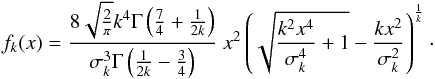 (B.3)Here σk is the dispersion. When the k-parameter tends to 1 again the standard Maxwellian distribution is attained. The CDF of Kaniadakis distribution is:
(B.3)Here σk is the dispersion. When the k-parameter tends to 1 again the standard Maxwellian distribution is attained. The CDF of Kaniadakis distribution is: ![\appendix \setcounter{section}{2} \begin{eqnarray} F_k(x)&= 1 - \left( \frac{2^{\frac{5}{2}-\frac{1}{k}} \Gamma \left(\frac{7}{4}+\frac{1}{2 k}\right) \Gamma \left(\frac{1}{k}\right) \left(\frac{k x^2}{\sigma_k ^2}\right)^{\frac{3}{2}-\frac{1}{k}}}{\sqrt{\pi }} \right) \nonumber\\[2mm] &\quad\times \, _3\tilde{F}_2\left(\frac{1}{2 k}-\frac{3}{4},\frac{k+1}{2 k},\frac{1}{2 k};\frac{k+2}{4 k},\frac{1}{k}+1;-\frac{\sigma_k ^4}{k^2 x^4}\right) \end{eqnarray}](/articles/aa/full_html/2014/05/aa23344-13/aa23344-13-eq133.png) (B.4)where
(B.4)where 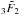 is the regularized generalized hypergeometric function.
is the regularized generalized hypergeometric function.
All Tables
All Figures
 |
Fig. 1 Histogram of a synthetic sample of y = v sin i with n = 1000 from the PDF (Eq. (13)), with σ = 8. The solid black line plots the corresponding theoretical (Maxwellian) PDF. The dashed line shows the corresponding KDE of this sample calculated with a Gaussian kernel. |
| In the text | |
 |
Fig. 2 CDF values calculated from Eq. (8) with a step of 1 km s-1 (black dots). The theoretical Maxwellian distribution is shown as a solid black line. |
| In the text | |
 |
Fig. 3 Histogram of the ISE for a set of 500 samples with 1000 data each, shown in light-gray and a set of 500 samples of 10 000 data each shown in dark-gray (see text for details). |
| In the text | |
 |
Fig. 4 Estimated CDF from the sample of 11 818 stars are shown as black dots, with an approximated confidence interval (error bar). All the bootstrap CDFs are also plotted in light-gray . The zoomed inset shows the error bar calculated using the methodology from Efron (1993). |
| In the text | |
 |
Fig. 5 Empirical CDF from the sample, shown as black dots without error bar. The fitted CDF function from a Maxwellian distribution with σ = 5.64 is shown as a solid black line, fitted Tsallis distribution with σq = 3.46 and q = 1.41 is shown as a dashed line and fitted Kaniadakis distribution with σk = 4.64 and k = 0.45 is shown as a dotted line. |
| In the text | |
 |
Fig. B.1 Distribution of sin i. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


