| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A136 | |
| Number of page(s) | 15 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201423617 | |
| Published online | 18 April 2014 | |
An empirical mass-loss law for Population II giants from the Spitzer-IRAC survey of Galactic globular clusters⋆,⋆⋆
1 INAF – Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
e-mail: livia.origlia@oabo.inaf.it
2 University of Bologna, Physics & Astronomy Dept., Viale Berti Pichat 6-2, 40127 Bologna, Italy
3 Department of Physics and Astronomy, University of California at Los Angeles, Los Angeles, CA 90095-1547, USA
4 ESO – European Southern Observatory, Karl-Schwarzschild Str. 2, 85748 Garching bei München, Germany
Received: 11 February 2014
Accepted: 2 March 2014
Aims. The main aim of the present work is to derive an empirical mass-loss (ML) law for Population II stars in first and second ascent red giant branches.
Methods. We used the Spitzer InfraRed Array Camera (IRAC) photometry obtained in the 3.6–8 μm range of a carefully chosen sample of 15 Galactic globular clusters spanning the entire metallicity range and sampling the vast zoology of horizontal branch (HB) morphologies. We complemented the IRAC photometry with near-infrared data to build suitable color-magnitude and color-color diagrams and identify mass-losing giant stars.
Results. We find that while the majority of stars show colors typical of cool giants, some stars show an excess of mid-infrared light that is larger than expected from their photospheric emission and that is plausibly due to dust formation in mass flowing from them. For these stars, we estimate dust and total (gas + dust) ML rates and timescales. We finally calibrate an empirical ML law for Population II red and asymptotic giant branch stars with varying metallicity. We find that at a given red giant branch luminosity only a fraction of the stars are losing mass. From this, we conclude that ML is episodic and is active only a fraction of the time, which we define as the duty cycle. The fraction of mass-losing stars increases by increasing the stellar luminosity and metallicity. The ML rate, as estimated from reasonable assumptions for the gas-to-dust ratio and expansion velocity, depends on metallicity and slowly increases with decreasing metallicity. In contrast, the duty cycle increases with increasing metallicity, with the net result that total ML increases moderately with increasing metallicity, about 0.1 M⊙ every dex in [Fe/H]. For Population II asymptotic giant branch stars, we estimate a total ML of ≤0.1 M⊙, nearly constant with varying metallicity.
Key words: techniques: photometric / Hertzsprung-Russell and C-M diagrams / stars: evolution / stars: mass-loss / stars: Population II / globular clusters: general
This work is based on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided by NASA through an award issued by JPL/Caltech.
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Mass loss (ML) affects all stages of stellar evolution and its parametrization remains a vexing problem in any modeling, since satisfactory empirical determinations as well as a comprehensive physical description of the involved processes are still lacking. This is especially true for Population II red giant branch (RGB) and asymptotic giant branch (AGB) stars.
The astrophysical impact of ML in Population II giants is huge and affects not only stellar evolution modeling, but also related subjects, like, for example, the UV excess in ellipticals or the interaction between the cool intracluster medium and hot halo gas. There is a great deal of indirect, but quantitative evidence for ML during the RGB evolution, namely the horizontal branch (HB) morphology and the 2nd parameter problem, the pulsational properties of RR Lyrae, the absence of AGB stars significantly brighter than the RGB tip, and the masses of white dwarfs (WDs) in Galactic globular clusters (GCs; see, e.g., Rood 1973; Fusi Pecci & Renzini 1975, 1976; Renzini 1977; Fusi Pecci et al. 1993; Ferraro et al. 1998; D’Cruz et al. 1996; Hansen 2005; Kalirai et al. 2007; Catelan 2009). On the contrary, there is no empirical ML law directly calibrated on Population II giants with varying metallicity and only a few estimates of ML for giants on the brightest portion of the RGB and AGB exist. As a consequence, ML timescales, driving mechanisms, dependence on stellar parameters, and metallicity are still open issues. There is little theoretical or observational guidance on how to incorporate ML into models.
With no better recipe, models of stellar evolution incorporate ML by using analytical ML formulae calibrated on bright Population I giants. The first and most used of these is the Reimers (1975a,b) formula, extrapolated toward lower luminosity and introducing a free parameter η (typically equal to 0.3) to account for a somewhat less efficient ML along the RGB. A few other formulae, which are variants of the Reimers formula, have been proposed in the subsequent years (see, e.g., Mullan 1978; Goldberg 1979; Judge 1991). More recently, Catelan (2000) revised these formulae by using a somewhat larger database of stars than in previous studies, but still amounting to 20–30 giants only, the majority being AGB stars. Schröder & Cuntz (2005) propose a new semi-empirical formula that explicitly includes a dependence from all the stellar parameters. Further advances clearly require empirical estimates of ML rates in low-mass giants along the entire RGB and AGB extension.
There are two major diagnostics of ML in giant stars: the detection of outflow motions in the outer regions of the stellar atmosphere or the detection of circumstellar (CS) envelopes at much larger distances from the star.
After the pioneering work by Reimers (1975a,b), the systematic investigation of chromospheric lines in giants stars with possible emission wings started in the 1980s. Gratton (1983); Cacciari & Freeman (1983); Gratton et al. (1984) measured Hα emission in old, bright giants near the RGB tip, members of Galactic globular and open clusters. They found Hα emission in a significant fraction of them and, by using the simple recombination model by Cohen (1976), they estimated average dM/ dt ≈ 10-8 M⊙ yr-1 ML rates. However, Dupree et al. (1984) and Dupree (1986) argued that the Hα wings could naturally arise in a static stellar chromospheres. Other authors (e.g., Peterson 1981, 1982; Dupree et al. 1992, 1994; Lyons et al. 1996; Smith et al. 2004; Cacciari et al. 2004; Mauas et al. 2006; Vieytes et al. 2011) investigated the possible presence of profile asymmetries and coreshifts in a large number of chromospheric lines, by means of high resolution spectroscopy over a wide spectral range, from UV (MgII h, k λ2800 Å) to optical (CaII K, NaI D, Hα) and IR (HeI λ10830.3 Å). These line asymmetries and coreshifts can be accounted for only by an active chromosphere and/or mass outflow, with typical velocity fields of 10–20 km s-1. The difficulty of converting the chromospheric line diagnostics into ML rates is certainly related to modeling uncertainties, for example because of the lack of any detailed knowledge of the structure and excitation mechanism of the wind region. However, it is also clear that the outflow region traced by the chromospheric lines is still too close to the star, to sample the bulk of the mass lost, likely accumulated at larger distances. Hence, the chromospheric line method seems more effective in tracing the region of wind formation and acceleration, rather than most of the outflow. Finally, it must be recalled that even with 8 m-class telescopes it is at best expensive and often impossible to obtain high-resolution, high signal-to-noise (S/N) spectra of Population II giants along the entire RGB extension.
A CS envelope around a cool giant can be detected by measuring IR dust emission, linear polarization, microwave CO emission and radio OH masers. However, CS envelopes of low-mass giants have intrinsically low surface brightness. Far IR and radio receivers have neither sufficient spatial resolution nor sensitivity to study Population II CS envelopes in dense stellar fields. Linear polarization, intrinsically well below 1%, is also hardly measurable. Hence, array photometry in the 3–20 μm region remains the most effective way to detect Population II CS envelopes. Mid-IR observations have the advantage of sampling an outflowing gas fairly far from the star (typically, tens/hundreds stellar radii). Such gas left the star a few decades previously, hence the inferred ML rate is also smoothed over such a timescale. In the late 1980s, the first measurements of dust excess in Galactic GC giants by means of mid-IR photometry from the ground (Frogel & Elias 1988) and with IRAS (Gillet et al. 1988; Origlia et al. 1996) became available, although the spatial resolution of these detectors was insufficient to properly resolve most of the stars. A decade later, the Infrared Space Observatory (ISO) satellite allowed new observations, but was still limited in spatial resolution and sensitivity. A few bright AGB stars in 47 Tuc have been measured by Ramdani & Jorissen (2001), finding dust excess in two objects only. Our group performed a deep survey with the ISO Infrared Camera ISOCAM of six massive GCs (Origlia et al. 2002), namely 47 Tuc, NGC 362, ω Cen, NGC 6388, M 15 and M 54, in the 10 μm window. From a combined physical and statistical analysis, our ISOCAM study provided ML rates and frequency for some giants near the tip (see also Origlia et al. 2007). However, the small sample of observed giants and the limited capabilities of ISOCAM allowed us to reach only weak conclusions on the ML dependence on luminosity, metallicity, and HB morphology.
The advent of Spitzer with its mid-InfraRed Array Camera (IRAC) has opened a new window in the study of CS envelopes around Population II giants. Indeed, the IRAC bands between 3.6 and 8 μm are effective in detecting warm dust with spatial resolution good enough to resolve a large fraction of the GC giants. By using the (3.6−8) Spitzer-IRAC color as a diagnostic, dust excess has been detected around some of the brightest giants in ω Cen, M 15, NGC 362 and 47 Tuc (Boyer et al. 2006, 2008, 2009, 2010).
In Cycle 2 (program ID #20298), our group was granted 26 h of Spitzer-IRAC observing time to map 17 Galactic GCs down to the HB level. We combined Spitzer-IRAC photometry with high-resolution near-IR photometry from the ground and used (K-IRAC) colors as diagnostics of possible circumstellar dust excess. Results for 47 Tuc have been published in Origlia et al. (2007, 2010), while those for the complex stellar system ω Cen will be presented in a forthcoming paper.
Here we present the photometric analysis for the remaining 15 GCs in our sample, we discuss ML rates and duty cycles in Population II giants and we derive an empirical law of ML for Population II giants with varying metallicity.
Observed sample of GCs and main parameters.
2. Observations, data reduction, and photometric analysis
The 15 GCs presented in this paper are listed in Table 1. They span metallicities from about 1/100 to about solar; at a given metallicity, clusters with different HB morphologies were chosen.
-
M 92, M 15, M 30 – These are the most metal-poor clusters in our sample, with M 15 and, to a lesser extent, M 30, showing very blue HB tails compared to M 92.
-
M80, M13, M3 – This is the popular cluster triplet at intermediate metallicity with different HB morphologies, including red clumps, gaps, and blue tails (see, e.g., Ferraro et al. 1997, 1998; Dalessandro et al. 2013a).
-
NGC 6752, NGC 288, NGC 2808, NGC 362, NGC 1851 – This group of clusters at intermediate metallicity also shows very different HB morphologies, with purely blue (NGC 6752, NGC 288), purely red (NGC 362), and multimodal distributions with blue tails (NGC 2808 and NGC 1851).
-
NGC 6440, NGC 6388, NGC 6441, NGC 6539 – These are the most metal-rich clusters in our sample. While NGC 6440 and NGC 6539 have a red HB, typical of their high metallicity, NGC 6441 and NGC 6388 have a multimodal HB distribution, with a well populated red clump and a peculiar blue HB tail (Rich et al. 1997; Pritzl et al. 2001, 2002, 2003; Busso et al. 2007; Dalessandro et al. 2008).
We observed these GCs between September 2005 and July 2006, using the mid-IR camera IRAC, onboard the Spitzer Space Telescope. A frame time of 12 s and a 25–30 cycling position dithering pattern with the small scale factor, repeated a few times for on-source integration times between 1000 s and 2700 s, and total observing time between 1.1 h and 2.05 h, allowed us to cover a 5′ × 5′ field of view in all the four IRAC channels, at 3.6, 4.5, 5.8, and 8.0 μm. Figure 1 shows the three color (3.6 μm (blue), 6 μm (green), 8 μm (red)) mosaicked images for the 15 observed GCs.
The [Post Basic Calibrated Data] mosaic frames from the Spitzer Pipeline (Software Version: S13.2.0), with signal per pixel in unit of MJy sr-1, have been photometrically reduced with ROMAFOT (Buonanno et al. 1983), a software package optimized for point spread function (PSF) fitting in crowded and undersampled stellar fields.
We used a constant PSF over the entire IRAC field of view. Indeed, we verified that in all of our IRAC images the PSF is constant within ±2%. Such a small (if any) variation of the PSF has a negligible impact on the computed magnitudes (a few hundredths of a magnitude at most), well within the overall error budget of our Spitzer photometry (see Appendix A.3).
 |
Fig. 1 Spitzer-IRAC three color (3.6 μm (blue), 6 μm (green), 8 μm (red)) images of the 15 GCs in our sample. |
We converted the instrumental magnitudes of each star into the Vega magnitude system by using the zero-magnitude flux densities of Reach et al. (2005).
We obtained complementary ground-based near-IR photometry of the central region at higher, sub-arcsec spatial resolution at ESO, La Silla (Chile) and at the TNG for the southern and northern clusters, respectively. A detailed description of the observations can be found in Valenti et al. (2004a,b, 2007). Both instrumental magnitudes and star positions were placed into the Two Micron All Sky Survey (2MASS) system. Then we supplemented these photometric catalogs with 2MASS data in the most external regions. We cross-correlated the Spitzer-IRAC catalogs with the near-IR ones and we constructed a final catalog for each cluster, including stars with both near- and mid-IR photometry. The fact that the Spitzer-IRAC catalogs are combined with high-resolution near-IR stellar photometric catalogs, suitably cleaned by spurious detections and background sources/galaxies, also has the advantage of automatically excluding contamination by non stellar objects and/or IRAC instrumental artifacts from the final Spitzer-IRAC catalogs.
We corrected the IR magnitudes for extinction using the E(B − V) values reported in Table 1 and the Rieke & Lebofsky (1985) and Indebetouw et al. (2005) interstellar extinction laws.
3. Color–magnitude and color–color diagrams
The combination of near-IR and Spitzer-IRAC photometries allows for many effective diagnostic planes to search for stars with color excess, thus tracing the presence of dusty CS envelopes.
The 1–2.5 μm spectral range is especially suitable to measure the photospheric emission of cool stars. We computed suitable transformations between near-IR colors and bolometric corrections and effective temperatures as obtained from the Kurucz’s model spectra convolved with the 2MASS broad-band filters. Very similar transformations were obtained by Montegriffo et al. (1998) using a large database of observed colors for GC giants and suitable grids of different model atmospheres. In this respect, we note that old GC stars have age, distance, and reddening determined with great accuracy and consequently their mass and photospheric parameters can be constrained by using more robust calibrations than a mere spectral energy distribution fitting, as used for field stars. The (J − K) color is especially effective in sensing the temperature of low-mass RGB and AGB stars and these temperature estimates are in very good agreement (normally well within 100 K) with those obtained from other colors like the (V − K) or the (V − I). Bolometric corrections in the K-band are very effective for estimating the bolometric magnitude. Hence, for each star detected in our Spitzer-IRAC survey we derived the bolometric magnitude and temperature from its dereddened (J − K)0 color and MK absolute magnitude, by using the distance moduli by Ferraro et al. (1999a, 2000) and Valenti et al. (2007). The use of bolometric magnitudes allows for a direct comparison of color-magnitude diagrams (CMDs) from different GCs and also with model predictions.
 |
Fig. 2 Mbol, (K − 8)0 CMDs of the 15 GCs in our sample. The mean ridge lines centered at (K − 8)0 = 0 are also plotted (dashed lines). Stars with color excess are marked with black dots, candidate dusty AGB stars as triangles. |
 |
Fig. 3 (K − 5.8)0, (K − 8)0 CCDs of the 15 GCs in our sample. RGB stars with color excess are marked with black dots, while candidate dusty AGB stars with filled triangles. |
In very cool, luminous giants the 3–5 μm spectral range is still largely dominated by the photospheric emission. However, CS dusty envelopes can also radiate in this spectral range. Indeed, in relatively warm and low luminosity giants, like low-mass RGB stars, the fractional contribution of warm, optically thin dust emission from a CS envelope is not negligible in the 3–5 μm spectral range. Hence, as detailed in Origlia et al. (2010), a combination of near- and mid-IR colors like (K − 5.8) and (K − 8), is more effective in tracing the possible presence of small amounts of warm dust around low-mass RGB stars than the pure Spitzer-IRAC (3.6−8) color, which is mostly sensitive to detect relatively large amount of cold dust around the coolest (hence the most luminous) giants. Since the 8 μm IRAC band is the most sensitive to warm dust and the least contaminated by photospheric emission, we use the (K − 8)0 color as a primary diagnostic to select stars with possible dust excess.
We first constructed suitable Mbol, (K − 8)0 CMDs for the 15 GCs in our sample, reported in Fig. 2. The results are fully consistent with a vertical, ridge line centered at color (K − 8)0 ≈ 0. Indeed, small zero point shifts, if any (on average 0.00±0.04), with respect to a nominal value of zero were obtained. Although very small, we apply these offsets to the measured (K − 8)0 color of all the sampled stars in each GC, in order to consistently get the mean ridge line centered at (K − 8)0 = 0. This observational evidence is also predicted by models. In stars with no extra-flux, the 8 micron filter measures only the photospheric emission of the giants, and for example, theoretical model atmospheres from the Kurucz’s database in the temperature range Teff = 3500–5000 K predict (K − IRAC)0 colors ≈0.0 ± 0.1 along the entire RGB range sampled by our survey, which is down to Mbol ≈ 0.0 mag.
Once we established the mean ridge line in each CMD, we computed the color standard deviation (σ) for the stars on the blue side of the line (i.e., those with sure photospheric emission, only) in different magnitude bins. Based on this definition, stars on the red side are flagged as “dusty” if they show a (K − 8)0 color excess ≥+ 3σ from the mean ridge line. We note that these objects are the brightest at the Spitzer wavelengths and therefore, they have on average smaller photometric errors (see Appendix). These stars are also normally the reddest in the other IRAC bands, so as a secondary diagnostic tool we also use the (K − 5.8)0, (K − 8)0 color-color diagram (CCD) to confirm selection of dusty star candidates. As for the (K − 8)0 color, we also measured very small zero point offsets (on average −0.02 ± 0.04) for the (K − 5.8)0 color with respect to a nominal value of (K − 5.8)0 = 0. Figure 3 shows the (K − 5.8)0, (K − 8)0 CCDs for the 15 observed clusters.
Star counts from the photometric Spitzer-IRAC survey.
In both the CMDs and CCDs, we marked our final candidate RGB and AGB dusty stars with filled symbols. The method used to separate RGB from AGB stars is discussed in Sect. 4.
3.1. Mass-losing stars: previous identifications
The NGC 362, NGC 6388, and M 15 clusters were previously observed with ISOCAM by Origlia et al. (2002).
Three sources in NGC 362 were identified as having IR excess in our ISOCAM survey. McDonald & van Loon (2007) obtained VLT/UVES spectra for these three sources, which they designated as x01, x02, and x03. All three sources show Spitzer excess, but we only confirmed x03 as a genuine dusty giant, while x01 and x02 turn out to be complex blends of a few stars with moderate (if any) color excess.
Six sources in NGC 6388 were identified as having IR excess in our ISOCAM survey. All of these sources have also been detected by Spitzer and confirmed as dusty giants.
Two sources in M 15 were identified as having IR excess in ISOCAM survey. Both sources have been detected by Spitzer and confirmed as dusty stars. One of the ISO sources was also flagged as dusty by Boyer et al. (2006, their IR13).
Spitzer observations of M 15 and NGC 362 were analyzed by Boyer et al. (2006) and Boyer et al. (2009), respectively.
Boyer et al. (2006) found 23 dusty IR sources in M 15, but they suggested that these giants are mostly AGB and post-AGB stars. Twenty sources are also present in our catalog, while one (identified as IR4 by Boyer et al. 2006) is out of our field of view, and two (identified as IR3a and IR3b by Boyer et al. 2006) are too faint (both have K> 15). We classify only their IR13 source as a dusty RGB star, and we also detect the planetary nebula K648.
Boyer et al. (2009) find ten candidate mass-losing stars in NGC 362: they classify s02, s05, s06, s07, s08 as strong mass-loss candidates because are very bright and have strong excess; s01, s03, s04, s09, s10 are identified as moderate ML candidates. Their s02 and s10 sources are out of our field of view. Sources s05 and s08 appear to be one component with Spitzer, but our near-IR images reveal that they have two and three components, respectively (McDonald & van Loon 2007 also noted the multiple components of s05). Hence, we identify s05 and s08 as blends. Among the remaining six sources we only classified s01, s06, and s07 as dusty RGB stars.
4. Star counts, frequency of dusty stars, and ML timescales
By inspecting the observed CMDs of Fig. 2, one can clearly see that i) all GCs, also the most metal-poor ones, have giant stars with color excess; ii) in each GC only a fraction of giant stars show color excess and this fraction quickly decreases with luminosity1.
This observational evidence cannot be simply ascribed to the somewhat stochastic formation of dust, since it cannot explain the observed trend with luminosity in all GCs. A natural explanation of the star-to-star variation in IR-excess is that the ML process is somewhat episodic and operates only a fraction of the evolutionary time along the RGB and AGB. We also find that iii) dusty giants at lower luminosity are preferentially detected in GCs of higher metallicity. This is at least in part a matter of sensitivity. For a given CS envelope mass there is less dust to detect at low metallicity.
Recently, Groenewegen (2012) also found dust excess in relatively low-luminosity Population I giants down to Mbol ≈ − 1.3, which is well below the RGB tip.
The fractional number of giant stars with color excess is an important quantity. In fact, if the color excess is a signature of a dusty CS envelope due to ML, it can give an empirical estimate of the so-called duty cycle – the fraction of the evolutionary time along the RGB and AGB during which ML is active (see Sect. 4 of Origlia et al. 2007). To properly evaluate it one needs i) to separate RGB from AGB stars and ii) to correct observed star counts for possible incompleteness and field contamination.
The (K,J − K) plane is not a very effective means to well separate the AGB and RGB evolutionary sequences and identify the AGB stars. Hence, we used complementary high-resolution HST where available, and ground-based wide field photometry in the optical bands and we computed suitable CMDs in the V, (U − V), V, (B − V) and/or V, (V − I) planes, where the RGB and AGB sequences are better separated. References to the already published photometry are listed in Table 2. The photometric reduction of those datasets not published yet was carried out using DAOPHOTII/ALLSTAR (Stetson 1987, 1994). We also used the Clement et al. (2001) compilation to identify long period variable stars.
We estimated the completeness of our catalogs by making extensive use of artificial star tests. The degree of completeness of the near-IR photometric catalogs is always ≈100% over the full magnitude range covered by our Spitzer survey. On the contrary, the completeness of the Spitzer-IRAC photometric catalogs, which is dominated by non-dusty giants, is not 100%. It is normally >80% down to Mbol = − 1.5, with the exception of the very central 10″–20″ regions of the most concentrated clusters (NGC 6440, NGC 6441, NGC 6388) where it can drop down to ≤60%2. At fainter Mbol> − 1.5 mag, the degree of completeness depends on both crowding and distance and does not exceed ≈60% in most clusters.
To estimate the degree of possible field contamination, we used 2MASS and selected an annular region at a distance larger than the cluster tidal radii, typically at 20′ <r< 22′ around each cluster and counted the stars within the same color and magnitude range of the sampled Spitzer population. Field contamination is negligible in most clusters except in NGC 6388, NGC 6440, and NGC 6441 where it turns out to be ≈3%, ≈19% and ≈20% at Mbol ≤ − 1.5, and ≈5%, ≈32% and ≈27% at −1.5 <Mbol ≤ − 0.6, respectively.
We computed the fractional number f = ndusty/ntot defined as the number of candidate dusty stars divided by the total number of stars, as counted in the near-IR sample, in suitable luminosity bins, by correcting star counts for incompleteness and field contamination and separating RGB from AGB and LPV stars. To estimate the values of the episodic ML timescale, we use the fractional numbers f in each luminosity bin along the RGB and AGB, and we multiply them for the corresponding evolutionary time Δt. The evolutionary times are derived from canonical evolutionary tracks (Pietrinferni et al. 2006) for low-mass (0.8–0.9 M⊙) RGB stars at the metallicity most suited for each individual GC, Z ranging between 0.008 for the most metal-rich and 0.0003 for the most metal-poor. The total time ΔtML during which a star can lose mass is thus given by the simple formula 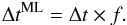 (1)The fractional numbers f of dusty RGB stars were computed in two suitable luminosity intervals, namely Mbol ≤ − 1.5 and −1.5 <Mbol ≤ − 0.6. These two bins correspond to approximately equal evolutionary times of 14 ± 1 Myr at all metallicities. We did not consider in this analysis fainter RGB stars, since only a few metal-rich giants show color excess, therefore star counts are more uncertain because of the intrinsic low number statistics, larger corrections for incompleteness, and lower photometric accuracy near the detection limit. The fractional numbers of dusty AGB stars apply only to the brightest luminosity bin at Mbol ≤ − 1.5, where most AGB stars have been detected. This luminosity bin corresponds to an evolutionary time of ≈4 Myr at all metallicities.
(1)The fractional numbers f of dusty RGB stars were computed in two suitable luminosity intervals, namely Mbol ≤ − 1.5 and −1.5 <Mbol ≤ − 0.6. These two bins correspond to approximately equal evolutionary times of 14 ± 1 Myr at all metallicities. We did not consider in this analysis fainter RGB stars, since only a few metal-rich giants show color excess, therefore star counts are more uncertain because of the intrinsic low number statistics, larger corrections for incompleteness, and lower photometric accuracy near the detection limit. The fractional numbers of dusty AGB stars apply only to the brightest luminosity bin at Mbol ≤ − 1.5, where most AGB stars have been detected. This luminosity bin corresponds to an evolutionary time of ≈4 Myr at all metallicities.
 |
Fig. 4 Fraction f of dusty RGB and AGB stars (left panels) and effective ML timescales (right panels) as a function of metallicity and for different magnitude bins (see Sect. 4 for details). Open circles refer to clusters with normal HB, filled circles to clusters with extended HB. Solid lines are best-fit relations. |
Our final observed numbers ndusty of dusty RGB and AGB stars as well as the fractional numbers f (corrected for incompleteness and field contamination) in each GC are reported in Table 2.
In the brightest luminosity bin such a fractional number varies from a few hundredths to a few tenths by increasing metallicity, while in the lower luminosity bin it can reach about one tenth in the most metal-rich clusters. The typical Poissonian error 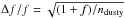 of the estimated fractional number ranges between 30% and 60%. The fractional numbers of dusty AGB stars at Mbol ≤ − 1.5 also increase with metallicity, ranging from ≈0.1 in the metal-poor GCs to ≈0.3 in the metal-rich ones with typical errors of 50%.
of the estimated fractional number ranges between 30% and 60%. The fractional numbers of dusty AGB stars at Mbol ≤ − 1.5 also increase with metallicity, ranging from ≈0.1 in the metal-poor GCs to ≈0.3 in the metal-rich ones with typical errors of 50%.
There is no significant trend between the fractional number of dusty giants and the cluster concentration (Harris 1996). Indeed, for a given metallicity range, very similar fractional numbers are measured in GCs with concentrations ranging from 1.5 to 2.5.
Figure 4 (left panels) shows the fractional numbers of dusty RGB and AGB stars in each GC of our sample for different magnitude bins and corresponding ML timescales (with typical uncertainty of ≤0.5 Myr). We also included the values for 47 Tuc (Origlia et al. 2007), as computed in the same magnitude bins. In the following, 47 Tuc has been classified as a metal-rich GC with normal HB. At Mbol< − 1.5 the inferred ML timescales (right panels of Fig. 4) for RGB stars increase by a factor of ≈6 (from ≈0.5 to ≈3 Myr) when increasing metallicity from [ Fe / H ] ≈ − 2.2 to [ Fe / H ] ≈ − 0.5, while for AGB stars the ML timescales increase only by a factor of ≈3 (from ≈0.5 to ≈1.5 Myr). At lower luminosities ML is only detectable around metal-rich RGB stars on a ≈1.5 Myr timescale. There are not appreciable differences in the inferred ML timescales between clusters with normal and extended HB.
5. Dust excess and ML rates
For the candidate dusty stars in each GC, ML rates can be estimated by properly modeling the circumstellar dust emission. To obtain the ML rates we use our modified version (Origlia et al. 2007) of the DUSTY code (Ivezić et al. 1999; Elitzur & Ivezić 2001) to compute the emerging spectrum and dust emission at the IRAC wavelengths. We adopt Kurucz model atmospheres for the heating source and assume the dust to be a mixture of warm silicates with an average grain radius a = 0.1 μm. We tested that slightly different choices for the dust properties have negligible impact in the resulting IRAC colors and ML rates. While radiation pressure acting on dust might plausibly drive winds in luminous, metal-rich red giants (Willson 2000), the GC stars are generally neither luminous nor metal rich enough for this mechanism to be efficient (Origlia et al. 2007; Groenewegen 2012). Hence, we run the DUSTY code under the general assumption of an expanding envelope at constant velocity vexp with a density profile η ∝ r-2, a dust temperature for the inner boundary rin of 1000 K and a shell outer boundary rout = 1000 × rin. The average rin value in the observed giants turns out to be ≈1014 cm, corresponding to tens of stellar radii. We then computed a large grid of DUSTY models with stellar temperatures in the 3500–5000 K range and optical depths at 8 μm (τ8) between 10-5 and 10-1. For each candidate star with dust excess, we enter the grid with its empirical stellar temperature (as derived from its (J − K)0 color, see Sect. 2) and (K − IRAC)0 colors, and we exit the grid with predictions for the dust optical depth, emerging flux, and envelope radius.
In the range of temperatures and colors shown by the giants sampled in our Spitzer survey, for a given input (K − 8)0 color, if the input photospheric temperature varies by 100K, the output opacity τ8 μm varies by 10% and the amount of dust by less than 5%. Hence, the input photospheric temperature is not a major critical parameter in the determination of the dust parameters, unless it is uncertain by more than several hundred degrees, which is normally never the case for GC giants.
As discussed in Origlia et al. (2007), the ML rates are computed by using the formula: 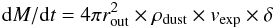 where
where 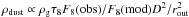 is the dust density, ρg = 3 g cm-3 is the grain density, F8 are the observed and model dust emission at 8 μm, D the GC distance, rout the envelope outer radius and δ the gas-to-dust ratio.
is the dust density, ρg = 3 g cm-3 is the grain density, F8 are the observed and model dust emission at 8 μm, D the GC distance, rout the envelope outer radius and δ the gas-to-dust ratio.
The vexp and δ quantities and especially their scaling with metallicity are somewhat free parameters. At variance, the linear density of dust mass 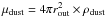 depends on observed quantities. Its absolute value also depends on the assumed individual grain density and overall circumstellar geometry, which, however, are normally considered independent of the metallicity of the central star. This is also the only working scenario that one can approach with the today’s knowledge of the field, given that we do not know whether and how dust and circumstellar envelope properties, especially around low-mass giants, may or may not change with metallicity.
depends on observed quantities. Its absolute value also depends on the assumed individual grain density and overall circumstellar geometry, which, however, are normally considered independent of the metallicity of the central star. This is also the only working scenario that one can approach with the today’s knowledge of the field, given that we do not know whether and how dust and circumstellar envelope properties, especially around low-mass giants, may or may not change with metallicity.
5.1. Dust ML
Figure 5 (bottom panel) shows the average μdust for the stars with Mbol< − 1.5 in each GC of our sample as a function of the cluster metallicity. We also included the value for 47 Tuc (Origlia et al. 2007), as computed in the same magnitude bin. The linear dust mass density increases by a factor of ≈3 by increasing metallicity from [Fe/H] = − 2.2 to [Fe/H] = − 0.5. By computing the ratio between μdust and ΔtML one can also get an estimate of the linear dust mass density rate and its behavior with varying metallicity (see Fig. 5, top panel). Such a rate decreases by a factor of ≈2 with increasing [Fe/H] from −2.2 to −0.5.
We derived these trends without any specific assumption on the metallicity dependence, hence they can be considered as an observational finding.
 |
Fig. 5 Average μdust (bottom panel) and the μdust/ΔtML ratio (top panel) for the stars with Mbol< − 1.5 in each GC as a function of the cluster metallicity. Open circles refer to clusters with normal HB, filled circles to clusters with extended HB. Solid lines are best-fit relations. |
5.2. Gas + dust ML rates: assumptions
If dust and gas are coupled and no mechanism preferentially removing one of the two components is at work, one should expect to get similar trends for total (gas + dust) ML rates and amount of mass lost with varying metallicity as observed for the dust alone. Hence, we can now attempt to compute total ML rates under reasonable assumptions for the gas-to-dust ratio and the expansion velocity of the envelope.
A lower limit to δ is given by 1 /Z (see, e.g., Leroy et al. 2007), where Z = (10[ M / H ] × Z⊙) is the global metallicity (see Table 1). A slower than 1/Z scaling for the gas-to-dust ratio would imply a concentration of metals higher in the envelope than in the photosphere, which is problematic unless for some reasons a large fraction of gas (hydrogen) is quickly escaping from the envelope while dust does not. At variance, a faster scaling is always possible but it will quickly raise the ML rates to prohibitive values at low metallicity, resulting in a total ML exceeding the stellar mass, which is unphysical.
As a reference zero point value for the gas-to-dust ratio we use δ0 ≈ 200 at the global metallicity (Z0 ≈ 0.005) of 47 Tuc, so δ = δ0 × Z0/Z.
This zero point value is also a somewhat lower limit, requiring that already ≈50% of the α-elements (O and Si in particular, among the main constituents of dust grains in these low-mass stars) available from the star atmosphere (and typically enhanced by a factor of 2−3 with respect to the iron abundance in GCs) condensate into dust once reaching the equilibrium radius at a distance of several tens/hundreds stellar radii. On the other hand, such a zero point value cannot be much higher (or equivalently the condensation fraction much lower than 50%), otherwise the total mass lost will quickly exceed the stellar mass.
In summary, both a faster than 1/Z scaling of the gas-to-dust ratio and/or a condensation fraction significantly lower than 50% would result in unphysically high ML. On the other hand, a slower than 1/Z scaling of the gas-to-dust ratio would result in an anomalously high (even higher than in the photosphere) concentration of metals in the envelopes of metal-poor stars. The condensation fraction of metals into dust grains cannot be much higher (a factor of 2 at most) than 50%, by definition.
Given that low-mass giants have very similar gravities, hence very similar escape velocities, regardless of their metallicity, for a given input energy the expansion velocity vexp of their circumstellar envelopes is expected to scale as δ-0.5 if dust and gas are coupled. Indeed, by increasing the number of gas particles (i.e., for higher value of δ), the momentum per particle (either gas or dust) is smaller, hence vexp decreases (Habing et al. 1994; van Loon 2000), independent of the nature of the input energy source. The alternative assumption of both a constant or increasing expansion velocity with decreasing metallicity would require a much higher input energy in metal-poor stars, which is possible, given also that such an energy source is unknown, but it would also quickly raise their ML to unphysically high values, exceeding the stellar mass.
As a reference zero point value for the expansion velocity, we adopt 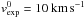 at the metallicity/gas-to-dust ratio of 47 Tuc, and we scale it accordingly to (δ0/δ)0.5. This gives values similar to typical expansion velocities measured in luminous, nearby giants (see, e.g., Netzer & Elitzur 1993; Schoeier & Olofsson 2001), which can range between a few and ≈20 km s-1. Very recently, Groenewegen (2014) detected rotational CO line emission in a nearby, low luminosity giant and measured an expansion velocity of 12 km s-1. Even in the most metal-poor stars where vexp ≈ 1 km s-1, vexp exceeds the sound speed. These envelope velocities are typically lower than the wind velocities derived from the measurements of chromospheric lines in field giants (see, e.g., Dupree et al. 2009), although such lines are better tracers of the region where wind forms and accelerates.
at the metallicity/gas-to-dust ratio of 47 Tuc, and we scale it accordingly to (δ0/δ)0.5. This gives values similar to typical expansion velocities measured in luminous, nearby giants (see, e.g., Netzer & Elitzur 1993; Schoeier & Olofsson 2001), which can range between a few and ≈20 km s-1. Very recently, Groenewegen (2014) detected rotational CO line emission in a nearby, low luminosity giant and measured an expansion velocity of 12 km s-1. Even in the most metal-poor stars where vexp ≈ 1 km s-1, vexp exceeds the sound speed. These envelope velocities are typically lower than the wind velocities derived from the measurements of chromospheric lines in field giants (see, e.g., Dupree et al. 2009), although such lines are better tracers of the region where wind forms and accelerates.
5.3. Gas + dust ML rates: results
Under the assumptions for the zero point values and trends with metallicity of the gas-to-dust ratio and expansion velocity discussed in Sect. 5.2, we can compute ML rates for RGB and AGB stars as a function of luminosity normalized using the Reimers parameter, (L∗/g∗R∗)⊙, where L∗, g∗, and R∗ are the stellar luminosity, gravity, and radius in solar units3.
Our best-fit empirical formulae for such ML rates in units of [M⊙ yr-1] are as follows. ![\begin{eqnarray*} ({\rm d}M/{\rm d}t)_{\rm RGB} &=& C \times 4.57 \times 10^{-10} \times (L_*/g_*R_*)_{\odot}^{0.43} \times f({\rm [Fe/H]}), \\ ({\rm d}M/{\rm d}t)_{\rm AGB} &=& C \times 2.24 \times 10^{-11} \times (L_*/g_*R_*)_{\odot}^{0.70} \times f({\rm [Fe/H]}), \end{eqnarray*}](/articles/aa/full_html/2014/04/aa23617-14/aa23617-14-eq143.png) where
where 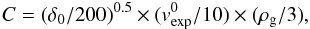 and
and ![\begin{eqnarray*} {f({\rm [Fe/H]}) = 10^{-0.25\times ({\rm [Fe/H]}+0.7)}}. \end{eqnarray*}](/articles/aa/full_html/2014/04/aa23617-14/aa23617-14-eq145.png) The rms uncertainty of these ML rate fitting formulae is ≈30%.
The rms uncertainty of these ML rate fitting formulae is ≈30%.
The ML rates increase with increasing luminosity and with decreasing metallicity. Our best-fit relations for RGB and AGB stars have shallower slopes with varying luminosity than the Reimers’ law ![\begin{eqnarray*} {{\rm d}M/{\rm d}t} = \eta_{\rm R} \times \, 4 \times 10^{-13} \times (L_*/g_*R_*)_{\odot} \qquad \left[\msun\,{\rm yr}^{-1}\right]. \end{eqnarray*}](/articles/aa/full_html/2014/04/aa23617-14/aa23617-14-eq146.png) The latter, however, can still fit our AGB ML rates at ≈2σ level of confidence.
The latter, however, can still fit our AGB ML rates at ≈2σ level of confidence.
The ML rates can be also conveniently computed as a function of bolometric magnitude and metallicity. Our best-fit formulae are as follows. ![\begin{eqnarray} \log_{10} ({\rm d}M/{\rm d}t)_{\rm RGB} &=& C' - 0.28 \times M_{\rm bol} - f'({\rm [Fe/H]}) - 8.00, \\ \log_{10} ({\rm d}M/{\rm d}t)_{\rm AGB} &=& C' - 0.40 \times M_{\rm bol} - f'({\rm [Fe/H]}) - 8.25, \end{eqnarray}](/articles/aa/full_html/2014/04/aa23617-14/aa23617-14-eq148.png) where
where 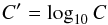 and
and ![\begin{eqnarray*} {f'({\rm [Fe/H]}) = 0.25\times ({\rm [Fe/H]}+0.7)}. \end{eqnarray*}](/articles/aa/full_html/2014/04/aa23617-14/aa23617-14-eq150.png) According to the inferred best-fit relations, ML rates (both in AGB and RGB) decrease by a factor of ≈2.6 with increasing [Fe/H] from −2.2 to −0.5. This factor is fully consistent with the factor of ≈2 obtained for the average linear mass density rates of the dust alone (mostly an observational finding).
According to the inferred best-fit relations, ML rates (both in AGB and RGB) decrease by a factor of ≈2.6 with increasing [Fe/H] from −2.2 to −0.5. This factor is fully consistent with the factor of ≈2 obtained for the average linear mass density rates of the dust alone (mostly an observational finding).
Such a similarity of trends seems to suggest that (i) the assumed scaling laws for the gas-to-dust ratio and expansion velocity with metallicity, based on common-sense/current-knowledge physics, are self-consistent with the assumption of gas and dust being coupled in the outflow of low-mass giants; and (ii) the modest anti-correlation between ML rates and metallicity is not a mere consequence of assumptions.
6. Total mass loss
Once rates and timescales at different stellar luminosity and metallicity are estimated, total ML at a given metallicity can be computed by integrating over the evolutionary time along the RGB and AGB.
By using the simple equation: 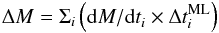 and multiplying the average ML rate by the ML timescale (see Eq. (1)) in each ith luminosity bin, we find the total ML on the RGB and AGB. For each GC, including 47 Tuc, average ML rates are computed by averaging the values obtained for the individual stars.
and multiplying the average ML rate by the ML timescale (see Eq. (1)) in each ith luminosity bin, we find the total ML on the RGB and AGB. For each GC, including 47 Tuc, average ML rates are computed by averaging the values obtained for the individual stars.
 |
Fig. 6 Total ML on RGB as a function of metallicity. For each GC, rates are computed by averaging the values of the single stars, duty cycles from the fitting relation. Only the two upper magnitude bins are used. Empty circles: GCs with normal HB. Filled circles: GCs with extended HB. Solid line: best-fit relation. |
Figure 6 shows total ML in RGB as a function of metallicity, summing the contribution of the two magnitude bins defined before, i.e. at Mbol< − 0.6 M⊙. In a similar fashion, Fig. 7 shows total ML in AGB as a function of metallicity at Mbol< − 1.5 M⊙.
The resulting fitting formulae are: ![\begin{eqnarray} ML^{\rm RGB} &=& 0.08 \times {\rm [Fe/H]} + 0.24 \pm 0.03~({\rm rms})\qquad [\msun], \\ ML^{\rm AGB} &=& 0.02 \times {\rm [Fe/H]} + 0.10 \pm 0.03~({\rm rms})\qquad [\msun]. \end{eqnarray}](/articles/aa/full_html/2014/04/aa23617-14/aa23617-14-eq155.png) If we separately fit clusters with normal and extended HB, we find fitting formulae with the same slope and minor (∓ 0.02) zero point variations.
If we separately fit clusters with normal and extended HB, we find fitting formulae with the same slope and minor (∓ 0.02) zero point variations.
 |
Fig. 7 Total ML on AGB as a function of metallicity. For each GC, rates are computed by averaging the values of the single stars, duty cycles from the fitting relation. Only the upper magnitude bin is used. Empty circles: GCs with normal HB. Filled circles: GCs with extended HB. Solid line: best-fit relation. |
If we compute the average ML rates by means of Eqs. (2), (3) instead of averaging the values of individual stars, we still obtain very similar fitting formulae within 1σ uncertainty.
It is interesting to note that the total amount of lost gas and dust increases by a factor of ≈3 with increasing [Fe/H] from −2.2 to −0.5 as in the case of the total amount of lost dust alone (see Sect. 5.1).
The inferred absolute values for the total ML are somewhat lower limits. Indeed, as mentioned in Sect. 5, we adopt a lower limit for the gas-to-dust ratio δ ∝ 1 /Z, and ML rates are proportional to 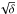 . Hence, if for example, we assume that δ ∝ 1 / (Z/ 2), the total ML would increase by
. Hence, if for example, we assume that δ ∝ 1 / (Z/ 2), the total ML would increase by 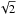 , i.e., by ≈40%. Moreover, although the bulk of the ML occurs in the brightest portion of the RGB, some ML can also occur at lower luminosities than those sampled by our Spitzer survey.
, i.e., by ≈40%. Moreover, although the bulk of the ML occurs in the brightest portion of the RGB, some ML can also occur at lower luminosities than those sampled by our Spitzer survey.
7. Discussion and conclusions
We have inspected the near- and mid-infrared color-magnitude and color-color diagrams of a carefully chosen sample of 15 Galactic GCs spanning the entire metallicity range from about one hundredth up to almost solar and, for a given metallicity, with different HB morphology.
All GCs, including the most metal-poor ones, have RGB and AGB giant stars with color excess, plausibly due to dust formation in mass flowing from them. Such dusty giants are detected down to Mbol ≤ − 1.5 at all metallicities and down to Mbol ≈ 0 in the most metal-rich GCs.
We find that the fractional number of giants stars with color excess increases toward higher luminosities and metallicities.
By modeling the mid-infrared color excess of our sample of GC giants, we are able to derive ML rates in a representative sample of Population II RGB and AGB stars with varying metallicity. At a given Mbol only a fraction of stars are losing mass4. From this, we conclude that the ML is episodic. The observed fraction of dusty giants gives the time that the ML is “on.” Combining this duty cycle with the ML rates yields the total ML. In the following subsections, we summarize our findings about ML and its possible dependence on the metallicity and HB morphology of the parent cluster.
7.1. Mass loss and metallicity
Our estimates of ML in Population II RGB stars indicate that ML depends only moderately on metallicity. Indeed, ML rates slowly decrease with increasing metallicity, while duty cycles more rapidly increase with increasing metallicity, with the net result that total ML moderately increases with increasing metallicity, about 0.08 M⊙ every dex in [Fe/H]. By using an indirect method based on the estimate of stellar masses on the HB, Gratton et al. (2010) find a similar dependence of total ML on metallicity.
The ML rates in Population II AGB stars show a similar dependence on metallicity as RGB stars, while duty cycles increase more slowly with it (see Sect. 4). We estimate ≤0.1 M⊙ of total ML on the AGB, nearly constant with varying metallicity.
The fact that ML rates in both Population II RGB and AGB stars seem to increase with decreasing metallicity, although rather slowly, would suggest that the outflow cannot be mainly driven by mechanisms involving opacity from metals.
7.2. Mass loss rates and HB morphology
The last generation of HST color-magnitude diagrams in the optical (see, e.g., Rich et al. 1997; Dotter et al. 2010) and UV (see, e.g., Ferraro et al. 1998; Dalessandro et al. 2013a,b) prove that the HB morphology of GCs is even more complex than previously believed and several 2nd parameters can be invoked (see, e.g., Rood 1973; Fusi Pecci & Renzini 1975, 1976; Renzini 1977; Fusi Pecci et al. 1993; D’Cruz et al. 1996; Catelan 2009; Dotter et al. 2010; Gratton et al. 2010). Some quantitative investigations of the HB morphology of the massive GCs NGC 2808, NGC 6388, and NGC 6441 HB, were recently performed (Busso et al. 2007; Dalessandro et al. 2008, 2011; Brown et al. 2010).
A significant population of blue, extreme blue, and blue hook HB stars (hereafter BHB, EHB and BHk, respectively) was found. For example, in the metal-intermediate GC NGC 2808 Dalessandro et al. (2011) account for 39% BHB, 11% EHB, and 9% BHk, while in the metal-rich GC NGC 6388 Dalessandro et al. (2008) account for 15% BHB, 2% EHB, and 2% BHk. In these GCs, HB models with normal He abundance (Y ≈ 0.24) and ML can account for red HB stars. On the contrary the hotter BHB and EHB could be explained by a higher He content. BHk stars are extremely hot HB stars with a significant spread in luminosity, likely due to a delayed, hot He-flash. It has been suggested that these stars could have experienced an enhanced ML during the RGB evolution (Cassisi et al. 2009; Moehler et al. 2007; Dalessandro et al. 2011), or alternatively, they could have an extremely large He content (Y> 0.5) (D’Antona & Caloi 2008) due to extra mixing processes undergone during their RGB phase.
In the following, we briefly explore whether and in which terms our results on ML could eventually provide additional constraints to these working scenarios.
We computed the ratio between the measured ML rates in each RGB star and the corresponding best-fit value or equivalently the difference of their logarithmic values. We then constructed global histograms of Δlog(ML rates) for metal-rich ([Fe/H] > − 1.0) and metal-intermediate/poor ([Fe/H] ≤ −1.0) clusters, grouped in two sub-samples, namely those with normal and extended HB, as shown in Fig. 8. The histograms of GCs with normal HBs have Gaussian dispersion σ ≈ 0.2 dex (rich) and σ ≈ 0.12 dex (metal-intermediate/poor). A larger dispersion of Δlog(ML rates) in metal-rich GCs is not surprising, given that these stars have a larger turnoff mass and a wider range of possible masses in the red part of the HB. The histograms of GCs with extended HBs have Gaussian dispersion similar to those of GCs with normal HBs, but have a tail (that is an excess of stars) toward higher ML rates.
 |
Fig. 8 Global histograms of Δ[log(ML rates)] (measured − bestfit) for metal-rich (left panel) and metal intermediate/poor (right panel) GCs, grouped in two subsamples, namely with normal (empty histograms) and extended (gray histograms) HB. |
 |
Fig. 9 Cumulative distributions of Δ[log(ML rates) (measured − bestfit) for metal-rich (gray lines) and metal intermediate/poor (black lines) GCs, grouped in two subsamples, namely with normal (solid lines) and extended (dashed lines) HB. |
Independent of metallicity, the bulk (>90%) of RGB stars in GCs with normal HB have rates within a factor of two from the average value. In GCs with extended HB about 15% of RGB stars have ML rates in excess by a factor of two (i.e., by 2–3σ) from the average value.
We also computed cumulative distributions Δ[log(ML rates)] for the ML rates, as shown in Fig. 9. The cumulative distribution of Δ[log(ML rates)] in metal-rich GCs with normal HB is more bent than the corresponding distribution for metal-intermediate/poor GCs, in agreement with the larger Gaussian dispersion. The cumulative distributions of Δ[log(ML rates)] in GCs with extended HB are also more bent (particularly for metal-poor GCs) and shifted toward higher ML rates, compared to those GCs with normal HBs. The KS-tests give probabilities of ≈5% (metal-rich) and <0.1% (metal-intermediate/poor) that normal and extended HB distributions be extracted from the same parent population.
By comparing the ≈15% estimated percentage of stars with ML rates in excess by a factor of two from the average values with the HB population ratios in NGC 6388 (metal-rich) and NGC 2808 (metal intermediate) reported above, we can speculate that: (1) metal-rich GC RGB stars with ML rates within a factor of two from the average value will probably evolve as red clump stars or moderate BHB, depending on their actual ML rate, duty cycle, and He content, while those with the highest ML rates will likely evolve as hot BHB, EHB, or BHs stars. It is also possible that those stars with extreme ML rates will move directly to the WD cooling sequence, without experiencing any He-flash; (2) metal-intermediate/poor GC RGB stars with ML rates within a factor of two from the average value can evolve either as red or BHB and EHB stars, depending on their actual ML rate, duty cycle, and He content. Those RGB stars with the highest ML rates (in excess by a factor of two from the average value) can be precursors of the hottest EHB and BHk stars.
In practice, for a given temperature on the HB, there can be a certain level of degeneracy between ML and He content, the two parameters being somehow anti-correlated. Indeed, according to evolutionary tracks (Pietrinferni et al. 2006) with normal and enhanced He content, for equal age and metallicity, a star with higher He content has a smaller Turnoff mass compared to a star with normal He, hence the former should need less ML than the latter to reach a given temperature on the HB.
Online material
Appendix A: Impact of crowding and photometric errors
In this section, we briefly discuss the major biases and sources of errors in our photometric analysis that could potentially affect the results.
Appendix A.1: Crowding and blending
Since the Spitzer-IRAC pixel size is relatively large (~1.2′′ pixel-1), it is possible that more than one star actually falls in it. Hence blending due to crowding is an obvious worry near cluster centers. However, as discussed in Origlia et al. (2010), our approach of combining the relatively low-resolution IRAC photometry with high-resolution near-IR photometry (in some cases also supported by HST photometry) has been designed to minimize this problem.
In fact, the most common cases of two relatively bright giants falling within the 8 μm PSF, thus potentially mimicking spurious dusty stars, should be easily identified in the higher resolution near-IR images. Hence, to avoid any spurious detection of color excess due to blend, for each candidate dusty star in the surveyed GCs, we directly inspected a 5″ × 5′′ high-resolution and deep K band sub-image centered on it. If we identified star(s) within the PSF and with comparable brightness (well within an order of magnitude, the exact value depending on their distance from the target) at 8 μm as well as in the K band (given that stars with pure photospheric emission have (K − 8)0 ≈ 0), the target star was rejected as a dusty candidate and not included in the final samples of dusty giants shown in Figs. 2 and 3. In addition, in a few suspect cases we performed the same procedure using HST images in the F814W band, as already done in Origlia et al. (2010). This provides the most solid evidence that the IR excess is not due to blends.
As stated in Sect. 4, we performed artificial star experiments to estimate the degree of completeness of our Spitzer and near-IR catalogs. These experiments have also been used to evaluate the fraction of expected blending due to crowding (either cluster or field stars), from a statistical approach. We found that this fraction is always below 5%, and in agreement with the values estimated by the direct inspection of high-resolution near-IR and HST images.
Appendix A.2: Unresolved background
We emphasize that the main source of background noise in the Spitzer images of our GCs is neither zodiacal light (also tabulated in the header of the fits images) nor unresolved galaxy emissions, but, as a matter of fact, unresolved stellar light (a few to several times the zodiacal light at 8 μm and fully dominant at shorter wavelengths). In the observed clusters, zodiacal light at 8 μm ranges between 4 and 8 el s-1 (i.e., between 5 and 10 MJy sr-1, in perfect agreement with the very recent estimates by Krick et al. 2012)5, while the unresolved stellar background ranges between 10 and 40 el s-1. These background levels correspond to Vega magnitudes ranging between 11.5 and 13.5 at 8 μm. The large majority of the stars sampled in our survey are still brighter than the background, especially those we target as candidate dusty stars, and only the lower RGB sequence in the most distant clusters is fainter than the unresolved background. However, even these fainter stars are always many times brighter than the background noise. The PSF fitting procedure we used (see Sect. 2) also provides a local estimate of the background level, hence possible contamination and local variations by diffuse light is accounted for and automatically subtracted from the computed instrumental magnitudes.
Appendix A.3: Photometric errors
To properly quantify the photometric errors, we define the S/N as the ratio between the signal of the star in el s-1 (background subtracted) and the square root of the total (star+background) signal in el s-1, multiplied by the square root of the on-source integration time (in sec). In all clusters, the faintest stars that we measured always have S/N> 15 and those with color excess always have S/N> 100 in all Spitzer bands. This implies that pure dust emission (which is always >30% of the total light at 8 μm) has always been detected at S/N> 30 and we can thus firmly exclude that the 8 μm flux in excess of the photospheric emission is due to background fluctuations. In summary, we obtain that random photometric errors of the stars we reliably measured are always less than 10% (i.e., <0.1 mag) in all Spitzer bands. Such relatively small random errors are not surprising, given that the final on-source integration time in each filter of our Spitzer observations has been quite long, ranging between 1000 and 2700 s. Our complementary near-IR photometry also has very small (typically <0.03 mag) random errors (see Valenti et al. 2004, 2004b, 2007 for details). Zero points calibrations in both the near-IR and Spitzer bands are uncertain by a few percent.
Appendix A.4: 47 Tuc: a test-bench target
An optimized photometric reduction and overall random errors well below <0.1 mag both in the near- and mid-IR bands are mandatory in order to safely detect small color excesses. A clear example of how large photometric uncertainties in both pass-bands can lead to misleading results is offered by the case of 47 Tuc. Indeed, our finding of dusty stars down to about the HB level Origlia et al. (2007, 2010) has been questioned by McDonald et al. (2011) and Momany et al. (2012). However, an accurate comparison of the datasets has shown that their claims were mostly a consequence of an insufficient accuracy of their near- and mid-IR photometry.
In fact, the photometry by McDonald et al. (2011) has larger photometric errors at any given magnitude than that presented in Origlia et al. (2010). Indeed, by comparing the CMDs in Figs. 1 and 2 of Origlia et al. (2010) with the CMDs in Fig. 12 of McDonald et al. (2011), one can clearly see that the color scatter in the latter is significantly larger than in the former. Moreover, McDonald et al. (2011) made an extensive use of 2MASS photometry in the inner region, which is less accurate and likely affected by blending because of its lower resolution than the data used by Origlia et al. (2007). In fact, by comparing the K-band and 8 μm photometry for a subsample of candidate dusty stars in common between Origlia et al. (2007) and McDonald et al. (2011, see their Fig. 13), one finds that 8 μm photometries differ by about +0.1 mag only, while K-band photometries differ by about −0.3 mag, implying average 0.2 mag = bluer (K − 8)0 colors for the dusty stars in McDonald et al. (2011). This indicates that the main discriminant between the two analyses is the K band, not the Spitzer photometry. The bluer K − 8 colors and the overall larger errors of McDonald et al. (2011) photometry largely prevent the detection of color excesses (a few tenths of a magnitude) as measured by Origlia et al. (2007).
Similar arguments apply to the Momany et al. (2012) photometric survey of 47 Tuc using the mid-IR imager VISIR at the VLT. While VISIR has an optimal, high spatial resolution, unfortunately its sensitivity is insufficient to probe small color excesses along the RGB in GCs. Indeed, Fig. 3 and Table 2 of Momany et al. (2012) show that about two magnitudes below the tip their photometric error rapidly increases from 0.1
up to 0.3 mag. Such errors are comparable with (at 1−2σ level) if not exceeding, the majority of color excesses measured by Origlia et al. (2007). This is not surprising, in fact even at an 8 m-class telescope and with the use of narrow band filters, the thermal background is still so high and variable that it is very difficult to obtain accurate, deep photometry from the ground (as required for this scientific goal) compared to a space facility like Spitzer.
There are very few candidate dusty stars in M 30, NGC 288, and NGC 6539. In particular, M 30 has a high central concentration but an intrinsic low luminosity; NGC 288 has a low central concentration and low intrinsic luminosity; finally, NGC 6539 has a relatively low central concentration. For all the three GCs the resulting CMDs and CCDs are poorly populated in the bright portion of the RGB. This prevented us from performing any quantitative analysis on their population of dusty stars and mass loss. Hence, these three GCs have not been used to derive ML timescales and rates.
The cluster centers have been estimated typically from IR photometric catalogs by adopting the procedure described in Montegriffo et al. (1995).
This evidence is in agreement with the consideration that it is impossible for a low-mass (≈ 0.8 M⊙) giant to lose mass at the estimated rates (see Sect. 5.3) during the entire time of its ascent of the RGB and AGB, simply because it would eject an amount of gas exceeding its total mass.
Acknowledgments
The authors dedicate this paper to the memory of Bob Rood, a pioneer scientist in the theory of low-mass star evolution, who inspired this work, and a friend, who sadly passed away on November 2nd, 2011. This research is part of the COSMIC-LAB (http://www.cosmic-lab.eu/Cosmic-Lab/Home.html) project funded by the European Research Council (under contract ERC-2010-AdG-267675).
References
- Boyer, M. L., Woodward, C. E., van Loon, J. T., et al. 2006, AJ, 132, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Boyer, M. L., McDonald, I., Loon, J. Th., et al. 2008, AJ, 135, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- Boyer, M. L., McDonald, I., van Loon, J. Th., et al. 2009, ApJ, 705, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Boyer, M. L., van Loon, J. Th., McDonald, I., et al. 2010, ApJ, 711, 99 [Google Scholar]
- Brown, T. M., Swigart, A. V., Lanz, T., et al. 2010, ApJ, 718, 1332 [NASA ADS] [CrossRef] [Google Scholar]
- Buonanno, R., Buscema, G., Corsi, C. E., Ferraro, I., & Iannicola, G. 1983, A&A, 126, 278 [NASA ADS] [Google Scholar]
- Busso, G., Cassisi, S., Piotto, G., et al. 2007, A&A, 474, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cacciari, C., & Freeman, K. C. 1983, ApJ, 268, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Cacciari, C., Bragaglia, A., Rossetti, E., et al. 2004, A&A, 413, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassisi, S., Salararis, M., Anderson, J., et al. 2009, ApJ. 702, 1530 [Google Scholar]
- Catelan, M. 2000, ApJ, 531, 826 [NASA ADS] [CrossRef] [Google Scholar]
- Catelan, M. 2009, Ap&SS, 320, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Clement, C. M., Muzzin, Ad., Dufton, Q., et al. 2001, AJ, 122, 2587 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G. 1976, ApJ, 203, 127 [Google Scholar]
- Dalessandro, E., Lanzoni, B., Ferraro, F. R., et al. 2008, ApJ, 677, 1069 [NASA ADS] [CrossRef] [Google Scholar]
- Dalessandro, E., Salaris, M., Ferraro, F. R., et al. 2011, MNRAS, 410, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Dalessandro, E., Salaris, M., Ferraro, F. R., Mucciarelli, A., & Cassisi, S. 2013a, MNRAS, 430, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Dalessandro, E., Ferraro, F. R., Massari, D., et al. 2013b, ApJ, 778, 135 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., & Caloi, V. 2008, MNRAS, 390, 693 [NASA ADS] [CrossRef] [Google Scholar]
- D’Cruz, N. L., Dorman, B., Rood, R. T., & O’Connell, R. W. 1996, ApJ, 466, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Sarajedini, A., Anderson, J., et al. 2010, ApJ, 708, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K. 1986, ARA&A, 24, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K., Hartmann, L., & Avrett, E. H. 1984, ApJ, 281, 37 [Google Scholar]
- Dupree, A. K., Sasselov, D. D., & Lester, J. B. 1992, ApJ, 387, 85 [Google Scholar]
- Dupree, A. K., Hartmann, L., Smith, G. H., et al. 1994, ApJ, 421, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K., Smith, G. H., & Strader, J. 2009, AJ, 138, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M., & Ivezić, Z. 2001, MNRAS, 327, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Paltrinieri, B., Fusi Pecci, F., et al. 1997, ApJ, 484, 145 [Google Scholar]
- Ferraro, F. R., Paltrinieri, B., Pecci, F. F., Rood, R. T., & Dorman, B. 1998, ApJ, 500, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Messineo, M., Fusi Pecci, F., et al. 1999a, AJ, 118, 1738 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Paltrinieri, B., Rood, R. T., & Dorman, B. 1999b, ApJ, 522, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Montegriffo, P., Origlia, L., & Fusi Pecci, F. 2000, AJ, 119, 1282 [NASA ADS] [CrossRef] [Google Scholar]
- Frogel, J. A., & Elias, J. H. 1988, ApJ, 324, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Fusi Pecci, F., & Renzini, A. 1975, A&A, 39, 413 [NASA ADS] [Google Scholar]
- Fusi Pecci, F., & Renzini, A. 1976, A&A, 46, 447 [NASA ADS] [Google Scholar]
- Fusi Pecci, F., Ferraro, F. R., Bellazzini, M., et al. 1993, AJ, 105, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Gillet, F. C., de Jong, T., Neugebauer, G., Rice, W. L., & Emerson, J. P. 1988, AJ, 96, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Goldberg, L. 1979, QJRAS, 20, 361 [Google Scholar]
- Gratton, R. G. 1983, ApJ, 264, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Pilachowski, C. A., & Sneden, C. 1984, A&A, 132, 11 [NASA ADS] [Google Scholar]
- Gratton, R., Carretta, E., Bragaglia, A., Lucatello, S., & d’Orazi, V. 2010, A&A, 517, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2012, A&A, 540, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2014, A&A, 561, A11 [Google Scholar]
- Habing, H. J., Tignon, J., & Tielens, A. G. G. M. 1994, A&A, 286, 523 [NASA ADS] [Google Scholar]
- Hansen, B. M. S. 2005, ApJ, 635, 526 [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Indebetouw, R., Mathis, J. S.,Babler, B. L., Meade, M. R., & Watson, C. 2005 [Google Scholar]
- Ivezić, Z., Nenkova, M., & Elitzur, M. 1999, User Manual for DUSTY (Lexington: Univ. Kentucky) [Google Scholar]
- Judge, P. G., & Stencel, R. E. 1991, ApJ, 371, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Kalirai, J. S., Bergeron, P., Hansen, Brad, M. S., et al. 2007, ApJ, 671, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Krick, J. E., Glaccum, W. J., Carey, S. J., et al. 2012, ApJ, 754, 53 [Google Scholar]
- Leroy, A., Bolatto, A., Stanimirovic, S., et al. 2007, ApJ, 658, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Lyons, M. A., Kemp, S. N., Bates, B., & Shaw, C. R. 1996, MNRAS, 280, 835 [NASA ADS] [Google Scholar]
- Mauas, P. J. D., Cacciari, C., & Pasquini, L. 2006, A&A, 454, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McDonald, I., & van Loon, J. Th. 2007 A&A, 476, 1261 [Google Scholar]
- McDonald, I., Boyer, M. L., van Loon, J. Th., et al. 2011, ApJS, 193, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Moehler, S., Dreizler, S., Lanz, T., et al. 2007, A&A, 475, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Momany, Y. A., Saviane, I., Smette, A., et al. 2012, A&A, 537, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montegriffo, P., Ferraro, F. R., Fusi Pecci, F., & Origlia, L. 1995, MNRAS, 276, 739 [NASA ADS] [Google Scholar]
- Montegriffo, P., Ferraro, F. R., Fusi Pecci, F., & Origlia, L. 1998, MNRAS, 297, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Mullan, D. J. 1978, ApJ, 226, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, N., & Elitzur, M. 1993, ApJ, 410, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Ferraro, F. R., & Fusi Pecci, F. 1996, MNRAS, 280, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Ferraro, F. R., Fusi Pecci, F., & Rood, R. T. 2002, ApJ, 571, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Valenti, E., Rich, R. M., & Ferraro, F. R. 2005 MNRAS, 363, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Rood, R. T., Fabbri, S., et al. 2007, ApJ, 667, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Valenti, E., & Rich, R. M. 2008, MNRAS, 388, 1419 [NASA ADS] [Google Scholar]
- Origlia, L., Rood, R. T., Fabbri, S., et al. 2010, ApJ, 718, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, R. C. 1981, ApJ, 248, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, R. C. 1982, ApJ, 258, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., King, I. R., Djorgovski, S. G., et al. 2002, A&A, 391, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pritzl, B. J., Smith, H. A., Catelan, M., & Sweigart, A. V. 2001, AJ, 122, 2600 [NASA ADS] [CrossRef] [Google Scholar]
- Pritzl, B. J., Smith, H. A., Catelan, M., & Sweigart, A. V. 2002, Observed HR Diagrams and Stellar Evolution, ASP Conf. Proc., eds. T. Lejeune, & J. Fernandez, 274, 335 [Google Scholar]
- Pritzl, B. J., Smith, H. A., Stetson, P. B., et al. 2003, AJ, 126, 1381 [NASA ADS] [CrossRef] [Google Scholar]
- Ramdani, A., & Jorissen, A. 2001, A&A, 372, 8 [Google Scholar]
- Reach, W. T., Megeath, S. T., Cohen, M., et al. 2005, PASP, 117, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers D. 1975a, in Problems in Stellar Atmospheres and Envelopes, eds. B. Baschek, W. H. Kegel, & G. Traving (Berlin: Springer), 229 [Google Scholar]
- Reimers D. 1975b, in Mem. Soc. R. Sci. Liège 6 Ser., 8, 369 [Google Scholar]
- Renzini, A. 1977, in Advanced Stages of Stellar Evolution, eds. P. Bouvier, & A. Maeder (Geneva: Geneva Obs.), 151 [Google Scholar]
- Rich, M. R., Sosin, C., Djorgovski, S. G., et al. 1997, ApJ, 484, 25 [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Rood, R. T. 1973, ApJ, 184, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbi, E., Ferraro, F. R., Sills, A., & Rood, R. T. 2004, ApJ, 617, 1296 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Chieffi, A., & Straniero, O. 1993, ApJ, 414, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Schoeier, F. L., & Olofsson, H. 2001, A&A, 368, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schröder, K.-P., & Cuntz, M. 2005, ApJ, 630, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. H., Dupree, A. K., Strader, J. 2004, PASP, 116, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1994, PASP, 106, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, E., Ferraro, F. R., & Origlia, L. 2004a, MNRAS, 351, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, E., Ferraro, F. R., & Origlia, L. 2004b, MNRAS, 354, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, E., Ferraro, F. R., & Origlia, L. 2007, AJ, 133, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J. T. 2000, A&A, 354, 125 [NASA ADS] [Google Scholar]
- Vieytes, M., Mauas, P., Cacciari, C., Origlia, L., & Pancino, E. 2011, A&A, 526, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willson, L. A. 2000, ARA&A, 38, 573 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Spitzer-IRAC three color (3.6 μm (blue), 6 μm (green), 8 μm (red)) images of the 15 GCs in our sample. |
| In the text | |
 |
Fig. 2 Mbol, (K − 8)0 CMDs of the 15 GCs in our sample. The mean ridge lines centered at (K − 8)0 = 0 are also plotted (dashed lines). Stars with color excess are marked with black dots, candidate dusty AGB stars as triangles. |
| In the text | |
 |
Fig. 3 (K − 5.8)0, (K − 8)0 CCDs of the 15 GCs in our sample. RGB stars with color excess are marked with black dots, while candidate dusty AGB stars with filled triangles. |
| In the text | |
 |
Fig. 4 Fraction f of dusty RGB and AGB stars (left panels) and effective ML timescales (right panels) as a function of metallicity and for different magnitude bins (see Sect. 4 for details). Open circles refer to clusters with normal HB, filled circles to clusters with extended HB. Solid lines are best-fit relations. |
| In the text | |
 |
Fig. 5 Average μdust (bottom panel) and the μdust/ΔtML ratio (top panel) for the stars with Mbol< − 1.5 in each GC as a function of the cluster metallicity. Open circles refer to clusters with normal HB, filled circles to clusters with extended HB. Solid lines are best-fit relations. |
| In the text | |
 |
Fig. 6 Total ML on RGB as a function of metallicity. For each GC, rates are computed by averaging the values of the single stars, duty cycles from the fitting relation. Only the two upper magnitude bins are used. Empty circles: GCs with normal HB. Filled circles: GCs with extended HB. Solid line: best-fit relation. |
| In the text | |
 |
Fig. 7 Total ML on AGB as a function of metallicity. For each GC, rates are computed by averaging the values of the single stars, duty cycles from the fitting relation. Only the upper magnitude bin is used. Empty circles: GCs with normal HB. Filled circles: GCs with extended HB. Solid line: best-fit relation. |
| In the text | |
 |
Fig. 8 Global histograms of Δ[log(ML rates)] (measured − bestfit) for metal-rich (left panel) and metal intermediate/poor (right panel) GCs, grouped in two subsamples, namely with normal (empty histograms) and extended (gray histograms) HB. |
| In the text | |
 |
Fig. 9 Cumulative distributions of Δ[log(ML rates) (measured − bestfit) for metal-rich (gray lines) and metal intermediate/poor (black lines) GCs, grouped in two subsamples, namely with normal (solid lines) and extended (dashed lines) HB. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


