| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 11 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201323163 | |
| Published online | 31 March 2014 | |
Calculations with spectroscopic accuracy: energies, transition rates, and Landé gJ-factors in the carbon isoelectronic sequence from Ar XIII to Zn XXV⋆,⋆⋆
1 Materials Science and Applied Mathematics, Malmö University, 21120 Malmö, Sweden
e-mail: jorgen.ekman@mah.se
2 Vilnius University, Institute of Theoretical Physics and Astronomy, A. Goštauto 12, 01108, Vilnius, Lithuania
3 Chimie Quantique et Photophysique, CP160/09, Université Libre de Bruxelles, Av. F.D. Roosevelt 50, 1050 Brussels, Belgium
4 Department of Electrical Engineering and Computer Science, Box 1679B, Vanderbilt University, TN 37235, USA
Received: 1 December 2013
Accepted: 5 February 2014
Extensive self-consistent multiconfiguration Dirac-Hartree-Fock (MCDHF) calculations and subsequent relativistic configuration interaction calculations are performed for 262 states belonging to the 15 configurations 2s22p2, 2s2p3, 2p4, 2s22p3l, 2s2p23l, 2p33l and 2s22p4l(l = 0,1,2) in selected carbon-like ions from Ar XIII to Zn XXV. Electron correlation effects are accounted for through large configuration state function expansions. Calculated energy levels are compared with existing theoretical calculations and data from the Chianti and NIST databases. In addition, Landé gJ-factors and radiative electric dipole transition rates are given for all ions. The accuracy of the calculations are high enough to facilitate the identification of observed spectral lines.
Key words: atomic data
Research supported in part by the Swedish Research council, Swedish Institute and by the IUAP-Belgian State Science Policy (BriX network P7/12).
Tables of energy levels and transition rates (Tables 3−22) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/564/A24
© ESO, 2014
1. Introduction
The observation of emission lines from carbon-like ions in spectra consitutes an important tool for diagnostics of astrophysical and fusion plasmas. For instance, lines in Fe XXI are strong candidates for spectral diagnostics of solar flares observed with the Solar Dynamics Obervatory (Del Zanna et al. 2013) where the transitions between the lowest configurations, 2s22p2 and 2s2p3, are found in the wavelength region 100−150 Å. Ratios of these lines are used as density probes. Depending on the plasma density and the blending lines from other species in the spectrum of the source studied, different lines must be used. Transitions between the 2s22p2 and 2s22p3d configurations appear in the region around 12 Å. These lines are closely spaced, and higher resolution observations are required to avoid blended lines. On the other hand, the line ratios are less sensitive to instrumental response. A third group of lines are the M1 transitions within the ground configuration, 2s22p2, with terms 3P, 1D, and 1S. The transitions within the 3P term appear at 1380 Å and 2295 Å, whereas lines from the singlet levels have shorter wavelengths, 300−800 Å. The triplet lines are excellent for electron density, ne, diagnostics in the range 1011−1013 cm-3, typical solar flare conditions. The singlet levels reach Boltzmann equilibrium at higher densities and the corresponding lines can be used for densities up to 1015 cm-3. The lines are thus ideal for tokamak conditions (Mason et al. 1979).
To interpret observed spectra, knowledge of accurate transition parameters such as transition rates is necessary. Previously a plethora of theoretical calculations and a few experimental studies on carbon-like systems have been made. A lot of work has been devoted to describe autoionization states in the isoelectronic sequence. Using the HFR (Cowan 1981) and AUTOSTRUCTURE (Eissner et al. 1974; Badnell 1986, 1997) atomic structure codes, Palmeri et al. (2008) reported calculations on K-vacancy level energies and transition rates for carbon-like Ne, Mg, Si, S, Ar and Ca ions. Autoionization- and radiative transition rates for carbon-like ions with 6 ≤ Z ≤ 54 have been calculated by Safronova et al. (1999) using the 1/Z pertubation theory method and by Chen et al. (1997) with the multiconfiguration Dirac-Hartree-Fock (MCDHF) approach. Other publications report on transition and energy level data below the first ionization limit. For example, oscillator strengths have been calculated for transions between F IV and Ar XIII and between Ar XIII and Mn XX (Aggarwal et al. 2001, 2003, 2005). Transition energies and probabilities for Ar XIII from MCDHF calculations have been reported by Costa et al. (2001). Calculated energy levels and oscillator strengths in Ti XVII and Ni XXIII have been reported in Hu et al. (2011a) and Hu et al. (2011b), respectively. In addition, intercombination transitions for a wide range of ions in the C-like sequence between the 2s22p2 3P1,2 and 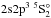 levels have been calculated by Liu et al. (2013) and observed spin-forbidden lines in the 500 − 1600 Å range emitted by solar coronal plasmas have been compiled and improved energy levels have been deduced by Feldman et al. (2007). However, the extensive calculations on 2l → 3l′ transitions in L-shell Fe and Ni ions by Gu (2005a) are so far the most accurate reported in the sequence, when compared with observed level energies. In these calculations a combined configuration interaction and relativistic many-body pertubation theory (RMBPT) approach was used. Later work by the same author has been extended to include higher-n energies and transitions (Gu 2005b, 2007).
levels have been calculated by Liu et al. (2013) and observed spin-forbidden lines in the 500 − 1600 Å range emitted by solar coronal plasmas have been compiled and improved energy levels have been deduced by Feldman et al. (2007). However, the extensive calculations on 2l → 3l′ transitions in L-shell Fe and Ni ions by Gu (2005a) are so far the most accurate reported in the sequence, when compared with observed level energies. In these calculations a combined configuration interaction and relativistic many-body pertubation theory (RMBPT) approach was used. Later work by the same author has been extended to include higher-n energies and transitions (Gu 2005b, 2007).
The present work aims at improving and extending the calculations by Gu, providing data of spectroscopic accuracy for a number of ions in the carbon-like sequence. In this context spectroscopic accuracy is related to the notion of calculated transition energies that are accurate enough to directly confirm or revise experimental identifications. In addition, the calculations also serve as benchmarks for other theoretical works (Jönsson et al. 2013b).
2. Multiconfiguration Dirac-Hartree-Fock
In the relativistic MCDHF method a natural starting point is the Dirac-Coloumb Hamiltonian. Using Hartree atomic units and subtracting the electron rest mass the latter is given by 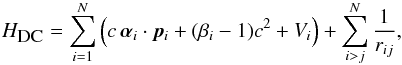 (1)where Vi is the monopole part of the electron-nucleus interaction, rij the distance between electrons i and j, and α and β are the Dirac matrices. The atomic state functions Ψ(γPJ) are expanded in terms of configuration state functions (CSFs), Φ(γjPJ), with appropriate J symmetry and parity P, namely
(1)where Vi is the monopole part of the electron-nucleus interaction, rij the distance between electrons i and j, and α and β are the Dirac matrices. The atomic state functions Ψ(γPJ) are expanded in terms of configuration state functions (CSFs), Φ(γjPJ), with appropriate J symmetry and parity P, namely 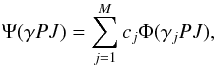 (2)where γj represents the configuration and other quantum numbers needed to uniquely specify the state j. The CSFs are built from products of one-electron Dirac orbitals. The radial parts of the latter and the expansion coefficients cj of the multiconfiguration expansion (2) are obtained in the relativistic self-consistent field (RSCF) procedure (Grant 2007). The Breit interaction
(2)where γj represents the configuration and other quantum numbers needed to uniquely specify the state j. The CSFs are built from products of one-electron Dirac orbitals. The radial parts of the latter and the expansion coefficients cj of the multiconfiguration expansion (2) are obtained in the relativistic self-consistent field (RSCF) procedure (Grant 2007). The Breit interaction ![\begin{eqnarray} \label{eq:Breit} H_{\mbox{{\footnotesize Breit}}} & = & - \sum_{i<j}^N \left[ \bm{\alpha}_{i} \cdot \bm{\alpha}_{j}\frac{ \cos(\omega_{ij} r_{ij}/c)}{r_{ij}} \right. \nonumber \\ & & + \left. (\bm{\alpha}_{i} \cdot \bm{\nabla}_i ) (\bm{\alpha}_{j} \cdot \bm{\nabla}_j )\frac{ \cos(\omega_{ij}r_{ij}/c) -1}{\omega_{ij}^2 r_{ij}/c^2} \right] \end{eqnarray}](/articles/aa/full_html/2014/04/aa23163-13/aa23163-13-eq41.png) (3)as well as leading quantum electrodynamic (QED) corrections can be included in subsequent relativistic configuration interaction (RCI) calculations (McKenzie et al. 1980). Calculations can be done for single levels, but also for portions of a spectrum in the extended optimal level (EOL) scheme, where optimization is applied on a weighted sum of energies (Dyall et al. 1989). All calculations were performed with a new release (Jönsson et al. 2013a) of the GRASP2K code (Jönsson et al. 2007).
(3)as well as leading quantum electrodynamic (QED) corrections can be included in subsequent relativistic configuration interaction (RCI) calculations (McKenzie et al. 1980). Calculations can be done for single levels, but also for portions of a spectrum in the extended optimal level (EOL) scheme, where optimization is applied on a weighted sum of energies (Dyall et al. 1989). All calculations were performed with a new release (Jönsson et al. 2013a) of the GRASP2K code (Jönsson et al. 2007).
3. Computation of Landé gJ-factors and transition parameters
Given a set of atomic state functions, measurable properties whose operators are expressed in tensor form, T(k), can be obtained as reduced matrix elements, 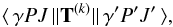 (4)which, after inserting the CSF expansions, reduce to a sum over matrix elements between CSFs. Using Racah algebra techniques these matrix elements are finally obtained as sums over radial integrals (Gaigalas et al. 2001).
(4)which, after inserting the CSF expansions, reduce to a sum over matrix elements between CSFs. Using Racah algebra techniques these matrix elements are finally obtained as sums over radial integrals (Gaigalas et al. 2001).
3.1. Landé gJ-factors
Under the influence of an external magnetic field, the Landé gJ-factors describe the first-order magnitude of the splitting of atomic levels into magnetic sub-levels of an atom (or ion). Moreover they provide information about the coupling in the system (Froese Fischer & Jönsson 2001). The gJ-factors are given by ![\begin{eqnarray} g_J &=& \frac{2}{\sqrt{J(J+1)}}\nonumber\\ && \times \left\langle {\mathit \gamma} PJ \left\|\sum_{j=1}^N \left[ -{\rm i} \frac{c^2}{\sqrt{2}} \, r_j \left( {\boldsymbol \alpha}_j\, {\bf C}^{(1)}(j) \right)^{(1)} + \frac{g_s-2}{2} \beta_j {\boldsymbol \Sigma}_j \right] \right\| {\mathit \gamma} PJ \right\rangle, \end{eqnarray}](/articles/aa/full_html/2014/04/aa23163-13/aa23163-13-eq44.png) (5)where
(5)where 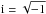 is the imaginary unit, Σj is the relativistic spin-matrix and gs = 2.00232 is the QED-corrected g-factor of the electron spin. The gJ-factors were calculated using the Zeeman module of GRASP2K (Andersson & Jönsson 2008).
is the imaginary unit, Σj is the relativistic spin-matrix and gs = 2.00232 is the QED-corrected g-factor of the electron spin. The gJ-factors were calculated using the Zeeman module of GRASP2K (Andersson & Jönsson 2008).
In the context of astrophysics it should be pointed out that strong magnetic fields have been detected in hot [O, B, and A] stars (Petit 2011). The magnetic field strength is of the order of several tens of kG. The study of these magnetic fields in stars requires accurate Landé gJ-factors.
3.2. Transition parameters
The transition rates for electric dipole transitions between atomic states γPJ and γ′P′J′ can be expressed in terms of reduced matrix elements 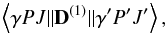 (6)where D(1) is the electromagnetic dipole operator in length (Babushkin) or velocity (Coulomb) gauge (Grant 1974). Using standard techniques the reduced matrix elements can be derived under the assumption that the atomic state functions are built from the same orthogonal radial orbital set (Gaigalas et al. 2001). However, this restriction can be relaxed and when two atomic state functions are described by independently optimized orbital sets, transformations of the atomic state functions are performed in such a way that the orbital sets become biorthogonal, in which case the calculation can proceed using standard Racah algebra (Olsen et al. 1995; Jönsson & Froese Fischer 1998).
(6)where D(1) is the electromagnetic dipole operator in length (Babushkin) or velocity (Coulomb) gauge (Grant 1974). Using standard techniques the reduced matrix elements can be derived under the assumption that the atomic state functions are built from the same orthogonal radial orbital set (Gaigalas et al. 2001). However, this restriction can be relaxed and when two atomic state functions are described by independently optimized orbital sets, transformations of the atomic state functions are performed in such a way that the orbital sets become biorthogonal, in which case the calculation can proceed using standard Racah algebra (Olsen et al. 1995; Jönsson & Froese Fischer 1998).
4. Calculations
The 7 even parity 2s22p2, 2p4, 2s22p3p, 2s2p23s, 2s2p23d, 2p33p and 2s22p4p configurations and the 8 odd parity 2s2p3, 2s22p3s, 2s22p3d, 2s2p23p, 2p33s, 2p33d, 2s22p4s and 2s22p4d configurations were chosen as reference configurations. Two MCDHF calculations in the EOL scheme were performed as a starting point: one calculation describing the 130 even parity levels and another the 132 odd parity levels with CSFs obtained from single- and double- (SD) excitations from all occupied orbitals of the odd and even parity reference configurations, respectively, to active sets {4s3p2d } (4 s-orbitals, 3 p-orbitals, and 2 d-orbitals). To account for electron correlation these calculations were followed by a series of calculations where the active sets were consecutively enlarged, layer by layer, by adding one orbital for each l up to {9s8p7d5f5g3h }. For the last three layers, the SD excitations from the outer orbitals of the reference configurations were included, keeping 1s orbital closed. In the process the calculated properties were carefully monitored to ensure that a satisfactory convergence was obtained. These calculations were followed by final RCI calculations, one for each parity, where SD excitations were allowed from all orbitals of the reference configurations to the largest active sets {9s8p7d5f5g3h } and with QED- and Breit contributions taken into account. The resulting expansions consisted of 1 633 000 and 1 703 000 CSFs distributed over the J = 0,1,...,5 angular symmetries for even and odd parity, respectively.
4.1. Labeling of states
The wave functions are given as expansions over jj-coupled CSFs. However, in the jj-coupling scheme the states are often not well described and in the expansions, many CSFs may have nearly the same weight. In this work we used a module in the latest release of the GRASP2K code (Jönsson et al. 2013a) to transform from jj- to LS-coupling and to obtain the leading LS-percentage composition. In general, this gives a good consistency with the labeling system used by the experimentalists as well as with the NIST database and other sources. It should be noted that also in LS-coupling, although to a less extent, different states sometimes share the same configuration and shell-coupling, as the leading component in the LS-percentage eigenvector composition. For these states an extended, but still truncated, composition can be used as the label.
5. Results and discussion
Figure 1 shows the gross structure of the calculated energy levels for ions in the carbon isoelectronic sequence. It is seen that the energy levels are clearly divided in two parts. The lower part consists of levels originating from the even parity 2s22p2 and 2p4 configurations and the odd parity 2s2p3 configuration whereas the upper part consists of configurations of both parities that include one electron in either the n = 3 or n = 4 shell.
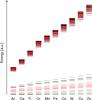 |
Fig. 1 Gross structure of calculated energy levels in the carbon isoelectronic sequence. Levels for odd parity states are colored red whereas levels for even parity states are displayed in black. Level energies are shown to scale, but given in arbitrary units. |
In terms of experimental work and accurate calculations, Fe XXI is currently the most studied ion in the carbon isoelectronic sequence so far. Therefore results from the present calculations are validated against experimental data and other theoretical predictions for this system. In Table 1 level energies for Fe XXI from calculations in this work are compared with calculated energies from a previous MCDHF/RCI calculation (RCI2) by Jönsson et al. (2011), relativistic many-body pertubation theory (RMBPT) by Gu (2005a) and from a calculation using the Flexible Atomic Code (FAC) by Landi & Gu (2006). Collected in Table 1 are also observed experimental level energies from NIST (NIST Atomic Spectra Database 2013) and Chianti (Landi et al. 2012) databases. Observed levels from the NIST database are from Sugar & Corliss (1985) and observed levels from the Chianti database are from Feldman et al. (2000); Martin et al. (1999); Brown et al. (2002); Landi & Phillips (2005). Whereas there is an excellent general agreement for the lower part (levels 1 − 20) between present calculations, calculations by Jönsson et al. (2011), Gu (2005a), and experimental data it is seen that Landi & Gu (2006) overestimated excitation energies significantly. These observations are manifested in a mean relative energy difference between calculations and observations of 0.028% − 0.032% for this work, 0.023% − 0.027% for RCI2, 0.035% − 0.038% for RMBPT and 0.641% − 0.646% for FAC, where lower (higher) values refer to experimental data from NIST (Chianti) databases. To quantify shifted absolute energy differences the mean level devation (MLD) according to 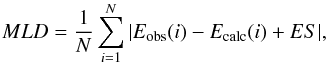 (7)was used. The energy shift (ES) is chosen as to minimize the sum and indicates to what extent the ground state level is favored (ES positive) or unfavored (ES negative) in the theoretical binding energy balance. The obtained MLD (ES) values for level 1 − 20 are 137 (130) cm-1 for this work, 141 (100) cm-1 for RCI2, 175 (215) cm-1 for RMBPT and 5017 (3800) cm-1 for FAC, where recommended NIST values where used as Eobs. Going beyond level 20 experimental observations are more scarce and the identification of levels becomes problematic in some cases. For example, the
(7)was used. The energy shift (ES) is chosen as to minimize the sum and indicates to what extent the ground state level is favored (ES positive) or unfavored (ES negative) in the theoretical binding energy balance. The obtained MLD (ES) values for level 1 − 20 are 137 (130) cm-1 for this work, 141 (100) cm-1 for RCI2, 175 (215) cm-1 for RMBPT and 5017 (3800) cm-1 for FAC, where recommended NIST values where used as Eobs. Going beyond level 20 experimental observations are more scarce and the identification of levels becomes problematic in some cases. For example, the 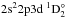 (8 098 000 cm-1),
(8 098 000 cm-1), 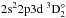 (8 187 400 cm-1) and
(8 187 400 cm-1) and 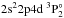 (10 548 000 cm-1) levels in the NIST database do not have any obvious counterparts in calculated energies or in the Chianti database. In addition, the
(10 548 000 cm-1) levels in the NIST database do not have any obvious counterparts in calculated energies or in the Chianti database. In addition, the 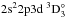 (8 195 000 cm-1) level (Sugar & Corliss 1985) from the NIST database is observed at a considerably lower energy (>30 000 cm-1) than in other sources and a misidentification cannot be ruled out. The agreement with observed energies from the Chianti database is better. In two cases (level 37 and 75) the leading LS terms in this work do not agree with the LS terms given in the Chianti database. However, for these levels significant term mixing is present and taking into account the second largest contribution in the LS-composition (see Table 9 at the CDS), identification is possible. Comparing with experimental data from the Chianti database, mean relative energy differences above level 20 are 0.050% for this work, 0.058% for RMBPT and 0.076% for FAC. A closer inspection of Table 1 reveals that the RMBPT energies above level 20 are on average predicted 800 cm-1 above the energies from the RCI calculation. RMBPT level energies in the lower part, below level 21, are also overpredicted, but to a less extent. The same observation was made in Jönsson et al. (2013b), where spectroscopic calculations were performed on boron-like Si using the same method as in the present work and compared with results from RMBPT calculations. All together it is fair to argue that the present RCI level energies reach spectroscopic accuracy and that the accuracy is better than for RMBPT calculated energies.
(8 195 000 cm-1) level (Sugar & Corliss 1985) from the NIST database is observed at a considerably lower energy (>30 000 cm-1) than in other sources and a misidentification cannot be ruled out. The agreement with observed energies from the Chianti database is better. In two cases (level 37 and 75) the leading LS terms in this work do not agree with the LS terms given in the Chianti database. However, for these levels significant term mixing is present and taking into account the second largest contribution in the LS-composition (see Table 9 at the CDS), identification is possible. Comparing with experimental data from the Chianti database, mean relative energy differences above level 20 are 0.050% for this work, 0.058% for RMBPT and 0.076% for FAC. A closer inspection of Table 1 reveals that the RMBPT energies above level 20 are on average predicted 800 cm-1 above the energies from the RCI calculation. RMBPT level energies in the lower part, below level 21, are also overpredicted, but to a less extent. The same observation was made in Jönsson et al. (2013b), where spectroscopic calculations were performed on boron-like Si using the same method as in the present work and compared with results from RMBPT calculations. All together it is fair to argue that the present RCI level energies reach spectroscopic accuracy and that the accuracy is better than for RMBPT calculated energies.
The material at the CDS also contain Landé gJ factors for all levels and ions considered. It is wortwhile to point out that in the presence of strong LS-mixing, the gJ factors differ substantially from what is obtained in the LS-coupling scheme. For example, the gJ-value obtained in this work for the highly mixed 2s22p3p 3P1:2 level in Fe XXI (level 29 in Table 9) is a factor of 2 larger than the corresponding value in the LS-scheme.
5.1. Transition rates
In Table 2 transition rates for transitions between levels in the 2s22p2, 2s2p3, and 2p4 configurations are shown. Transition rates from this work, A(RCI), are compared for Fe XXI with calculated rates from Landi & Gu (2006), A(FAC), and NIST Atomic Spectra Database (2013), A(NIST). The NIST recommended values are from Shirai et al. (2000). The overall agreement between the present and previous work is good and the average deviation compared to NIST values and FAC calculations amounts to 9.7% and 4.8%, respectively.
Also included in Table 2 is the ratio R of the obtained transition probabilities in length and velocity gauge. For accurate wave functions and strong transitions the ratio R is expected to be close to unity, whereas ratios far from 1 are often associated with weaker transitions where uncertainties normally are larger. On the other hand, ratios close to unity do not necessarily imply accurate wave functions, but together with a thorough validation of calculated level energies these are still strong indicators on the quality of the calculations. As seen in Table 2 the ratios are almost exclusively close to or at unity with only a few exceptions where the transition rates are smaller.
Differences in calculated transition probabilities in length and velocity gauge also reflect the theoretical uncertainty, which must be estimated when experimental observations are lacking. Boron-like O IV, a system for which numerous calculations have been performed, where the scattering in calculated transition rates from different models turns out to be correlated with the ratio R (Rynkun et al. 2012), serves as a good example. In Froese Fischer (2009), the use of the resulting rates in the two gauges as a measure of the theoretical uncertainty is discussed in detail and it is argued that a plausible estimate of the accuracy of LS allowed transition rates, δA, is given by 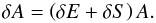 (8)In the expression above A is the transition rate computed using the transition energy from observed energy levels (Eobs), δE = | Ecalc − Eobs | /Eobs and δS = | Slength − Svelocity | /max(Slength,Svelocity) where Slength and Svelocity is the line strength using length and velocity gauge, respectively. Following this method, an average uncertainty of 2.4% is obtained for all transitions between levels in the lower structure. It should be noted that this value probably represents an overestimate since it includes contributions from LS-forbidden transitions for which a comparison of length and velocity values is no longer reliable (Froese Fischer 2009). Based on the above analysis we expect that the calculated transition rates in this work have the better accuracy compared to values from FAC calculations and NIST recommended values, although in a more thorough analysis the transition rates calculated by Landi & Gu (2006) should be corrected with observed transition energies.
(8)In the expression above A is the transition rate computed using the transition energy from observed energy levels (Eobs), δE = | Ecalc − Eobs | /Eobs and δS = | Slength − Svelocity | /max(Slength,Svelocity) where Slength and Svelocity is the line strength using length and velocity gauge, respectively. Following this method, an average uncertainty of 2.4% is obtained for all transitions between levels in the lower structure. It should be noted that this value probably represents an overestimate since it includes contributions from LS-forbidden transitions for which a comparison of length and velocity values is no longer reliable (Froese Fischer 2009). Based on the above analysis we expect that the calculated transition rates in this work have the better accuracy compared to values from FAC calculations and NIST recommended values, although in a more thorough analysis the transition rates calculated by Landi & Gu (2006) should be corrected with observed transition energies.
In Fig. 2 a synthetic Fe XXI spectrum obtained from calculated transition rates is shown. The intensity of each transition in the spectrum is represented by a Gaussian distribution with a full width at half maximum (FWMH) of 0.05 Å, corresponding to a temperature T = 107 K, a typical solar flare temperature (Del Zanna et al. 2013). The intensity is set in proportion to gjAij exp(−Ei/kT), where gj is the statistical weight for the upper level, Aij the transition rate in s-1 between the upper level j and the lower i and Ei the excitation energy of the upper level. This scenario corresponds to a high temperature condition where the level population is dominated by collisions. For a low density environment the deexcitation is dominated by the spontaneous decay, and the intensity of each line depends on the excitation rate and the branching fraction. Prominent transitions in the spectrum are
-
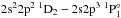 (98.35 Å),
(98.35 Å), -
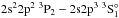 (102.19 Å),
(102.19 Å), -
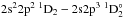 (113.26 Å), and
(113.26 Å), and -
2s2p3 1P1 −
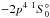 (127.08 Å).
(127.08 Å).
The strongest resonance transition in the spectrum is 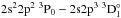 (128.75 Å).
(128.75 Å).
 |
Fig. 2 Synthetic Fe XXI spectrum containing transitions between 90 − 200 Å from the present calculation. See text for details. |
6. Conclusions
Self-consistent MCDHF and subsequent RCI calculations have been performed in selected carbon-like ions from Ar XIII to Zn XXV using the GRASP2K program suite. Level energies, Landé gJ-factors, transition energies and transition rates involving the 2s22p2, 2s2p3, 2p4, 2s22p3l, 2s2p23l, 2p33l and 2s22p4l(l = 0,1,2) configurations have been deduced. To facilitate labeling of states, a transformation from jj-coupling to LS-coupling to obtain LS-precentage compositions has been used. Even so a number of states with identical configuration and leading LS-composition are found. Previous theoretical and experimental data for Fe XXI were used to validate computational methods. The energy results from RCI calculations are in excellent agreement with observations. For the 2s22p2, 2p4 and 2s2p3 configurations, the mean relative energy differences are 0.028% (NIST Atomic Spectra Database 2013) − 0.032% (Landi et al. 2012) whereas, for all other configurations, they are 0.050% (Landi et al. 2012). The uncertainties in transition rates between the lower states have been estimated from the expressions suggested by Froese Fischer (2009) giving an average of only 2.4%. We thus argue that the transition rates are highly accurate and may serve as benchmark for other calculations. The average difference in transition rates from the present calculations and the calculations by Landi & Gu (2006) is 4.8%.
To summarize, the present work has significantly increased the amount of available data for ions in the carbon-like sequence and the resulting level energies and transition rates represent an improvement in accuracy compared with observations as well as with RMBPT calculations by Gu (2005a). A reanalysis of electron temperature and density in solar or astrophysical plasma using the current extended data set allows for a more thorough consistency check with the possibility to identify and include new lines of diagnostic value. In addition, the high accuracy of the current data may rule out the possibility that wrongly identified lines enter the analysis. In the case of Landé gJ-factors the complete data set fills a gap and there is no longer any need to use values derived in the LS-coupling scheme that are of limited accuracy for the more ionized ions.
Energies in cm-1 for levels in Fe XXI.
Transition rates A(RCI) in units of s-1 for E1 transitions in Fe XXI for upper levels 6−20.
References
- Aggarwal, K. M., & Keenan, F. P. 2001, ApJ, 136, 763 [Google Scholar]
- Aggarwal, K. M., Keenan, F. P., & Msezane, A. Z. 2003, A&A, 401, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aggarwal, K. M., Keenan, F. P., & Nakazaki, S. 2005, A&A, 436, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andersson, M., & Jönsson, P. 2008, Comput. Phys. Commun., 178, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 1986, J. Phys. B., 19, 3827 [Google Scholar]
- Badnell, N. R. 1997, J. Phys. B., 30, 1 [Google Scholar]
- Brown, G. V., Beiersdorfer, P., Liedahl, D. A., et al. 2002, ApJS, 140, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, M. H., Reed, K. J., McWilliams, D. M., et al. 1997, Atom. Data Nucl. Data Tables, 65, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, A. M., Martins, M. C., & Parente, F. 2001, Atom. Data Nucl. Data Tables, 79, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, R. 1981, The theory of atomic structure and spectra (Berkeley: University of California Press) [Google Scholar]
- DelZanna, G., & Woods, T. N. 2013, A&A, 555, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dyall, K. G., Grant, I. P., Johnson, C. T., Parpia, F. A., & Plummer, E. P. 1989, Comput. Phys. Commun., 55, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Eissner, W., Jones, M., & Nussbaumer, H. 1974, Comput. Phys. Commun., 8, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U., & Doschek, G. A. 2007, Atom. Data Nucl. Data Tables, 93, 779 [Google Scholar]
- Feldman, U., Curdt, W., Landi, E., & Wilhelm, K. 2000, ApJ, 544, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Froese Fischer, C., & Jönsson, P. 2001, J. Mol. Struct., 537, 55 [CrossRef] [Google Scholar]
- Froese Fischer, C. 2009, Phys. Scr. T, 134, 014019 [Google Scholar]
- Gaigalas, G., Fritzsche, S., & Grant, I. P. 2001, Comput. Phys. Commun., 139, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Grant, I. P. 1974, J. Phys. B, 7, 1458 [Google Scholar]
- Grant, I. P. 2007, Relativistic Quantum Theory of Atoms and Molecules (New York: Springer) [Google Scholar]
- Gu, M. F. 2005a, ApJS, 156, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. F. 2005b, Atom. Data Nucl. Data Tables, 89, 267 [Google Scholar]
- Gu, M. F. 2007, ApJS, 169, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, F., Yang, J., Jiang, G., Wang, C.K., & Zhao, X. F. 2011a, Phys. Scr. T144, 014006 [Google Scholar]
- Hu, F., Jiang, G., Yang, J. M., Zhang, J. Y., & Zhao, X. F. 2011b, Acta Physica Polonica A, 120, 429 [Google Scholar]
- Jönsson, P., & Froese Fischer, C. 1998 Phys. Rev. A, 57, 4967 [Google Scholar]
- Jönsson, P., He, X., Froese Fischer, C., & Grant, I. P. 2007, Comput. Phys. Commun., 177, 597 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jönsson, P., Rynkun, P., & Gaigalas, G. 2011, Atom. Data Nucl. Data Tables, 97, 648 [Google Scholar]
- Jönsson, P., Gaigalas, G., Bieroń, J., Froese Fischer, C., & Grant, I. P. 2013a, Comput. Phys. Commun., 184, 2197 [NASA ADS] [CrossRef] [Google Scholar]
- Jönsson, P., Ekman, J., Gustafsson, S., et al. 2013b, A&A, 559, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramida, A., Ralchenko, Yu., Reader, J., & and NIST ASD Team 2012 NIST Atomic Spectra Database (ver. 5.0), National Institute of Standards and Technology, Gaithersburg, MD, http://physics.nist.gov/asd [2013, March 10] [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., Dere, K. P., & Mason, H. E. 2012, ApJS, 744, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., & Gu, M. F. 2006, ApJ, 640, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., & Phillips, K. J. H. 2005, ApJS, 160, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H., Jiang, G., Hu, F., Wang, C.-K., Wang, Z.-B., & Yang, J.-M. 2013, Chin. Phys. B, 22, 073202 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, W. C., Fuhr, J. R., Kelleher, D. E., et al. 1999, NIST Atomic Spectra Database (ver. 2.0), National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
- McKenzie, B. J., Grant, I. P., & Norrington, P. H. 1980, Comput. Phys. Commun., 21, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, H. E., Doschek, G. A., Feldman, U., & Bhatia, A. K. 1979, A&A, 73, 74 [NASA ADS] [Google Scholar]
- Olsen, J., Godefroid, M., Jönsson, P., Malmqvist, P. Å., & Froese Fischer, C., 1995, Phys. Rev. E, 52, 4499 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeri, P., Quinet, P., Mendoza, C., et al. 2008, ApJS, 177, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, V. 2011, Active OB stars: structure, evolution, mass loss, and critical limits, Proc. IAU Symp., 272, 106 [NASA ADS] [Google Scholar]
- Rynkun, P., Jönsson, P., Gaigalas, G., & Froese Fischer, C. 2012, Atom. Data Nucl. Data Tables, 98, 481 [Google Scholar]
- Safronova, U. I., & Shlyaptseva, A. S. 1999, Phys. Scr., 60, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Shirai, T., Sugar, J., Musgrove, A., & Wiese, W. L. 2000, Spectral Data for Highly Ionized Atoms, Monograph No. 8 (AIP) [Google Scholar]
- Sugar, J., & Corliss, C., 1985, J. Phys. Chem. Ref. Data, 14, 1 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Transition rates A(RCI) in units of s-1 for E1 transitions in Fe XXI for upper levels 6−20.
All Figures
 |
Fig. 1 Gross structure of calculated energy levels in the carbon isoelectronic sequence. Levels for odd parity states are colored red whereas levels for even parity states are displayed in black. Level energies are shown to scale, but given in arbitrary units. |
| In the text | |
 |
Fig. 2 Synthetic Fe XXI spectrum containing transitions between 90 − 200 Å from the present calculation. See text for details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


