EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 563 (March 2014) A&A, 563 (2014) A17 Full HTML
Free Access
Issue
A&A
Volume 563, March 2014
Article Number A17
Number of page(s) 5
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201323334
Published online 26 February 2014

© ESO, 2014

1. Introduction

Relativistic radiation hydrodynamics provides the natural framework of several high-energy astrophysical processes, essentially all those for which the interaction of photons with matter takes place in a strong gravity regime or in the presence of relativistic motions. One such relativistic system is represented by geometrically thick disks (tori) around black holes. Considered as inviscid purely fluid solutions, these objects have always attracted much interest, partly because they allow for relatively simple analytic or semi-analytic configurations (Fishbone & Moncrief 1976; Abramowicz et al. 1978; Kozlowski et al. 1978; Font & Daigne 2002; Daigne & Font 2004; Qian et al. 2009; Penna et al. 2013) and partly because they can be adopted to study various types of fluid instabilities and potentially observable physical effects in the vicinity of black holes (Abramowicz et al. 1980, 1983; Papaloizou & Pringle 1984; Abramowicz et al. 1998; Rezzolla et al. 2003; Zanotti et al. 2003; Blaes et al. 2006; Montero et al. 2010). Moreover, a renewed interest for them has been motivated by the outcome of recent numerical simulations in full general relativity, showing that high-density tori are indeed produced after the merger of unequal-mass neutron star binaries that form a black hole (Rezzolla et al. 2010).

In spite of all these analyses, and although tori have been extensively studied in numerical simulations also for the effects of magnetic fields (Villiers & Hawley 2003; Komissarov 2006; Fragile & Meier 2009; Barkov & Baushev 2011; Narayan et al. 2012; McKinney et al. 2012), the role of radiation fields has often been disregarded. This has certainly been due to the complexity inherent in the time-dependent solution of the relativistic radiation hydrodynamics equations, which, at a rigorous level, would require the solution of the Boltzmann equation for the distribution function of photons1. For this reason, a few more pragmatic approaches have been developed over the years, which become useful both from a theoretical and from a numerical point of view. Perhaps the most successful one is represented by the so-called projected symmetric trace-free (PSTF) moment formalism of Thorne (1981), which defines the moments of the radiation field similarly to how density, momentum and pressure of a fluid are defined as moments of the corresponding distribution function.

In the recent past, by adopting this procedure, a number of time-dependent numerical codes have been developed and subsequently applied to various scenarios related to accretion flows in a relativistic context (Shapiro 1996; Farris et al. 2008; Zanotti et al. 2011; Fragile et al. 2012; Roedig et al. 2012; Sa¸dowski et al. 2013; Takahashi & Ohsuga 2013). Sadowski et al. (2014), in particular, have studied the super-critical accretion onto a black hole from a radiative torus, showing that most of the luminosity emerges through the funnels and confirmed, broadly speaking, the physical importance of these objects for high-energy astrophysics after so many years of active research.

The goal of this paper is to provide a simple model for an optically thick radiative torus around a black hole. Local thermodynamic equilibrium is assumed, and it is shown that a radiation field can be added while keeping the underlying hydrodynamic solution unmodified. The new model can be useful both on theoretical grounds, for clarifying the physics of radiative tori, and on numerical grounds, since it offers a test for general relativistic radiation codes in the optically thick regime. However, the time-dependent numerical investigation and the study of the stability properties of the proposed model are not the focus of this work and will be considered elsewhere.

In the following, we set the speed of light c = 1, and the gravitational constant G = 1. We extend the geometric units by setting mp/kB = 1, where mp is the mass of the proton, while kB is the Boltzmann constant. However, we have maintained c in an explicit form in expressions of particular physical interest.

2. Physics of the model

2.1. Basics assumptions

We considered a stationary and axisymmetric space-time around a Kerr black hole, which may be written either in Boyer-Lindquist or in Kerr-Schild coordinates. The energy-momentum tensor of the system is given by 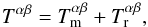(1)which clearly contains two contribution. The first term is due to matter and can be written as 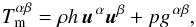(2)where gαβ is the metric of the background space-time, uα is the four-vector velocity of the fluid, while ρ, h = 1 + ϵ + p/ρ, ϵ and p are the rest-mass density, the specific (i.e. per unit mass) enthalpy, the specific internal energy, and the pressure, respectively. For the time being, we keep the equation of state unspecified. The fluid is in circular motion around the black hole and its four-vector velocity is uα = ut(1,0,0,Ω), where Ω = uφ/ut is the angular velocity as observed from infinity.

The second contribution to the energy-momentum tensor is due to the radiation field, and, in terms of its moments, can be written as (Hsieh & Spiegel 1976) 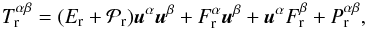(3)where the energy density, the radiation flux and the radiation stress tensor, all measured in the comoving frame of the fluid, are given by 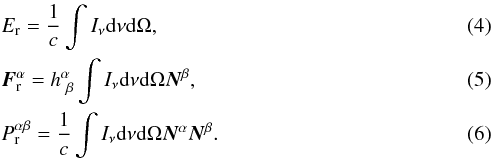We recall that Iν = Iν(xα,Ni,ν) is the specific (i.e. an energy flux per unit time, frequency, and solid angle) intensity of the radiation, Nα is the four-vector defining the photon propagation direction, dν is the infinitesimal frequency and dΩ is the infinitesimal solid angle around the direction of propagation. Finally, hαβ = uαuβ + gαβ is the projector operator into the space orthogonal to the four-velocity uα. In full generality, the four-force density of the radiation field, which describes the interaction of radiation with matter, is given by (Mihalas & Mihalas 1984; Shapiro 1996) 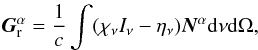(7)where 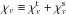and 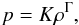are the total opacity and emissivity coefficients, each containing a thermal contribution, indicated with superscript t, and a scattering contribution, indicated with superscript s. However, if additionally assume that the fluid is optically thick and in local thermodynamic equilibrium with the radiation, then the radiation four-force vanishes, and the energy density is just 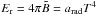, where 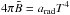is the equilibrium black-body intensity, T is the local temperature of the fluid, and arad is the radiation constant. Under these conditions, the radiation is isotropic in the comoving frame of the fluid, the radiation pressure is 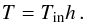and the radiation fluxes 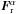also vanish (Farris et al. 2008). As a result, the energy-momentum tensor (3) of the radiation field reduces to 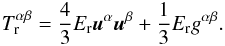(8)

2.2. Description of the model

Table 1

Main parameters of a few representative tori in local thermodynamic equilibrium with a radiation field.

We searched for a stationary, that is, ∂t ≡ 0, and axisymmetric, that is, ∂φ ≡ 0, solution to the full set of equations describing the dynamics of the system, that is,

The continuity equation is of course trivially satisfied when the velocity field is purely toroidal. In addition, since local thermodynamic equilibrium is assumed, and the radiation four-force vanishes, Eq. (10) effectively decouples into 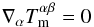(12)and 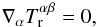(13)which must be satisfied separately. From (12), after contracting with the operator hαβ, we can write the Euler equation in the form (Abramowicz et al. 1978) 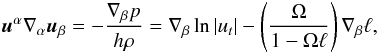(14)where the last term is the four-acceleration of the fluid in circular motion. This equation was extensively studied in the context of geometrically thick disks around black holes, and depending on the specific2 angular momentum ℓ = −uφ/ut, different classes of equilibrium tori can be obtained3 whose structure and properties have been discussed in detail (Abramowicz et al. 1978; Kozlowski et al. 1978; Font & Daigne 2002; Daigne & Font 2004). Here we investigate the possibility of adding an optically thick radiation field to those solutions without affecting their hydrodynamics. This extension is possible, but only for a limited class of equations of state. First of all, we contract Eq. (13) with hαβ to find, after a few tensor operations, that 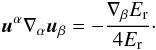(15)To make (14) and (15) compatible, it must be (16)We now need to address the thermodynamic properties of the fluid. We limited our attention to isentropic fluids, for which dp = ρdh. This has two important consequences. The first one is that the specific enthalpy can be computed as 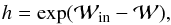(17)which follows from the second equality of Eq. (14) after introducing the potential 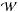as (Kozlowski et al. 1978) 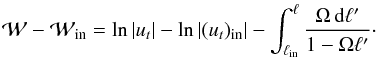(18)Note that subscript in refers to the inner edge of the disk in the equatorial plane, where hin = 1. The second consequence of the isentropic assumption is that Eq. (16) can be integrated to give 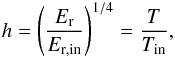(19)where 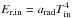is the energy density of the radiation field at r = rin, while Tin is the surface temperature. Equation (19) poses some restrictions on the equations of state that can be accepted. For instance, an ideal fluid equation of state p = ρϵ(γ − 1), for which T = p/ρ and h = 1 + γ/(γ − 1)T, would imply a constant temperature from Eq. (19). This is clearly not acceptable, since p/ρ is not uniform within the torus. Hence, we need an equation of state for which the temperature is a free parameter. This is the case of the polytropic equation of state 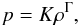(20)where K is the polytropic constant and Γ is the adiabatic index of the polytrope. We stress that the equation of state of isentropic polytropes can still be written formally like p = ρϵ(Γ−1). However, there are two important differences with respect to the equation of state of an ideal fluid, even when the latter is isentropic. The first difference is that the exponent Γ of Eq. (20) is not necessarily given by the ratio of the specific heats at constant pressure and at constant volume. The second difference is that for polytropes like (20), the temperature T is not necessarily given by the ratio p/ρ and can therefore be regarded as a free parameter4. It is interesting to note that while a purely hydrodynamic torus is compatible with the ideal fluid equation of state, in which case its temperature is given by p/ρ, the radiation hydrodynamic torus that we are describing is not.

After adopting the equation of state (20), Eq. (19) can be used to fix the temperature of the torus as 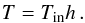(21)Hence, the isocurves of the temperature T and those of the specific enthalpy h of the torus coincide.

A well-known property of polish doughnuts is that they possess an internal Keplerian point, rc, lying on the equatorial plane, where the rest-mass density reaches a maximum ρc. This also corresponds to the highest temperature of the torus, and the ratio of the central to the surface temperature is given by 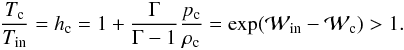(22)We note that the surface temperature Tin, or, alternatively, the central temperature Tc, is the only missing parameter that must be specified in addition to those necessary for constructing the hydrodynamic model. We also stress that since the temperature scales like the specific enthalpy, and the specific enthalpy is given by Eq. (17), the temperature does not depend on the polytropic constant K or on the index of the polytrope Γ. This is reminiscent of a similar result originally proved by Rezzolla et al. (2003) for purely hydrodynamic relativistic tori, namely that they have ratios p/ρ, which do not depend on the polytropic constant K.

Finally, a consistency check can be performed to show that even in the presence of a temperature gradient, the relativistic radiation flux is zero. In fact, in the framework of Eckart’s formulation of relativistic standard irreversible thermodynamics (Eckart 1940), the flux is given by the relativistic form of Fourier’s law, namely (Israel 1976) 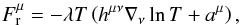(23)where λ is the thermal conductivity. It is easy to see that if the four-vector acceleration is given by the right-hand side of Eq. (15), 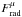as given by Eq. (23) is indeed zero.

2.3. A few representative examples

As a first illustrative example, we consider a Schwarzschild space-time with the fluid having a constant (in radius) specific angular momentum ℓ. In these circumstances the rest-mass density distribution can be solved analytically and is (Font & Daigne 2002) (24)where (25)is the potential. If we fix the position of the inner edge of torus rin at the position of the cusp rcusp of the potential 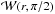, the torus will exactly fill its Roche lobe. Under this assumption, we have considered a few tori orbiting around a M = 2.5  M⊙ black hole. The first four rows of Table 1 report four models previously considered by Zanotti et al. (2003) in the Schwarzschild space-time, but without the radiation field5. All the models have the same disk-to-hole mass ratio Mt/M = 0.1, but different sizes. The last column reports the ratio Tc/Tin, computed according to Eq. (22). As can be seen, tori that are in local thermodynamic equilibrium and obey Eq. (19) are close to be isothermal, with deviations from T = const that increase as the inner edge of the torus approaches the black hole.

The property of being almost isothermal remains true also when power-law distributions of the specific angular momentum are adopted, namely when 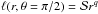, although a richer phenomenology is possible for them6. We recall that in the Kerr metric the radius rms of the marginally stable orbit is a decreasing function of the black-hole spin parameter a. On the other hand, when the power law-index q is increased, the inner radius of the torus increases as well. Hence, for low values of q, the torus penetrates deeper into the potential well, placing the cusp below the marginally stable orbit. In these circumstances the highest values of Tc/Tin are found. The last two rows of Table 1 report two representative models of this class, which were previously considered by Zanotti et al. (2005) in Kerr space-time, but without the radiation field.7

In contrast, when the exponent q is close to 1/2, the rotation law tends to the Keplerian one, with a torus that flattens toward the equatorial plane. Tori of this kind are generally much larger than ℓ = const tori (Zanotti et al. 2010), with radii at the maximum rest-mass density point as high as rc ~ 1000. Consequently, they are very mildly relativistic, with values of the specific enthalpy hc very close to unity. We have verified this trend for a few representative cases, not reported in Table 1, and found that Tc/Tin ≈ 1 to a few parts over 106.

3. Discussion and conclusions

We have shown that purely hydrodynamical geometrically thick disks around a black hole, extensively studied in the past and sometimes referred to as polish doughnuts, can be dressed with a radiation field in local thermodynamic equilibrium with the fluid. The equation of state required for this extension is that of an isentropic and polytropic fluid, with a temperature that scales like the specific enthalpy. The resulting models, computed for a few representative cases of both constant and varying distributions of the specific angular momentum, are almost isothermal, with deviations of only a few percent.

Since the equation of state of the model is nonthermal and well-suited to describe degenerate matter, the most natural astrophysical scenario where such a model can become relevant is that of a high-density torus, with densities close to those of neutron stars. Although still rather simplified, these models may indeed offer a better description of high-density tori produced after the merger of unequal-mass neutron star binaries collapsing onto a black hole, as reported by fully relativistic and purely hydrodynamical numerical simulations (Rezzolla et al. 2010). This marks an important difference with respect to the radiation torus discussed in McKinney et al. (2014), which adopts a thermal equation of state and is instead well-suited to describe (much) lower density accretion disks around black holes.

The model discussed here may also offer a stationary test for numerical codes that solve the equations of general relativistic radiation hydrodynamics. However, a few words of caution need to be said in this respect. The first warning is that since the torus is isentropic, the evolution should preferably be performed without integrating the energy density of the fluid, which can be computed algebraically from the remaining quantities by exploiting Eq. (20). Secondly, since the opacity is typically a function of the rest-mass density, which drops at the surface of the torus, the assumption of rigorous optical thickness is likely to fail in a thin shell at the surface of the torus. However, this problem is mitigated by the possibility of building models for which such a shell is arbitrarily thin. Thirdly, any modern numerical code for the solution of the general relativistic radiation hydrodynamics equations will require the treatment of a tenuous “atmosphere”, that is, of a low-density region filling the supposedly vacuum space around the torus. The atmosphere is intrinsically optically thin and this requires a code capable of handling both the optically thick and the optically thin regimes. Significant progress in this respect has recently been obtained by Sa¸dowski et al. (2013); Takahashi & Ohsuga (2013); McKinney et al. (2014).

Finally, the stability properties of these new models and their response to perturbations remain an open question, which may deserve a dedicated investigation, both analytical and numerical.

1

See McClarren & Hauck (2010) and Radice et al. (2013) for some promising progress in this direction.

2

When referred to the angular momentum, the adjective specific means “per unit energy”.

3

See Rezzolla & Zanotti (2013) for a pedagogic exposition.

4

A famous example is given by the degenerate Fermi fluid, whose equation of state can be written like Eq. (20).

5

Models (a)–(d) in Table 1 are the same as models (e)–(h) of Zanotti et al. (2003).

6

See Daigne & Font (2004) for an extended discussion about tori with a power-law distribution of the specific angular momentum.

7

Models (e)–(f) in Table 1 are the same as models (D2a) and (E1a) of Zanotti et al. (2005).

Acknowledgments

I thank John C. Miller and the referee Jonathan McKinney for very useful suggestions that helped me to improve the quality of the manuscript. This work has been financed in parts by the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013) in the frame of the research project STiMulUs, ERC Grant agreement No. 278267.

References

  1. Abramowicz, M., Jaroszynski, M., & Sikora, M. 1978, A&A, 63, 221 [NASA ADS] [Google Scholar]
  2. Abramowicz, M. A., Calvani, M., & Nobili, L. 1980, ApJ, 242, 772 [NASA ADS] [CrossRef] [Google Scholar]
  3. Abramowicz, M. A., Calvani, M., & Nobili, L. 1983, Nature, 302, 597 [NASA ADS] [CrossRef] [Google Scholar]
  4. Abramowicz, M. A., Karas, V., & Lanza, A. 1998, A&A, 331, 1143 [NASA ADS] [Google Scholar]
  5. Barkov, M. V., & Baushev, A. N. 2011, New Astron., 16, 46 [NASA ADS] [CrossRef] [Google Scholar]
  6. Blaes, O. M., Arras, P., & Fragile, P. C. 2006, MNRAS, 369, 1235 [NASA ADS] [CrossRef] [Google Scholar]
  7. Daigne, F., & Font, J. A. 2004, MNRAS, 349, 841 [NASA ADS] [CrossRef] [Google Scholar]
  8. Eckart, C. 1940, Phys. Rev., 58, 919 [NASA ADS] [CrossRef] [Google Scholar]
  9. Farris, B. D., Li, T. K., Liu, Y. T., & Shapiro, S. L. 2008, Phys. Rev. D, 78, 024023 [NASA ADS] [CrossRef] [Google Scholar]
  10. Fishbone, L. G., & Moncrief, V. 1976, ApJ, 207, 962 [NASA ADS] [CrossRef] [Google Scholar]
  11. Font, J. A., & Daigne, F. 2002, MNRAS, 334, 383 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fragile, P. C., & Meier, D. L. 2009, ApJ, 693, 771 [NASA ADS] [CrossRef] [Google Scholar]
  13. Fragile, P. C., Gillespie, A., Monahan, T., Rodriguez, M., & Anninos, P. 2012, ApJS, 201, 9 [NASA ADS] [CrossRef] [Google Scholar]
  14. Hsieh, S., & Spiegel, E. A. 1976, ApJ, 207, 244 [NASA ADS] [CrossRef] [Google Scholar]
  15. Israel, W. 1976, Ann. Phys., 100, 310 [Google Scholar]
  16. Komissarov, S. S. 2006, MNRAS, 368, 993 [NASA ADS] [CrossRef] [Google Scholar]
  17. Kozlowski, M., Jaroszynski, M., & Abramowicz, M. A. 1978, A&A, 63, 209 [NASA ADS] [Google Scholar]
  18. McClarren, R. G., & Hauck, C. D. 2010, J. Comput. Phys., 229, 5597 [NASA ADS] [CrossRef] [Google Scholar]
  19. McKinney, J. C., Tchekhovskoy, A., & Blandford, R. D. 2012, MNRAS, 423, 3083 [NASA ADS] [CrossRef] [Google Scholar]
  20. McKinney, J. C., Tchekhovskoy, A., Sadowski, A., & Narayan, R. 2014, MNRAS, submitted [arXiv:1312.6127] [Google Scholar]
  21. Mihalas, D., & Mihalas, B. 1984, Foundations of radiation hydrodynamics (New York: Oxford University Press) [Google Scholar]
  22. Montero, P. J., Font, J. A., & Shibata, M. 2010, Phys. Rev. Lett., 104, 191101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  23. Narayan, R., SÄ dowski, A., Penna, R. F., & Kulkarni, A. K. 2012, MNRAS, 426, 3241 [NASA ADS] [CrossRef] [Google Scholar]
  24. Papaloizou, J. C. B., & Pringle, J. E. 1984, MNRAS, 208, 721 [NASA ADS] [CrossRef] [Google Scholar]
  25. Penna, R. F., Kulkarni, A., & Narayan, R. 2013, A&A, 559, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Qian, L., Abramowicz, M. A., Fragile, P. C., et al. 2009, A&A, 498, 471 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Radice, D., Abdikamalov, E., Rezzolla, L., & Ott, C. D. 2013, J. Comp. Phys., 242, 648 [NASA ADS] [CrossRef] [Google Scholar]
  28. Rezzolla, L., & Zanotti, O. 2013, Relativistic Hydrodynamics (Oxford: Oxford University Press) [Google Scholar]
  29. Rezzolla, L., Yoshida, S., & Zanotti, O. 2003, MNRAS, 344, 978 [NASA ADS] [CrossRef] [Google Scholar]
  30. Rezzolla, L., Baiotti, L., Giacomazzo, B., Link, D., & Font, J. A. 2010, Class. Quant. Grav., 27, 114105 [NASA ADS] [CrossRef] [Google Scholar]
  31. Roedig, C., Zanotti, O., & Alic, D. 2012, MNRAS, 426, 1613 [NASA ADS] [CrossRef] [Google Scholar]
  32. Sądowski, A., Narayan, R., Tchekhovskoy, A., & Zhu, Y. 2013, MNRAS, 429, 3533 [NASA ADS] [CrossRef] [Google Scholar]
  33. Sadowski, A., Narayan, R., McKinney, J. C., & Tchekhovskoy, A. 2014, MNRAS, submitted [arXiv:1311.5900] [Google Scholar]
  34. Shapiro, S. L. 1996, ApJ, 472, 308 [NASA ADS] [CrossRef] [Google Scholar]
  35. Takahashi, H. R., & Ohsuga, K. 2013, ApJ, 772, 127 [NASA ADS] [CrossRef] [Google Scholar]
  36. Thorne, K. S. 1981, MNRAS, 194, 439 [NASA ADS] [Google Scholar]
  37. Villiers, J. P. D., & Hawley, J. F. 2003, ApJ, 592, 1060 [NASA ADS] [CrossRef] [Google Scholar]
  38. Zanotti, O., Rezzolla, L., & Font, J. A. 2003, MNRAS, 341, 832 [NASA ADS] [CrossRef] [Google Scholar]
  39. Zanotti, O., Font, J. A., Rezzolla, L., & Montero, P. J. 2005, MNRAS, 356, 1371 [NASA ADS] [CrossRef] [Google Scholar]
  40. Zanotti, O., Rezzolla, L., DelZanna, L., & Palenzuela, C. 2010, A&A, 523, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Zanotti, O., Roedig, C., Rezzolla, L., & Del Zanna, L. 2011, MNRAS, 417, 2899 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Main parameters of a few representative tori in local thermodynamic equilibrium with a radiation field.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.