Fig. 5
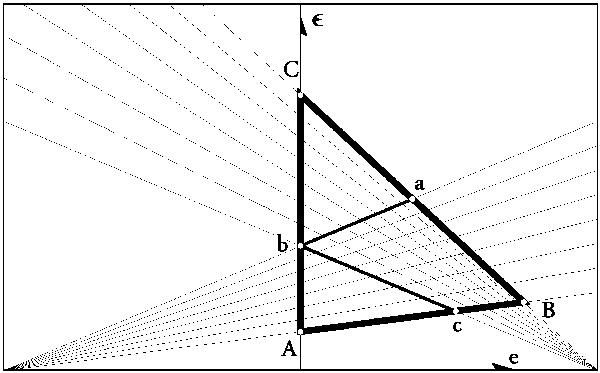
Each point on the (e,ϵ) plane represents an elliptical orbit
with eccentricity e and energy − ϵ. The ABC
triangle with vertices A 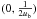 , B
, B
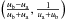 ,
C
,
C 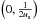 is a locus of all confocal ellipses lying entirely in-between two bounding spheres
of fixed radii ua and ub and
centered on the focal point. The two families of mutually crossing lines
is a locus of all confocal ellipses lying entirely in-between two bounding spheres
of fixed radii ua and ub and
centered on the focal point. The two families of mutually crossing lines
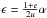 through point (− 1,0) and
through point (− 1,0) and
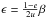 through point (1,0) give rise to a new coordinate system
(α,β) on the (e,ϵ) plane. When
through point (1,0) give rise to a new coordinate system
(α,β) on the (e,ϵ) plane. When
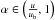 and
and 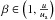 the coordinates cover a u-dependent quadrilateral integration
domain abcB with vertices a
the coordinates cover a u-dependent quadrilateral integration
domain abcB with vertices a  ,
b
,
b 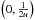 ,
c
,
c  ,
and B, which is the locus of all orbits (e,ϵ) crossing at least once a sphere of a
given radius ua < u < ub.
,
and B, which is the locus of all orbits (e,ϵ) crossing at least once a sphere of a
given radius ua < u < ub.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


