| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201322966 | |
| Published online | 14 January 2014 | |
Analytical models of X-shape magnetic fields in galactic halos
IRAP, Université de Toulouse, CNRS, 9 avenue du Colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
e-mail: katia.ferriere@irap.omp.eu
Received: 1 November 2013
Accepted: 5 December 2013
Context. External spiral galaxies seen edge-on exhibit X-shape magnetic fields in their halos. Whether the halo of our own Galaxy also hosts an X-shape magnetic field is still an open question.
Aims. We would like to provide the necessary analytical tools to test the hypothesis of an X-shape magnetic field in the Galactic halo.
Methods. We propose a general method to derive analytical models of divergence-free magnetic fields whose field lines are assigned a specific shape. We then utilize our method to obtain four particular models of X-shape magnetic fields in galactic halos. In passing, we also derive two particular models of predominantly horizontal magnetic fields in galactic disks. All our field models have spiraling field lines with spatially varying pitch angle.
Results. Our four halo field models do indeed lead to X patterns in synthetic synchrotron polarization maps. Their precise topologies can all be explained by the action of a wind blowing outward from the galactic disk or from the galactic center. In practice, our field models may be used for fitting purposes or as inputs to various theoretical problems.
Key words: galaxies: magnetic fields / galaxies: halos / galaxies: spiral / Galaxy: halo / Galaxy: disk / ISM: magnetic fields
© ESO, 2014
1. Introduction
Low-frequency radio continuum observations provide a powerful tool to detect and measure magnetic fields in the disks and halos of external galaxies (see, e.g., the recent review by Beck & Wielebinski 2013). Polarization observations of nearby edge-on spiral galaxies show that most galactic disks harbor large-scale magnetic fields that are horizontal, i.e., parallel to the disk plane (e.g., Wielebinski & Krause 1993; Dumke et al. 1995). In the past few years, high-sensitivity polarization observations have also revealed the presence in galactic halos of magnetic fields forming a general X pattern. These so-called X-shape magnetic fields are characterized by a vertical (i.e., perpendicular to the disk plane) component that increases with both galactic radius and height in the four quadrants (Tüllmann et al. 2000; Soida 2005; Krause et al. 2006; Krause 2009; Heesen et al. 2009; Braun et al. 2010; Soida et al. 2011; Haverkorn & Heesen 2012).
At first thought, the denomination of X-shape magnetic fields could be reminiscent of magnetic reconnection. However, in contrast to X-type reconnection configurations, which truly form a complete and well-defined X, the observed X-shape magnetic fields often have the central part of the X missing or distorted – in that sense, the term “X-shape” may be a little misleading. More importantly, X-shape magnetic fields appear on global galactic scales, which are vastly larger than the resistive scales on which reconnection presumably takes place.
Since X-shape magnetic fields generally stand out best at large distances from the galactic center, it is often hard to guess what their complete magnetic topology is and how their field lines connect together, i.e., horizontally near the rotation axis or vertically across the disk plane. This, in turn, makes it difficult to pin down the exact nature of X-shape magnetic fields and to trace back to their origin. Various physical scenarios have been proposed in the literature, involving either the operation of a classical galactic dynamo in the halo (Tüllmann et al. 2000; Soida 2005) or, more likely, the action of a large-scale galactic wind from the disk (Tüllmann et al. 2000; Beck 2008; Heesen et al. 2009; Soida et al. 2011). Alternatively, it has been suggested that the X pattern does not pertain to the large-scale regular magnetic field, but rather to a small-scale anisotropic random field which would be associated with extremely elongated magnetic loops produced by a spiky wind (Michał Hanasz, priv. comm.; see also Elstner et al.1995, who first used the term “spiky wind”). Only rotation measure (RM) studies can distinguish between regular and anisotropic random fields. In the cases of NGC 5775 (Soida et al. 2011) and NGC 4631 (Mora & Krause 2013), the large values and the rather smooth distributions of the RMs measured toward their halos may speak in favor of regular X-shape fields, but little information is available for other galaxies. In the present study, we will proceed on the premise that the X pattern is really an attribute of the large-scale regular field.
Now the question that naturally comes to mind is whether the halo of our own Galaxy also possesses an X-shape magnetic field. The most widely used description of the Galactic halo field relies on the double-torus picture, originally sketched by Han (2002) and later modeled by Prouza & Šmída (2003); Sun et al. (2008); Jansson & Farrar (2012a), where the halo field is purely azimuthal, forms a torus on each side of the Galactic plane and has opposite signs above and below the plane. For the first time, Jansson & Farrar (2012a,b) added to this double-torus component a simple X-shape component, which they chose to be axisymmetric and purely poloidal1. They found that this addition improved the overall fit to the RM and synchrotron data combined.
In this paper, we will not attempt to settle the question of whether the Galactic halo possesses or not an X-shape magnetic field, but we will provide the analytical tools required to seriously address this question in view of the existing observations. More specifically, we will propose a general method to derive analytical models of divergence-free, X-shape magnetic fields that can be applied to galactic halos. We will then derive four particular X-shape models having a small number of free parameters, and we will verify that these models truly produce X patterns in synchrotron polarization maps.
We emphasize that the method proposed here to obtain analytical field models is very general, in the sense that it can be applied to all sorts of magnetic configurations, with or without an X shape. Our four X-shape models, which represent a particular application of our general method to halo magnetic fields, have themselves broad applicability. First of all, they can be applied to our own Galaxy, with different purposes in mind. For instance, they can be used to construct synthetic maps of RMs, of synchrotron total and polarized intensities or of any other relevant observables, which can then be confronted to existing observational maps with the aim of placing constraints on the properties of a putative X-shape magnetic field in the Galactic halo. In a different perspective, our X-shape models can serve as a framework to study theoretical problems, such as cosmic-ray propagation and large-scale magnetohydrodynamic phenomena, in our Galaxy. Similarly, they can be applied to external galaxies, both to construct various synthetic maps which can help to constrain their true magnetic morphologies and to study the same kind of theoretical problems as in our own Galaxy.
For pedagogical reasons, we will start by developing models of purely poloidal magnetic fields, and since our intended application is to galactic halos, we will restrict our attention to poloidal fields with an overall X shape (Sect. 2). We will then extend our poloidal field models to three dimensions, by including an azimuthal field component that is directly linked to the poloidal component, as expected from dynamo theory (Sect. 3). Taking advantage of the analytical expressions obtained for magnetic fields in galactic halos, we will, with a little extra work, derive three-dimensional models of magnetic fields in galactic disks; these disk field models can be utilized either independently or in combination with our halo field models (Sect. 4). As a necessary check of the relevance of our halo field models, we will use them to simulate synchrotron polarization maps of a hypothetical external galaxy seen edge-on and make sure that these maps display the expected X patterns (Sect. 5). Finally, we will conclude our study with a short summary (Sect. 6).
2. Analytical models of poloidal, X-shape magnetic fields
2.1. Euler potentials
To model magnetic fields in galactic halos (in particular, in the halo of our own Galaxy), we will consider various magnetic configurations characterized by field lines that form a general X pattern. For each considered configuration, we will adopt a simple analytical function to describe the shape of field lines, and we will derive the analytical expression of the corresponding magnetic field vector, B, as a function of galactocentric cylindrical coordinates, (r,ϕ,z).
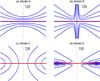 |
Fig. 1 Small set of field lines for each of our four models of poloidal, X-shape magnetic fields in galactic halos, in a vertical plane through the galactic center: a) model A (described by Eq. (12)) with r1 = 3 kpc and a = 1/(10 kpc)2; b) model B (Eq. (17)) with r1 = 3 kpc and n = 2; c) model C (Eq. (26)) with a = 1/(10 kpc)2 (and, as always, z1 = 0); and d) model D (Eq. (31)) with | z1 | = 1.5 kpc and n = 2. Field lines are separated by a fixed magnetic flux per unit azimuthal angle; thus, in models A and B, their vertical spacing at r1 is determined by Eq. (16) or (21) with H = 1.5 kpc, while in models C and D, their radial spacing at z1 is determined by Eq. (30) or (35) with L = 10 kpc. Each panel is 30 kpc × 30 kpc in size and is centered on the galactic center. The trace of the galactic plane is indicated by the horizontal, solid red line, and the z-axis by the vertical, dot-dashed black line. |
A convenient way to proceed is to use the Euler potentials, α and β, defined (Northrop 1963; Stern 1966) such that 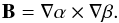 (1)A first great advantage of the Euler representation is that the magnetic field is automatically divergence-free. Another important advantage, particularly relevant in the present context, is that field lines can be directly visualized. Indeed, according to Eq. (1), any given field line is the line of intersection between a surface of constant α and a surface of constant β. As an immediate consequence, each field line can be defined by, or labeled with, a given pair (α,β).
(1)A first great advantage of the Euler representation is that the magnetic field is automatically divergence-free. Another important advantage, particularly relevant in the present context, is that field lines can be directly visualized. Indeed, according to Eq. (1), any given field line is the line of intersection between a surface of constant α and a surface of constant β. As an immediate consequence, each field line can be defined by, or labeled with, a given pair (α,β).
In this section, we focus on the particular case when the magnetic field is poloidal (Bϕ = 0), postponing discussion of the general three-dimensional case to Sect. 3. We can then identify one of the Euler potentials, say β, with galactic azimuthal angle: 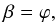 (2)whereupon Eq. (1) yields
(2)whereupon Eq. (1) yields  where subscripts r and z indicate that the partial derivatives with respect to z and r are to be taken at constant r and z, respectively. It appears that α represents the (poloidal) magnetic flux per unit azimuthal angle (taken with the appropriate sign) between the considered field line (α,ϕ) and a reference field line (α0,ϕ).
where subscripts r and z indicate that the partial derivatives with respect to z and r are to be taken at constant r and z, respectively. It appears that α represents the (poloidal) magnetic flux per unit azimuthal angle (taken with the appropriate sign) between the considered field line (α,ϕ) and a reference field line (α0,ϕ).
2.2. Magnetic field in a given meridional plane
For a poloidal, X-shape magnetic field, the equation of field lines in a given meridional plane ϕ can generally be written in the form 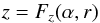 (6)or
(6)or 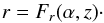 (7)These two classes of field lines are successively studied in Sects. 2.2.1 and 2.2.2.
(7)These two classes of field lines are successively studied in Sects. 2.2.1 and 2.2.2.
2.2.1. Field lines given by z as a function of r
Each field line can be identified by a value of α or, equivalently, by a value of any monotonic function of α. A convenient such function is z1(α), where z1 denotes the height of the considered field line at a specified (and fixed) radius r1 (e.g., r1 = 3 kpc). The equation of field lines, Eq. (6), can be rewritten in terms of z1, as 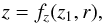 (8)and, accordingly, the expressions for the radial and vertical field components, Eqs. (3) and (5), can be transformed into
(8)and, accordingly, the expressions for the radial and vertical field components, Eqs. (3) and (5), can be transformed into 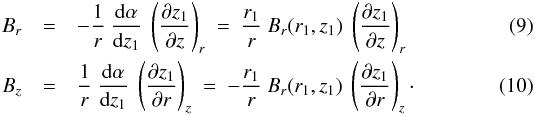 Clearly, Eq. (9) expresses magnetic flux conservation (in the radial direction) between (r1,z1) and (r,z), while the ratio of Eqs. (10) to (9),
Clearly, Eq. (9) expresses magnetic flux conservation (in the radial direction) between (r1,z1) and (r,z), while the ratio of Eqs. (10) to (9), 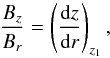 (11)simply states that the magnetic field is tangent to field lines.
(11)simply states that the magnetic field is tangent to field lines.
Model A. To describe field lines with an X shape, we choose a function z = fz(z1,r) such that |z| increases as a positive power of r for r → ∞. We discard the simple linear function of r, which leads to a cusp at r = 0, and consider the quadratic function 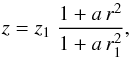 (12)where r1 and a are two strictly positive free parameters (see Fig. 1a). Let us emphasize that the values of r1 and a are unique and common to all field lines, in contrast to z1, which has a different value on each field line. By inverting Eq. (12) to obtain z1 as a function of (r,z):
(12)where r1 and a are two strictly positive free parameters (see Fig. 1a). Let us emphasize that the values of r1 and a are unique and common to all field lines, in contrast to z1, which has a different value on each field line. By inverting Eq. (12) to obtain z1 as a function of (r,z): 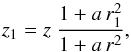 (13)calculating the partial derivatives of z1 with respect to z and r, and introducing these derivatives into Eqs. (9) and (10), we find for the radial and vertical field components:
(13)calculating the partial derivatives of z1 with respect to z and r, and introducing these derivatives into Eqs. (9) and (10), we find for the radial and vertical field components:  To complete the model, it remains to specify the z1-dependence of Br(r1,z1), which, for simplicity, we choose to be linear-exponential:
To complete the model, it remains to specify the z1-dependence of Br(r1,z1), which, for simplicity, we choose to be linear-exponential: 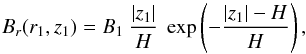 (16)with B1 ≷ 0 and H > 0 two additional free parameters. As usual, the exponential factor ensures a fast enough decline at high |z|, while the linear factor guarantees that the X-shape halo field remains weaker than the horizontal disk field (modeled in Sect. 4) at low |z|. The peak value of Br(r1,z1), reached at | z1 | = H, is [Br(r1,z1)] peak = B1.
(16)with B1 ≷ 0 and H > 0 two additional free parameters. As usual, the exponential factor ensures a fast enough decline at high |z|, while the linear factor guarantees that the X-shape halo field remains weaker than the horizontal disk field (modeled in Sect. 4) at low |z|. The peak value of Br(r1,z1), reached at | z1 | = H, is [Br(r1,z1)] peak = B1.
It directly follows from Eq. (14) that Br → ∞ for r → 0. Evidently, this unphysical behavior arises because all field lines (from all meridional planes) converge to, or diverge from, the z-axis. Nevertheless, in non-axisymmetric configurations (discussed in Sect. 2.4), a slight modification of the magnetic topology near the z-axis, involving the addition of a local azimuthal field component, may be sufficient to remove the singularity.
Model B. An alternative way of avoiding the singularity inherent in the parabolic form of Eq. (12) is to prevent field lines from reaching the z-axis. This can be done by replacing the constant term in the right-hand side of Eq. (12) by a negative power of r. The second term can remain quadratic, but it can also be replaced by a linear term without a cusp appearing at r = 0. We prefer the second possibility, which we feel reproduces the observational situation better. We adjust the ratio of both terms by requiring that each field line reaches its minimum height at (r1,z1). Altogether, we write the equation of field lines as ![\begin{equation} \label{eq_mfl_z_divlinear} z = \frac{1}{n+1} \ z_1 \ \left[ \left( \frac{r}{r_1} \right)^{-n} + n \, \frac{r}{r_1} \right] , \end{equation}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq49.png) (17)with r1 and n two strictly positive free parameters (see Fig. 1b). As before, we invert this equation in favor of z1:
(17)with r1 and n two strictly positive free parameters (see Fig. 1b). As before, we invert this equation in favor of z1: ![\begin{equation} \label{eq_mfl_z1_divlinear} z_1 = (n+1) \ z \ \left[ \left( \frac{r}{r_1} \right)^{-n} + n \, \frac{r}{r_1} \right]^{-1} , \end{equation}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq51.png) (18)and we insert the partial derivatives of z1 into Eqs. (9) and (10), to obtain:
(18)and we insert the partial derivatives of z1 into Eqs. (9) and (10), to obtain: ![\begin{eqnarray} B_r & = & \frac{r_1}{r} \ \frac{z_1}{z} \ B_r(r_1,z_1) \label{eq_Br_z1_divlinear} \\ B_z & = & - \frac{n}{n+1} \ \frac{r_1 \, z_1^2}{r^2 \, z} \ \left[ \left( \frac{r}{r_1} \right)^{-n} - \frac{r}{r_1} \right] \ B_r(r_1,z_1) \cdot \label{eq_Bz_z1_divlinear} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq52.png) The z1-dependence of Br(r1,z1) is again chosen to follow Eq. (16). Finally, the requirement that Br and Bz remain finite in the limit r → 0, where Br ∝ rn − 1 Br(r1,z1) ∝ r2n − 1 and Bz ∝ rn − 2 Br(r1,z1) ∝ r2n − 2, leads to the constraint n ≥ 1.
The z1-dependence of Br(r1,z1) is again chosen to follow Eq. (16). Finally, the requirement that Br and Bz remain finite in the limit r → 0, where Br ∝ rn − 1 Br(r1,z1) ∝ r2n − 1 and Bz ∝ rn − 2 Br(r1,z1) ∝ r2n − 2, leads to the constraint n ≥ 1.
Brief description of our four models of poloidal, X-shape magnetic fields in galactic halos.
In both model A (Eqs. (14), (15)) and model B (Eqs. (19), (20)), Br and Bz are, respectively, even and odd functions of z. The magnetic field is, therefore, symmetric with respect to the galactic midplane2. In principle, it is possible to obtain antisymmetric magnetic fields with the same families of field lines, by choosing for Br(r1,z1) an odd function of z1 – for instance, by replacing the linear factor in the right-hand side of Eq. (16) by (z1/H): 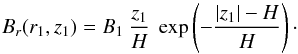 (21)
(21)
2.2.2. Field lines given by r as a function of z
Here, each field line is identified by a value of the function r1(α), where r1 denotes the radius of the considered field line at a specified (and fixed) height z1 (e.g., z1 = 0). In magnetic configurations where field lines do not cross the midplane, one has to adopt two values of z1 with opposite signs and select the positive/negative value of z1 for field lines lying above/below the midplane. The equation of field lines, Eq. (7), can be rewritten in terms of r1, as 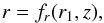 (22)and the expressions for the radial and vertical field components, Eqs. (3) and (5), can be transformed into
(22)and the expressions for the radial and vertical field components, Eqs. (3) and (5), can be transformed into 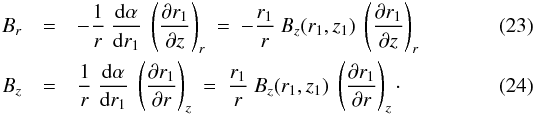 It is now Eq. (24) which expresses magnetic flux conservation (in the vertical direction) between (r1,z1) and (r,z), while the ratio of Eqs. (23) to (24),
It is now Eq. (24) which expresses magnetic flux conservation (in the vertical direction) between (r1,z1) and (r,z), while the ratio of Eqs. (23) to (24), 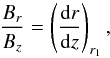 (25)corresponds again to the standard definition of field lines.
(25)corresponds again to the standard definition of field lines.
Model C. For the same reasons as in Sect. 2.2.1, our first choice to describe X-shape field lines is the quadratic function 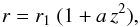 (26)obtained for z1 = 0 and containing the free parameter a > 0 (see Fig. 1c). The inverse equation,
(26)obtained for z1 = 0 and containing the free parameter a > 0 (see Fig. 1c). The inverse equation, 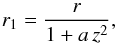 (27)combines with Eqs. (23) and (24) to yield
(27)combines with Eqs. (23) and (24) to yield 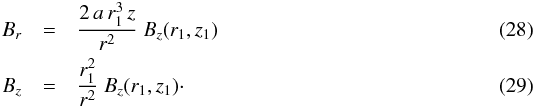 For the r1-dependence of Bz(r1,z1), we assume a simple exponential:
For the r1-dependence of Bz(r1,z1), we assume a simple exponential: 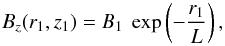 (30)with B1 ≷ 0 and L > 0 two free parameters.
(30)with B1 ≷ 0 and L > 0 two free parameters.
It is interesting to note that, in contrast to the parabolic field derived in Sect. 2.2.1 (Eqs. (14), (15)), the parabolic field obtained here (Eqs. (28), (29)) is perfectly regular. The physical explanation is straightforward: whereas the field lines governed by Eq. (12) all converge to, or diverge from, the same z-axis, the field lines governed by Eq. (26) only cross the r-axis of their own meridional plane.
Model D. For completeness, we also examine the counterpart of Eq. (17), ![\begin{equation} \label{eq_mfl_r_divlinear} r = \frac{1}{n+1} \ r_1 \ \left[ \left( \frac{z}{z_1} \right)^{-n} + n \, \frac{z}{z_1} \right] , \end{equation}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq78.png) (31)with | z1 | and n two strictly positive free parameters and z1 required to take on the same sign as z, i.e., z1 = | z1 | sign z, such that the ratio (z/z1) is always positive (see Fig. 1d). With the inverse equation,
(31)with | z1 | and n two strictly positive free parameters and z1 required to take on the same sign as z, i.e., z1 = | z1 | sign z, such that the ratio (z/z1) is always positive (see Fig. 1d). With the inverse equation, ![\begin{equation} \label{eq_mfl_r1_divlinear} r_1 = (n+1) \ r \ \left[ \left( \frac{z}{z_1} \right)^{-n} + n \, \frac{z}{z_1} \right]^{-1} , \end{equation}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq80.png) (32)Eqs. (23) and (24) reduce to
(32)Eqs. (23) and (24) reduce to ![\begin{eqnarray} B_r & = & - \frac{n}{n+1} \ \frac{r_1^3}{r^2 \, z} \ \left[ \left( \frac{z}{z_1} \right)^{-n} - \frac{z}{z_1} \right] \ B_z(r_1,z_1) \label{eq_Br_r1_divlinear} \\ B_z & = & \frac{r_1^2}{r^2} \ B_z(r_1,z_1) \cdot \label{eq_Bz_r1_divlinear} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq81.png) The r1-dependence of Bz(r1,z1) is again assumed to follow Eq. (30), while the exponent n must now satisfy the constraint
The r1-dependence of Bz(r1,z1) is again assumed to follow Eq. (30), while the exponent n must now satisfy the constraint 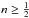 , as can be seen from the behavior Br ∝ z2n − 1 Bz(r1,z1) ∝ z2n − 1 and Bz ∝ z2n Bz(r1,z1) ∝ z2n in the limit z → 0.
, as can be seen from the behavior Br ∝ z2n − 1 Bz(r1,z1) ∝ z2n − 1 and Bz ∝ z2n Bz(r1,z1) ∝ z2n in the limit z → 0.
In both model C (Eqs. (28), (29)) and model D (Eqs. (33), (34)), Br and Bz are, respectively, odd and even functions of z, so that the magnetic field is anti-symmetric with respect to the midplane (see footnote 2). Model D can also be made symmetric, by linking the sign of Bz(r1,z1) to the sign of z1 – for instance, by multiplying the right-hand side of Eq. (30) by sign z1: 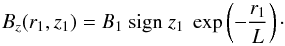 (35)On the other hand, model C cannot be made symmetric, because field lines actually cross the midplane, so that Bz cannot change sign across the midplane.
(35)On the other hand, model C cannot be made symmetric, because field lines actually cross the midplane, so that Bz cannot change sign across the midplane.
2.3. Vertical symmetry
In Sect. 2.2, we presented four different analytical models of poloidal, X-shape magnetic fields for application to galactic halos. Our models in their original form are either symmetric or antisymmetric with respect to the midplane, but their parity can generally be reversed, simply by flipping the parity of the function chosen for Br(r1,z1) or Bz(r1,z1). Thus, models A and B are originally symmetric, with Br(r1,z1) given by an even function of z1 (Eq. (16)), but they also have an antisymmetric version, obtained by turning Br(r1,z1) into an odd function of z1 (Eq. (21)). Similarly, models C and D are originally antisymmetric, with Bz(r1,z1) independent of the sign of z1 (Eq. (30)), but model D also has a symmetric version, obtained by linking the sign of Bz(r1,z1) to the sign of z1 (Eq. (35)). For convenience, the descriptive equations and parameters of the four models, in their original and modified versions, are summarized in Table 1.
Let us now discuss the possible physical origin of X-shape magnetic fields, in connection with their vertical parity. The natural tendency of a conventional galactic dynamo is to generate a symmetric, mainly horizontal, field in the disk and an antisymmetric, possibly dipole-like, field in the halo (e.g., Sokoloff & Shukurov 1990). In general, though, the disk and halo fields are coupled together and do not evolve independently. What usually happens is that one field enslaves and imposes its natural parity to the other, so that the total (disk + halo) field ends up being either symmetric (if the disk dynamo dominates) or antisymmetric (if the halo dynamo dominates) (Moss & Sokoloff 2008). However, in the presence of a moderate galactic wind, the total field can sometimes have mixed parity, being approximately symmetric in the disk and approximately antisymmetric in the halo (Moss et al. 2010).
All-sky RM maps point to such a mixed-parity magnetic configuration in our Galaxy (Rand & Lyne 1994; Oren & Wolfe 1995; Han et al. 1997, 1999; Frick et al. 2001). The situation in external galaxies remains uncertain, but the available data would also tend to suggest mixed parity. In the particular case of NGC 5775, a preliminary derivation of RMs toward the halo revealed a flip in the RM sign across the midplane, consistent with an antisymmetric poloidal halo field (Tüllmann et al. 2000); however, a subsequent RM analysis using additional data at a shorter wavelength (almost free of Faraday rotation) found the RM sign to be continuous across, and out to large distances from, the midplane (Soida et al. 2011). In a more comprehensive study, RM synthesis of a sample of 21 WSRT-SINGS galaxies suggests that the halo field generally possesses a symmetric (axisymmetric spiral quadrupole) component, which would be a mere extension of the symmetric thick-disk field, plus an antisymmetric (almost purely poloidal dipole) component, which would become dominant in the upper halo (Braun et al. 2010).
Regardless of vertical parity, conventional dynamo fields do not naturally come with an X shape, but they can potentially acquire one under the action of a galactic wind (e.g., Brandenburg et al. 1993; Moss et al. 2010). Quite naturally, symmetric X-shape fields would be related to the disk dynamo, while antisymmetric X-shape fields would be related to the halo dynamo. More specifically, the former could be explained with a wind originating near the galactic plane and advecting the disk dynamo field into the halo, while the latter could be explained with a wind blowing from the base of the halo and stretching out the halo dynamo field into an X shape.
From a morphological point of view, in models A, B and D, where low-|z| field lines tend to follow the galactic plane, the X-shape field could conceivably be traced back to an initially horizontal disk field, assuming the wind has the following properties: in model A, the wind would blow obliquely outward from the disk (possibly due to pressure gradients; see the hydrodynamical simulations of Dalla Vecchia & Schaye 2008); in model B, the wind would have a weak oblique component emanating from the disk plus a strong bipolar-jet component emanating from the galactic center (most likely driven by an AGN or by a nuclear starburst); and in model D, the wind would take the form of a champagne flow originating in the central region (probably due to strong stellar activity). In these three models, the X-shape field could a priori be either symmetric or antisymmetric, but if it is indeed connected to the disk field and if the latter has evolved to and retained its natural parity (two non-trivial conditions), the X-shape field should be symmetric. In contrast, in model C, where field lines cross the galactic plane, the X-shape field is easily reconciled with an initially dipole-like halo field, which was blown open either along the plane by an oblique wind from the disk or along the z-axis by a champagne flow from the central region. In this model, the X-shape field would obvioulsy keep the antisymmetric character of the initial dipole-like field.
Somewhat different conclusions on the vertical parity of the halo field emerged from the galactic dynamo calculations of Moss et al. (2010). They found that halo fields that are antisymmetric tend to come with an X shape – a tendency which is reinforced by the presence of a modest wind, whereas halo fields that have become symmetric, presumably under the influence of the disk, tend to lose all resemblance to an X pattern.
2.4. Azimuthal variation
The expressions derived in Sect. 2.2 and discussed in Sect. 2.3 are valid in any given meridional plane. They can be generalized to full three-dimensional space by letting the free parameters (listed in the last column of Table 1) be functions of the azimuthal angle, ϕ.
Here, we consider the very simple case when the only free parameter allowed to vary with ϕ is the normalization field, B1, defined as B1 = Br(r1,H) in models A and B (see Eqs. (16) and (21)) and B1 = Bz(0, | z1 |) in models C and D (see Eqs. (30) and (35)). We further assume that the variation of B1 with ϕ is sinusoidal: 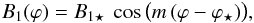 (36)with m the azimuthal wavenumber (taken to be positive) and B1 ⋆ and ϕ⋆ two free parameters (allowed to take on either sign). Clearly, m = 0 corresponds to a purely axisymmetric magnetic field, m = 1 to a bisymmetric field, m = 2 to a quadrisymmetric field, and so on.
(36)with m the azimuthal wavenumber (taken to be positive) and B1 ⋆ and ϕ⋆ two free parameters (allowed to take on either sign). Clearly, m = 0 corresponds to a purely axisymmetric magnetic field, m = 1 to a bisymmetric field, m = 2 to a quadrisymmetric field, and so on.
We now return to model A and show that the nature of its singularity at r = 0 depends on whether the magnetic field is axisymmetric or not. Consider a cylinder of radius R and semi-infinite length, centered on the z-axis and extending from z = 0 to z → + ∞. The magnetic flux across the surface of this cylinder reads 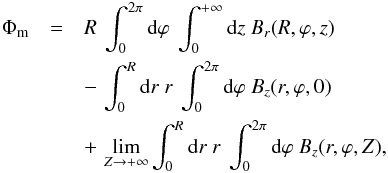 (37)where the three terms in the right-hand side represent, respectively, the flux through the side surface at r = R, the flux through the bottom surface at z = 0 and the flux through the top surface at z → + ∞. These terms can be calculated using Eqs. (14) and (15), in conjunction with Eq. (13) and Eq. (16) or (21). The second and third terms are easily shown to vanish, leaving only
(37)where the three terms in the right-hand side represent, respectively, the flux through the side surface at r = R, the flux through the bottom surface at z = 0 and the flux through the top surface at z → + ∞. These terms can be calculated using Eqs. (14) and (15), in conjunction with Eq. (13) and Eq. (16) or (21). The second and third terms are easily shown to vanish, leaving only 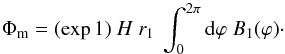 (38)Now, the divergence-free condition implies that Φm must vanish, which, in turn, implies
(38)Now, the divergence-free condition implies that Φm must vanish, which, in turn, implies 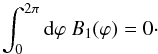 (39)For the sinusoidally-varying field given by Eq. (36), this is possible only if the azimuthal wavenumber m ≠ 0.
(39)For the sinusoidally-varying field given by Eq. (36), this is possible only if the azimuthal wavenumber m ≠ 0.
In consequence, an axisymmetric (m = 0) magnetic field in model A is intrinsically unphysical, in the sense that it automatically leads to a non-vanishing magnetic flux out of, or into, the considered cylinder – in contradiction with the divergence-free condition. This occurs because, in the axisymmetric case, the magnetic field on the side surface of the cylinder points everywhere outward or inward. It then follows that the magnetic field must necessarily become singular along the axis of the cylinder.
In contrast, a non-axisymmetric (m ≠ 0) magnetic field has no net magnetic flux across the side surface of the cylinder, because the magnetic field points alternatively outward and inward. The singularity found at r = 0 arises only because the magnetic field is required to be poloidal everywhere and to become radial as r → 0, so that field lines have no other choice but to run into each other at r = 0. This unacceptable situation could be avoided by simply introducing an azimuthal field component within a small radius, which would enable field lines to remain separate from each other, except for connecting two by two to ensure field line continuity. In this manner, the magnetic field would remain finite everywhere.
Hence, model A can be retained to describe non-axisymmetric magnetic fields outside a small radius. Inside this radius, an azimuthal component must be added to the poloidal field so as to remove the singularity at r = 0. Note that, in practice, it may not be necessary to specify the exact form of the azimuthal component; knowing that the model can be made physical may be sufficient.
Model B does not become singular at r = 0, even in the axisymmetric case, because all the magnetic flux leaving/entering through the side surface of the cylinder finds its way in/out through the top surface (see Fig. 1b). This can be verified mathematically by examining the three terms in the right-hand side of Eq. (37). The first term (flux through the side surface) has the same expression as in model A, because in both models z1 is a linear function of z (see Eq. (13) for model A and Eq. (18) for model B). The second term (flux through the bottom surface) vanishes, because, like in model A, Bz = 0 at z = 0 (see Eq. (15) for model A and Eq. (20) for model B). The difference between the two models comes from the third term (flux through the top surface), which vanishes in model A, but is equal and opposite to the first term (flux through the side surface) in model B.
3. Analytical models of three-dimensional magnetic fields in galactic halos
3.1. Magnetic field with a spiral horizontal component
In this section, we let the magnetic field have both poloidal and azimuthal components. Moreover, based on observations of external face-on spiral galaxies, we assume that the magnetic field projected onto the galactic plane forms a spiral pattern, in which each spiral line satisfies an equation of the type 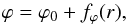 (40)where ϕ0 is the azimuthal angle at which the line passes through a chosen (and fixed) radius r0, and fϕ(r) is a monotonic function of r which vanishes at r0. The pitch angle of the spiral, p, defined as the angle between the tangent to the spiral and the azimuthal direction, is given by
(40)where ϕ0 is the azimuthal angle at which the line passes through a chosen (and fixed) radius r0, and fϕ(r) is a monotonic function of r which vanishes at r0. The pitch angle of the spiral, p, defined as the angle between the tangent to the spiral and the azimuthal direction, is given by 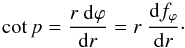 (41)In most studies of galactic magnetic fields, p is supposed to be constant, which implies a logarithmic spiral, with
(41)In most studies of galactic magnetic fields, p is supposed to be constant, which implies a logarithmic spiral, with 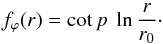 (42)However, the assumption of constant pitch angle is generally not realistic, either in external galaxies or in our own Galaxy (e.g., Fletcher 2010). This unrealistic assumption is not made in our formalism, which naturally allows the pitch angle to vary with galactic radius.
(42)However, the assumption of constant pitch angle is generally not realistic, either in external galaxies or in our own Galaxy (e.g., Fletcher 2010). This unrealistic assumption is not made in our formalism, which naturally allows the pitch angle to vary with galactic radius.
When the magnetic field has an azimuthal component (Bϕ ≠ 0), ϕ is no longer constant along field lines and, therefore, may no longer serve as one of the Euler potentials. Instead, one can use ϕ0 and, accordingly, replace Eq. (2) by 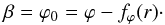 (43)With this choice of β, Eq. (1) gives for the radial, azimuthal and vertical field components
(43)With this choice of β, Eq. (1) gives for the radial, azimuthal and vertical field components 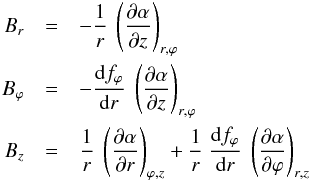 or, equivalently,
or, equivalently, 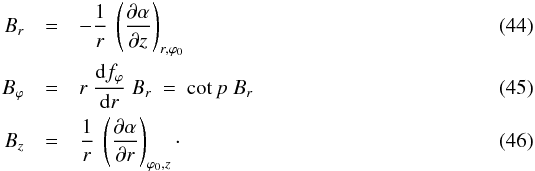 Equations (44) and (46) are the direct counterparts of Eqs. (3) and (5) in Sect. 2; the only difference between both pairs of equations is that the partial derivatives of α in Eqs. (3) and (5) are taken at constant ϕ, i.e., in meridional planes, whereas those in Eqs. (44) and (46) are taken at constant ϕ0, i.e., along the spiral surfaces defined by Eq. (40). Equation (45), for its part, states that the horizontal magnetic field has pitch angle p and, therefore, follows the spiral lines defined in the galactic plane by Eq. (40). Let us emphasize again that p is not required to remain constant along field lines.
Equations (44) and (46) are the direct counterparts of Eqs. (3) and (5) in Sect. 2; the only difference between both pairs of equations is that the partial derivatives of α in Eqs. (3) and (5) are taken at constant ϕ, i.e., in meridional planes, whereas those in Eqs. (44) and (46) are taken at constant ϕ0, i.e., along the spiral surfaces defined by Eq. (40). Equation (45), for its part, states that the horizontal magnetic field has pitch angle p and, therefore, follows the spiral lines defined in the galactic plane by Eq. (40). Let us emphasize again that p is not required to remain constant along field lines.
3.2. Magnetic field with a spiral horizontal component and an X-shape poloidal component
The similarity between the pair of Eqs. (3), (5) and the pair of Eqs. (44), (46) indicates that the derivation presented in Sect. 2.2 can be repeated here, with this only difference that the working space is now a spiral surface of constant ϕ0 rather than a meridional plane of constant ϕ. Likewise, the azimuthal variation introduced in Sect. 2.4 can be taken up here, with Eq. (36) written as a function of ϕ0 instead of ϕ. For future reference, we recall that (see Eq. (40)) 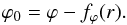 (47)In the same spirit as in Sect. 2.2, we distinguish between two classes of poloidal field lines, which we successively study in Sects. 3.2.1 and 3.2.2. Note that we only need to worry about the radial and vertical field components, as the azimuthal field, given by Eq. (45), can easily be obtained from the radial field once the shape of the spiral has been specified.
(47)In the same spirit as in Sect. 2.2, we distinguish between two classes of poloidal field lines, which we successively study in Sects. 3.2.1 and 3.2.2. Note that we only need to worry about the radial and vertical field components, as the azimuthal field, given by Eq. (45), can easily be obtained from the radial field once the shape of the spiral has been specified.
3.2.1. Poloidal field lines given by z as a function of r
As in Sect. 2.2.1, we start by adopting a reference radius r1. Each field line can then be identified by the coordinates (ϕ1,z1) at which it intersects the cylinder of radius r1. Since the reference radius, r1, and the normalization radius of the spiral, r0, both have unique values (common to all field lines), we may, for convenience, let r1 = r0, and hence ϕ1 = ϕ0.
Following the procedure of Sect. 2.2.1, on a surface of constant ϕ0 rather than constant ϕ, we transform Eqs. (44) and (46) into 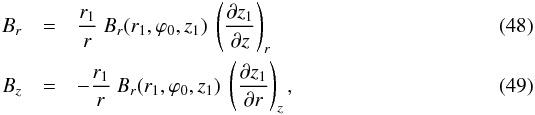 with r1 the reference radius, z1 set by our adopted X shape (Eq. (13) in model A and Eq. (18) in model B), and ϕ0 set by our adopted spiral (Eq. (47)). A comparison with Eqs. (9), (10) shows that the expressions of Br and Bz obtained in Sect. 2.2.1 remain valid here provided only that Br(r1,z1) be replaced by Br(r1,ϕ0,z1).
with r1 the reference radius, z1 set by our adopted X shape (Eq. (13) in model A and Eq. (18) in model B), and ϕ0 set by our adopted spiral (Eq. (47)). A comparison with Eqs. (9), (10) shows that the expressions of Br and Bz obtained in Sect. 2.2.1 remain valid here provided only that Br(r1,z1) be replaced by Br(r1,ϕ0,z1).
Thus, in model A, Eqs. (14), (15) become 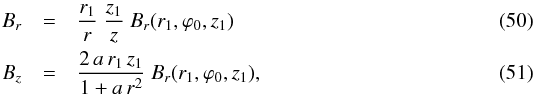 and in model B, Eqs. (19), (20) become
and in model B, Eqs. (19), (20) become ![\begin{eqnarray} B_r & = & \frac{r_1}{r} \ \frac{z_1}{z} \ B_r(r_1,\varphi_0,z_1) \label{eq_Br_z1_divlinear_spiral} \\ B_z & = & - \frac{n}{n+1} \ \frac{r_1 \, z_1^2}{r^2 \, z} \ \left[ \left( \frac{r}{r_1} \right)^{-n} - \frac{r}{r_1} \right] \ B_r(r_1,\varphi_0,z_1) \cdot \label{eq_Bz_z1_divlinear_spiral} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq124.png) We assume that Br(r1,ϕ0,z1) has the same vertical variation as in Sect. 2.2.1 (see Eqs. (16) and (21)) and that its azimuthal variation is governed by Eq. (36) written as a function of ϕ0 instead of ϕ (see first paragraph of Sect. 3.2). The result is
We assume that Br(r1,ϕ0,z1) has the same vertical variation as in Sect. 2.2.1 (see Eqs. (16) and (21)) and that its azimuthal variation is governed by Eq. (36) written as a function of ϕ0 instead of ϕ (see first paragraph of Sect. 3.2). The result is 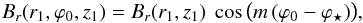 (54)with Br(r1,z1) given by Eq. (16) for symmetric magnetic fields and by Eq. (21) for antisymmetric magnetic fields, m the azimuthal wavenumber and ϕ⋆ a free parameter.
(54)with Br(r1,z1) given by Eq. (16) for symmetric magnetic fields and by Eq. (21) for antisymmetric magnetic fields, m the azimuthal wavenumber and ϕ⋆ a free parameter.
3.2.2. Poloidal field lines given by r as a function of z
Here, we adopt a reference height z1 – or two opposite-signed values of z1 if field lines do not cross the midplane. Each field line can then be identified by the coordinates (r1,ϕ1) at which it intersects the horizontal plane – or one of the two horizontal planes – of height z1. Since the value of r1 now depends on the considered field line, we may no longer equate r1 to r0, which must remain a separate free parameter. According to Eq. (40), the azimuthal angles associated with r1 and r0 are related through ϕ1 = ϕ0 + fϕ(r1).
In the same fashion as in Sect. 2.2.2, we transform Eqs. (44) and (46) into 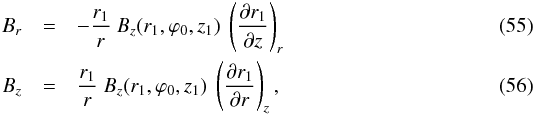 with z1 the reference height, r1 set by our adopted X shape (Eq. (27) in model C and Eq. (32) in model D), and ϕ0 set by our adopted spiral (Eq. (47)). A comparison with Eqs. (23), (24) shows that the results obtained in Sect. 2.2.2 remain valid with Bz(r1,z1) replaced by Bz(r1,ϕ0,z1).
with z1 the reference height, r1 set by our adopted X shape (Eq. (27) in model C and Eq. (32) in model D), and ϕ0 set by our adopted spiral (Eq. (47)). A comparison with Eqs. (23), (24) shows that the results obtained in Sect. 2.2.2 remain valid with Bz(r1,z1) replaced by Bz(r1,ϕ0,z1).
Thus, in model C, Eqs. (28), (29) become 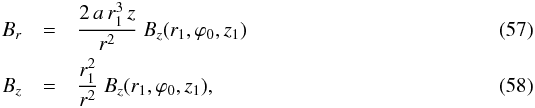 and in model D, Eqs. (33), (34) become
and in model D, Eqs. (33), (34) become ![\begin{eqnarray} B_r & = & - \frac{n}{n+1} \ \frac{r_1^3}{r^2 \, z} \ \left[ \left( \frac{z}{z_1} \right)^{-n} - \frac{z}{z_1} \right] \ B_z(r_1,\varphi_0,z_1) \label{eq_Br_r1_divlinear_spiral} \\ B_z & = & \frac{r_1^2}{r^2} \ B_z(r_1,\varphi_0,z_1) \cdot \label{eq_Bz_r1_divlinear_spiral} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq131.png) If we assume that Bz(r1,ϕ0,z1) has the same radial variation as in Sect. 2.2.2 (see Eqs. (30) and (35)) and that its azimuthal variation is governed by Eq. (36) written as a function of ϕ0, we obtain
If we assume that Bz(r1,ϕ0,z1) has the same radial variation as in Sect. 2.2.2 (see Eqs. (30) and (35)) and that its azimuthal variation is governed by Eq. (36) written as a function of ϕ0, we obtain 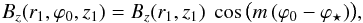 (61)with Bz(r1,z1) given by Eq. (30) for antisymmetric magnetic fields and by Eq. (35) for symmetric magnetic fields, m the azimuthal wavenumber and ϕ⋆ a free parameter.
(61)with Bz(r1,z1) given by Eq. (30) for antisymmetric magnetic fields and by Eq. (35) for symmetric magnetic fields, m the azimuthal wavenumber and ϕ⋆ a free parameter.
Brief description of our four models of three-dimensional, X-shape + spiral magnetic fields in galactic halos.
3.3. Generalization to z-dependent pitch angles
A remaining limitation of our formalism is that the magnetic pitch angle depends only on galactic radius. Yet, because galactic differential rotation probably decreases with distance from the midplane (e.g., Levine et al. 2008; Marasco & Fraternali 2011; Jałocha et al. 2011, and references therein), we expect field lines to become less tightly wound up, and hence to have a larger pitch angle, at higher altitudes. Note that this is just a qualitative argument, and one should not try to directly link the vertical variation of the pitch angle to that of the rotational velocity. For instance, while a vertical decrease in rotational velocity does indeed reduce the generation of azimuthal field through the shearing of radial field, the vertical velocity gradient itself generates azimuthal field through the shearing of vertical field. Furthermore, the pitch angle depends on other factors, such as the intensity of helical turbulence and the scale height of the interstellar gas (e.g., Fletcher 2010).
Mathematically, we can allow the pitch angle to vary with both r and z by letting each field line obey an equation similar to Eq. (40), with fϕ(r) replaced by fϕ(r,z): 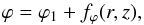 (62)where ϕ1 is the azimuthal angle at which the field line passes through either the reference radius, r1 (in models A and B), or the reference height, z1 (in models C and D). In both cases, one must have3fϕ(r1,z1) = 0. The pitch angle, p(r,z), associated with a given winding function, fϕ(r,z), is easily obtained by differentiation:
(62)where ϕ1 is the azimuthal angle at which the field line passes through either the reference radius, r1 (in models A and B), or the reference height, z1 (in models C and D). In both cases, one must have3fϕ(r1,z1) = 0. The pitch angle, p(r,z), associated with a given winding function, fϕ(r,z), is easily obtained by differentiation: 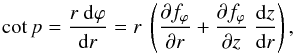 (63)where the factor (dz/dr) = (Bz/Br) depends on the chosen model for the poloidal field. Conversely, the winding function associated with a given pitch angle is obtained by integrating Eq. (63) along the poloidal field line through (r,z):
(63)where the factor (dz/dr) = (Bz/Br) depends on the chosen model for the poloidal field. Conversely, the winding function associated with a given pitch angle is obtained by integrating Eq. (63) along the poloidal field line through (r,z): 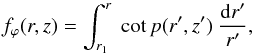 (64)where r1 is either the reference radius (in models A and B) or the radial label of the field line (in models C and D; see Eqs. (27) and (32), respectively); z1 is either the vertical label of the field line (in models A and B; see Eqs. (13) and (18), respectively) or the reference height (in models C and D); and z′ is the height of the field line at radius r′ (given by the primed versions of Eqs. (12), (17), (26) and (31) for models A, B, C and D, respectively)4
(64)where r1 is either the reference radius (in models A and B) or the radial label of the field line (in models C and D; see Eqs. (27) and (32), respectively); z1 is either the vertical label of the field line (in models A and B; see Eqs. (13) and (18), respectively) or the reference height (in models C and D); and z′ is the height of the field line at radius r′ (given by the primed versions of Eqs. (12), (17), (26) and (31) for models A, B, C and D, respectively)4
A possible simple choice for the pitch angle, which accounts for the decrease in differential rotation with height, is 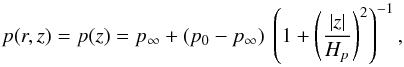 (65)with p0 the pitch angle at midplane, p∞ the pitch angle at infinity and Hp the scale height.
(65)with p0 the pitch angle at midplane, p∞ the pitch angle at infinity and Hp the scale height.
The three components of the magnetic field can now be derived in the same manner as in Sect. 3.1. With 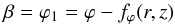 (66)chosen for the second Euler potential, Eq. (1) yields
(66)chosen for the second Euler potential, Eq. (1) yields 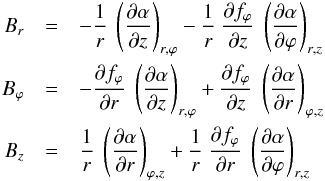 or, equivalently,
or, equivalently, 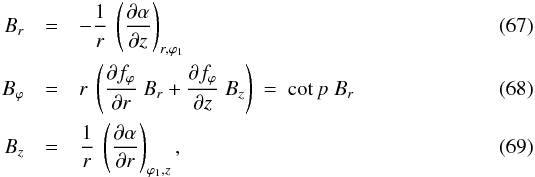 where Eq. (63) was used to write the second equality in Eq. (68). The expressions of Br and Bz are the same as those obtained in Sect. 3.1 (Eqs. (44) and (46)), with ϕ1 substituting for ϕ0. The final expression of Bϕ is also the same as in Sect. 3.1 (Eq. (45)), which is a direct consequence of the definition of the pitch angle. On the other hand, the intermediate expression of Bϕ is more general, containing not only a term ∝Br (as in Eq. (45)), but also a term ∝Bz. This new term reflects the explicit z-dependence of the azimuthal winding of field lines, as described by fϕ (see Eq. (62)). The first equality in Eq. (68) can also be viewed as the mathematical statement that the magnetic field is tangent to the surfaces defined by Eq. (62).
where Eq. (63) was used to write the second equality in Eq. (68). The expressions of Br and Bz are the same as those obtained in Sect. 3.1 (Eqs. (44) and (46)), with ϕ1 substituting for ϕ0. The final expression of Bϕ is also the same as in Sect. 3.1 (Eq. (45)), which is a direct consequence of the definition of the pitch angle. On the other hand, the intermediate expression of Bϕ is more general, containing not only a term ∝Br (as in Eq. (45)), but also a term ∝Bz. This new term reflects the explicit z-dependence of the azimuthal winding of field lines, as described by fϕ (see Eq. (62)). The first equality in Eq. (68) can also be viewed as the mathematical statement that the magnetic field is tangent to the surfaces defined by Eq. (62).
While Eq. (68) provides a general expression of Bϕ, common to the four different models, Eqs. (67) and (69) need to be specifically worked out for each model. The resulting expressions of Br and Bz can be directly taken from Sects. 3.2.1 and 3.2.2, with ϕ0 replaced by ϕ1, keeping in mind that (see Eq. (62)) 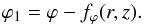 (70)The final equations are shown below, a summary is presented in Table 2 and the four models are illustrated in Fig. 2.
(70)The final equations are shown below, a summary is presented in Table 2 and the four models are illustrated in Fig. 2.
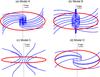 |
Fig. 2 Small set of field lines for each of our four models of three-dimensional, X-shape + spiral magnetic fields in galactic halos, as seen from an oblique angle. The parameters of the poloidal field take on the same values as in Fig. 1, while the pitch angle is assigned a constant value of p = −30°, plausibly representative of galactic halos. The selected field lines correspond to those displayed in Fig. 1 (i.e., they have the same labels (z1,ϕ1) or (r1,ϕ1)), except in model D, where only four field lines are drawn for clarity. Each box is a (30 kpc)3 cube centered on the galactic center. The trace of the galactic plane is indicated by the solid red circle, and the z-axis by the vertical, dot-dashed black line. |
3.3.1. Poloidal field lines given by z as a function of r
As a reminder, r1 is the reference radius, z1 the vertical label of field lines (dependent on the chosen X-shape model) and ϕ1 their azimuthal label (always set by Eq. (70)). For a general function z1(r,z), 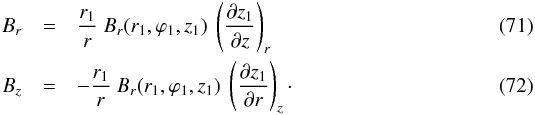 In model A, where z1 is given by Eq. (13),
In model A, where z1 is given by Eq. (13), 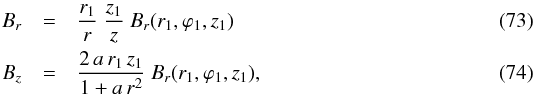 and in model B, where z1 is given by Eq. (18),
and in model B, where z1 is given by Eq. (18), ![\begin{eqnarray} B_r & = & \frac{r_1}{r} \ \frac{z_1}{z} \ B_r(r_1,\varphi_1,z_1) \label{eq_Br_z1_divlinear_spiral_rz} \\ B_z & = & - \frac{n}{n+1} \ \frac{r_1 \, z_1^2}{r^2 \, z} \ \left[ \left( \frac{r}{r_1} \right)^{-n} - \frac{r}{r_1} \right] \ B_r(r_1,\varphi_1,z_1) \cdot \label{eq_Bz_z1_divlinear_spiral_rz} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq168.png) In the above equations,
In the above equations, 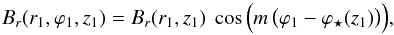 (77)with Br(r1,z1) taken from Eq. (16) for symmetric magnetic fields and from Eq. (21) for antisymmetric magnetic fields, m the azimuthal wavenumber and ϕ⋆(z1) a smoothly varying function of z1. When ϕ⋆(z1) reduces to a constant, one recovers exactly the results of Sect. 3.2.1, where ϕ1 = ϕ0.
(77)with Br(r1,z1) taken from Eq. (16) for symmetric magnetic fields and from Eq. (21) for antisymmetric magnetic fields, m the azimuthal wavenumber and ϕ⋆(z1) a smoothly varying function of z1. When ϕ⋆(z1) reduces to a constant, one recovers exactly the results of Sect. 3.2.1, where ϕ1 = ϕ0.
3.3.2. Poloidal field lines given by r as a function of z
Here, z1 is the reference height, r1 the model-dependent radial label of field lines and ϕ1 their azimuthal label set by Eq. (70). For a general function r1(r,z), 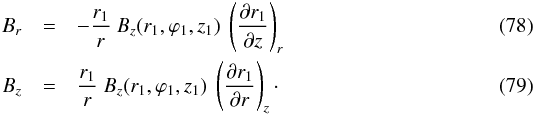 In model C, where r1 is given by Eq. (27),
In model C, where r1 is given by Eq. (27), 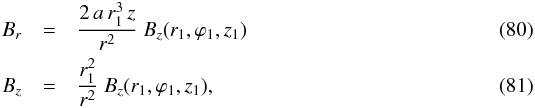 and in model D, where r1 is given by Eq. (32),
and in model D, where r1 is given by Eq. (32), ![\begin{eqnarray} B_r & = & - \frac{n}{n+1} \ \frac{r_1^3}{r^2 \, z} \ \left[ \left( \frac{z}{z_1} \right)^{-n} - \frac{z}{z_1} \right] \ B_z(r_1,\varphi_1,z_1) \label{eq_Br_r1_divlinear_spiral_rz} \\ B_z & = & \frac{r_1^2}{r^2} \ B_z(r_1,\varphi_1,z_1) \cdot \label{eq_Bz_r1_divlinear_spiral_rz} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq173.png) In the above equations,
In the above equations, 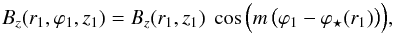 (84)with Bz(r1,z1) taken from Eq. (30) for antisymmetric magnetic fields and from Eq. (35) for symmetric magnetic fields, m the azimuthal wavenumber and ϕ⋆(r1) a smoothly varying function of r1. To recover the results of Sect. 3.2.2, where ϕ1 = ϕ0 + fϕ(r1), it suffices to identify ϕ⋆(r1) with fϕ(r1) to within a constant.
(84)with Bz(r1,z1) taken from Eq. (30) for antisymmetric magnetic fields and from Eq. (35) for symmetric magnetic fields, m the azimuthal wavenumber and ϕ⋆(r1) a smoothly varying function of r1. To recover the results of Sect. 3.2.2, where ϕ1 = ϕ0 + fϕ(r1), it suffices to identify ϕ⋆(r1) with fϕ(r1) to within a constant.
Brief description of our two models of three-dimensional, X-shape + spiral magnetic fields in galactic disks.
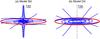 |
Fig. 3 Small set of field lines for our two models of three-dimensional, X-shape + spiral magnetic fields in galactic disks, as seen from an oblique angle: a) model Bd (poloidal component described by Eq. (87)) with r1 = 3 kpc and n = 2; and b) model Dd (Eq. (31)) with | z1 | = 1.5 kpc and |
4. Analytical models of three-dimensional magnetic fields in galactic disks
Magnetic fields in most galactic disks are approximately horizontal and follow a spiral pattern (e.g., Wielebinski & Krause 1993; Dumke et al. 1995; Beck 2009; Braun et al. 2010). In Sect. 3, we already derived the general expression of a magnetic field having a spiral horizontal component (Eqs. (67)–(69)), and we applied this general expression to our four models of magnetic fields with an X-shape poloidal component (Sects. 3.3.1 and 3.3.2). We now use the results of Sect. 3 to discuss and model magnetic fields in galactic disks.
4.1. Purely horizontal magnetic field with a spiral pattern
In most studies of magnetic fields in galactic disks (in particular, in the disk of our own Galaxy), the field is assumed to be purely horizontal (Bz = 0). This simplifying assumption has important implications for the r-dependence of Br, which are generally overlooked. These implications, which directly emerge from our formalism, are discussed below.
When Bz = 0, Eq. (69) implies that α(r,ϕ1,z) reduces to a function of ϕ1 and z only, with the dependence on r dropped out. It then follows from Eq. (67) that Br can be written as 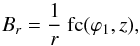 (85)or, in the case of a sinusoidal variation with ϕ1,
(85)or, in the case of a sinusoidal variation with ϕ1, 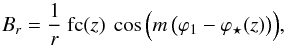 (86)where ϕ1 (given by Eq. (70)) is the azimuthal angle at which the field line passing through (r,ϕ,z) crosses a reference radius r1, m is the azimuthal wavenumber, and fc(z) and ϕ⋆(z) are two function of z. The key point here is that, unless fc(z) = 0 (trivial case of a perfectly circular field), Br ∝ (1/r), regardless of azimuthal symmetry, i.e., in axisymmetric (m = 0) as well as bisymmetric (m = 1) and higher-order (m ≥ 2) configurations. Aside from the fact that this (1/r) dependence is hardly consistent with radio (synchrotron) observations of spiral galaxies (Rainer Beck, priv. comm.), the field becomes singular, with Br → ∞ for r → 0. The physical reason for this singularity is similar to that put forward in model A (see below Eq. (16)), namely, all field lines (with all values of ϕ1) in a given horizontal plane converge to, or diverge from, the z-axis.
(86)where ϕ1 (given by Eq. (70)) is the azimuthal angle at which the field line passing through (r,ϕ,z) crosses a reference radius r1, m is the azimuthal wavenumber, and fc(z) and ϕ⋆(z) are two function of z. The key point here is that, unless fc(z) = 0 (trivial case of a perfectly circular field), Br ∝ (1/r), regardless of azimuthal symmetry, i.e., in axisymmetric (m = 0) as well as bisymmetric (m = 1) and higher-order (m ≥ 2) configurations. Aside from the fact that this (1/r) dependence is hardly consistent with radio (synchrotron) observations of spiral galaxies (Rainer Beck, priv. comm.), the field becomes singular, with Br → ∞ for r → 0. The physical reason for this singularity is similar to that put forward in model A (see below Eq. (16)), namely, all field lines (with all values of ϕ1) in a given horizontal plane converge to, or diverge from, the z-axis.
Many existing studies completely ignore this (1/r) dependence of Br (e.g., Han & Qiao 1994; Sun et al. 2008). Others correctly include the (1/r) factor in the expression of Br, but either they choose to turn a blind eye to the singular behavior of Br at r = 0 (e.g., Sofue & Fujimoto 1983; Prouza & Šmída 2003) or they artificially get rid of it by replacing, inside a certain radius, the factor (1/r) by a constant or a regular function of r (e.g., Stanev 1997; Harari et al. 1999; Jansson et al. 2009; Pshirkov et al. 2011) – which leads to a violation of the divergence-free condition.
Like in model A, there are basically two ways of removing the singularity at r = 0, while keeping the magnetic field divergence-free. The first way is to let the horizontal field at small radii deviate from a pure spiral (defined here by Eq. (62)), in such a way that field lines connect two by two away from the z-axis and remain separate from all other field lines. This re-configuration is possible only for non-axisymmetric fields, because connecting field lines must necessarily have opposite signs of Br for the field direction to remain continuous at their connection point.
The alternative approach is to allow for a departure from a strictly horizontal magnetic field. With an adequate vertical component, field lines can bend away from the midplane as they approach the z-axis and continue into the halo without ever reaching the z-axis. The advantage of this approach is that it can be implemented in both axisymmetric and non-axisymmetric configurations. Two illustrative examples are provided in Sect. 4.2.
4.2. Three-dimensional magnetic field with a spiral horizontal component
Two of the four models developed in Sects. 2 and 3 for magnetic fields in galactic halos (models B and D) have specific properties which should make them easily adapted to galactic disks: unlike model A, they are regular at r = 0; unlike model C, they can be symmetric with respect to the midplane; and they both have nearly horizontal field lines at low |z|. In this section, we present disk versions of these two models, which we refer to as models Bd and Dd, respectively. The descriptive equations of these two models are listed in Table 3, and a few representative field lines are plotted in Fig. 3.
The notation used for disk fields is the same as that used for halo fields, namely, (r1,ϕ1,z1) denotes the point where the field line passing by (r,ϕ,z) crosses the chosen reference coordinate, r1 (in model Bd) or z1 (in model Dd). In practice, z1 (in model Bd) and r1 (in model Dd) are related to (r,z) via the shape of poloidal field lines (see Eqs. (88) and (32), respectively). Moreover, ϕ1 is related to (r,ϕ,z) via the winding function of the spiral, fϕ(r,z) (see Eq. (70)), which, in turn, can be expressed in terms of the pitch angle, p(r,z), through Eq. (64). The pitch angle also links the azimuthal field to the radial field through Eq. (68).
Model Bd. Model B is not immediately fit to represent disk magnetic fields, for two reasons. First, low-|z| field lines outside the reference radius, r1, rise up too steeply into the halo (see Fig. 1b). Second, the magnetic field strength peaks too high above the midplane (the reference field Br(r1,z1) peaks at | z1 | = H; see Eqs. (16) and (21)). As we now show, both shortcomings can easily be overcome.
First, to reduce the slope of low-|z| field lines outside r1, we replace the linear term ∝(r/r1) in Eq. (17) by a slower-rising term ∝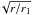 . Under our previous requirement that each field line reaches its minimum height at (r1,z1), the equation of field lines becomes
. Under our previous requirement that each field line reaches its minimum height at (r1,z1), the equation of field lines becomes ![\begin{equation} \label{eq_mfl_z_divlinear_disk} z = \frac{1}{2n+1} \ z_1 \ \left[ \left( \frac{r}{r_1} \right)^{-n} + 2n \, \sqrt{\frac{r}{r_1}} \right] , \end{equation}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq194.png) (87)and, after inversion, the vertical label of field lines reads
(87)and, after inversion, the vertical label of field lines reads ![\begin{equation} \label{eq_mfl_z1_divlinear_disk} z_1 = (2n+1) \ z \ \left[ \left( \frac{r}{r_1} \right)^{-n} + 2n \, \sqrt{\frac{r}{r_1}} \right]^{-1} \cdot \end{equation}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq195.png) (88)In view of Eqs. (71), (72), the poloidal field components are then given by
(88)In view of Eqs. (71), (72), the poloidal field components are then given by ![\begin{eqnarray} B_r & = & \frac{r_1}{r} \ \frac{z_1}{z} \ B_r(r_1,\varphi_1,z_1) \label{eq_Br_z1_divlinear_disk} \\ B_z & = & - \frac{n}{2n+1} \ \frac{r_1 \, z_1^2}{r^2 \, z} \ \left[ \left( \frac{r}{r_1} \right)^{-n} - \sqrt{\frac{r}{r_1}} \right] \ B_r(r_1,\varphi_1,z_1) \cdot \label{eq_Bz_z1_divlinear_disk} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq196.png) The value of the exponent n in Eq. (90) is a little more restricted than for halo magnetic fields, not because of differences in the expressions of Bz itself (Eq. (90) for disk fields vs. Eq. (76) for halo fields), but because of differences in the expressions of Br(r1,z1) (Eq. (91) for disk fields vs. Eq. (16) or (21) for halo fields). Here, the behavior Br ∝ rn − 1 Br(r1,z1) ∝ rn − 1 and Bz ∝ rn − 2 Br(r1,z1) ∝ rn − 2 in the limit r → 0 imposes n ≥ 2.
The value of the exponent n in Eq. (90) is a little more restricted than for halo magnetic fields, not because of differences in the expressions of Bz itself (Eq. (90) for disk fields vs. Eq. (76) for halo fields), but because of differences in the expressions of Br(r1,z1) (Eq. (91) for disk fields vs. Eq. (16) or (21) for halo fields). Here, the behavior Br ∝ rn − 1 Br(r1,z1) ∝ rn − 1 and Bz ∝ rn − 2 Br(r1,z1) ∝ rn − 2 in the limit r → 0 imposes n ≥ 2.
Second, to bring the peak in magnetic field strength from the halo down to the midplane, we keep the expression of Br(r1,ϕ1,z1) provided by Eq. (77), but we change the vertical profile of the function Br(r1,z1) entering Eq. (77) from a linear-exponential (as in Eqs. (16) and (21)) to a pure exponential: 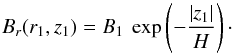 (91)With this simple choice, Br(r1,z1) is an even function of z1, so that the magnetic field is symmetric with respect to the midplane, as appropriate for galactic disks (e.g., Krause 2009; Braun et al. 2010; Beck & Wielebinski 2013). Let us just mention for completeness that model Bd could in principle be made antisymmetric, simply by mutliplying the right-hand side of Eq. (91) by sign z1.
(91)With this simple choice, Br(r1,z1) is an even function of z1, so that the magnetic field is symmetric with respect to the midplane, as appropriate for galactic disks (e.g., Krause 2009; Braun et al. 2010; Beck & Wielebinski 2013). Let us just mention for completeness that model Bd could in principle be made antisymmetric, simply by mutliplying the right-hand side of Eq. (91) by sign z1.
Model Dd. Model D is more straightforward to adapt to galactic disks. Indeed, low-|z| field lines are already closely aligned with the disk plane, and the magnetic field is clearly much stronger in a narrow band around the plane than in the halo (see Fig. 1d).
To obtain a disk version of model D, it suffices to introduce two simple restrictions. First, in the equation of field lines (Eq. (31)), the exponent n must be such that the magnetic field strength peaks, while remaining finite, at the midplane. Since Br ∝ z2n − 1 and Bz ∝ z2n in the limit z → 0 (see below Eq. (34)), this can be achieved with, and only with, 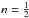 . Second, if disk magnetic fields are indeed symmetric with respect to the midplane, one must select Eq. (35) rather than Eq. (30) for the radial profile of the reference field Bz(r1,z1).
. Second, if disk magnetic fields are indeed symmetric with respect to the midplane, one must select Eq. (35) rather than Eq. (30) for the radial profile of the reference field Bz(r1,z1).
To conclude, we point out a very nice aspect of model Dd. Since its field lines are densely packed and quasi-horizontal in the disk, while they are broadly spread out and X-shaped in the halo, model Dd could potentially serve as a single model for complete galactic magnetic fields, including both the disk and the halo contributions. Similarly, although less strikingly, model Bd could potentially serve as a single, complete field model in the cases of galaxies harboring strong vertical fields near their centers. Such a use of models Dd and Bd would, of course, be conceivable only to the extent that the disk and halo fields have the same vertical parity (namely, symmetric with respect to the midplane).
 |
Fig. 4 Maps of the normalized synchrotron polarization bars (or headless vectors) rotated by 90° toward a hypothetical external galaxy seen edge-on, as predicted by our four models of three-dimensional, X-shape + spiral magnetic fields in galactic halos. The magnetic field is supposed to be axisymmetric (m = 0), the parameters of its poloidal component have the same values as in Figs. 1 and 2, and the pitch angle is given by Eq. (65) with p0 = −10°, p∞ = −90° and Hp = 3 kpc. The trace of the galactic plane is indicated by the horizontal, solid red line, and the z-axis by the vertical, dot-dashed black line. The rotated polarization bars trace the average magnetic field orientation in the plane of the sky, and their level of grey reflects the magnitude of the polarized intensity (with a logarithmic scale). |
5. Synchrotron polarization maps
By construction, our models of magnetic fields in galactic halos are characterized by a poloidal component that has an X shape at large r and |z| (see Fig. 1). However, in the presence of an azimuthal field component, this X shape can be partly masked by the spiraling of field lines (see Fig. 2). How does this affect synchrotron polarization maps? Does the azimuthal field wash out the X pattern formed by the poloidal field alone?
To address this question, we simulate synchrotron polarization maps of a hypothetical external galaxy seen edge-on, for our four models in their axisymmetric versions (m = 0). The parameters of the poloidal field are assigned the same values as in Figs. 1 and 2, the normalization field, B1, is set to an arbitrary value (irrelevant here), and the pitch angle, p, is assumed to obey Eq. (65) with p0 = −10°, p∞ = −90° and Hp = 3 kpc. We compute the synchrotron emissivity, 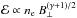 , where B⊥ is the magnetic field perpendicular to the line of sight, ne is the density of relativistic electrons and γ is the power-law index of the relativistic-electron energy spectrum. Here, we adopt the conservative value γ = 3, and we make the standard double assumption that (1) relativistic electrons represent a fixed fraction of the cosmic-ray population and (2) cosmic rays and magnetic fields are in (energy or pressure) equipartition5, so that
, where B⊥ is the magnetic field perpendicular to the line of sight, ne is the density of relativistic electrons and γ is the power-law index of the relativistic-electron energy spectrum. Here, we adopt the conservative value γ = 3, and we make the standard double assumption that (1) relativistic electrons represent a fixed fraction of the cosmic-ray population and (2) cosmic rays and magnetic fields are in (energy or pressure) equipartition5, so that 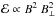 . We then compute the associated Stokes parameters U and Q, remembering that synchrotron emission is (partially) linearly polarized perpendicular to B⊥ and assuming that the intrinsic degree of linear polarization is uniform throughout the galaxy (consistent with the power-law index, γ, being uniform). We define a grid of sightlines through the galaxy, integrate the Stokes parameters along every sightline and rotate the resulting polarized-intensity bar (or headless vector) by 90° to recover the magnetic field orientation in the plane of the sky. The polarization maps obtained in this manner are displayed in Fig. 4. We emphasize that these maps do not include any Faraday rotation, Faraday depolarization or beam depolarization effects.
. We then compute the associated Stokes parameters U and Q, remembering that synchrotron emission is (partially) linearly polarized perpendicular to B⊥ and assuming that the intrinsic degree of linear polarization is uniform throughout the galaxy (consistent with the power-law index, γ, being uniform). We define a grid of sightlines through the galaxy, integrate the Stokes parameters along every sightline and rotate the resulting polarized-intensity bar (or headless vector) by 90° to recover the magnetic field orientation in the plane of the sky. The polarization maps obtained in this manner are displayed in Fig. 4. We emphasize that these maps do not include any Faraday rotation, Faraday depolarization or beam depolarization effects.
The synchrotron polarization patterns predicted by models A, C and D are reminiscent of the run of poloidal field lines in Fig. 1. By the same token, they are consistent with the X shapes observed in the halos of external edge-on galaxies. Model B leads to an X pattern as well, but because the polarization bars fade away (logarithmically) with decreasing polarized intensity, this X pattern is completely overshadowed by the strong polarized emission arising from the strong vertical field along the z-axis.
The impact of the main model parameters on the polarization maps can be understood by running a large number of simulations with different parameter values. One of the most critical parameters is the pitch angle, p, whose effect is found to conform to our physical expectation. As a general rule, a small pitch angle entails a strong azimuthal field in regions where the poloidal field (shown in Fig. 1) has a significant radial component (see Eq. (68)). This strong azimuthal field, in turn, tends to make the magnetic orientation bars (i.e., the polarization bars rotated by 90°) more horizontal, especially at short projected distances from the z-axis, where the azimuthal field along most of the line of sight lies close to the plane of the sky. This effect is particularly pronounced toward the central galactic region in models B and D, where the magnetic orientation bars are almost perfectly horizontal (see Figs. 4b and d), while they would have been nearly vertical for a purely poloidal field.
The scale height of the pitch angle, Hp, is also found to have the expected impact on the polarization maps. Choosing, somewhat arbitrarily, Hp = 3 kpc, we obtain the X patterns of Fig. 4. With a larger value of Hp, we find that the magnetic orientation bars either remain nearly horizontal up to higher altitudes (in models A, B and D) or start turning toward the horizontal closer to the midplane (in model C). As a result, the X pattern either emerges higher up (in models A, B and D) or is squeezed toward the midplane (in model C).
Another parameter affecting the polarization maps is the azimuthal wavenumber, m. The results presented in Fig. 4 pertain to axisymmetric (m = 0) configurations. Bisymmetric (m = 1) configurations are found to lead to a broader range of polarization arrangements, in which the X pattern can be either enhanced or weakened, depending on the viewing angle. For higher-order (m ≥ 2) modes, the distribution of magnetic orientation bars becomes more complex and does not always display a recognizable X pattern.
The variety of polarization structures produced by our four models may be representative of the variety observed in the real world of external galaxies (e.g., Soida 2005; Krause 2009). Model A could a priori be used to describe the halo fields of galaxies like NGC 891, where the X pattern appears to cross the rotation axis almost horizontally (Krause 2009) – under the condition that the magnetic configuration is not axisymmetric. Model D would be more appropriate to describe the halo fields of galaxies like NGC 4217, where the magnetic orientation bars are nearly horizontal near the midplane and gradually turn more vertical with increasing latitude away from the central region (Soida 2005). Note, however, that both models A and D predict a strong polarized intensity from the disk, which is not always observed in the polarization maps of external edge-on galaxies. This can be because, at low radio frequencies, the (intrinsically polarized) emission from the disk is subject to strong Faraday depolarization. Model C could be the best candidate to describe the halo fields of galaxies like the starburst galaxy NGC 4631, which appears to host the superposition of an X-shape halo field crossing the midplane at nearly right angles plus a horizontal disk field (Irwin et al.2012; Mora & Krause2013; Marita Krause, priv. comm.). Finally, model B could probably be used in the case of galaxies with strong bipolar outflows from their central regions. In that respect, it is noteworthy that many, if not all, of the highly inclined galaxies studied by Braun et al. (2010) show evidence for circumnuclear, bipolar-outflow fields. On the other hand, such strong vertical fields should be observable through large RM values in face-on galaxies, but have not been detected (Rainer Beck, priv. comm.).
6. Summary
In this paper, we proposed a general method, based on the Euler potentials, to derive the analytical expression (as a function of galactocentric cylindrical coordinates) of a magnetic field defined by the shape of its field lines and by the distribution of its normal component on a given reference surface (e.g., a vertical cylinder of radius r1 or a horizontal plane of height z1). Utilizing the Euler formalism ensures that the calculated magnetic field is divergence-free.
The first and primary application of our method was to magnetic fields in galactic halos, which are believed to come with an X shape. We derived four specific analytical models of X-shape magnetic fields, starting with purely poloidal fields (Sect. 2) and generalizing to three-dimensional fields that have an X-shape poloidal component and a spiral horizontal component (Sect. 3). The pitch angle of the spiral was allowed to vary with both galactic radius and height. The descriptive equations and the free parameters of our four halo models (models A–D) are summarized in Table 2 (see also Table 1 for the poloidal component alone) and the shapes of their field lines are shown in Fig. 2 (see also Fig. 1 for the poloidal component alone).
In models A and C, field lines have nice and simple X shapes in meridional planes (see Figs. 1a and c), and synchrotron polarization maps showcase the best-looking X patterns (see Figs. 4a and c). Unfortunately, model A is unphysical, insofar as field lines from all meridional planes converge to the rotation axis, thereby causing the radial field component to become infinite. For non-axisymmetric fields, this difficulty can possibly be circumvented with a slight re-organization of field lines at small radii, but for axisymmetric fields, model A must definitely be ruled out (see Sect. 2.4). Model C, for its part, is always physical, but because field lines cross the midplane vertically, it is restricted to antisymmetric fields.
In models B and D, field lines have slightly more complicated shapes in meridional planes (see Figs. 1b and d): their outer parts form a well-defined X figure, while their inner parts concentrate along the rotation axis (in model B) or along the midplane (in model D). This geometry is a direct consequence of magnetic flux conservation in a setting where field lines tend to converge toward the rotation axis (in model B) or the midplane (in model D), but are not allowed to cross it. An effect of this concentration of field lines is to overshadow the underlying X pattern in synchrotron polarization maps (see Figs. 4b and d). Otherwise, the strong vertical field near the rotation axis in model B is not unrealistic, as it could be explained by strong bipolar outflows from the central region. The strong horizontal field near the midplane in model D is also realistic, but it would be more appropriate for a model of the disk field than a model of the halo field.
A secondary application of our general method was to magnetic fields in galactic disks, which were assumed to be approximately horizontal near the midplane and to have a spiral horizontal component everywhere, again with spatially varying pitch angle (Sect. 4). Instead of going through an entire new derivation, we took up two of our halo models (models B and D) and modified them slightly in such a way as to adapt them to galactic disks. The descriptive equations of our two disk models (models Bd and Dd) are summarized in Table 3 and the shapes of their field lines are shown in Fig. 3.
Models Bd and Dd were both designed to represent disk magnetic fields, with a high density of nearly horizontal field lines near the midplane. However, field lines do not remain strictly confined to the disk; at some point, they leave the disk and enter the halo, where they continue along X-shaped lines. Therefore, models Bd and Dd could potentially represent the disk and halo fields combined and, thus, provide complete models of galactic magnetic fields. One necessary condition for this to be possible would be that the disk and halo fields have a common vertical parity (presumably, symmetric with respect to the midplane), which would be expected on theoretical grounds, but does not seem to be fully supported by current observations (see Sect. 2.3).
Anyway, because galactic disks and halos are different structures, formed at different times and shaped differently (e.g., Silk 2003; Agertz et al. 2011; Guo et al. 2011; Aumer & White 2013), it may be warranted to appeal to separate models for the disk and halo fields. This keeps open the possibility for these fields to possess different vertical parities, azimuthal symmetries, pitch angles, etc. This also makes it possible to consider the disk or halo field alone, as required in some specific problems.
Our magnetic field models can serve a variety of purposes, related to either our Galaxy or external spiral galaxies. Most obviously, they can be used to test the hypothesis of X-shape magnetic fields in galactic halos against existing RM and synchrotron observations, and, if relevant, they can help to constrain their observational characteristics. Equally important, they can provide the galactic field models needed in a number of theoretical problems and numerical simulations.
The interested readers can resort to one of the specific field models derived in this paper (see Table 2 for the halo fields and Table 3 for the disk fields), but they can also derive their own field models, relying on Eqs. (67)–(69), once they have settled on a given network of field lines. These new field models may in principle apply to galactic disks or halos, come with an X shape or not, have one or several lobes in each quadrant, etc., the main difficulty being to find a workable analytical function for the first Euler potential, α.
Throughout this paper, we will follow the usual convention of employing the term “poloidal” to refer to magnetic fields with only radial and vertical components, i.e., with no azimuthal component, in galactocentric cylindrical coordinates. Strictly speaking, this terminology is correct only for axisymmetric magnetic fields (e.g., Moffatt 1978).
We may no longer take the surface r = r0 to be the normalization surface on which fϕ vanishes, since not all field lines cross r0 in models C and D. This was not an issue in Sect. 3.1, where we didn’t consider individual field lines, but the spiral lines defined by the magnetic field projection onto the galactic plane.
Acknowledgments
Katia Ferrière would like to express her gratitude to the many colleagues with whom she had lively and enlightening discussions on X-shape magnetic fields: Robert Braun, Chris Chyży, Ralf-Jürgen Dettmar, Andrew Fletcher, Michał Hanasz, Marijke Haverkorn, Anvar Shukurov, with special thanks to Rainer Beck and Marita Krause. The authors also thank the referee, Marian Soida, for his careful reading of the paper and his valuable comments.
References
- Agertz, O., Teyssier, R., & Moore, B. 2011, MNRAS, 410, 1391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aumer, M., & White, S. D. M. 2013, MNRAS, 428, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 2008, in AIP Conf. Ser. 1085, eds. F. A. Aharonian, W. Hofmann, & F. Rieger, 83 [Google Scholar]
- Beck, R. 2009, in IAU Symp. 259, eds. K. G. Strassmeier, A. G. Kosovichev, & J. E. Beckman, 3 [Google Scholar]
- Beck, R., & Wielebinski, R. 2013, Magnetic Fields in Galaxies, Planets, Stars and Stellar Systems, Vol. 5: Galactic Structure and Stellar Populations, eds. T. D. Oswalt, & G. Gilmore (Dordrecht: Springer Science, Business Media), 641 [Google Scholar]
- Brandenburg, A., Donner, K. J., Moss, D., et al. 1993, A&A, 271, 36 [NASA ADS] [Google Scholar]
- Braun, R., Heald, G., & Beck, R. 2010, A&A, 514, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalla Vecchia, C., & Schaye, J. 2008, MNRAS, 387, 1431 [NASA ADS] [CrossRef] [Google Scholar]
- Dumke, M., Krause, M., Wielebinski, R., & Klein, U. 1995, A&A, 302, 691 [NASA ADS] [Google Scholar]
- Elstner, D., Golla, G., Rudiger, G., & Wielebinski, R. 1995, A&A, 297, 77 [NASA ADS] [Google Scholar]
- Fletcher, A. 2010, in ASP Conf. Ser. 438, eds. R. Kothes, T. L. Landecker, & A. G. Willis, 197 [Google Scholar]
- Frick, P., Stepanov, R., Shukurov, A., & Sokoloff, D. 2001, MNRAS, 325, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Boylan-Kolchin, M., et al. 2011, MNRAS, 413, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Han, J. 2002, in Astrophysical Polarized Backgrounds, eds. S. Cecchini, S. Cortiglioni, R. Sault, & C. Sbarra, AIP Conf. Ser., 609, 96 [Google Scholar]
- Han, J. L., & Qiao, G. J. 1994, A&A, 288, 759 [NASA ADS] [Google Scholar]
- Han, J. L., Manchester, R. N., Berkhuijsen, E. M., & Beck, R. 1997, A&A, 322, 98 [NASA ADS] [Google Scholar]
- Han, J. L., Manchester, R. N., & Qiao, G. J. 1999, MNRAS, 306, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Harari, D., Mollerach, S., & Roulet, E. 1999, J. High Energy Phys., 8, 22 [Google Scholar]
- Haverkorn, M., & Heesen, V. 2012, Space Sci. Rev., 166, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Krause, M., Beck, R., & Dettmar, R.-J. 2009, A&A, 506, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Irwin, J., Beck, R., Benjamin, R. A., et al. 2012, AJ, 144, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Jałocha, J., Bratek, Ł., Kutschera, M., & Skindzier, P. 2011, MNRAS, 412, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Jansson, R., & Farrar, G. R. 2012a, ApJ, 757, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Jansson, R., & Farrar, G. R. 2012b, ApJ, 761, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Jansson, R., Farrar, G. R., Waelkens, A. H., & Enßlin, T. A. 2009, JCAP, 7, 21 [Google Scholar]
- Krause, M. 2009, Rev. Mex. Astron. Astrofis. Conf. Ser., 36, 25 [NASA ADS] [Google Scholar]
- Krause, M., Wielebinski, R., & Dumke, M. 2006, A&A, 448, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levine, E. S., Heiles, C., & Blitz, L. 2008, ApJ, 679, 1288 [NASA ADS] [CrossRef] [Google Scholar]
- Marasco, A., & Fraternali, F. 2011, A&A, 525, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moffatt, H. K. 1978, Magnetic field generation in electrically conducting fluids (Cambridge, England: Cambridge University Press) [Google Scholar]
- Mora, S. C., & Krause, M. 2013, A&A, 560, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., & Sokoloff, D. 2008, A&A, 487, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Sokoloff, D., Beck, R., & Krause, M. 2010, A&A, 512, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Northrop, T. G. 1963, Rev. Geophys. Space Phys., 1, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Oren, A. L., & Wolfe, A. M. 1995, ApJ, 445, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Prouza, M., & Šmída, R. 2003, A&A, 410, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pshirkov, M. S., Tinyakov, P. G., Kronberg, P. P., & Newton-McGee, K. J. 2011, ApJ, 738, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Rand, R. J., & Lyne, A. G. 1994, MNRAS, 268, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 2003, Ap&SS, 284, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Sofue, Y., & Fujimoto, M. 1983, ApJ, 265, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Soida, M. 2005, in Proc. Conf. The Magnetized Plasma in Galaxy Evolution, eds. K. T. Chyzy, K. Otmianowska-Mazur, M. Soida, & R.-J. Dettmar (Kraków: Jagiellonian University), 185 [Google Scholar]
- Soida, M., Krause, M., Dettmar, R.-J., & Urbanik, M. 2011, A&A, 531, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sokoloff, D., & Shukurov, A. 1990, Nature, 347, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Stanev, T. 1997, ApJ, 479, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, D. P. 1966, Space Sci. Rev., 6, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X. H., Reich, W., Waelkens, A., & Enßlin, T. A. 2008, A&A, 477, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tüllmann, R., Dettmar, R.-J., Soida, M., Urbanik, M., & Rossa, J. 2000, A&A, 364, L36 [Google Scholar]
- Wielebinski, R., & Krause, F. 1993, A&ARv, 4, 449 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Brief description of our four models of poloidal, X-shape magnetic fields in galactic halos.
Brief description of our four models of three-dimensional, X-shape + spiral magnetic fields in galactic halos.
Brief description of our two models of three-dimensional, X-shape + spiral magnetic fields in galactic disks.
All Figures
 |
Fig. 1 Small set of field lines for each of our four models of poloidal, X-shape magnetic fields in galactic halos, in a vertical plane through the galactic center: a) model A (described by Eq. (12)) with r1 = 3 kpc and a = 1/(10 kpc)2; b) model B (Eq. (17)) with r1 = 3 kpc and n = 2; c) model C (Eq. (26)) with a = 1/(10 kpc)2 (and, as always, z1 = 0); and d) model D (Eq. (31)) with | z1 | = 1.5 kpc and n = 2. Field lines are separated by a fixed magnetic flux per unit azimuthal angle; thus, in models A and B, their vertical spacing at r1 is determined by Eq. (16) or (21) with H = 1.5 kpc, while in models C and D, their radial spacing at z1 is determined by Eq. (30) or (35) with L = 10 kpc. Each panel is 30 kpc × 30 kpc in size and is centered on the galactic center. The trace of the galactic plane is indicated by the horizontal, solid red line, and the z-axis by the vertical, dot-dashed black line. |
| In the text | |
 |
Fig. 2 Small set of field lines for each of our four models of three-dimensional, X-shape + spiral magnetic fields in galactic halos, as seen from an oblique angle. The parameters of the poloidal field take on the same values as in Fig. 1, while the pitch angle is assigned a constant value of p = −30°, plausibly representative of galactic halos. The selected field lines correspond to those displayed in Fig. 1 (i.e., they have the same labels (z1,ϕ1) or (r1,ϕ1)), except in model D, where only four field lines are drawn for clarity. Each box is a (30 kpc)3 cube centered on the galactic center. The trace of the galactic plane is indicated by the solid red circle, and the z-axis by the vertical, dot-dashed black line. |
| In the text | |
 |
Fig. 3 Small set of field lines for our two models of three-dimensional, X-shape + spiral magnetic fields in galactic disks, as seen from an oblique angle: a) model Bd (poloidal component described by Eq. (87)) with r1 = 3 kpc and n = 2; and b) model Dd (Eq. (31)) with | z1 | = 1.5 kpc and |
| In the text | |
 |
Fig. 4 Maps of the normalized synchrotron polarization bars (or headless vectors) rotated by 90° toward a hypothetical external galaxy seen edge-on, as predicted by our four models of three-dimensional, X-shape + spiral magnetic fields in galactic halos. The magnetic field is supposed to be axisymmetric (m = 0), the parameters of its poloidal component have the same values as in Figs. 1 and 2, and the pitch angle is given by Eq. (65) with p0 = −10°, p∞ = −90° and Hp = 3 kpc. The trace of the galactic plane is indicated by the horizontal, solid red line, and the z-axis by the vertical, dot-dashed black line. The rotated polarization bars trace the average magnetic field orientation in the plane of the sky, and their level of grey reflects the magnitude of the polarized intensity (with a logarithmic scale). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



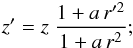
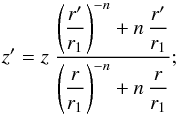
![\begin{eqnarray*} z' = {\rm sign}~z \ \sqrt{ \frac{1}{a} \ \left[ \frac{r'}{r} \ (1 + a \, z^2) - 1 \right] } ; \end{eqnarray*}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq148.png)
![\begin{eqnarray*} \left[ \left( \frac{z'}{z_1} \right)^{-n} + n \, \frac{z'}{z_1} \right] = \frac{r'}{r} \ \left[ \left( \frac{z}{z_1} \right)^{-n} + n \, \frac{z}{z_1} \right] \cdot \end{eqnarray*}](/articles/aa/full_html/2014/01/aa22966-13/aa22966-13-eq149.png)