| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322595 | |
| Published online | 17 January 2014 | |
Modulated gamma-ray emission from compact millisecond pulsar binary systems
Department of Astrophysics, University of Łódź, ul. Pomorska 149/153, 90-236 Łódź, Poland
e-mail: bednar@uni.lodz.pl
Received: 3 September 2013
Accepted: 28 November 2013
Context. A significant number of the millisecond pulsars (MSPs) have been discovered within binary systems. Tens of these MSPs emit γ-rays that are modulated with the pulsar period since this emission is produced in the inner pulsar magnetosphere. In several such binary systems, the masses of the companion stars have been derived allowing two classes of objects to be distinguished, which are called the black widow and the redback binaries. Pulsars in these binary systems are expected to produce winds that create conditions for acceleration of electrons, when colliding with stellar winds. These electrons should interact with the anisotropic radiation from the companion stars producing γ-ray emission modulated with the orbital period of the binary system, similar to what is observed in the massive TeV γ-ray binary systems.
Aims. We consider the interaction of a MSP wind with a very inhomogeneous stellar wind from the companion star within binary systems of the black widow and redback types. Our aim is to determine the features of γ-ray emission produced in the collision region of the winds from a few typical MSP binary systems.
Methods. It is expected that the pulsar wind should mix efficiently with the inhomogeneous stellar wind. The mixed winds move outside the binary with relatively low velocity. Electrons accelerated in such mixed, turbulent winds can interact with the magnetic field and strong radiation from the companion star, producing not only synchrotron radiation but also γ-rays in the inverse Compton process, fluxes of which are expected to be modulated on the periods of the binary systems. Applying numerical methods, we calculated the GeV-TeV gamma-ray spectra and the light curves expected from some MSP binary systems.
Results. Gamma-ray emission, produced within the binary systems, is compared with the sensitivities of the present and future gamma-ray telescopes. It is concluded that energetic MSP binary systems create a new class of TeV γ-ray sources that could be detectable by the future Cherenkov arrays (e.g., CTA) and possibly also by the extensive campains with the present arrays (HESS, MAGIC, VERITAS). However, γ-ray emission from the MSP binary systems is predicted to have different features than those observed in the case of massive TeV gamma-ray binaries such as LS I 303 61 or LS 5039. The maximum in the TeV γ-ray orbital light curve should appear when the MSP is behind the companion star. This is in contrast to the observations of the orbital light curves from the massive TeV γ-ray binaries (LS I 303 61 or LS 5039). Moreover, the GeV and orbital TeV γ-ray light curves should be positively correlated unlike the case of massive TeV γ-ray binaries.
Conclusions. We conclude that TeV γ-ray emission, modulated on the orbital period of MSP binary systems, should be detected by the future CTA. Moreover, some MSP binary systems of the Redback type might also show GeV γ-ray emission modulated on the binary periods on the level detectable by Fermi-LAT.
Key words: binaries: general / pulsars: general / radiation mechanisms: non-thermal / gamma rays: stars
© ESO, 2014
1. Introduction
Most of the millisecond pulsars (MSPs) are members of binary systems (Manchester et al. 2005). It is supposed that this feature is related to their formation mechanism (Alpar et al. 1982; Bhattacharya & van den Heuvel 1991). Several such binaries have surprisingly low-mass companion stars. Their masses are a few percent of the solar mass in the case of black widow binaries and a few tens percent of solar mass in the case of redback binaries (Roberts 2012). Clearly, the lower masses of the companion stars in black widow systems with respect to redback systems are probably due to the more effective evaporation of the companion stars caused by the energy released by the MSPs in these binaries (Ruderman et al. 1989). The energy realized by the MSP also heats the surface of the companion star to temperatures significantly above what is expected from the nuclear burning in black widow systems. Therefore, optical emission from the companions in black widow systems is often modulated on the periods of the binary systems (e.g. Breton et al. 2013), in contrast to the emission from the companion stars in the redback systems.
As observed in the famous binary system containing the pulsar PSR B1259−63, it is expected that electrons can also be accelerated within the MSP binaries at the shock that appears to be a result of the interaction of winds from the MSP and the companion star. Electrons can reach energies allowing them to produce of synchrotron X-rays and inverse Compton (IC) γ-rays in collisions with the radiation from the companion stars. One of the best studied MSP binary system of the black widow type is PSR B1957+20 (Fruchter et al. 1988). The X-ray emission from this binary system is modulated on the orbital period (Huang et al. 2012), suggesting that its origin is in the wind-collision shock as considered by Harding & Gaisser (1990) and Arons & Tavani (1993). In fact, the presence of the shock within the binary system has been expected from the discovery of binary system PSR B1957+20, since the pulsed radio emission shows the eclipse lasting for about 10% of the orbital phase (Fruchter et al. 1988). The binary system PSR B1957+20 was claimed in the past to be a GeV-TeV γ-ray source (Brink et al. 1990). But, this report was not confirmed by EGRET observations (Buccheri et al. 1996). Only recently Fermi has discovered pulsed γ-ray emission from PSR B1957+20 (Guillemot et al. 2012). It is clear at present that MSPs create one of the major classes of pulsed γ-ray sources in the Galaxy. There is also evidence of an additional higher energy component in the GeV emission from the black widow binary system PSR B1957+20 (Wu et al. 2012). This component is modulated on the period of the binary system reaching the maximum when the MSP is behind the companion star. This additional emission component, modulated on the orbital period of the binary system, is interpreted as produced by relativistic electrons moving in the pulsar wind (Wu et al. 2012). They up-scatter radiation field from the companion star.
Similar general features of the pulsed GeV γ-ray emission from the MSPs and classical pulsars (efficiencies and shape of the spectra) suggest that acceleration processes in the inner magnetospheres of these two classes of pulsars occur in similar way (Abdo et al. 2009a, 2013). Therefore, it is likely that binary systems containing MSPs also show modulated high-energy emission, as recently discovered in the case of TeV γ-ray binaries, such as those containing PSR B1259−63 (Abdo et al. 2011; Aharonian et al. 2005a) and maybe also LS 5039 (Abdo et al. 2009b; Aharonian et al. 2005b) and LSI 61 303 (Abdo et al. 2009c; Albert et al. 2006), provided that these two binary systems contain energetic pulsars as suggested by, e.g., Dubus (2006).
In this paper we consider a specific model for the interaction of winds from the MSP and the companion star. In contrast to previous models (Harding & Gaisser 1990; Arons & Tavani 1993), we assume that the wind from the companion star is highly inhomogeneous. Then, the pulsar and stellar winds should mix very efficiently at the location where the pressure of both winds becomes comparable. The mixed winds expand from the binary system with relatively low velocity owing to the barion loading of the relativistic pulsar wind with the matter from the relatively slow stellar wind. Relativistic electrons, which are captured in such mixed winds, can interact efficiently with the radiation from the nearby companion star producing TeV γ-rays, which are supposed to be modulated on the orbital period of the binary system. We calculate the γ-ray and synchrotron spectra, produced by these electrons and compare them with the available X-ray observations from these binary systems and also with the sensitivities of the Fermi-LAT telescope and of the present and future Cherenkov telescopes.
2. Interaction of winds in MSP binary systems
We consider the standard picture for the compact binary systems containing energetic MSPs of the black widow and redback type following previous works by Harding & Gaisser (1990) and Arons & Tavani (1993). In this scenario a MSP produces a relativistic pulsar wind that interacts with the stellar wind of the low-mass companion (see Fig. 1 on the left). As a result of this interaction, a shock structure appears within the binary system that separates the pulsar and stellar winds. We modify this standard scenario by assuming that the wind from the companion star is highly inhomogeneous. In this case, the interaction of winds produces a very turbulent mixed pulsar-stellar wind that moves together with the velocity determined by the momentum conservation. The velocity of the mixed pulsar-stellar wind can be estimated by assuming that the relativistic pulsar wind is loaded with the matter from the stellar wind, ![\begin{eqnarray} v_{\rm mix} = \left[{{2L_{\rm pul}\Delta\Omega_{\rm pul}}\over{{\dot M}_\star\Delta\Omega_{\star}}}\right]^{1/2}\approx 4\times 10^9\left({{\xi_{-1}L_{35}}\over{M_{-11}}}\right)^{1/2}~~~{\rm {{cm}\over{s}}} \label{eq1} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22595-13/aa22595-13-eq4.png) (1)where Lpul = 1035L35 erg s-1 is the power of the pulsar wind, and Ṁ = 10-11M-11 M⊙ yr-1 is the mass loss rate of the companion star. The power of the pulsar wind is assumed to be equal to the rotational energy loss rate of the pulsar that is estimated for known values of the rotational period, P, and period derivative of the pulsar, Ṗ, based on the standard formula that assumes the rotating dipole model for the pulsar magnetosphere: Lpul = 3.95 × 1031(Ṗ / 10-15)(P / 1s)-3 erg s-1. The solid angles, ΔΩpul and ΔΩ⋆, describe a part of the solid angles that are over-taken by the collision region as observed from the pulsar site and from the companion star site, respectively. These solid angles can be estimated as ΔΩpul = (1 − cosφpul) / 2, and ΔΩ⋆ = (1 − cosφ⋆) / 2. We introduced the parameter χ = 0.1χ-1 = ΔΩpul / ΔΩ⋆, and φpul is the half opening angle calculated from φ = 2.1(1 − η2 / 5 / 4)η1 / 3 rad (see Eichler & Usov 1993). Here η is the minimum value from
(1)where Lpul = 1035L35 erg s-1 is the power of the pulsar wind, and Ṁ = 10-11M-11 M⊙ yr-1 is the mass loss rate of the companion star. The power of the pulsar wind is assumed to be equal to the rotational energy loss rate of the pulsar that is estimated for known values of the rotational period, P, and period derivative of the pulsar, Ṗ, based on the standard formula that assumes the rotating dipole model for the pulsar magnetosphere: Lpul = 3.95 × 1031(Ṗ / 10-15)(P / 1s)-3 erg s-1. The solid angles, ΔΩpul and ΔΩ⋆, describe a part of the solid angles that are over-taken by the collision region as observed from the pulsar site and from the companion star site, respectively. These solid angles can be estimated as ΔΩpul = (1 − cosφpul) / 2, and ΔΩ⋆ = (1 − cosφ⋆) / 2. We introduced the parameter χ = 0.1χ-1 = ΔΩpul / ΔΩ⋆, and φpul is the half opening angle calculated from φ = 2.1(1 − η2 / 5 / 4)η1 / 3 rad (see Eichler & Usov 1993). Here η is the minimum value from 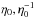 , η0 is defined by the parameters of the pulsar and stellar winds
, η0 is defined by the parameters of the pulsar and stellar winds 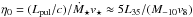 , and the velocity of the stellar wind is v⋆ = 108v8 cm s-1 (Girard & Willson 1987). The half opening angle of the collision region, φ⋆, is seen from the location of the companion star. The closest approach of the shock from the companion star is at
, and the velocity of the stellar wind is v⋆ = 108v8 cm s-1 (Girard & Willson 1987). The half opening angle of the collision region, φ⋆, is seen from the location of the companion star. The closest approach of the shock from the companion star is at 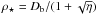 , where Db is the separation of the stars. The distance of the shock for other angles, φ⋆, is approximated by ρ(φ⋆) ≈ ρ⋆ × φ⋆ / sin(φ⋆). We estimate the angle φ⋆ by solving the approximate equation: Dbcosφ⋆ ≈ ρ⋆(φ⋆ / sinφ⋆). For typical parameters of the MSP binary systems (L = 1035 erg s-1, M = 10-11 M⊙ yr-1 and v⋆ = 700 km s-1, expected for PSR B1957+20), η is estimated on ~7, the angle φpul on ~0.45 rad and the angle φ⋆ on 1.2 rad. Then, the value of the parameter ξ is equal to ~0.14. For these parameters, the typical velocity of the mixed pulsar/stellar wind is ~4.6 × 109 cm s-1.
, where Db is the separation of the stars. The distance of the shock for other angles, φ⋆, is approximated by ρ(φ⋆) ≈ ρ⋆ × φ⋆ / sin(φ⋆). We estimate the angle φ⋆ by solving the approximate equation: Dbcosφ⋆ ≈ ρ⋆(φ⋆ / sinφ⋆). For typical parameters of the MSP binary systems (L = 1035 erg s-1, M = 10-11 M⊙ yr-1 and v⋆ = 700 km s-1, expected for PSR B1957+20), η is estimated on ~7, the angle φpul on ~0.45 rad and the angle φ⋆ on 1.2 rad. Then, the value of the parameter ξ is equal to ~0.14. For these parameters, the typical velocity of the mixed pulsar/stellar wind is ~4.6 × 109 cm s-1.
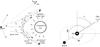 |
Fig. 1 Schematic representation of the compact binary system containing a energetic MSP (on the left) and the picture on which the basic angles defining the binary system are shown (on the right). On the left: the pulsar creates a strong wind that contains relativistic electrons (γe). The companion star creates turbulent stellar wind mainly as a result of irradiation from the pulsar. The winds collide, creating a turbulent, non-stationary shock structure. Both winds mix effectively in this region. Relativistic electrons (from the pulsar wind or additionally re-accelerated in the turbulent pulsar-stellar winds) are isotropized by the random magnetic field of the mixed winds. They are advected along the shock structure. During this process, electrons comptonize stellar radiation producing γ-rays. Owing to the anisotropy of the stellar radiation field, γ-rays tend to be produced in the general direction of the companion star. As a result, the γ-ray signal, produced towards the observer (obs.) located at the angle β, should be modulated with the phase of the binary system. On the right: the binary system is inclined at the angle i towards the observer’s (Obs) line of sight. The orbital phase, ω, is equal to zero when the pulsar is in front of the companion star. The angle between the observer and the pulsar (and also injection place of relativistic electrons) is marked by β. |
The above estimated relatively low velocity of the mixed winds (with respect to the velocity of the pulsar wind) guarantees that relativistic electrons stay relatively close to the stellar surface for long enough that their interactions with soft radiation from the stellar surface is efficient. These electrons are isotropized in the reference frame of the mixed wind. They lose energy mainly on the synchrotron process and the IC scattering of stellar radiation.
In Table 1, we report the basic parameters of a few MSP binary systems. Up to now, several MSP binary systems have been identified as belonging to the black widow type and a few such systems have been classified as the redback type (Roberts 2012). For illustration purposes, we have selected two MSP binaries of the black widow type, PSR B1957+20 (Fruchter et al. 1988) and PSR J1810+1744 (Hessels et al. 2011), and two of the Redback type, PSR J1023+0038 (Archibald et al. 2009) and PSR J1816+4510 (Kaplan et al. 2012). The basic parameters of these MSP binaries are quite well known. The distances to these binaries are estimated based on the dispersion measure using the Cordes & Lazio (2002) model (see Gentile et al. 2013) and from parallax measurements for PSR 1023+0038 (Deller et al. 2012).
The parameters of the companion stars (stellar radius and surface temperature) and the parameters of the binary systems (semimajor axis, inclination angle) are taken from Manchester et al. (2005), Fruchter et al. (1990), Reynolds et al. (2007), Archibald et al. (2009), Hessels et al. (2011), Breton et al. (2013), and Kaplan et al. (2012). The inclination angles of these binary systems are not very well defined since their estimates depend on the unknown masses of the neutron stars in these binary systems. These four binaries are expected to provide good conditions for γ-ray production by electrons accelerated at the collision region of the pulsar and stellar winds. These binary systems are compact and contain MSPs with a high rotational energy loss rate (estimated for the known rotational periods and period derivatives, see Manchester et al. 2005; Archibald et al. 2009 and Kaplan et al. 2012). The collision regions of their winds are close to the stellar surfaces, and their measured surface temperatures are relatively high. The distances of the collision regions from the companion stars, Rsh (reported in Table 1), are estimated by the value of the closest approach of the collision region to the companion star, ρ⋆ (defined above).
Basic parameters of MSPs and their binary systems.
3. High-energy processes within binary systems
We consider the role of the high-energy processes that are expected to be important in the general scenario discussed above. We are interested in processes which could explain X-ray emission produced within the MSP binary systems of the PSR B1957+20 type. This emission cannot be produced by relativistic electrons that escape from the inner pulsar magnetosphere and move rectilinearly in the pulsar wind. On the other hand, such synchrotron X-ray emission can be produced within the binary system when the relativistic electrons move in the region of turbulent, mixed MSP-stellar wind discussed above. In fact, the phase dependent X-ray emission is observed up to at least εsyn ~ 8 keV (Huang et al. 2012). We assume that this emission originates in the synchrotron process. In such a case, the magnetic field in the emission region and the Lorentz factor of electrons should fulfill the following condition, 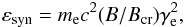 (2)where mec2 is the electron rest energy, B the magnetic field strength in the emission region, Bcr = 4.4 × 1013 G is the critical magnetic field strength, and γe the Lorentz factor of electrons. This synchrotron emission is likely to originate in the transition region of colliding winds. The magnetic field strength in this region can be estimated by a simple extrapolation from the pulsar surface, assuming the dipole structure of the magnetic field below the light cylinder and the toroidal structure in the pulsar wind region. Then,
(2)where mec2 is the electron rest energy, B the magnetic field strength in the emission region, Bcr = 4.4 × 1013 G is the critical magnetic field strength, and γe the Lorentz factor of electrons. This synchrotron emission is likely to originate in the transition region of colliding winds. The magnetic field strength in this region can be estimated by a simple extrapolation from the pulsar surface, assuming the dipole structure of the magnetic field below the light cylinder and the toroidal structure in the pulsar wind region. Then, 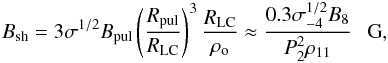 (3)where Bpul = 108B8 G and Ppul = 2P2 ms are the surface magnetic field strength and the period of the pulsar, RLC = cPpul / 2π is the light cylinder radius of the pulsar, σ = 10-4σ-4 is the magnetization parameter of the pulsar wind, ρo = a − RshR⋆ is the distance of the wind collision region from the MSP, and a is the semimajor axis of the binary system. The surface magnetic field of the pulsar is estimated from the standard formula, which assumes the rotating dipole model for the inner pulsar magnetosphere, Bpul = 3.2 × 1019(PṖ)1 / 2 G. This formula bases on the known values of the pulsar period and of period derivative. The magnetic field is expected to reconnect very efficiently in this highly turbulent region of the mixed winds. Therefore, the magnetic field strengths, described by very low values of the magnetization parameter, σ ≪ 10-2, should not be surprising. For the above value of the magnetic field at the transition region (Eq. (3)), the Lorentz factor of electrons, have to be at least
(3)where Bpul = 108B8 G and Ppul = 2P2 ms are the surface magnetic field strength and the period of the pulsar, RLC = cPpul / 2π is the light cylinder radius of the pulsar, σ = 10-4σ-4 is the magnetization parameter of the pulsar wind, ρo = a − RshR⋆ is the distance of the wind collision region from the MSP, and a is the semimajor axis of the binary system. The surface magnetic field of the pulsar is estimated from the standard formula, which assumes the rotating dipole model for the inner pulsar magnetosphere, Bpul = 3.2 × 1019(PṖ)1 / 2 G. This formula bases on the known values of the pulsar period and of period derivative. The magnetic field is expected to reconnect very efficiently in this highly turbulent region of the mixed winds. Therefore, the magnetic field strengths, described by very low values of the magnetization parameter, σ ≪ 10-2, should not be surprising. For the above value of the magnetic field at the transition region (Eq. (3)), the Lorentz factor of electrons, have to be at least 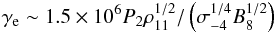 (4)to produce the observable X-ray emission in synchrotron process (Eq. (2)). We conclude that the TeV electrons have to be present within the turbulent region of the colliding winds of the MSP binary system PSR B1957+20, to explain the X-ray emission modulated with the period of the binary system.
(4)to produce the observable X-ray emission in synchrotron process (Eq. (2)). We conclude that the TeV electrons have to be present within the turbulent region of the colliding winds of the MSP binary system PSR B1957+20, to explain the X-ray emission modulated with the period of the binary system.
We determine the conditions in which electrons can reach TeV energies. The maximum energies of electrons accelerated at the transition region are determined by the acceleration time scale and the time scales for the energy losses or the escape from the acceleration region. The acceleration time scale can be estimated from 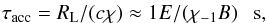 (5)where the electron energy is in TeV and χ = 0.1χ-1 is the acceleration parameter. We assume that the acceleration parameter can be related to the velocity of the mixed winds in the following way:
(5)where the electron energy is in TeV and χ = 0.1χ-1 is the acceleration parameter. We assume that the acceleration parameter can be related to the velocity of the mixed winds in the following way:  , where the mixed wind velocity is vmix = 1010v10 cm s-1.
, where the mixed wind velocity is vmix = 1010v10 cm s-1.
The maximum energies of electrons might be constrained by their escape from the acceleration region with the velocity of the mixed pulsar/stellar wind. The advection time scale of the mixed wind is 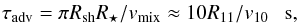 (6)where R ≈ πRshR⋆ = 1011R11 cm is the characteristic distance scale for the propagation of the turbulent wind around the companion star. By comparing this time scale with the acceleration time scale, we get the limit on the electron energies,
(6)where R ≈ πRshR⋆ = 1011R11 cm is the characteristic distance scale for the propagation of the turbulent wind around the companion star. By comparing this time scale with the acceleration time scale, we get the limit on the electron energies, 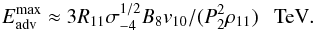 (7)We conclude that electrons can be accelerated to TeV energies in the turbulent collision region of the mixed pulsar and stellar winds.
(7)We conclude that electrons can be accelerated to TeV energies in the turbulent collision region of the mixed pulsar and stellar winds.
To fully understand their importance of the energy losses of accelerated electrons, we compare the electron acceleration time scale with the synchrotron or the IC energy-loss time scales. The synchrotron energy-loss time scale can be calculated from 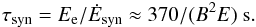 (8)The synchrotron energy losses dominate the IC energy losses in the Thomson regime (T regime) provided that the magnetic field in the acceleration region is stronger than
(8)The synchrotron energy losses dominate the IC energy losses in the Thomson regime (T regime) provided that the magnetic field in the acceleration region is stronger than 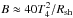 G (see e.g. Bednarek 1997), where Rsh is the distance of the electron acceleration from the companion star in units of the stellar radius. For the parameters of considered binary systems (see Table 1), the IC energy losses in the Thomson regime usually dominate the synchrotron energy losses. However, the IC energy losses in the Klein-Nishina (KN) regime declines, and the synchrotron losses can start to dominate at high energies. In this case, the maximum energy of accelerated electrons is determined by the balance between the acceleration time scale and the synchrotron time scale. They are estimated on
G (see e.g. Bednarek 1997), where Rsh is the distance of the electron acceleration from the companion star in units of the stellar radius. For the parameters of considered binary systems (see Table 1), the IC energy losses in the Thomson regime usually dominate the synchrotron energy losses. However, the IC energy losses in the Klein-Nishina (KN) regime declines, and the synchrotron losses can start to dominate at high energies. In this case, the maximum energy of accelerated electrons is determined by the balance between the acceleration time scale and the synchrotron time scale. They are estimated on 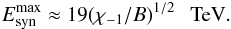 (9)Then, electrons can reach energies as large as (see Eq. (3)),
(9)Then, electrons can reach energies as large as (see Eq. (3)), 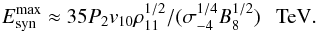 (10)In the situation considered above, electrons with maximum energies lose energy mainly in the synchrotron process but lower energy electrons can lose most of their energy still on the IC process. We now estimate the electron energy at which synchrotron losses become comparable to the IC losses in the KN regime. For the IC energy loss time scale in the KN regime, we apply the approximate formula by assuming that the IC energy losses in the KN regime are comparable to the IC energy losses on the border between T and KN regimes (see e.g. Eq. (7) in Bednarek 2011). Then, the IC losses in KN regime can be estimated from
(10)In the situation considered above, electrons with maximum energies lose energy mainly in the synchrotron process but lower energy electrons can lose most of their energy still on the IC process. We now estimate the electron energy at which synchrotron losses become comparable to the IC losses in the KN regime. For the IC energy loss time scale in the KN regime, we apply the approximate formula by assuming that the IC energy losses in the KN regime are comparable to the IC energy losses on the border between T and KN regimes (see e.g. Eq. (7) in Bednarek 2011). Then, the IC losses in KN regime can be estimated from 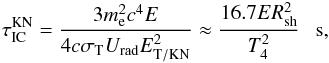 (11)where σT is the Thomson cross section, Urad is the density of stellar radiation at the acceleration region, T = 104T4 K is the surface temperature of the companion star, and ET / KN = (mec2)2 / 3kBT ≈ 0.1 / T4 TeV is the electron energy corresponding to transition between the T and KN regimes. By comparing
(11)where σT is the Thomson cross section, Urad is the density of stellar radiation at the acceleration region, T = 104T4 K is the surface temperature of the companion star, and ET / KN = (mec2)2 / 3kBT ≈ 0.1 / T4 TeV is the electron energy corresponding to transition between the T and KN regimes. By comparing 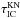 with τsyn, we can estimate the critical energy below which electrons lose energy mainly in the IC process,
with τsyn, we can estimate the critical energy below which electrons lose energy mainly in the IC process, 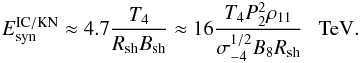 (12)This critical electron energy is usually not far from the maximum electron energy determined from the comparison of the acceleration time scale and the synchrotron energy-loss time scale. Therefore, we conclude that a relatively small part of electron’s energy can go to the synchrotron emission with respect to the IC emission, provided that electrons have the differential power law spectrum and spectral index close to − 2. The IC γ-ray emission should in this case extend up to TeV energies. The presence of electrons with TeV energies can also explain observations of the non-thermal synchrotron emission from the binary system PSR B1957+20 mentioned above.
(12)This critical electron energy is usually not far from the maximum electron energy determined from the comparison of the acceleration time scale and the synchrotron energy-loss time scale. Therefore, we conclude that a relatively small part of electron’s energy can go to the synchrotron emission with respect to the IC emission, provided that electrons have the differential power law spectrum and spectral index close to − 2. The IC γ-ray emission should in this case extend up to TeV energies. The presence of electrons with TeV energies can also explain observations of the non-thermal synchrotron emission from the binary system PSR B1957+20 mentioned above.
The Larmor radii of the TeV electrons are lower than the characteristic dimension of the binary system, RL < a, for the magnetic field strength above B ~ 0.03E / a11 G, where a = 1011a11. This condition is fulfilled in our scenario (see Eq. (3)), which means that electrons are trapped in the turbulent region. They have to be advected with the mixed winds.
We conclude that the most important process, which determines the maximum energies of electrons accelerated in the turbulent region, is the advection from the acceleration region (Eq. (7)). However, electrons can lose a significant amount of their energy on radiation processes, such as the IC scattering of soft photons from the companion star and the synchrotron radiation in the magnetic field in the colliding wind region.
4. Gamma rays from comptonization of stellar radiation
A few MSP binary systems (shown in Table 1) have been selected for their well known parameters of the pulsars and binary systems. We assume that electrons are accelerated in the turbulent collision region of the pulsar and stellar winds to TeV energies as discussed in the section above. These electrons are isotropized in the reference frame of the mixed pulsar-stellar wind. They are advected from the acceleration region (assumed the apex of the collision region) with the velocity of the mixed winds. Since electrons are isotropized, they can efficiently interact with the stellar radiation. The injection place of electrons is located outside the isotropic source of stellar radiation, therefore the IC scattering process has to occur anisotropically because the electron-photon collision rate depends on the angle between the direction of propagation of the electron and the soft photon. The production rate (and spectra) of γ-rays should depend on the observation angle of the binary system with respect to the direction defined by the stars.
To calculate the γ-ray spectra expected in terms of our model, we applied the Monte Carlo code that follows the IC e± pair cascade processes. This code has been developed for the anisotropic radiation processes within the massive binary systems (Bednarek 1997, 2000, 2006). In the modified version of this code, we take not only radiation processes characteristic of the IC e± pair cascade within the binary system into account but also energy losses of electrons on the synchrotron process. Therefore, we calculated the γ-ray spectra from the IC process and the synchrotron spectra produced by these same electrons. In fact, in the case of MSP binary systems, in which radiation field is much weaker than within massive binary systems, some production of secondary e± pairs, owing to absorption of IC γ-rays, can only happen for γ-rays that appear close to the stellar surface. We note that the radiation effects, connected with the production of secondary e± pairs, are negligible in the case of MSP binary systems.
In the example calculations, we assume that electrons are injected with the differential power law spectrum (spectral index − 2), extending to the maximum energies allowed by their escape from the binary system (Eq. (7)). The γ-ray spectra, escaping from the binary system, are obtained as a function of the cosine angle β (cosβ), where β is the angle between the direction defined by the stars and the direction towards the observer. The angle β depends on the inclination angle of the binary system i and the phase, ω, of the injection place of relativistic electrons according to cosβ = cos(90° − ι)cosω. These angles are defined in Fig. 1 (on the right).
The synchrotron spectra were also calculated. In contrast to the IC spectra, the synchrotron spectra are isotropic, since the magnetic field and electron distribution in the mixed wind reference frame are assumed to be isotropic. The velocity of the mixed wind is relatively low, so relativistic beaming effects can then be safely neglected. The only modulation effect on the X-ray emission is due to its absorption in the inhomogeneous wind of the companion star as observed in the case of PSR B1957+20.
 |
Fig. 2 Spectral energy distribution (energy flux versus energy, SED) of the γ-rays from the IC process and X-rays from the synchrotron process, produced by electrons accelerated in the wind collision region in the binary systems: PSR J1816+4510 (right column), PSR J1810+1744 (right-middle column), PSR J1023+0038 (left-middle column), and PSR B1957-20 (left column). a) Dependence on different advection velocities of the mixed pulsar-stellar winds: vadv = 1010 cm s-1 (dashed), 3 × 109 cm s-1 (solid), and 109 cm s-1 (dotted). The other parameters are fixed on σ = 10-3, − 0.5 ≤ cosβ ≤ − 0.4. The differential spectrum of electrons is assumed to be a power-law type (spectral index − 2) between the maximum energy given by Eq. (7) and minimum energy equal to Emin = 0.5 GeV. The power in this electron spectrum is normalized to 1% of the pulsar rotational energy lost by the pulsar. b) Dependence on magnetization parameter of the pulsar wind: σ = 10-2 (dotted), 10-3 (solid), and 10-4 (dashed). The other parameters are fixed on − 0.5 ≤ cosβ ≤ − 0.4 and Ee given by Eq. (7), and vadv = 3 × 109 cm s-1. c) Dependence on the cosine of the observation angle (measured from the direction defined by the centers of the stars): 0.9 ≤ cosβ ≤ 1.0 (dashed, outwards from the companion star), 0.5 ≤ cosβ ≤ 0.6 (solid), − 0.1 ≤ cosβ ≤ 0 (dotted), − 0.5 ≤ cosβ ≤ − 0.4 (dot-dashed), − 1.0 ≤ cosβ ≤ − 0.9 (dot-dot-dashed), the electron energy Ee is given by Eq. (7), σ = 10-3, and vadv = 3 × 109 cm s-1. |
5. γ-ray emission features from specific binaries
Two of the four MSP binary systems are the black widow type, PSR B1957+20 (Fruchter et al. 1988) and PSR J1810+1744 (Hessels et al. 2011), and two are redback, PSR J1023+0038 (Archibald et al. 2009) and PSR J1816+4510 (Kaplan et al. 2012). Some basic parameters of these binary systems, important for our calculations, are shown in Table 1. The X-ray emission, modulated with the period of the binary system, has been reported from three of these MSP binary systems: PSR B1957+20 (Huang et al. 2012), PSR J1023+0038 (Bogdanov et al. 2011), and PSR J1810+1744 (Gentile et al. (2013). For PSR J1816+4510, only the upper limit on the X-ray flux has been reported based on the Swift data (Kaplan et al. 2012). These X-ray positive detections (and the upper limit) are also used for the normalization for the synchrotron X-ray emission calculated in terms of our model. Such procedure allows us to predict the absolute level of the TeV γ-ray emission expected from the IC scattering of stellar radiation by this same population of relativistic electrons. In this calculation, we fixed the injection place of relativistic electrons between the pulsar and the companion star at the distance of the collision region from the companion star (also reported in Table 1).
At first, we investigate how the synchrotron and IC γ-ray spectra depend on the free parameters of the considered model for all four binary systems. In Fig. 2a we show how the spectra depend on the velocity of the mixed pulsar-stellar winds considering the range between vadv = vmix = 109 − 1010 cm s-1. This range of velocities of the mixed pulsar-stellar winds is expected for the typical parameters of the MSP binary systems, i.e., pulsar energy loss rate L35 = 1, the mass loss rate of the companion star Ṁ-11 = 1, and the solid angle overtaken by the collision region ξ-1 = 1 (see Eq. (1)). Another important parameter, which determines the model, is the magnetization parameter of the pulsar wind. We applied the value for σ = 10-3. This value is derived for the pulsar wind termination shock in the Crab nebula (~0.003, Kennel & Coroniti 1984), but clearly below this value since we expect that the recconnection of the magnetic field in the collision region of the turbulent stellar wind, and the pulsar wind will occur more efficiently within the MSP binary systems. We also fix the range of cosine of observation angles on − 0.5 ≤ cosβ ≤ − 0.4, since for this range of angles, the largest γ-ray fluxes are expected from the MSP binary systems. Electrons are injected with the differential power-law spectrum (spectral index − 2) at an energy range between the maximum energy given by Eq. (7) and the minimum energy Emin = 0.5 GeV. For illustration purposes, we normalize the power in this electron spectrum to 1% of the rotational energy lost by the pulsar. This normalization coefficient is the product of the solid angle overcome by the colliding winds and the efficiency of electron acceleration in turbulent regions. The shock wave, formed in the interaction of the pulsar and stellar winds, is expected to typically overcome about ~10% of the whole solid angle (for the parameters reported in Table 1). On the other hand, the efficiency of particle acceleration in the pulsar shock is expected to be in the range 10% to 30% (e.g. nebula around the Crab pulsar). In fact, this coefficient is close to magnitude of the one derived further in Sect. 5.1 from the normalization of synchrotron spectra, calculated in terms of our model, to the X-ray observations of the considered MSP binary systems.
Only the lower energy part of the IC γ-ray spectrum strongly depend on the velocity of the mixed winds. For faster winds, the γ-ray emission below ~100 GeV is suppressed since electrons do not spend enough time close to the companion star in order to cool completely. The higher energy part of the IC spectrum is not very sensitive to the maximum energy of electrons owing to the importance of the synchrotron process. However, the synchrotron spectra for faster winds peak at higher energies since the maximum energies of electrons accelerated in the transition region strongly depend on the mixed wind velocity (see Eq. (7)).
In Fig. 2b, we show the dependence of the synchrotron and IC spectra on the magnetization parameter of the pulsar wind that, in our model, determines the strength of the magnetic field in the transition region. We fix in this case the mixed wind velocity on 3 × 109 cm s-1, the maximum energy of electrons by applying Eq. (7), and the range of the cosine of observation angles on − 0.5 ≤ cosβ ≤ − 0.4. The synchrotron spectra are very sensitive to the magnetization parameter σ (flux, maximum energies). On the other hand, the IC γ-ray spectra only weakly depend on the magnetization of the mixed wind, except for the PSR J1023+0038 binary system in which the radiation field created by the companion star is the weakest among all considered binaries.
Finally, in Fig. 2c we show the dependence of the IC γ-ray spectra on the range of the observation angles. The peak in the γ-ray spectra shifts slowly to higher energies, but the flux increases fast for larger angles β. Both effects are due to more efficient cooling of relativistic electrons directed towards the companion star. These directions correspond to the lower values of the cosine of the observation angles (i.e., higher values of the angles β). Therefore, our model predicts clearly stronger IC γ-ray production at phases when the pulsar is behind the companion star.
5.1. Expected gamma-ray spectra
 |
Fig. 3 Comparison of the high-energy emission (energy flux versus energy) expected from the MSP binary systems with the sensitivities of Fermi-LAT (10 yrs – extragalactic background, see thin dashed curve, Funk et al. 2013), MAGIC (thin dotted curve, Aleksić et al. 2012) and CTA (thin dot-dashed, Bernlohr et al. 2012), for different ranges of observation angles: 0.9 ≤ cosβ ≤ 1.0 (dot-dashed, away from the companion star), 0.5 ≤ cosβ ≤ 0.6 (dotted), − 0.1 ≤ cosβ ≤ 0. (dashed), − 0.5 ≤ cosβ ≤ − 0.4 (solid), − 1.0 ≤ cosβ ≤ − 0.9 (dot-dot-dashed). The other parameters of the models have been fixed on σ = 10-4, and vadv = 1010 cm s-1, and Ee is given by Eq. (7). The spectra are normalized to the X-ray fluxes observed from PSR B1957+20 (Huang et al. 2012), PSR J1023+0038 (Bogdanov et al. 2011), PSR J1810+1744 (Gentile et al. 2013). For PSR J1816+4510, the upper limit derived from the Swift data (Kaplan et al. 2012). The spectra have been calculated for the energy conversion efficiencies from pulsars to relativistic electrons estimated on 1.6 × 10-2 (for PSR J1023+0038), 6.5 × 10-2 (PSR J1810+1744), 5 × 10-3 (PSR J1816+4510), and 1.8 × 10-3 (PSR B1957+20). |
The synchrotron and IC γ-ray spectra, calculated for likely parameters defining considered model, were compared with the observations of the modulated synchrotron emission in the X-ray energy range (or with derived upper limit) reported in different works. The constraints on the modulated X-ray emission from these four binary systems are reported in Table 1. We apply the velocity of the mixed pulsar-stellar wind equal to 1010 cm s-1, which is close to the one in Sect. 2. For the assumed magnetization parameter, σ = 10-4, and the other typical parameters of the pulsar and its binary system, we estimated the maximum energies of accelerated electrons by using Eq. (7). The assumed value of the magnetization parameter is clearly lower than estimated for the Crab nebula (~0.003, Kennel & Coroniti 1984). However, in our model the pulsar wind is expected to mix very efficiently with the inhomogeneous stellar wind in the transition region. Then, thanks to the magnetic recconnection process, a relatively weak magnetic field is expected in the acceleration and radiation region. In Fig. 3 we show the expected IC γ-ray spectra produced by electrons with the differential power-law spectrum (spectral index − 2), after normalization to the observed modulated X-ray emission from binary systems, PSR J1023+0038, PSR J1810+1744, and PSR B1957+20, and consistent with the upper limit derived for the binary system J1816+4510. Specific curves show the results for different ranges of the cosine of the observation angles, i.e., related to different phases of the binary system. The IC γ-ray spectra in the sub-TeV energy range are on the level of sensitivity of the present Cherenkov telescopes (such as HESS, MAGIC, and VERITAS), for the observation angles that are optimal for efficient γ-ray production (i.e., pulsar behind the companion star).
 |
Fig. 4 The γ-ray light curves in the TeV energies (>100 GeV) expected from considered MSP binary systems: PSR J1023+0038 (on the left), PSR J1810+1744 (left middle), PSR J1816+4510 (right middle), and PSR B1957+20 (right). Specific curves show the results for different inclination angles of the binary systems: i = 0° (dotted), 30° (dot-dot-dashed), 45° (dashed), 60° (solid), and 90° (dot-dashed). The phase is counted from the location of the MSP in front of the companion star. The parameters of the companion stars and the binary systems are reported in Table 1. It is assumed that the MSP moves in a circular orbit around the companion star. The parameters describing the spectrum and escape of electrons are the same as in Fig. 3. The injection place of electrons is assumed to be at the apex of the collision region (described by Rsh in Table 1). The γ-ray fluxes are collected in the range of phases with the width equal to 0.05. |
In the case of three binary systems, PSR B1957+20, PSR J1023+0038, and PSR J1810+1744, the estimates of the inclination angles are available in the literature: 65° for PSR B1957+20 (Reynolds et al. 2007) and 46° for PSR J1023+0038 (assuming that the neutron star mass is equal to the 1.4 solar masses, Archibald et al. 2009, Archibald et al. 2010), and 48° for PSR J1810+1744. The values of these angles depend on the masses of the neutron stars in these binary systems, which are in fact not well known. The values of the inclination angles determine the lowest values of the cosine of the angle β for the pulsar and the observer located on the opposite site of the companion star (i.e., ω = π). Then, cosβ equals to − 0.9 (for PSR B1957+20), − 0.72 (for PSR J1023+0038), and − 0.74 (for PSR J1810+1744). It is clear from Fig. 3 that for these locations of pulsars on the orbits, the TeV γ-ray fluxes are expected to be close to the maximum values. However, when the pulsar is in front of the companion star, the fluxes should be a factor of 2 − 3 lower in the TeV γ-ray energy range and about an order of magnitude lower in the GeV γ-ray energies (see Fig. 3).
We conclude that the TeV γ-ray signals from these binary systems have a chance to be detected in the extensive observations with the present Cherenkov telescopes only during specific range of orbital phases. The situation should be much better with the construction of the next generation of Cherenkov telescope arrays such as CTA. In the case of CTA, the TeV γ-ray emission from MSP binary systems is expected to be probed for most of the range of orbital phases. Modulated GeV γ-ray emission from the considered binary systems is not likely to be detected in the Fermi-LAT data. The exception can only be the redback-type binary, PSR J1816+4510, which contains an exceptionally luminous companion star with surface temperature above ~104 K (Kaplan et al. 2013). Recently identified γ-ray sources in the direction of this pulsar show clear pulsations with the MSP period (Kaplan et al. 2012). Interestingly, the γ-ray spectrum calculated for PSR J1816+4510 seems to be atypical of the MSP population. It shows emission above the characteristic cut-off in the pulsar’s spectra at ~2–3 GeV. It might be that a part of this emission comes from the binary system itself. This interesting binary system should be clearly studied again in the future since positive detection (or even the upper limits) of the γ-ray component modulated with the binary period will provide important constraints for the scenario discussed in this paper.
5.2. Gamma-ray light curves
For more quantitative predictions, which could be tested by the extensive observations in the TeV γ-ray energy range, we calculated the expected γ-ray light curves at energies above >100 GeV from all four MSP binaries (see Fig. 4). The phase zero is measured from the location of the pulsar on the orbit when it is in front of the companion star. Different curve styles indicate the cases with the observer located at different inclination angles starting from i = 0° up to 90°.
For the large inclination angles, the light curves show a clear dip (around the phase 0.5), caused by a shadowing effect by the companion star. The extent of the dip depends on the relative separation of the stars in the binary system (with respect to the stellar radius). The TeV γ-ray flux also depends rather weakly on the inclination angle of the binary system for the range of phases when the pulsar is behind the companion star. On the other hand, we notice a strong change in the TeV flux with the inclination angle for the phases when the pulsar is in front of the star. This behavior is due to the basic feature of the IC scattering process in the case of a strongly anisotropic radiation field. The efficiency of IC scattering depends much more strongly on the collision angle between electron and soft photon when the photon arrives from the hemisphere behind the direction of the electron.
We now discuss the case of three MSP binaries for which the inclination angles are known in detail. For the redback MSP binary, PSR J1023+0038, and the black widow binary, PSR J1810+1744, we predict modulation of the TeV γ-ray signal with the orbital period of the binary system by a factor of ~3–5. However, the black widow binary system, PSR B1957+20, the predicted modulation of the signal is clearly over one order of magnitude. Therefore, it is very important to observe MSP binary systems at the correct phase intervals in order to guarantee positive detection. The stronger modulation pattern in the case of PSR B1957+20 is due to the larger inclination angle and weaker radiation field created by the companion star in this binary system in respect to the redback binary PSR J1023+0038.
The TeV γ-ray flux is expected to be the most sensitive to the inclination angle of the binary system when the pulsar is in front of the companion star (corresponding to phase zero, see Fig. 4). In principle, CTA upper limits in this phase, or positive detection that will be rather difficult due to the low fluxes, should allow putting a limit on the inclination angle of the binary system. However, this limit may not be very restrictive due to relatively low TeV γ-ray fluxes at these phases, which are comparable to the sensitivity of CTA.
The TeV γ-ray light curves, predicted by our model for the MSP binary systems, basically show different emission features than observed from the massive TeV γ-ray binary systems, such as LS 5039 (Aharonian et al. 2006) or LSI 303 +61 (Albert et al. 2009). The massive binaries show the maximum of the TeV emission at phases when the compact objects are generally in front of the massive stars. In contrast, we predict here that the TeV γ-ray light curves from MSP binaries should behave in a completely opposite manner, i.e., the maximum of the TeV emission should occur at phases shifted by half of the period with respect to massive TeV binaries. Therefore, observations of MSP binary systems with Cherenkov telescopes should concentrate on phases when the pulsar is behind the companion star in order to increase the chances for detection of the TeV γ-ray signal.
6. Discussion and conclusion
We have considered the high-energy processes that are expected to occur within the MSP binary systems of the redback and black widow types. We modified the general scenario proposed for those objects (acceleration of particles and their radiation in the region of the colliding pulsar and companion star winds, e.g., Harding & Gaisser 1990; Arons & Tavani 1993) by assuming that the wind of the companion star, induced by the energy realized by the pulsar, is very inhomogeneous. This assumption has two important consequences. Firstly, winds should mix efficiently at the collision region and move with velocity that is clearly lower than the velocity of light. Secondly, thanks to the efficient mixing, the reconnection of the magnetic field should be very efficient. As a consequence, a relatively low value of the magnetic field is expected at the transition region. This magnetic field is described by the magnetization parameter of plasma σ, which in our case can have values clearly below what is estimated for the Crab nebula (i.e., σ ~ 0.003, Kennel & Coroniti 1984). Since the mixed winds move relatively slowly, relativistic electrons stay a relatively long time in the dense radiation of the companion star, losing energy on the IC scattering process. Thanks to the relatively weak magnetic field at the transition region, the cooling process of relativistic electrons is not completely dominated by synchrotron radiation, as considered by Arons & Tavani (1993), among others.
As an example, we applied our model to the four MSP binary systems, two of the black widow type and two of the Redback type. We show that electrons can be accelerated in these binary systems to TeV energies. A significant amount of their energy is lost on the production of TeV γ-rays in collisions with the stellar radiation. We calculated the synchrotron and IC γ-ray spectra escaping to the observer located at different angles in respect to direction defined by the stars. Synchrotron spectra are independent of the location of the observer owing to isotropization of relativistic electrons in the mixed winds and the relatively low velocity of this winds. However, the IC γ-ray spectra clearly depend on the location of the observer since the companion star creates anisotropic radiation field for relativistic electrons. We made a simplified assumption that all relativistic electrons are injected at the apex of the collision region between the pulsar and stellar winds whose distance from the companion star is reported in Table 1. In fact, the injection distance should extend along the transition region as discussed in Sect. 2. Therefore, in a more realistic injection scenario for electrons, the γ-ray spectra at the observer can be obtained by integrating over the specific solid angle subtracted by the extend of the transition region. However, such a process will require introducing a few, not well constrained, free parameters that should describe the extent of the injection region of electrons. We did not consider these geometric effects in detail in the present calculations, which are more oriented to investigating general emission features.
From normalization of calculated synchrotron spectra to the observed non-thermal X-ray flux from these binary systems (or to the upper limit in the case of PSR J1816+4510), we predicted the absolute level of the TeV γ-ray flux from these binaries (see Figs. 3 and 4) and concluded that the TeV emission is comparable to the sensitivities of the present Cherenkov telescopes. Therefore, extensive observations of some MSP binary systems by the HESS, MAGIC, or VERITAS telescopes should give a chance for positive detection of the new class of the TeV γ-ray sources.
The expected TeV γ-ray emission from MSP binary systems should have different emission features than those discovered in the recent years from the massive TeV γ-ray binaries such as LS 5039 or LS I 303 +61. After all, the maximum (minimum) of the TeV emission is predicted to appear at the range of phases when the pulsar is behind (in front of) the companion star. Moreover, we predict the synchronization of the GeV and TeV γ-ray emission in the light curve of the MSP binary systems; however, predicted modulated GeV flux cannot be observed with the present, even extensive monitoring with the Fermi-LAT telescope, possibly excepting the cases of some Redback type binaries that contain especially luminous companion stars as observed in the case of PSR J1816+4510. These two basic emission features clearly distinguish MSP binary systems from the massive TeV binary systems. They are due to the much weaker radiation field created by the companion stars in the MSP binary systems when compared to the massive binaries. Therefore, the IC e± pair cascading processes within the MSP binary systems are also not expected to play a major role in contrast to the massive TeV binary systems.
The results of our calculations are based on the assumption that the winds from the pulsar and the companion star are spherically symmetric. In fact, this is probably not the case. The wind of the companion star is probably much stronger towards the pulsar owing to irradiation. On the other hand, the pulsar wind is also expected to be stronger in the equatorial plane with respect to the rotational axis of the pulsar (see, e.g., Bogovalov & Khangoulian 2002; Lyubarsky 2002). Thanks to the non-spherical pulsar wind, the wind power can be more efficiently transferred to relativistic electrons and the predicted above γ-ray fluxes can be enhanced as also considered by Wu et al. (2012).
Acknowledgments
This work is supported by grants through the Polish NCN No. 2011/01/B/ST9/00411 and NCBiR No. ERA-NET-ASPERA/01/10.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi-LAT Collaboration) 2009a, Science, 325, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi-LAT Collaboration) 2009b, ApJ, 706, 56 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi-LAT Collaboration) 2009c, ApJ, 701, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi-LAT Collaboration) 2011, ApJ, 736, 11 [Google Scholar]
- Abdo, A. A., Ajello, M., Allafort, A., et al. (Fermi-LAT Collaboration) 2013, ApJS, 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Acharya, B. S., Actis, M., Aghajani, T., et al. (CTA Consortium) 2013, Astropart. Phys., 43, 3 [Google Scholar]
- Aharonian, F. A., Akhperjanian, A. G., Aye, K.-M., et al. (HESS Collaboration) 2005a, A&A, 442, 1 [Google Scholar]
- Aharonian, F. A., Akhperjanian, A. G., Aye, K.-M., et al. (HESS Collaboration) 2005b, Science, 309, 746 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F. A., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS Collaboration) 2006, A&A, 460, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. (MAGIC Collaboration) 2006, Science, 312, 1771 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. (MAGIC Collaboration) 2009, ApJ, 693, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Alvarez, E. A., Antonelli, L. A., et al. (MAGIC Collaboration) 2012, Astropart. Phys., 35, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Archibald, A. M., Stairs, I. H., Ransom, S. M., et al. 2009, Science, 324, 1411 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Archibald, A. M., Kaspi, V. M., Bogdanov, S., et al. 2010, ApJ, 722, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Arons, J., & Tavani, M. 1993, ApJ, 403, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W. 1997, A&A, 322, 523 [NASA ADS] [Google Scholar]
- Bednarek, W. 2000, A&A, 362, 646 [NASA ADS] [Google Scholar]
- Bednarek, W. 2006, MNRAS, 368, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W. 2011, MNRAS, 418, L49 [NASA ADS] [Google Scholar]
- Bernlöhr, K., Barnacka, A., Becherini, Y., et al. (CTA Consortium) 2013, Astropart. Phys., 43, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanov, S., Archibald, A. M., Hessels, J. W. T., et al. 2011, ApJ, 742, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Bogovalov, S. V., & Khangoulian, D. V. 2002, MNRAS, 336, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Breton, R. P., van Kerkwijk, M. H., Roberts, M. S. E., et al. 2013, ApJ, 769, 108 [Google Scholar]
- Brink, C., de Jager, O. C., Raubenheimer, B. C., et al. 1990, ApJ, 364, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Buccheri, R., Salamone, V., Bennett, K., et al. 1996, A&AS, 115, 305 [NASA ADS] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002 [arXiv:astro-ph/0207156] [Google Scholar]
- Dubus, G. 2006, A&A, 456, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deller, A. T., Archibald, A. M., Brisken, W. F., et al. 2012, ApJ, 756, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Eichler, D., & Usov, V. 1993, ApJ, 402, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., Berman, G., Bower, G., et al. 1990, ApJ, 351, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., Stinebring, D. R., Taylor, J. H., et al. 1988, Nature, 333, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Funk, S., & Hinton, J. A. (CTA Consortium) 2013, Astropart. Phys., 43, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, P., Roberts, M., McLaughlin, M., et al. 2013, ApJ, submitted [arXiv:1305.6799] [Google Scholar]
- Girard, T., & Willson, L. A. 1987, A&A, 183, 247 [NASA ADS] [Google Scholar]
- Guillemot, L., Johnson, T. J., Venter, C., et al. 2012, ApJ, 744, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, A. K., & Gaisser, T. K. 1990, ApJ, 358, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W. T., Roberts, M. S. E., McLaughlin, M. A., et al. 2011, in AIP Conf. Ser. 1357, eds. M. Burgay et al., 40 [Google Scholar]
- Huang, R. H. H., Kong, A. K. H., Takata, J., et al. 2012, ApJ, 760, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplan, D. L., Stovall, K., Ransom, S. M., et al. 2012, ApJ, 753, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplan, D. L., Bhalerao, V. B., van Kerkwijk, M. H., et al. 2013, ApJ, 765, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Kennel, C. F., & Coroniti, F. V. 1984, ApJ, 283, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarsky, Y. E. 2002, MNRAS, 329, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, M. T., Callanan, P. J., Fruchter, A. S., et al. 2007, MNRAS, 379, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, M. S. E. 2012, in Proc. Neutron Stars and Pulsars: Challenges and Opportunities after 80 years, ed. J. van Leeuwen, IAU Symp., 291 [Google Scholar]
- Ruderman, M., Shaham, J., & Tavani, M. 1989, ApJ, 336, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, E. M. H., Takata, J., Cheng, K. S., et al. 2012, ApJ, 761, 181 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Schematic representation of the compact binary system containing a energetic MSP (on the left) and the picture on which the basic angles defining the binary system are shown (on the right). On the left: the pulsar creates a strong wind that contains relativistic electrons (γe). The companion star creates turbulent stellar wind mainly as a result of irradiation from the pulsar. The winds collide, creating a turbulent, non-stationary shock structure. Both winds mix effectively in this region. Relativistic electrons (from the pulsar wind or additionally re-accelerated in the turbulent pulsar-stellar winds) are isotropized by the random magnetic field of the mixed winds. They are advected along the shock structure. During this process, electrons comptonize stellar radiation producing γ-rays. Owing to the anisotropy of the stellar radiation field, γ-rays tend to be produced in the general direction of the companion star. As a result, the γ-ray signal, produced towards the observer (obs.) located at the angle β, should be modulated with the phase of the binary system. On the right: the binary system is inclined at the angle i towards the observer’s (Obs) line of sight. The orbital phase, ω, is equal to zero when the pulsar is in front of the companion star. The angle between the observer and the pulsar (and also injection place of relativistic electrons) is marked by β. |
| In the text | |
 |
Fig. 2 Spectral energy distribution (energy flux versus energy, SED) of the γ-rays from the IC process and X-rays from the synchrotron process, produced by electrons accelerated in the wind collision region in the binary systems: PSR J1816+4510 (right column), PSR J1810+1744 (right-middle column), PSR J1023+0038 (left-middle column), and PSR B1957-20 (left column). a) Dependence on different advection velocities of the mixed pulsar-stellar winds: vadv = 1010 cm s-1 (dashed), 3 × 109 cm s-1 (solid), and 109 cm s-1 (dotted). The other parameters are fixed on σ = 10-3, − 0.5 ≤ cosβ ≤ − 0.4. The differential spectrum of electrons is assumed to be a power-law type (spectral index − 2) between the maximum energy given by Eq. (7) and minimum energy equal to Emin = 0.5 GeV. The power in this electron spectrum is normalized to 1% of the pulsar rotational energy lost by the pulsar. b) Dependence on magnetization parameter of the pulsar wind: σ = 10-2 (dotted), 10-3 (solid), and 10-4 (dashed). The other parameters are fixed on − 0.5 ≤ cosβ ≤ − 0.4 and Ee given by Eq. (7), and vadv = 3 × 109 cm s-1. c) Dependence on the cosine of the observation angle (measured from the direction defined by the centers of the stars): 0.9 ≤ cosβ ≤ 1.0 (dashed, outwards from the companion star), 0.5 ≤ cosβ ≤ 0.6 (solid), − 0.1 ≤ cosβ ≤ 0 (dotted), − 0.5 ≤ cosβ ≤ − 0.4 (dot-dashed), − 1.0 ≤ cosβ ≤ − 0.9 (dot-dot-dashed), the electron energy Ee is given by Eq. (7), σ = 10-3, and vadv = 3 × 109 cm s-1. |
| In the text | |
 |
Fig. 3 Comparison of the high-energy emission (energy flux versus energy) expected from the MSP binary systems with the sensitivities of Fermi-LAT (10 yrs – extragalactic background, see thin dashed curve, Funk et al. 2013), MAGIC (thin dotted curve, Aleksić et al. 2012) and CTA (thin dot-dashed, Bernlohr et al. 2012), for different ranges of observation angles: 0.9 ≤ cosβ ≤ 1.0 (dot-dashed, away from the companion star), 0.5 ≤ cosβ ≤ 0.6 (dotted), − 0.1 ≤ cosβ ≤ 0. (dashed), − 0.5 ≤ cosβ ≤ − 0.4 (solid), − 1.0 ≤ cosβ ≤ − 0.9 (dot-dot-dashed). The other parameters of the models have been fixed on σ = 10-4, and vadv = 1010 cm s-1, and Ee is given by Eq. (7). The spectra are normalized to the X-ray fluxes observed from PSR B1957+20 (Huang et al. 2012), PSR J1023+0038 (Bogdanov et al. 2011), PSR J1810+1744 (Gentile et al. 2013). For PSR J1816+4510, the upper limit derived from the Swift data (Kaplan et al. 2012). The spectra have been calculated for the energy conversion efficiencies from pulsars to relativistic electrons estimated on 1.6 × 10-2 (for PSR J1023+0038), 6.5 × 10-2 (PSR J1810+1744), 5 × 10-3 (PSR J1816+4510), and 1.8 × 10-3 (PSR B1957+20). |
| In the text | |
 |
Fig. 4 The γ-ray light curves in the TeV energies (>100 GeV) expected from considered MSP binary systems: PSR J1023+0038 (on the left), PSR J1810+1744 (left middle), PSR J1816+4510 (right middle), and PSR B1957+20 (right). Specific curves show the results for different inclination angles of the binary systems: i = 0° (dotted), 30° (dot-dot-dashed), 45° (dashed), 60° (solid), and 90° (dot-dashed). The phase is counted from the location of the MSP in front of the companion star. The parameters of the companion stars and the binary systems are reported in Table 1. It is assumed that the MSP moves in a circular orbit around the companion star. The parameters describing the spectrum and escape of electrons are the same as in Fig. 3. The injection place of electrons is assumed to be at the apex of the collision region (described by Rsh in Table 1). The γ-ray fluxes are collected in the range of phases with the width equal to 0.05. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


