| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 14 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201322565 | |
| Published online | 22 January 2014 | |
ynogkm: A new public code for calculating time-like geodesics in the Kerr-Newman spacetime⋆
1 Yunnan Observatories, Chinese Academy of Sciences, 650011 Kunming, PR China
e-mail: yangxl@ynao.ac.cn
2 Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, 650011 Kunming, PR China
3 University of Chinese Academy of Sciences, 100049 Beijing, PR China
Received: 29 August 2013
Accepted: 9 November 2013
In this paper, we present a new public code, named ynogkm (Yun-Nan observatories geodesic in a Kerr-Newman spacetime for massive particles), for the fast calculation of time-like geodesics in the Kerr-Newman (K-N) spacetime, which is a direct extension of ynogk (Yun-Nan observatories geodesic Kerr) calculating null geodesics in a Kerr spacetime. Following the strategies used in ynogk, we also solve the equations of motion analytically and semi-analytically by using Weierstrass’ and Jacobi’s elliptic functions and integrals in which the Boyer-Lidquist (B-L) coordinates r, θ, φ, t and the proper time σ are expressed as functions of an independent variable p (Mino time). All of the elliptic integrals are computed by Carlson’s elliptic integral method, which guarantees the fast speed of the code. Finally, the code is applied to a couple of toy problems.
Key words: accretion, accretion disks / black hole physics / relativistic processes / methods: numerical
The current version of the code is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/561/A127
© ESO, 2014
1. Introduction
In the vicinity of the black hole and any other compact objects, the gravitational field is extremely strong and the spacetime is significantly warped and twisted. Thus, the general relativity effects cannot be ignored. The motion of photons and test particles in this curved spacetime is along geodesics if we do not consider the external forces or perturbations exerting on them. The assumption that photons and particles propagate along geodesic trajectories is valid in most astrophysical contexts. The fast calculation of the null and time-like geodesics in curved spacetime is significantly important and has been widely used in astrophysical research (e.g., Cunningham & Bardeen 1973; Luminet 1979; Rauch & Blandford 1994; Hackmann 2010).
The calculation and applications of null geodesics in a curved spacetime, especially in a Kerr spacetime, have been discussed by many authors in different attempts to date (Dexter & Agol 2009; Hackmann 2010; Hackmann & Xu 2013; Chan et al. 2013; Yang & Wang 2013,and the references therein). To compute the geodesics it is possible to integrate a set of second-order differential equations in any relativistic spacetime directly, or to evaluate a set of elliptic integrals of motion in a Kerr-Newman (K-N) spacetime. In the present paper, we focus on the latter approach. There are four constants for any geodesic motions in a K-N spacetime (Carter 1968), which makes the reduction of the order of motion equations possible.
To obtain the optical appearance of a star orbiting around an extreme Kerr black hole, Cunningham & Bardeen (1973) calculated the null geodesics in a Kerr spacetime based on the elliptic integral method and proposed the impact parameters for the first time. After that, a method called ray-tracing was developed (e.g., Luminet 1979). Rauch & Blandford (1994) researched the optical caustics in a Kerr spacetime with an attempt to explain rapid X-ray variability in AGN. As a bonus they presented, in tabular form, cases that need to be considered for the calculation of both the null and time-like geodesics in a Kerr spacetime. Similar discussions and results are also given by Li et al. (2005) in their appendix.
The cases discussed by the above authors are very detailed and very complicated. As discussed in Yang & Wang (2013), this sophisticated situation can be significantly simplified by the introductions of Mino time p (Mino 2003) and the Weierstrass elliptic integrals and functions. Hackmann (2010) and Hackmann & Xu (2013) systematically discuss how to solve equations of geodesic motion, instead of restricting their research to the Kerr or K-N spacetime by Mino time and many types of elliptic functions. Carlson’s elliptic approach is quite suitable and efficient for evaluating elliptic integrals and functions, which has been demonstrated by Dexter & Agol (2009) and Yang & Wang (2013).
Motivated by the above discussions and the fact that there is currently no public code available to calculate time-like geodesics in a K-N spacetimes for all coordinates (including the proper times) at the same time, in this paper, we extend the scheme of Yang & Wang (2013) from null geodesics in a Kerr spacetime to time-like geodesics in a K-N spacetime. As a result, we developed a new public code, named ynogkm.
Analogous to ynogk, in ynogkm we also express the Boyer-Lidquist (B-L) coordinates r, θ, φ, t and the proper time σ as functions of the Mino time p semianalytically by using Weierstrass’ and Jacobi’s elliptic functions and integrals. Such treatment allows us to handle the practical applications conveniently. The Mino time p is an integral value along a particular geodesic. All of the elliptical integrals are computed using Carlson’s approach. Similarly to ynogk, we discuss how to compute the constants of motion from the initial conditions, i.e., the initial four-momentum of the particles measured under the local nonrotating frame (LNRF, Bardeen et al. 1972). For a massive particle with electric charge in a K-N spacetime, the number of constants of motion becomes 4. For a photon whose rest mass μm and electric charge ϵ are both zero, the number of constants of motion is 2. When taking μm and ϵ to be zero, the discussions here are reduced to those for null geodesics.
The paper is organized as follows. In Sect. 2, we provide the equations of motion for an electrically charged massive particle in a K-N spacetime. In Sect. 3, we discuss the expressions of the B-L coordinates and proper time as functions of parameter p. Then we reduce all of the elliptic integrals to standard forms that are evaluated by Carlson’s approach. Next, we discuss the calculation of constants of motion from initial conditions in Sect. 4. A brief introduction and discussion about the code are given in Sect. 5. In Sect. 6, we demonstrate the applications of our code to toy problems in the literature. Finally, a brief summary is presented in Sect. 7. Throughout this paper, the natural unit is used in which the constants G = c = 1. The mass of central black hole M is also taken to be 1, unless otherwise stated.
2. Equations of motion for time-like geodesics
We assume that the spin and electric charge of the black hole are a and e, respectively. Using the notation of Bardeen et al. (1972), we can write the K-N metric under the B-L coordinate as 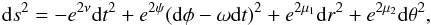 (1)where
(1)where 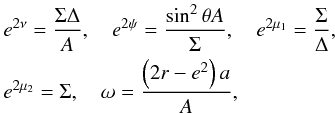 (2)and
(2)and 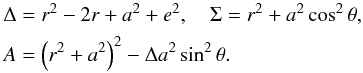 (3)Carter (1968) gave the first-order differential equations of motion for electrically charged massive particles as follows:
(3)Carter (1968) gave the first-order differential equations of motion for electrically charged massive particles as follows: 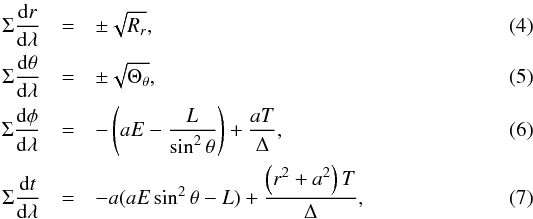 where
where
![\begin{eqnarray} \label{Rr} && T=E\left(r^2+a^2\right)-L a+e\epsilon r,\\ && R_r=T^2-\Delta\left[\mu_m^2r^2+(L-aE)^2+Q\right],\\ && \Theta_\theta=Q-\cos^2\theta\left[a^2\left(\mu_m^2-E^2\right)+L^2/\sin^2\theta\right], \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq17.png) and λ = τ/μm, τ is the proper time, μm is the rest mass of the particle, Q is the Carter constant, E is the energy tested by an observer at infinity, L is the angular momentum of the particle about the black hole spin axis, and ϵ is the electric charge of the particle. From Eqs. (4)–(7) we can obtain the expression of the four-momentum for a particle
and λ = τ/μm, τ is the proper time, μm is the rest mass of the particle, Q is the Carter constant, E is the energy tested by an observer at infinity, L is the angular momentum of the particle about the black hole spin axis, and ϵ is the electric charge of the particle. From Eqs. (4)–(7) we can obtain the expression of the four-momentum for a particle 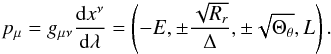 (11)Equivalently, the equations of motion with integral forms can be written as:
(11)Equivalently, the equations of motion with integral forms can be written as:
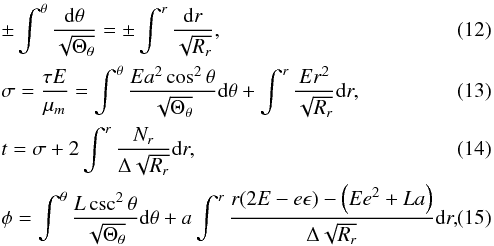 where
where ![\begin{eqnarray} N_r&=&(2E+e\epsilon)r^3-Ee^2r^2+\bigg[2a(Ea-L) \nonumber\\ &&+~a^2e\epsilon\bigg]r-e^2a(Ea-L). \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq25.png) (16)Here σ is a new variable, which is related to the proper time τ of the particle. For a photon, it becomes an affine parameter.
(16)Here σ is a new variable, which is related to the proper time τ of the particle. For a photon, it becomes an affine parameter.
In many cases, we only need the equations of motion with integral forms. But in two special cases, i.e., the equatorial plane motion and the spherical motion, we need the differential equations of motion. In the case of the former, the particle is confined to the equatorial plane, one has Q = 0, θ ≡ π/2, and thus Θθ ≡ 0. Then the equations of motion with integral forms become invalid, since Θθ ≡ 0 appears in the denominator. But, from the differential equations, we can obtain the right equations to describe the plane motion. From Eq. (4), we have 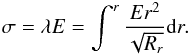 (17)Dividing both sides of Eq. (7) by Eq. (4), we obtain
(17)Dividing both sides of Eq. (7) by Eq. (4), we obtain 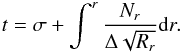 (18)Similarly, from Eqs. (4) and (6), we obtain
(18)Similarly, from Eqs. (4) and (6), we obtain 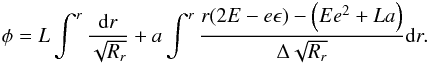 (19)For spherical motion, we have Rr ≡ 0, thus the equations of motion with integral forms become invalid, because Rr appears in the denominator. Similarly, from Eq. (5) we obtain
(19)For spherical motion, we have Rr ≡ 0, thus the equations of motion with integral forms become invalid, because Rr appears in the denominator. Similarly, from Eq. (5) we obtain 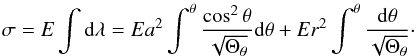 (20)From Eqs. (5) and (7), we obtain
(20)From Eqs. (5) and (7), we obtain 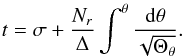 (21)And from Eqs. (5) and (6), we find
(21)And from Eqs. (5) and (6), we find 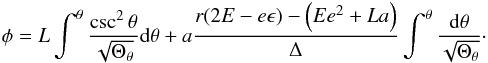 (22)With Eqs. (12)–(22), we can calculate the geodesics by evaluating the elliptical integrals, instead of solving the differential equations of motion, and we can also express the B-L coordinates and proper time as functions of a parameter p. In the next section, we discuss how to get these functions semianalytically with elliptical functions and integrals.
(22)With Eqs. (12)–(22), we can calculate the geodesics by evaluating the elliptical integrals, instead of solving the differential equations of motion, and we can also express the B-L coordinates and proper time as functions of a parameter p. In the next section, we discuss how to get these functions semianalytically with elliptical functions and integrals.
3. Expressions of B-L coordinates and proper time as functions of p
3.1. The turning points
As discussed in Yang & Wang (2013), when we introduce a new parameter p with following definition from Eq. (12) 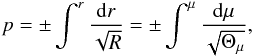 (23)we can obtain functions r(p),μ(p),φ(p),t(p), and σ(p) from the equations of motion with integral forms, where μ = cosθ and
(23)we can obtain functions r(p),μ(p),φ(p),t(p), and σ(p) from the equations of motion with integral forms, where μ = cosθ and
![\begin{eqnarray} && R(r) = \frac{R_r}{E^2} = \left(1-m^2\right)r^4+2\left(m^2+e\varepsilon\right)r^3- \bigg[q+\lambda^2 \nonumber \\ &&\qquad \;\; +~a^2\left(m^2-1\right)+e^2\left(m^2-\varepsilon^2\right)\bigg]r^2+ 2\bigg[q+\left(a-\lambda\right)^2\nonumber \\ &&\qquad \;\; +~ea\varepsilon\left(a-\lambda\right)\bigg]r-e^2\left(a-\lambda\right)^2-\left(a^2+e^2\right)q, \\ &&\Theta_\mu(\mu) = \frac{\Theta_\theta \sin^2\theta}{E^2}\nonumber \\ &&\qquad\;\;\, =a^2\left(m^2-1\right)\mu^4 - \left[q+\lambda^2+a^2\left(m^2-1\right)\right]\mu^2 + q.~~~~ \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq42.png) Since the signs before the integrals are the same with dr and dθ, the parameter p monotonously increases along a particular geodesic. Here λ = L/E, q = Q/E2, m = μm/E, and ε = ϵ/E, which are defined as constants of motion throughout this paper. Because R and Θμ are quartic (when m ≠ 1) or cubic (when m = 1) polynomials, the integrals about r and μ are elliptical integrals, which are reduced to the Weierstrass standard elliptic integrals (or those of Legendre’s when equation R(r) = 0 has no real roots).
Since the signs before the integrals are the same with dr and dθ, the parameter p monotonously increases along a particular geodesic. Here λ = L/E, q = Q/E2, m = μm/E, and ε = ϵ/E, which are defined as constants of motion throughout this paper. Because R and Θμ are quartic (when m ≠ 1) or cubic (when m = 1) polynomials, the integrals about r and μ are elliptical integrals, which are reduced to the Weierstrass standard elliptic integrals (or those of Legendre’s when equation R(r) = 0 has no real roots).
Since both R and Θθ appear under the radical sign in the equations of motion, they must be nonnegative. The critical points satisfying R(r) = 0 or Θθ(θ) = 0 are so-called turning points in which the corresponding coordinate velocity is zero. When the motion of a particle is bounded in r or in θ coordinate, two turning points exist for the coordinate. We use rtp1,rtp2 and θtp1, θtp2 to denote the coordinates of these points, and assume that rtp1 ≤ rtp2, θtp1 ≤ θtp2. Since 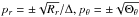 , when pr = 0 or pθ = 0 at the initial point, we have Rr(rini) = 0,Θθ(θini) = 0, implying that the initial point is a turning point and rini (or θini) is equal to one of rtp1,rtp2 (or θtp1, θtp2). Then we find rini ∈ [rtp1,rtp2] and θini ∈ [θtp1,θtp2].
, when pr = 0 or pθ = 0 at the initial point, we have Rr(rini) = 0,Θθ(θini) = 0, implying that the initial point is a turning point and rini (or θini) is equal to one of rtp1,rtp2 (or θtp1, θtp2). Then we find rini ∈ [rtp1,rtp2] and θini ∈ [θtp1,θtp2].
When rtp2 does not exist at all (or equivalently, rtp2 = ∞) and rtp1 > rh (rh is the radius of the event horizon), the particle will eventually go to infinity far away. When rtp1 does not exist (or rtp1 < rh) and rtp2 > rh, then the particle will eventually fall into the event horizon of the black hole. If (1) both rtp1 and rtp2 do not exist, this case equivalently corresponds to the fact that the equation R(r) = 0 has no real roots; or (2) rtp2 does not exist and rtp1 exists, but rtp1 < rh, for both cases the particle can move from infinity to the event horizon freely.
To obtain the θ coordinate of a turning point, we usually solve the equation Θμ(μ) = 0 to get μtp (=cosθtp) instead of solving the equation Θθ(θ) = 0. The roots of two equations are exactly the same except these special cases with constant λ = 0. The equation Θμ(μ) = 0 with λ = 0 has real roots ± 1, or 0,π, which are not the roots of equation Θθ(θ) = 0, indicating that a particle with λ = 0 can move from 0 to π freely and can go through the spin axis due to non-zero poloidal velocity pθ = ±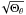 at the spin axis. Meanwhile, the particle changes the sign of its angular velocity dθ/dλ, and its azimuthal coordinate jumps from φ to φ ± π (Shakura 1987) instantaneously.
at the spin axis. Meanwhile, the particle changes the sign of its angular velocity dθ/dλ, and its azimuthal coordinate jumps from φ to φ ± π (Shakura 1987) instantaneously.
Expression of μ(p).
Expression of r(p).
3.2. Coordinates μ and r
In this section, we express μ and r as functions of parameter p, i.e., μ = μ(p),r = r(p). The procedure to obtain these explicit expressions for electrically charged massive particles is quite tedious, but similar to the procedure for photons (refer to the discussions in Yang & Wang 2013). Thus, there is no need to present the details of the procedure. For reference, we present expressions of μ(p),r(p) in tabular form. See Tables 1 and 2.
Definitions of Table 2.
Expression of p.
For r, there are five cases:
-
1.
m ≠ 1 and equation R(r) = 0 has at least one real root.
-
2.
1 − m2 > 0 (or | E | > μm) and R(r) = 0 has no real roots.
-
3.
1 − m2 < 0 (or | E | < μm) and R(r) = 0 has no real roots.
-
4.
| m | = 1 (or | E | = μm) and the geodesic is unbounded.
-
5.
| m | = 1 (or | E | = μm) and the geodesic is bounded.
In case 1, R(r) = 0 with m ≠ 1 has at least one real root. We are not concerned with the number of real roots in the equation or with their practical distribution. When the equation R(r) = 0 has real roots, turning point rtp1 (or rtp2) does exist, and can be easily determined with given rini1.
In cases 2 and 3, R(r) = 0 has no real roots, but two pairs of complex conjugate roots are written as: 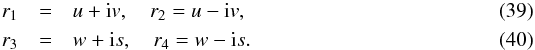 To avoid dealing with a complex integral, we use Jacobi’s elliptic function to express r instead of that of Weierstrass.
To avoid dealing with a complex integral, we use Jacobi’s elliptic function to express r instead of that of Weierstrass.
For cases 4 and 5, 1 − m2 = 0, thus R(r) reduces to ![\begin{eqnarray} R(r) &=& 2(1+e\varepsilon)r^3-[q+\lambda^2+e^2(1-\varepsilon^2)]r^2+2[q+(a-\lambda)^2 \nonumber \\ &&+~ea\varepsilon(a-\lambda)]r-e^2(a-\lambda)^2-(a^2+e^2)q. \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq146.png) (41)From the expression of r(p) in Eq. (30), we know that when p + Πr = ω′, ℘(p + Πr;g2,g3) = ∞, i.e., r(p) = ∞, meaning that no matter what initial value pr takes, the particle shall reach infinity eventually. As a result, the particular geodesic is unbounded.
(41)From the expression of r(p) in Eq. (30), we know that when p + Πr = ω′, ℘(p + Πr;g2,g3) = ∞, i.e., r(p) = ∞, meaning that no matter what initial value pr takes, the particle shall reach infinity eventually. As a result, the particular geodesic is unbounded.
3.3. Coordinates φ, t and the proper time σ
As discussed in Yang & Wang (2013), the expressions φ,t, and σ as functions of parameter p can be converted to evaluate the elliptic integrals appeared in the equations of motion with a given p. We divide the process into two steps. In the first step, the path and limits of the integrals are determined. In the second step, the integrals are reduced to standard forms, which are evaluated by Carlson’s approach.
3.3.1. The path and limits of integrals
For convenience, we use Fr and Fμ to represent the complicated integrands in integrals of r and μ, respectively.
The path is not monotonic when one or more than one turning points exist for r and μ. The path is divided into several parts in which each one has the maximum monotonic length, and the integrals are the sum of all individual parts. In Fig. 1, the integral path of r coordinate for a particular bounded geodesic is illustrated schematically. The motion of the particle is confined between two turning points, rtp1 and rtp2.
 |
Fig. 1 Motion of r illustrated schematically. It has been projected onto the equatorial plane of the black hole. The radial turning points are rtp1 and rtp2 between which the motion is confined. Point P indicates the position for a given p. The whole integral path is not monotonous and should be divided into several sections, each with a maximum proper length, such as DA, DG, HG, HI, PI. From the definitions of I0αr,I1αr, and I2αr (see text), one obtains |
There are four important points in a particular path for r (or for μ), which are related to the integral limits. They are: 1. the initial position rini (or μini); 2. the two turning points, rtp1 and rtp2 (or μtp1, μtp2); 3. the position corresponding to a given p, rp, and μp. The z values of these points are zini, ztp1, ztp2, and zp. The former three can be evaluated from z(r) functions listed in the right column of Table 3. The value of zp can be evaluated from function z(p) = ℘(p + Πr;g2,g3) for cases 1, 4, 5 and 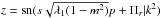 for case 2, and
for case 2, and 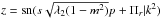 for case 3. For μ, the value of zp can be computed from z = ℘(p + Πμ;g2,g3). It is noted that the functions z(r) are monotonously decreasing, we have ztp1 ≥ zini ≥ ztp2 and ztp1 ≥ zp ≥ ztp2. For μ, since the function z(μ) given in Table 1 is monotonously increasing, the two relationships are still valid.
for case 3. For μ, the value of zp can be computed from z = ℘(p + Πμ;g2,g3). It is noted that the functions z(r) are monotonously decreasing, we have ztp1 ≥ zini ≥ ztp2 and ztp1 ≥ zp ≥ ztp2. For μ, since the function z(μ) given in Table 1 is monotonously increasing, the two relationships are still valid.
In addition to zp, for a given p, we also obtain the number of times that the particle meets the two turning points. We assume that the particle meets rtp1 (or μtp1) for Nt1 times, and rtp2 (or μtp2) for Nt2 times. If rtp1 or rtp2 does not exist, Nt1 or Nt2 is zero. To get Nt1 and Nt2 for a given p, we define the following five integrals with the help of Table 4: ![\begin{eqnarray} \begin{array}{@{}ll} p_0=&\int^{z_p}_{z_{\mathrm{ini}}}W(z) {\rm d}z,\quad p_1=\int^{z_{\mathrm{tp}_1}}_{z_p}W(z) {\rm d}z,\quad p_2=\int^{z_p}_{z_{\mathrm{tp}_2}}W(z) {\rm d}z,\\[2mm] I_1=&\int^{z_{\mathrm{tp}_{1}}}_{z_{_{\mathrm{ini}}}}W(z) {\rm d}z,\quad I_2=\int_{z_{\mathrm{tp}_{2}}}^{z_{_{\mathrm{ini}}}}W(z) {\rm d}z, \end{array} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq185.png) (42)where W(z) represents the integrands in Table 4. Apparently, we have p1 ≥ 0 and p2 ≥ 0, and
(42)where W(z) represents the integrands in Table 4. Apparently, we have p1 ≥ 0 and p2 ≥ 0, and  (43)With the above definitions, we get the following identity
(43)With the above definitions, we get the following identity ![\begin{eqnarray} \begin{aligned} \label{t1t2}p =& -\mathrm{sign}(p_\beta)p_0+2Nt_1p_1+2Nt_2p_2,\\ =&-[\mathrm{sign}(p_\beta)+2Nt_1-2Nt_2]p_0+2Nt_1I_1+2Nt_2I_2, \end{aligned} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq190.png) (44)where β = r or θ, and pβ is the initial value of r or θ component of the four-momentum. We obtain Nt1 and Nt2 from the above equations by trial and error because Nt1 and Nt2 increase regularly as the particle moves, i.e., when pβ > 0 (or, pβ = 0 and zini = ztp1), Nt1 and Nt2 increase as:
(44)where β = r or θ, and pβ is the initial value of r or θ component of the four-momentum. We obtain Nt1 and Nt2 from the above equations by trial and error because Nt1 and Nt2 increase regularly as the particle moves, i.e., when pβ > 0 (or, pβ = 0 and zini = ztp1), Nt1 and Nt2 increase as: 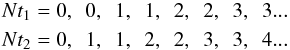 When pβ < 0 (or, pβ = 0 and zini = ztp2), Nt1 and Nt2 increase as:
When pβ < 0 (or, pβ = 0 and zini = ztp2), Nt1 and Nt2 increase as: 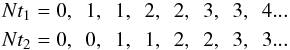 Note the path and limits of integrals in t, φ, and σ are exactly the same with those of p. We introduce the following definitions:
Note the path and limits of integrals in t, φ, and σ are exactly the same with those of p. We introduce the following definitions: ![\begin{eqnarray} \begin{array}{@{}ll} I_{0\alpha\beta} = &\int^{z_p}_{z_{\mathrm{ini}}}F_{\beta}(z){\rm d}z,\; I_{1\alpha\beta}= \int^{z_{\mathrm{tp}_1}}_{z_p}F_{\beta}(z){\rm d}z,\;I_{2\alpha\beta}=\int^{z_p}_{z_{\mathrm{tp}_2}}F_{\beta}(z){\rm d}z,\\[2mm] IT_{1\alpha\beta}=&\int^{z_{\mathrm{tp}_{1}}}_{z_{_{\mathrm{ini}}}}F_{\beta}(z){\rm d}z,\quad IT_{2\alpha\beta}=\int_{z_{\mathrm{tp}_{2}}}^{z_{_{\mathrm{ini}}}}F_{\beta}(z){\rm d}z. \end{array} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq200.png) (45)where α = t, φ, σ. Similarly, we have
(45)where α = t, φ, σ. Similarly, we have  (46)Then the integrals in t, φ, and σ can be written as
(46)Then the integrals in t, φ, and σ can be written as ![\begin{eqnarray} \label{integral} I_{\alpha\beta}&=&-\mathrm{sign}(p_\beta) I_{0\alpha\beta}+2Nt_1I_{1\alpha\beta}+2Nt_2I_{2\alpha\beta},\\ &=&-[\mathrm{sign}(p_\beta)+2Nt_1-2Nt_2]I_{0\alpha\beta}+2Nt_1IT_{1\alpha\beta}+2Nt_2IT_{2\alpha\beta}. \nonumber \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq203.png) (47)Finally, we have
(47)Finally, we have 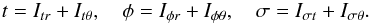 (48)
(48)
3.3.2. The computation of elliptic integrals by Carlson’s approach
In this section, we discuss how to compute the elliptic integrals appeared in t, φ, and σ using Carlson’s approach. First, we reduce these integrals to the standard forms. Before the reductions we introduce two notations Jk(h) and Ik(h) with the following definition: ![\begin{eqnarray} J_k(h) &=& \int^x_y\frac{{\rm d}t}{(t-h)^k\sqrt{4t^3-g_2t-g_3}},\\ I_k(h) &=& \int^x_y\frac{{\rm d}r}{(r-h)^k\sqrt{[(r-u)^2+v^2][(r-w)^2+s^2]}}, \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq207.png) where k = −2, − 1,0,1,2. From Eqs. (13)–(15), we have
where k = −2, − 1,0,1,2. From Eqs. (13)–(15), we have
![\begin{eqnarray} &&\sigma_\mu = t_\mu= a^2\left[\frac{b_0^2}{16}J_2\left(\frac{b_1}{4}\right)+\frac {b_0\mu_{\mathrm{tp}_1}}{2}J_1\left(\frac{b_1}{4}\right)+\mu^2_{\mathrm{tp}_1}p\right],\\ &&\phi_\mu = \lambda\left[\frac{ p}{1-\mu_{\mathrm{tp}_1}^2}-\frac{C_-}{2}J_1(z_-)+\frac{C_+}{2}J_1(z_+)\right], \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq209.png) where
where 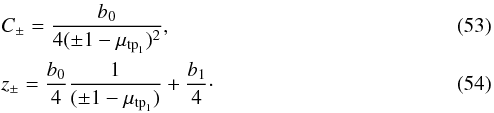 Noting the definition of parameter p, we have replaced J0 with p in the above equations.
Noting the definition of parameter p, we have replaced J0 with p in the above equations.
Standard forms of integrals.
Definitions of Table 5.
The reduced standard forms of integrals for r are given in Tables 5 and 6. The standard forms for the special cases, such as the equatorial plane motion and the spherical motion, can be obtained directly and are not given here anymore.
Carlson (1988, 1989, 1991, 1992) developed a new approach to compute elliptic integrals (Press et al. 2007). He gave new definitions of the standard elliptic integrals of the first and third kind
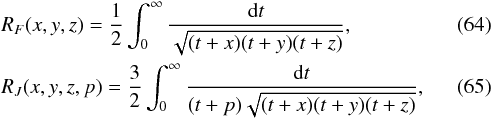 and the degenerate cases of RC(x,y) = RF(x,y,y) and RD(x,y,z) = RJ(x,y,z,z). Case RD can be regarded as the standard elliptic integral of the second kind. Carlson denotes the elliptic integrals with a symbol with the following definition:
and the degenerate cases of RC(x,y) = RF(x,y,y) and RD(x,y,z) = RJ(x,y,z,z). Case RD can be regarded as the standard elliptic integral of the second kind. Carlson denotes the elliptic integrals with a symbol with the following definition: ![\begin{eqnarray} [p_1,\cdots,p_k]=\int^x_y\prod^k_{i\,=\,1}(a_i+b_it)^{p_i/2}{\rm d}t. \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq229.png) (66)If ai + bit is complex, then its complex conjugate
(66)If ai + bit is complex, then its complex conjugate  must exist and guarantee the integral is real. And,
must exist and guarantee the integral is real. And, 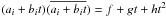 . Thus,
. Thus, ![\begin{eqnarray} \begin{aligned}{} [p_1,p_1,p_3\cdots,p_k]=\,&\int^x_y(f+gt+ht^2)^{p_1/2}\\ &\times\prod^k_{j\,=\,3}(a_j+b_jt)^{p_j/2}{\rm d}t. \end{aligned} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq233.png) (67)For a particular elliptic integral, there is an unique formula to evaluate it. We give a simple example here:
(67)For a particular elliptic integral, there is an unique formula to evaluate it. We give a simple example here: ![\begin{eqnarray} [-1,-1,-1,-1]=2R_F(U^2_{12},U^2_{13},U^2_{14}), \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq234.png) (68)where
(68)where
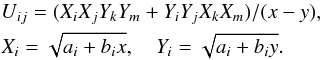 The elliptic integrals we need to evaluate in this paper are: J1,J2,I2,I-1,I-2, which can be recast with Carlson’s notations. When equation 4t3 − g2t − g3 = 0 has three real roots denoted by e1,e2,e3, we obtain (Carlson 1988)
The elliptic integrals we need to evaluate in this paper are: J1,J2,I2,I-1,I-2, which can be recast with Carlson’s notations. When equation 4t3 − g2t − g3 = 0 has three real roots denoted by e1,e2,e3, we obtain (Carlson 1988) ![\begin{eqnarray} \begin{aligned} J_k(h)&= s_h\frac{1}{2}\int^x_y\frac{{\rm d}t}{\sqrt{(t-e_1)(t-e_2)(t-e_3) (t-h)^{2k}}}\\ &=s_h\frac{1}{2}[-1,-1,-1,-2k], \end{aligned} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq238.png) (69)where sh = sign [(y − h)k]. When equation 4t3 − g2t − g3 = 0 has one pair of complex roots and one real root e1, we obtain (Carlson 1991)
(69)where sh = sign [(y − h)k]. When equation 4t3 − g2t − g3 = 0 has one pair of complex roots and one real root e1, we obtain (Carlson 1991) ![\begin{eqnarray} \begin{aligned} J_k(h)&= s_h\frac{1}{2}\int^x_y\frac{{\rm d}t}{\sqrt{(t-e_1) (t^2+gt+f)(t-h)^{2k}}}\\ &=s_h\frac{1}{2}[-1,-1,-1,-2k]. \end{aligned} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq241.png) (70)The integral Ik(h) corresponds to the case that equation Rr(r) = 0 has no real roots and can be expressed as (Carlson 1992):
(70)The integral Ik(h) corresponds to the case that equation Rr(r) = 0 has no real roots and can be expressed as (Carlson 1992): ![\begin{eqnarray} \begin{aligned} I_{k}(h)&=s_h\int^x_y\frac{{\rm d}r}{\sqrt{[(r-u)^2+v^2][(r-w)^2+s^2](r-h)^{2k}}},\\ &=s_h[-1,-1,-1,-1,-2k]. \end{aligned} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq244.png) (71)Up to now, we have expressed all coordinates and proper time as functions of parameter p semi-analytically. As discussed in Yang & Wang (2013), such treatment is very convenient for massive particles whose geodesics can be bounded, and the number of times that the particle meets the turning points can be arbitrary both for r and μ coordinates. In addition to p, one needs to prescribe the constants of motion. In the next section, we discuss how to get them from the initial four-momentum of a particle.
(71)Up to now, we have expressed all coordinates and proper time as functions of parameter p semi-analytically. As discussed in Yang & Wang (2013), such treatment is very convenient for massive particles whose geodesics can be bounded, and the number of times that the particle meets the turning points can be arbitrary both for r and μ coordinates. In addition to p, one needs to prescribe the constants of motion. In the next section, we discuss how to get them from the initial four-momentum of a particle.
4. Constants of motion
As mentioned above, the constants of motion throughout this paper are defined as 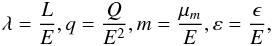 (72)which can be obtained from the initial four-momentum of a particle given in an LNRF reference. But to handle more complicated applications, we want to specify the initial four-momentum in the reference of an assumed emitter, instead of an LNRF reference directly. However, the initial four-momentum is finally transformed into an LNRF reference by a Lorentz transformation.
(72)which can be obtained from the initial four-momentum of a particle given in an LNRF reference. But to handle more complicated applications, we want to specify the initial four-momentum in the reference of an assumed emitter, instead of an LNRF reference directly. However, the initial four-momentum is finally transformed into an LNRF reference by a Lorentz transformation.
Now we introduce the LNRF reference, which is also called zero angular momentum observers (ZAMO, Bardeen et al. 1972). The orthonormal tetrad is given by 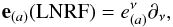 (73)where
(73)where 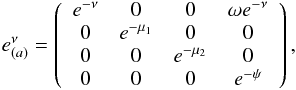 (74)and the dual form of which is
(74)and the dual form of which is 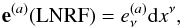 (75)where
(75)where 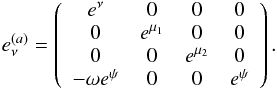 (76)We assume that the particle is emitted by an emitter at the initial position, where the emitter has coordinate velocities ṙ = dr/dt,
(76)We assume that the particle is emitted by an emitter at the initial position, where the emitter has coordinate velocities ṙ = dr/dt, 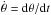 , and
, and 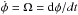 , then its physical velocities υr,υθ,υφ, with respect to the LNRF fixed at the same point, can be written as (Bardeen et al. 1972):
, then its physical velocities υr,υθ,υφ, with respect to the LNRF fixed at the same point, can be written as (Bardeen et al. 1972): 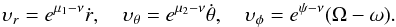 (77)The orthonormal tetrad of the emitter can be obtained by rotating the tetrad of the LNRF reference in the local four dimension spacetime. The rotation is simply a Lorentz transformation. We denote the matrix of the rotation by Λ, and find
(77)The orthonormal tetrad of the emitter can be obtained by rotating the tetrad of the LNRF reference in the local four dimension spacetime. The rotation is simply a Lorentz transformation. We denote the matrix of the rotation by Λ, and find 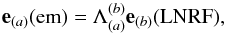 (78)where (Misner et al. 1973)
(78)where (Misner et al. 1973) 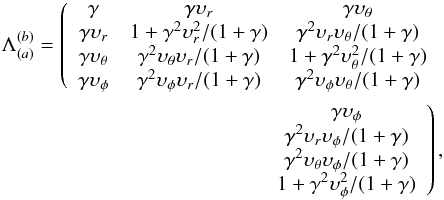 (79)where
(79)where ![\hbox{$\gamma=[1-(\upsilon_r^2+\upsilon_{\theta}^2+\upsilon_{\phi}^2)]^{-1/2}$}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq258.png) , and the covariant tetrad of the emitter is
, and the covariant tetrad of the emitter is 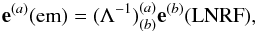 (80)where
(80)where 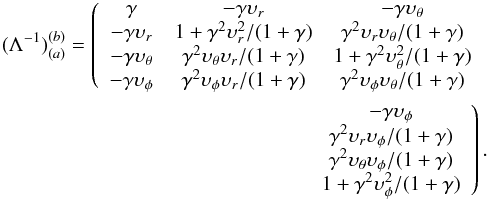 (81)Equivalently, we have
(81)Equivalently, we have
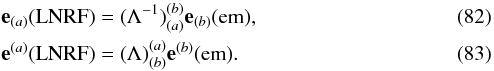 In the rest frame of the emitter, the components of the four-momentum of the particle are denoted by
In the rest frame of the emitter, the components of the four-momentum of the particle are denoted by 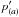 , which can be regarded as the projections of the momentum p on the corresponding basis vectors, i.e.,
, which can be regarded as the projections of the momentum p on the corresponding basis vectors, i.e., 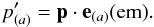 (84)Multiplying both sides of Eq. (82) by p, we find
(84)Multiplying both sides of Eq. (82) by p, we find 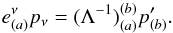 (85)By assuming that the physical velocities of the particle with respect to the emitter are:
(85)By assuming that the physical velocities of the particle with respect to the emitter are: 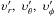 , we find
, we find 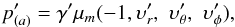 (86)where
(86)where ![\hbox{$\gamma' =[1-(\upsilon_r'^2+\upsilon_\theta'^2+\upsilon_\phi'^2)]^{-1/2}$}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq268.png) is the Lorentz factor. Equation (85) can be expanded explicitly with Eqs. (11) and (74):
is the Lorentz factor. Equation (85) can be expanded explicitly with Eqs. (11) and (74):
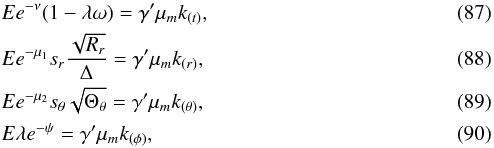 where
where 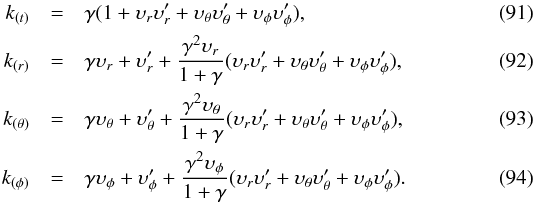 If we solve Eqs. (87) and (90) for λ, we obtain
If we solve Eqs. (87) and (90) for λ, we obtain 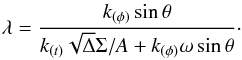 (95)With λ, from Eq. (87), we find
(95)With λ, from Eq. (87), we find 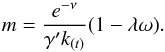 (96)With λ and m, from Eq. (89), we find
(96)With λ and m, from Eq. (89), we find ![\begin{eqnarray} \begin{aligned} q =\,& \left[\left(\frac{k_{(\phi)}}{k_{(t)}\sqrt{\Delta}\Sigma/A+k_{(\phi)}\omega\sin\theta}\right)^2+a^2(m^2-1)\right] \cos^2\theta\\ &+m^2\Sigma\gamma'^2k^2_{(\theta)}. \end{aligned} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq274.png) (97)With λ, m, and q, from Eq. (88), we obtain a quadratic equation for ε,
(97)With λ, m, and q, from Eq. (88), we obtain a quadratic equation for ε, 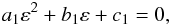 (98)where
(98)where ![\begin{eqnarray} a_1&=&e^2r^2, \\ b_1&=&2er(r^2+a^2-a\lambda),\\ \nonumber c_1&=&(1-m^2)r^4+2m^2r^3-[q+\lambda^2+a^2(m^2-1)+e^2m^2]r^2\\ \nonumber &&+2[q+(a-\lambda)^2]r-e^2(a-\lambda)^2-(a^2+e^2)q\\ &&-\Delta\Sigma(m\gamma'k_{(r)})^2. \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq278.png) We then find two values,
We then find two values, 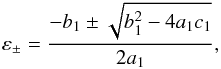 (102)where ε+ represents positive electric charge, and ε− represents negative electric charge. In Fig. 2, we plot a set of geodesic orbits of particles emitted isotropically in an LNRF reference. These particles are confined in the equatorial plane. The particles have ε+ in the top panel, and ε− in the bottom panel.
(102)where ε+ represents positive electric charge, and ε− represents negative electric charge. In Fig. 2, we plot a set of geodesic orbits of particles emitted isotropically in an LNRF reference. These particles are confined in the equatorial plane. The particles have ε+ in the top panel, and ε− in the bottom panel.
 |
Fig. 2 Trajectories of a set of particles, which are confined in the equatorial plane and conduct plane motions. The spin and electric charge of the black hole are 0.96 and 0.1, respectively. The electric charges of particles are ε+ (top panel) and ε− (bottom panel). The initial physical speed of the particles is isotropical and equal to 0.35 with respect to the LNRF. The initial coordinates of the particles are r = 5 rg, θ = 90°, and φ = 0. A circle at the left represents the event horizon. |
5. A brief introduction to the code
According to the discussions above, we have developed a new public code for computing null and time-like geodesics in a K-N spacetime2. We name the code ynogkm, which is written in fortran 95, and the object-oriented method is used. The code consists of several independent modules, in which each one completes a special goal. The most important two modules are ellfunction and blcoordinates. The former contains the supporting functions and subroutines computing elliptic integrals by Carlson’s approach. The latter contains the functions and routines computing the B-L coordinate functions: r(p), μ(p), φ(p), and t(p), as well as proper time function σ(p). In blcoordinates, we provide a subroutine named ynogkm to compute all coordinates and proper times simultaneously for a given p. We also provide two functions named radius and mucos to compute r(p) and μ(p), respectively. In an axis-symmetry case, we only need to compute r and μ.
Before calling these functions and subroutines to compute the B-L coordinates, we need to provide the constants of motion, namely, λ, q, m, and ε. As discussed in the above section, we have provided a set of formulae to compute these constants from  , which are the physical velocities of the particle with respect to an assumed emitter, which also has physical velocities υi with respect to an LNRF reference. According to these formulae, we provide a subroutine named lambdaqm to calculate λ, q, m, ε, and k(a) defined by Eqs. (91)–(94). Except for a factor γ′μm, k(a) actually are exactly equal to the initial four-momentum of the test particle given in an LNRF. Thus, k(a) can be used to determine the signs in front of Πr or Πμ. The other initial parameters that need to be specified include: (1) the initial coordinates of the particle, rini, θini, φini, and tini. The latter two are usually set at zero; (2) the physical velocities of the assumed emitter with respect to an LNRF, υr, υθ, and υφ; (3) the physical velocities of the particle with respect to the assumed emitter,
, which are the physical velocities of the particle with respect to an assumed emitter, which also has physical velocities υi with respect to an LNRF reference. According to these formulae, we provide a subroutine named lambdaqm to calculate λ, q, m, ε, and k(a) defined by Eqs. (91)–(94). Except for a factor γ′μm, k(a) actually are exactly equal to the initial four-momentum of the test particle given in an LNRF. Thus, k(a) can be used to determine the signs in front of Πr or Πμ. The other initial parameters that need to be specified include: (1) the initial coordinates of the particle, rini, θini, φini, and tini. The latter two are usually set at zero; (2) the physical velocities of the assumed emitter with respect to an LNRF, υr, υθ, and υφ; (3) the physical velocities of the particle with respect to the assumed emitter,  ,
, 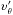 , and
, and 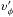 ; (4) the spin parameter a and the electric charge e of the black hole. With a given p and those initial parameters, we can do the calculations directly without giving the number of times that the particle meets the two turning points, namely Nt1 and Nt2.
; (4) the spin parameter a and the electric charge e of the black hole. With a given p and those initial parameters, we can do the calculations directly without giving the number of times that the particle meets the two turning points, namely Nt1 and Nt2.
 |
Fig. 3 A set of geodesics of massive particles orbit around a black hole with a = 0.9. The physical velocities of the emitter with respect to the LNRF are υr = 0, υθ = 0, and υφ = 0.4, υφ = 0.5, υφ = 0.6, υφ = 0.7, υφ = 0.8, υφ = 0.9 for panels from left to right, top to bottom. The velocities of these particles are specified isotropically in the rest frame of the emitter and |
In our code, the parameter p is an independent variable, which is always positive and monotonously increasing along a particular geodesic. When the geodesic is unbounded, it has a termination, either at infinity or the event horizon. The value of p corresponding to the termination is a finite number, denoted by pmax. We provide a subroutine named ptotal to calculate this number. Apparently, when a p given by the user is bigger than pmax, it has no meaning and the code resets it to be pmax mandatorily. When a geodesic is bounded, its termination does not exist at all and p can take any positive value.
For a more detailed introduction, refer to the README3 file. In the next section, we provide the results of our code for toy problems.
6. Applications for toy problems
To show the utility of our code, we apply it to toy problems. The results for six such examples are illustrated in this section.
6.1. Geodesic orbits of massive particles
The most important application of the code is to compute the geodesics of massive particles in a K-N spacetime. As in the first application, we use the code to compute the orbits of a set of test particles that are emitted isotropically in the local rest frame of an assumed emitter. The particles have a constant speed 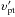 , but different directions in the local reference, and
, but different directions in the local reference, and 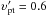 . The orientation of the velocity is described by ϑ and ϕ, thus the components of the velocity under the reference of the emitter are
. The orientation of the velocity is described by ϑ and ϕ, thus the components of the velocity under the reference of the emitter are  The physical velocities of the emitter with respect to the LNRF reference are υr = 0, υθ = 0, in which only the φ component is not zero and can take on different values. We demonstrate the results in Fig. 3. It is shown that as the speed of emitter increases, more particles become unbounded, and the beaming effect becomes more significant.
The physical velocities of the emitter with respect to the LNRF reference are υr = 0, υθ = 0, in which only the φ component is not zero and can take on different values. We demonstrate the results in Fig. 3. It is shown that as the speed of emitter increases, more particles become unbounded, and the beaming effect becomes more significant.
6.2. The orbits of spherical motion
The circular orbits in the Kerr spacetime have significant applications in the standard geometrically thin accretion disk systems. A particle in the accretion flow loses its angular momentum by viscosity and moves inward slowly. Its angular velocity is far greater than its radial velocity. Thus, to be a good approximation, the particle moves in a circular orbit. The inner radius of the disk is usually located at the innermost stable circular orbit (ISCO). Based on this assumption, one can measure the black hole spin by fitting the line profiles or the continuous spectra. Actually, the circular orbit, in which the particle is confined in the equatorial plane of the black hole, can be regarded as a special case of spherical orbit. The radial velocity and acceleration of the particle in a spherical orbit are vanished, leading to two conditions: dr/dτ = 0 and d2r/dτ2 = 0. Using Eq. (4), these conditions reduce to (Bardeen et al. 1972; Wilkins 1972): 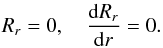 (106)We use θ∗ to denote the coordinate of one of the θ turning points, therefore we have Θθ(θ∗) = 0. Using the same strategy discussed in Shakura (1987), we can obtain the angular velocity of the particle at θ∗
(106)We use θ∗ to denote the coordinate of one of the θ turning points, therefore we have Θθ(θ∗) = 0. Using the same strategy discussed in Shakura (1987), we can obtain the angular velocity of the particle at θ∗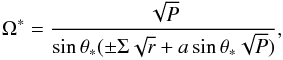 (107)where P = M(r2 − a2cos2θ∗) − e2r, and the constants of motion:
(107)where P = M(r2 − a2cos2θ∗) − e2r, and the constants of motion: ![\begin{eqnarray} \label{evm}\frac{E}{\mu_m} &=& \frac{\pm a \sin\theta_*\sqrt{P}+(\Delta-a^2\sin^2\theta_*)\sqrt{r}}{\sqrt{\Sigma} \sqrt{-P+(\Delta-a^2\sin^2\theta_*)r\pm2a\sin\theta_*\sqrt{rP}}}, \\[2mm] \label{lvm}\frac{L}{\mu_m}&=& \frac{\sin\theta_*[\pm(r^2+a^2)\sqrt{P}-\sqrt{r}a\sin\theta_*(2Mr-e^2)] }{\sqrt{\Sigma}\sqrt{-P+(\Delta-a^2\sin^2\theta_*)r\pm2a\sin\theta_*\sqrt{rP}}}, \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq333.png)
![\begin{eqnarray} \nonumber\label{qvm} \frac{Q}{\mu_m^2}&=&\cos^2\theta_*\left[a^2\left(1-\frac{E^2}{\mu_m^2}\right)+ \frac{1}{\sin^2\theta_*}\frac{L^2}{\mu_m^2}\right],\\ &=&\frac{r\cos^2\theta_*\left[A_Q\mp2a\sin\theta_* (2Mr-e^2)r\sqrt{rP}\right]}{ \Sigma[ -P+(\Delta-a^2\sin^2\theta_*)r\pm2a\sin\theta_*\sqrt{rP}]}, \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq334.png) (110)where
(110)where ![\begin{eqnarray} A_Q &=& (r^2+a^2)^2(Mr-e^2)+a^2\left\{\left[Mr(r^2-a^2)\right.\right. \nonumber\\ &&\left.\left.+\,e^2a^2\right]\sin^2\theta_*-(2Mr-e^2)^2\cos^2\theta_*\right\}. \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq335.png) (111)In these formulae, the upper sign refers to the prograde orbits (i.e., corotating with L > 0), while the lower sign refers to retrograde orbits (counter rotating with L < 0).
(111)In these formulae, the upper sign refers to the prograde orbits (i.e., corotating with L > 0), while the lower sign refers to retrograde orbits (counter rotating with L < 0).
 |
Fig. 4 Orbit of a particle in a spherical motion. The parameters are: the black hole spin a = 0.998, the radius of the orbit r = 2 rg, the turning point θ∗ = 30°, the inclination angle of the observer θobs = 90°. |
In Fig. 4, we plot the orbit of a particle in a spherical motion. Given the parameters: a,e,r, and θ∗, from Eqs. (108)–(110), we can obtain the constants of motion: λ,q,m, with which from equation Rr = 0 (or dRr/dr = 0), we can obtain the final constant ε. For simplicity, we let both e and ε be zero in this figure. In comparison with circular motion, the most significant effect of spherical motion is the precession of the orbit.
Correspondingly, the spherical motion also has three kinds of marginal orbits, which are:
(1): The photon orbit rph, which is the innermost boundaryof the spherical orbits for particles, occurs when the de-nominator of Eqs. (108)–(110) vanishes, i.e.,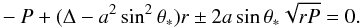 (112)
(112)
(2): The marginally bound spherical orbit rmb, which occurs when E/μm = 1.
(3): The innermost stable spherical orbit (ISSO) rms. The stable condition requires that d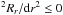 , which yields the equivalent condition,
, which yields the equivalent condition, 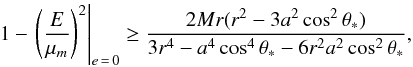 (113)
(113)
In our code, we provide three functions named r_ms,r_mb, and r_ph to compute the radii of these orbits with given a,θ∗,e. In Fig. 5, we plot the radii of inner most stable spherical orbits as functions of a for various θ∗. For simplicity, we also let e = 0 in this figure. One can see that as θ∗ increases, the radii become smaller for a > 0 and larger for a < 0. For a = 0, the radii remain unchanged. When θ∗ = 0°, the curve becomes symmetry for a > 0 and a < 0. Similar properties can be obtained for the radii of photon orbits and marginally bound orbits.
 |
Fig. 5 Radii of the innermost stable orbits for the spherical motion around a Kerr black hole, as functions of the specific angular momentum a of the black hole. |
6.3. Orbits inside rms
The region inside ISSO is usually called the plug region in which a particle moves along geodesics with constants of motion of the marginally stable spherical geodesic (Cunningham 1975) when its initial radial perturbation velocity υr = 0. With the results presented in the above section, we obtain the constants of motion for the marginally stable spherical orbits ![\begin{eqnarray} \left(\frac{E}{\mu_m}\right)^2&=&1-\frac{2Mr_{\mathrm{ms}}(r_{\mathrm{ms}}^2- 3a^2\cos^2\theta_{*})}{D_{\mathrm{ms}}},\\ \left(\frac{L}{\mu_m}\right)^2&=&2Mr_{\mathrm{ms}}\sin^2\theta_{*}[3r_{\mathrm{ms}}^4-r_{\mathrm{ms}}^2a^2(1+ \cos^2\theta_{*})\nonumber \\ &&+3a^4\cos^2\theta_{*}]/D_{\mathrm{ms}}, \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq364.png)
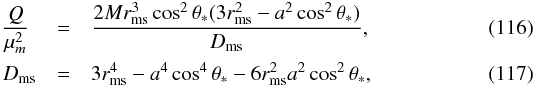 and
and
![\begin{eqnarray} &&R_r=2M(r_{\rms{ms}}-r)^3[rr_{\rms{ms}}^3-3a^2r_{\rms{ms}} \cos^2\theta_{*}(r_{\rms{ms}}+r) \nonumber\\ &&\qquad\,\, +\,a^4\cos^4\theta_{*}]/D_{\rms{ms}}, \\ &&\Theta_\mu=2Mr_{\rms{ms}}(\cos^2\theta_{*}-\mu^2) [(3a^4\cos^2\theta_{*}-r_{\rms{ms}}^2a^2)\mu^2 \nonumber \\ &&\qquad \,\,-\, r_{\rms{ms}}^2a^2\cos^2\theta_{*}+3r_{\rms{ms}}^4]/D_{\rms{ms}}. \end{eqnarray}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq366.png) From the above two equations, we know that both rms and θ∗ are the turning points. With these expressions, we can find the constants of motion immediately to compute the geodesic orbits inside rms. In Fig. 6, we plot such an orbit. We take a = 0.998 and θ∗ = 0, namely the particle goes through the spin axis of the black hole. Using the function r_ms(θ∗,a,e) in our code, we find rms = 5.2781 rg. From this figure, one can see that the orbit is almost the same with a spherical motion because the radial velocity is much smaller than the poloidal and azimuthal velocities.
From the above two equations, we know that both rms and θ∗ are the turning points. With these expressions, we can find the constants of motion immediately to compute the geodesic orbits inside rms. In Fig. 6, we plot such an orbit. We take a = 0.998 and θ∗ = 0, namely the particle goes through the spin axis of the black hole. Using the function r_ms(θ∗,a,e) in our code, we find rms = 5.2781 rg. From this figure, one can see that the orbit is almost the same with a spherical motion because the radial velocity is much smaller than the poloidal and azimuthal velocities.
 |
Fig. 6 Orbit of a particle moving inside the ISSO with the constants of motion of the ISSO. The black hole spin a = 0.998 and the turning point θ∗ = 0°. The radius of ISSO is r = 5.2781 rg. The inclination angle θobs = 90° for the top panel and θobs = 0° for the bottom panel. |
6.4. Accretion flow of disk
Now we use our code to construct a toy model for mimicking the accretion flows of a skewed geometrically thin disk. The flows are composed of non-interacting particles, which fall freely into the black hole along the geodesic trajectories. This implies that we make a ballistic treatment to the fluid flow, and the dynamics and the structure of the disk are uniquely determined by the gravitational field of the black hole. It is also convenient to regard the accretion flow as a collection of test particles with the same mass. The boundary conditions of the disk are assumed to be a ring at r = r0, from which the test particles are continuously injected. The plane of the ring has an inclination angle β with respect to the spin axis.
To describe the initial conditions of the test particles, namely the velocities, an orthonormal tetrad is established on the ring. We choose three spacial basis vectors of the tetrad as : ex,ey,ez, where ex is the tangent vector of the ring, ey is aligned along the radial direction and pointed inward, ez is the normal vector of the plane of the ring, and these vectors satisfy right hand rule. In the local rest frame of the tetrad, the physical velocities of the particle are 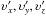 . According to the discussions in Sect. 4, to compute the constants of motion from these velocities, we need to transform them into the LNRF reference for getting υr,υθ,υφ.
. According to the discussions in Sect. 4, to compute the constants of motion from these velocities, we need to transform them into the LNRF reference for getting υr,υθ,υφ.
We denote the transformation matrix by T(θ,φ,β). The explcit expression of T is presented in Appendix A. Hence, we have 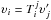 . Since the tetrad is attached on the ring, θ and φ are not independent variables, actually they satisfy the following equation,
. Since the tetrad is attached on the ring, θ and φ are not independent variables, actually they satisfy the following equation, 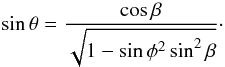 (120)Therefore, we have
(120)Therefore, we have 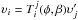 . Taking φ as an independent variable that varies from 0 to 2π, we can set the initial conditions for all test particles. In Fig. 7, we plot such a set of geodesic orbits of test particles with the same mass. The physical velocities are
. Taking φ as an independent variable that varies from 0 to 2π, we can set the initial conditions for all test particles. In Fig. 7, we plot such a set of geodesic orbits of test particles with the same mass. The physical velocities are 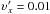 ,
, 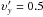 , and
, and 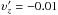 , respectively. From the figure, one can see that all trajectories form a smooth but curved surface.
, respectively. From the figure, one can see that all trajectories form a smooth but curved surface.
 |
Fig. 7 Orbits of equal mass test particles flow inward to a black hole along geodesic trajectories, which form a smooth and curved surface. The black hole spin is a = 0.96, the initial tiled angle of the disk is β = 30°. The initial physical velocities of the particles under the tetrad are: |
Using the ray-tracing approach (Luminet 1979), we can image the curved surface. In Yang & Wang (2013), we presented a new public code named ynogk to compute the null geodesics in a Kerr spacetime and a more general method to image a target object. The method requires one to provide the function describing the surface, i.e., F(r,θ,φ) = 0, or F(x,y,z) = 0. For this curved surface formed by geodesic orbits of test particles, we cannot write out its explicit form, and only use the interpolation approach. To approximate the surface, we take N particles with N geodesic orbits. We take M points in each orbit, and get a total of N × M points. We can get the coordinates of each point easily and write them as: zij = zij(xi,yj). Using the interpolation approaches provided in Press et al. (2007), we can obtain an approximation function z = z(x,y) that describes the surface.
In Fig. 8, we plot the images of a skewed accretion disk that is composed of test particles falling freely into a black hole along geodesics viewed from different inclinations. The initial tiled angle of the disk is β = 30°. Due to the frame drag effect, the particles drift into the black hole along spiral orbits, instead of a straight lines. The orbits make a gradual transition into the equatorial plane. The disk is significantly warped as it moves inward. In the figure, the false color represents the redshift of emission coming from the disk surface. The approaching and receding sides of the disk are no longer the left and right sides, but the regions are farthest and nearest with respect to the observer, respectively.
 |
Fig. 8 Images of a skewed disk, whose inner and outer radii are 1.5 rg and 10 rg. The parameters: β = 30°, γ0 = 135°, black hole spin a = 0.998, inclination angles θobs are 15°, 30°, 45°, 60°, 75° and 90° for panels from left to right, top to bottom. |
6.5. Stationary axisymmetric accretion flow
Tejeda et al. (2013) presented an analytic toy model to mimic the stationary axisymmetric accretion flow of a rotating cloud of non interacting particles falling onto a Kerr black hole in which the streamlines are described analytically in terms of time-like geodesics. Thus, they solve the equations of motion with integral forms with elliptic functions. However, their results are completely different from ours. In addition, they just obtain the solutions for r and μ.
As a check of the validation of our code, we model a similar accretion flow. Since the flow is axisymmetric, we just need to consider the spacial projections onto the r − θ plane. The boundary of the flow is a spherical shell at r = r0 from which test particles are continuously injected. On the shell, the four-velocity of particles are taken to be constants, i.e., 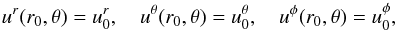 (121)with which and the identity gμνuμuν = −1, we obtain the time component
(121)with which and the identity gμνuμuν = −1, we obtain the time component 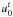 . The four-velocity
. The four-velocity 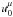 at r0 are taken as the initial conditions for the calculation of geodesics. Using Eq. (77) the physical velocities υr,υθ,υφ can be computed from
at r0 are taken as the initial conditions for the calculation of geodesics. Using Eq. (77) the physical velocities υr,υθ,υφ can be computed from 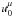 . Then the constants of motion are uniquely determined. The results are illustrated in Fig. 9, which agree well with those of Tejeda et al. (2013).
. Then the constants of motion are uniquely determined. The results are illustrated in Fig. 9, which agree well with those of Tejeda et al. (2013).
 |
Fig. 9 Streamlines of axisymmetric accretion flow, the parameters are: black hole spin a = 0.998; initial four-velocity |
6.6. The tidal disruption of a ball
As the final application of our code, we model a tidal disruption event of a ball, which falls freely to the central black hole. To use the code, we have to assume that the ball consists of a set of equal mass test particles without any interactions. At the initial point the ball has a kick velocity, the physical components of which measured under the LNRF reference are υr,υθ,υφ. All of the particles share the same initial velocities, but different positions. Then with the given initial conditions, each particle freely falls inward along a geodesic trajectory.
 |
Fig. 10 An assumed ball composed of a set of massive test particles without interactions is disrupted by the strong tidal force of a Kerr black hole. The black hole spin is a = 0.8. The radius of the ball is 4 rg. The initial coordinates are r = 20 rg, θ = 90°, φ = 0°. The coordinate times are t = 0, 22.5, 45, 67.5, 90 for images from right to left. A circle at the left represents the event horizon. |
In Fig. 10, we show the deformed images of the ball for five different coordinate times. Initially, we assume that the shape of the ball is a regular sphere and the center of the ball is located in the equatorial plane of the black hole. The velocities are υr = −0.1,υθ = 0,υφ = 0.1. The shape of the ball is significantly deformed and stretched as it approaches the central black hole due to the strong tidal disruption force. The former part is stretched more seriously than the latter part. The debris of the ball orbits around the black hole along a spiral trajectory and goes inward slowly instead of falling into the black hole directly because of the frame drag effect. However, the picture illustrated by this example is definitely a toy model.
7. Discussion and conclusion
We have developed a new fast public code named ynogkm for calculating time-like geodesics under a K-N spacetime, which is a direct extension of Yang & Wang (2013). In ynogkm, we adopt the same strategies used in ynogk, i.e., expressing all coordinates and proper times as functions of a parameter p and calculating all elliptic integrals with Carlson’s approach. The former guarantees the convenience of the code in practical application and the latter guarantees the fast speed of the code. The extension is involved in many more complicated cases.
In the expressions, we also use the Weierstrass elliptic function ℘(z;g2,g3) and integral as investigated by many authors in the literature. They not only investigate the geodesic motion itself but also the properties of the spacetime, while what we discussed in this paper focuses on the potential real applications of the calculation of geodesic orbits in astrophysics. To avoid complex integrals, we also adopt the Jacobi’s elliptic functions sn(z | k2),cn(z | k2) when equation R(r) = 0 has no real roots.
Since ynogkm uses the same strategies as ynogk and their speeds are almost the same, we do not present the speed test results. As discussed in Chan et al. (2013), a powerful approach to improve the speed of tracing the trajectories of billions of photons in a curved spacetime is based on the massively parallel algorithm and GPU graphic cards. Their results show that this approach is two orders of magnitude faster than the CPU-based tracing codes. Therefore, a future work will involve the extension of ynogkm from a serial program to a parallel program.
To demonstrate the utility of ynogkm, we apply it to six toy problems and present the results simply. Its application to more complicated and practical cases will be provided in a future work.
The source FORTRAN code can be download on our Web site http://www1.ynao.ac.cn/~yangxl/yxl.html and at the CDS.
Acknowledgments
We acknowledge the anonymous referee for his/her valuable comments and advice, which significantly improved the manuscript. We acknowledge financial support from the National Natural Science Foundation of China 11133006, 11163006, 11173054, the National Basic Research Program of China (973 Program 2009CB824800), and the Policy Research Program of Chinese Academy of Sciences (KJCX2-YW-T24).
References
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, B. C. 1988, Math. Comput., 51, 267 [CrossRef] [Google Scholar]
- Carlson, B. C. 1989, Math. Comput., 53, 327 [CrossRef] [Google Scholar]
- Carlson, B. C. 1991, Math. Comput., 56, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, B. C. 1992, Math. Comput., 59, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, B. 1968, Phys. Rev., 174, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, C.-K., Psaltis, D., & Ozel, F. 2013, ApJ, 777, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Cunningham, C. T. 1975, ApJ, 202, 788 [Google Scholar]
- Cunningham, C. T., & Bardeen, J. M. 1973, ApJ, 183, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., & Agol, E. 2009, ApJ, 696, 1616 [NASA ADS] [CrossRef] [Google Scholar]
- Hackmann, E. 2010, Ph.D. Thesis, University of Bremen [Google Scholar]
- Hackmann, E., & Xu, H. X. 2013, Phys. Rev. D, 87, 124030 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L.-X., Zimmerman, E. R., Narayan, R., & McClintock, J. E. 2005, ApJS, 157, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Luminet, J. P. 1973, A&A, 75, 228 [Google Scholar]
- Mino, Y. 2003, Phys. Rev. D, 67, 084027 [NASA ADS] [CrossRef] [Google Scholar]
- Misner, C. W., Thorne, K. S., & Wheeler, J. A. 1973, Gravitation (San Francisco: W.H. Freeman and Co.) [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical recipes in FORTRAN. The art of scientific computing, 3rd edn. (Cambridge University Press) [Google Scholar]
- Rauch, K. P., & Blandford, R. D. 1994, ApJ, 421, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I. 1987, Soviet Ast., 13, 99 [Google Scholar]
- Tejeda, E., Taylor, P. A., & Miller, J. C. 2013, MNRAS, 429, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, D. C. 1972, Phys. Rev. D, 5, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X.-L., & Wang, J.-C. 2013, ApJS, 207, 6 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Transformation matrix
Here we discuss how to get the explicit expression for the matrix T, which transforms the physical velocities 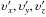 of a particle specified in the reference of the tetrad
of a particle specified in the reference of the tetrad 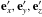 into the LNRF reference whose origin is fixed at the same point. As shown in Fig. A.1, we have four references, i.e., R′: {p,
into the LNRF reference whose origin is fixed at the same point. As shown in Fig. A.1, we have four references, i.e., R′: {p, 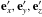 }, R′′: {O,x′′,y′′,z′′}, R: {O,x,y,z}, and Rrθφ: {p, er,eθ,eφ}.
}, R′′: {O,x′′,y′′,z′′}, R: {O,x,y,z}, and Rrθφ: {p, er,eθ,eφ}.
 |
Fig. A.1 Geometry between the skewed disk plane and the equatorial plane of a black hole. The boundary of the disk is a ring, at which equal mass test particles are injected continuously. At the initial position, indicated by p, there are two orthonormal tetrads, i.e., {p, er,eθ,eφ} and {p, |
The matrix of transformation T1 from R′ into R′′ can be obtained directly, 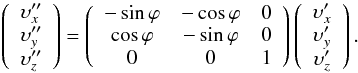 (A.1)The transformation T2 from R′′ into R is given by,
(A.1)The transformation T2 from R′′ into R is given by, 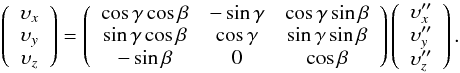 (A.2)The transformation T3 from R into Rrθφ is given by,
(A.2)The transformation T3 from R into Rrθφ is given by, 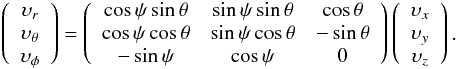 (A.3)Thus the transformation T from R′ into Rrθφ is given by
(A.3)Thus the transformation T from R′ into Rrθφ is given by 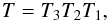 (A.4)and noting that ψ = γ + φ, one has
(A.4)and noting that ψ = γ + φ, one has 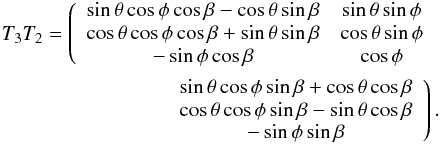 Finally, we obtain
Finally, we obtain 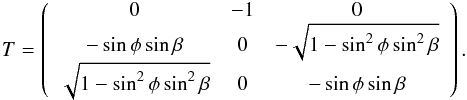 (A.5)In the reduction, the following identities are used
(A.5)In the reduction, the following identities are used
Appendix B: Taking t and σ to be the independent variable
In some practical applications, we prefer using t or σ as the independent variable to parameter p. Since we have expressed all B-L coordinates and proper times as functions of the parameter p, when a value of t or σ is given, there is an unique p corresponds to it. Namely, both the equations t(p) = t0 and σ(p) = σ0 have one and only one real root, which is denoted by p0. Apparently, if we can solve these equations efficiently and precisely to get p0, we can take t or σ as the independent variable, for p0 is obtained, the other three coordinates r,μ, and φ are also uniquely determined.
Definitions of Cσ and Ct.
Actually, we can solve both equations t(p) = t0 and σ(p) = σ0 by the bisection method or iterative method. From the expressions for tr,tμ and σr,σμ given in Sect. 3.3.2 we can rewrite functions t(p) and σ(p) as 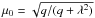 (B.1)where the definitions of Cσ and Ct are provided in Table B.1. Thus for a given σ0 and t0, we have
(B.1)where the definitions of Cσ and Ct are provided in Table B.1. Thus for a given σ0 and t0, we have 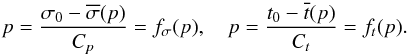 (B.2)
(B.2)
We illustrate schematically how to solve these equations using an iterative method in Fig. B.1. To use the bisection method, we define two new functions 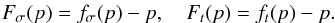 (B.3)Figure B.1 shows that when p < p0, Fσ(p) or Ft(p) > 0; when p > p0, Fσ(p) or Ft(p) < 0. Thus through the use of bisection method, we can solve the equations Fσ(p) = 0 and Ft(p) = 0 immediately.
(B.3)Figure B.1 shows that when p < p0, Fσ(p) or Ft(p) > 0; when p > p0, Fσ(p) or Ft(p) < 0. Thus through the use of bisection method, we can solve the equations Fσ(p) = 0 and Ft(p) = 0 immediately.
 |
Fig. B.1 Curve of fσ(p) (or ft(p)) as function of p. The parameter p0 is the unique real root of equation σ(p) = σ0 (or t(p) = t0). Starting from an appropriate initial value, pini, one can approach p0 through an iterative process. |
All Tables
All Figures
 |
Fig. 1 Motion of r illustrated schematically. It has been projected onto the equatorial plane of the black hole. The radial turning points are rtp1 and rtp2 between which the motion is confined. Point P indicates the position for a given p. The whole integral path is not monotonous and should be divided into several sections, each with a maximum proper length, such as DA, DG, HG, HI, PI. From the definitions of I0αr,I1αr, and I2αr (see text), one obtains |
| In the text | |
 |
Fig. 2 Trajectories of a set of particles, which are confined in the equatorial plane and conduct plane motions. The spin and electric charge of the black hole are 0.96 and 0.1, respectively. The electric charges of particles are ε+ (top panel) and ε− (bottom panel). The initial physical speed of the particles is isotropical and equal to 0.35 with respect to the LNRF. The initial coordinates of the particles are r = 5 rg, θ = 90°, and φ = 0. A circle at the left represents the event horizon. |
| In the text | |
 |
Fig. 3 A set of geodesics of massive particles orbit around a black hole with a = 0.9. The physical velocities of the emitter with respect to the LNRF are υr = 0, υθ = 0, and υφ = 0.4, υφ = 0.5, υφ = 0.6, υφ = 0.7, υφ = 0.8, υφ = 0.9 for panels from left to right, top to bottom. The velocities of these particles are specified isotropically in the rest frame of the emitter and |
| In the text | |
 |
Fig. 4 Orbit of a particle in a spherical motion. The parameters are: the black hole spin a = 0.998, the radius of the orbit r = 2 rg, the turning point θ∗ = 30°, the inclination angle of the observer θobs = 90°. |
| In the text | |
 |
Fig. 5 Radii of the innermost stable orbits for the spherical motion around a Kerr black hole, as functions of the specific angular momentum a of the black hole. |
| In the text | |
 |
Fig. 6 Orbit of a particle moving inside the ISSO with the constants of motion of the ISSO. The black hole spin a = 0.998 and the turning point θ∗ = 0°. The radius of ISSO is r = 5.2781 rg. The inclination angle θobs = 90° for the top panel and θobs = 0° for the bottom panel. |
| In the text | |
 |
Fig. 7 Orbits of equal mass test particles flow inward to a black hole along geodesic trajectories, which form a smooth and curved surface. The black hole spin is a = 0.96, the initial tiled angle of the disk is β = 30°. The initial physical velocities of the particles under the tetrad are: |
| In the text | |
 |
Fig. 8 Images of a skewed disk, whose inner and outer radii are 1.5 rg and 10 rg. The parameters: β = 30°, γ0 = 135°, black hole spin a = 0.998, inclination angles θobs are 15°, 30°, 45°, 60°, 75° and 90° for panels from left to right, top to bottom. |
| In the text | |
 |
Fig. 9 Streamlines of axisymmetric accretion flow, the parameters are: black hole spin a = 0.998; initial four-velocity |
| In the text | |
 |
Fig. 10 An assumed ball composed of a set of massive test particles without interactions is disrupted by the strong tidal force of a Kerr black hole. The black hole spin is a = 0.8. The radius of the ball is 4 rg. The initial coordinates are r = 20 rg, θ = 90°, φ = 0°. The coordinate times are t = 0, 22.5, 45, 67.5, 90 for images from right to left. A circle at the left represents the event horizon. |
| In the text | |
 |
Fig. A.1 Geometry between the skewed disk plane and the equatorial plane of a black hole. The boundary of the disk is a ring, at which equal mass test particles are injected continuously. At the initial position, indicated by p, there are two orthonormal tetrads, i.e., {p, er,eθ,eφ} and {p, |
| In the text | |
 |
Fig. B.1 Curve of fσ(p) (or ft(p)) as function of p. The parameter p0 is the unique real root of equation σ(p) = σ0 (or t(p) = t0). Starting from an appropriate initial value, pini, one can approach p0 through an iterative process. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



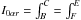
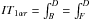
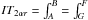
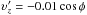
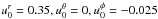
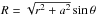
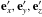
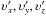
![\appendix \setcounter{section}{1} \begin{eqnarray*} &&\sin\theta = \frac{\cos\beta}{\sqrt{1-\sin^2\phi\sin^2\beta}},\quad \cos\theta = -\frac{\cos\phi\sin\beta}{\sqrt{1-\sin^2\phi\sin^2\beta}},\\[3mm] &&\sin\varphi = \frac{\sin\phi\cos\beta}{\sqrt{1-\sin^2\phi\sin^2\beta}},\quad \cos\varphi = \frac{\cos\phi}{\sqrt{1-\sin^2\phi\sin^2\beta}}\cdot \end{eqnarray*}](/articles/aa/full_html/2014/01/aa22565-13/aa22565-13-eq445.png)