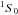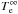| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | L5 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201322514 | |
| Published online | 03 January 2014 | |
The neutron star in Cassiopeia A: equation of state, superfluidity, and Joule heating
1 INAF, Osservatorio Astrofisico di Catania, via S.Sofia 78, 95123 Catania, Italy
e-mail: abo@oact.inaf.it
2 INFN, Sezione di Catania, via S.Sofia 72, 95123 Catania, Italy
3 A. F. Ioffe Institute of Physics and Technology, 194021 St. Petersburg, Russia
Received: 20 August 2013
Accepted: 6 November 2013
The thermomagnetic evolution of the young neutron star in Cassiopea A is studied by considering fast neutrino emission processes. In particular, we consider neutron star models obtained from the equation of state computed in the framework of the Brueckner-Bethe-Goldstone many-body theory and variational methods, and models obtained with the Akmal-Pandharipande-Ravenhall equation of state. It is shown that it is possible to explain a fast cooling regime as the one observed in the neutron star in Cassiopea A if the Joule heating produced by dissipation of the small-scale magnetic field in the crust is taken into account. We thus argue that it is difficult to put severe constraints on the superfluid gap if the Joule heating is considered.
Key words: dense matter / equation of state / stars: neutron / stars: magnetic field / supernovae: individual: Cassiopeia A
© ESO, 2014
1. Introduction
The neutron star identified with the historical supernova SN 1680 in Cassiopea A (Cas A) is the youngest one to be discovered in the Milky Way. Its estimated age of 330 yrs is in agreement with its kinematic age (Fesen et al. 2006) and its thermal X-ray spectrum is consistent with a nonmagnetized carbon atmosphere with a surface temperature of 2 × 106 K (Ho & Heinke 2009). The estimated values of radius and mass vary from R = 8.3 km and M = 2.01 M⊙ to R = 10.3 km and M = 1.65 M⊙ depending on the reduction procedure of Chandra X-ray Observatory archival data (Heinke & Ho 2010). In particular, the authors argued that the surface temperature has rapidly decreased from 2.12 × 106 to 2.04 × 106 in almost one decade, from 2000 to 2009. This cooling rate is significantly stronger than expected when compared to the standard cooling model (Page et al. 2006; Yakovlev & Pethick 2004) or to the medium modified Urca model (Grigorian & Voskresensky 2005). It is also unlikely that the observed cooling can be attributed to fast cooling models alone, such as direct Urca (DU) processes or neutrino emission from Bose condensates, for instance.
In a recent work Page et al. (2011) interpreted the Cas A data within the frame of the minimal cooling paradigm (Page et al. 2004) and explained that the onset of enhanced neutrino emission resulting from the neutron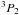 
pairing in the core is enough to explain the cooling data. In particular, a critical temperature Tc = 5 × 108 K for the triplet neutron superfluidity is implied in this process. A similar scenario has also been put forward by Shternin et al. (2011). While in these works the basic idea is that neutrons have recently become superfluid in the core, in Blaschke et al. (2012) it has been argued that this cooling is produced by a reduction of thermal conductivity caused by a nuclear medium effect.
In this paper we argue that the data can instead be explained by dissipation of the magnetic field and subsequent Joule heating in the surface layers of the crust, even in the framework of fast emission processes. There is no evidence for the presence of a significant magnetic field in this neutron star. A strong field should lead to hot spots at the surface and spin-induced variations in the X-ray flux, which are not observed. However, if the magnetic field is distributed mostly on small-scales, the global field can be rather weak and the corresponding variations in the X-ray flux might not be observable. The existence of a class of neutron stars with a predominant small-scale field at the surface has been theoretically predicted by Bonanno et al. (2005, 2006) and subsequently observed by Gotthelf & Halpern (2007) who introduced the term antimagnetars for this class of objects.
Rapid motions caused by hydrodynamic instabilities in protoneutron stars (Epstein 1979; Burrows & Lattimer 1986) can lead to the onset of a turbulent dynamo action that amplifies the magnetic field during the first 30−40 s of a neutron star life (Thompson & Duncan 1993; Bonanno et al. 2003). However, if the initial rotational period is too slow this mechanism might not be sufficient to produce a large-scale field. On the contrary, turbulence in a highly conducting plasma is always accompanied by the generation of small-scale fields that are approximately in equipartition with the turbulent motions (Urpin & Gil 2004). These fields will then be frozen into the crust which starts forming soon after the end of the unstable stage. Therefore, the magnetic field of neutron stars can have a very complex geometry. In the crust, their subsequent evolution is determined essentially by ohmic dissipation, a relatively slow process because of the high conductivity of the crust. Small-scale fields can generally be stronger than large-scale fields and for this reason can produce more efficient heating in certain conditions. Estimates of a small-scale field are uncertain and range from ~1015 − 1016 G to ~(1−3) × 1013 G (Bonanno et al. 2006; Urpin & Gil 2004).
2. Joule heating in the crust
The effect of Joule heating on the thermal evolution of neutron star was considered for the first time by Miralles et al. (1998) who argued that this heating can have a significantly impact on the thermal evolution of old neutron stars with age t > 106 − 107 yrs. The general relativistic treatment proposed by Page et al. (2000) led to similar conclusions. More recent works (Urpin & Konenkov 2008; Pons et al. 2009) have further clarified that Joule heating can also be important in very young neutron stars (with age ≲104), thus it is important to include this effect when discussing the thermal evolution of Cas A. The induction equation in the crust reads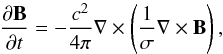 
(1)where σ is the conductivity; we have neglected the Hall currents because these are important only for very strong magnetic fields ≳1014 G.
The Joule heating term is an additional source of heat in the thermal balance equation which depends on the strength and configuration of the magnetic field. For the sake of simplicity, we assume that the radial length-scale of a small-scale field Lr is smaller than those in the azimuthal and polar directions L∥. This is reasonable because the thickness of the crust (1−1.5 km) is much smaller than the radius (10−15 km). This assumption does not qualitatively influence our results, but it simplifies calculations because we can neglect terms on the order of 1/r compared to ∂/∂r, being r the radial spherical coordinate. It is convenient to introduce the vector potential B = ∇ × A. The potential A and electric current j can be expanded in terms of the vector spherical harmonics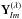 
where λ = 0, ± 1, and l and m are the polar and azimuthal wavenumbers (Akhiezer & Berestetskii 1965): 
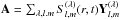and 
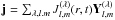. Then, Eq. (1) yields 
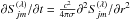(Urpin et al. 1994). Continuity of the field at the stellar surface r = R leads to the boundary condition 
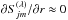with the accuracy in terms of the lowest order in Lr/L∥. The spherical components of j can be expressed in terms of 
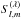. Then, the rate of Joule heating is 
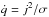and in general it will depend on θ and ϕ, the polar and azimuthal spherical coordinates. The cooling codes for neutron stars usually do not take into account departure from spherical symmetry and we will thus use the angle-averaged expression for 
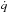. Using orthogonality of the vector spherical harmonics, we finally obtain 
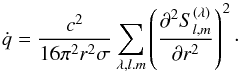(2)In our model, 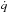depends on the radial distribution of the small-scale field. At the beginning of the evolution, the instabilities occur almost in the whole volume of a neutron star. Hence, motions caused by instabilities generate small-scale fields almost everywhere within the neutron star. The characteristic length-scales of these fields range from the main turbulent scale (~1 km) up the dissipative length scale. During the cooling these fields will be frozen into the crustal matter and their evolution is determined mainly by ohmic dissipation. Dissipation in the core is very slow because of large σ, and we neglect it. In the crust, fields with different length-scales λ located at different depths decay on different time scales, τλ ~ 4πσλ2/c2. Depending on the age, the main contribution to 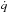is given by fields with different characteristic length scales. Using the expression for τλ, it is easy to estimate that the main contribution to 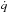at the age ~300 yrs is determined by magnetic fields with a characteristic length scale 300−600 m. Fields with smaller characteristic length scales have already disappeared, but those with greater length scales do not contribute yet to the Joule heating. Therefore, in the sum in Eq. (2) we can consider only a dominant term with the characteristic radial length scale 300−600 m and the corresponding field strength.
 |
Fig. 1 Critical temperatures of the neutron |
| Open with DEXTER | |
3. Equation of state
In this paper, we concentrate on the thermal evolution of a neutron star with the fast neutrino emission processes. We consider two models based on different equation of state (EOS) to be representative of these stars. The first is derived within the Brueckner-Bethe-Goldstone many-body theory (Baldo 1999), the BHF EOS. In this many-body approach one introduces the Brueckner reaction matrix G, which can be interpreted as the effective in-medium nucleon-nucleon (NN) interaction, and the single particle potential U(k;ρ) = ∑ k′ ≤ kF ⟨ kk′ | G(ρ) | kk′ ⟩ a . The subscript “a” indicates antisymmetrization and ρ is the baryon density. From the potential U the EOS can be obtained, and the in-medium nucleon effective mass m∗ at the Fermi surface can be derived according to the relation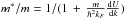 
where the derivative of U is taken at k = kF. The accuracy and convergence of the expansion have been extensively studied (Song et al. 1998; Baldo et al. 2000) and it turns out that in order to reproduce the correct saturation point of symmetric nuclear matter one needs to introduce three-body force, which are reduced to density dependent two-body force by averaging over the position of the third particle (Baldo et al. 1997). We took the Argonne v18 as NN potential Wiringa et al. (1995), supplemented by the so-called Urbana model (Carlson et al. 1983) as the three-body force. The saturation point (ρ0 ≈ 0.16 fm-3, E/A ≈ − 16 MeV) is then well reproduced, and incompressibility and symmetry energy are compatible with those extracted from phenomenology (Taranto et al. 2013). The second EOS is the so-called APR EOS by Akmal et al. (1998) obtained from the Argonne v18 NN interaction and a variational procedure as well as Urbana three-nucleon interactions. Although the BHF and variational methods are connected (Baldo & Moshfegh 2012), they give different EOS at high density. We assume that the matter is composed of neutrons, protons, and leptons in beta-equilibrium where electrons and muons are treated as relativistic Fermi gas.
 |
Fig. 2 Left panel: redshifted effective temperature |
| Open with DEXTER | |
The two EOS start to deviate at nucleon densities >2ρ0 and the symmetry energy for APR EOS becomes smaller than for the BHF EOS. The symmetry energy determines the proton fraction, hence the onset of the DU process. In the BHF approach it already takes place at 3ρ0, whereas in the APR case it is allowed at larger density, close to 1fm-3 (Zhou et al. 2004). Therefore, in the BHF case NS with mass around 1.2 M⊙ can cool rapidly through DU, whereas in the APR case DU is allowed only for heavy NS, close to the maximum mass. We note that the values of the maximum allowed mass is different in the two approaches, being slightly above 2 M⊙ in the BHF case and close to 2.2 M⊙ in the APR case (Taranto et al. 2013).
4. Numerical results
Our numerical simulations use the public code NSCool1 in which the magnetothermal evolution has been taken into account by coupling the induction equation with the thermal equation via the Joule heating source. In particular, the induction equation was solved via an implicit scheme and the electron conductivity was calculated with the approach described in Potekhin (1999). We assumed that the composition of the crust corresponds to the so-called accreted matter with an envelope mass of ΔM = 3.6 × 10-15 M⊙ and an impurity parameter Q = 0.01.
The critical temperature of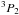 
pairing of neutrons is 109 K in all our models. In particular, we followed the estimate of Baldo et al. (1998) for the proton and neutron superfluidity where the gap extends up to the center of the neutron star. For actual computations we have thus modeled the density dependence of this gap with a sharp increase after ρ ~ 4 × 1014 gm/cm3 which extends up to the center of the star in all the models (see Fig. 1 for the 1.4M⊙ example).
The small-scale magnetic field is assumed to be anchored in the crust and its characteristic length scale should vary around λr ~ 300 − 600 m as estimated in the previous section. We expect that the initial field strength lies in the range (1 − 3) × 1013 G, according to the estimate of Bonanno et al. (2006) for a dynamo generated small-scale field. The crucial feature, from the observational point of view, is the occurrence of a sharp transition, a transit time (Page et al. 2011) of a few decades, during which the cooling can be characterized by an almost constant slope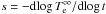 
, as shown in the center and right panels in Fig. 2. In determining the observed slope and effective temperature, the strength of the magnetic field and its length scale play antagonistic roles. By increasing the strength, it is possible to slow down the cooling, and the slope s decreases. On the contrary, by increasing the length scale it is possible to decrease the efficiency of the Joule heating. This is expected since 
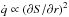, and therefore the greater the gradients of S are, the more efficient the Joule heating will be. In our numerical simulations we tried to find the best compromise between the field strength and its length scale in order to explain both the slope and the observed effective temperature of Cas A.
Our results are summarized in the three panels in Fig. 2, where our best models with different EOS are displayed. We found that the length scale of the initial magnetic field should be ~600 m in the models with the BHF EOS and ~300 m in the model with the APR EOS. It is reassuring to notice that these values are comparable to the main length scale of turbulence in protoneutron stars, ~1 km (see, e.g., Burrows & Lattimer 1986).
On the other hand, the obtained values of the field are 2.2, 1.3, and 1.5 × 1013 G for models with the BHF EOS and with 1.4, 1.6, and 2.0 M⊙, respectively, while for the model with the APR EOS, we obtain 9.5 × 1012 G, in agreement with the estimate discussed in Bonanno et al. (2006).
5. Discussion
Most probably all neutron stars have small-scale magnetic fields amplified in the course of a short unstable stage soon after collapse. Turbulent motions generate small-scale fields on a very short time scale 1−10 ms. The strength of these fields is (1 − 3) × 1013 G at the end of a convective stage. Generation of a global magnetic field is determined by rotation and can be suppressed if the neutron star rotates slowly at birth. Therefore, there should exist a particular class of neutron stars that has relatively strong small-scale fields and has no (or a very weak) global field. Perhaps, Cas A is representative of this class.
Dissipation of small-scale fields ~1013 G can lead to departures from the standard cooling scenario of non-magnetic neutron stars. Our calculations show that Joule heating can provide a sufficient amount of heat to account for the temperature and cooling rate of Cas A even for the neutron star models with fast cooling. Since the presence of small-scale fields is a general feature of neutron stars, our model predicts that departures from the standard cooling should be detected in all young stars. According to our calculations, the cooling rate of Cas A will remain approximately unchanged during at least a few hundred years.
It is important to stress that in our calculation the presence of a gap extending up to the center was needed only to suppress the fast cooling due to the DU, otherwise it did not play an essential role in explaining the rapid cooling during the transit phase. In this model it is impossible to put severe constraints on Tc from the observed slope during this phase. In particular, although in actual calculations the critical temperature Tc = 109 K for the triplet neutron superfluidity has been used, we found that a successful fit can also be obtained with Tc = 5 × 108 K. Generally, a good fit for the temperature and cooling rate can be obtained for other values of Tc by varying the magnetic field and its length scale.
While this work was in progress a new analysis of the Cas A appeared (Elshamouty et al. 2013) where the cooling of Cas A is less extreme than previously reported. Clearly, all our conclusions would remain valid even in this case, provided the strength of the initial magnetic field is slightly reduced.
Acknowledgments
V.U. thanks INFN-Sezione di Catania and INAF-Osservatorio Astrofisico di Catania for hospitality and financial support. A.B. would like to thank Dany Page for his help in using the public code NSCool.
References
- Akhiezer, A. I., & Berestetskii, V. B. 1965, Quantum Electrodynamics (New York: Interscience) [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M. 1999, Int. Rev. Nucl. Phys., 8, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., & Moshfegh, H. R. 2012, Phys. Rev. C, 86, 024306 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., Bombaci, I., & Burgio, G. F. 1997, A&A, 328, 274 [NASA ADS] [Google Scholar]
- Baldo, M., Elgarøy, Ø., Engvik, L., Hjorth-Jensen, M., & Schulze, H.-J. 1998, Phys. Rev. C, 58, 1921 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baldo, M., Giansiracusa, G., Lombardo, U., & Song, H. Q. 2000, Phys. Lett. B, 473, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Blaschke, D., Grigorian, H., Voskresensky, D. N., & Weber, F. 2012, Phys. Rev. C, 85, 022802 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanno, A., Rezzolla, L., & Urpin, V. 2003, A&A, 410, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonanno, A., Urpin, V., & Belvedere, G. 2005, A&A, 440, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonanno, A., Urpin, V., & Belvedere, G. 2006, A&A, 451, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burrows, A., & Lattimer, J. M. 1986, ApJ, 307, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, J., Pandharipande, V. R., & Wiringa, R. B. 1983, Nucl. Phys. A, 401, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Elshamouty, K. G., Heinke, C. O., Sivakoff, G. R., et al. 2013, ApJ, 777, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Epstein, R. I. 1979, MNRAS, 188, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Fesen, R. A., Hammell, M. C., Morse, J., et al. 2006, ApJ, 645, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Gotthelf, E. V., & Halpern, J. P. 2007, ApJ, 664, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Grigorian, H., & Voskresensky, D. N. 2005, A&A, 444, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinke, C. O., & Ho, W. C. G. 2010, ApJ, 719, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, W. C. G., & Heinke, C. O. 2009, Nature, 462, 71 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Miralles, J. A., Urpin, V., & Konenkov, D. 1998, ApJ, 503, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Geppert, U., & Zannias, T. 2000, A&A, 360, 1052 [NASA ADS] [Google Scholar]
- Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W. 2004, ApJS, 155, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Geppert, U., & Weber, F. 2006, Nucl. Phys. A, 777, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Prakash, M., Lattimer, J. M., & Steiner, A. W. 2011, Phys. Rev. Lett., 106, 081101 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Pons, J. A., Miralles, J. A., & Geppert, U. 2009, A&A, 496, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potekhin, A. Y. 1999, A&A, 351, 787 [NASA ADS] [Google Scholar]
- Shternin, P. S., Yakovlev, D. G., Heinke, C. O., Ho, W. C. G., & Patnaude, D. J. 2011, MNRAS, 412, L108 [NASA ADS] [Google Scholar]
- Song, H. Q., Baldo, M., Giansiracusa, G., & Lombardo, U. 1998, Phys. Rev. Lett., 81, 1584 [NASA ADS] [CrossRef] [Google Scholar]
- Taranto, G., Baldo, M., & Burgio, G. F. 2013, Phys. Rev. C, 87, 045803 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, C., & Duncan, R. C. 1993, ApJ, 408, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Urpin, V., & Gil, J. 2004, A&A, 415, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urpin, V., & Konenkov, D. 2008, A&A, 483, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urpin, V. A., Chanmugam, G., & Sang, Y. 1994, ApJ, 433, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Wiringa, R. B., Stoks, V. G. J., & Schiavilla, R. 1995, Phys. Rev. C, 51, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Zhou, X. R., Burgio, G. F., Lombardo, U., Schulze, H.-J., & Zuo, W. 2004, Phys. Rev. C, 69, 018801 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
|
Fig. 1 Critical temperatures of the neutron |
| Open with DEXTER | |
| In the text | |
|
Fig. 2 Left panel: redshifted effective temperature |
| Open with DEXTER | |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.