| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A133 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321321 | |
| Published online | 22 January 2014 | |
The chromosphere above sunspots at millimeter wavelengths
1 Max-Planck-Institut for Sonnensystemforschung, 37191 Katlenburg-Lindau, Germany
e-mail: lukicheva@mps.mpg.de
2 Astronomical Institute, St. Petersburg University, Universitetskii pr. 28, 198504 St. Petersburg, Russia
3 School of Space Research, Kyung Hee University, Yongin, Gyeonggi 446-701, Korea
4 Space Vehicles Directorate, Air Force Research Laboratory, Kirtland AFB, NM, USA
Received: 19 February 2013
Accepted: 19 December 2013
Aims. The aim of this paper is to demonstrate that millimeter wave data can be used to distinguish between various atmospheric models of sunspots, whose temperature structure in the upper photosphere and chromosphere has been the source of some controversy.
Methods. We use observations of the temperature contrast (relative to the quiet Sun) above a sunspot umbra at 3.5 mm obtained with the Berkeley-Illinois-Maryland Array (BIMA), complemented by submm observations from Lindsey & Kopp (1995) and 2 cm observations with the Very Large Array. These are compared with the umbral contrast calculated from various atmospheric models of sunspots.
Results. Current mm and submm observational data suggest that the brightness observed at these wavelengths is low compared to the most widely used sunspot models. These data impose strong constraints on the temperature and density stratifications of the sunspot umbral atmosphere, in particular on the location and depth of the temperature minimum and the location of the transition region.
Conclusions. A successful model that is in agreement with millimeter umbral brightness should have an extended and deep temperature minimum (below 3000 K). Better spatial resolution as well as better wavelength coverage are needed for a more complete determination of the chromospheric temperature stratification above sunspot umbrae.
Key words: Sun: chromosphere / Sun: radio radiation / sunspots
© ESO, 2014
1. Introduction
There have been numerous attempts to build a comprehensive semiempirical model of the atmosphere above a sunspot umbra. Deriving such models is a complicated process that tries to balance observations of a range of optical and UV lines (mostly formed in non-local thermodynamical equilibrium (LTE) conditions, see, e.g., Avrett 1981; Maltby et al. 1986; Obridko & Staude 1988, for a review see Solanki 2003) and, when available, radio measurements of brightness spectra, together with ionization equilibrium and radiative transfer calculations that include heat transfer down from the corona as well as other factors (e.g., Fontenla et al. 1993). The radio data are particularly valuable for solar diagnostics because the measurements are in the Rayleigh-Jeans limit, meaning that measured brightness temperatures actually represent thermal electron temperatures in the optically thick atmosphere. The temperature, at which a given frequency is optically thick, is sensitive to density and temperature, and hence the radio data provide important constraints for modeling (e.g., Loukitcheva et al. 2004).
However, while there are numerous radio temperature measurements of the quiet-Sun atmosphere, there are very few for sunspots, particularly at millimeter wavelengths, since good spatial resolution is required to isolate the brightness temperature of the sunspot from its surroundings, and single-dish measurements generally do not have enough resolution. The highest-resolution single-dish data, at 10 − 20′′, are from James Clerk Maxwell Telescope (JCMT; Lindsey & Kopp 1995) and CSO (Bastian et al. 1993), but at submm wavelengths, which sample deeper in the atmosphere, closer to photospheric heights. The sunspot umbra appears darker than the quiet Sun at these wavelengths and umbral contrast decreases towards longer wavelengths. It is more interesting, however, to use millimeter wavelength radio data, which can constrain the temperature in the chromosphere and address the controversy regarding the umbral temperature in these layers (see, e.g., Maltby et al. 1986; Severino et al. 1994; Fontenla et al. 2009, and Sect. 3). At millimeter wavelengths the instrument best suited for high-resolution observations of sunspots until recently was the 10-element Berkeley-Illinois-Maryland Array (BIMA) operating at 3.5 mm (Welch et al. 1996). The BIMA antennas are now part of the Combined Array for Millimeter Astronomy (CARMA; Bock et al. 2006).
 |
Fig. 1 Active region NOAA 10448 observed on August 31, 2003. a) BIMA image at 3.5 mm, b) MDI photospheric magnetogram and c) BBSO Ca ii K image. White contours mark sunspot umbrae and penumbrae. The box contains the region shown in Fig. 4 as a blowup. The zero brightness in the BIMA image corresponds to the weakest flux. |
In this work we use BIMA observations of the temperature contrast (relative to the quiet Sun) above a sunspot umbra at 3.5 mm. At this wavelength models predict rather different umbral brightnesses, so that such measurements can be used to distinguish between the various atmospheric models of sunspots. In Sect. 2 we report the observations of the active region at 3.5 mm, evaluate umbral brightness at this wavelength relative to the quiet Sun, and investigate the influence of spatial resolution on the appearance of the sunspot at mm wavelengths. In Sect. 3 we discuss the differences between the temperature and density stratifications in the existing sunspot models as well as between mm brightness spectra calculated from these models. We demonstrate that observations of sunspots at mm wavelengths impose strong constraints on temperature and density stratifications of the sunspot atmosphere, particularly on the location and depth of the temperature minimum and the location of the transition region in the umbral models. In Sect. 4 we complement the investigation of submm and mm umbral brightnesses with two examples of the observations of sunspot umbra at short cm wavelengths.
2. Observational data and their analysis
On August 31, 2003 BIMA observed a small active region NOAA 10448 north of the solar equator (coordinates N20W07 on 31-Aug-2003 23:30 UT). The BIMA images were deconvolved using the maximum entropy method (MEM) and restored with a Gaussian beam of 12′′ (White et al. 2006). Contemporaneous images of NOAA 10448 at 3 wavelengths are shown in Fig. 1 including the BIMA image at 3.5 mm wavelength, a photospheric magnetogram from the Michelson Doppler Imager (MDI) on the SOHO satellite (Scherrer et al. 1995), and a Ca ii K image obtained at the Big Bear Solar Observatory. Prior to the analysis solar differential rotation was compensated, so that all image locations correspond to the AR’s location at a single time. Then the images were spatially coaligned. In Fig. 2 we show the results of the coalignment depicting the mm emission contours overlaid on the Ca ii K image and the magnetogram. The pixel size for all images was set to 1′′. Images are 241 by 241 pixels which corresponds to a 241′′ by 241′′ FOV.
 |
Fig. 2 BBSO Ca ii K image and MDI photospheric magnetogram with the overlaid contours of 3.5 mm emission plotted as iso-intensity lines corresponding to 10, 20, 30, 40, 50, 60, 70% of maximum brightness. |
For analysis and comparison with the umbral models we chose the largest sunspot in the field, which is located at the trailing (eastern) edge of the active region. Its photospheric magnetic field does not exceed 2000 G according to recalibrated MDI full disk magnetograms1. This sunspot had a well-defined umbra and penumbra, with the penumbra linking to a smaller sunspot with a weaker umbra to the west of the larger spot (see corresponding umbral and penumbral contours overlaid in Fig. 1). Hereafter we refer to the umbra under consideration, associated with the largest sunspot, as “the big” umbra, and for comparison we usually provide the observational quantities obtained for “the small” umbra of the western sunspot as well. The umbral and penumbral boundaries were derived from the MDI continuum image as, respectively, 0.65 and 0.90 of the surrounding photospheric white-light intensity following Mathew et al. (2007).
Due to a positivity constraint applied in the maximum entropy deconvolution method the zero level in the BIMA maps corresponds to the weakest flux in the image. Therefore, to determine umbral brightness decrement relative to the QS we first need to establish the quiet Sun level in the BIMA images. To that end we used the MDI/SOHO photospheric magnetograms and applied a threshold of 40 G in the absolute value of the magnetogram signal to determine quiet-Sun regions. After that we degraded the resolution of the (absolute-valued) magnetogram to the BIMA resolution (12′′) and found the contour carrying the same amount of magnetic flux as the 40 G contour in the magnetogram at the original MDI resolution (2.6′′). The resulting quiet-Sun brightness was determined as the average of brightness outside this iso-Gauss contour, which turns out to lie at 26 G at the 12′′ resolution of the mm data. The results of the procedure are demonstrated in Fig. 3a, where we show the magnetogram with the overlaid 40 G and 26 G contours, represented by dotted and solid lines, respectively. The latter corresponds to the threshold defining the resulting quiet-Sun mask, depicted in Fig. 3b. Note that we consider the flux only within the BIMA field of view of 3′ by 3′ (white circle in Fig. 3).
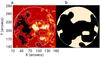 |
Fig. 3 a) MDI magnetogram in the range (− 200, 200) Gauss. The dotted and solid lines mark the 40 G and 26 G contours, corresponding to the quiet-Sun level at the original resolution of the magnetogram and at the resolution of the mm data, respectively. The white circle corresponds to the BIMA primary beam of 3′ by 3′ containing flux. b) The resulting quiet-Sun mask restricted to BIMA’s primary beam. Quiet-Sun areas are white. |
We acknowledge that there is considerable uncertainty in choosing the pixels that correspond to the “quiet-Sun atmosphere”, since there is always some arbitrariness in the criterion chosen to identify such pixels. The criterion applied here is consistent with other investigations (e.g., Wang et al. 2009) and leads to a reasonable proportion of pixels in quiet Sun regions. Using even stronger thresholds (based on the mm brightness histogram) we would get lower values for the level of quiet-Sun emission in the millimeter images, but they are always higher than the derived umbral brightness.
A high level of correspondence between the mm brightness contours and the magnetic field structures, as well as between the mm brightness contours and calcium intensity, found in Fig. 2, indicates that the mm brightness decrement at the location of the umbrae can provide an estimate of umbral brightness at 3.5 mm even if there is no obvious umbral feature found in the mm image. We calculate the umbral millimeter brightness as the average brightness of pixels lying within the umbral boundaries. Special attention was paid to the fact that in the mm image the location of the weakest emission (the zero level in the maximum entropy maps) does not match the exact position of the umbra, while the darkest feature in the calcium image lies within the umbral boundary. Lindsey & Kopp (1995) also reported that the location of dark features corresponding to sunspot umbrae in the submm images often appeared to be noticeably offset from their locations in the Ca K images. To study the influence of image resolution on the appearance of the umbral depression and its position relative to the photospheric umbral counterpart we convolved the Ca ii K image with the 12′′ beam corresponding to the BIMA resolution and plotted a blowup (marked with a box in Fig. 1) of the convolved image together with the calcium image at the original resolution and the 3.5 mm image in Fig. 4. In the calcium image, smoothed to the resolution of the mm image (Fig. 4c), the brightness minimum is no longer within the umbral boundaries and the depression in brightness becomes less pronounced and more diffuse due to an admixture of signal from neighboring bright points. Therefore smearing of the brightness distribution reduces umbral contrast relative to the quiet-Sun background. This result is demonstrated nicely in Fig. 5, where we show the east-west cuts through the two spot umbrae at y = 203.6′′ north of apparent disk center for the mm image and calcium images at original and degraded (12′′) resolution respectively. In Fig. 5 we adopted for convenience Tb = 6730 K as the absolute quiet Sun level at 3.5 mm as an average of the several single-dish quiet-Sun brightness temperature measurements (Nagnibeda & Piotrovitch 1994; Loukitcheva 2005).
For the big umbra (which is used further for comparison with umbral models below) the average calcium umbral contrast changes from 0.83 of the quiet-Sun brightness in the original image to 1.04 in the smoothed image (see Figs. 5b and c), i.e. the big umbra in the degraded Ca images is slightly brighter than the QS, mainly due to admixture of bright emission from nearby plage. For the small umbra located in the region of the enhanced calcium flux the values are 1.01 and 1.14 respectively. Degrading the image resolution also decreases the contrast between the big and the small umbrae. The ratio of umbral brightnesses changes from 0.80 in the original image to 0.88 in the smeared image. The latter value is close to the ratio derived from the mm image, which is 0.90 (Fig. 5a). Therefore the results shown in Figs. 4 and 5 confirm that the relatively low resolution of the mm images leads to an overestimate of the umbral brightness and is a plausible reason for the displacement of the location of the minimum in the mm image relative to its photospheric umbral counterpart.
 |
Fig. 4 A blowup of the sunspot region marked in Fig. 1. a) BIMA image at 3.5 mm, b) BBSO Ca ii K image at the original resolution and c) the Ca ii K image convolved to the resolution of the mm image (12′′). Thick white contours mark the locations of two umbrae. The other are iso-intensity lines corresponding to 10, 20, 30, 40, 50, 60, 70% of maximum brightness for the mm image and 30, 40, 50, 60, 70% of maximum brightness for the original and convolved calcium images. The zero brightness in the BIMA image corresponds to the weakest flux. |
The distribution of brightness in the mm and degraded calcium images is sufficiently different that we cannot use the comparison between original and degraded calcium images to correct the BIMA umbral brightness, but we can use it to estimate the uncertainty in the mm umbral contrast relative to the QS. Thus, in the upper panel of Fig. 5 we plot (thick dashed lines) the potential reduction of the umbral brightness at 3.5 mm when going to 4′′ resolution if we assume the same contrast between the umbrae and the QS for the mm and calcium images. The same effect is shown also in Fig. 8 with downward arrows for the mm brightness of the big and small umbrae depicted with filled and open circles, respectively. We estimate this uncertainty to be 17% and 9% of the QS brightness at 12′′ resolution for the big and small umbrae, respectively. Note that this correction can be considered to be an upper limit, so that the true contrast is expected to lie between thick solid and dashed bars in Fig. 5.
From the above analysis of the BIMA observations, we estimate the “3.5 mm umbra” to be approximately 400 K cooler than the quiet sun (roughly 6% of the QS brightness temperature at this wavelength) at the resolution of 12′′ with an uncertainty of order 100 K. This is the value we will use primarily for comparison with the atmospheric models, but in addition we will also reference the resolution-corrected (based on Ca ii) value of 1500 K as the upper limit to the umbral decrement at 3.5 mm. For comparison with the model calculations we also use the submm umbral brightness temperatures measured at 0.35 mm, 0.85 mm, and 1.2 mm from Lindsey & Kopp (1995). The observed submm and mm umbral brightness and corresponding measurement error estimates are plotted in Figs. 8 and 9 together with the output of the sunspot models discussed in the following section.
 |
Fig. 5 Horizontal cuts through the umbrae at y = 203.6′′ north of apparent solar disk center for BIMA image at 3.5 mm a), for BBSO Ca ii K image at the original resolution b) and at 12′′ resolution of the mm image c). Thick solid lines mark the location and size of the two umbrae. Thick dashed lines correspond to the potential reduction of the mm umbral brightness when going to 4′′ resolution. The QS level is indicated by the thin dotted lines. |
 |
Fig. 6 a) Electron temperature as a function of height in a number of standard models of the solar chromosphere above a sunspot umbra. (i) The model of Avrett (1981), (ii) of Maltby et al. (1986), (iii) of Severino et al. (1994), (iv) of Socas-Navarro (2007), (v) of Fontenla et al. (2009). The thin solid black line (vi) is the reference quiet-Sun atmosphere of Fontenla et al. (1993) known as FAL − C. b) The electron number density as a function of height for the same models as shown in panel a). |
3. Model simulations
In order to distinguish between the sunspot models, we have calculated the expected submm/mm brightness temperatures at 24 selected wavelengths in the range 0.1 − 20 mm for a set of classical sunspot models as well as their more recent updates. The models we analyzed are the sunspot model of Avrett (1981), model M of Maltby et al. (1986), the sunspot model of Severino et al. (1994), models A (dark umbra) and B (bright umbra) of Socas-Navarro (2007), and model S of Fontenla et al. (2009). The first two models are classical semiempirical sunspot models covering the umbral photosphere, chromosphere and transition region. The model of Severino et al. (1994) is an update of the model of Caccin et al. (1993) which is in its turn a modified version of one of the Maltby et al. (1986) models with a steeper temperature gradient in the photosphere. The model of Socas-Navarro (2007) was derived from non-LTE inversions of high-resolution spectropolarimetric observations of four Ca ii and Fe i lines. The most recent model of Fontenla et al. (2009) is based on the EUV spectrum from the SOHO/SUMER atlas (Curdt et al. 2001). We complemented this set of the one-component umbral models with the two-component model of Obridko & Staude (1988). Their umbral atmosphere consists of the main (dark) component and a secondary (bright) component with a filling factor in the range 0.05 − 0.1 depending on the spot size and solar cycle phase.
The height dependence of the electron temperature and electron number density of each of these models are plotted in Fig. 6, together with the reference quiet-Sun atmosphere. As a reference model for this plot we chose the model that represents the average quiet Sun (model C of Fontenla et al. 1993, commonly referred to as FAL − C). We preferred it to the more recent quiet-Sun models of Fontenla et al. (2007) and of Avrett & Loeser (2008). Although the quiet-Sun model of Fontenla et al. (2007) is constructed at moderate resolution it represents not the average quiet Sun but the internetwork. Furthermore, the model parameters in the upper chromosphere and transition region in this model are described as tentative (see Sect. 3 of Fontenla et al. 2007) and consequently the model cannot account accurately for the formation of the mm emission at the spatial resolution achieved by BIMA. The model of Avrett & Loeser (2008), an updated average quiet-Sun model, produces millimeter brightness temperatures substantially lower than any of the observed values (see Fig.3 of Avrett & Loeser 2008).
We note that each of the umbral models analyzed in this paper compared their results with corresponding quiet-Sun atmosphere models, but that different umbral models used different quiet-Sun models as their reference. For instance, the average QS model by Vernazza et al. (1981), VAL − C, was used as a reference point by Maltby et al. (1986) and Obridko & Staude (1988). The model by Gingerich et al. (1971), HSRA model, was chosen to represent the QS in the umbral models of Socas-Navarro (2007).
Calculations of the expected brightness temperature as a function of wavelength in the submm/mm range were carried out under the assumption that bremsstrahlung opacity is responsible for the mm continuum radiation. We distinguish two sources of opacity: due to encounters between free electrons and protons, and between free electrons and neutral hydrogen. They are usually referred to as H0 opacity and H − opacity, respectively. We assume that gyroresonance opacity is negligible at these high frequencies. The expression for bremsstrahlung opacity in magnetic media was taken from Zheleznyakov (1996). The magnetic field was modeled by a vertical dipole buried under the photosphere, following the approach of Zlotnik (1968). For the calculations we adopted the value of 2000 G for photospheric umbral magnetic field strength and a penumbral size (outer diameter) of 12′′, which corresponds to a dipole depth of 10 000 km.
From Fig. 6 it is seen that the sunspot models differ significantly from the FAL − C quiet-Sun model and from each other in the depth and extension of the temperature minimum region and also in the location of the transition region. A number of classical models, such as Avrett (1981), marked in Fig. 6 with (i), Maltby et al. (1986) (ii), and also their update by Severino et al. (1994) (iii), and the model of Socas-Navarro (2007) (iv), have the transition region at heights similar to the FAL − C model (about 2000 km and above). However, the more recent model of Fontenla et al. (2009) (v) places the transition region at much lower heights (around 1000 km). The temperature minimum in the sunspot umbra models generally lies deeper than in the FAL − C model. Furthermore the temperature in the temperature minimum region drops to below 3000 K in the models of Severino et al. (1994) (iii) and of Socas-Navarro (2007) (iv). However, the model of Severino et al. (1994) (iii) possesses an extended temperature minimum, i.e. the temperature minimum reaches to much greater heights in the atmosphere than do those of the other models.
 |
Fig. 7 Brightness-temperature contribution functions (with maxima normalized to unity) at 3 mm a) and at 1 mm b) for a number of sunspot models including the model of Avrett (1981) (dot-dashed curve), of Severino et al. (1994) (dashed curve), and of Fontenla et al. (2009) (dotted curve). For comparison the contribution function for the model FAL − C is shown with a thin solid black line. |
To study the contribution of various atmospheric layers to the emergent intensity of the radiation we calculated the brightness temperature contribution functions for the sunspot umbral models introduced in Fig. 6. In Fig. 7 we show the contribution functions at 3 mm and 1 mm for the umbral models of Avrett (1981), Severino et al. (1994), and Fontenla et al. (2009). For comparison we also plot the contribution function for model FAL − C with a thin solid line in Fig. 7.
The models of Avrett (1981) and Severino et al. (1994) both attribute the major contribution to radiation at 3 mm wavelength to a similar range of heights, of order 1200–1800 km, and moreover the contribution functions are of similar shape (see corresponding dot-dashed and dashed curves in Fig. 7a). The reason for this is the similarity of the electron temperature and number density distributions for these two models in this range of heights (see (i) and (iii) in Fig. 6). In the model of Fontenla et al. (2009) (dotted line in Fig. 7a) the effective emitting region at 3 mm is sharply defined due to the fact that the coronal contribution is negligible and the absorption coefficient varies rapidly with height at the base of the (low-lying) transition region.
Going to shorter wavelengths the formation heights move lower in the chromosphere (see Fig. 7b for 1 mm). However, for the model of Fontenla et al. (2009) the only difference between the contribution functions at 3 and 1 mm is a small bump of additional contribution from heights close to 500 km. The other models also exhibit a substantial contribution from heights at around 500 km. At these heights all the models investigated provide favorable conditions, namely low temperatures together with sufficiently high neutral hydrogen and electron densities for H − opacity to become appreciable, which leads to the observed peaks in the contribution functions. The contribution function (dashed line in Fig. 7b) for the model of Severino et al. (1994) is characterized by an additional peak at 800 km which is also due to effective collisions between electrons and neutral hydrogen at this height.
Thus, analysis of the contribution functions for different umbral models demonstrates that at 3 mm we should sample mostly the middle and upper umbral chromosphere, but in the model of Fontenla et al. (2009) the transition region also contributes significantly due to its location low in the atmosphere. For radiation at 1 mm and shorter wavelengths a substantial contribution comes from the heights of the temperature minimum region.
 |
Fig. 8 Difference between the umbral brightness (in temperature units) and the QS brightness, plotted as a function of wavelength for the model (i) of Avrett (1981), (ii) model M of Maltby et al. (1986), (iii) of Severino et al. (1994), (iv) model A of Socas-Navarro (2007), (v) model S of Fontenla et al. (2009) and (vi) the two-component umbral model of Obridko & Staude (1988) employing a filling factor of 0.05 for the hot component. Filled and open circles mark the observational values obtained from BIMA maps at 3.5 mm for the big and small umbrae, respectively. Arrowheads mark the shift of umbral brightness when extrapolating to 4′′ resolution. Diamonds stand for the measurements from JCMT at 0.35, 0.85 and 1.2 mm made by Lindsey & Kopp (1995). |
 |
Fig. 9 Absolute brightness temperature as a function of wavelength for the same umbral models as in Fig. 8. Also plotted is (viii) FAL − C model representing the Quiet Sun. |
Figures 8 and 9 show the predicted umbral brightness temperature spectra from each model, together with the BIMA observational results and measurements culled from Lindsey & Kopp (1995) depicted by circles and diamonds, respectively. In Fig. 8 we consider each umbral model relative to the QS model that it refers to and plot the corresponding mm brightness contrast 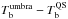 . We chose to depict the difference between the umbral and QS brightness in order to minimize the influence of the reference QS value on the umbral brightness and to make the models directly comparable with the observations which provide only the difference of the umbral brightness relative to the QS. For completeness, in Fig. 9 we compare the absolute brightness spectra from the umbral models with that from a single standard quiet-Sun model which is represented by the model FAL − C (plotted with black solid line in Fig. 9).
. We chose to depict the difference between the umbral and QS brightness in order to minimize the influence of the reference QS value on the umbral brightness and to make the models directly comparable with the observations which provide only the difference of the umbral brightness relative to the QS. For completeness, in Fig. 9 we compare the absolute brightness spectra from the umbral models with that from a single standard quiet-Sun model which is represented by the model FAL − C (plotted with black solid line in Fig. 9).
From Figs. 8 and 9 it is seen that the models by Severino et al. (1994) and Fontenla et al. (2009) reproduce the majority of the submm/mm observational data from Lindsey & Kopp (1995) relatively well. These models are characterized by deep and extended temperature minima (see Fig. 6) which dominates the contribution functions for umbral brightness at wavelengths up to 1 mm (Fig. 7b). However at 3.5 mm none of the models displays brightness in the umbra that is reduced relative to the individual reference quiet-Sun models (Fig. 8), in contrast to the observations which find at least the large sunspot umbra to be dark at this wavelength. Rather, these models predict that the umbra should be brighter than the surrounding quiet Sun at 3.5 mm wavelength. The model of Severino et al. (1994) predicts the lowest 3.5 mm umbral brightness and is therefore the closest to the observed value. In this model a wide range of heights in the upper chromosphere (1300–1700 km) contributes to the radiation at 3.5 mm wavelength (Fig. 7a) and a better fit to the observed values might need a revision of the temperature and electron density stratifications at these heights. The submm and mm brightnesses predicted by the classical umbral models of Avrett (1981) and Maltby et al. (1986), as well as the dark umbral model of Socas-Navarro (2007) and the two-component model of Obridko & Staude (1988), appear to be too high to account for the current submm/mm observations.
We expect the true 3.5 mm umbral brightness to be lower than the reported value of 400 K below the QS level (filled circle in Fig. 8) due to the dilution of the brightness-temperature reduction by the relatively low resolution of the data and also show in Figs. 8 and 9 the potential 3.5 mm brightness extrapolated (albeit crudely, based on Ca ii K images) to a resolution of 4′′ with a downward arrow.
 |
Fig. 10 Normalized brightness temperature as a function of sunspot photospheric magnetic field strength for the model of Fontenla et al. (2009) for 1 mm (cross), 3.6 mm (asterisk), 6 mm (diamond) and 10 mm (triangle). |
The magnetic field strength in the umbra can also affect the predictions of the models at millimeter wavelengths through its influence on the bremsstrahlung opacity. Therefore we also studied the dependence of sunspot brightness on the photospheric magnetic field. In Fig. 10 we show an example of normalized brightness temperature as a function of magnetic field strength at the photospheric level for wavelengths of 1, 3, 6 and 10 mm derived using the model of Fontenla et al. (2009). For mm wavelengths up to 6 mm (crosses, asterisks and diamonds in Fig. 10) the magnetic field influences the model brightness by less than 0.5% even for field strengths of 3500 G. Crucially, a stronger field increases the brightness of the umbra, so that we expect the discrepancy with the 3 mm data to be even larger if the 2000 G field strength obtained by MDI is too low. Starting from 10 mm the difference in brightness between sunspots with different magnetic fields becomes more significant. Thus, for a strong sunspot with photospheric magnetic field of 3500 G the model of Fontenla et al. (2009) predicts that the brightness at 10 mm should be 3% higher than for the sunspot analyzed in this work (2000 G). Longer wavelengths demonstrate a stronger dependence of sunspot brightness on magnetic field, but this can be difficult to measure due to the presence of a significant contributions from other sources, discussed in the next section.
4. Umbrae at centimeter wavelengths
One consequence of the umbral brightness analysis at submm and mm wavelengths is that we expect the radio umbra to change its appearance from darker than the quiet Sun at short wavelengths to brighter than the quiet Sun at longer wavelengths. The turnover wavelength beyond which (i.e., at longer wavelengths) an umbra should appear brighter than the quiet Sun depends on the exact temperature distribution in the model and can be used as an independent test for existing sunspot models. For the models considered here it ranges from 2.5 mm in the case of Fontenla et al. (2009) to 0.3 mm in the Maltby et al. (1986) model (see Fig. 8). As reported in Sect. 3, none of the models investigated has the turnover wavelength in agreement with the 3.5 mm measurements, which show the umbra to be cooler than the quiet Sun at this wavelength, whereas all the models predict a brighter umbra at wavelengths longer than 3 mm.
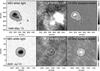 |
Fig. 11 Two observations of sunspots made with the Very Large Array radio telescope at 15 GHz. In both cases only the image in the sense of circular polarization that minimizes any contribution from gyroresonance emission (the “ordinary” mode) is shown. The upper panels compare a white light image from the MDI instrument on the SOHO satellite (left), showing the umbra and penumbra of a large sunspot observed on 1999 May 13, with a simultaneous 15 GHz image from the VLA in “D” configuration (middle, spatial resolution 5′′). The right panel shows what the VLA would have seen if the only emission were from the sunspot, i.e., the white-light image scaled linearly so that the darkest part of the umbra is 6000 K hotter than the surrounding atmosphere at 15 GHz. The lower panels show another comparison for a sunspot observed on 2001 July 15 when the VLA was in “C” configuration (resolution 2′′). Because the VLA “C” configuration is not sensitive to large structures, the model image in this case does not recover all the enhanced emission from the penumbra, but the umbra is well recovered. The actual and model radio images are displayed with a brightness temperature range of − 5000 to 5000 K relative to the background quiet-Sun level (the VLA is an interferometer and does not measure the absolute level). Contours mark sunspot umbrae and penumbrae. |
The difference between the predictions of the various models tends to increase rapidly towards longer wavelengths, making it attractive to observe at, say, 10 mm. However, it is more difficult to measure the umbral brightness-temperature offset at centimeter wavelengths because of the presence of additional contributions to the brightness temperature that are negligible at millimeter wavelengths: thus dense material in the solar corona above the chromosphere contributes optically thin thermal emission (brightness temperature ∝λ2) that can reach tens of thousands of K, and gyroresonance emission from strong magnetic fields in the umbra can reach coronal brightness temperatures (>106 K) at microwave wavelengths if the field strength is sufficiently high. Gyroresonance opacity is prominent only at low harmonics (2 or 3) of the electron gyrofrequency ΩB = 2.8 × 106B Hz, with B measured in G. The fact that the observed field strength rarely exceeds 4000 G (see, however, Livingston et al. 2006; van Noort et al. 2013, for exceptions) means that coronal gyroresonance emission is seldom seen above 20 GHz.
There have been a number of observations of large sunspots carried out with the Very Large Array (VLA) at 15 GHz (2 cm wavelength) that are suitable to investigate the umbral brightness temperature at centimeter wavelengths. At this frequency bright gyroresonance emission is often present, if at all, only in the sense of circular polarization that corresponds to the gyration motion of electrons about the electric field (the magnetoionic “extraordinary” mode), because the other polarization (the “ordinary” mode) requires a lower harmonic to produce significant opacity and therefore requires a higher magnetic field strength (2700 G for the 2nd harmonic) that is usually not present in the corona (e.g., see White & Kundu 1997).
Figure 11 shows two examples of VLA observations of sunspots at 15 GHz in the ordinary-mode polarization (in both cases bright gyroresonance sources are seen over the umbra in the opposite polarization). In the sunspot observed on May 13, 1999, optically thin thermal emission from dense coronal gas can be seen to the west-south-west of the sunspot with a brightness temperature of order 25 000 K (saturated in the figure). Fainter coronal contributions (1000–2000 K) can be seen to the south-west and east of the spot. These regions of emission match the distribution of denser coronal material seen in Extreme-Ultraviolet Imaging Telescope (EIT) Fe XII 195 Å images from the SOHO satellite. There is no clear bright or dark feature corresponding to the umbra of the sunspot. The noise level in regions away from the sunspot and from the bright coronal emission is 900 K. The spot of 2001 July 15 has no bright coronal emission near it (confirmed by inspection of the EIT 195 Å image): there is a small dark feature coincident with, but much smaller than the umbra that is 3000 K below the background level. The noise level in the VLA image is 800 K. Since the latter observation was carried out in the VLA’s “C”-configuration which is not sensitive to large sources, to confirm that the lack of an umbral feature is not an artefact of the observing conditions we modeled what the VLA would have seen in each case by assuming that the umbra should be 6000 K (a lower limit, from Fig. 9) brighter than the surrounding quiet Sun at 2 cm wavelength. We linearly scaled the corresponding white-light image accordingly, used it to generate model visibilities matching those used in the VLA observations, and then mapped those data exactly as for the real data. The results are shown in the right-hand column of Fig. 11, and they confirm that the absence of umbral features is not due to the observing conditions. The “C”-configuration model does indeed suggest that some of the penumbral emission is resolved out, but the bright umbral feature is recovered.
These examples are typical of VLA observations of sunspots at 15 GHz: when other contributions are sufficiently small so as not to obscure the umbra, the radio images at this frequency generally do not show a distinct feature (bright or dark) corresponding to the umbra, with an upper limit on the difference of order 1–2 thousand K. This result is again inconsistent with the umbral atmosphere models that predict that umbrae should be much brighter than the quiet Sun at centimeter wavelengths.
Once more among the considered models it is the model of Severino et al. (1994) that is in closest agreement with these data. However, we note that the inference here rests on the assumption that the brightness temperature surrounding the umbra in these radio images is truly representative of the quiet Sun and therefore corresponds to our reference model: given the additional contributions to brightness temperature at centimeter wavelengths, and the fact the VLA field of view at 15 GHz is only 3′, it is possible that the regions adjoining the umbra in our images are not truly representative of the quiet Sun. This should not be an issue in the case of the 2001 July 15 spot, which was isolated with very little coronal emission around it. However, pending better data, we emphasize that the results of this section are not yet definitive.
5. Conclusions
Millimeter brightness observations impose strong constraints on temperature and density stratifications of the sunspot atmosphere, in particular on the location and depth of the temperature minimum and the location of the transition region. Current submm/mm observational data suggest that existing sunspot models, including the models of Avrett (1981), Maltby et al. (1986), Obridko & Staude (1988), Socas-Navarro (2007) and Fontenla et al. (2009), fail to reproduce the millimeter observations and therefore are incomplete descriptions of the umbral atmosphere from the temperature minimum through the chromosphere up to the transition region. Only the model of Severino et al. (1994) lies within the error bars at all the wavelengths considered here.
From the analysis of the existing models we can conclude that a successful model that is in agreement with submm and mm umbral brightness should have an extended or/and deep temperature minimum (3000 K or below) as, for instance, in the models of Severino et al. (1994) and Fontenla et al. (2009).
Most atmospheric models are based on one-dimensional static atmospheres that try to reproduce observed umbral spectra. However, according to Fontenla (priv. comm.) there is an obvious reason why such 1D models will have difficulty. The atmosphere of a sunspot umbra is strongly irradiated from the sides by the penumbra in the walls produced by the Wilson depression, and this will affect the observed spectra. An example is the fact that Lyman-α has centrally-peaked profiles in the umbra but centrally-reversed profiles elsewhere (e.g., Tian et al. 2009): centrally-peaked profiles are expected if the umbral Lyα emission is dominated by scattered and redistributed emission coming in from the penumbral walls, rather than emission intrinsic to the umbral atmosphere. One-dimensional models cannot handle the complication introduced by scattering from a source with a different atmospheric structure. This implies that umbra is probably cooler and less dense than the current 1D models indicate, which is consistent with the fact that the radio data show the depression continuing to longer wavelengths than the 1D models suggest.
Due to the spatial resolution limit of 12′′ in the BIMA observations used here we are not able to fully resolve the umbra and cleanly separate it from penumbra. Therefore the results obtained in this work are preliminary. A detailed study of the appearance of sunspot umbrae at mm waves requires significantly higher spatial resolution. Furthermore, good wavelength coverage is needed for accurate diagnostics of the turnover wavelength, which is, in turn, required for the successful modeling of the sunspot atmospheric temperature structure based on mm-wavelength data. We place high expectations on the Atacama Large Millimeter/Submillimeter Array (ALMA), which has commenced Early Science observations. The current instrument wavelength range covers 0.4 to 3.6 mm and the field of view ranges from 8.5′′ at the shortest wavelengths to 72′′ at the longest wavelength. At the shortest wavelengths the single pointing field of view will be too small for umbral observations and the mosaicing observing mode will be essential to cover a sunspot together with surrounding quiet-Sun areas. With sub-arcsecond resolution and up to 66 antennas, ALMA will be an extraordinarily powerful instrument for studying the three-dimensional thermal structure of sunspots at chromospheric heights.
However, it is likely that the recalibrated magnetograms still significantly underestimate the total flux in the sunspot: see Ulrich et al. (2009).
Acknowledgments
We thank Gene Avrett and Juan Fontenla for valuable discussions and Giuseppe Severino for kindly providing his model.
References
- Avrett, E. H. 1981, in The Physics of Sunspots, eds. L. E. Cram, & J. H. Thomas (National Solar Obs., Sunspot, NM), 235 [Google Scholar]
- Avrett, E. H., & Loeser, R. 2008, ApJS, 175, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, T. S., Ewell, M. W., Jr., & Zirin, H. 1993, ApJ, 415, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Bock, D. C.-J., Bolatto, A. D., Hawkins, D. W., et al. 2006, Proc. SPIE, 6267, 13 [Google Scholar]
- Caccin, B., Gomez, M. T., & Severino, G. 1993, A&A, 276, 219 [NASA ADS] [Google Scholar]
- Curdt, W., Brekke, P., Feldman, U., et al. 2001, A&A, 375, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Balasubramaniam, K. S., & Harder, J. 2007, ApJ, 667, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Curdt, W., Haberreiter, M., Harder, J., & Tian, H. 2009, ApJ, 707, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Gingerich, O., Noyes, R. W., Kalkofen, W., & Cuny, Y. 1971, Sol. Phys., 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsey, C., & Kopp, G. 1995, ApJ, 453, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W., Harvey, J. W., Malanushenko, O. V., & Webster, L. 2006, Sol. Phys., 239, 41 [Google Scholar]
- Loukitcheva, M. 2005, Ph.D. Thesis, St.Petersburg University, Russia [Google Scholar]
- Loukitcheva, M., Solanki, S. K., Carlsson, M., & Stein, R. F. 2004, A&A, 419, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maltby, P., Avrett, E. H., Carlsson, M., Kjeldseth-Moe, O., Kurucz, R. L., & Loeser, R. 1986, ApJ, 306, 284 [Google Scholar]
- Mathew, S. K., Martínez Pillet, V., Solanki, S. K., & Krivova, N. A. 2007, A&A, 465, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagnibeda, V. G., & Piotrovitch, V. V. 1994, Sol. Phys., 152, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Obridko, V. N., & Staude, J. 1988, A&A, 189, 232 [NASA ADS] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Severino, G., Gomez, M. T., & Caccin, B. 1994, in Solar Surface Magnetism, eds. R. J. Rutten, & C. J. Schrijver (Dordrecht: Kluwer), 169 [Google Scholar]
- Socas-Navarro, H. 2007, ApJS, 169, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K. 2003, A&AR, 11, 153 [Google Scholar]
- Tian, H., Curdt, W., Teriaca, L., Landi, E., & Marsch, E. 2009, A&A, 505, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ulrich, R. K., Bertello, L., Boyden, J. E., & Webster, L. 2009, Sol. Phys., 255, 53 [NASA ADS] [CrossRef] [Google Scholar]
- van Noort, M., Lagg, A., Tiwari, S. K., & Solanki, S. K. 2013, A&A, 557, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, D., Zhang, M., Li, H., & Zhang, H. Q. 2009, Sol. Phys., 260, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Welch, W. J., Thornton, D. D., Plambeck, R. L., et al. 1996, PASP, 108, 93 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. M., & Kundu, M. R. 1997, Sol. Phys., 174, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, S., Loukitcheva, M., & Solanki, S. K. 2006, A&A, 456, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zheleznyakov, V. V. 1996, Radiation in Astrophysical Plasmas (Dordrecht: Kluwer Academic Publisher) [Google Scholar]
- Zlotnik, E. Ya. 1968, Sov. Astron., 12, 245 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Active region NOAA 10448 observed on August 31, 2003. a) BIMA image at 3.5 mm, b) MDI photospheric magnetogram and c) BBSO Ca ii K image. White contours mark sunspot umbrae and penumbrae. The box contains the region shown in Fig. 4 as a blowup. The zero brightness in the BIMA image corresponds to the weakest flux. |
| In the text | |
 |
Fig. 2 BBSO Ca ii K image and MDI photospheric magnetogram with the overlaid contours of 3.5 mm emission plotted as iso-intensity lines corresponding to 10, 20, 30, 40, 50, 60, 70% of maximum brightness. |
| In the text | |
 |
Fig. 3 a) MDI magnetogram in the range (− 200, 200) Gauss. The dotted and solid lines mark the 40 G and 26 G contours, corresponding to the quiet-Sun level at the original resolution of the magnetogram and at the resolution of the mm data, respectively. The white circle corresponds to the BIMA primary beam of 3′ by 3′ containing flux. b) The resulting quiet-Sun mask restricted to BIMA’s primary beam. Quiet-Sun areas are white. |
| In the text | |
 |
Fig. 4 A blowup of the sunspot region marked in Fig. 1. a) BIMA image at 3.5 mm, b) BBSO Ca ii K image at the original resolution and c) the Ca ii K image convolved to the resolution of the mm image (12′′). Thick white contours mark the locations of two umbrae. The other are iso-intensity lines corresponding to 10, 20, 30, 40, 50, 60, 70% of maximum brightness for the mm image and 30, 40, 50, 60, 70% of maximum brightness for the original and convolved calcium images. The zero brightness in the BIMA image corresponds to the weakest flux. |
| In the text | |
 |
Fig. 5 Horizontal cuts through the umbrae at y = 203.6′′ north of apparent solar disk center for BIMA image at 3.5 mm a), for BBSO Ca ii K image at the original resolution b) and at 12′′ resolution of the mm image c). Thick solid lines mark the location and size of the two umbrae. Thick dashed lines correspond to the potential reduction of the mm umbral brightness when going to 4′′ resolution. The QS level is indicated by the thin dotted lines. |
| In the text | |
 |
Fig. 6 a) Electron temperature as a function of height in a number of standard models of the solar chromosphere above a sunspot umbra. (i) The model of Avrett (1981), (ii) of Maltby et al. (1986), (iii) of Severino et al. (1994), (iv) of Socas-Navarro (2007), (v) of Fontenla et al. (2009). The thin solid black line (vi) is the reference quiet-Sun atmosphere of Fontenla et al. (1993) known as FAL − C. b) The electron number density as a function of height for the same models as shown in panel a). |
| In the text | |
 |
Fig. 7 Brightness-temperature contribution functions (with maxima normalized to unity) at 3 mm a) and at 1 mm b) for a number of sunspot models including the model of Avrett (1981) (dot-dashed curve), of Severino et al. (1994) (dashed curve), and of Fontenla et al. (2009) (dotted curve). For comparison the contribution function for the model FAL − C is shown with a thin solid black line. |
| In the text | |
 |
Fig. 8 Difference between the umbral brightness (in temperature units) and the QS brightness, plotted as a function of wavelength for the model (i) of Avrett (1981), (ii) model M of Maltby et al. (1986), (iii) of Severino et al. (1994), (iv) model A of Socas-Navarro (2007), (v) model S of Fontenla et al. (2009) and (vi) the two-component umbral model of Obridko & Staude (1988) employing a filling factor of 0.05 for the hot component. Filled and open circles mark the observational values obtained from BIMA maps at 3.5 mm for the big and small umbrae, respectively. Arrowheads mark the shift of umbral brightness when extrapolating to 4′′ resolution. Diamonds stand for the measurements from JCMT at 0.35, 0.85 and 1.2 mm made by Lindsey & Kopp (1995). |
| In the text | |
 |
Fig. 9 Absolute brightness temperature as a function of wavelength for the same umbral models as in Fig. 8. Also plotted is (viii) FAL − C model representing the Quiet Sun. |
| In the text | |
 |
Fig. 10 Normalized brightness temperature as a function of sunspot photospheric magnetic field strength for the model of Fontenla et al. (2009) for 1 mm (cross), 3.6 mm (asterisk), 6 mm (diamond) and 10 mm (triangle). |
| In the text | |
 |
Fig. 11 Two observations of sunspots made with the Very Large Array radio telescope at 15 GHz. In both cases only the image in the sense of circular polarization that minimizes any contribution from gyroresonance emission (the “ordinary” mode) is shown. The upper panels compare a white light image from the MDI instrument on the SOHO satellite (left), showing the umbra and penumbra of a large sunspot observed on 1999 May 13, with a simultaneous 15 GHz image from the VLA in “D” configuration (middle, spatial resolution 5′′). The right panel shows what the VLA would have seen if the only emission were from the sunspot, i.e., the white-light image scaled linearly so that the darkest part of the umbra is 6000 K hotter than the surrounding atmosphere at 15 GHz. The lower panels show another comparison for a sunspot observed on 2001 July 15 when the VLA was in “C” configuration (resolution 2′′). Because the VLA “C” configuration is not sensitive to large structures, the model image in this case does not recover all the enhanced emission from the penumbra, but the umbra is well recovered. The actual and model radio images are displayed with a brightness temperature range of − 5000 to 5000 K relative to the background quiet-Sun level (the VLA is an interferometer and does not measure the absolute level). Contours mark sunspot umbrae and penumbrae. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


