EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 560 (December 2013) A&A, 560 (2013) A60 Full HTML
Free Access
Issue
A&A
Volume 560, December 2013
Article Number A60
Number of page(s) 4
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201322389
Published online 06 December 2013

© ESO, 2013

1. Introduction

Chemical abundances in stellar atmospheres are key observational parameters in modern astrophysics and as a result, non-local thermodynamic equilibrium (non-LTE) modelling of stellar atmospheres is important for many fundamental problems (see, e.g., Lambert 1993; Asplund 2005; Barklem 2007; Bergemann et al. 2011; Barklem 2012). A non-LTE study requires detailed and complete information about the radiative and inelastic collision processes that affect the statistical equilibrium for a given atomic species. The most important collisions are ones with electrons and with H and H−. Atomic collisions are a main source of uncertainty for non-LTE studies owing to high concentrations of hydrogen atoms (Lambert 1993; Asplund 2005; Barklem 2012).

Considerable progress has recently been made in detailed quantum treatments of inelastic processes in collisions of H with atoms of different chemical elements. The accurate quantum cross sections were calculated for transitions between many low-lying atomic and ionic states for Na, Li, and Mg + H collisions (Belyaev et al. 1999, 2010; Croft et al. 1999b; Belyaev & Barklem 2003; Guitou et al. 2011; Belyaev et al. 2012) based on accurate ab initio or pseudopotential quantum-chemical data (Belyaev et al. 1999; Guitou et al. 2011, 2010; Croft et al. 1999a; Dickinson et al. 1999; Belyaev 2007). The excitation, de-excitation, ion-pair formation, and mutual neutralization processes have been studied in detail. The ion-pair formation and mutual neutralization processes belong to a general kind of charge exchange (charge transfer) reactions, and the names “ion-pair formation” and “mutual neutralization” indicate specific features of these processes1. The quantum cross sections from Belyaev et al. (1999, 2010, 2012), Croft et al. (1999b), Belyaev & Barklem (2003), Guitou et al. (2011) were used for computing the inelastic rates (Barklem et al. 2003, 2010, 2012) and finally for non-LTE astrophysical applications by Barklem et al. (2003), Lind et al. (2009, 2011), and Mashonkina (2013). It was shown that inelastic atomic collisions are important for non-LTE treatments.

For many atoms of interest, however, quantum cross sections for inelastic collisions with hydrogen atoms are still not available. For this reason, the so-called Drawin formula (Lambert 1993; Steenbock & Holweger 1984), which is an extension (Drawin 1968, 1969; Drawin & Emard 1973) of a classical Thomson model, is still widely employed for estimates of inelastic collision rates. Meanwhile, it has been shown by Barklem et al. (2011, see also references therein) that in case of low-energy atomic collisions, the Drawin formula does not have a correct physical background, overestimates inelastic rates up to several orders of magnitude for optically allowed atomic transitions, and underestimates rates for optically forbidden transitions. Scaling factors do not improve rates obtained by means of the Drawin formula. Variations in scaling factors are huge: For inelastic Mg + H collision rates a scaling factor was varied from 1 (Shimanskaya et al. 2000) up to 0.001 (Sundqvist et al. 2008) and even down to 3 × 10-10 (Zhao et al. 1998). Moreover, the Drawin formula provides incorrect relative efficiencies for different transitions: Even if a scaling factor is taken as a proper value for one transition, it does not provide reliable rates for other transitions. Obviously, using the Drawin formula is more or less equivalent to using a random number technique for inelastic collision rates, which is not physical. For this reason, Barklem et al. (2011) emphasized the importance of deriving an approximate approach to inelastic atomic collisions with hydrogen atoms, an approach that would be physically reliable, but computationally not as expensive as a complete quantum study.

Such a model approach has recently been proposed by Belyaev (2013) based on the asymptotic method for determination of molecular potential energies and on the branching probability current method for the nonadiabatic nuclear dynamics. The main goal of the approach is to calculate inelastic rates with high values and to estimate rates with moderate values, that is, rates of astrophysical interest. In the present paper, the approach is applied to low-energy inelastic Al + H and Al+ + H− collisions that are of interest for stellar atmosphere modelling (Andrievsky et al. 2008; Carretta et al. 2012).

2. Inelastic hydrogen-collision rates

The excitation, de-excitation, ion-pair formation, and mutual neutralization processes 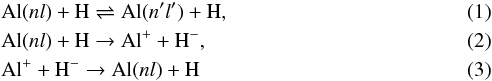are treated between the low-lying levels up to and including the ionic state. The treatment is performed within the Born-Oppenheimer (BO) approach based on a molecular state consideration, which is a standard for low-energy collisions. The BO approach treats inelastic collision processes in two steps: (i) electronic structure calculations for molecular states and (ii) nonadiabatic nuclear dynamical studies. In the present work, the inelastic rates for the processes (1)–(3) are calculated by means of the model that is derived within the BO approach and that simplifies both BO steps.

The model approach is described in detail elsewhere (Belyaev 2013), so only the main features are given below. The electronic structure calculations are performed by means of the asymptotic method. The long-range diabatic potentials are taken in the screened Coulomb form for the ionic state and are flat for covalent states; short-range contributions include exchange interactions and screened nuclear repulsion; the off-diagonal matrix elements are estimated by the semi-emperical formula from Olson et al. (1971). This approach allows one to calculate long-range adiabatic potentials, which are the main interest, and to estimate short-range potentials. The second step in the BO approach, the nonadiabatic nuclear dynamical treatment, is performed by means of the branching probability current method (Belyaev 2013), which is close to the branching classical trajectory method (Belyaev & Lebedev 2011) and based on the novel formula for a nonadiabatic transition probability within the Landau-Zener model. The novel formula allows one to calculate a nonadiabatic transition probability using only adiabatic potentials, while a complete quantal calculation requires information about nonadiabatic couplings as well.

The branching probability current method treats a collision as an evolution of probability currents in molecular states along the internuclear distance starting in the asymptotic region, going downwards to classical turning points, and then going out to the asymptotic region. In the quantum scattering theory, a probability current splits after a single traverse of a nonadiabatic region and this is taken into account by the branching probability current method. In each nonadiabatic region, a probability current branches into two currents in two neighbouring molecular states according to a nonadiabatic transition probability in this region. Finally, a single incoming probability current at a given collision energy and a given total angular momentum quantum number branches into many currents in all molecular states, proving transition probabilities, which allow one to calculate cross sections and rates. Only transitions between molecular states of the same symmetry (a symmetry of an ionic state) are taken into account, since they yield dominant contributions in inelastic rates with high values. Transitions due to rotational couplings are usually negligible at low energies (Belyaev et al. 1999; Guitou et al. 2011).

For the AlH hydride, the ground ionic state and the 15 lowest covalent states yielding the 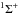molecular symmetry are taken into account resulting in adiabatic potentials (Belyaev 2013). As for many other hydrides, AlH exhibits a series of long-range avoided crossings due to the ionic-covalent interaction. The ten lowest atomic states have energies below the ionic limit, but only six of them produce covalent molecular states, Al(3p,4s,3d,4p,5s,nd)+H(1s), which when interacting with the ionic Al+ + H− state, create nonadiabatic regions resulting in large or at least noticeable inelastic cross sections and rates. Higher lying covalent-state potentials have avoided crossings with the ionic potential at internuclear distances greater than 100 au, resulting in negligible cross sections and rates for transitions between these states and the ionic one. For this reason only transitions between the seven low-lying states, including the six covalent states, Al(3p,4s,3d,4p,5s,nd)+H(1s), and the ionic state, Al+ + H−, are taken into account at present.

The calculated ground-state potential agrees perfectly with the accurate ab initio calculations performed by Wells & Lane (2011) for the short-range internuclear distances (R < 12 au). Since the semi-emperical formula (Olson et al. 1971) underestimates off-diagonal matrix elements at short distances, the two lowest model potentials are replaced by the ab initio potentials (Wells & Lane 2011), which have the avoided crossing at R = 7.8 au. To the best of our knowledge, no ab initio calculations for higher lying AlH(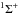) potentials have been performed2, although transitions between higher lying states, including the ionic one, are of the primary interest for astrophysical applications. On the other hand, the avoided crossings between higher lying covalent states and the ionic one take place at large internuclear distances where both the long-range diabatic potentials and the semiemperical formula (Olson et al. 1971) are reliable: The formula has been applied to a large number of charge transfer processes, including various mutual neutralization ones, and found to yield physically correct results. Thus, the model approach provides reliable long-range potentials. Short-range potential uncertainties, which might affect nonadiabatic transitions mainly at high energies, are taken into account within the extended model (see below and Belyaev 2013).

Table 1

Rate coefficients ⟨ σv ⟩, in units of cm3/s, for selected temperatures in the range T = 1000–10 000 K, for the excitation, de-excitation, ion-pair formation, and mutual neutralization processes (1)–(3).

The calculated potentials allow one to specify the nonadiabatic regions and determine nonadiabatic parameters needed for a nonadiabatic nuclear dynamics. At present, the dynamical study is done by means of the branching probability current method (Belyaev 2013). The inelastic cross sections and the rates are calculated for all transitions between the seven low-lying levels up to and including the ionic state, namely Al(3p,4s,3d,4p,5s,nd) + H(1s) and Al+ + H− (for details see Belyaev 2013). The calculated rates are presented in Table 1. The calculations were performed at two levels. At the first level, the simple model, only the long-range nonadiabatic regions due to the covalent-ionic interaction are included. This level provides low-limit estimates for inelastic rates. At the second level, the extended model, additional short-range nonadiabatic regions are taken into account as well. The presence of these additional regions are justified by physical arguments, though nonadiabatic parameters of these regions are determined by the model with less accuracy than the long-range regions. Inelastic rates with highest values are not changed by including short-range regions, while rates with low-to-moderate values can increase substantially but may not exceed moderate values. The rates obtained by the extended model are expected to be physically reliable and are collected in Table 1. To the best of our knowledge, there are no experimental or quantum data available for these collisions to compare with.

3. Discussion and conclusion

The analysis of the calculated cross sections and rates allows one to divide the treated processes into three groups. The first group consists of the processes with high values of cross sections and rates, roughly with cross sections larger than 1 Å2. The largest cross sections and rates (up to 20 Å2 and 10-9 cm3/s, respectively, for endothermic processes) correspond to the excitation and de-excitation processes between the Al(3d) and Al(4p), as well as the ion-pair formation and mutual neutralization processes involving the Al(3d), Al(4p), Al(4s) and ionic states. These inelastic processes are based on nonadiabatic transitions due to the ionic-covalent interaction at large internuclear distances. For these processes, a presence of additional nonadiabatic regions at short-to-intermediate internuclear distances (roughly, shorter than 10 au) hardly affects the cross sections obtained by means of the simple model based only on long-range regions. The parameters of the long-range nonadiabatic regions are well-defined by the model, so the calculated estimates for the corresponding cross sections and rates are expected to be accurate within a factor of 2−3. This fluctuation factor is taken from Miller & Morgner (1977) for the accuracy of using the semi-empirical formula (Olson et al. 1971). The inelastic processes involving the states from this group are expected to be important for astrophysical applications.

The second group includes processes with small-to-moderate cross sections and rates, the processes involving the Al(5s) and Al(nd) states, as well as higher lying states. For these states, the long-range nonadiabatic regions formed by the ionic-covalent interaction provide small cross sections and rates, if only these regions are taken into account. A presence of short-range nonadiabatic regions between these covalent states increases cross sections up to several orders of magnitude, but short-range transitions yield only moderate values for inelastic cross sections, typically not exceeding 10-3−1 Å2, and the increase is more significant at high collision energies while the main astrophysical interest is in low energies. The presence of short-range nonadiabatic regions is justified by physical reasons and provides substantial values for cross sections either via a direct covalent-transition mechanism for excitation and de-excitation processes involving these states, or via the loop mechanism (Belyaev et al. 2012) for the processes involving the ionic state. The estimates for this group are believed to be reliable within a factor of 2−10. This range is estimated from the factor of Miller & Morgner (1977), as well as from the comparison with the available quantum results for other collisions. The processes from this group have some effects in astrophysical applications.

The third group consists of the processes with negligible values of rates, lower than 10-20 cm3/s. Low-lying states (including the ground state) are typically in this group. Adiabatic potentials of low-lying molecular states usually have large energy gaps, so nonadiabatic transition probabilities are very low. Including additional nonadiabatic regions can increase them by several orders

of magnitude, but they are still negligible. These processes are unimportant for astrophysical applications.

It should be emphasized that although the present findings are based on the results of the particular case of Al + H and Al+ + H− collisions, the derived model and the conclusions are general. In particular, the derived model explains the results of quantum calculations for the inelastic processes in low-energy collisions Li + H (Croft et al. 1999a,b), Na + H (Belyaev et al. 2010), and Mg + H (Belyaev et al. 2012), and it can be used for estimates of inelastic cross sections and rates for other collisions.

1

The ion-pair formation process A∗ + H → A+ + H− should not be confused with the ionization process A∗ + H → A+ + H + e−.

2

Some additional estimates have been obtained by I. C. Lane (unpublished) for the 3   1Σ+ potential, which agrees with the model potential.

Acknowledgments

The author thanks Dr. P. S. Barklem for fruitful discussions and Dr. I. C. Lane for providing the ab initio AlH quantum-chemical data. The work was supported by the Wenner-Gren Foundation (Sweden), by the Max-Planck Institute for Astrophysics at Garching (Germany), and by the Russian Foundation for Basic Research (Grant No. 13-03-00163-a).

References

  1. Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2008, A&A, 481, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barklem, P. S. 2007, A&A, 466, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Barklem, P. S. 2012, J. Phys. Conf. Ser., 397, 012049 [NASA ADS] [CrossRef] [Google Scholar]
  5. Barklem, P. S., Belyaev, A. K., & Asplund, M. 2003, A&A, 409, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Barklem, P. S., Belyaev, A. K., Dickinson, A. S., & Gadéa, F. X. 2010, A&A, 519, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Barklem, P. S., Belyaev, A. K., Guitou, M., et al. 2011, A&A, 530, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Barklem, P. S., Belyaev, A. K., Spielfiedel, A., et al. 2012, A&A, 541, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Belyaev, A. K. 2007, Eur. Phys. J. D, 44, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Belyaev, A. K. 2013, Phys. Rev. A, 88, 052704 [NASA ADS] [CrossRef] [Google Scholar]
  11. Belyaev, A. K., & Barklem, P. S. 2003, Phys. Rev. A, 68, 062703 [NASA ADS] [CrossRef] [Google Scholar]
  12. Belyaev, A. K., & Lebedev, O. V. 2011, Phys. Rev. A, 84, 014701 [NASA ADS] [CrossRef] [Google Scholar]
  13. Belyaev, A. K., Grosser, J., Hahne, J., & Menzel, T. 1999, Phys. Rev. A, 60, 2151 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  14. Belyaev, A. K., Barklem, P. S., Dickinson, A. S., & Gadéa, F. X. 2010, Phys. Rev. A, 81, 032706 [NASA ADS] [CrossRef] [Google Scholar]
  15. Belyaev, A. K., Barklem, P. S., Spielfiedel, A., et al. 2012, Phys. Rev. A, 85, 032704 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bergemann, M., Lind, K., Collet, R., & Asplund, M. 2011, J. Phys. Conf. Ser., 328, 012002 [NASA ADS] [CrossRef] [Google Scholar]
  17. Carretta, E., D’Orazi, V., Gratton, R. G., & Lucatello, S. 2012, A&A, 543, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Croft, H., Dickinson, A. S., & Gadéa, F. X. 1999a, J. Phys. B, 32, 81 [NASA ADS] [CrossRef] [Google Scholar]
  19. Croft, H., Dickinson, A. S., & Gadéa, F. X. 1999b, MNRAS, 304, 327 [NASA ADS] [CrossRef] [Google Scholar]
  20. Dickinson, A. S., Poteau, R., & Gadéa, F. X. 1999, J. Phys. B, 32, 5451 [NASA ADS] [CrossRef] [Google Scholar]
  21. Drawin, H.-W. 1968, Z. Phys., 211, 404 [Google Scholar]
  22. Drawin, H.-W. 1969, Z. Phys., 225, 483 [Google Scholar]
  23. Drawin, H.-W., & Emard, F. 1973, Phys. Lett. A, 43, 333 [NASA ADS] [CrossRef] [Google Scholar]
  24. Guitou, M., Spielfiedel, A., & Feautrier, N. 2010, Chem. Phys. Lett., 488, 145 [NASA ADS] [CrossRef] [Google Scholar]
  25. Guitou, M., Belyaev, A. K., Barklem, P. S., et al. 2011, J. Phys. B, 44, 035202 [NASA ADS] [CrossRef] [Google Scholar]
  26. Lambert, D. L. 1993, Phys. Scr., T, 47, 186 [Google Scholar]
  27. Lind, K., Asplund, M., & Barklem, P. S. 2009, A&A, 503, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2011, A&A, 528, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Mashonkina, L. 2013, A&A, 550, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Miller, W. H., & Morgner, H. 1977, J. Chem. Phys., 67, 4923 [NASA ADS] [CrossRef] [Google Scholar]
  31. Olson, R. E., Smith, F. T., & Bauer, E. 1971, Appl. Opt ., 10, 1848 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. Shimanskaya, N. N., Mashonkina, L. I., & Sakhibullin, N. A. 2000, Astron. Rep., 44, 530 [NASA ADS] [CrossRef] [Google Scholar]
  33. Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 [NASA ADS] [Google Scholar]
  34. Sundqvist, J. O., Ryde, N., Harper, G. M., et al. 2008, A&A, 486, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Wells, N., & Lane, I. C. 2011, Phys. Chem. Chem. Phys., 13, 19018 [CrossRef] [Google Scholar]
  36. Zhao, G., Butler, K., & Gehren, T. 1998, A&A, 333, 219 [NASA ADS] [Google Scholar]

All Tables

Table 1

Rate coefficients ⟨ σv ⟩, in units of cm3/s, for selected temperatures in the range T = 1000–10 000 K, for the excitation, de-excitation, ion-pair formation, and mutual neutralization processes (1)–(3).

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.