| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322165 | |
| Published online | 29 November 2013 | |
Long gamma ray bursts from binary black holes
1 Center for Theoretical Physics, Polish Academy of Sciences, Al. Lotnikow 32/46, 02-668 Warsaw, Poland
e-mail: agnes@cft.edu.pl
2 Faculty of Mathematics and Natural Sciences, Cardinal Stefan Wyszyński University, ul. Wóycickiego 1/3, 01-938 Warsaw, Poland
e-mail: szycha@cft.edu.pl
3 Copernicus Astronomical Center, Bartycka 18, 00-716 Warsaw, Poland
e-mail: bejger@camk.edu.pl
Received: 28 June 2013
Accepted: 17 October 2013
Aims. We consider a scenario for the longest duration gamma ray bursts, resulting from the collapse of a massive rotating star in a close binary system with a companion black hole (BH).
Methods. The primary BH born during the core collapse is first being spun up and increases its mass during the fallback of the stellar envelope just after its birth. As the companion BH enters the outer envelope, it provides an additional angular momentum to the gas. After the infall and spiral-in toward the primary, the two BHs merge inside the circumbinary disk.
Results. The second episode of mass accretion and high final spin of the postmerger BH prolongs the gamma ray burst central engine activity. The observed events should have two distinct peaks in the electromagnetic signal, separated by the gravitational wave emission. The gravitational recoil of the burst engine is also possible.
Key words: accretion, accretion disks / black hole physics / gravitational waves / gamma-ray burst: general
© ESO, 2013
1. Introduction
Gamma ray bursts are transient sources of extreme brightness observed on the sky with isotropic distribution. Their prompt phase lasts between a fraction of a second and few hundreds seconds, and the long-duration events are believed to originate from collapsing massive stars. In the collapsar model, a newly-born black hole (BH), surrounded by a transient disk accreting a part of the fallback stellar envelope, helps launch relativistic jets (Woosley 1993; MacFadyen & Woosley 1999). These polar jets give rise to gamma rays produced far away from the engine in the circumstellar region (see, e.g., the reviews by Zhang & Mészáros 2004, Piran 2004). The model is supported by observed associations of many gamma ray bursts with bright supernovae (Woosley & Bloom 2006). These are the brightest I b/c type explosions of the so-called “hypernovae”, which constitute about 10% of this class (Fryer et al. 2007). What seems to be most important for a pre-supernova star to become a GRB progenitor, is its high rate of differential rotation (Podsiadlowski et al. 2004). The massive stars that are progenitors of GRBs go through the stage of a Wolf-Rayet (WR) star (Crowther 2007) at the end of their lives. Such a star may be spun up by the interaction in a binary system. In addition, the loss of angular momentum through the stellar wind may be avoided when the metallicity of the star is sufficiently low (Yoon & Langer 2005; Svensson et al. 2010).
A possible configuration in the binary star evolution history would be a close binary that consists of a massive OB star and a compact remnant resulting from an earlier core collapse. A system, such as a high-mass X-ray binary (Wellstein & Langer 1999), evolves to form a WR star–BH binary, such as the well known Cyg X-3 system discovered in our Galaxy (van Kerkwijk et al. 1992), or the extragalactic sources IC 10 X-1 and NGC 300 X-1 (Bauer & Brandt 2004; Carpano et al. 2007). Here, we consider the final stage of evolution of such a binary in which the BH ultimately enters the massive star’s envelope and spins it up (essentially, a common envelope phase of the binary). This process triggers the collapse of the core, possibly via the tidal squeezing interaction (Luminet & Marck 1985), and may provide an additional source of power to the GRB event. Similar scenarios were proposed in the past, for example by Zhang & Fryer (2001) and Barkov & Komissarov (2010), in which three phases can be distinguished: the spiral-in of the BH inside the envelope, possibly with a spherical accretion of some surrounding gas and transfer of orbital angular momentum into the envelope; an increase of the accretion rate through the high angular momentum shells of matter onto the BH residing already, or newly born, in the center (see Chevalier 2012 for a description of a collapse event triggered by the inspiral of a compact object to the central core of the companion star); and final accretion of the remaining gas during the ultimate GRB explosion accompanied by the jet ejection. In addition to the electromagnetic signal, such a process is followed by a characteristic gravitational-wave signal due to the collapse of the core into the BH, but mostly because of the binary BH inspiral and merger.
This article is composed as follows: Sect. 2 describes the models used to estimate the basic parameters of the process. Sect. 2.1 describes a model of the BH surrounded by a torus. Section 2.2 describes the homologous accretion without mass loss, whereas Sect. 2.3 considers the case of strong winds during the accretion of the in-falling shells. Section 2.4 pulls together the various premerger scenarios. The model of the binary BH merger is described in Sect. 3. Section 4 contains discussion and conclusions.
Throughout the text, the subscript 1 denotes the primary BH, a result of the collapse of the primary component in the binary system. Subscript 2 denotes the companion BH, whereas subscript 3 marks the final BH, which results from a merger of two BHs.
2. Collapsing star with a companion black hole
2.1. Model of a BH surrounded by a torus
First, we test the predictions of a model of a collapsing star that encounters a companion BH. We use a simple “toy model” calculation to quantify the behavior of the rotating BH in the center of the collapsing star and an accreting torus embedded in its envelope. We focus on the evolution of the BH spin and changes in the accretion rate within the torus to make predictions about the duration and power available for the gamma ray burst.
The primary component is a collapsing star, whose iron core has just formed a central BH of mass M1,init. The distribution of density in the envelope is the same as used in Janiuk et al. (2008), and is taken from the spherically symmetric presupernova star of a mass of 25 M⊙ (Woosley & Weaver 1995). The size of the star is Rout ≈ 6 × 1013 cm, so the free-fall timescale from this radius is about tff ≈ 107 s. The rotation of the stellar envelope leads to formation of the torus, i.e., high angular momentum shells located in the equatorial plane, that will subsequently accrete onto the core. The specific angular momentum distribution is in general given by 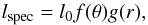 (1)where the normalization is scaled to the critical angular momentum, l0/lcrit = x. We express lcrit as
(1)where the normalization is scaled to the critical angular momentum, l0/lcrit = x. We express lcrit as 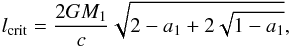 (2)where a1 is the primary BH dimensionless spin parameter. The above equation specifies the condition for the formation of a disk with the angular momentum exceeding that of the marginally-bound orbit (Bardeen et al. 1972). The dependence on polar angle θ is
(2)where a1 is the primary BH dimensionless spin parameter. The above equation specifies the condition for the formation of a disk with the angular momentum exceeding that of the marginally-bound orbit (Bardeen et al. 1972). The dependence on polar angle θ is 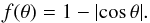 (3)In the present model we only take into account differential rotation, i.e., we neglect the radial dependence (see Janiuk & Proga (2008) for a discussion of other rotation laws).
(3)In the present model we only take into account differential rotation, i.e., we neglect the radial dependence (see Janiuk & Proga (2008) for a discussion of other rotation laws).
Both mass and spin of the primary BH change during the collapse of the envelope as the massive shells accrete onto the center. The BH absorbs only the angular momentum of the gas, which is smaller than the critical value. The rotating torus, however, is supported by the gas which has a larger angular momentum than the critical. The value of lcrit changes during the collapse, affecting the evolution of the BH spin and conditions for the existence of the torus.
We then introduce a secondary (companion) BH of a mass M2 and negligible spin, falling into the envelope of the primary star at the onset of its collapse. As the companion BH moves from the radius r to r − Δr inside the envelope, it transfers its specific orbital angular momentum to the shells: 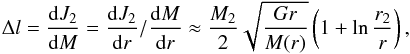 (4)where M(r) is the mass of the envelope inside the radius r. We assume here that the companion BH orbital angular momentum is Keplerian,
(4)where M(r) is the mass of the envelope inside the radius r. We assume here that the companion BH orbital angular momentum is Keplerian, 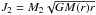 (see Barkov & Komissarov 2010). In addition, we assume explicitly that the companion enters the envelope close to the equatorial plane so that the specific angular momentum is transferred as lspec = lspec + Δlf(θ).
(see Barkov & Komissarov 2010). In addition, we assume explicitly that the companion enters the envelope close to the equatorial plane so that the specific angular momentum is transferred as lspec = lspec + Δlf(θ).
2.2. Homologous accretion without mass loss
First, we analyze the simplest scenario, where the whole envelope collapses via homologous accretion of subsequent shells. Therefore, not only the high angular momentum, but also the low lspec gas contributes to the BH evolution.
Figure 1 shows the evolution of the BH spin with time. The time is calculated as a free-fall time of the envelope shell that surrounds the central BH of mass M BH(t). We show two examples of the specific angular momenta of the envelope parameterized by x = lspec/lcrit = 1.5 (solid lines) and x = 7.0 (dashed lines).
 |
Fig. 1 Evolution of the primary BH spin during the collapse of the stellar envelope. Blue lines are for a1,init = 0.1 and red lines for a1,init = 0.85. The solid and dashed lines show the models with the envelope’s angular momentum normalized with x = lspec/lcrit = 1.5 and 7, respectively. The model assumes homologous accretion of the envelope shells onto the BH and no wind. The envelope is spun up by the companion BH of a mass M2 = 3 M⊙. The time is given as the free-fall timescale, so it scales with M1. |
Initially, the BH spin grows in a short timescale due to accretion of high angular momentum material from the rotating torus. Afterwards the spin decreases, sometimes even below the initial value. This is due to accretion of low angular momentum gas, i.e., gas with lspec smaller than the critical value lcrit for a current BH mass and spin (Janiuk et al. 2008). If the spin-up of the envelope is neglected, the rotationally-supported torus is present only temporarily. Here, however, the companion spins up the envelope again, so that high angular momentum gas is available to spin up the primary BH. Finally, the furthest shells of the envelope collapse onto the center. The duration of this episode is not sensitive to the initial BH spin and angular momentum normalization. The latter affects the minimum spin of the primary BH during this episode, and in our examples it is roughly a1,min = 0.4 − 0.5 for x = 1.5, and roughly a1,min = 0.9 − 0.95 for x = 7.0. In any case, at the end of the collapse the primary BH will spin at nearly the maximum rate.
Our calculations show two accretion episodes. The first lasts up to a few hundred seconds, depending on the angular momentum in the envelope, x, and the primary BH spin a1,init. The accretion rate in the torus is initially almost 0.1 M⊙ s-1, but steeply decreases following the density profile of gas in the subsequent shells of the envelope. The second accretion episode begins at ~500 s and is governed by the presence of the companion. This episode lasts until the whole envelope has collapsed; the accretion rate (estimated simply as Δmtorus/Δt) now rises to above 1 M⊙ s-1 because of the larger mass available in the shells.
2.3. Torus accretion with mass loss
In the above section, the accretion rate was estimated using the free-fall timescale. Primary BH was spun up to a maximum rotation, practically regardless of its initial spin. Moreover, the homologous accretion of shells led to the effective increase of the BH mass and at the end of the simulation it simply equals the initial mass of the precollapse star.
Now, we consider a more realistic scenario: when accretion onto the primary BH proceeds through a thick, viscous disk and a substantial fraction of the envelope mass is not accreted, but lost to the massive winds. Such winds were discussed in (MacFadyen & Woosley 1999) and have also been found in numerical simulations by McKinney (2006), who report on their mildly relativistic velocities and intermediate opening angles. In our recent work (Janiuk et al. 2013; Janiuk & Moscibrodzka 2012), we also studied the neutrino cooled disk/winds in the GRB central engine via the magnetohydrodynamical simulations of accretion. We found that the mass taken away by the winds and not accreted onto the BH through the event horizon might reach a fraction of as much as 50−72%. This fraction depends on the parameters such as BH mass and spin, and might also be sensitive to the adopted initial distribution of the specific angular momentum in the gas. These winds are launched by the magnetic pressure and are bright in neutrinos that cool the central engine. We checked that for some models the winds appear to be bound, so that they would actually result in some large-scale circularization movements. However, for other models the wind velocity exceeds the escape velocity. The mass loss of 72% must therefore be treated as an upper limit.
Here, we assume a fiducial value of a maximum fraction of the wind mass loss, so that the mass accreted onto the primary BH is 28% of the shell, the remaining fraction being lost from the system.
The viscous timescale in the accretion disk is given by 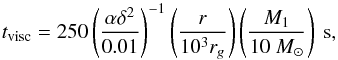 (5)where α is the viscosity parameter, and M BH and rg are the BH mass and gravitational radius, respectively. The ratio of disk thickness to radius h/r ≡ δ can be estimated from the model of a neutrino cooled disk in the GRB central engine (Janiuk & Yuan 2010); it is about 0.1 − 0.3 for the neutrino transparent (low accretion rate) models.
(5)where α is the viscosity parameter, and M BH and rg are the BH mass and gravitational radius, respectively. The ratio of disk thickness to radius h/r ≡ δ can be estimated from the model of a neutrino cooled disk in the GRB central engine (Janiuk & Yuan 2010); it is about 0.1 − 0.3 for the neutrino transparent (low accretion rate) models.
In Fig. 2, we plot the BH mass, accretion rate, and BH spin as a function of time. The time is expressed in viscous timescale of the accreting torus at the distance r from the center. The final BH spin in this model is always maximal and is reached very quickly after the onset of accretion. In this scenario, most of the envelope’s mass is blown out with the wind and not accreted onto the BH, while some of the matter is accreted but it contributes to the primary BH spin up more than to its mass increase. We assume that 72% of the envelope’s mass was ejected with the massive wind outflow.
 |
Fig. 2 Mass of the primary BH (top), accretion rate (middle), and the primary BH spin (bottom panel) as a function of time during the accretion of the viscous torus. In the top panel, the model assumes the specific angular momentum in the envelope: x = 1.5 to compare two cases: either 28% of the torus mass (solid line) and the rest is blown out, or its total mass (dashed line) is fully accreted. In the middle and bottom panels, the models assume the wind outflow, and the two lines show the cases with different angular momentum: x = 1.5 (solid) and x = 7.0 (dotted). |
The mass of the central BH grows as long as the torus exists. The torus is supported by both the specific angular momentum in the envelope and by the companion. For the smallest lspec normalization we have tested, x = 1.5, with no companion, we obtained M1,final = 4.4 M⊙ at the end of the simulation. The result is for the particular precollapse star density distribution and depends on the assumed fraction of the torus mass taken out by the wind. If no wind outflow was assumed, and the whole torus mass was accreted onto the BH, then its final mass was M1,final = 8.4 M⊙. This value is very weakly dependent on the angular momentum distributions in the stellar envelope.
We calculate the instantaneous accretion rate (middle panel of Fig. 2) in the torus as the ratio between the mass of an accreting shell and the local viscous timescale, ṁ = δmtorus/δtvisc. Initially, the accretion rate peaks at about 0.01 M⊙ s-1, for a large specific angular momentum in the envelope. The second peak in the accretion rate lasts much longer, but the accretion rate is lower than during the first peak because of a lower density of the accreted material. Finally, the accretion rate drops below 10-4 M⊙ s-1 even though the torus persists because of lower density and long viscous timescale.
The accretion in the torus proceeds through three episodes, as shown in Fig. 3. The figure shows the mass of a given accreting shell versus the free-fall timescale at the initial distance of this shell. The shells that are closest to the center have their free-falling timescales below ~900 s and masses up to 0.15 M⊙. The exact value of the shell mass, which is contained within the rotationally supported torus, is sensitive to the magnitude of specific angular momentum (the figure shows three different lines for x = 1.5, 3.0, and 7.0). The total shell mass (i.e., torus plus polar regions) is the same for any x, nevertheless, it is still governed by the onion-like distribution of the elements in the envelope. This leads to the two distinct peaks.
 |
Fig. 3 Mass of the envelope shell as a function of the free-fall time. The green solid line is the total mass in the shell, while the red lines corresponds to the mass contained in the rotationally supported torus. Here, the solid, long dashed and short dashed lines show the models with the specific angular momentum normalized with x = 1.5, 3, and 7, respectively. All models assume that 28% of the stellar envelope is accreted onto the BH, and the rest of the mass is evacuated as a massive wind. |
The outer shells are made of lighter elements and are less dense; their mass increases only due to the larger volume. Because the outermost envelope is first spun up by the companion, the effect of the intrinsic angular momentum distribution is not important and basically the entire outer envelope contributes to the rotationally supported torus. Therefore, the third accretion episode is the fallback of the material from the outer shells spun up by the companion and rotating in the torus.
2.4. Summary of the premerging scenarios
We considered the scenarios of a homologous or torus accretion onto the newly-formed BH in the core of the primary star. We tested a range of angular momentum normalizations in the envelope. We also included the possibility of the wind taking away most of the mass from the rotationally supported torus. In this scenario, the BH mass grows more slowly, however, its spin is still growing very quickly to the maximum limit, regardless of the initial value of the stellar core rotation.
Due to the accretion of the inner shells of the star’s envelope onto the core, the primary BH mass increases to M1,final and the spin obtains the value of a1,final. These values are checked at the time when the companion BH approaches the primary core to the shell thet have already been accreted (i.e., r2(tfinal) = rk and k is the number of the currently accreting shell). In our model, this moment corresponds to the distance of r2 = 1011 cm and the free-fall timescale at this distance is tfinal ~ 530 s (scaling with mass M1).
In the homologous accretion scenario, the primary BH mass is at tfinal equal to about M1,final = 9 M⊙ for our assumed progenitor star model. This value is independent on the initial core rotation rate and specific angular momentum distribution in the envelope. If the initial spin is a1,init = 0.5, it temporarily drops due to the in-fall of low angular momentum material, and then increases. The final value of the spin, for a moderately rapid rotation in the envelope, given by our parameter x = 3, is about a1,final = 0.69.
This primary BH then merges with the companion and we assume its mass of M2 = 3 M⊙ and negligible spin. After the merger, the remaining mass of the envelope, which in this example is equal to about Menv(tfinal) ~ 16 M⊙, accretes onto the product of the merger.
The second scenario is the accretion through the viscous, rotationally supported torus onto the primary BH, under the assumption that most of the material is blown out with a massive wind. We assume that only 28% of mass accretes onto the core and contributes to its growing mass and spin. The resulting BH will nevertheless be spinning at the maximum rate, as all the accreting material has large specific angular momentum. The mass of the primary BH after this accretion episode is about M1,final = 3.8 M⊙. As the companion BH mass is again assumed 3 M⊙, the final BH is produced of a merger of two comparable mass BHs. The product M3 subsequently accretes the remaining envelope. The mass of the gas available for accretion in the final episode is in this example equal to about 6 M⊙.
In both scenarios outlined above, the mass of the final BH, M3, and the remaining torus mass are comparable. We do not follow this final accretion process numerically here, as it would require enormous computational power to run a full general relativistic magnetohydrodynamic simulation in a nonstationary metric. In the stationary Kerr metric, such simulations of accretion onto a single BH have recently been shown elsewhere (e.g., McKinney et al. 2012). We aim, however, to treat the binary BH merger process in more detail. In that case, the merger timescale is much shorter than the timescale of accretion of the distant torus, and may be treated separately from the surrounding matter, i.e., in the vacuum approximation. Below we present several of our numerical simulations, focusing in particular on the two distinct scenarios that led to different initial parameters of the merging BHs.
Summary of the binary BH merger models.
3. Binary black hole merger
3.1. Physics of the model
The simulation covers the very last stage of the evolution of binary BH system, when the separation of the components becomes so small that the phases of inspiral, merger, and ringdown can be tracked. This is the stage of the evolution for which the full set of Einstein equations needs to be solved numerically to model the geometry of spacetime to obtain reasonable results.
The initial state of the system under consideration consists of two BHs in quasicircular orbits with mass ratio varying from 2 to 3. The more massive BH also carries spin perpendicular to the orbital plane, and the second component is spinless. The direction of the initial spin vector of the BH coincides with the direction of the orbital angular momentum of the binary system.
We performed several runs of simulations for different values of spin of the rotating BH. The parameters for each run are presented in Table 1. The initial separation of components is the same for each run and is equal to 6M, where the value of M is close to the Arnowitt, Deser and Misner (ADM) mass of the whole system (Arnowitt et al. 1959), defined as the mass measured by a distant observer in an asymptotically flat space time.
Despite the fact that we do not change mass parameters of punctures representing BHs (for numerical details see next section) for each run, the ADM mass of the system varies, since we vary the spin that contributes to the total ADM mass. This is a known property of rotating BHs, for example, for the analytical Kerr solution we have: 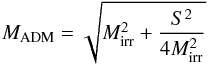 (6)where MADM is the ADM mass, S is the spin of BH, and Mirr is the irreducible mass, namely the mass related to the area of the event horizon (the mass of nonrotating BH with the same area of event horizon, for more details see Misner et al. 2003).
(6)where MADM is the ADM mass, S is the spin of BH, and Mirr is the irreducible mass, namely the mass related to the area of the event horizon (the mass of nonrotating BH with the same area of event horizon, for more details see Misner et al. 2003).
3.2. Numerics
We use the fifth release of the Einstein Toolkit1 (Löffler et al. 2012) based on the Cactus Computational Toolkit (Goodale et al. 2003).
The initial data are provided by the TwoPunctrures thorn (Ansorg et al. 2004). This module numerically solves the binary puncture equations for a pair of BHs (Brandt & Brügmann 1997). The initial state of space time is described by the extrinsic curvature in the Bowen-York form (Bowen & York 1980), for a given mass, momentum, and spin of each puncture. These are the controlled parameters in the first section of Table 1.
The evolution is performed by the McLachlan module (Brown et al. 2009), which is a numerical implementation of the 3 + 1 split of Einstein equations, solving the Cauchy initial value problem using the Baumgarte-Shapiro-Shibata-Nakamura (BSSN) method (Shibata & Nakamura 1995; Baumgarte & Shapiro 1999; Alcubierre et al. 2000).
The simulation is performed on the cartesian grid with the size of 60 × 60 × 60M and resolution of dx = dy = dx = 2M (runs R1−R7 in Table 1), or the size of 48 × 48 × 48M and resolution of dx = dy = dz = 1.6 (runs R8 and R9). We use seven levels of the adaptive mesh refinement in two regions around singularities. Each refinement is by a factor of two and the radii of refinement regions are: 0.5, 1, 2, 4, 8, and 16 around each singularity. The regions of refined grid follow the positions of singularities (Schnetter et al. 2004). We assume that the space time has a reflection symmetry with respect to the plane spanned by the initial momenta of components of the BH binary system, which reduces the number of grid points by a factor of two. The apparent horizons are localized around the components of the BH system and around the final merged black hole after it forms (Thornburg 2004). The proper integrals over the isolated horizons are calculated to extract the values of mass and spin of the merged BH (Dreyer et al. 2003).
In all simulations, we note the effect of gravitational recoil of the final BH. This effect is illustrated in Fig. 4. This is a known effect, see, for example, Tichy & Marronetti (2007). The calculation of the exact value of the recoil speed requires the evaluation of the momentum carried away by the gravitational radiation during the merger. We did not analyze the gravitational radiation in the first series of simulations performed. To estimate the recoil speed, we have done a last run of the simulation (R9 in the Table 1) once again ancluding an analysis of radiation. To calculate the total momentum carried by radiation, we have followed the algorithm described by Alcubierre (2008). We use the formula for dP/dt in terms of coefficients Alm of multipole expansion of the Weyl scalar ψ4. The coefficients Alm are computed by the thorns WeylScal4 and Multipole on the sphere of radius 22M and l ranging from 2 to 4. We integrate dP/dt over the time of the simulation to get total linear momentum radiated from the system through gravitational waves. Since total momentum has to be conserved we are able to compute the recoil of the merged BH.
3.3. Results
The results of the simulations are presented in Table 1. We also present a plot of the BH trajectories for the run R9 (Fig. 4). We note that there is a saturation of the final BH spin at about a3 ~ 0.8, (primary BH has a1 = 0 − 0.9, and companion BH a2 = 0 in all runs). Models with a1 = 0.9 do not result in a significant growth of the final BH spin.
In the last five simulations (R6-R10), the initial momentum of the BH system was varied.The initial spin parameter a1 was kept constant, a1 = 0.9 in runs R6-R9. These initial data therefore correspond to orbits that are not necessarily circular. The values of the final BH spin do not change significantly with the initial orbital angular momentum of the system. This can be understood as a manifestation of the emission of gravitational waves: part of the angular momentum is radiated away with the gravitational radiation. Above a certain limit, the increase of the total angular momentum of the initial system (orbital and spin) does not result in the increase of spin of the final BH; the amount of angular momentum radiated away increases, however.
We have done a quantitative analysis of gravitational radiation for the last two runs of simulations (R9 and R10 in the Table 1). The direction of the recoil is irrelevant, since it depends on which phase of the last orbit the components of the system meet (in our simulations, the recoil vector must remain in the orbital plane, since the reflection symmetry is assumed). The velocity of the final BH depends on spins and masses of the components and basically it is on the order of a few thousands km s-1 (see, e.g., Tichy & Marronetti 2007). In this particular case we obtained the values of recoil speeds of approximately 200 km s-1 and 300 km s-1, for the runs R9 and R10, respectively.
The runs that roughly correspond to the premerging scenarios outlined in Sect. 2, are R5 or R9 for the first (i.e., homologous accretion) scenario and R10 for the second (i.e., torus accretion and wind outflow) scenario. The second one, which is more realistic in the physical collapse models, leads to the approximately equal mass ratio of the merging holes and high spin of the primary. Our merger simulations confirm, therefore, that a high recoil velocity is obtained in this case, albeit not as high as in the runs with BH mass ratio of about 3 and moderate or high spins.
 |
Fig. 4 Trajectories of the component BHs for an exemplary simulation described in Table 1 (run R9). Simulation covers the last two orbits of BH binary (red and green) and the formation of the final BH (blue). |
4. Discussion and conclusions
The scenarios presented here consider the long gamma ray burst case, resulting from the massive rotating star collapse that occurs in a close binary system with a companion BH. The event can be divided into three stages. First, the innermost shells of the massive primary accrete onto the core that has collapsed to a BH. These massive shells add the mass and angular momentum to this newly-born BH, and the ultimate outcome depends on the fraction of envelope that is blown away from the system through the wind. The companion BH spins up the outer shells of the rotating envelope and subsequently falls into the gap after the inner torus has been accreted. The second stage consists of the merger of two BHs, surrounded by a remnant circumbinary disk. The product of the merger has a net spin and a recoil velocity that depends on the binary parameters. In the third stage, the final BH accretes the remaining material that constitutes the outer rotationally-supported torus.
We studied two classes of models: those with and without the massive wind launched from the primary star. In the first scenario, the primary BH is spun up to the maximum rotation rate due to accretion of only the high angular momentum material, while it accretes only a moderate amount of mass. Our calculations show, that the mass of the BH increases from 1.7 up to 3.8 M⊙. It then merges with the companion BH of mass M2 = 3 M⊙. In the second scenario, the primary BH accretes both high and low angular momentum material from the envelope in the first stage. Therefore, its mass prior to the binary BH merger is large, equal to 9.2 M⊙. The spin however may not increase significantly and even drops below the starting value. The details depend on the magnitude of specific angular momentum deposited in the stellar envelope. For our testing parameters, we obtain a = 0.40, 0.69, and 0.94 for the lspec normalizations x = 1.5, 3.0, and 7.0, respectively.
We found no significant dependence of our results on the companion mass, provided it is a stellar mass BH on the order of 1−3 M⊙. In all of the cases, we neglected the spin of the companion BH, as well as the increase of its mass in the Bondi-like accretion during its passage through the primary’s envelope. Prior to the merger of the binary BH system, in the central engine we have either a maximally spinning and moderately massive, or more massive and moderately spinning BH and circumbinary torus. After the merger, the final BH mass is between M3 = 7 − 12 M⊙ and the mass of the remnant torus is about 16 M⊙. We may expect that most of this material will eventually be lost from the envelope through massive outflows. The transfer of the orbital angular momentum from the companion to the envelope leads to a longer lifetime of the rotationally supported torus around the primary BH. The accretion rate through this torus is small, however, the infalling matter contributes to increasing BH mass and spin.
In the present work, we consider a fiducial value of the mass loss parameter from the accreting torus due to powerful winds. Kumar et al. (2008) discuss the problem of mass fallback in the long GRB central engine and notice that the advection dominated part of the accretion flow generates a strong mass outflow. In their model, the 14 solar mass star ends up with a BH of ten solar masses, which means that four solar masses (28 percent) were lost from the system through the wind.
Lindner et al. (2010), in their hydrodynamical simulations of a collapsar, also use a 14 solar mass WR star with low metallicity (of 0.01 Z⊙), which results in a very small mass loss. These authors use the radius dependent angular momentum profile l(r)sin2(θ) with a magnitude at 3/4 mass radius of 8 × 1017 cm2 s-1. In the models discussed in Janiuk et al. (2013), on which we base the fiducial value of the wind parameter, the specific angular momentum is about 6 × 1016 − 2 × 1017 cm2 s-1 and therefore the centrifugal force could help drive the wind outflow. However, as we also include the magnetic fields and neutrino emission in those calculations, more powerful winds are launched. Still, in some of the models the winds appear to be gravitationally bound, therefore our assumed fiducial number in the present paper must be treated as an upper limit for the wind mass loss. Nevertheless, we note that the results presented in Sect. 2 are mostly sensitive to the adopted accretion scenario (i.e., the homologous vs. torus accretion) and the assumed wind fraction in case of torus accretion does not affect them in great detail.
As for the progenitor star and its mass loss rate due to its wind, the rate is uncertain and observationally poorly constrained. Heger et al. (2003) found that a low metallicity reduces mass loss in supernovae (see also Woosley & Heger 2006). Mapelli et al. (2013) use the power-law dependence of mass loss rate Ṁ Zμ, where μ = 0.5 − 0.9 is the index for main sequence stars. However, in the case of luminous blue variable stars and WR stars this scaling might be different (Vink & de Koter 2005). Dwarkadas (2013) studies the supernova remnants and finds that the mass loss and wind velocities in the WR stars are on the order of 10-5 M⊙ yr-1 and 2000 km s-1, respectively. In case of red supergiants, the mass loss rate is larger, but the wind velocity is smaller.
Observationally, at least some long GRBs that are associated with supernovae must have strong winds, which do not make them “failed” supernovae. One example is GRB 021211 (Della Valle et al. 2003). On the other hand, GRB 060614, 100 seconds long duration, had no supernova signatures (Della Valle et al. 2006).
The merger of two BHs occurs when the inner torus has completely accreted onto the primary and a clean gap forms at the distance of approximately twice the orbital separation (see, e.g., Shi et al. 2012; Farris et al. 2011). For stellar mass BHs the timescale of the merger is on the order of milliseconds. The merger event in our simulations should occur at about ~1700 − 2000, which is related to the timescale of the progenitor star collapse and the crossing time of the secondary component through the outer envelope shells. Accretion after the merger then proceeds onto the product BH, with a smaller accretion rate than in the first episode. This is because despite a large mass of the outer envelope shells, most of it is blown out and not accreted, while the viscous timescale at large radii is long. The total duration of this phase is determined by the size and mass of the primary star. In our model, the parameters of the star used for a simulation imply the viscous timescale at tvisc(Rout) ≈ 107 s. This is therefore the source of a resulting GRB afterglow emission, observable at lower energies for a few months following the prompt event.
The total observed event should have two distinct components in the electromagnetic signal, separated by a gravitational wave emission. One of the accompanying effects will also be the product BH recoiled due to the gravitational waves. This effect has been intensively discussed recently for the scenarios of the supermassive BH mergers. For instance, Bogdanović et al. (2007) proposed a scenario of gas-rich binary BH mergers. In this scenario, torques from gas accretion align the spins of two BHs and their orbital axis with the large-scale disks. The authors argue that this alignment prevents large kicks from the gravitational radiation recoil and helps explain the observations that the ubiquity of BHs remain in the galaxy cores, despite their past mergers.
This reasoning is based on the results of the simulations. For instance, Baker et al. (2008) modeled the coalescence of nonspinning BHs with different mass ratios. Also, González et al. (2007) and Campanelli et al. (2007) studied the cases with general spin orientations. These simulations show that for mergers with BHs of low spins or the spins aligned, the maximum speeds of the kick are below 200 km s-1. For the spins oppositely directed and large a values, the kicks exceed 4000 km s-1, while the escape speed from the galaxy core is below 1000 km s-1 (Merritt et al. 2004). The simulations’ results are not conclusive enough to say however, that large kicks are prevented by the coaligned spins of merging BHs. For instance, Tichy & Marronetti (2007) performed simulations of equal mass BHs with spins of ~0.8 and random orientations. They showed that all recoil velocities are large, between 1000 and 2000 km s-1. Higher spins lead to even larger kicks. The kick velocity also depends on the mass ratio. The above mentioned authors did not calculate this, but they expect that smaller kicks would be obtained for unequal mass case. This is consistent with analytical estimates presented in Bogdanović et al. (2007). In our simulations, the mass ratios and spins are approximately either (i) q = 0.3, a1 = 0.9 and a2 = 0 or (ii) q = 1.35, a1 = 0.8 and a2 = 0, so the ratio between the two kicks will be about 0.8 with this simplified formula. Therefore, the kick of 200 km s-1 obtained in the first case (unequal masses) would scale up to about 250 km s-1 for the second case. We obtained only a kick of 300 km s-1 in model R10, which seems to be in rough agreement with these analytical estimates, taking also into account some numerical uncertainties.
The escape velocities estimated for a sample of short GRBs’ host galaxies from Svensson et al. (2010) with median mass of Mhost = 1.3109 M⊙ and an 80% light radius of r80 = 3.3 kpc would be about 2280 km s-1. It is therefore not possible that the merger product simulated in our models will leave the host galaxy. Such extreme kick velocities could however be obtained if both merger components had very large spins.
The gravitational wave emission is estimated at ≲10% of the rest mass energy of the system; similar figures can be obtained using the analytic phenomenological formulae derived from numerical-relativity simulations by Barausse et al. (2012). Our simulation covers the merger phase only, and the resulting gravitational wave emission is on the order of a few percent (see Table 1 for the ADM mass differences).
In comparison with our current understanding of a two supermasive BHs system residing in the centers of merging galaxies, we suspect that the interaction with the gas-rich environment will facilitate the transfer of kinetic energy and orbital angular momentum from the binary system to the gas2. This should result in “speeding up” the inspiral and fewer orbits before the merger. However, at smaller distances the two BHs may be orbiting in a region relatively cleared of matter, surrounded by a circumbinary disk/torus and the accretion from it may temporarily increase the binary system angular momentum, possibly prolonging the inspiral phase. The problem of exact GW signature from such a system depends on many unknown factors, like the recoil received during the creation of a second BH and subsequent eccentricity of the orbit as well as the details of the MHD interaction with matter, and deserves separate studies.
The electromagnetic emission can be divided into three phases. The first is related to the collapse of the progenitor star and creation of the primary BH, and its electromagnetic emission is approximately the SN emission. The second stage consists of the tidal interaction of the binary BH system with the circumbinary accretion disk. Rescaling the exploratory work results of Farris et al. (2011) shows that for the binary of ≃10 M⊙, the luminosity is ≃1025 erg/s, much fainter than the third and final phase, which pertains to the collapsar scenario. In the case of substantial recoil, the final BH drags the inner part of the disk out of the system, and the electromagnetic counterpart is altered.
The progenitors of such systems are evolved binaries in star-forming regions, most likely similar to Cyg X-1 or Cyg X-3. The first system most likely contains a high mass BH, while the latter shows significant contribution of a stellar wind component. The compact star in Cyg X-3 might already be a small mass BH (Zdziarski et al. 2013) or a neutron star that will eventually collapse into a BH during the inspiral phase.
The observations of binary galaxies in the process of merging are at present still poorly sampled. The only source for which the orbital modeling finds a tight BH system, i.e., a sub-parsec solution is OJ287 (Valtonen et al. 2012). The other pairs of supermassive BHs are rather wide, with separations on the order of hundreds of parsec (Kunert-Bajraszewska & Janiuk 2011), and the indirect evidence for the presence of binaries comes mostly from their semi-periodic lightcurves or the observations of “wiggles” in the radio jets, e.g., Xu & Komossa (2009). Therefore, the observational tests of such scenarios are also limited.
Acknowledgments
We thank Mikolaj Korzynski, Stefanie Komossa, and Magda Kunert-Bajraszewska for helpful discussions. This work was supported in part by the grants NN 203 512 638, DEC-2012/05/E/ST9/03914, and 2011/01/B/ST9/04838 from the Polish National Science Center.
References
- Alcubierre, M. 2008, Introduction to 3+1 Numerical Relativity (Oxford University Press) [Google Scholar]
- Alcubierre, M., Brügmann, B., Dramlitsch, T., et al. 2000, Phys. Rev. D, 62, 044034 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ansorg, M., Brügmann, B., & Tichy, W. 2004, Phys. Rev. D, 70, 064011 [NASA ADS] [CrossRef] [Google Scholar]
- Arnowitt, R., Deser, S., & Misner, C. W. 1959, Phys. Rev., 116, 1322 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baker, J. G., Boggs, W. D., Centrella, J., et al. 2008, Phys. Rev. D, 78, 044046 [NASA ADS] [CrossRef] [Google Scholar]
- Barausse, E., Morozova, V., & Rezzolla, L. 2012, ApJ, 758, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Barkov, M. V., & Komissarov, S. S. 2010, MNRAS, 401, 1644 [Google Scholar]
- Bauer, F. E., & Brandt, W. N. 2004, ApJ, 601, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgarte, T. W., & Shapiro, S. L. 1999, Phys. Rev. D, 59, 024007 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bogdanović, T., Reynolds, C. S., & Miller, M. C. 2007, ApJ, 661, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Bowen, J. M., & York, James, W. J. 1980, Phys. Rev. D, 21, 2047 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, S., & Brügmann, B. 1997, Phys. Rev. Lett., 78, 3606 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. D., Diener, P., Sarbach, O., Schnetter, E., & Tiglio, M. 2009, Phys. Rev. D, 79, 044023 [NASA ADS] [CrossRef] [Google Scholar]
- Campanelli, M., Lousto, C. O., Zlochower, Y., & Merritt, D. 2007, Phys. Rev. Lett., 98, 231102 [NASA ADS] [CrossRef] [Google Scholar]
- Carpano, S., Pollock, A. M. T., Wilms, J., Ehle, M., & Schirmer, M. 2007, A&A, 461, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chevalier, R. A. 2012, ApJ, 752, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A. 2007, ARA&A, 45, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Della Valle, M., Malesani, D., Benetti, S., et al. 2003, A&A, 406, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Valle, M., Chincarini, G., Panagia, N., et al. 2006, Nature, 444, 1050 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dreyer, O., Krishnan, B., Shoemaker, D., & Schnetter, E. 2003, Phys. Rev. D, 67, 024018 [NASA ADS] [CrossRef] [Google Scholar]
- Dwarkadas, V. V. 2013, MNRAS, 434, 3368 [NASA ADS] [CrossRef] [Google Scholar]
- Farris, B. D., Liu, Y. T., & Shapiro, S. L. 2011, Phys. Rev. D, 84, 024024 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., Mazzali, P. A., Prochaska, J., et al. 2007, unpublished [arXiv:astro-ph/0702338] [Google Scholar]
- González, J. A., Hannam, M., Sperhake, U., Brügmann, B., & Husa, S. 2007, Phys. Rev. Lett., 98, 231101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goodale, T., Allen, G., Lanfermann, G., et al. 2003, in Vector and Parallel Processing – VECPAR’2002, 5th International Conference, Lecture Notes in Computer Science (Berlin: Springer) [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., & Moscibrodzka, M. 2012, Int. J. Mod. Phys. Conf. Ser., 8, 352 [CrossRef] [Google Scholar]
- Janiuk, A., & Proga, D. 2008, ApJ, 675, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., Moderski, R., & Proga, D. 2008, ApJ, 687, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., Mioduszewski, P., & Moscibrodzka, M. 2013, ApJ, 776, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Narayan, R., & Johnson, J. L. 2008, MNRAS, 388, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Kunert-Bajraszewska, M., & Janiuk, A. 2011, ApJ, 736, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Lindner, C. C., Milosavljević, M., Couch, S. M., & Kumar, P. 2010, ApJ, 713, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Löffler, F., Faber, J., Bentivegna, E., et al. 2012, Class. Quant. Grav., 29, 115001 [NASA ADS] [CrossRef] [Google Scholar]
- Luminet, J.-P., & Marck, J.-A. 1985, MNRAS, 212, 57 [NASA ADS] [Google Scholar]
- MacFadyen, A. I., & Woosley, S. E. 1999, ApJ, 524, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Mapelli, M., Zampieri, L., Ripamonti, E., & Bressan, A. 2013, MNRAS, 429, 2298 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C. 2006, MNRAS, 368, 1561 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., Tchekhovskoy, A., & Blandford, R. D. 2012, MNRAS, 423, 3083 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D., Milosavljević, M., Favata, M., Hughes, S. A., & Holz, D. E. 2004, ApJ, 607, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Misner, C. W., Thorne, K. S., & Wheeler, J. A. 2003, Gravitation (W. H. Freeman and Company) [Google Scholar]
- Piran, T. 2004, Rev. Mod. Phys., 76, 1143 [Google Scholar]
- Podsiadlowski, P., Mazzali, P. A., Nomoto, K., Lazzati, D., & Cappellaro, E. 2004, ApJ, 607, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schnetter, E., Hawley, S. H., & Hawke, I. 2004, Class. Quantum Grav., 21, 1465 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Shi, J.-M., Krolik, J. H., Lubow, S. H., & Hawley, J. F. 2012, ApJ, 749, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, M., & Nakamura, T. 1995, Phys. Rev. D, 52, 5428 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Svensson, K. M., Levan, A. J., Tanvir, N. R., Fruchter, A. S., & Strolger, L.-G. 2010, MNRAS, 405, 57 [NASA ADS] [Google Scholar]
- Thornburg, J. 2004, Class. Quantum Grav., 21, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Tichy, W., & Marronetti, P. 2007, Phys. Rev. D, 76, 061502 [NASA ADS] [CrossRef] [Google Scholar]
- Valtonen, M. J., Ciprini, S., & Lehto, H. J. 2012, MNRAS, 427, 77 [NASA ADS] [CrossRef] [Google Scholar]
- van Kerkwijk, M. H., Charles, P. A., Geballe, T. R., et al. 1992, Nature, 355, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., & de Koter, A. 2005, A&A, 442, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wellstein, S., & Langer, N. 1999, A&A, 350, 148 [NASA ADS] [Google Scholar]
- Woosley, S. E. 1993, ApJ, 405, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Heger, A. 2006, ApJ, 637, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, D., & Komossa, S. 2009, ApJ, 705, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 443, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdziarski, A. A., Mikołajewska, J., & Belczyński, K. 2013, MNRAS, 429, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., & Mészáros, P. 2004, Int. J. Mod. Phys. A, 19, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, W., & Fryer, C. L. 2001, ApJ, 550, 357 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Evolution of the primary BH spin during the collapse of the stellar envelope. Blue lines are for a1,init = 0.1 and red lines for a1,init = 0.85. The solid and dashed lines show the models with the envelope’s angular momentum normalized with x = lspec/lcrit = 1.5 and 7, respectively. The model assumes homologous accretion of the envelope shells onto the BH and no wind. The envelope is spun up by the companion BH of a mass M2 = 3 M⊙. The time is given as the free-fall timescale, so it scales with M1. |
| In the text | |
 |
Fig. 2 Mass of the primary BH (top), accretion rate (middle), and the primary BH spin (bottom panel) as a function of time during the accretion of the viscous torus. In the top panel, the model assumes the specific angular momentum in the envelope: x = 1.5 to compare two cases: either 28% of the torus mass (solid line) and the rest is blown out, or its total mass (dashed line) is fully accreted. In the middle and bottom panels, the models assume the wind outflow, and the two lines show the cases with different angular momentum: x = 1.5 (solid) and x = 7.0 (dotted). |
| In the text | |
 |
Fig. 3 Mass of the envelope shell as a function of the free-fall time. The green solid line is the total mass in the shell, while the red lines corresponds to the mass contained in the rotationally supported torus. Here, the solid, long dashed and short dashed lines show the models with the specific angular momentum normalized with x = 1.5, 3, and 7, respectively. All models assume that 28% of the stellar envelope is accreted onto the BH, and the rest of the mass is evacuated as a massive wind. |
| In the text | |
 |
Fig. 4 Trajectories of the component BHs for an exemplary simulation described in Table 1 (run R9). Simulation covers the last two orbits of BH binary (red and green) and the formation of the final BH (blue). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


