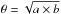| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322112 | |
| Published online | 10 December 2013 | |
Research Note
A revised distance scale of planetary nebulae⋆
Escola de Artes, Ciências e Humanidades, USP, Av. Arlindo Bettio 1000, 03828-000 São Paulo, SP Brazil
e-mail: rortiz@usp.br
Received: 20 June 2013
Accepted: 25 October 2013
Context. The advent of large-scale, high-sensitivity surveys of the Galaxy (2MASS, WISE, Spitzer, etc.) has allowed detection of a large number of planetary nebulae (PNe), some of them at large distances.
Aims. I propose a new distance scale of planetary nebulae, based on two main quantities: the flux density (or magnitude) at 8 μm and the nebular apparent size.
Methods. I used these quantities to calculate the specific intensity of the radiation I8 μm, which decreases as the nebula evolves. The PNe situated in the Large Magellanic Cloud (LMC) with 8 μm photometry obtained by Spitzer and diameter obtained from HST observations were used as calibrators.
Results. After calibration, I recalculated distances of PNe in the LMC, and they show a one-sigma spread of 10 kpc (20%). Eventually, I applied the method to a sample of 47 Galactic PNe observed during the Spitzer survey. These results showed agreement within 0.2 dex with the distances determined with another method of calibrating with PNe in the LMC.
Conclusions. The main advantage of the present distance scale is that it is nearly “extinction free”, which makes it especially suited to PNe severely affected by interstellar extinction, such as the Galactic disc and bulge. On the other hand, the method requires an unbiased determination of the nebular size, which might be quite uncertain for PNe with extended faint features, such as haloes and ansae.
Key words: planetary nebulae: general / infrared: ISM / stars: AGB and post-AGB / stars: distances / Galaxy: structure
Tables 1−3 are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Since the pioneering work by Shklovsky (1956), different attempts to determine the distances of PNe have been proposed with a wide variety of techniques. These methods can be divided into two main classes: (1) the statistical methods make use of the relationships among general characteristics of PNe (quantities that are distance-invariant are used to infer other physical quantities that depend on the distance, such as constant ionized mass, Shklovsky 1956; the radio flux, Milne & Aller 1975; the brightness temperature – nebular radius correlation, Zhang & Kwok 1993); and (2) individual methods, which apply to specific physical characteristics relative to the nebula or its central star. At first glance, individual methods seem to be more reliable. However, even among these direct methods, large discrepancies still exist. Thus, when correctly proposed, statistical methods still constitute a valid approach to the problem.
In an earlier paper, Ortiz et al. (2011) proposed a distance scale based on a minimal set of infrared data: the mid-infrared specific intensity Iλ and the apparent size, θ. Although the present method is based on the same set of physical quantities as used in Ortiz et al. (2011), the dependence among these parameters and the distance of PNe is modelled differently.
The discrepancy between some of the distances determined by Stanghellini et al. (2008, hereafter SSV) and Ortiz et al. (2011) also demanded a revision of the method. Some bias seems to affect the nearer objects, especially those within 2 kpc. For these PNe, the distances determined by Ortiz et al. (2011) were clearly overestimated by a factor 2, on average. Besides this, another bias seems to affect the farther objects: PNe with d > 7.5 kpc had their distances underestimated by 30−50% by Ortiz et al. (2011). Thus, a revision of the method became necessary, and this is the main goal of the present paper.
2. The method and its calibration
Like many of the distance scales previously described in the literature, the present method is based on a physical quantity that remains invariant with the distance: the specific intensity of the radiation, Iλ. The first studies of the behaviour of Iλ of PNe are from Volk (1992) and Zhang & Kwok (1993) who showed that Iλ of the IRAS bands keep a tight correlation with the brightness temperature measured at radio wavelengths. Van de Steene & Zijlstra (1994) developed a statistical distance scale based on an empirical correlation between the radio-continuum brightness temperature and the nebular radius. Eventually, Ortiz et al. (2011) derived a similar correlation for several wavelengths between 8 and 21 μm. According to these studies, as a nebula evolves, its optical depth at radio wavelengths decreases as the result of the geometrical dilution of the gas. At the same time, the specific intensity at mid-infrared wavelengths also decreases, approximately at the same rate.
Another physical parameter that varies monotonically with time is the nebular radius. Our present knowledge about this matter includes the interaction (or shock) of different stellar winds (Kwok et al. 1978) – each of them with its own distinct velocity − with the local interstellar medium (Wareing et al. 2007). All the studies of this matter point out that the central star wind must have at least two components: a slow wind, which is remmant of the asymptotic giant branch (AGB) phase, showing Vexp = 10 − 20 km s-1 (Mufson et al. 1975; Kwok 1982); a fast wind, revealed by the broad P-Cygni profiles of resonance lines observed in the UV, showing velocities as high as 2000−4000 km s-1 (Heap et al. 1978). Besides these two components, PNe are also shaped by additional physical mechanisms, which generate the complex structures, such as jets, knots, and tori.
As formerly defined in Ortiz et al. (2011), the specific intensity at any wavelength can be evaluated according to the following equation: 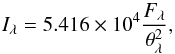 (1)where Iλ is given in MJy sr-1, Fλ is the flux density in Jansky, and θλ the apparent nebular diameter, in arcseconds. The infrared flux density in the equation above can be converted into magnitude units using the IRAC zero-magnitude flux density at 8 μm, Fzero,8 μm = 64.13 Jansky (Meade et al. 2009). After conversion, Eq. (1) can be rewritten as
(1)where Iλ is given in MJy sr-1, Fλ is the flux density in Jansky, and θλ the apparent nebular diameter, in arcseconds. The infrared flux density in the equation above can be converted into magnitude units using the IRAC zero-magnitude flux density at 8 μm, Fzero,8 μm = 64.13 Jansky (Meade et al. 2009). After conversion, Eq. (1) can be rewritten as 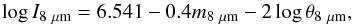 (2)where m8 μm refers to the magnitude corresponding to F8 μm.
(2)where m8 μm refers to the magnitude corresponding to F8 μm.
The distance scale proposed in this paper is calibrated with a sample of PNe situated in the Large Magellanic Cloud (LMC). All the 8 μm magnitudes of the calibrators were extracted from Hora et al. (2008). They were calculated from the solid angle-integrated intensity of IRAC images of previously identified PNe in the LMC-SAGE survey (Meixner et al. 2006).
2.1. The relationship between visual and 8 μm apparent sizes
As formerly discussed in Ortiz et al. (2011), the main source of uncertainty for any distance scale based on the parameters above is the definition of the nebular apparent size. Because PNe are diffuse and often display faint haloes around a prominent nebular bulk (Jewitt et al. 1986), the evaluation of θλ depends on various factors, such as the wavelength of the observation, the sensitivity and spatial resolution of the camera, and the morphology of the nebula. The compilation of a sample consisting of PNe situated only in the LMC imposes additional difficulties, especially concerning the sensitivity and spatial resolution of the observations. Shaw et al. (2007) discussed the discrepancy between LMC nebular sizes obtained from HST images and with ground-based telescopes. According to that study, faint, outer haloes may be overlooked in HST images. Besides, PNe with angular diameter smaller than the spatial resolution of ground-based telescopes have their sizes overestimated.
 |
Fig. 1 Filled circles represent apparent sizes of Galactic PNe, measured at both 8 μm and visual wavelengths. The continuous straight line represents the best fit to the data, excluding two objects with θ8 μm/θvis > 3 (plotted as open circles). |
Unfortunately, the spatial resolution of the IRAC camera at 8 μm does not allow correct determination of θ8 μm of LMC-PNe, and other determinations of this quantity still do not exist in the literature. It is well known that nebular apparent sizes depend on the wavelength, but these differences may not be significant in all cases. Bedding & Zijlstra (1994) compared nebular diameters obtained from images taken with the Hα filter with those determined from 6 cm radio observations with the VLA. They concluded that, even though the agreement between these quantities is very poor when only compact (<10′′) objects are selected, θrad generally equals θvis for larger (>10′′) objects. Ortiz et al. (2011) also compared sizes obtained at radio (the VLA, Siódmiak & Tylenda, 2001) with diameters measured at visual wavelengths (the compilation by SSV). Their results showed good agreement in 85% of the cases, confirming the previous results by Bedding & Zijlstra (1994). A comparison among sizes determined at different wavelengths in the visual range was carried out by Ruffle et al. (2004). They compared diameters obtained from images taken both at Hα and O[iii] wavelengths and showed that these quantities agree within 15% in more than 90% of the cases.
This scenario changes completely when nebular sizes obtained at visual and mid-infrared wavelengths are compared. Some nebulae show dusty envelopes far beyond the ionization front, a relic of the intense mass loss that occurred at the end of the AGB. Because this outer envelope contains large amounts of warm dust, its emission peaks at mid-infrared wavelengths. Thus, the nebular size used in the calculation of I8 μm must be measured or estimated at this same wavelength. In this work the nebular size of LMC-PNe at 8 μm is estimated from its visual value. I analysed a sample of Galactic PNe observed at 8 μm in order to obtain a relationship between θvis and θ8 μm (Table 1).
Figure 1 shows a comparison between apparent sizes of Galactic PNe observed by Spitzer and the sizes obtained at visual wavelengths1. The θ8 μm values were obtained from θ8 μm,10%, which was taken from isophotal maps and/or profile cuts, and deconvolved according to the following relationship proposed by Tylenda et al. (2003): 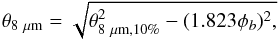 (3)where φb is the full width at half maximum (FWHM) of the resolution beam. Kwok et al. (2008) estimated the FWHM of the point-spread function of the IRAC camera at 8 μm as φb = 1.94″. A least-squared fit to the data shown in Fig. 1 resulted in ⟨ θ8 μm/θvis ⟩ = 1.23 ± 0.34. Two (10% of the sample) compact (<10″) PNe were not included in the calculation because of their discrepant diameters (θ8 μm/θvis > 3).
(3)where φb is the full width at half maximum (FWHM) of the resolution beam. Kwok et al. (2008) estimated the FWHM of the point-spread function of the IRAC camera at 8 μm as φb = 1.94″. A least-squared fit to the data shown in Fig. 1 resulted in ⟨ θ8 μm/θvis ⟩ = 1.23 ± 0.34. Two (10% of the sample) compact (<10″) PNe were not included in the calculation because of their discrepant diameters (θ8 μm/θvis > 3).
Sizes of LMC-PNe were determined by Shaw et al. (2001, 2006) from various HST images taken at broadband, O[iii]λ5007, and Hα + N[ii] images. The apparent diameter of a round nebula is defined as the isophotal diameter taken at the level of 10% of the maximum intensity. In the cases where the nebular shape deviates from a round shape, the diameter was calculated as the square root of the product of the larger and smaller dimensions (the major and minor axes, assuming the PN to be elliptical). After deconvolution, the spatial resolution of HST images is only ~0.1″ (~0.02 parsec at 50 kpc of distance, Mould et al. 2000), which allows including of a wide range of nebular sizes.
Unfortunately, high-resolution images of LMC-PNe still do not exist at mid-infrared wavelengths, and consequently their diameters at 8 μm can only be estimated from the values obtained in visual bands. In this study, I used the relationship between visual and 8 μm apparent diameters of Galactic PNe (Fig. 1) to estimate the 8 μm diameters of LMC-PNe. Because these data show a considerable spread, 8 μm diameters cannot be calculated by simply multiplying the visual sizes by the ⟨ θ8 μm/θvis ⟩ average ratio. Instead, artificial 8 μm diameters were generated by a Monte Carlo simulation applied to the visual diameters of LMC-PNe given by Shaw et al. (2001, 2006), assuming that these data follow a Gaussian distribution with ⟨ θ8 μm/θvis ⟩ = 1.23 ± 0.34.
Table 2 shows various characteristics of PNe, as well as the results of the Monte Carlo method used in the calibration. Nebular sizes at 8 μm (θ8 μm) are not individually valid because they represent sizes calculated by the Monte Carlo simulation. Therefore, 8 μm sizes are artificial, and have been included to simulate the distribution of mid-infrared sizes of LMC-PNe in the diagram, which do not exist in the literature.
Figure 2 shows the results of this technique. For each nebula, a second I8 μm was calculated by substituting θvis by θ8 μm, generated by a Monte Carlo simulation. These 8 μm data are plotted in Fig. 2 according to the morphological type of the nebula.
An analysis of Fig. 2 reveals that (1) the shift caused by exchanging θvis by θ8 μm in the calculation of I8 μm is, on average, almost parallel to the distribution of data, i.e. the diagonal in the diagram (2) Worst-fit data correspond mostly to bipolar nebulae, confirming the previous conclusion by SSV, who state that distance scales of this kind do not work well for bipolar PNe; (3) there is only one PN (SMP11, near log D(pc) ≃ 0.75 and log I8 μm(MJy sr-1) ≃ 4.5) in disagreement with the fit curve. This object is described by Shaw et al. (2006) as one of the smallest known bipolar PNe in the LMC. A misevaluation of its diameter might have been the cause of its detached position in the diagram. (4) All PNe situated near the bottom right-hand corner of the diagram have been classified as bipolar or other than round or elliptical. The combination of large diameter with low-intensity radiation (near the threshold detecting level of the HST images) may have caused the overestimation of I8 μm.
 |
Fig. 2 Statistically adjusted nebular diameter (D, in parsecs) versus the specific intensity of the radiation at 8 μm. Crosses represent the intensity at 8 μm, calculated with the visual nebular size θvis. Each filled symbol was generated by a Monte Carlo simulation that transformed the original data θvis into θ8 μm, assuming θ8 μm/θvis = 1.23 ± 0.34. |
2.2. Estimation of the physical nebular diameter from the intensity of the nebular radiation at 8 μm
The plot shown in Fig. 2 reinforces the interpretation formerly proposed by Zhang & Kwok (1993) which states that Iλ at mid-infrared wavelengths decreases as the nebula evolves. The data situated near the top left-hand corner of Fig. 2 correspond to young, compact PNe. The most compact objects in the present sample show log I8 μm ≃ 4.7, similar to log I8 μm ≃ 4.8 observed in the sample compiled by Ortiz et al. (2011), carried out at a similar wavelength. At the other end of the sequence, where there are PNe showing low I8 μm, a comparison between the present data with the sample studied by Ortiz et al. (2011) confirms the higher sensitivity of the Spitzer IRAC camera compared to the Spirit instrument used in the MSX survey.
The following equation has been obtained from a least-squared fit to the data shown in Fig. 2: 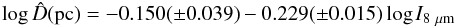 (4)where
(4)where 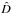 represents the estimated diameter of the nebula, obtained from its I8 μm. The correlation coefficient of the fit is R2 = 0.804. One nebula, SMP11, was excluded from the fit owing to its divergent position in the diagram.
represents the estimated diameter of the nebula, obtained from its I8 μm. The correlation coefficient of the fit is R2 = 0.804. One nebula, SMP11, was excluded from the fit owing to its divergent position in the diagram.
Equation (4) is similar to the relationship between the nebular radius and the brightness temperature in the radio domain, which is used to calibrate other distance scales (van de Steene & Zijlstra 1995, SSV). However, as pointed out by Urosevic et al. (2009), there are large discrepancies among the various distance scales based on relationships of this kind. According to their analysis, the slope of brightness-radius relationship varies according to the sample used in the calibration. Slopes vary from − 0.25 (for PNe with d > 2 kpc, SSV) up to − 0.68 (for nearby PNe, with d < 0.4 kpc, SSV and Phillips 2002). The slope in Eq. (4) is distinct from the values determined with other distance scales, but this may result from the different hypotheses assumed by the other methods, such as the definition of angular size.
Once the nebular diameter is estimated, the distance d of a PN can be estimated from the well-known relationship: 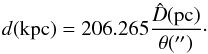 (5)The substitution of the previous equations into the relationship above results in
(5)The substitution of the previous equations into the relationship above results in 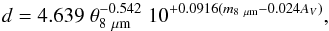 (6)where d is the distance (in kiloparsecs), θ8 μm(′′) the apparent size (diameter, or its equivalent) at 8 μm, m8 μm is the nebular magnitude at 8 μm (Spitzer), and AV the visual extinction of the nebula.
(6)where d is the distance (in kiloparsecs), θ8 μm(′′) the apparent size (diameter, or its equivalent) at 8 μm, m8 μm is the nebular magnitude at 8 μm (Spitzer), and AV the visual extinction of the nebula.
2.3. Estimation of errors
This method contains intrinsic shortcomings that produce errors in the distance. Figure 2 shows the data distributed along the fitted curve with a one-sigma spread of ~0.2 dex in log (D). This scattering is the main source of error in the present method and is caused mainly by (1) errors in the θ measurements of the LMC-PNe, i.e. the calibration; (2) intrinsic variation in I8 μm, due to the various features seen among PNe spectra. These variations include the intensity of the continuum (which depends on thermal emission by dust), the strength of emission molecular bands caused by various chemical compounds in the nebula, especially those deposited onto grains, etc. The uncertainty intrinsic to the method (the 0.2 dex scattering in Fig. 2) directly affect the distance calculated by Eq. (5), resulting in a one-sigma error bar of 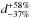 .
.
A second cause of error in the distance is the misevaluation of the nebular angular diameter, but this does not affect all PNe equally. Figure 2 shows that bipolar or peculiar-type PNe are more subject to this error. Misevaluation of nebular sizes can also result from observational factors, such as instrumental limitations and low signal-to-noise ratio of the image. As an example, if the angular diameter was overmeasured by 20%, its estimated diameter (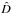 ) would be 8.7% larger than its real size (by Fig. 2 and Eq. (4)). However, its distance, calculated according to Eq. (6), would be underestimated by 10%. On the other hand, a misevaluation of the angular diameter by 20% less than its real size would produce a distance in excess of 13%.
) would be 8.7% larger than its real size (by Fig. 2 and Eq. (4)). However, its distance, calculated according to Eq. (6), would be underestimated by 10%. On the other hand, a misevaluation of the angular diameter by 20% less than its real size would produce a distance in excess of 13%.
 |
Fig. 3 Histogram, showing the distance of PNe situated in the LMC, determined by the present method. The sample consists of the same set as used to compose the data shown in Fig. 2. |
The interstellar extinction is another factor that can affect determination of the distance, especially those PNe located in the Galactic bulge. Schultheis et al. (1999) estimate the average visual extinction up to the Galactic centre as 25m. When assuming A8 μm = 0.024 × AV (Li & Greenberg 1997; Cox 2000), the extinction at 8 μm to the Galactic bulge would amount to 0.6m, which would cause the distance to be overestimated by 13%. In this study, only Pe 2-12 might have had its distance affected a little by interstellar extinction. Generally, this effect has little influence on the determination of disc PNe.
There are only a few distance determinations obtained with “direct” methods that could be used as a independent calibration, such as trigonometric and expansion parallaxes and binary planetary nebula nucleii. Statistical methods rely on physical hypotheses with various restrictions: PNNi spectroscopic distances (Méndez et al. 1988), constant ionized mass (Shklovsky 1956), etc. Unfortunately a comparison between the “direct” and the statistical methods is very difficult to make, especially because there are only a few objects with distances determined by both types of methods. For example, until now there have only been four PNe near the Galactic plane (| b | < 5°) with distances determined by trigonometric parallax, NGC 6853 (Benedict et al. 2009; Harris et al. 2007), NGC 6881 (Gúzman-Ramírez et al. 2011), Sh 2-216 (Harris et al. 2007), and Hen 2-11 (Gutierrez-Moreno et al. 1999), but none of these objects was observed in the GLIMPSE survey. There are also a few objects with distances obtained by expansion parallaxes observed by GLIMPSE. However this method also has its limitations, especially concerning the derivation of the nebular expansion velocity (Mellema 2004), and the distances determined by this method may be underestimated by a factor 1.3 ~ 3 (Schoenberner et al. 2005).
 |
Fig. 4 Comparison between the distances obtained in the present work with others: a) Stanghellini et al. (2008, SSV); b) Phillips (2004); c) SSV versus Phillips (2004); d) van de Steene & Zijlstra (1994). The error bars correspond to the average value in the original reference, whilst the error bar of this method corresponds to its minimum value: 0.2 dex or |
3. Results and discussion
To test the new distance scale, I applied the method to PNe situated in the LMC and the Galaxy. The first test was to recalculate the distance of LMC-PNe using the same data set as was used to compose the calibration obtained in Sect. 2. The histogram depicted in Fig. 3 peaks at d = 50 kpc and has a half width of ~10 kpc. This scatter, corresponding to a relative uncertainty of 20%, is mainly due to the dispersion of the data near the fitted curve shown in Fig. 2, as discussed in Sect. 2.3. The distance of a few objects have been severely under- or overestimated in this test. SMP11, the discrepant data point in Fig. 2 has had its distance underestimated as 18.1 kpc. On the other hand, four objects have clearly overestimated distances: SMP80, SMP82, SMP84, and MG40 (with distances of 107.9, 92.0, 80.8, and 88.3 kpc, respectively). Among them, only MG40 seems to exhibit special morphological features: a bipolar core and an attached outer shell (Shaw et al. 2006). SMP84 has a visual diameter of 0.57 × 0.48′′ (Shaw et al. 2006), but its distance was calculated assuming a 8 μm diameter of 0.380′′ generated by the Monte Carlo simulation. This is one of the very few cases where the 8 μm size is smaller than its visual value. If the average ⟨ θ8 μm/θvis ⟩ = 1.23 ratio had been used to calculate θ8 μm instead of generating a 8 μm size by the Monte Carlo simulation, its distance would be calculated as 60.7 kpc. SMP82, showing θvis = 0.305′′ is among the four smallest objects in the sample, resulting in the large relative uncertainty of its size. SMP-80 is the faintest PN in the sample, resulting in the large uncertainty of its 8 μm magnitude and consequently I8 μm.
A second test of the method consisted in determining the distances of Galactic PNe. Different authors have measured the total flux density and size of these nebulae, and a compilation of data collected from the literature resulted in 47 PNe with 8 μm magnitudes and diameters (Table 3). In the cases where the 8 μm intensity was given by brightness profiles or isophote maps, the outer border was defined at the level corresponding to one tenth of the maximum intensity.
The validity of a distance scale calibrated with LMC-PNe but applied to Galactic objects can be questioned if these two classes of objects have different luminosity distributions, for example. Stanghellini et al. (2012) compared these two populations of PNe and conclude that Galactic PNe exhibit higher infrared luminosity when compared to LMC-PNe. However, this conclusion may be a selection effect. In fact, their sample of compact Galactic PNe only contains objects with radius smaller than 0.1 parsec, which show Tdust > 102 K. If their radius versus log Tdust relationship can be extended to larger PNe, objects with R > 0.1 parsec (and Tdust < 102 K) would be added to their sample, and those show log (LIR/L⊙) < 2. In this case the interval of infrared luminosities of LMC and Galactic PNe would be similar.
A comparison among different distance scales is shown in Fig. 4, where only methods based on the specific intensity of the radiation, i.e. infrared intensity or brightness temperature, have been included. The comparison with the method proposed by SSV (panel a) is interesting because SSV’s method was also calibrated using PNe in the LMC. Their model is based on the Shklovsky/Daub distance technique, but with several improvements designed to fix its main limitation: the assumption that all PNe are optically thick and thus that they would all have the same ionized mass. According to SSV, the uncertainty of their method is 30% at least, and this figure cannot be reduced significantly by improving the sample of calibrators, for instance. The uncertainty of the present method is 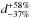 , but this figure may be greater if the apparent size is misevaluated, for example. A comparison between the results produced by these two methods must consider that there are important differences between them: SSV’s is based on the 5 GHz brightness temperature (or its equivalent Hβ flux) and the nebular size is defined by the photometric radius, i.e. the isocontour that contains 85% of the nebular flux. Figure 4a shows that these two methods are in good agreement within their respective uncertainties. The case of H1-7 might have been caused by its misidentification by SSV.
, but this figure may be greater if the apparent size is misevaluated, for example. A comparison between the results produced by these two methods must consider that there are important differences between them: SSV’s is based on the 5 GHz brightness temperature (or its equivalent Hβ flux) and the nebular size is defined by the photometric radius, i.e. the isocontour that contains 85% of the nebular flux. Figure 4a shows that these two methods are in good agreement within their respective uncertainties. The case of H1-7 might have been caused by its misidentification by SSV.
The comparison with the method proposed by Phillips (2004) is shown in Fig. 4b. The uncertainty of that method is estimated as 35%, on average. The plot reveals the existence of a bias over the whole range of distances, which makes that distance scale “short” when compared with the present method. However, a similar bias appears when Phillips’ method is compared with SSV (Fig. 4c). This suggests that this bias is probably restricted to Phillips’ method. The present distance scale agrees more with the distance scale proposed by van de Steene & Zijlstra (1994, Fig. 4d), which was calibrated with Galactic bulge PNe, assuming that their average distance is 8 kpc. The uncertainty of that method is estimated by the authors as 40%, on average. A closer inspection of the original data reveals the cause of the larger differences between the two methods: Pe2-12 (d = 8.51 kpc, dvdSZ = 13.59 kpc), Pe1-15 (d = 6.09 kpc, dvdSZ = 8.47 kpc), and Pe1-6 (d = 2.43 kpc, dvdSZ = 4.27 kpc). The difference in the distance of Pe2-12 is probably due to an error in the measurement of the flux density at 5 GHz, 2 mJy, the lowest value among all PNe in the bulge. The difference observed in the case of Pe1-15 may have been caused by incorrect determination of its apparent size: observations at 5 GHz point out a diameter of only 4.8′′, whereas Spitzer observations at 8 μm suggest 11.3′′. The distance produced by both methods would show better agreement if similar apparent diameters were considered. The discrepancy between the sizes at 8 μm (48.6′′) and at 5 GHz (7.2′′) seems to be also the problem with the distance of Pe1-6. These two latter examples illustrate the sensitivity of the method well with respect to the determination of θ8 μm.
4. Conclusions
A new distance scale was proposed that is based on a relationship between the specific intensity of the nebular radiation at 8 μm and its diameter. The calibration, based on a sample of 56 PNe in the LMC, shows a one-sigma spread of 0.2 dex in the nebular size.
Two main sources of error in the method are (1) the intrinsic spread of 0.2 dex in the D versus I8 μm relationship; and (2) the misevaluation of the angular diameter. The former causes the distance scale to be accurate to 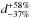 . An uncertainty of 20% in the apparent diameter alone generates an additional error of
. An uncertainty of 20% in the apparent diameter alone generates an additional error of 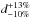 .
.
Distances of PNe in the LMC show one-sigma uncertainty of 20%. A comparison between the new method and the distance scale proposed by Stanghellini et al. (2008) does not show significant bias, and they generally agree with each other within 30%.
Online material
Flux density and apparent diameters of Galactic PNe observed during the Spitzer survey.
PNe in the LMC and their characteristics.
Acknowledgments
This research made use of the SIMBAD database, operated at the CDS, Strasbourg, France, and the NASA Astrophysics Data System. This work is partially based on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA. The author acknowledges the grant awarded by FAPESP (proc. 2010/18835-3) entitled “Planetary nebulae, stars, and the chemical evolution of stellar systems”. The author thanks the anonymous referee for the excellent critical review of the original manuscript.
References
- Bedding, T. R., & Zijlstra, A. A. 1994, A&A, 283, 955 [NASA ADS] [Google Scholar]
- Benedict, G. F., MacArthur, B. E., Napiwotski, R., et al. 2009, AJ, 138, 1969 [NASA ADS] [CrossRef] [Google Scholar]
- Cerrigone, L., Hora, J. L., Umana, G., & Trigilio, C. 2008, ApJ, 682, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., Parker, Q. A., Green, A. J., et al. 2011, MNRAS, 413, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Cox A. N. 2000, Allen’s Astrophysical Quantities (Springer) [Google Scholar]
- Gutiérrez-Moreno, A., Anguita, C., Loyola, P., & Moreno, H. 1999, PASP, 111, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Guzmán-Ramírez, L., Gómez, Y., Loinard, L., & Tafoya, D. 2011, MNRAS, 414, 3129 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, H. C., Dahn, C. C., Canzian, B., et al. 2007, AJ, 133, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Heap, S. R., Boggess, A., Holm, A., et al. 1978, Nature, 275, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hora, J. L., Cohen, M., Ellis, R. G., et al. 2008, AJ, 135, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C., Danielson, G. E., & Kupferman, P. N. 1986, ApJ, 302, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Kwok, S. 1982, ApJ, 258, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Kwok, S., Purton, C. R., & FitzGerald, P. M. 1978, ApJ, 219, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Kwok, S., Zhang, Y., Koning, N., Huang, H. H., & Churchwell, E. 2008, ApJS, 174, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., & Greenberg, J. M. 1997, A&A, 323, 566 [NASA ADS] [Google Scholar]
- Meade, M. R., Whitney, B. A., Babler, B. L., et al. 2009, Glimpse II – v. 2.0 data release, 31 [Google Scholar]
- Meixner, M., Gordon, K. D., Indebetouw, R., et al. 2006, AJ, 132, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Mellema, G. 2004, A&A, 416, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Méndez, R. H., Kudritzki, R. P., Herrero, A., Husfeld, D., & Groth, H. G. 1988, A&A, 190, 113 [NASA ADS] [Google Scholar]
- Milne, D. K., & Aller, L. H. 1975, A&A, 38, 183 [NASA ADS] [Google Scholar]
- Mould, J. R., Huchra, J. P., Freedman, W. L., et al. 2000, ApJ, 529, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Mufson, S. L., Lyon, J., & Marionni, P. A. 1975, ApJ, 201, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, R., Copetti, M. V. F., & Lorenz-Martins, S. 2011, MNRAS, 418, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, J. P. 2002, ApJS, 138, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, J. P. 2004, MNRAS, 353, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, J. P., & Ramos-Larios, G. 2008a, MNRAS, 383, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, J. P., & Ramos-Larios, G. 2008b, MNRAS, 386, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, J. P., & Ramos-Larios, G. 2010, MNRAS, 405, 2179 [NASA ADS] [Google Scholar]
- Phillips, J. P., Ramos-Larios, G., Schoereder, K.-P., & Verbena Contreras, J. L. 2009, MNRAS, 399, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Quino-Mendoza, J. A., Phillips, J. P., & Ramos-Lario, G. 2011, Rev. Mex. Astron. Astrofis., 47, 31 [NASA ADS] [Google Scholar]
- Ramos-Lario, G., & Phillips, J. P. 2008, MNRAS, 390, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos-Lario, G., & Phillips, J. P. 2009, MNRAS, 400, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos-Lario, G., & Phillips, J. P. 2012, MNRAS, 425, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos-Lario, G., Guerrero, M. A., Vazquez, R., & Phillips, J. P. 2012, MNRAS, 420, 1977 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffle, P. M. E., Zijlstra, A. A., Walsh, J. R., et al. 2004, MNRAS, 353, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Schoenberner, D., Jacob, R., & Steffen, M. 2005, A&A, 441, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schultheis, M., Ganesh, S., Simon, G., et al. 1999, A&A, 349, L69 [NASA ADS] [Google Scholar]
- Shaw, R. A., Stanghellini, L., Mutchler, M., Balick, B., & Blades, J. C. 2001, ApJ, 548, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, R. A., Stanghellini, L., Villaver, E., & Mutchler, M. 2006, ApJS, 167, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, R. A., Reid, W. A., & Parker, Q. A. 2007, PASP, 119, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Shklovsky, I. 1956, Astron. Zh., 33, 222 [Google Scholar]
- Siódmiak, N., & Tylenda, R. 2001, A& A, 373, 1032 [Google Scholar]
- Stanghellini, L., Shaw, R. A., & Villaver, E. 2008, ApJ, 689, 194 (SSV) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stanghellini, L., García-Hernández, D. A., García-Lario, P., et al. 2012, ApJ, 753, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Tylenda, R., Siódmiak, N., Górny, S. K., Corradi, R. L. M., & Schwarz, H. E. 2003, A&A, 405, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urosevic, D., Vukotic, B., Arbutina, B., et al. 2009, A&A, 495, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van de Steene, G. C., & Zijlstra, A. A. 1994, A&AS, 108, 485 [NASA ADS] [Google Scholar]
- van de Steene, G. C., & Zijlstra, A. A. 1995, A&A, 293, 541 [NASA ADS] [Google Scholar]
- Volk, K. 1992, ApJS, 80, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Wareing, C. J., Zijlstra, A. A., & O’Brien, T. J. 2007, MNRAS, 382, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, C. Y., & Kwok, S. 1993, ApJS, 88, 137 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Flux density and apparent diameters of Galactic PNe observed during the Spitzer survey.
All Figures
 |
Fig. 1 Filled circles represent apparent sizes of Galactic PNe, measured at both 8 μm and visual wavelengths. The continuous straight line represents the best fit to the data, excluding two objects with θ8 μm/θvis > 3 (plotted as open circles). |
| In the text | |
 |
Fig. 2 Statistically adjusted nebular diameter (D, in parsecs) versus the specific intensity of the radiation at 8 μm. Crosses represent the intensity at 8 μm, calculated with the visual nebular size θvis. Each filled symbol was generated by a Monte Carlo simulation that transformed the original data θvis into θ8 μm, assuming θ8 μm/θvis = 1.23 ± 0.34. |
| In the text | |
 |
Fig. 3 Histogram, showing the distance of PNe situated in the LMC, determined by the present method. The sample consists of the same set as used to compose the data shown in Fig. 2. |
| In the text | |
 |
Fig. 4 Comparison between the distances obtained in the present work with others: a) Stanghellini et al. (2008, SSV); b) Phillips (2004); c) SSV versus Phillips (2004); d) van de Steene & Zijlstra (1994). The error bars correspond to the average value in the original reference, whilst the error bar of this method corresponds to its minimum value: 0.2 dex or |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.