| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321333 | |
| Published online | 28 November 2013 | |
On the use of the ratio of small to large separations in asteroseismic model fitting
Astronomy Unit, Queen Mary University of London Mile End Road London E1 4NS UK
e-mail: I.W.Roxburgh@qmul.ac.uk
Received: 21 February 2013
Accepted: 1 November 2013
Aims. We aim to show that model fitting by searching for a best fit of observed and model separation ratios at the same radial orders n is in principle incorrect, and to show that a correct procedure is to compare the model ratios interpolated to the observed frequencies.
Methods. We compare models with different interior structures and outer layers, relate the separation ratios to phase shift differences, conduct model fitting experiments using separation ratios, and relate phase shift differences to internal phase shifts.
Results. We show that the separation ratios of stellar models with the same interior structure, but different outer layers, are not the same when compared at the same radial order n, but are the same when evaluated at the same frequencies by interpolation. The separation ratios trace the phase shift differences as a function of frequency, not of n, and it is the phase shift differences which are determined by the interior structure. We give examples from model fitting where the ratios at the same n values agree but the models have different interior structure, and where the ratios agree when interpolated to the same frequencies and the models have the same interior structure. The correct procedure is to compare observed ratios with model values interpolated to the observed frequencies.
Key words: stars: oscillations / asteroseismology / stars: interiors / methods: analytical / methods: numerical / stars: solar-type
© ESO, 2013
1. Introduction
The ratio of small to large separations of stellar p-modes as a diagnostic of the internal structure of stars was proposed in Roxburgh & Vorontsov (2003) (see also Roxburgh 2004, 2005; Otí Floranes et al. 2005) and is increasingly being used in model fitting, that is finding that model (or models), out of a set models, whose separation ratios best fit the ratios of the observed frequencies. These ratios, defined in terms of the frequencies νnℓ as (Roxburgh & Vorontsov 2003) 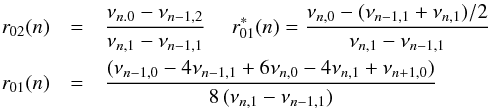 (1)(and similarly defined ratios
(1)(and similarly defined ratios 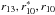 ) subtract off the major contribution of the outer layers of a star and so constitute a diagnostic of the stellar interior that is almost independent of the structure of the outer layers of a star which are subject to considerable uncertainties in modelling.
) subtract off the major contribution of the outer layers of a star and so constitute a diagnostic of the stellar interior that is almost independent of the structure of the outer layers of a star which are subject to considerable uncertainties in modelling.
This validity of this procedure rests on the result that that the contribution of the outer layers of a star to the oscillation frequencies νnℓ is very nearly independent of the degree ℓ; the separation ratios are combinations of frequencies that seek to subtract off this ℓ independent contribution.
We here point out that seeking a best fit model by direct comparison of observational and model ratios at the same {n,ℓ} values, e.g. searching for minimum in the reduced  where
where 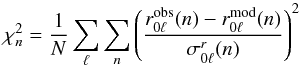 (2)is, in principle, incorrect, and can give misleading, indeed erroneous results. Here
(2)is, in principle, incorrect, and can give misleading, indeed erroneous results. Here 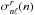 are the error estimates on the ratios derived from σnℓ, the error estimates on the frequencies νnℓ, and N is the number of ratios. We show below that the correct procedure is to compare the observed ratios with the model ratios interpolated to the observed frequencies.
are the error estimates on the ratios derived from σnℓ, the error estimates on the frequencies νnℓ, and N is the number of ratios. We show below that the correct procedure is to compare the observed ratios with the model ratios interpolated to the observed frequencies.
2. Examples
To illustrate this we take a model “observed” star of mass 1.2 M⊙, radius 1.34 R⊙, luminosity 2.45 L⊙, effective temperature Teff = 6242° K, central hydrogen abundance Xc = 0.30 and age of 2.90 × 109 ys. We assume a total of 33 “observed” frequencies (11 n values, ℓ = 0,1,2) in the range 1534 − 2550 μHz which have a mean large separation Δ = ⟨νn,0 − νn − 1,0⟩ = 96.2 μHz. For illustrative purposes, we assume a constant error on the frequencies of σν = 0.2 μHz since, for the “best” observed stars from CoRoT and Kepler (eg HD 43587, 16CygA) the errors typically lie in the range 0.1 − 0.3 μHz (cf. Appourchaux et al. 2012).
 |
Fig. 1 Internal structure of the “observed” and model stars. |
 |
Fig. 2 Top panel: the separation ratios r01(n) for model99 (triangles) and scaled model (squares) superimposed on those for the “observed” star; bottom panel: the same but for the r02 ratios. |
We then constructed two extreme comparison models:
- 1.
A “scaled model” with the same dimensionless interior structure: density ρ(r)/(M/R3), pressure P(r)/(GM2/R4) and adiabatic exponent Γ1(r) as functions of the dimensionless radius x = r/R as the “observed’ star, but with a mass of 1.35 M⊙, and radius of 1.25 R⊙. This model has a mean large separation of ~ 114 μHz;
- 2.
“model99” which has the same interior structure as our “observed” star ρ(r),P(r),Γ1(r) but is truncated at a radius 0.99 Ro where Ro is the radius of the “observed” star. This model has a mean large separation Δ ~ 112 μHz.
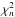 for model99 of 2.2 which for 20 ratios has a probability of being due to chance of 0.1%. In Fig. 3 we plot the ratios r0ℓ(n) against frequencies ν0n for the “observed” and comparison models. The scaled model does not agree with the “observed” model, whereas the truncated model values, whilst not evaluated at the same frequencies as the “observed” model, lie on a cubic interpolated curve through the “observed” values. Comparing ratios at the same n values (Eq. (2)) therefore tests the functional form of the dimensionless structure of the stellar interior but not the physical values, nor the mass and radius. If the scaled model has the same M/R3 as the “observed” star then the r0ℓ(n) would coincide since the frequencies are invariant under a scaling that keeps M/R3 constant.
for model99 of 2.2 which for 20 ratios has a probability of being due to chance of 0.1%. In Fig. 3 we plot the ratios r0ℓ(n) against frequencies ν0n for the “observed” and comparison models. The scaled model does not agree with the “observed” model, whereas the truncated model values, whilst not evaluated at the same frequencies as the “observed” model, lie on a cubic interpolated curve through the “observed” values. Comparing ratios at the same n values (Eq. (2)) therefore tests the functional form of the dimensionless structure of the stellar interior but not the physical values, nor the mass and radius. If the scaled model has the same M/R3 as the “observed” star then the r0ℓ(n) would coincide since the frequencies are invariant under a scaling that keeps M/R3 constant.
 |
Fig. 3 Top panel: the separation ratios r01(ν) for model99 (triangles) and scaled model (squares) superimposed on those for the “observed” star; bottom panel: the same but for the r02 ratios. |
3. Separation ratios and phase shifts ϵ(ν)
The eigenfrequencies of a slowly rotating star can always be expressed in the form ![\begin{equation} \nu_{n\ell} ={\bar \Delta}\,\left[ n + \ell/2 + \epsilon_\ell(\nu_{n\ell}) \right] \end{equation}](/articles/aa/full_html/2013/12/aa21333-13/aa21333-13-eq46.png) (3)where
(3)where 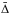 is some estimate of the mean large separation, and the phase shifts ϵℓ(νnℓ) are determined at the eigenfrequencies from this equation. The ϵℓ(νnℓ) contain all the information on the departure of the structure of the star from a uniform sphere whose frequencies are the roots of the spherical Bessel functions which rapidly approach
is some estimate of the mean large separation, and the phase shifts ϵℓ(νnℓ) are determined at the eigenfrequencies from this equation. The ϵℓ(νnℓ) contain all the information on the departure of the structure of the star from a uniform sphere whose frequencies are the roots of the spherical Bessel functions which rapidly approach ![\hbox{${\bar \Delta}\, [n + \ell/2 ]$}](/articles/aa/full_html/2013/12/aa21333-13/aa21333-13-eq49.png) as n increases (Rayleigh 1894).
as n increases (Rayleigh 1894).
As shown in Roxburgh & Vorontsov (2000, 2003) (see Sect. 6 below) the ϵℓ(ν) can be effectively split into an ℓ dependent inner contribution determined by the structure of the interior of the star, and an (almost) ℓ independent outer contribution determined by the structure of the outer layers. Interpolating in ϵℓ(ν), which is known at the frequencies νnℓ, to determine the value at any ν, and subtracting values for different ℓ, cancels out both the ℓ independent contribution from the outer layers and the linear term 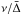 ; the differences ϵ0(ν) − ϵℓ(ν) as a function of ν being determined solely by the structure of the inner layers. The separation ratios r0ℓ are approximations to values of ϵ0(ν) − ϵℓ(ν) at the frequencies νn0.
; the differences ϵ0(ν) − ϵℓ(ν) as a function of ν being determined solely by the structure of the inner layers. The separation ratios r0ℓ are approximations to values of ϵ0(ν) − ϵℓ(ν) at the frequencies νn0.
 |
Fig. 4 Top panel: phase shifts ϵℓ(νnℓ), and interpolated curves ϵℓ(ν); middle panel: phase shift differences ϵ0(ν) − ϵ1(ν) and the 9 separation ratios r01: bottom panel as above but for the 11 r02. |
The top panel in Fig. 4 shows the phase shifts ϵℓ(νnℓ) at the “observed” frequencies for our “observed” star, and the cubic interpolated curves ϵℓ(ν), the bottom panels show the phase shift differences ϵ0(ν) − ϵℓ(ν) together with the separation ratios r01,r02 which lie on or close to the curves ϵ0(ν) − ϵℓ(ν).
If we now compare the separation ratios of a star with observed frequencies 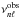 to those of a model with different frequencies
to those of a model with different frequencies 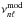 (as in Eq. (2)) then we are comparing the values of the phase shift differences ϵℓ(ν) − ϵ0(ν) at different frequencies so, even if the star and model have the same interior structure, that is the same ϵℓ(ν) − ϵ0(ν) as a function of ν, they will not have the same values of the separation ratios at their respective {n,ℓ} values. This explains why the ratios for model99 in Fig. 3 are offset from the “observed” values. The scaled model on the other hand has a different interior structure and therefore a different function for its phase shift differences.
(as in Eq. (2)) then we are comparing the values of the phase shift differences ϵℓ(ν) − ϵ0(ν) at different frequencies so, even if the star and model have the same interior structure, that is the same ϵℓ(ν) − ϵ0(ν) as a function of ν, they will not have the same values of the separation ratios at their respective {n,ℓ} values. This explains why the ratios for model99 in Fig. 3 are offset from the “observed” values. The scaled model on the other hand has a different interior structure and therefore a different function for its phase shift differences.
In summary the separation ratios of model99 with the same interior structure as the “observed” star lie on the same ϵ0(ν) − ϵℓ(ν) curves as those of the “observed” star when considered as a function of frequency, but disagree as a function of radial order n. Conversely the ratios for the scaled model which has a different interior structure from that of the “observed” star agree with the observations when considered as a function of n, but do not lie on the same ϵ0(ν) − ϵℓ(ν) curves as those of the “observed” star when considered as a function of frequency.
This demonstrates that seeking a best fit model by comparing separation ratios at the same n values can give erroneous results.
This is not surprising, the radial order n of an eigenfrequency depends on the structure of the outer layers of a star as well as on the interior structure, being determined approximately by the integral number of wavelengths that fit into the acoustic radius of the star T = ∫dr/c where c is the sound speed. Since c is small in the outer layers these layers can make a significant contribution to the acoustic radius. So the n values are not independent of the structure of the outer layers; comparing observed and model separation ratios at the same n does not subtract off the effect of the outer layers.
 |
Fig. 5 Comparison of “observed” with model99 ratios interpolated to the “observed” frequencies. |
4. Correcting the model fitting
This comparison procedure can be corrected by interpolating the values of the model separation ratios 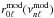 , which can be calculated for any { n,ℓ } values, to derive values
, which can be calculated for any { n,ℓ } values, to derive values 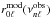 at the observed frequencies, and then comparing the interpolated model ratios to the observed ratios. The results using local cubic interpolation on model99 ratios are shown in Fig. 5 along with the separate
at the observed frequencies, and then comparing the interpolated model ratios to the observed ratios. The results using local cubic interpolation on model99 ratios are shown in Fig. 5 along with the separate 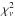 for the r0ℓ separations. The total
for the r0ℓ separations. The total 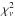 defined as
defined as 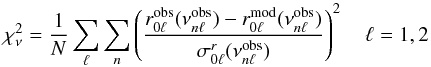 (4)is 0.006 (with σν = 0.2 μHz). The “observed” and interpolated model values are in excellent agreement. This is the procedure to be used in comparing observed and model separation ratios; it is independent of the n values the astronomer assigns to the frequencies.
(4)is 0.006 (with σν = 0.2 μHz). The “observed” and interpolated model values are in excellent agreement. This is the procedure to be used in comparing observed and model separation ratios; it is independent of the n values the astronomer assigns to the frequencies.
 |
Fig. 6 “Observed” and model ratios r01,r02 as functions of radial order n for 4 models within the L,Teff error box in the H-R diagram and their separate |
5. Examples from model fitting
The above example is somewhat extreme, although it illustrates the point we are making. We therefore undertook a study which closely follows a realistic model fitting procedure, taking our “observed” star and seeking best fit models out of a large data base of models. The data base we use was kindly supplied by Miglio (priv. comm.) and contains over 200 000 models, computed using the CLES and OSC codes (Scuflaire et al. 2008a,b). The model set has masses in the range 1.04 − 1.5 M⊙, 4 values of the initial Hydrogen abundance XH = 0.684,0.694,0,704,0.714, 4 values of heavy element abundance Z = 0.015,0.02,0.025,0.03, 2 values of the mixing length parameter αcon = 1.705,1.905, 2 values of a chemical overshoot parameter αov = 0,0.2Hp and with and without microscopic diffusion (details of the physics are given in Scuflaire et al. 2008a). The models are evolved from the pre-main sequence to the sub-giant phase. Our “observed” star has similar physics with XH = 0.7,Z = 0.02,αcon = 1.6,αov = 0 and no diffusion (cf. Roxburgh 2008a).
We searched for best fit models that lie within an error box in the HR-diagram around the “observed” star defined by Teff = 6242 ± 70°K, L/L⊙ = 2.45 ± 0.245, these being realistic error estimates. Some 1,324 models lie within the error box in the HR diagram of which 53 have both 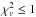 and
and 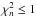 ; 38 have
; 38 have 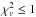 and
and 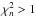 ; and 17 have
; and 17 have 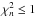 and
and 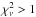 . The fact that a large proportion of the models which have
. The fact that a large proportion of the models which have 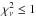 also have
also have 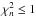 is not a great surprise; if the ϵ0(ν) − ϵℓ(ν) are slowly varying functions of ν, their difference,
is not a great surprise; if the ϵ0(ν) − ϵℓ(ν) are slowly varying functions of ν, their difference, 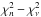 , is given by
, is given by ![\begin{equation} \chi^2_{n}-\chi^2_\nu \approx {1\over N} \sum_\ell \sum_n \left( {1\over\sigma^r_{n\ell}} {{\rm d}\left(\epsilon_0-\epsilon_\ell\right)\over {\rm d}\nu} \left[\nu^{\rm mod}_{n\ell} -\nu^{\rm obs}_{n\ell}\right] \right)^2 \end{equation}](/articles/aa/full_html/2013/12/aa21333-13/aa21333-13-eq95.png) (5)so if d(ϵℓ − ϵ0)/dν is small, and the frequency offset
(5)so if d(ϵℓ − ϵ0)/dν is small, and the frequency offset 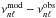 is not too large, this difference is small.
is not too large, this difference is small.
 |
Fig. 7 “Observed” and model ratios r01,r02 for the 4 models within the L,Teff error box in the H-R diagram interpolated to the “observed” frequencies, and their separate |
To illustrate the point that matching observed and model ratios at the same n values can lead to erroneous inferences we show in Fig. 6 the ratios for 4 models that lie within the L,Teff error box in the HR diagram and have a combined 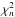 of 0.32,0.42,0.53,0.66; apparently good fits to the “observed” data. Details of the models are given in Table 1, they all include diffusion, have the same heavy element abundance Z and similar ages (age9 is the age in units of 109 years). However if we interpolate for the values of the ratios at the “observed” frequencies the fit is not so good – this is shown in Fig. 7; the combined
of 0.32,0.42,0.53,0.66; apparently good fits to the “observed” data. Details of the models are given in Table 1, they all include diffusion, have the same heavy element abundance Z and similar ages (age9 is the age in units of 109 years). However if we interpolate for the values of the ratios at the “observed” frequencies the fit is not so good – this is shown in Fig. 7; the combined 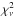 for the 4 models are 2.06,2.45,2.61,2.10 which for for the best case has has a probability of being due to chance of 0.22%.
for the 4 models are 2.06,2.45,2.61,2.10 which for for the best case has has a probability of being due to chance of 0.22%.
Properties of the 4 models with 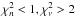 .
.
 |
Fig. 8 Internal structure of the “observed” star and that of the 4 models obtained by fitting at the same n values. |
Properties of the 10 models with the lowest 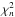 .
.
In Fig. 8 we compare the sound speed and density of the 4 models in the inner layers with that of the “observed” star; the models have a higher central temperature, lower central density and larger convective core (the core boundary being at the point of increase in c2). This demonstrates that models that fit the observed ratios when compared at the same n values (within reduced 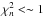 for σν = 0.2 μHz) may not fit the observed ratios when compared at the observed frequencies and can have an interior structure that is not that of the observed star.
for σν = 0.2 μHz) may not fit the observed ratios when compared at the observed frequencies and can have an interior structure that is not that of the observed star.
 |
Fig. 9 Internal structure of the observed star and that of the best 10 models obtained by fitting at the same n values. |
 |
Fig. 10 Comparison of “observed” ratios with those of the best 10 models interpolated to the observed frequencies. |
The above examples were chosen to illustrate the argument advanced in this paper – but they are not the models with the lowest reduced 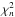 . The 10 best fit models when compared at the same n values have a combined reduced
. The 10 best fit models when compared at the same n values have a combined reduced 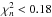 ; details of these models are given in Table 2 and their inner structure is shown in Fig. 9. 4 of the 10 models (numbers 2,4,7,10) fit the structure very well; but all 4 also have a very small reduced
; details of these models are given in Table 2 and their inner structure is shown in Fig. 9. 4 of the 10 models (numbers 2,4,7,10) fit the structure very well; but all 4 also have a very small reduced 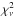 (also shown in Table 2) and are amongst the 10 best fit models obtained by comparing at the “observed” frequencies (see Table 3 below). As pointed out above the difference between ν and n comparison (Eq. (5)) can be small. The other 6 models, which includes the model with the lowest
(also shown in Table 2) and are amongst the 10 best fit models obtained by comparing at the “observed” frequencies (see Table 3 below). As pointed out above the difference between ν and n comparison (Eq. (5)) can be small. The other 6 models, which includes the model with the lowest 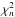 , are not such good fits, having larger convective cores, lower central densities and higher central temperatures.
, are not such good fits, having larger convective cores, lower central densities and higher central temperatures.
Were one to seek a best fit model by comparing ratios at the same n values, the model with the lowest 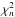 would not necessarily reproduce the internal structure of the observed star. Matching ratios at the same n values can therefore give erroneous results on the interior structure of an observed star, and on the physical processes that govern stellar evolution.
would not necessarily reproduce the internal structure of the observed star. Matching ratios at the same n values can therefore give erroneous results on the interior structure of an observed star, and on the physical processes that govern stellar evolution.
 |
Fig. 11 Comparison of the internal structure of the observed star with those of the best 10 models. |
Properties of the 10 models with the lowest 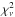 .
.
The 10 best fit models when comparing ratios interpolated to the “observed” frequencies are illustrated in Fig. 10 and details of the models are given in Table 3. The fits are very good with 9 of the 10 models having a 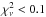 . The internal structure of these models is shown in Fig. 11; all the models satisfactorily reproduce the internal structure of the “observed” star. Note that models 1,4,5,7 in Table 3 are the same as models 7,4,10,2 in Table 2 and are the 4 models that fit the internal structure of the “observed” star in Fig. 9.
. The internal structure of these models is shown in Fig. 11; all the models satisfactorily reproduce the internal structure of the “observed” star. Note that models 1,4,5,7 in Table 3 are the same as models 7,4,10,2 in Table 2 and are the 4 models that fit the internal structure of the “observed” star in Fig. 9.
The properties of the best fit model with 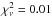 are very close to those of the “observed” star and all 10 models have very similar central hydrogen abundances and ages. But the masses range from 1.16 − 1.22 M⊙, the smaller masses having lowest initial hydrogen content, some models incorporate diffusion and some do not, and all models have a large separation Δ greater than that of the “observed” model (96.2 μHz).
are very close to those of the “observed” star and all 10 models have very similar central hydrogen abundances and ages. But the masses range from 1.16 − 1.22 M⊙, the smaller masses having lowest initial hydrogen content, some models incorporate diffusion and some do not, and all models have a large separation Δ greater than that of the “observed” model (96.2 μHz).
 |
Fig. 12 Offset of frequencies of the 10 best fit models from those of the “observed” star. |
The difference between the observed frequencies 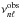 and the model frequencies
and the model frequencies 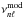 , often referred to as the “frequency offset” is plotted in Fig. 12 for the all 10 models. These offsets can be extremely large even though the interior structure of the models agrees well with that of the “observed” star. This reflects the fact that the large separations Δ of the models are larger than that of the “observed” star by 1.4 − 7.4 μHz; to lowest order the frequencies νnℓ are approximately (n + ℓ/2)Δ and for modes of radial order n = 20 this gives an approximate offset in the range 30 − 150 μHz, in agreement with that shown in Fig. 12.
, often referred to as the “frequency offset” is plotted in Fig. 12 for the all 10 models. These offsets can be extremely large even though the interior structure of the models agrees well with that of the “observed” star. This reflects the fact that the large separations Δ of the models are larger than that of the “observed” star by 1.4 − 7.4 μHz; to lowest order the frequencies νnℓ are approximately (n + ℓ/2)Δ and for modes of radial order n = 20 this gives an approximate offset in the range 30 − 150 μHz, in agreement with that shown in Fig. 12.
6. Separation ratios and internal phase shifts
The frequencies of a spherical star satisfy an Eigenfrequency equation of the form (Roxburgh & Vorontsov 2000) ![\begin{equation} 2 T \nu_{n\ell}= \big[n+\ell/2 + \alpha_\ell(\nu) -\delta_\ell(\nu)\big],~~~{\rm where}~~T=\int_0^R{{\rm d}r\over c} \end{equation}](/articles/aa/full_html/2013/12/aa21333-13/aa21333-13-eq199.png) (6)is the acoustic radius of the star and c the sound speed. The inner phase shift δℓ(ν) is determined by the structure interior to some fitting point rf, and outer phase shifts αℓ(ν) by the structure above rf. This is exactly true for modes of degree ℓ = 0,1 where the oscillation equations reduce to 2nd order (Takata 2005; Roxburgh 2006, 2008b), and holds to high accuracy for ℓ = 2 provided rf is in the low density outer layers of the star. Eq. (6) is identical in form to that of Eq. (3) with ϵℓ = αℓ − δℓ and
(6)is the acoustic radius of the star and c the sound speed. The inner phase shift δℓ(ν) is determined by the structure interior to some fitting point rf, and outer phase shifts αℓ(ν) by the structure above rf. This is exactly true for modes of degree ℓ = 0,1 where the oscillation equations reduce to 2nd order (Takata 2005; Roxburgh 2006, 2008b), and holds to high accuracy for ℓ = 2 provided rf is in the low density outer layers of the star. Eq. (6) is identical in form to that of Eq. (3) with ϵℓ = αℓ − δℓ and 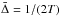 . The important difference is that since the density, sound speed, and curvature effects are small in the outer layers, the αℓ(ν) are almost independent of degree ℓ.
. The important difference is that since the density, sound speed, and curvature effects are small in the outer layers, the αℓ(ν) are almost independent of degree ℓ.
To see this we define αℓ(ν,t),δℓ(ν,t) at any radius and frequency in terms of the functions ψℓ(ν,t) = rp′/(ρc)1/2 by ![\begin{eqnarray} &&\tan[2\pi\nu\,t -\ell\pi/2+ \pi \delta_\ell(\nu, t)] = {2\pi\nu\psi_\ell\over {\rm d}\psi_\ell/{\rm d}t} ~~~~~~~~t =\int_0^r {{\rm d}r\over c(r)} \notag \\ &&\tan[2\pi\nu\,\tau - \pi \alpha_\ell(\nu, \tau)] = {2\pi\nu\psi_\ell\over {\rm d}\psi_\ell/{\rm d}\tau} ~~~~~~~~~~~~~~\tau=\int_R^r {{\rm d}r\over c(r)} \end{eqnarray}](/articles/aa/full_html/2013/12/aa21333-13/aa21333-13-eq209.png) (7)where p′ is the Eulerian pressure perturbation, t is the acoustic radius, τ = T − t the acoustic depth, and ν any frequency (not restricted to an eigenfrequency). In the outer sub-surface layers the functions ψℓ(ν,t) are almost pure sine waves with constant phase shift, and the phase shifts are almost independent of the choice of fitting point rf (or tf) (Roxburgh & Vorontsov 1996). In Fig. 13 we show the differences α2(ν) − α0(ν) and δℓν) − δ0(ν) for the “observed” 1.2 M⊙ star, evaluated at radii xf = rf/R = 0.93,0.95, 0.97; the differences α1(ν) − α0(ν) ≈ [ α2(ν) − α0(ν) ] /3.
(7)where p′ is the Eulerian pressure perturbation, t is the acoustic radius, τ = T − t the acoustic depth, and ν any frequency (not restricted to an eigenfrequency). In the outer sub-surface layers the functions ψℓ(ν,t) are almost pure sine waves with constant phase shift, and the phase shifts are almost independent of the choice of fitting point rf (or tf) (Roxburgh & Vorontsov 1996). In Fig. 13 we show the differences α2(ν) − α0(ν) and δℓν) − δ0(ν) for the “observed” 1.2 M⊙ star, evaluated at radii xf = rf/R = 0.93,0.95, 0.97; the differences α1(ν) − α0(ν) ≈ [ α2(ν) − α0(ν) ] /3.
As can be seen in Fig. 13 the αℓ(ν) − α0(ν) are less than 1% of the differences δℓ(ν) − δ0(ν), and the values of δℓ(ν) − δ0(ν) are almost independent of the fitting point xf. So, to a good approximation, the phase differences 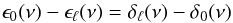 (8)and are therefore determined by the interior structure of the star.
(8)and are therefore determined by the interior structure of the star.
 |
Fig. 13 Phase shift differences α2(ν) − α0(ν) and δℓ(ν) − δ0(ν) at fractional radii xf = 0.93,0.95,0.97 for the “observed” “star”. |
7. Conclusions and comments on model fitting
The separation ratios are an approximation to the phase shift differences ϵ0(ν) − ϵℓ(ν) which are determined by the structure of the stellar interior and are almost independent of the structure of the outer layers. One should not compare the ratios 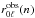 of an observed frequency set with the
of an observed frequency set with the 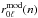 of a model at the same n values since one is not comparing values of ϵ0(ν) − ϵℓ(ν) at the same frequencies. This can be corrected by interpolating in the model values
of a model at the same n values since one is not comparing values of ϵ0(ν) − ϵℓ(ν) at the same frequencies. This can be corrected by interpolating in the model values 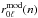 to determine the model ratios at the observed frequencies
to determine the model ratios at the observed frequencies 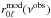 and then comparing observed and model values. Alternatively one could compute the phase shift differences from the model and compare the observed ratios with the values of the model phase shift differences at the observed frequencies.
and then comparing observed and model values. Alternatively one could compute the phase shift differences from the model and compare the observed ratios with the values of the model phase shift differences at the observed frequencies.
The error in comparing ratios at the same n values depends both on the scale of variation of ϵ0 − ϵℓ and the difference in frequencies at the same n values (Eq. (5)). For the model fitting examples given here, where the models and the “observed” star have almost the same governing physics, we find many models that have both 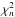 and
and 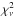 less than one (with an error on the frequencies of 0.2 μHz), but even so we find examples where
less than one (with an error on the frequencies of 0.2 μHz), but even so we find examples where 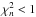 but
but 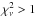 and the models do not have the same interior as the “observed” star, the difference being large enough to lead to erroneous conclusions on the structure, age, and physical processes that govern stellar evolution.
and the models do not have the same interior as the “observed” star, the difference being large enough to lead to erroneous conclusions on the structure, age, and physical processes that govern stellar evolution.
The fact that we find so many models (91) with 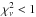 indicates the limits of model fitting using ratios. We have only 20 data to match, each being an integral over the interior structure, different structures can therefore give approximately the same ratios, differences in structure in one region being compensated by differences in other regions. To overcome this one needs considerably higher precision on the data – in the examples given here a σν ~ 0.06 μHz – or considerable more data points.
indicates the limits of model fitting using ratios. We have only 20 data to match, each being an integral over the interior structure, different structures can therefore give approximately the same ratios, differences in structure in one region being compensated by differences in other regions. To overcome this one needs considerably higher precision on the data – in the examples given here a σν ~ 0.06 μHz – or considerable more data points.
In the above analysis we have taken the error estimate on the frequencies to be independent of frequency whereas, in general, both the error estimates on observed frequencies (σν), and the error in comparing ratios at the same n values, are larger at high frequencies leading to a somewhat smaller value of 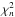 than obtained using a constant average value of σν. But the general point remains valid; a model that has the same values of the separation ratios as an observed set when compared at the same n values, and which does not have the same frequencies, does not have the same internal structure as the observed star.
than obtained using a constant average value of σν. But the general point remains valid; a model that has the same values of the separation ratios as an observed set when compared at the same n values, and which does not have the same frequencies, does not have the same internal structure as the observed star.
A further comment is in order. Since the objective of using separation ratios is to subtract off the unknown effect of the outer layers of a star it can only yield a best fit to the interior structure. It is inconsistent to impose strict constraints on the radius, effective temperature, surface gravity, metallicity, and large separations derived by observations, since these all depend on the structure of the outer layers and non-adiabatic effects, which we seek to eliminate by using ratios. The luminosity on the other hand is determined by the interior structure alone, as is the mass which, in principle, can be estimated from surface gravity and surface radius; these can provide additional surface layer independent constraints on the model fitting.
Acknowledgments
We thank Andrea Miglio who generously provided the large data base of models used in the model fitting. I. W. Roxburgh gratefully acknowledges support from the Leverhulme Foundation under grant EM-2012-035/4.
References
- Appourchaux, T., Chaplin, W. J., García, R. A., et al. 2012, A&A, 543, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Otó Floranes, H., Christensen-Dalsgaard, J., & Thompson, M. J. 2005, MNRAS, 356, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Rayleigh, Lord (J. W. Strutt) 1894, Theory of Sound, 2nd edn. (Macmillan) [Google Scholar]
- Roxburgh, I. W. 2004, Proc 2nd Eddington Workshop, Palermo, 2003, ESA SP, 538, 23 [NASA ADS] [Google Scholar]
- Roxburgh, I. W. 2005, A&A, 434, 665 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roxburgh, I. W. 2006, http://www.maths.qmul.ac.uk/~iwr/oscodes/L1modes.pdf [Google Scholar]
- Roxburgh, I. W. 2008a, Ap&SS, 316, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W. 2008b, Ap&SS, 316, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 1996, MNRAS, 278, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 2000, MNRAS, 317, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 2003, A&A, 411, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scuflaire, R., Théado, S., Montalbán, J., et al. 2008a, Ap&SS, 316, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Scuflaire, R., Montalbán, J., Théado, S., et al. 2008b, Ap&SS, 316, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Takata, M. 2005, PASJ, 57, 375 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Internal structure of the “observed” and model stars. |
| In the text | |
 |
Fig. 2 Top panel: the separation ratios r01(n) for model99 (triangles) and scaled model (squares) superimposed on those for the “observed” star; bottom panel: the same but for the r02 ratios. |
| In the text | |
 |
Fig. 3 Top panel: the separation ratios r01(ν) for model99 (triangles) and scaled model (squares) superimposed on those for the “observed” star; bottom panel: the same but for the r02 ratios. |
| In the text | |
 |
Fig. 4 Top panel: phase shifts ϵℓ(νnℓ), and interpolated curves ϵℓ(ν); middle panel: phase shift differences ϵ0(ν) − ϵ1(ν) and the 9 separation ratios r01: bottom panel as above but for the 11 r02. |
| In the text | |
 |
Fig. 5 Comparison of “observed” with model99 ratios interpolated to the “observed” frequencies. |
| In the text | |
 |
Fig. 6 “Observed” and model ratios r01,r02 as functions of radial order n for 4 models within the L,Teff error box in the H-R diagram and their separate |
| In the text | |
 |
Fig. 7 “Observed” and model ratios r01,r02 for the 4 models within the L,Teff error box in the H-R diagram interpolated to the “observed” frequencies, and their separate |
| In the text | |
 |
Fig. 8 Internal structure of the “observed” star and that of the 4 models obtained by fitting at the same n values. |
| In the text | |
 |
Fig. 9 Internal structure of the observed star and that of the best 10 models obtained by fitting at the same n values. |
| In the text | |
 |
Fig. 10 Comparison of “observed” ratios with those of the best 10 models interpolated to the observed frequencies. |
| In the text | |
 |
Fig. 11 Comparison of the internal structure of the observed star with those of the best 10 models. |
| In the text | |
 |
Fig. 12 Offset of frequencies of the 10 best fit models from those of the “observed” star. |
| In the text | |
 |
Fig. 13 Phase shift differences α2(ν) − α0(ν) and δℓ(ν) − δ0(ν) at fractional radii xf = 0.93,0.95,0.97 for the “observed” “star”. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


