| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 4 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201322452 | |
| Published online | 29 October 2013 | |
Research Note
Measuring galaxy [O ii] emission line doublet with future ground-based wide-field spectroscopic surveys
1
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de
Marseille) UMR 7326,
13388
Marseille,
France
e-mail:
johan.comparat@lam.fr
2
Laboratoire d’astrophysique, École Polytechnique Fédérale de
Lausanne (EPFL), Observatoire de Sauverny, 1290
Versoix,
Switzerland
3
CRAL, Observatoire de Lyon, Université Lyon 1,
9 avenue Ch. André,
69561
Saint-Genis-Laval Cedex,
France
4
Lawrence Berkeley National Laboratory,
1 Cyclotron Road,
Berkeley, CA
94720,
USA
5
Department of Physics and Astronomy, University of Pittsburgh and
PITT-PACC, 3941 O’Hara
St., Pittsburgh,
PA
15260,
USA
6
CEA, Centre de
Saclay, IRFU, 91191
Gif-sur-Yvette,
France
Received:
6
August
2013
Accepted:
20
September
2013
The next generation of wide-field spectroscopic redshift surveys will map the large-scale galaxy distribution in the redshift range 0.7 ≤ z ≤ 2 to measure baryonic acoustic oscillations (BAO). The primary optical signature used in this redshift range comes from the [Oii] emission line doublet, which provides a unique redshift identification that can minimize confusion with other single emission lines. To derive the required spectrograph resolution for these redshift surveys, we simulate observations of the [Oii] (λλ 3727, 3729) doublet for various instrument resolutions, and line velocities. We foresee two strategies for the choice of the resolution for future spectrographs for BAO surveys. For bright [Oii] emitter surveys ([Oii] flux ~30 × 10-17 erg cm-2 s-1 like SDSS-IV/eBOSS), a resolution of R ~ 3300 allows the separation of 90 percent of the doublets. The impact of the sky lines on the completeness in redshift is less than 6 percent. For faint [Oii] emitter surveys ([Oii] flux ~10 × 10-17 erg cm-2 s-1 like DESi), the detection improves continuously with resolution, so we recommend the highest possible resolution, the limit being given by the number of pixels (4k by 4k) on the detector and the number of spectroscopic channels (2 or 3).
Key words: instrumentation: spectrographs / techniques: spectroscopic / cosmology: observations / galaxies: statistics
© ESO, 2013
1. Introduction
Following the successful baryonic acoustic oscillation (BAO) measurement in the galaxy clustering from the Sloan Digital Sky Survey (SDSS; Eisenstein et al. 2005), and the 2 degree Field Galaxy Redshift Survey (2dFGRS; Cole et al. 2005), WiggleZ (Blake et al. 2011), and the Baryonic Oscillation Spectroscopic Survey (BOSS; Anderson et al. 2012), there is a strong motivation in the community to plan the next generation of spectroscopic redshift surveys for BAO. In particular, the future ground-based surveys plan to map the galaxy distribution in the redshift range 0.7 ≤ z ≤ 2 and use the galaxy power spectrum to precisely measure the BAO signature and constrain the cosmological parameters.
Two examples of this new paradigm are the following projects: the Sloan Digital Sky Survey, extended Baryonic Oscillation Spectroscopic Survey (SDSS-IV/eBOSS) and the Dark Energy Spectroscopic instrument (DESi). The SDSS-IV/eBOSS dark energy experiment starts observing in 2014 with SDSS-III/BOSS infrastructure (1000 fibers on ~7 deg2). This survey will measure about 1.5 million spectroscopic redshifts of QSOs in the redshift range 0.9 < z < 2.5 and galaxies with a redshift in 0.6 < z < 1.2. The DESi project plans to map 14 000 deg2 of sky using 5000 motorized fibers over a 7 deg2 field of view and to measure 22 million galaxy redshifts (see Schlegel et al. 2011, for a global survey description and Mostek et al. 2012, for the current survey parameters).
Galaxy redshifts will be mostly determined from the emission line features of star-forming galaxies between 0.7 ≤ z ≤ 2. Table 1 lists the primary emission lines that are available at optical and near-infrared wavelengths within this redshift range. Of these lines, the [Oii] doublet at (λ3727,λ3729) will provide the most consistently available feature. In order to avoid confusion with other prominent emission lines (Hα, Hβ, [Oiii]), the [Oii] doublet should be resolved over the instrumented wavelength range where no other lines are available to make an unambiguous identification.
Emission lines available at optical and near-infrared wavelengths.
Previous emission line redshift surveys have had different strategies concerning the use of emission lines for measuring the redshift. The WiggleZ Survey with a spectral resolution of 1300, obtained 60% of reliable redshifts (18% based on the detection of the [Oii] doublet, i.e. the doublet is resolved or partially resolved), and 40% of unreliable redshifts (Drinkwater et al. 2010). The DEEP2 Survey, with a resolution of 6000, obtained 71% of reliable redshifts (14.8% based on the detection of the [Oii] doublet, i.e. the doublet is resolved or partially resolved), 10% between reliable and unreliable, and 19% of unreliable redshifts (Newman et al. 2013). The difference between these redshift efficiencies is related to the resolution of the spectrograph and the wavelength it covers. If the [Oii] emission is the only one available in the spectrum, at high resolution the doublet is split and the redshift is reliable. Instead, at lower resolution the [Oii] doublet is not always split and may be taken for another emission line.
In Sect. 2, we derive the minimum resolution necessary to resolve the doublet in the case of an observation without noise. In Sect. 3, we describe our simulation of [Oii] doublet detections based on DEEP2 spectral observations. We discuss the results of our simulation in Sect. 4.
2. Instrument requirements
First, we define our notation: R = λ/FWHMλ is the resolution of the spectrograph; λa = 3727.092 Å and λb = 3729.875 Å are the individual [Oii] emission wavelengths and λ[Oii] = (λa ∗ 3.326568 + λb ∗ 3.324086)/(3.326568 + 3.324086) = 3728.483 Å is the energy-weighted mean [Oii] wavelength. The observed wavelength separation between the emission lines depends on the redshift δ[Oii](z) = (λb − λa)(1 + z) = 2.783(1 + z). We can thus define the resolution R[Oii] as the minimal resolution required to properly sample a theoretical [Oii] doublet (with zero intrinsic width) without loss of information by R[Oii] = 2(1 + z)λ[Oii]/δ[Oii](z) = 2679 (Nyquist-Shannon sampling theorem, Shannon & Weaver 1975). We note that R[Oii] is independent of redshift.
A real galaxy, however, has an intrinsic velocity dispersion
Δv that broadens the emission lines from a theoretical Dirac
δ-function profile. Assuming the line profile is dominated by thermal
Doppler broadening in the host galaxy interstellar medium, the observed wavelength width
δλv of the broadened
[Oii] line profiles is defined in Eq. (1) where c is the speed of light: 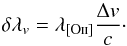 (1)In this simplified
case, the intrinsic velocity dispersion is equivalent to the standard deviation in a
Gaussian profile. For example, a galaxy at z = 1 with
Δv = 50 km s-1 has a line width of
δλv ~ 0.6 Å, which
represents ~10% of the wavelength separation between the doublet peaks.
(1)In this simplified
case, the intrinsic velocity dispersion is equivalent to the standard deviation in a
Gaussian profile. For example, a galaxy at z = 1 with
Δv = 50 km s-1 has a line width of
δλv ~ 0.6 Å, which
represents ~10% of the wavelength separation between the doublet peaks.
Furthermore, the spectral resolution of the instrument also broadens the width of the
[Oii] lines. The change in line width due to resolution is given by
δλR(z)
defined in Eq. (2). We note that the
broadening due to instrumental resolution depends on the redshift because the position of
[Oii] changes with redshift while the resolution element
FWHMλ is roughly constant with the wavelength (for a grism
spectrograph): 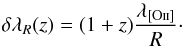 (2)By performing a
squaring sum of the components in Eqs. (1)
and (2), we obtain the observed width,
denoted w[Oii](z), of an individual
line in the [Oii] doublet:
(2)By performing a
squaring sum of the components in Eqs. (1)
and (2), we obtain the observed width,
denoted w[Oii](z), of an individual
line in the [Oii] doublet: 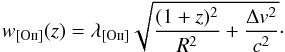 (3)In order to Nyquist sample
the observed [Oii] doublet at redshift z, the individual line
width of the doublet has to be at least twice the doublet separation, or
w[Oii](z) = 2δ[Oii](z).
Rewriting Eq. (3) in terms of this minimum
sampling requirement gives the minimal resolution, denoted
R(z,Δv), required to split an
[Oii] doublet emitted at redshift z with a velocity dispersion
Δv,
(3)In order to Nyquist sample
the observed [Oii] doublet at redshift z, the individual line
width of the doublet has to be at least twice the doublet separation, or
w[Oii](z) = 2δ[Oii](z).
Rewriting Eq. (3) in terms of this minimum
sampling requirement gives the minimal resolution, denoted
R(z,Δv), required to split an
[Oii] doublet emitted at redshift z with a velocity dispersion
Δv, ![\begin{equation} R(z,\Delta v) = \left[ \frac{1}{R_{\rm \OII}^{2}}- \frac{\Delta v^{2}}{(1+z)^{2}c^{2}} \right]^{-1/2}, \label{eq:6:Rzv} \end{equation}](/articles/aa/full_html/2013/11/aa22452-13/aa22452-13-eq44.png) (4)where
R(z,Δv) decreases with redshift,
increases with the velocity dispersion, and converges asymptotically towards
R[Oii].
(4)where
R(z,Δv) decreases with redshift,
increases with the velocity dispersion, and converges asymptotically towards
R[Oii].
For a galaxy at z = 1 ([Oii] is observed at λ ~ 7456 Å) with Δv = 100 km s-1, the minimum resolution required is Rmin = 3000. For a galaxy at z = 1 with Δv = 70 km s-1, it is Rmin = 2800. The spectrograph currently used by SDSS-III/BOSS reaches R ~ 2700 > R[Oii] at 9320 Å, and therefore it theoretically splits the [Oii] doublet for galaxies with Δv < 50 km s-1 at z ≥ 1.5. With this spectrograph, the observation of the [Oii] doublet of galaxies with Δv = 100 km s-1 will be highly-blended.
At low resolution, it is possible to actually see [Oii] doublets when the lines peak and the valleys fall exactly right opposite to the pixels. In the following, when we state “the doublet is resolved”, it is true wherever the emission line lands on the detector.
In classical spectrographs, the resolution element FWHMλ is roughly constant with wavelength, and therefore the spectral resolution R is a linear function of the observed wavelength λ. We must therefore define the minimum resolution requirement to be at the lowest redshift limit where [Oii] becomes the only emission line available in the spectrum. The resolution requirement will automatically be satisfied for all higher redshifts.
In this study, we consider the more common case where the spectral range is limited to <1 μm.
3. Simulation
To confirm the theoretical considerations of Sect. 2, we simulate observations of [Oii] doublets in the presence of Poisson noise. Future massive spectroscopic redshift surveys are primarily focused on obtaining redshifts with only emission lines, which is less demanding in terms of exposure time than requiring the detection of the continuum. For these applications, a Gaussian profile is sufficient to simulate the resolution effects.
Because spectrograph resolution increases with wavelength, the minimal resolution requirement is determined at the shortest wavelength where the [Oii] doublet becomes the only major emission line feature in the spectrum. Assuming an instrumental wavelength limit of 1 μm, the resolution requirement for [Oii] is therefore defined at λobs([Oii] ,z = 1) ~ 7450 Å.
Of interest for this work, DEEP2 has obtained a complete spectroscopic sample of [Oii] emitters at redshift z = 1. Its magnitude limit is r = 24.1 and its [Oii] flux limit is 5 × 10-17 ergcm-2s-1 (Newman et al. 2013). These limits are deeper than the target selection limits for BAO surveys currently under development. The DEEP2 Survey used the DEep Imaging Multi-Object Spectrograph (DEIMOS grism spectrograph) at Keck with a resolution R = 6000 (Faber et al. 2003) and was limited by the galaxy continuum signal-to-noise.
The range of velocity dispersions used in our simulation is empirically determined by observations of z ~ 1 [Oii] emitters within the DEEP2 redshift survey. We set the lower (upper) limit of the investigated range at Δv = 20 km s-1 (120 km s-1), which encompasses most of the galaxies down to r < 24.
In terms of instrumental resolution, we explore the range of 2500 < R < 6000 sampled by steps of δR = 3 in resolution. To avoid aliasing problems, for each doublet we add a random number smaller than 3 to the resolution to correctly sample the complete resolution range. We use a sampling of 3 pixels per resolution element. Our results will span a meaningful range of resolutions for numerous spectrographs at λobs([Oii] ) ~ 7500 Å, including the current SDSS-III/BOSS spectrograph (R ~ 2500; Smee et al. 2013) and future spectrographs such as PFS-SUMIRE (R ~ 3000; Vivès et al. 2012) or DESi (R ~ 4000; Jelinsky et al. 2012).
We use a Gaussian function, to model the [Oii] doublet, given by
![\hbox{$f_\mathrm{gaussian}(\lambda,\lambda_0,\sigma_{\rm g},F_0)= \frac{F_0}{\sqrt{2\pi} \sigma_{\rm g}} {\rm Exp} \left[ \frac{(\lambda-\lambda_0)^2}{2 \sigma_{\rm g}^2} \right]$}](/articles/aa/full_html/2013/11/aa22452-13/aa22452-13-eq72.png) .
This produces an emission line centered at λ0 of total flux
F0. The profile width σg is linked
to the velocity dispersion by
σg = λ[Oii]Δv/c.
The Gaussian profile has an exponential drop off from the emission peak value, and therefore
it may not represent systematic effects like scattered light within the spectrograph. A
Moffat profile recovers the information in the wings of the emission line when
β is allowed to vary. However, the Moffat model is only attractive if the
data has a high spectral resolution and high signal-to-noise ratio (S/N), otherwise the
information in the wings will have low significance owing to measurement noise.
.
This produces an emission line centered at λ0 of total flux
F0. The profile width σg is linked
to the velocity dispersion by
σg = λ[Oii]Δv/c.
The Gaussian profile has an exponential drop off from the emission peak value, and therefore
it may not represent systematic effects like scattered light within the spectrograph. A
Moffat profile recovers the information in the wings of the emission line when
β is allowed to vary. However, the Moffat model is only attractive if the
data has a high spectral resolution and high signal-to-noise ratio (S/N), otherwise the
information in the wings will have low significance owing to measurement noise.
We calibrate the flux f and the sky level to a recent emission line galaxy observational study performed at the SDSS Telescope (Comparat et al. 2013). This study showed that the nominal observed total line flux is ~30 × 10-17 erg cm-2 s-1 and the nominal sky brightness is ~3 × 10-18 erg cm-2 s-1 Å-1arcsec-2 at ~7400 Å. This noise level corresponds to detections with a S/N above 7 which should be typical of observations in future BAO survey. In the simulation, we use fluxes f from a broader range, 6 < f < 100 × 10-17 erg cm-2 s-1. We determine the relative abundance of emission lines at a given flux with the [Oii] luminosity function at z ~ 1 measured by Zhu et al. (2009) on the DEEP2 survey.
First, we make a Gaussian doublet at
λobs([Oii] ) ~ 7450 Å for a given resolution
R, velocity dispersion Δv , and flux f.
The flux ratio between the two lines is fixed at 1; the impact of a varying flux ratio is
discussed in Sect. 4.3. Next, we sample the doublet
spectrum at resolution R with 3 pixel per resolution element. We add
Poisson sky noise on each pixel (this is the dominating contribution of the observed noise).
This creates a mock observation of the [Oii] emission doublet for the Gaussian
profile. Finally, we fit two models to the simulated doublet: a single Gaussian profile, and
a double Gaussian profile. To compare the detections from each fit, we compute the S/N and
the χ2, which is defined as the usual reduced chi-square
statistics by 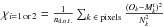 ,
where nd.o.f.
is the number of degrees of freedom, O is the array of observed values,
M1 is the model with one line, M2
is the model with 2 lines, and N is the noise. The number of degrees of
freedom vary from 35 to 94 depending on the spectral resolution used. The S/N is calculated
with a Fisher matrix.
,
where nd.o.f.
is the number of degrees of freedom, O is the array of observed values,
M1 is the model with one line, M2
is the model with 2 lines, and N is the noise. The number of degrees of
freedom vary from 35 to 94 depending on the spectral resolution used. The S/N is calculated
with a Fisher matrix.
 |
Fig. 1 Share of doublets at the 3σ (confidence level of 99.7%) vs. resolution for r < 24 doublets at z = 1 for different flux bins and with a flux ratio between the lines of 1. Each line corresponds to a survey with a the flux detection limit given on the right end of each line in units of 10-17 erg cm-2 s-1. SDSS-IV/eBOSS corresponds to line 30 and DESi to line 10. |
4. Results
The simulation contains ~15 × 106 simulated [Oii] lines sampling the velocity dispersion, resolution, and flux range set in the above.
To statistically differentiate whether an observation of [Oii] is identified as a doublet or a single emission line (SEL), given that the numbers of degrees of freedom is high (35 < nd.o.f. < 94), we use the difference Δχ2 = χ1/nd.o.f.1 − χ2/nd.o.f.2 of the normalized χ2. A Δχ2 = 9 means the single line emission model is ruled out at 3σ or with a 99.7% confidence level. We compute the share of emission line with r < 24 (convolved by the velocity dispersion distribution of DEEP2) detected as a doublet at the 3σ confidence level at redshift 1 as function of the resolution for different [Oii] flux detection limit (see Fig. 1).
The main trend is that the percentage of doublets increases as a function of the resolution. We can distinguish two regimes. In the regime of low [Oii] fluxes the gain is linear, i.e. for surveys with a lower limit of [Oii] detection of 10 × 10-17erg cm-2 s-1 or below, the increase of the share of doublet is linear as a function of the resolution (which corresponds to line 10 of Fig. 1). For such survey, it indicates the resolution should be the highest possible. For higher [Oii] fluxes, the marginal increase of the doublet share is large for low resolutions and small for higher resolutions. For a survey aiming only to observe the brightest [Oii] emitters (Fig. 1), it is not necessary to aim for the highest resolution; R = 3300 is sufficient to obtain 90% of the doublets. And for R > 3300, the marginal cost of an extra percent of doublets decreases.
The DEEP 2 Survey dealt with SEL using a neural network (Kirby et al. 2007). They showed that given a fair spectroscopic sample of an observed population with reliable redshifts, it is possible to infer correct redshifts to nearly 100% of the [Oii] SEL. The Hα, Hβ, and [Oiii] SEL cases are not as well handled by the neural network with efficiencies of ~90%, ~60%, and ~60% respectively.
The combination of the last two points shows that it will be possible to derive robust [Oii] redshifts where [Oii] is the only emission line available in the spectrograph, even if the fraction of 3σ doublet detections is small.
4.1. Higher redshift, sky lines, completeness
The sky lines have an observed width of one resolution element; therefore, their width varies with the resolution. In the case of a single sky line located on a doublet, it is not a problem to subtract the sky line and obtain an accurate redshift. In the case of many contiguous sky lines, they can cover a doublet completely and prevent getting any redshift in this zone. This causes the survey to have a varying [Oii] flux limit as a function of the redshift. To quantify the impact of the sky line obstruction as a function of redshift, we simulate at various resolutions the observation of a sky spectrum. The sky spectrum is taken from Hanuschik (2003).
At a given resolution, we convert the wavelength array of the sky into a redshift array corresponding to the [Oii] redshift. We scan the redshift array by steps of 0.0005 (which corresponds to the desired precision of a spectroscopic redshift). At each step, we compare the median value of the sky (assuming a sky subtraction efficient at 90%) to the flux measured in the middle of an [Oii] doublet (where it is the lowest). If the median value of the sky is greater than the value of the doublet, we consider that we cannot fit a redshift. Finally, we compute the percentage of the redshift range where we can fit spectroscopic redshifts.
We run this test for two settings. A bright survey with [Oii] fluxes ~30 × 10-17 erg cm-2 s-1 and fibers of 2′′ diameter (SDSS-IV/eBOSS-like). A faint survey with [Oii] fluxes ~10 × 10-17 erg cm-2 s-1 and fibers of 1.5′′ diameter (DESi-like). It shows that the impact of the sky lines on the completeness depends weakly on the resolution; the discrepancy between the different resolution settings is smaller than two percentage points. For the bright scenario the completeness is greater than 95%. For the faint survey case, the completeness is greater than 80%. This demonstrates how the sky lines impact the redshift completeness of an [Oii] spectroscopic survey. It shows that it is necessary to have the smallest fiber possible to diminish the impact of the sky. The increase in resolution is not useful for coping with this problem.
Finally the completeness in redshift is not driven by the resolution at the first order, but by the robustness of sky subtraction and the strength of the [Oii] flux. To obtain a precise estimate of the impact of sky lines on the redshift distribution completeness, a full end-to-end simulation is needed.
4.2. Integrated velocity profile
In this study, the integrated velocity profile of each galaxy within a fiber is assumed to be Gaussian, although galaxy rotation may create complications. Current data is not sufficient to explore this particular difficulty. Nearby galaxies are not representative of the properties of these higher-redshift galaxies, and surveys like the Mass Assembly Survey with SINFONI in the VIMOS-VLT Deep Survey (MASSIV) are limited to a sample of only 50 galaxies in the redshift range 0.6 < z < 1.6 (Epinat et al. 2012).
4.3. Emission line flux ratio
The flux ratio between the forbidden fine structure [Oii] lines varies with the surrounding electronic density between 0.35 (high electron density limit) and 1.5 (low density limit) (Pradhan et al. 2006). A precise estimation of the distribution of this ratio at z ~ 1 has not been measured, although observations show the ratio does not take the extreme values 0.35 or 1.5, but seems to stay around 1. A ratio of one is the best for separating the doublet. A different ratio can only decrease the efficiency
of recognizing the doublet. Furthermore, this effect is symmetric: a ratio of 0.7 or 1.4 implies the loss of the same amount of doublets. We quantify this effect by varying the flux ratio of the lines simulated between 0.7 and 1. For emission lines with total flux of 10-16 erg cm-2 s-1 (DESi-like), a flux ratio of 0.7 (or 1.4) induces a decrease in the amount of doublets seen of 8.3% at R ~ 4500. The total number of doublets detected at 3σ goes from ~25% to ~22.9%. For emission lines with total flux of 3 × 10-16 erg cm-2 s-1 (SDSS-IV/eBOSS-like), a flux ratio of 0.7 (or 1.4) induces a decrease in the amount of doublets seen of 9.1% at R ~ 3300. The total number of doublets detected at 3σ diminishies from ~90% to ~81.8%.
5. Conclusion
Large spectroscopic redshift surveys are being designed to measure galaxy redshifts using the [Oii] emission line doublet and trace the large-scale matter distribution. This study shows we should be optimistic regarding their feasibility. We have shown how the observation of the doublet evolves with the instrumental resolution and the line velocity dispersion. We also quantified the impact of sky lines on the redshift completeness of this type of survey.
In light of the numbers obtained, we foresee two strategies about the choice of the resolution for future spectrographs. For bright [Oii] emitter surveys (like SDSS-IV/eBOSS), a resolution of R ~ 2500 (current SDSS spectrograph) is sufficient to obtain a fair sample of doublets (60%) in order to train the pipeline to recover all the [Oii] redshifts. Increasing the resolution to 3300 allows us to get 90% of the doublets. For a small increase in resolution, the redshift determination efficiency doubles. The impact of the sky lines on the completeness in redshift is smaller than 6%. For faint [Oii] emitter surveys (like DESi), we recommend pushing the resolution to the highest level. Knowing there is a limited number of pixels on the detector (4k), and that the highest resolution possible on a three channel spectrograph is R ~ 4500 at 7500 Å, to go beyond it is necessary to use a four-channel spectrograph. With a resolution of 4500, one would obtain 25% of the doublets, which is enough to train the pipeline to assign correct redshift.
Acknowledgments
J.P.K. acknowledges support from the ERC advanced grant “LIDA”. This work was supported by the United States Department of Energy Early Career program via grant DE-SC0003960 and by the National Science Foundation via grant AST-0806732.
References
- Anderson, L., Aubourg, E., Bailey, S., et al. 2012, MNRAS, 427, 3435 [Google Scholar]
- Blake, C., Kazin, E. A., Beutler, F., et al. 2011, MNRAS, 418, 1707 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Cole, S., Percival, W. J., Peacock, J. A., et al. 2005, MNRAS, 362, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Comparat, J., Kneib, J.-P., Escoffier, S., et al. 2013, MNRAS, 428, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Drinkwater, M. J., Jurek, R. J., Blake, C., et al. 2010, MNRAS, 401, 1429 [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Epinat, B., Tasca, L., Amram, P., et al. 2012, A&A, 539, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faber, S. M., Phillips, A. C., Kibrick, R. I., et al. 2003, SPIE, 4841, 1657 [Google Scholar]
- Hanuschik, R. W. 2003, A&A, 407, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jelinsky, P., Bebek, C., Besuner, R., et al. 2012, SPIE, 8446 [Google Scholar]
- Kirby, E. N., Guhathakurta, P., Faber, S. M., et al. 2007, ApJ, 660, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Mostek, N., Barbary, K., Bebek, C. J., et al. 2012, SPIE, 8446 [Google Scholar]
- Newman, J. A., Cooper, M. C., Davis, M., et al. 2013, ApJS, 208, 5 [Google Scholar]
- Pradhan, A. K., Montenegro, M., Nahar, S. N., & Eissner, W. 2006, MNRAS, 366, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D., Abdalla, F., Abraham, T., et al. 2011 [arXiv:1106.1706] [Google Scholar]
- Shannon, C. E., & Weaver, W. 1975, The mathematical theory of communication (Urbana: University of Illinois Press) [Google Scholar]
- Smee, S. A., Gunn, J. E., Uomoto, A., et al. 2013, AJ, 146, 32 [Google Scholar]
- Vivès, S., Le Mignant, D., Madec, F., et al. 2012, SPIE, 8446 [Google Scholar]
- Zhu, G., Moustakas, J., & Blanton, M. R. 2009, ApJ, 701, 86 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Share of doublets at the 3σ (confidence level of 99.7%) vs. resolution for r < 24 doublets at z = 1 for different flux bins and with a flux ratio between the lines of 1. Each line corresponds to a survey with a the flux detection limit given on the right end of each line in units of 10-17 erg cm-2 s-1. SDSS-IV/eBOSS corresponds to line 30 and DESi to line 10. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


