| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 4 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322122 | |
| Published online | 01 October 2013 | |
Research Note
Incomplete-exclusion statistical mechanics in violent relaxation
1
International Space Science Institute,
3012
Bern,
Switzerland
e-mail:
Wolfgang.Baumjohann@oeaw.ac.at
2
Department of Geophysics, Munich University,
80333
Munich,
Germany
3
Space Research Institute, Austrian Academy of Sciences,
8042
Graz,
Austria
Received:
24
June
2013
Accepted:
27
August
2013
Violent relaxation was proposed half a century ago as responsible for non-collisional dynamics in gravitationally bound systems of extended celestial objects after reaching an equilibrium state that can be described thermodynamically. It is based on a complete spatial exclusion principle that formally leads to a distribution function resembling the Fermi distribution. We extend this theory to incomplete spatial exclusion by assuming that Fermi states can only be partially occupied. This is made possible by analogy to Fermi statistics. A new form of distribution function has been obtained. Formally it does not resemble the Fermi distribution. It consists of a difference of two Bose distributions but has the same properties as the Fermi distribution. Using it in the violent relaxation equation for the global gravitational potential extends the violent relaxation theory to incomplete exclusion. Though this refines violent relaxation theory, it does not resolve its basic deficiencies: the mass problem and those problems related to the mean field assumption.
Key words: equation of state / galaxies: interactions
© ESO, 2013
1. Introduction
Fermi statistics got a new application when Lynden-Bell (1967) suggested his “principle of (volume) exclusion” to arrive at a statistical mechanical description of interacting stellar systems and of the formation of galaxies. The underlying idea was that two extended celestial bodies cannot occupy the same volume at the same time. This culminated in so-called violent relaxation statistics of gravitationally bound non-collisional systems, which presumably leads to a final “thermodynamic equilibrium” state. Violent relaxation theory found widespread application (for a review see Gott 1977) in galaxy formation and clusters of galaxies, in particular in the presence of cold dark matter (Treumann et al. 2000). It also received critical reviews (Shu 1978; Arad & Lynden-Bell 2005; Chavanis 1998) and improvements (Kull et al. 1996, 1997; Lynden-Bell 1999; Lynden-Bell & Lynden-Bell 1999; Arad & Lynden-Bell 2005).
Indeed, two gravitationally interacting bodies necessarily exclude each other from occupying the same volume; otherwise, they collide, merge, or are disrupted – all complicated non-equilibrium processes outside any simple statistical mechanical description.
2. Complete exclusion in violent relaxation
Within Lynden-Bell’s exclusion principle, the obtained volume-excluding equilibrium
distribution, 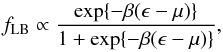 (1)formally resembles
the Fermi distribution of zero-spin fermions. Here, ϵ is energy and
β and μ are the Lagrange multipliers arising in the
counting-of-states procedure. They are identified with an inverse temperature and a chemical
potential, respectively. Since the assumption of exclusion in the counting-of-states
procedure is identical to the basic assumption of Pauli’s exclusion principle that underlies
Fermi statistics, the above result is obvious, even without derivation. The proportionality
factor is defined through the mass distribution of the interacting objects.
(1)formally resembles
the Fermi distribution of zero-spin fermions. Here, ϵ is energy and
β and μ are the Lagrange multipliers arising in the
counting-of-states procedure. They are identified with an inverse temperature and a chemical
potential, respectively. Since the assumption of exclusion in the counting-of-states
procedure is identical to the basic assumption of Pauli’s exclusion principle that underlies
Fermi statistics, the above result is obvious, even without derivation. The proportionality
factor is defined through the mass distribution of the interacting objects.
With the above distribution in Poisson’s equation 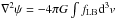 for the gravitational potential
ψ, and v the velocity of gravitationally interacting
“particles” (objects: stars, galaxies, etc.), this yields Lynden-Bell’s “equation of violent
relaxation” of a bound non-collisional system:
for the gravitational potential
ψ, and v the velocity of gravitationally interacting
“particles” (objects: stars, galaxies, etc.), this yields Lynden-Bell’s “equation of violent
relaxation” of a bound non-collisional system: ![\begin{equation} \label{eq-poisson} \nabla^2\psi=-C\int\limits_0^\infty \frac{\zeta^2\mathrm{d}\zeta\exp(-\zeta^2/2)}{\exp[-\beta(\psi+\mu)]+\exp(-\zeta^2/2)}\cdot \end{equation}](/articles/aa/full_html/2013/10/aa22122-13/aa22122-13-eq8.png) (2)The integral on the
right is the mass density, a self-consistent function of both chemical potential
μ and gravitational potential ψ. Integration is over the
velocity space volume. The dimensional constant is
(2)The integral on the
right is the mass density, a self-consistent function of both chemical potential
μ and gravitational potential ψ. Integration is over the
velocity space volume. The dimensional constant is 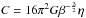 , and
η is some initial phase space density (for its specification see, e.g.,
Chavanis 1998), the normalization constant appearing
in Eq. (1). The distribution
fLB – or the equivalent Eq. (7) derived below – can be taken for the equilibrium distribution in the
Vlasov theory of linear eigenmodes.
, and
η is some initial phase space density (for its specification see, e.g.,
Chavanis 1998), the normalization constant appearing
in Eq. (1). The distribution
fLB – or the equivalent Eq. (7) derived below – can be taken for the equilibrium distribution in the
Vlasov theory of linear eigenmodes.
Violent relaxation based on fLB is a mean-field theory (cf., e.g., Chavanis et al. 2002, 2005; Chavanis & Ispolatov 2002; Chavanis & Bouchet 2005; Bouchet et al. 2010). It supposes that a mean gravitational potential field can be defined and that a thermodynamic equilibrium state of self-gravitating matter moving in this field can be achieved.
The distribution fLB, if applied to gravitating systems, suffers from several deficiencies. Integration over an infinite spatial volume causes the total mass to diverge. This can be circumvented by restricting it to a finite – say spherical – volume (cf., e.g., Arad & Lynden-Bell 2005, and others). The most severe deficiency is that self-gravitating systems barely reach the supposed stationary thermodynamic quasi-equilibrium. Violent relaxation is only an intermediate state in their gravitational evolution. Cosmological expansion may balance the large-scale merging on the universal scale. This seems to occur in cosmological comoving particle-in-cell simulations. Our improvement of the basic distribution function below is also in the realm of mean field theories. It resolves neither of these principal problems.
3. Incomplete population of states
The assumption of complete volume exclusion is very strong, even for stars. Stars have extended atmospheres, are magnetized, and they blow out winds. Galaxies are extended objects that by no means resemble solid bodies or point-like particles. They occupy large volumes and necessarily spatially overlap when approaching each other. Considering them as point-like objects in a statistical description is convenient but can only be justified as a rather weak approximation of reality.
Modern approaches have turned to massive numerical particle-in-cell simulations of large numbers of gravitating particles. They allow their temporal evolution to be followed, but they do not deviate from the assumption of non-extended objects. Therefore, they all fall into the same category as Lynden-Bell’s statistical mechanical approach (Lynden-Bell 1967, 1979) and its refinements by Shu (1978) and others (Kull et al. 1996, 1997; Chavanis 1998, 2006b; Chavanis & Sommeria 1998; Chavanis et al. 2002; Lynden-Bell 1999; Lynden-Bell & Lynden-Bell 1999; Arad & Lynden-Bell 2005).
Relaxing the assumption of complete exclusion would be desirable. Fortunately, with this goal in mind we can exploit the analogy to Fermi statistics, thereby circumventing the necessity of precisely including any object overlap in state-counting statistics. Below we show that the Pauli principle can be extended to the case of incomplete (or partial) occupation of states.
3.1. Discrete states
There are three kinds of particles, bosons, fermions, and anyons. Anyons obey fractional statistics (Wilczek 1982; Haldane 1983; Arovas et al. 1984; Wu 1994), which is a mixture of bosonic and fermionic statistics. Haldane (1991) proposed a generalization of the Pauli principle for anyons. Bosons are allowed to occupy energy states to arbitrary numbers; they do not resemble gravitationally interacting systems, so do not need to be considered here.
For fermions, multiparticle states are inhibited by the Pauli principle, which allows for
only two occupations, empty states or (when neglecting the particle spin) one particle per
state. Fermi’s ingenious truncation of the infinite sum in the partition function
![\begin{equation} Z_i=\sum_i\{\exp[(\mu-\epsilon_i)/k_{\rm B}T]\}^{n_i}, \end{equation}](/articles/aa/full_html/2013/10/aa22122-13/aa22122-13-eq12.png) (3)by boldly assuming
only binary occupations
ni = [0,1] of states
ϵi with i ∈ N, immediately
led him to the proposal of the celebrated Fermi distribution
⟨ ni ⟩ F = { 1 + exp [−(μ − ϵi)/kBT] } -1.
Here, T is the temperature;
(3)by boldly assuming
only binary occupations
ni = [0,1] of states
ϵi with i ∈ N, immediately
led him to the proposal of the celebrated Fermi distribution
⟨ ni ⟩ F = { 1 + exp [−(μ − ϵi)/kBT] } -1.
Here, T is the temperature; 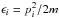 is the kinetic energy of the
ith particle; pi is its
momentum, and m its mass. The Fermi distribution had profound
consequences for the statistical mechanics of solids at low temperatures. Fermi’s
assumption was justified by the Pauli principle and, for
spin-
is the kinetic energy of the
ith particle; pi is its
momentum, and m its mass. The Fermi distribution had profound
consequences for the statistical mechanics of solids at low temperatures. Fermi’s
assumption was justified by the Pauli principle and, for
spin-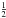 particles, was ultimately given its quantum mechanical interpretation based on the
complete asymmetry of fermionic wave functions. Discovery of the quantum Hall effect, in
particular the fractional effect, had temporarily shaken Fermi statistics, until Laughlin (1983) proposed his wave function, which
includes interaction with collective bosonic fields.
particles, was ultimately given its quantum mechanical interpretation based on the
complete asymmetry of fermionic wave functions. Discovery of the quantum Hall effect, in
particular the fractional effect, had temporarily shaken Fermi statistics, until Laughlin (1983) proposed his wave function, which
includes interaction with collective bosonic fields.
One may ask what happens when enough states are available for fermions, e.g., electrons, and the electrons are allowed to fill those states incompletely, e.g., in fractions? We may think of the loosely interacting stars or galaxies mentioned above, but for clarity we instead stay in the framework of having to deal with elementary particles, fermions in our case.
There are no experimentally known examples of incompletely filled fermionic states.
Fermion populations are binary. However, as for a theoretical example, one may think of
small numbers of gyrating electrons that bounce in a magnetic mirror geometry at frequency
ωb ≪ ωce.
In this case, all Landau levels (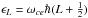 , L ∈ N)
split into several bounce levels
, L ∈ N)
split into several bounce levels 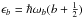 , b ∈ N,
b/L < ωce/ωb.
The total electron energy
ϵb,L = ϵL + ϵb
in Landau level L is then shared by the two kinds of oscillatory states
of the electron (Treumann & Baumjohann
2013). Under these circumstances, all the electron energy is only in the Landau
levels at the magnetic mirror points, while a substantial part of energy is transferred to
the bounce levels in the field minima. Bounce levels might become partially (hence
incompletely) filled under these circumstances during the short gyration time, even though
only fermionic states are involved, and partial population of states may not necessarily
mean that the Pauli principle is violated when not involving bosonic interactions. The
occupation may still be a fraction below one that the Pauli principle does not explicitly
exclude. Though this example may only serve as illustration, we simply assume that
fermionic states can sometimes – hypothetically – become incompletely filled. In the
following, we rewrite the formalism for this case of partial (or incomplete) population,
keeping in mind that it possibly is never realized in elementary particle statistical
mechanics, while becoming useful for some classical systems.
, b ∈ N,
b/L < ωce/ωb.
The total electron energy
ϵb,L = ϵL + ϵb
in Landau level L is then shared by the two kinds of oscillatory states
of the electron (Treumann & Baumjohann
2013). Under these circumstances, all the electron energy is only in the Landau
levels at the magnetic mirror points, while a substantial part of energy is transferred to
the bounce levels in the field minima. Bounce levels might become partially (hence
incompletely) filled under these circumstances during the short gyration time, even though
only fermionic states are involved, and partial population of states may not necessarily
mean that the Pauli principle is violated when not involving bosonic interactions. The
occupation may still be a fraction below one that the Pauli principle does not explicitly
exclude. Though this example may only serve as illustration, we simply assume that
fermionic states can sometimes – hypothetically – become incompletely filled. In the
following, we rewrite the formalism for this case of partial (or incomplete) population,
keeping in mind that it possibly is never realized in elementary particle statistical
mechanics, while becoming useful for some classical systems.
Rewriting Fermi statistics for the case of partially filled states is easily done,
starting as usual (cf., e.g., Huang 1987; Landau & Lifschitz 1994) from the logarithm
Ωi [ni] of
the Γ-phase-space volume corresponding to the population numbers
[ni] of the particles in an ideal gas:
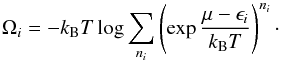 (4)The sum is taken
over Gibbs’ distributions in all the ni
states.
(4)The sum is taken
over Gibbs’ distributions in all the ni
states.
We assume that the states can become partially occupied by fermions alone. The Pauli
principle categorically excludes occupation numbers
ni > 1. As a
result, partial population of states implies that, given the number interval
[0,ℓ] with fixed natural number ℓ ∈N, and
j any integer, such that
j ∈ [0,ℓ], the thermodynamic potential
Ωi can be written as
![\begin{equation} \Omega_i=-k_{\rm B}T\log\sum_{j\,=\,0}^\ell\left(\exp\frac{\mu-\epsilon_i}{\ell k_{\rm B}T}\right)^j, \qquad j\in[0,\ell], \end{equation}](/articles/aa/full_html/2013/10/aa22122-13/aa22122-13-eq42.png) (5)where
j = 0 andj = ell just reproduce the
two permitted Fermi occupations. In the intermediate interval, the populations follow the
simple partial chain { j/ℓ }, with
fixed ℓ ≥ j. The sum represents a truncated geometric
progression with ratio
exp [(μ − ϵi)/ℓkBT]
yielding after summation
(5)where
j = 0 andj = ell just reproduce the
two permitted Fermi occupations. In the intermediate interval, the populations follow the
simple partial chain { j/ℓ }, with
fixed ℓ ≥ j. The sum represents a truncated geometric
progression with ratio
exp [(μ − ϵi)/ℓkBT]
yielding after summation ![\begin{equation} \Omega_i=-k_{\rm B}T\log\left\{\frac{\exp[x_i(\ell+1)]-1}{\exp(x_i) - 1}\right\}, \qquad x_i\equiv \frac{\mu-\epsilon_i}{\ell k_{\rm B}T}\cdot \end{equation}](/articles/aa/full_html/2013/10/aa22122-13/aa22122-13-eq48.png) (6)One trivially
shows that this becomes the thermodynamic Fermi potential
ΩiF = −kBTlog {1 + exp[(μ − ϵi)/kBT ]}
for ℓ = 1. By taking the derivative
− ∂Ωi/∂μ,
the average incompletely filled partial distribution
⟨ ni ⟩ ℓ in
the ith quantum state follows as
(6)One trivially
shows that this becomes the thermodynamic Fermi potential
ΩiF = −kBTlog {1 + exp[(μ − ϵi)/kBT ]}
for ℓ = 1. By taking the derivative
− ∂Ωi/∂μ,
the average incompletely filled partial distribution
⟨ ni ⟩ ℓ in
the ith quantum state follows as ![\begin{equation} \langle n_i\rangle_\ell =\frac{1}{\ell}\left[\frac{(\ell+1)\mathrm{e}^{x_i(\ell\,+\,1)}}{\mathrm{e}^{x_i(\ell\,+\,1)}-1}-\frac{\mathrm{e}^{x_i}}{\mathrm{e}^{x_i}-1}\right],\quad \ell\geq 1.\label{eq-fracferm} \end{equation}](/articles/aa/full_html/2013/10/aa22122-13/aa22122-13-eq53.png) (7)It is easily
shown that the ordinary Fermi distribution
⟨ ni ⟩ F is reproduced for
ℓ = 1. The partial Fermi distribution Eq. (7) is a bit more complicated than the (integer)
Fermi distribution. Apparently, it looks more like a Boson distribution. However, this is
an illusion that becomes clear when checking its low- and high-temperature forms, which
agree with those for the Fermi distribution. For T → 0, one obtains
μ = ϵ = ϵF,
⟨ ni ⟩ → 1. For
T ≫ μ ~ ϵF, one recovers
the Boltzmann distribution. Thus the fermionic property of the distribution is maintained.
Obviously it results from the subtraction of two bosonic distributions in Eq. (7): The preserved antisymmetric property of the
partial many-particle fermionic system is caused by subtraction.
(7)It is easily
shown that the ordinary Fermi distribution
⟨ ni ⟩ F is reproduced for
ℓ = 1. The partial Fermi distribution Eq. (7) is a bit more complicated than the (integer)
Fermi distribution. Apparently, it looks more like a Boson distribution. However, this is
an illusion that becomes clear when checking its low- and high-temperature forms, which
agree with those for the Fermi distribution. For T → 0, one obtains
μ = ϵ = ϵF,
⟨ ni ⟩ → 1. For
T ≫ μ ~ ϵF, one recovers
the Boltzmann distribution. Thus the fermionic property of the distribution is maintained.
Obviously it results from the subtraction of two bosonic distributions in Eq. (7): The preserved antisymmetric property of the
partial many-particle fermionic system is caused by subtraction.
From the partial distribution
⟨ ni ⟩ ℓ as a
function of energy ϵi(p),
which in its turn is a function of momentum p, all thermodynamic
quantities like the equation of state can be derived by formally defining the appropriate
moments. For the ideal Fermi gas, one then has for pressure P and density
N, 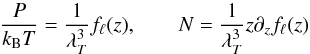 (8)respectively, with
log z = μ/kBT,
when introducing an appropriate new function
(8)respectively, with
log z = μ/kBT,
when introducing an appropriate new function 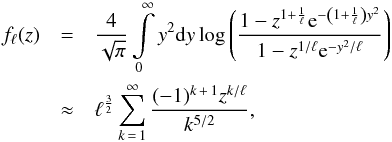 (9)which
replaces the common function
f5/2(z). Here,
(9)which
replaces the common function
f5/2(z). Here,
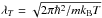 is the thermal wavelength. As usual,
is the thermal wavelength. As usual, 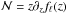 is the particle number per volume spanned by the thermal wavelength.
is the particle number per volume spanned by the thermal wavelength.
3.2. Continuous states
One may formally extend the partial-occupation case to the extreme case of a continuity
of partial states. Then j/ℓ becomes a
continuous variable in the interval
j/ℓ ∈ [0,1],
and the sum in the expression for the thermodynamic potential
Ωi turns into an integral yielding ![\begin{equation} \label{contpot} \Omega_i = -k_{\rm B}T \log \left\{ \frac{k_{\rm B}T}{\mu-\epsilon_i} \left[ \exp \left( \frac{\mu-\epsilon_i}{k_{\rm B}T} \right) -1\right] \right\}\cdot \end{equation}](/articles/aa/full_html/2013/10/aa22122-13/aa22122-13-eq71.png) (10)For the average
distribution
(10)For the average
distribution ![\begin{equation} \label{eq-fracferm-a} \langle n_i\rangle = \frac{\exp\left[(\mu-\epsilon_i)/k_{\rm B}T\right]}{\exp\left[(\mu-\epsilon_i)/k_{\rm B}T\right]-1}-\frac{k_{\rm B}T}{\mu-\epsilon_i}\cdot \end{equation}](/articles/aa/full_html/2013/10/aa22122-13/aa22122-13-eq72.png) (11)The first term on the
right looks again like a Bose distribution. It is straightforward to show by expanding
that, in the limit kBT → 0, it becomes
(11)The first term on the
right looks again like a Bose distribution. It is straightforward to show by expanding
that, in the limit kBT → 0, it becomes
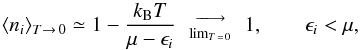 (12)which is the
completely degenerate Fermi distribution case. At high temperatures, the second term on
the right cancels the first term, and the distribution algebraically approaches zero. This
can already be seen from Eq. (10) where
one has
ϵi > μ
for high T, in which case the argument of the logarithm approaches unity.
Consequently, Ωi → 0 for a high temperature.
(12)which is the
completely degenerate Fermi distribution case. At high temperatures, the second term on
the right cancels the first term, and the distribution algebraically approaches zero. This
can already be seen from Eq. (10) where
one has
ϵi > μ
for high T, in which case the argument of the logarithm approaches unity.
Consequently, Ωi → 0 for a high temperature.
4. Discussion and conclusions
In the statistical mechanics of elementary particles, to which Fermi statistics apply, the case of an incomplete population of states is uncommon. Elementary particles like electrons either can or cannot be found in a particular state. The exeptions are anyons, which are collectively mixed fermionic and bosonic states, obeying statistics that exhibit properties of both fermions and bosons (Wilczek 1982; Haldane 1983, 1991; Halperin 1984; Wu 1994). They play a role in the fractional quantum Hall effect (Wilczek 1982; Arovas et al. 1984). Even though violent relaxation resembles Fermi statistics, anyon statistics have not found an application in astrophysics yet. This is not for the reason of its complication, but for the obvious lack of objects where its application would make physical sense. Such objects might indeed be found in self-gravitating systems that are prototypes of quasi-fermionic systems in interaction with the bosonic gravitational field. Anyon statistics might be more appropriate to them, in which case exclusive fermion statistics – whether complete or incomplete – should be replaced by anyon statistics. On the other hand, our partially-exclusive (or incompletely- exclusive) Fermi statistics is of a simple enough form that is suited for application in violent relaxation.
The partial Fermi distribution Eq. (7) is a variant of the (integer occupation) Fermi distribution, which it reproduces for ℓ = 1. The low- and high-temperature limits are identical to those of the Fermi distribution, as is the definition of Fermi energy. Fermions occupying partial states at T = 0 remain degenerate, even for the case of continuous occupation of states below filling number one. As an interesting observation, we note that for this type of distribution the fermionic character comes about by subtraction of two bosonic distributions.
After this excursion into Fermi statistics we return to the violent relaxation case. For
incomplete exclusion of “order ℓ”, we may use the new distribution function
Eq. (7), which we write in the conventional
form as ![\begin{eqnarray} \label{eq-dist1} {\tilde f}_{\ell}&\propto& \frac{1}{\ell}\Bigg\{\frac{\exp\left[-\beta(\epsilon-\mu)/\ell\right]}{1-\exp\left[-\beta(\epsilon-\mu)/\ell\right]}\nonumber\\[4mm] &&-\, \frac{(\ell+1)\exp\left[-(\ell+1)\beta(\epsilon-\mu)/\ell\right]}{1-\exp\left[-(\ell+1)\beta(\epsilon-\mu)/\ell\right]}\Bigg\}\cdot \end{eqnarray}](/articles/aa/full_html/2013/10/aa22122-13/aa22122-13-eq79.png) (13)The
tilde indicates that we are dealing here with the Lynden-Bell distribution function, which
now is reformulated for the incomplete exclusion case. The degree of incompleteness is
contained in the parameter ℓ > 1. Its value must be
specified from observations. When solving the violent relaxation Eq. (2), it is Eq. (13) that enters the density integral. Since
(13)The
tilde indicates that we are dealing here with the Lynden-Bell distribution function, which
now is reformulated for the incomplete exclusion case. The degree of incompleteness is
contained in the parameter ℓ > 1. Its value must be
specified from observations. When solving the violent relaxation Eq. (2), it is Eq. (13) that enters the density integral. Since
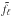 consists of two terms,
the density integral also splits into two different terms:
consists of two terms,
the density integral also splits into two different terms:
![\begin{eqnarray} \nabla^2\psi&=&-{\tilde C} \int\limits_0^\infty\zeta^2\mathrm{d}\zeta\left\{\frac{\exp\left(-\zeta^2/2\ell\right)}{\exp\left[-\beta(\psi+\mu)/\ell\right]-\exp\left(-\zeta^2/2\ell\right)}\right.\nonumber\\[2mm] &&-\, \left.\frac{(\ell+1)\exp\left[-(\ell+1)\zeta^2/2\ell\right]}{\exp\left[-(\ell+1)\beta(\psi+\mu)/\ell\right]-\exp\left[-(\ell+1)\zeta^2/\ell\right]}\right\} \end{eqnarray}](/articles/aa/full_html/2013/10/aa22122-13/aa22122-13-eq82.png) (14)and
(14)and
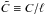 . This equation has to be solved
numerically for any particular object by applying some Poisson solver. By fitting the data
to the solution, one might be able to determine ℓ, the “degree of
exclusion”, in our terminology. These expressions can easily be extended to formally include
either a finite number or a continuity of mass shells (cf., e.g., Arad & Lynden-Bell 2005). The exponentials in Eq. (7) then turn into either sums or integrals over
shells. As noted before, the incomplete-exclusion violent relaxation that is based on this
distribution, suffers from the mass problem and is intransitive in the sense discussed by
Arad & Lynden-Bell (2005).
. This equation has to be solved
numerically for any particular object by applying some Poisson solver. By fitting the data
to the solution, one might be able to determine ℓ, the “degree of
exclusion”, in our terminology. These expressions can easily be extended to formally include
either a finite number or a continuity of mass shells (cf., e.g., Arad & Lynden-Bell 2005). The exponentials in Eq. (7) then turn into either sums or integrals over
shells. As noted before, the incomplete-exclusion violent relaxation that is based on this
distribution, suffers from the mass problem and is intransitive in the sense discussed by
Arad & Lynden-Bell (2005).
The continuous distribution Eq. (12) is
responsible, when there is a continuous spectrum of overlaps. Its two parts are just the sum
of the Bose form of Lynden-Bell’s exclusion distribution, which is corrected by the second
term to account for the fermionic properties. At high β (zero temperature)
the problem becomes the completely degenerate case. For low β (high
temperature) the two terms compensate for each other, as can be checked by expanding,
causing the distribution to vanishes. There is no continuous distribution of incompletely
filled states at large temperature. Accordingly, using the continuous distribution in
Poisson’s equation of violent relaxation yields
![\begin{eqnarray} \nabla^2\psi&= &-C\int\limits_0^\alpha\zeta^2\mathrm{d}\zeta\left\{\frac{1}{\beta(\psi+\mu)+\zeta^2/2}\ \right.\nonumber \\[2mm] &&-\, \left.\frac{\exp(-\zeta^2/2)}{\exp\left[-\beta(\psi+\mu)\right]-\exp(-\zeta^2/2)}\right\}\cdot \end{eqnarray}](/articles/aa/full_html/2013/10/aa22122-13/aa22122-13-eq84.png) (15)In
spite of the vanishing of the thermal mass distribution, the integral of the first term with
infinite upper limit α → ∞ does not exist and is, moreover, not compensated
by the second term. The integral would thus only make sense up to a finite upper energy
limit α ≪ ∞. This indicates that for arbitrary exclusion modes at high
energies and temperatures the assumption of spatial exclusion will become violated, and
effects such as collisions and merging cannot be neglected a priori.
(15)In
spite of the vanishing of the thermal mass distribution, the integral of the first term with
infinite upper limit α → ∞ does not exist and is, moreover, not compensated
by the second term. The integral would thus only make sense up to a finite upper energy
limit α ≪ ∞. This indicates that for arbitrary exclusion modes at high
energies and temperatures the assumption of spatial exclusion will become violated, and
effects such as collisions and merging cannot be neglected a priori.
Chavanis & Sommeria (1998), de Vega & Sanchez. (2001), Chavanis et al. (2002), Chavanis (2002), and Chavanis & Ispolatov (2002) suggested that distributions like Eq. (7) open up the possibility of coexistence of phases and phase transitions. This requires investigating the phase diagram as function of the gravitational potential ψ and the model parameters. Granting that
a thermodynamical state has been reached, this is a most interesting problem of mean field statistical theory. In the statistical mechanics of gravitationally interacting many-body systems it may not easily be realized. For Lynden-Bell’s complete exclusion statistics the occurrence of phase transitions has been investigated extensively in the canonical and microcanonical ensemble theories (Chavanis 2002, 2006a) for the fermionic and also for the bosonic models.
The results culminated in the identification of zeroth- and first-order phase transitions, their parametric dependencies, and the identification of microcanonical and canonical critical points. Phase transition theory has been developed further from the point of view of thermodynamic stability (Chavanis 2006a, 2011a,b,c,d; Chavanis & Delfini 2010; Staniscia et al. 2011). Similar behavior for the phase diagram and existence of critical points is expected in the incomplete-exclusion violent relaxation statistics.
Acknowledgments
We thank A. Kull and H. Böhringer for their participation in earlier work. RT thanks the referee for valuable suggestions.
References
- Arad, I., & Lynden-Bell, D., 2005, MNRAS, 361, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Arovas, D., Schrieffer, J. R., & Wilczek, F. 1984, Phys. Rev. Lett., 53, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchet, F., Gupta, S., & Mukamel, D. 2010, Physica A, 389, 4389 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chavanis, P. H. 1998, MNRAS, 300, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P. H. 2002, Phys. Rev. E, 65, 056123 [Google Scholar]
- Chavanis, P. H. 2006a, Int. J. Mod. Phys. B, 389, 3113 [Google Scholar]
- Chavanis, P. H. 2006b, Physica A, 365, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P. H. 2011a, Phys. Rev. E, 84, 031101 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chavanis, P. H. 2011b, EPJ B, 80, 275 [Google Scholar]
- Chavanis, P. H. 2011c, Physica A, 390, 1546 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P. H. 2011d, J. Stat. Mech. Theory Exp., 8, 2 [Google Scholar]
- Chavanis, P. H., & Bouchet, F. 2005, A&A, 430, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chavanis, P. H., & Delfini, L. 2010, Phys. Rev. E, 81, 051103 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chavanis, P. H., & Ispolatov, I. 2002, Phys. Rev. E, 66, 036109 [Google Scholar]
- Chavanis, P. H., & Sommeria, J. 1998, MNRAS, 296, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P. H., Rosier, C., & Sire, C. 2002, Phys. Rev. E., 66, 036105 [Google Scholar]
- Chavanis, P. H., Vatteville, J., & Bouchet, F. 2005, EPJ B, 46, 61 [Google Scholar]
- de Vega, H. J., & Sanchez, N. 2001, Nucl. Phys. B, 625, 409 [Google Scholar]
- Gott, J.-R. III, 1977, ARA&A, 15, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Haldane, F. D. M. 1983, Phys. Rev. Lett., 51, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Haldane, F. D. M. 1991, Phys. Rev. Lett., 67, 937 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Halperin, B. I. 1984, Phys. Rev. Lett., 52, 1583 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, K. 1987, Statistical Mechanics, 2nd edn. (New York: John Wiley & Sons) [Google Scholar]
- Kull, A., Treumann, R. A., & Böhringer, H. 1996, ApJ, 466, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Kull, A., Treumann, R. A., & Böhringer, H. 1997, ApJ, 484, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1994, Statistical Physics, 3rd Edition, Part 1 (Oxford: Pergamon Press, Elsevier Science) [Google Scholar]
- Laughlin, R. B. 1983, Phys. Rev. Lett., 50, 1392 [Google Scholar]
- Lynden-Bell, D. 1967, MNRAS, 136, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1979, MNRAS, 187, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1999, Physica A, 263, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Lynden-Bell, R. M. 1979, Proc. Roy. Soc. London, Ser. A, 455, 3261 [CrossRef] [Google Scholar]
- Shu, F. H. 1978, ApJ, 225, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Staniscia, F., Chavanis, P. H., & de Ninno, G. 2011, Phys. Rev. E, 83, 051111 [NASA ADS] [CrossRef] [Google Scholar]
- Treumann, R. A., Kull, A., & Böhringer, H. 2000, New J. Phys., 2, 1 [CrossRef] [Google Scholar]
- Treumann, R. A., & Baumjohann, W. 2013 [arXiv:1305.1000] [Google Scholar]
- Wilczek, F. 1982, Phys. Rev. Lett., 49, 957 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wu, Y.-S. 1994, Phys. Rev. Lett., 73, 922 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


