| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 6 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322006 | |
| Published online | 27 September 2013 | |
Broad Balmer line emission and cosmic ray acceleration efficiency in supernova remnant shocks
1 INAF/Osservatorio Astrofisico di Arcetri, Largo E. Fermi, 5, 50125 Firenze, Italy
e-mail: morlino@arcetri.astro.it
2 INFN/Gran Sasso Science Institute, viale F. Crispi 7, 67100 L’Aquila, Italy
Received: 31 May 2013
Accepted: 27 July 2013
Context. Balmer emission may be a powerful diagnostic tool for testing the paradigm of cosmic ray (CR) acceleration in young supernova remnant (SNR) shocks. The width of the broad Balmer line is a direct indicator of the downstream plasma temperature. In the case of efficient particle acceleration, an appreciable fraction of the total kinetic energy of the plasma is channeled into CRs, therefore the downstream temperature decreases and so does the broad Balmer line width. This width also depends on the level of thermal equilibration between ions and neutral hydrogen atoms in the downstream. Since generally only a few charge exchange (CE) reactions occur before ionization in young SNR shocks, equilibration between ions and neutrals is not reached, and a kinetic description of the neutrals is required to properly compute Balmer emission.
Aims. We provide a method for calculating Balmer emission using a self-consistent description of the shock structure in the presence of neutrals and CRs, which also accounts for the non-Maxwellian distribution of neutrals.
Methods. We use a recently developed semi-analytical approach, where neutral particles, ionized plasma, accelerated particles, and magnetic fields are all coupled together through the mass, momentum, and energy flux-conservation equations. The distribution of neutrals is obtained from the full Boltzmann equation in velocity space, coupled to Maxwellian ions through ionization and CE processes. The computation is also an improvement over previous work thanks to a better approximation of the atomic interaction rates.
Results. We find that for shock speeds ≳2500 km s-1, the distribution of broad neutrals never approaches a Maxwellian and its moments differ from those of the ionized component. These differences lead to a smaller FWHM than predicted in previous calculations, where thermalization was assumed.
Conclusions. The method presented here provides a realistic estimate of particle acceleration efficiency in Balmer-dominated shocks.
Key words: shock waves / ISM: supernova remnants / cosmic rays / acceleration of particles
© ESO, 2013
1. Introduction
Optical spectra of a few young supernova remnant (SNR) shocks essentially consist of Balmer emission. Observations show that the Hα line produced in these so-called Balmer dominated shocks is made of two components (see Heng 2010, for a review): a narrow line, with a full width at half maximum (FWHM) of few tens of km s-1 produced by excitation of cold atoms entering the shock region, and a broad line with a FWHM resembles the shock speed produced by atoms that undergo a charge exchange (CE) process before being excited (Chevalier & Raymond 1978; Chevalier et al. 1980). Measuring the shape of this complex Balmer line allows one to infer information on the conditions around the shock, which in turn are affected by the presence of accelerated particles. Balmer emission from young SNR shocks can be used to measure the cosmic ray (CR) acceleration efficiency at such shocks and even to gather information on a CR induced precursor upstream of the shock as predicted by nonlinear theories of diffusive shock acceleration.
Efficient CR acceleration at SNR shocks changes the Balmer line emission in (at least) two ways. For CR modified shocks, the temperature of the ions downstream of the shock is expected to be lower than in the absence of particle acceleration. This leads to a narrower width of the broad Balmer line. On the other hand, the pressure carried by accelerated particles also produces a CR-induced precursor in which ions can be heated by adiabatic heating (the plasma slows down) and interaction with magnetic turbulence, possibly induced by the same accelerated particles. This second effect leads to a broadening of the narrow component of the Balmer line.
An anomalous width of the narrow Balmer line was first reported as early as 1994 (Smith et al. 1994; Hester et al. 1994): a FWHM ranging from 30 to 50 km s-1 was detected in several SNRs, implying a preshock temperature around 25 000–50 000 K, which is clearly in excess of the temperature for which hydrogen would stay neutral, in the presence of collisional ionization. This suggests that the line is broadened in some sort of preshock region small enough to make collisional ionization unimportant. This is exactly the effect expected from a CR-induced precursor, as already speculated by Smith et al. (1994). From the theoretical point of view, the first attempt at calculating the broadening of the narrow Balmer lines due to a CR-induced precursor was done by Wagner et al. (2009), who used a two-fluid model to treat ions and CRs but neglected the dynamical role of neutrals. A different model was proposed by Raymond et al. (2011) where momentum and energy transfer between ions and neutrals are included, but both the CR spectrum and the profile of the CR-precursor are assumed rather than calculated. Both works conclude that the observed width of 30–50 km s-1 can be explained by postulating some level of CR acceleration at the shock. A more detailed calculation has been developed in Morlino et al. (2013) to take the mutual interplay between CRs, neutrals, ionized plasma and magnetic turbulence into account. The conclusion of this latter work is that, as far as the broadening of the narrow line is concerned, the main physical effect to take into account is the damping of magnetic turbulence in the CR precursor, while adiabatic compression alone is ineffective.
A smaller FWHM of the broad Balmer line, such as the one expected from the presence of CRs (van Adelsberg et al. 2008), has been inferred in two SNRs: RCW 86 inside our own Galaxy (Helder et al. 2009), and SNR 0509–67.5 in the LMC (Helder et al. 2010). In the first case, the authors combined proper motion measurements of nonthermal X-ray filaments observed by Chandra and optical measurements by the VLT of the width of the broad Hα component from the same region to show that the temperature behind the shock is lower than expected based on Rankine-Hugoniot relations. The conclusion was that a sizable fraction of the energy (≥50%) is being channeled into CRs. In fact this conclusion has somehow been retracted by the same authors in a recent paper (Helder et al. 2013) where they use new measurements of the proper motion of optical filaments, which imply a lower shock velocity than inferred from the X-ray proper motion. Using the new measurements, the CR acceleration efficiency that the authors estimate is lower and depends on the assumed distance of the remnant, which is compatible with zero for d ≲ 2.5 kpc. For the second remnant, SNR 0509–67.5, Helder et al. (2010) estimate that the CR pressure behind the SW region of the shock is >15% of the total post-shock pressure.
In both these papers, the CR acceleration efficiency was estimated through a relation between the FWHM of the broad line and the shock velocity found by van Adelsberg et al. (2008, hereafter vAHMR) using the formalism developed in Heng & McCray (2007). This relation was based on the assumption that after three CE reactions, the distributions of atoms and ions reach thermal equilibrium (namely the same temperature and bulk velocity). Here we use a kinetic approach to show that this condition is not fulfilled and this fact substantially changes the expected width of the broad Balmer line.
An accurate calculation of the Balmer emission requires a proper description of the distribution function of the neutral particles in the shock region. Neutrals may undergo a number of CE events before being ionized, but in general they do not thermalize with ions, so that the neutral distribution function can only be determined using the full Boltzmann equation. Moreover, when CRs are also present, the shock structure is determined by the mutual interaction between ions, neutrals, CRs and magnetic field, which are all coupled together through different processes, resulting in a highly nonlinear system. In a series of three papers (Blasi et al. 2012; Morlino et al. 2012, 2013, hereafter Papers I, II, and III), we developed a semi-analytical method for describing the diffusive shock acceleration process in the presence of neutral particles. Our method also estimates the Balmer emission produced by excited hydrogen atoms in the shock region.
In the present paper we use the previously developed formalism to assess the relation between broad Balmer line width, shock speed, and CR acceleration efficiency. Compared with our previous work, we improved our calculations by better approximating of the ion-neutral scattering rate. We show that, for shock speed ≳2500 km s-1, the neutrals experience only a few CE events before ionization. As a consequence, the assumption that the neutral distribution function converges to the ion distribution function (quasi-Maxwellian assumption) is a bad approximation that leads to overestimating the width of the broad line by a factor up to ~20%. When measuring the Balmer line width in real sources, one can then easily obtain unrealistically high values for the CR acceleration efficiency, simply as a result of an erroneous prediction of the line width for any given shock velocity. We find that for an acceleration efficiency of ~20%, the FWHM of the broad Balmer line only decreases by 10% compared to the case in which CRs are absent. Because the effect is so modest, it is clear that if one erroneously expects a very broad line for a given shock velocity, based on the assumption of equilibration between ions and neutrals, a very strong acceleration efficiency (>50%) could easily be inferred.
In Sect. 2 we summarize the calculations of the neutral distribution function and discuss the improvements we implemented with respect to our previous work. In Sect. 3 we discuss our results for the distribution of neutrals and the FWHM of the broad Balmer line and compare them with those in the literature. We conclude in Sect. 4.
2. Improved calculation of atomic rates
We consider a plane-parallel shock wave propagating in a partially ionized proton-electron plasma with velocity Vsh along the z direction. The ionization fraction is fixed at upstream infinity (ISM) where ions and neutrals are assumed to be in thermal equilibrium with each other. The shock structure is determined by the interaction of CRs and neutrals with the background plasma, as discussed in detail in Paper III. In this section we limit ourselves to summarizing the computational method we used to determine the distribution function of neutral atoms in phase space and illustrate an improved approximation for the ion-neutral scattering rates.
The basic equations that describe the behavior of neutral hydrogen have been discussed in our Paper I: neutral hydrogen atoms interact with protons through CE and ionization and with electrons through ionization alone. The hydrogen distribution function, fN(v,z) satisfies the stationary Boltzmann equation ![\begin{equation} \label{eq:vlasov} v_z \frac{\partial f_{N}(\vec v, z)}{\partial z} = \beta_{N} f_{i}(\vec v, z) - \left[ \beta_{i} + \beta_{\rm e} \right] f_{N}(\vec v, z) , \end{equation}](/articles/aa/full_html/2013/10/aa22006-13/aa22006-13-eq12.png) (1)where z is the distance from the shock (which is located at the origin, z = 0), vz is the velocity component along the z-axis, and where the electron and proton distribution functions, fe(v,z) and fi(v,z), are assumed to be Maxwellian at each position.
(1)where z is the distance from the shock (which is located at the origin, z = 0), vz is the velocity component along the z-axis, and where the electron and proton distribution functions, fe(v,z) and fi(v,z), are assumed to be Maxwellian at each position.
The collision terms, βkfl, describe the interaction (due to CE and/or ionization) between the species k and l. The interaction rate βk can be formally written as 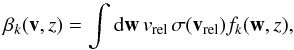 (2)where vrel = | v − w | is the relative velocity, and σ is the cross section for the relevant interaction process. More precisely, βN is the rate of CE of an ion that becomes a neutral, βi is the rate of CE plus ionization of a neutral due to collisions with protons, while βe is the ionization rate of neutrals due to collisions with electrons. A full description of the cross sections used in the calculations can be found in our Paper II.
(2)where vrel = | v − w | is the relative velocity, and σ is the cross section for the relevant interaction process. More precisely, βN is the rate of CE of an ion that becomes a neutral, βi is the rate of CE plus ionization of a neutral due to collisions with protons, while βe is the ionization rate of neutrals due to collisions with electrons. A full description of the cross sections used in the calculations can be found in our Paper II.
Since the dynamics of electrons are not well known, we parametrize the electron temperature as a given fraction of the proton temperature and investigate the dependence of the results on such a parameter. In particular, we define βdown ≡ Te/Tp in the region downstream of the shock and a similar parameter upstream of the shock.
A semi-analytical method for solving Eq. (1) was discussed in Paper I, where we showed how to calculate fN starting from the distribution of protons and electrons. The method is based on decomposing the distribution function fN at each location, upstream and downstream, as the sum of the neutrals that have undergone 0, 1, 2, ..., k CE processes. Each distribution function is named 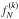 , and clearly
, and clearly 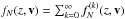 . Using this formalism, Eq. (1) can be rewritten as a set of k + 1 equations, one for each component:
. Using this formalism, Eq. (1) can be rewritten as a set of k + 1 equations, one for each component: ![\begin{eqnarray} \label{eq:vlasov_0} &&v_z \partial_z f_{N}^{(0)} = -\left[ \beta_{i} + \beta_{\rm e} \right] f_{N}^{(0)} \quad {\rm for} \; k=0 , \quad {\rm and} \\[2mm] \label{eq:vlasov_k} &&v_z \partial_z f_{N}^{(k)} = \beta_{N}^{(k-1)} f_{i} - \left[ \beta_{i} + \beta_{\rm e} \right] f_{N}^{(k)} \quad {\rm for} \; k>0 . \end{eqnarray}](/articles/aa/full_html/2013/10/aa22006-13/aa22006-13-eq32.png) Each one of these equations is linear, and the solution for
Each one of these equations is linear, and the solution for 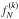 can be obtained from
can be obtained from 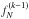 . The boundary conditions are imposed at upstream infinity where ions and neutrals are assumed to start with the same bulk velocity and temperature, so that CE occurs at equilibrium and the distributions do not change. The resulting boundary conditions are
. The boundary conditions are imposed at upstream infinity where ions and neutrals are assumed to start with the same bulk velocity and temperature, so that CE occurs at equilibrium and the distributions do not change. The resulting boundary conditions are 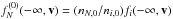 and
and 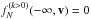 . We can write the solution of these equations in the following implicit form:
. We can write the solution of these equations in the following implicit form: ![\begin{equation} f_{N}^{(0)} (z,v_{\parallel},v_{\perp}) = f_{N}^{(0)} (-\infty, v_{\parallel}, v_{\perp}) \, \exp\left[-\int_{-\infty}^{z} \frac{{\rm d} z'}{v_{\parallel}} \beta_{i} (z',v_{\parallel},v_{\perp})\right] , \end{equation}](/articles/aa/full_html/2013/10/aa22006-13/aa22006-13-eq36.png) (5)for k = 0, and
(5)for k = 0, and ![\begin{equation} f_N^{(k)}= - \int_{z}^{+\infty} \frac{{\rm d}z'}{v_{\parallel}} \beta_{N}^{(k-1)} f_{i} \exp \left[ \int_{z}^{z'} \frac{{\rm d}z''}{v_{\parallel}} \beta_{i} \right], ~~~v_{\parallel}<0, \label{eq:fnk<} \end{equation}](/articles/aa/full_html/2013/10/aa22006-13/aa22006-13-eq38.png) (6)and
(6)and ![\begin{equation} f_N^{(k)}= \int_{-\infty}^{z} \frac{{\rm d}z'}{v_{\parallel}} \beta_{N}^{(k-1)} f_{i} \exp \left[ \int_{z}^{z'} \frac{{\rm d}z''}{v_{\parallel}} \beta_{i} \right], ~~~v_{\parallel}>0, \label{eq:fnk>} \end{equation}](/articles/aa/full_html/2013/10/aa22006-13/aa22006-13-eq39.png) (7)for k > 0. Notice that v| | = vz is the velocity component along z, while v⊥ is orthogonal to z.
(7)for k > 0. Notice that v| | = vz is the velocity component along z, while v⊥ is orthogonal to z.
A good approximation for the total distribution function of neutrals is obtained by adding a sufficiently large number of 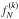 . How many are added is determined by the physical scale of the problem. A rough estimate can be obtained by comparing the length scale for CE with the maximum between the ionization length scale and the precursor length. In general, for typical values of the ambient parameters, the longest scale, hence the one relevant to this comparison, is the size of the CR-induced precursor.
. How many are added is determined by the physical scale of the problem. A rough estimate can be obtained by comparing the length scale for CE with the maximum between the ionization length scale and the precursor length. In general, for typical values of the ambient parameters, the longest scale, hence the one relevant to this comparison, is the size of the CR-induced precursor.
The most expensive part for computation is calculating the interaction rates 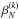 from Eq. (2). To reduce the computational time, we used an approximated expression in Paper I, originally proposed by Pauls et al. (1995), which is based on two assumptions: i) the partial distribution functions
from Eq. (2). To reduce the computational time, we used an approximated expression in Paper I, originally proposed by Pauls et al. (1995), which is based on two assumptions: i) the partial distribution functions 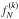 are assumed to be Maxwellian, and ii) the cross section is assumed to be constant (or slowly changing as a function of the relative velocity). Under these assumptions, the interaction rates can be expressed as
are assumed to be Maxwellian, and ii) the cross section is assumed to be constant (or slowly changing as a function of the relative velocity). Under these assumptions, the interaction rates can be expressed as 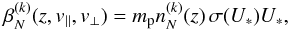 (8)where
(8)where 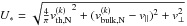 , and σ(U∗) is the relevant cross section calculated at U∗. Here
, and σ(U∗) is the relevant cross section calculated at U∗. Here 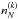 is the numerical density of particles in the distribution function
is the numerical density of particles in the distribution function 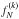 , while
, while 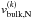 and
and 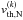 are the moments of the same distribution corresponding to bulk and thermal speed.
are the moments of the same distribution corresponding to bulk and thermal speed.
In our calculations the 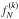 are neither assumed to be Maxwellian nor found to be Maxwellian, and most of the difference between the results presented here and in previous literature arises exactly from our more realistic treatment of the neutral distribution in phase space. However, we find that the scattering rates can be computed in an accurate way through the following procedure, which allows us to save a large amount of computation time: we compute the moments of the
are neither assumed to be Maxwellian nor found to be Maxwellian, and most of the difference between the results presented here and in previous literature arises exactly from our more realistic treatment of the neutral distribution in phase space. However, we find that the scattering rates can be computed in an accurate way through the following procedure, which allows us to save a large amount of computation time: we compute the moments of the 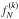 and then introduce an equivalent Maxwellian, with the same moments, only with the purpose of calculating the scattering rates. We checked that this procedure does not introduce any critical aspect in the calculations and therefore retained this part of the computation here as well. On the other hand, we relaxed the assumption here that the cross sections are weak functions of the relative velocity. Following Chevalier et al. (1980) the three-dimensional integral in Eq. (2) can be reduced to only one dimension with a change of variable. The final result can be written as
and then introduce an equivalent Maxwellian, with the same moments, only with the purpose of calculating the scattering rates. We checked that this procedure does not introduce any critical aspect in the calculations and therefore retained this part of the computation here as well. On the other hand, we relaxed the assumption here that the cross sections are weak functions of the relative velocity. Following Chevalier et al. (1980) the three-dimensional integral in Eq. (2) can be reduced to only one dimension with a change of variable. The final result can be written as ![\begin{equation} \label{eq:beta_new} \beta_{N}^{(k)}(v,v_{\rm th},z) = n_N^{(k)}(z) \int_0^{\infty} {\rm d}v_{\rm r} \frac{\sigma(v_{\rm r}) v_{\rm r}^2}{v v_{\rm th} \sqrt{\pi}} \left[ {\rm e}^{-\left(\frac{v-v_{\rm r}}{v_{\rm th}} \right)^2} - {\rm e}^{-\left(\frac{v+v_{\rm r}}{v_{\rm th}} \right)^2} \right] , \end{equation}](/articles/aa/full_html/2013/10/aa22006-13/aa22006-13-eq54.png) (9)where σ is now an arbitrary function of the relative velocity vr. The integration in Eq. (9) is performed numerically only once and for each cross section involved in the calculation on a two-dimensional grid in the variables (v,vth). Using Eq. (9) rather than Eq. (8) the value of
(9)where σ is now an arbitrary function of the relative velocity vr. The integration in Eq. (9) is performed numerically only once and for each cross section involved in the calculation on a two-dimensional grid in the variables (v,vth). Using Eq. (9) rather than Eq. (8) the value of 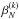 is more accurate by ~10%. At the same time, this improved version of the calculation is also found to be computationally faster by roughly 20%.
is more accurate by ~10%. At the same time, this improved version of the calculation is also found to be computationally faster by roughly 20%.
3. Results
The most important result of this work is that for shocks moving with speed over ~2500 km s-1, the neutral distribution function does not reach thermal equilibrium with the ions distribution, not even after many CE reactions. As a consequence, we predict that the widths of the broad Balmer line appreciably smaller than estimated in previous calculations, where the assumption was made that ions and neutrals would thermalize after three CE reactions (vAHMR). The implications for the estimates of the CR acceleration efficiency are rather dramatic and discussed below.
As a benchmark case, we consider a shock with speed Vsh = 4000 km s-1, total upstream density 1 cm-3, and ionization fraction xion = 50%. With these values for the parameters, the typical interaction length for both CE and ionization is ~ 1016 cm. For this specific case, we assume, as may be expected for a collisionless shock, that the background electrons and protons are not in thermal equilibrium. We take βdown = 0.01, although this assumption is not crucial for our conclusions. We first consider a case with no particle acceleration.
In Fig. 1 we plot the partial distribution functions 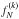 for k = 1–6 at three different locations downstream, as a function of v| | and for v⊥ = 0, comparing them with the downstream distribution function of ions. Each
for k = 1–6 at three different locations downstream, as a function of v| | and for v⊥ = 0, comparing them with the downstream distribution function of ions. Each 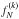 includes three different contributions: a broad component emitted by neutrals that suffered at least one CE downstream, an intermediate component produced by atoms resulting from CE in the neutral return flux precursor upstream (Paper I), and finally a narrow component emitted by truly cold (T ~ 104 K) atoms. As far as the atoms responsible for the broad component are concerned, we clearly see that even for k = 6 (namely after six CE events, basically all in the downstream in this case), their distribution does not approach a Maxwellian, and one can easily judge that its peak is still at a different velocity than for ions. We can make this argument more quantitative by calculating the moments of the distributions.
includes three different contributions: a broad component emitted by neutrals that suffered at least one CE downstream, an intermediate component produced by atoms resulting from CE in the neutral return flux precursor upstream (Paper I), and finally a narrow component emitted by truly cold (T ~ 104 K) atoms. As far as the atoms responsible for the broad component are concerned, we clearly see that even for k = 6 (namely after six CE events, basically all in the downstream in this case), their distribution does not approach a Maxwellian, and one can easily judge that its peak is still at a different velocity than for ions. We can make this argument more quantitative by calculating the moments of the distributions.
In Fig. 2 we plot several quantities related to the neutral distribution as a function of the position downstream, for the same benchmark case. Panels (b), (c), and (d) show, for each 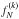 , the behavior of density, bulk speed and “equivalent” thermal speed of the broad component (the bulk and thermal velocities are normalized to the same quantities as computed for the ions’ distribution function). The region in which these parameters are most important is where the bulk of Balmer emission is produced. This region is easily identified from panel (a), which shows the numerical density and the Hα emission of both the broad and narrow line emitting components: the bulk of the broad Hα component is produced in the region 1015 < z < 1016 cm.
, the behavior of density, bulk speed and “equivalent” thermal speed of the broad component (the bulk and thermal velocities are normalized to the same quantities as computed for the ions’ distribution function). The region in which these parameters are most important is where the bulk of Balmer emission is produced. This region is easily identified from panel (a), which shows the numerical density and the Hα emission of both the broad and narrow line emitting components: the bulk of the broad Hα component is produced in the region 1015 < z < 1016 cm.
It is easy to see from panel (c) that in the region between 1015 and 1016 cm, the bulk speed of all 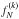 is greater than the bulk speed of ions, although vbulk decreases for higher values of k. We also note that for z ≲ 1014 cm, vbulk becomes negative, which is a consequence of the neutral return flux (see Paper I). We see in panel (d) that the thermal speed as calculated for any
is greater than the bulk speed of ions, although vbulk decreases for higher values of k. We also note that for z ≲ 1014 cm, vbulk becomes negative, which is a consequence of the neutral return flux (see Paper I). We see in panel (d) that the thermal speed as calculated for any 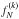 is less than the thermal speed of ions by ~ (25−30)%. These two facts prove that the ionization starts dominating CE before neutrals and ions may reach thermal equilibrium.
is less than the thermal speed of ions by ~ (25−30)%. These two facts prove that the ionization starts dominating CE before neutrals and ions may reach thermal equilibrium.
 |
Fig. 1 Partial distribution functions of neutrals, |
 |
Fig. 2 Panel a) total density of broad (dashed) and narrow neutrals (dot-dashed) and the sum of the two (solid line). The thin lines show the Balmer emission of narrow (dashed) and broad (dot-dashed) components (the first divided by 3). Panel b) density of the partial component of broad neutrals normalized to the total density of broad neutrals, for k = 1 to 6. Panel c) bulk speed of the partial component of broad neutrals normalized to the bulk speed of ions. Panel d) thermal speed of the partial component of broad neutrals normalized to the thermal speed of ions. The labels in panel c) also refer to panels b) and d). |
Finally, from panel (b) of Fig. 2 we see that for z < 1015 cm the partial distribution functions with k > 2 contribute about half of the total density of broad neutrals, while for z > 1015 cm their contribution increases to more than 50%. In other words, the bulk of broad Balmer line emission is dominated by neutrals that have undergone more than two CE events. This is especially important in the comparison of our results with those of van Adelsberg et al. (2008). Like us, they also separate the neutral distribution function into a sum of partial functions, each defined by the number of CE events undergone by the particles. Unlike ours, their partial functions are averaged over the downstream region. There is no description of the upstream region in van Adelsberg et al. (2008). However, what is most important, and makes the biggest difference between our results and those of vAHMR, is their assumption that after two CE events the neutral distribution function acquires the same moments as fion, namely, same temperature and same bulk speed.
In the following, we compare our results with those of vAHMR, and show how their assumptions can easily lead to overestimate the CR energy content at the shock. Before proceeding, however, we want caution that a direct comparison is actually difficult, because of the differences in the two methods: vAHMR only account for the dynamics in the downstream, while we also consider the dynamics of ions and neutrals in the upstream, so that our 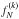 ’s also include particles that undergo one or more CE events in the upstream.
’s also include particles that undergo one or more CE events in the upstream.
In Fig. 3 we plot the FWHM of the broad Balmer line as a function of the shock speed. Three different sets of curves are shown: the results obtained using our full method and the results of vAHMR. For the sake of comparison of our calculations with those of vAHMR, we also plot the FWHM that would be obtained from our calculations if we made the artificial assumption that all distributions 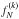 with k > 2 Maxwellians with the same moments as the ions’ distribution. For each set of curves, thick and thin lines represent the non equilibration (NE: βdown = 0.01) and full equilibration (FE: βdown = 1) cases between protons and electrons, respectively.
with k > 2 Maxwellians with the same moments as the ions’ distribution. For each set of curves, thick and thin lines represent the non equilibration (NE: βdown = 0.01) and full equilibration (FE: βdown = 1) cases between protons and electrons, respectively.
Our results and those of vAHMR coincide for shock speeds ≲2000 km s-1 for the NE case (or ≲2500 km s-1 for the FE case), as one may expect based on the fact that ionization becomes important for such low velocities only after a large number of CE path lengths, thereby making the assumption of thermalization between ions and neutrals a better approximation.
 |
Fig. 3 Comparison between the FWHM of the broad Balmer line as calculated in the present work (solid lines) with those calculated by van Adelsberg et al. (2008, dot-dashed lines). The dashed lines represent the FWHM calculated using our technique, but requiring that the partial distribution functions of broad neutrals are Maxwellian for k > 2, with the same temperature and the same bulk velocity as the ions. Dots show the FWHM calculated in the presence of CRs with acceleration efficiency equal to 0.1 and 0.2 and for shock speeds of 4000 and 6000 km s-1. |
To provide an easy way to compare our results with measured values of the FWHM of broad Balmer lines, we looked for a fit to the curves shown in Fig. 3. A good fit is provided by the expression, ![\begin{equation} \label{eq:fit} W_0(V_{\rm sh},\beta_{\rm down}) = A \sqrt{ \frac{3 \ln 2}{2 (1+\beta_{\rm down})} } \, \frac{V_{\rm sh}}{{\left[ 1 + {(V_{\rm sh}/V_{\rm br})}^3 \right]}^{1/5}} , \end{equation}](/articles/aa/full_html/2013/10/aa22006-13/aa22006-13-eq92.png) (10)which in the limit of low Vsh gives back the linear dependence of line width on shock speed. The term in the square root gives the slope expected if the neutrals have a Maxwellian distribution with exactly the same temperature as ions (see e.g. Heng 2010). The parameter A represents the deviation from this ideal situation, and its value changes only slightly between the NE case (A = 1.126) and the FE case (A = 1.096), while the value of the break velocity Vbr changes from Vbr = 2104 km s-1 (for NE) to Vbr = 3184 km s-1 (for FE). Equation (10) provides a good fit, giving an error less than 2%, if the shock speed value is in the range between 500 and 7000 km s-1.
(10)which in the limit of low Vsh gives back the linear dependence of line width on shock speed. The term in the square root gives the slope expected if the neutrals have a Maxwellian distribution with exactly the same temperature as ions (see e.g. Heng 2010). The parameter A represents the deviation from this ideal situation, and its value changes only slightly between the NE case (A = 1.126) and the FE case (A = 1.096), while the value of the break velocity Vbr changes from Vbr = 2104 km s-1 (for NE) to Vbr = 3184 km s-1 (for FE). Equation (10) provides a good fit, giving an error less than 2%, if the shock speed value is in the range between 500 and 7000 km s-1.
Aside from the level of equilibration between electrons and protons, the FWHM of the broad Balmer line can also be affected, at least in principle, by the presence of He. The main effect of He is associated to the possibility that fully ionized He by itself can thermalize to a downstream temperature which is mHe/mp times the proton temperature. If collisionless processes lead to thermal equilibrium of the two species (Coulomb collisions are too slow to have any effect on the relevant time scales), then the presence of He would be reflected in a downstream temperature possibly as high as ~ 1.3Tp. Clearly, in order for this effect to affect Balmer emission, thermalization would have to occur on a spatial scale smaller than the ionization length of hydrogen atoms. On the other hand, if He+ and He++ were present, they could play an active role in CE and ionization of H atoms, thereby modifying the distribution function relevant for the Balmer emissivity.
While in our calculations we neglect the contribution of He, vAHMR take it into account, under the assumption that it is completely neutral upstream. With this assumption, the effects of He can only appear after it is ionized downstream at least once. This immediately suggests that the differences shown in Fig. 3 between the two calculations (ours and vAHMR’s) cannot be accounted for by the different treatments of He. The results of the two calculations are in fact coincident for slow shocks. But this is exactly the regime for which the effects of He should be most important, because the ratio between its ionization length and that of hydrogen atoms is lower for low shock speeds.
The conclusion we draw is that neglecting the presence of He in our calculations cannot be the main source of the differences between our results and those of vAHMR. At the same time we can conclude, based on vAHMR’s calculations, that He has negligible effects on the system. In fact, their assumption (namely of negligible He ionization upstream) should apply to most (if not all) of the sources of interest, since from Saha’s formula one easily sees that having an appreciable fraction of He+/He implies a totally negligible fraction of neutral H, if the overall plasma is in thermal equilibrium. A possible exception to this scenario could be produced by the presence of ionizing radiation which tends to ionize He.
We now turn our attention to the main point we want to address in this paper, namely estimating the CR acceleration efficiency from measurement of the FWHM of the broad Balmer line. It is apparent that our refined treatment of the neutral distribution downstream leads us to expect a FWHM of the broad Balmer line that is smaller than in previous calculations. As a consequence, for a given measured value of the FWHM, we infer a lower CR acceleration efficiency. In fact, in some SNRs, it may turn out to be difficult or even impossible to reach a definite conclusion concerning the presence of CR acceleration.
The theory of Balmer-dominated CR modified shocks has been outlined in our Paper III, where we showed in a quantitative way how the FWHM of the broad Balmer line decreases with increasing acceleration efficiency, as expected on qualitative grounds. This approach has been improved further here with a more accurate calculation of the CE and ionization scattering rates, as discussed in Sect. 2.
Figure 3 represents the FWHM of the broad Balmer line for the cases of NE (βdown = 0.01) and full equilibration (βdown = 1) and for acceleration efficiency of 10% and 20%. Two values of the shock speed have been considered: 4000 and 6000 km s-1. Here we define the acceleration efficiency as 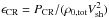 , where PCR is the CR pressure at the shock position, and ρ0,tot is the total density at upstream infinity (ions plus neutrals). This definition could be somewhat misleading, in that the shock can only accelerate the ionized component. In this sense, the actual efficiency would be
, where PCR is the CR pressure at the shock position, and ρ0,tot is the total density at upstream infinity (ions plus neutrals). This definition could be somewhat misleading, in that the shock can only accelerate the ionized component. In this sense, the actual efficiency would be 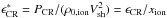 . Since in Fig. 3 we assumed an ionization fraction of 50%, we have
. Since in Fig. 3 we assumed an ionization fraction of 50%, we have 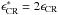 .
.
From Fig. 3, it is clear that, given the strong dependence of the implied efficiency on the assumed level of electron-proton thermalization (parametrized by the value of βdown), it is generally difficult to draw firm conclusions about the CR acceleration efficiency unless additional information on βdown is available. However, if the measured value of the FWHM of the broad line falls below the thin solid line, then one can derive a robust lower limit on the CR acceleration efficiency, provided a reliable measurement of the shock speed is available.
To first approximation, the FWHM of the broad line decreases linearly with ϵCR, for ϵCR ≲ 20%. A simple linear fit to the FWHM in the presence of CRs reads as ![\begin{equation} W(V_{\rm sh}, \epsilon_{\rm CR}) \approx W_0(V_{\rm sh}) \left[1-B/W_0(V_{\rm sh}) \, \epsilon_{\rm CR} \right], \end{equation}](/articles/aa/full_html/2013/10/aa22006-13/aa22006-13-eq114.png) (11)where W0(Vsh) is the FWHM in the absence of CR acceleration, and B = 2000 km s-1. This implies that, in order to obtain a lower limit on the acceleration efficiency, equal, say, to a given value
(11)where W0(Vsh) is the FWHM in the absence of CR acceleration, and B = 2000 km s-1. This implies that, in order to obtain a lower limit on the acceleration efficiency, equal, say, to a given value 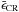 , the accuracy needed in the measurement of W should satisfy the condition
, the accuracy needed in the measurement of W should satisfy the condition 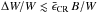 . Needless to say, the shock velocity is needed as well with decent accuracy: the lower limit should satisfy
. Needless to say, the shock velocity is needed as well with decent accuracy: the lower limit should satisfy 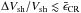 . Such constraints can provide hints on the observational requirements needed to determine the presence of CRs in Balmer-dominated shocks.
. Such constraints can provide hints on the observational requirements needed to determine the presence of CRs in Balmer-dominated shocks.
Finally we note that in the absence of accelerated particles, the FWHM does not depend upon the choice of the density and ionization fraction. What does depend on these two parameters is the absolute value of the length scale where the processes of charge exchange and ionization take place. In the presence of accelerated particles, the results depend upon the gas density very weakly, while the dependence of the inferred acceleration efficiencies on the ionization fraction is more substantial, but it does need to be assesses on a case-by-case basis. This is why we decided to calculate the FWHM for nominal values of the gas density and ionization fraction, since the arguments presented in the paper remain valid in a qualitative way, irrespective of the exact values of parameters.
4. Conclusions
The possibility of using optical telescopes to measure the width of the Balmer lines in SNRs, and then inferring the CR acceleration efficiency, is one of the big hopes for the future of any investigations of the CR origin. The technique is, in a way, calorimetric in that the broad Balmer line contains information about the temperature of the hot proton plasma behind the SNR shock and this temperature is lower when the shock accelerates CRs efficiently. Although this is a simple consequence of energy conservation arguments, a detailed knowledge of the physical phenomena that couple ions and H atoms is needed to achieve a quantitative estimate of the CR acceleration efficiency. A complete theory of the dynamics of a Balmer-dominated, CR-modified shock has recently been presented in Paper III, where we used the mathematical formalism introduced in our Paper I.
In the present paper we have improved on one aspect of that work, by better calculating scattering rates of CE and ionization, the two physical processes responsible for the coupling between ionized and neutral material at the shock. However, the main point we want to stress in this work is that to accurately estimate the CR acceleration efficiency one has to have a space-dependent, kinetic approach to the neutrals, such as the one we put forward in Paper III. To highlight this, we compared our predicted FWHM of the broad Balmer line with the results of vAHMR, which is widely used in the literature to infer information on CR acceleration from optical measurements. In the work by vAHMR, the simplifying assumption was made that neutrals that suffered more than two CE reactions would reach thermal equilibrium with ions. Moreover, their calculation does not provide any space dependence of the distribution functions. In the absence of CRs, at 4000 km s-1 the difference in the FWHM between the two calculations is ~1000 km s-1 in the NE case and a few hundred km s-1 for full equilibration between electrons and protons. This is also the order of magnitude of the reduction in the FWHM expected for CR acceleration, which implies that a proper treatment of the neutral distribution function is absolutely crucial for a reliable quantitative assessment of the CR energy content of SNRs. The assumption of ion-neutral equilibration has been shown to be incorrect for shock speeds above ~2500 km s-1. The physical reason for this behavior is in the relative importance of CE and ionization: ions and neutrals tend to reach thermal equilibrium through CE, but unless this happens within a length equal to a few times the ionization path length at most, Maxwellian neutrals (with the same temperature as ions) are not what the Balmer line will reflect. For low shock speeds, ionization is inefficient, and thermal equilibrium between ions and neutrals is reached approximately, but for high speed shocks ionization dominates CE and the neutrals do not thermalize.
The application of these calculations has far-reaching implications: the modeling described in Paper III, when including the improvements in terms of accuracy and computation time given in the present paper, provides all the necessary tools to determine the dynamical state of a Balmer-dominated CR-modified shocks and to calculate the shape of the Balmer line (narrow, intermediate, and broad) for any CR acceleration efficiency. The whole computation is fast enough to allow for extensive applications to several SNRs of interest. Future combined observations of the overall shape of the Balmer line, as well as of shock velocity and a multifrequency spectrum from individual remnants, may open the door to a systematic estimate of the CR acceleration efficiency in SNRs. In two forthcoming papers, we will illustrate the results of our investigation of the Balmer emission from the two remnants discussed in the introduction, RCW 86 and SNR 0509–67.5.
Acknowledgments
We are grateful to D. Caprioli and K. Heng for discussions of this topic. This work was partially funded through grant PRIN INAF 2010 and ASTRI.
References
- van Adelsberg, M., Heng, K., McCray, R., & Raymond, J. C. 2008, ApJ, 689, 1089 (vAHMR) [CrossRef] [Google Scholar]
- Blasi, P., Morlino, G., Bandiera, R., Amato, E., & Caprioli, D. 2012, ApJ, 755, 121 (Paper I) [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Raymond, J. C. 1978, ApJ, 225, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., Kirshner, R. P., & Raymond, J. C. 1980, ApJ, 235, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Helder, E. A., Vink, J., Bassa, C. G., et al. 2009, Science, 325, 719 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Helder, E. A., Kosenko, D., & Vink, J. 2010, ApJ, 719, 140 [Google Scholar]
- Helder, E. A., Vink, J., Bamba, A., et al. 2013, MNRAS, accepted [arXiv:1306.3994] [Google Scholar]
- Heng, K. 2010, PASA, 27, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., & McCray, R. 2007, ApJ, 654, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Hester, J. J., Raymond, J. C., & Blair, W. P. 1994, ApJ, 470, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Morlino, G., Bandiera, R., Blasi, P., & Amato, E. 2012, ApJ, 760, 137 (Paper II) [NASA ADS] [CrossRef] [Google Scholar]
- Morlino, G., Blasi, P., Bandiera, R., Amato, E., & Caprioli, D. 2013, ApJ, 768, 148 (Paper III) [NASA ADS] [CrossRef] [Google Scholar]
- Pauls, H. L., Zank, G. P., & Williams, L. L. 1995, J. Geophys. Res., 100, 21 [Google Scholar]
- Raymond, J. C., Vink, J., Helder, E. A, & de Laat, A. 2011, ApJ, 731, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. C., Raymond, J. C., & Laming, J. M. 1994, ApJ, 420, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, A. Y., Lee, J.-J., Raymond, J. C., Hartquist, T. W., & Falle, S. A. E. G. 2009, ApJ, 690, 1412 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Partial distribution functions of neutrals, |
| In the text | |
 |
Fig. 2 Panel a) total density of broad (dashed) and narrow neutrals (dot-dashed) and the sum of the two (solid line). The thin lines show the Balmer emission of narrow (dashed) and broad (dot-dashed) components (the first divided by 3). Panel b) density of the partial component of broad neutrals normalized to the total density of broad neutrals, for k = 1 to 6. Panel c) bulk speed of the partial component of broad neutrals normalized to the bulk speed of ions. Panel d) thermal speed of the partial component of broad neutrals normalized to the thermal speed of ions. The labels in panel c) also refer to panels b) and d). |
| In the text | |
 |
Fig. 3 Comparison between the FWHM of the broad Balmer line as calculated in the present work (solid lines) with those calculated by van Adelsberg et al. (2008, dot-dashed lines). The dashed lines represent the FWHM calculated using our technique, but requiring that the partial distribution functions of broad neutrals are Maxwellian for k > 2, with the same temperature and the same bulk velocity as the ions. Dots show the FWHM calculated in the presence of CRs with acceleration efficiency equal to 0.1 and 0.2 and for shock speeds of 4000 and 6000 km s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


