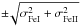| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 10 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201321844 | |
| Published online | 01 October 2013 | |
FAMA: An automatic code for stellar parameter and abundance determination⋆
1
INAF – Osservatorio Astrofisico di Arcetri,
Largo E. Fermi, 5, 50125
Firenze,
Italy
e-mail: laura@arcetri.astro.it
2
Department of Astronomy, Indiana University,
Bloomington,
USA
3
MIT Kavli Institute, Boston, USA
4
Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122
Padova,
Italy
5
Dipartimento di Fisica e Astronomia, Vicolo dell’Osservatorio 3, 35122
Padova,
Italy
6
INAF – Osservatorio Astronomico di Bologna,
Via Ranzani 1, 40127
Bologna,
Italy
7
Dipartimento di Fisica e Astronomia, Via Ranzani 1, 40127
Bologna,
Italy
8
Dipartimento di Fisica, sezione Astronomia, Largo E. Fermi 2,
50125
Firenze,
Italy
Received: 6 May 2013
Accepted: 27 June 2013
Context. The large amount of spectra obtained during the epoch of extensive spectroscopic surveys of Galactic stars needs the development of automatic procedures to derive their atmospheric parameters and individual element abundances.
Aims. Starting from the widely-used code MOOG by C. Sneden, we have developed a new procedure to determine atmospheric parameters and abundances in a fully automatic way. The code FAMA (Fast Automatic MOOG Analysis) is presented describing its approach to derive atmospheric stellar parameters and element abundances. The code, freely distributed, is written in Perl and can be used on different platforms.
Methods. The aim of FAMA is to render the computation of the atmospheric parameters and abundances of a large number of stars using measurements of equivalent widths (EWs) as automatic and as independent of any subjective approach as possible. It is based on the simultaneous search for three equilibria: excitation equilibrium, ionization balance, and the relationship between log n(Fe i) and the reduced EWs. FAMA also evaluates the statistical errors on individual element abundances and errors due to the uncertainties in the stellar parameters. The convergence criteria are not fixed “a priori” but are based on the quality of the spectra.
Results. In this paper we present tests performed on the solar spectrum EWs that assess the method’s dependency on the initial parameters and we analyze a sample of stars observed in Galactic open and globular clusters.
Key words: methods: data analysis / techniques: spectroscopic / stars: abundances / Galaxy: abundances / surveys / open clusters and associations: general
The current version of FAMA is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/558/A38
© ESO, 2013
1. Introduction
The most recent years have been characterized by a large number of ambitious spectroscopic surveys, such as, the Gaia-ESO Survey (GES) with the Very Large Telescope (VLT) at the European Southern Observatory (Gilmore et al. 2012; Randich & Gilmore 2012), the APOGEE Survey at the Apache Point Observatory (Allende Prieto et al. 2008), the RAVE Survey at the Anglo-Australian Observatory (Zwitter et al. 2008), and the BRAVA (Kunder et al. 2012) and ARGOS (Freeman et al. 2013) surveys dedicated to the Galactic bulge. Moreover, wide-field multifiber facilities such as, HERMES (Barden et al. 2010) at the Anglo-Australian Observatory, 4MOST (de Jong 2011) at the New Technology Telescope, and MOONS (Cirasuolo et al. 2011) at the VLT are planned for the near future.
These surveys yield spectra for a very large number of stars which need automatic or semi-automatic procedures to analyze their spectra. To satisfy the requests for an automatic and rapid analysis, several new codes have been designed during the past few years. Some of them are based on the χ2 minimization of the differences between the observed spectrum and a grid of synthetic spectra, such as the codes ABBO (Bonifacio & Caffau 2003) and SME (Valenti & Piskunov 1996), or the projection of the observed spectra on a grid of synthetic spectra as in MATISSE (Recio-Blanco et al. 2006). Other methods are based on the analysis of the equivalent widths (EWs) of the metal lines, as in the codes developed by Takeda et al. (2002) and in GALA (Mucciarelli et al. 2013).
The two methodologies, the global χ2 minimization and the traditional analysis with EWs, differ particularly in their use of the knowledge of the physics, the Boltzmann and Saha statistical physics, governing the stellar atmospheres. While classical methods make an intensive use of statistical physics, taking advantage of the physical-state indicators that are available in high-resolution stellar spectra, the χ2 minimization methods lose part of the information trying to optimize the atmospheric parameters by seeking the best match between the observed spectrum and a synthetic spectrum. The possible risk of this latter approach is, for instance, described by Torres et al. (2012) who analyzed a sample of high-resolution spectra with both the classical EW method and the χ2 minimization techniques. Comparing the results obtained with different methods, they found that correlations between the stellar parameters exist, and that they are much stronger for parameters derived with χ2 minimization due to one spectroscopic quantity that can play against another to some extent which leads to nearly the same cross-correlation value or χ2 value. For example, stronger lines produced by adopting a higher metallicity for the synthetic spectrum can be compensated by a suitable increase in the effective temperature to first order. A similar degeneracy exists between surface gravity and temperature. Torres et al. (2012) found that the effect of these correlations is evidently much weaker in the case of classical EW analysis, in which their work was performed with MOOG. For these reasons we believe that traditional analysis has still a strong potential in the framework of high-resolution spectra, and, with the help of automatic procedures, it will be competitive as one of the more appealing χ2 minimization techniques.
In this context, we have decided to automate the well-known, widely-used MOOG code1 (Sneden 1973; Sneden et al. 2012) to allow the computation of a fully self-operating spectral analysis. MOOG was originally designed at the beginning of the 1970s, and it has been periodically updated by Sneden and his collaborators. The typical use of MOOG is to assist in the determination of the chemical composition of a star, following the basic equations of one dimensional local thermodynamic equilibrium (1D LTE) stellar line analysis. MOOG performs a variety of line analysis and spectrum synthesis tasks.
The classical version of MOOG makes use of the Abfind driver with a model atmosphere to derive the stellar parameters and the abundances. MOOG needs a continuous human intervention to adjust the stellar parameters satisfying three requirements: the ionization balance, the excitation balance, and the minimization of the trend between log n(Fe i) and the observed (or predicted) reduced EWs [log(EW/λ)]. Each of these three well-known steps allows one to fix one of the stellar parameters: The effective temperature (Teff) is obtained by eliminating trends between log n(Fe i) and the excitation potential (EP). The surface gravity is optimized by assuming the ionization equilibrium condition, i.e. log n(Fe ii) = log n(Fe i). The microturbulence is set by minimizing the slope of the relationship between log n(Fe i) and the logarithm of the reduced EWs. However the three steps are interconnected, for example a variation in effective temperature produces a variation in log n(Fe ii) and log n(Fe i) and thus could require an adjustment in the surface gravity. The changes on gravity can sometimes be of second order. As long as changes to Teff and ξ are not radical from iteration to iteration, we can thus neglect the variation in log g by adjusting it every few iterations. The determination of the atmospheric parameters is usually done with an iterative process, which could take a relatively long time to complete the analysis of a single star. This process is acceptable, if the number of stars is limited, but it is completely infeasible for a large survey.
To make the analysis of a large number of stars possible, we have designed an automation of MOOG, also called FAMA (Fast Automatic MOOG Analysis), that does not need any human intervention during the phase of determination of abundances and atmospheric parameters. It is able to minimize the slopes of the correlations in a coherent way that considers the quality of the spectra and of the EW measurement. FAMA is developed at the Arcetri Observatory and it can be freely obtained with the installation manual sending an email to laura@arcetri.astro.it, at http//www.arcetri.astro.it/~laura, or at CDS. It is a Perl code2, which performs a complete 1D LTE (local thermodynamic equilibrium) spectral analysis of high-resolution spectra. Composed of several modules and a parameter file that allow the user to derive the stellar parameters and abundances, the Perl code starts from two files with EWs (one with iron EWs and the other with EWs of other elements) and a file with first-guess atmospheric parameters.
In the present paper we show the working principles of FAMA with some tests on the Sun and on a sample of stars in open clusters (OCs) and in globular clusters (GCs). The paper is structured as follows: In Sect. 2 we present the philosophy of the code together with the definition of the quality parameter QP. In Sect. 3, we will describe how the errors are computed, whereas in Sect. 4 we present the test data analysis. Finally, our summary and conclusions are given in Sect. 5.
2. The working principles of the code
The ingredients with which FAMA is fed are: i) EW files: two files, one containing EWs of iron in the two ionization stages and the second one containing EWs belonging to the complete list of elements; and ii) parameter file: a file with the first-guess atmospheric parameters which includes the effective temperature, Teff, the surface gravity, log g , the microturbulent velocity, ξ, and the abundance of iron with respect to the solar value, [Fe/H]3.
The philosophy of the code is based on an iterative search for the three equilibria (excitation, ionization, and the trend between log n(Fe i) and log(EW/λ)) with a series of recursive steps starting from a set of initial atmospheric parameters, and arriving at a final set of atmospheric parameters which fulfills the three equilibrium conditions. The order followed in the search for the three equilibria is also important since Teff is the controlling parameter for the ultimate solution. Thus it is necessary first to regulate it, then to move to the second most important parameter, the surface gravity, which adjusts the ionization equilibrium, and finally to fix the microturbulence.
-
1.
Excitation equilibrium: According to theclassical equation of Saha-Boltzmann, as summarized byTakeda et al. (2002) and byGray (2005), the abundance of Fe iincreases with an increase inTeff, while it is less sensitive to a variation in the surface gravity. The relation is given by the following formula:
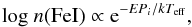 (1)where log n(Fe i) is the logarithmic abundance of iron and EPi is the excitation potential of each line corresponding to the level i. This relation is valid in the approximation that most of the iron atoms are neutral. This means that the variation in temperature causes changes in iron abundance of lines with different EPi, and we can constrain Teff by requiring that the abundances derived from Fe i lines, for which the values of the excitation potential spread over a sufficiently wide range, be independent of EP.
(1)where log n(Fe i) is the logarithmic abundance of iron and EPi is the excitation potential of each line corresponding to the level i. This relation is valid in the approximation that most of the iron atoms are neutral. This means that the variation in temperature causes changes in iron abundance of lines with different EPi, and we can constrain Teff by requiring that the abundances derived from Fe i lines, for which the values of the excitation potential spread over a sufficiently wide range, be independent of EP. -
2.
Ionization equilibrium: The surface gravity, log g, is related to the Fe ii abundance by the following relation
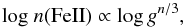 (2)derived in the approximation of the classical equation of Saha-Boltzmann and with n = 1 when iron is mostly ionized and n = 2 for an iron population dominated by neutral atoms. Thus, the same abundance should be derived for neutral and ionized lines in the condition of ionization equilibrium for a given element. The equality of the abundances log n(Fe i) and log n(Fe ii) gives us a direct measurement of the surface gravity.
(2)derived in the approximation of the classical equation of Saha-Boltzmann and with n = 1 when iron is mostly ionized and n = 2 for an iron population dominated by neutral atoms. Thus, the same abundance should be derived for neutral and ionized lines in the condition of ionization equilibrium for a given element. The equality of the abundances log n(Fe i) and log n(Fe ii) gives us a direct measurement of the surface gravity. -
3.
Microturbulence equilibrium: The minimization of the trend between log n(Fe i) and the reduced EWs, log(EWs/λ), are necessary to set the microturbulent velocity, ξ. The microturbulent velocity is a quantity incorporated in the Doppler width of the profile of a line, which was introduced to increase the strength of the lines near or on the flat part of the curve of growth to reconcile them with the observations. The classical way to set ξ is to nullify any trend between the abundance log n(Fe i) and the reduced EW. The justification for this requirement is that ξ preferentially affects the moderately/strong lines, while the weak ones are less affected by ξ. As noted by Magain (1984), this classical method might lead to a systematic overestimate of ξ, when the observed EWs are affected by random errors. This overestimate is due to the correlation between errors in EWs and in abundances of each line. This might be avoided by using theoretical EWs instead of observed ones.
Thus, the aim of FAMA is to reach the three equilibria with a series of iterations. A block diagram of FAMA is shown in Fig. 1. The iteration strategy is the following: First the Teff is adjusted by an amount that depends on how far the initial Teff is from the excitation equilibrium. Subsequently the surface gravity is modified by an initial amount that depends on the difference between log n(Fe i) and log n(Fe ii). Finally, ξ is varied on the basis of the slope of reduced EW versus log n(Fe i). This is repeated in three cycles (see the first and last cycle in Fig. 1). In each cycle, the minimization requirements on the slopes and neutral/ionized iron abundances are varied and become stricter with each cycle. In particular, the minimization requirements for the first cycle are three times larger than those of the last cycle, and those of the second cycle are two times larger. The value of the smallest minimization requirement is calculated using the information on the quality of the EW measurements. Since the EW measurements are affected by errors, it is not reasonable to minimize the slopes to infinitely low values, yielding zero slopes. This would have no physical justification and would lead us to find local minima in the three-dimensional space of Teff, log g, and ξ. Thus the minimum reachable slopes (MRS) in FAMA are strictly linked to the quality of the spectra, as expressed by the dispersion of log n(Fe i) (σFeI) around the average value ⟨log n(Fe i)⟩. This is correct in the approximation that the main contribution to the dispersion is due to the error in the EW measurement rather than to an inaccuracy in atomic parameters, as e.g., the strengths (log gf). The MRS are defined as the following:
-
i)
MRS
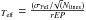 , where rEP is the range spanned in excitation potential (EP) by the measured lines and
, where rEP is the range spanned in excitation potential (EP) by the measured lines and 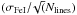 is the standard deviation with Nlines the number of lines employed;
is the standard deviation with Nlines the number of lines employed; -
ii)
MRS
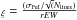 , where rEW is the range spanned in reduced EW;
, where rEW is the range spanned in reduced EW; -
iii)
MRS
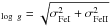 , where
, where 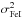 and
and 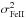 are the dispersions around the mean of log n(Fe i) and log n(Fe ii), respectively.
are the dispersions around the mean of log n(Fe i) and log n(Fe ii), respectively.
This means that we are allowed to minimize the excitation equilibrium up to a MRSTeff ~ 0.001 for a spectrum with a very high signal-to-noise ratio (S/N) having a σFeI = 0.06 dex derived from about one hundred Fe i lines, and a typical rEP = 5, while we cannot reach MRSTeff ≤ 0.003 for a spectrum of average quality with a σFeI = 0.12 dex, derived from ~60 lines. The same is true for the ionization equilibrium and for the microturbulent velocity trend.
During the first iteration, the file containing the EWs of Fe i and Fe ii are treated with the σ-clipping, a procedure that allows us to remove EWs producing abundances more discrepant than nσ from the average abundance. The σ-clipping thresholds may be easily changed on the basis of the needs of the user and of the quality and spectral coverage of the spectrum via a file containing the main parameters that can be set by the user.
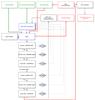 |
Fig. 1 Block diagram of FAMA: the input files in green, the main codes in blue, the iterative steps in black, and finally, the final outputs in red. |
 |
Fig. 2 Example of the final control plot of FAMA. In the first three panels, the filled (red) circles are the abundances from the Fe i EWs accepted after the σ-clipping, while the empty circles are those rejected. In the first two panels the excitation and microturbulence equilibria are shown. The blue long-dashed line is the zero-slope curve, and the dashed magenta line is the slope of the final convergence point. In the third panel the dependence on iron abundances on λ is shown, and in the fourth panel, the ionization equilibrium is presented with the green circles being the Fe ii abundances used for gravity determination. The cyan horizontal line in the last panel is the average Fe ii abundance, while the magenta line is the average Fe i. |
2.1. The QP parameter
The first-guess atmospheric parameters should be derived from photometric information or from other sources, if possible, and should preferably allow one to start close to the final values. That is a dwarf star should be treated with the initial parameters suitable for a dwarf star, and a giant star should have appropriate first guess parameters. To ensure the final solution independence of the initial parameters, FAMA is however designed to repeat the complete convergence path up to six times, starting each time from the previous set of stellar parameters which ensured the convergence. At each step, the requirements of minimization of the three slopes become stricter and they are parametrized by the so-called QP quality parameter. This parameter QP assumes six values, 10, 8, 6, 4, 2, and 1, which means that the requirement for the first step is that, e.g., a MRS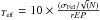 . In the specific example described above, the high S/N spectrum would indicate MRSTeff ~ 0.01. In the later steps, MRS
Teff will move from 0.01 to 0.001, passing from 0.008 to 0.006, 0.004, and 0.002. Note that each step starts with initial parameters that are the convergence point of the previous step and with the original EW list. The sequence of several steps is necessary, because it allows us to move toward the final set of stellar parameters while maintaining the initial line list. If we were to reach a minimization of the slope with QP = 1 with a single step, by starting from stellar parameters that were far from the true ones, we would risk both losing several lines with the first σ-clipping and finding a convergence point that could be far from the true value. The values assumed by the QP parameter can be set by the user on the basis of the quality of spectra.
. In the specific example described above, the high S/N spectrum would indicate MRSTeff ~ 0.01. In the later steps, MRS
Teff will move from 0.01 to 0.001, passing from 0.008 to 0.006, 0.004, and 0.002. Note that each step starts with initial parameters that are the convergence point of the previous step and with the original EW list. The sequence of several steps is necessary, because it allows us to move toward the final set of stellar parameters while maintaining the initial line list. If we were to reach a minimization of the slope with QP = 1 with a single step, by starting from stellar parameters that were far from the true ones, we would risk both losing several lines with the first σ-clipping and finding a convergence point that could be far from the true value. The values assumed by the QP parameter can be set by the user on the basis of the quality of spectra.
From the block diagram of FAMA shown in Fig. 1 we can see the structure of the code. At the top of the diagram, in green, are the three input files. The flow of the analysis is the following: The file containing the first guess stellar atmospheric parameters is given to an interpolator code of model atmosphere, in our specific case the Kurucz (Kurucz 1979; Castelli & Kurucz 2004) or MARCS models (Gustafsson et al. 2008), and a model atmosphere with the input parameters is produced. The model atmosphere and the files containing the EWs of iron are given to MOOG. A σ-clipping is performed on Fe i and Fe ii lines based on an initial run of MOOG, and MOOG is run again with the cleaned list of EW. Then, the first step begins with the QP parameter set to 10. Each step is composed of a series of iterations (shown with dotted arrows), which allow FAMA to reach the required minimization criteria. The iterations continue until the final convergence criteria are reached. The last step (indicated with red lines and arrows) corresponds to QP = 1. At the end of this step when the final stellar parameters are obtained, the EWs of all elements are given to MOOG, a σ-clipping is then performed on them, and a final evaluation of the error is done. At this point, the final results are written in two files, one containing the final stellar parameters with errors, and the other with the individual element abundances and their errors (in red in the diagram).
2.2. Quality plots
At the end of the run of FAMA a control plot is produced with the aim of helping to visually check the quality of the result4. In Fig. 2, we show an example of the control plot with four panels. In the first three panels, the filled (red) circles are the abundances from the Fe i EWs accepted after the σ-clipping, while the empty circles are those rejected. In the first two panels, the excitation and microturbulence equilibria are shown. The blue long dashed line is the zero-slope line, and the dashed magenta line is the slope of the final convergence point. In the case of good convergence these two lines are coincident. In the third panel, the dependence on iron abundances on λ is shown giving us a further test on the quality of the data and of the EW measurements. In spectra of good quality, we do not expect any dependence of EWs on the wavelength. Finally, the ionization equilibrium is presented in the fourth panel with the green circles, where the Fe ii abundances are used for gravity determination, and with empty circles showing rejected lines. The cyan horizontal line in the last panel is the average Fe ii abundance, while the magenta line is the average Fe i.
3. The evaluation of errors
Solar analysis.
FAMA is designed to evaluate the errors on the final stellar parameters. This is done with a further last step after the final convergence, in which the slopes of the excitation equilibrium, the slope of the trend between log n(Fe i) and reduced EWs, and the difference between Fe i and Fe ii abundances are not completely minimized but kept to the values given by the dispersion of the abundances. To do this, FAMA derives the stellar parameters which correspond to following:
-
1)
For the Teff: a slope equal to the ratio between the dispersion around the mean value of iron abundance and the range of EP ±
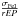 ;
; -
2)
For ξ: a slope corresponding to ±
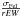 , where rEW is the range spanned in reduced EW;
, where rEW is the range spanned in reduced EW; -
3)
For gravity: a difference between log n(Fe i) and log n(Fe ii) equal to
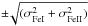 , where
, where 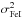 and
and 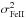 are the dispersions around the mean of log n(Fe i) and log n(Fe ii), respectively. This allows us to find the maximum and minimum values for Teff, log g, and ξ, which are acceptable within errors due to the dispersion of the abundances. This choice is shown in Fig. 3, where the slopes corresponding to the dispersion of the Fe i and Fe ii abundances are shown.
are the dispersions around the mean of log n(Fe i) and log n(Fe ii), respectively. This allows us to find the maximum and minimum values for Teff, log g, and ξ, which are acceptable within errors due to the dispersion of the abundances. This choice is shown in Fig. 3, where the slopes corresponding to the dispersion of the Fe i and Fe ii abundances are shown.
Concerning the error in the final individual element abundances, there are two types of errors which are considered by FAMA: i) the statistical uncertainties due to the random errors in the EW measurements and to uncertainties on the atomic parameters; and ii) the errors on the abundances generated by the uncertainties in the determination of the atmospheric parameters. The first source of errors is simply evaluated during the analysis with MOOG by the standard deviation around the average value of the abundance of each elements. The second source of error is instead evaluated recomputing the element abundances with the stellar parameters corresponding to the minimum and maximum slope and Fe i and Fe ii difference. Their difference with respect to the abundances computed with the best parameters gives us an estimate of the error due to the uncertainties in stellar parameters.
 |
Fig. 3 Evaluation of errors on the stellar parameters. The green circles are the lines accepted after the σ-clipping. The blue long-dashed line is the zero-slope curves, and the dashed magenta line is the slope of the final convergence point. The two dotted lines in the upper panel indicate |
 |
Fig. 4 Solar parameters derived from a sample of different first guess stellar parameters. The different symbols indicate the different initial parameters shown in Table 1. The (red) empty large squares are the final parameters shown in the last four columns of Table 1. |
Sample of analyzed stars in OCs.
4. Code validation
The aim of the present paper is to introduce the FAMA code testing it on a set of literature EW measurements. We have used the EWs of the Sun and of a set of stars in OCs and GCs present in published papers to perform a set of tests described in the following sections.
4.1. Checking the independency of the starting point with the Sun
First, we have considered the EWs of the Sun measured by Magrini et al. (2010. hereafter M10) from a high-resolution spectrum that is obtained with the spectrograph UVES at VLT. We have performed the analysis with FAMA starting from six different sets of atmospheric parameters. The aim of this first test is to check the possibility of retrieving with initial parameters that stay very far from the known parameters. In Table 1, we show the results of FAMA, with the literature accepted solar values: All results are in excellent agreement with the Solar parameters. In Fig. 4 the paths followed by FAMA are shown. The left panel shows the full range of Teff and log g while the right panel is a zoom around the region of the final solutions. Different symbols indicate the path obtained from each of the six starting values of Table 1. The red squares mark the final values. Note that FAMA is already approaching the final values after the first step. The following steps allow us to fine-tune the parameters and to approach as close as possible the final values. The uncertainties shown in Table 1 are obtained with the procedure described in Sect. 3, and the error in the iron abundance considers both sources of errors from EWs and stellar parameters. We note that all solutions are consistent within error5 of the accepted solar parameters given in the first row of the Table 1.
 |
Fig. 5 Comparison of the parameters derived with FAMA with those available in the literature for the open clusters. The continuous (black) lines are the mean least squares fit of the FAMA vs. literature results for each of the four parameters. The dashed (magenta) lines are the one-to-one relations for each parameter. |
4.2. Stars in open clusters
We have selected a sample of stars belonging to OCs, observed by several authors during the past few years and analyzed with MOOG. The sample includes nine evolved stars in the old, distant open clusters Be18, Be21, Be22, Be32, and PWM4 (Yong et al. 2012, hereafter Y12), 16 evolved stars in the old open clusters Be 31, Be 32, Be 39, M 67, NGC 188, and NGC 1193 (Friel et al. 2010, hereafter F10), and 10 stars (Magrini et al. 2010) in three inner-Galaxy clusters, NGC 6192, NGC 6404, NGC 6583. We have preferred to use literature measurements to separate the effects due to EWs and the choice of atomic parameters from the effects due to minimization criteria. Thus, we use the Fe i and Fe ii EWs available in the original papers and the atomic data adopted by each author for each star. The aim of this paper is indeed to compare the Fama results to those of the literature which are obtained in the same conditions (same atomic parameters and EWs). A future work will be devoted to a re-analysis using a common line list and a common method of measuring EWs and deriving parameters.
This test focuses on stars analyzed with the classical procedure. That is the author using the classical procedure start from the photometric values of Teff and log g and from an assumed ξ ~ 1.5 km s-1 for giant stars, and manually adjust effective temperatures to remove any trends of Fe i abundance with EP. Then, they alter log g values to achieve ionization equilibrium, vary ξ to minimize trends of Fe i abundance with line strength and iterate as necessary on the parameters until the trends are removed. Starting from the same photometric values we have performed the analysis on the EW values published in the paper of Y12, F10, and M10, with also their EP and log gf values. In our analysis we have considered the line broadening computed with tabulated damping constants (Barklem et al. 2000; Barklem & Aspelund-Johansson 2005) whenever possible, and we have used the Unsöld approximation for other lines. In the works of M10, F10 and Y12, the Unsöld approximation has been adopted.
In Table 2, we show the literature parameters of the selected stars with the errors quoted by the authors and the results obtained with our code. The literature parameters are given in Cols. 2 to 5. Our results are in Cols. 8 to 12. The iron abundances computed with FAMA are re-scaled to the Solar abundances quoted in each paper (references and values in the 6th and 7th columns, respectively). For the FAMA results, the error on the iron abundance considers both the error due to stellar parameters and the error due to the dispersion of the abundance around the average. In Fig. 5 we plot the literature vs. FAMA parameters. In the four panels of Fig. 5 we show the mean least squares fit of the literature vs. FAMA results for each of the four parameters with continuous (black) lines and the one-to-one relations for each parameter with dashed (magenta) lines. There is general good agreement. Note that the correlation between the two results is close to unity for the four parameters with some small offsets. In particular, the offset in temperature is very small being around ~14 K, while the offset in gravity is more consistent with FAMA tending to have higher gravity than the literature values. This effect seems to be more marked at low gravity. For microturbulence the relationship is very good with a very small offset. For [Fe/H] the results of FAMA have an offset of 0.04 dex with respect to the literature results.
The offsets are likely due to different aspects: for example different versions of MOOG adopted in the present work (MOOG v.2010), in Y12, in F10 and in M10 (MOOG v.2002), and to different model atmosphere grids. Y12 computed model atmospheres using the ATLAS99 program (Kurucz 1993), F10 adopted the plane-parallel MARCS models of (Bell et al. 1976), and M10 used the Kurucz model atmospheres (Kurucz 1979). On the other hand, the version of FAMA we adopted for this test, uses the complete grid of MARCS models (Gustafsson et al. 2008) which includes both spherical and plane-parallel models. Spherical models are adopted for stars with log g< 3.5, thus we practically used spherical models for the whole sample of evolved stars that we have analyzed. Another source of the differences with literature results might be the result of different treatments of the line broadening. As noticed above, the results shown in the present paper have been obtained by considering the line broadening from collisions with neutral hydrogen for lines with tabulated damping constants (Barklem et al. 2000; Barklem & Aspelund-Johansson 2005) while using the Unsöld approximation for other lines. The different treatment of damping might lead to differences in abundances up to 0.1 dex.
To probe how these dependences work in our stars, we have analyzed one of them, namely Be18-1383, by adopting different choices of damping treatment, MOOG version, and model atmospheres. These choices lead to the following differences:
-
i)
Unsöld approximation for the damping treatment: we foundnegligible differences in all atmospheric parameters withvariation [Fe/H] on the order of ~0.01 dex;
-
ii)
MOOG v.2009: we found differences in temperature ~+20 K, gravity ~+0.04 dex, ξ ~ + 0.05 km s-1, and no differences in [Fe/H];
-
iii)
with plane-parallel Kurucz model atmospheres: we found no differences in temperature, but differences in gravity ~+0.20 dex, ξ ~ + 0.06 km s-1, and [Fe/H] ~ − 0.08 dex.
Sample of analyzed stars in GCs.
4.3. Stars in globular clusters
We have selected a sample of stars that belong to GCs observed by Carretta et al. (2009, hereafter C09) and span a wide metallicity range ([Fe/H] from − 0.8 to − 2.3) to check the applicability of our method in the metal poor regime. The selected stars6 belong to the clusters 47Tuc, M4, M10, M15, and NGC 6397. The literature values of temperature and gravity of these stars are derived from photometry, and thus, a direct comparison with the parameters obtained from our spectral analysis is not possible, with the exception of metallicity. The only free parameter in C09 is the microturbolent velocity and, of course, the metallicity. We mention that the group of E. Carretta uses a private line analysis code, known as the ROSA code (Gratton & Sneden 1988), which produces solid results in accord with our work.
As in our test on OC stars, we have started the analysis with FAMA from the photometric values of Teff and log g and from the values of ξ given in C09. In Table 3, we show these values of Teff, log g, [Fe/H], and ξ. Then we report the results of our spectroscopic analysis in the following columns, with Teff, log g, [Fe/H], and ξ derived using FAMA, which is rescaled to the Solar abundance adopted by C09.
Figure 6 summarizes the literature vs. FAMA metallicity for both OCs and GCs, and shows the good agreement over the whole metallicity range: The coefficient of the mean least squares fit is very close to unity, at 1.09.
 |
Fig. 6 Comparison of the metallicity derived with FAMA to the literature values for the sample of OC and GC stars. The continuous (black) lines are the mean least squares fit of the FAMA vs. literature results for each of the four parameters. The dashed (magenta) lines are the one-to-one relations for each parameter. |
5. Summary and conclusions
We have presented a new FAMA code designed for an automatic spectral analysis using EWs obtained from high-resolution stellar spectra. The code is written in Perl and is based in the widely used Fortran code, MOOG, by C. Sneden. FAMA is freely distributed (via email to laura@arcetri.astro.it, web page http//www.arcetri.astro.it/~laura, and CDS) and it works on different platforms (tested on Mac OSX (Leopard, Mountain Lion) and Linux (Ubuntu, Centos)).
In the present paper, we have described the code with its general structure, starting from the determination of the atmospheric parameters that are defined by the excitation and ionization equilibria, and by the nullification of the trend between log n(Fe i) and reduced EWs. We then described how metallicity is computed, and how errors on stellar parameters and on abundances are obtained. We have also described how the convergence criteria are set and how they are chosen and varied depending on the quality of the spectra and of the EW measurements.
We have presented three tests: the first one on the reproducibility of the final results, analyzing the Solar spectrum starting from six different starting points, the second one computing a complete spectral analysis of a set of 34 evolved stars belonging to Galactic OCs, and the third one computing the spectral analysis of 10 stars belonging to GCs with literature metallicity [Fe/H] values that range from − 0.7 to − 2.3. To separate the effects due to EW measurements from the choice of atomic parameters, we have used published EWs and log gf for all tests. We have demonstrated the independence of FAMA on the initial set of stellar parameters, and its capability to reproduce the literature results obtained with a completely manual and time-consuming technique. Small offsets and differences with literature OC results might be due to different versions of MOOG, to a different adopted grid of model atmospheres, and to line broadening treatment. In GCs, we could compare [Fe/H] to literature values, finding a good agreement, even if we have a slightly higher dispersion than in more metal-rich stars.
FAMA is an easily installable Perl code, which performs a complete spectral analysis of high-resolution spectra. It starts from two files with EWs and a file with first-guess atmospheric parameters and gives a file with stellar parameters with their uncertainties, a file with the element abundances with their errors, and a control plot to check the final solution as main final results. Due to its versatility and its low CPU requirement7, it is a perfect code to perform spectral analysis on large samples of spectra.
MOOG is available at http://www.as.utexts.edu/~chris/moog
The quality plots are produced making use of a supermongo macro http://www.astro.princeton.edu/~rhl/sm/.
Acknowledgments
We warmly thank the referee, Chris Sneden, for his support to the paper and for his useful comments and suggestions which helped us to improve the paper. We thank Eugenio Carretta for providing us the EWs of the sample of GC stars. We finally thank the language editor, C.-J. Lin, for improving the quality of our English. This research has made use of NASA’s Astrophysics Data System.
References
- Allen de Prieto, C., Majewski, S. R., Schiavon, R., et al. 2008, Astron. Nachr., 329, 1018 [Google Scholar]
- Barden, S. C., Jones, D. J., Barnes, S. I., et al. 2010, Proc. SPIE, 7735 [Google Scholar]
- Barklem, P. S., & Aspelund-Johansson, J. 2005, A&A, 435, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&AS, 142, 467 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Bell, R. A., Eriksson, K., Gustafsson, B., & Nordlund, A. 1976, A&AS, 23, 37 [NASA ADS] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, in Modelling of Stellar Atmospheres, Proc. IAU Symp. 210, poster A20 [Google Scholar]
- Bonifacio, P., & Caffau, E. 2003, A&A, 399, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cirasuolo, M., Afonso, J., Bender, R., et al. 2011, The Messenger, 145, 11 [NASA ADS] [Google Scholar]
- de Jong, R. 2011, The Messenger, 145, 14 [NASA ADS] [Google Scholar]
- Freeman, K., Ness, M., Wylie-de-Boer, E., et al. 2013, MNRAS, 428, 3660 [NASA ADS] [CrossRef] [Google Scholar]
- Friel, E. D., Jacobson, H. R., & Pilachowski, C. A. 2010, AJ, 139, 1942 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres, 3rd edn. (UK: Cambridge University Press) [Google Scholar]
- Gratton, R. G., & Sneden, C. 1988, A&A, 204, 193 [NASA ADS] [Google Scholar]
- Kunder, A., Koch, A., Rich, R. M., et al. 2012, AJ, 143, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1993, IAU Colloq. 138: Peculiar versus Normal Phenomena in A-type and Related Stars, ASPC, 44, 87 [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magain, P. 1984, A&A, 134, 189 [NASA ADS] [Google Scholar]
- Magrini, L., Randich, S., Zoccali, M., et al. 2010, A&A, 523, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mucciarelli, A., Pancino, E., Lovisi, L., Ferraro, F. R., & Lapenna, E. 2013, ApJ, 766, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Randich, S., & Gilmore, G. 2012, in Science from the Next Generation Imaging and Spectroscopic Surveys, ESO Garching, 15–18 October, Online at: http://www.eso.org/sci/meetings/2012/surveys2012/program.html, 21 [Google Scholar]
- Recio-Blanco, A., Bijaoui, A., & de Laverny, P. 2006, MNRAS, 370, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. A. 1973, Ph.D. Thesis [Google Scholar]
- Sneden, C., Bean, J., Ivans, I., Lucatello, S., & Sobeck, J. 2012, Astrophysics Source Code Library, 2009 [Google Scholar]
- Takeda, Y., Ohkubo, M., & Sadakane, K. 2002, PASJ, 54, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Fischer, D. A., Sozzetti, A., et al. 2012, ApJ, 757, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yong, D., Carney, B. W., & Friel, E. D. 2012, AJ, 144, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Zwitter, T., Siebert, A., Munari, U., et al. 2008, AJ, 136, 421 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Block diagram of FAMA: the input files in green, the main codes in blue, the iterative steps in black, and finally, the final outputs in red. |
| In the text | |
 |
Fig. 2 Example of the final control plot of FAMA. In the first three panels, the filled (red) circles are the abundances from the Fe i EWs accepted after the σ-clipping, while the empty circles are those rejected. In the first two panels the excitation and microturbulence equilibria are shown. The blue long-dashed line is the zero-slope curve, and the dashed magenta line is the slope of the final convergence point. In the third panel the dependence on iron abundances on λ is shown, and in the fourth panel, the ionization equilibrium is presented with the green circles being the Fe ii abundances used for gravity determination. The cyan horizontal line in the last panel is the average Fe ii abundance, while the magenta line is the average Fe i. |
| In the text | |
 |
Fig. 3 Evaluation of errors on the stellar parameters. The green circles are the lines accepted after the σ-clipping. The blue long-dashed line is the zero-slope curves, and the dashed magenta line is the slope of the final convergence point. The two dotted lines in the upper panel indicate |
| In the text | |
 |
Fig. 4 Solar parameters derived from a sample of different first guess stellar parameters. The different symbols indicate the different initial parameters shown in Table 1. The (red) empty large squares are the final parameters shown in the last four columns of Table 1. |
| In the text | |
 |
Fig. 5 Comparison of the parameters derived with FAMA with those available in the literature for the open clusters. The continuous (black) lines are the mean least squares fit of the FAMA vs. literature results for each of the four parameters. The dashed (magenta) lines are the one-to-one relations for each parameter. |
| In the text | |
 |
Fig. 6 Comparison of the metallicity derived with FAMA to the literature values for the sample of OC and GC stars. The continuous (black) lines are the mean least squares fit of the FAMA vs. literature results for each of the four parameters. The dashed (magenta) lines are the one-to-one relations for each parameter. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.