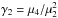| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201321606 | |
| Published online | 01 October 2013 | |
Model comparison of the dark matter profiles of Fornax, Sculptor, Carina and Sextans
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: breddels@astro.rug.nl
Received: 28 March 2013
Accepted: 16 August 2013
Aims. We compare dark matter profile models of four dwarf spheroidal galaxies satellites of the Milky Way using Bayesian evidence.
Methods. We use orbit based dynamical models to fit the 2nd and 4th moments of the line of sight velocity distributions of the Fornax, Sculptor, Carina and Sextans dwarf spheroidal galaxies. We compare NFW, Einasto and several cored profiles for their dark halos and present the probability distribution functions of the model parameters.
Results. For each galaxy separately we compare the evidence for the various dark matter profiles, and find that it is not possible to distinguish between these specific parametric dark matter density profiles using the current data. Nonetheless, from the combined evidence, we find that is unlikely that all galaxies are embedded in the same type of cored profiles of the form ρDM ∝ 1/(1 + r2)β/2, where β = 3,4. For each galaxy, we also obtain an almost model independent, and therefore accurate, constraint on the logarithmic slope of the dark matter density distribution at a radius ~r-3, i.e. where the logarithmic slope of the stellar density profile is −3.
Conclusions. For each galaxy, we find that all best fit models essentially have the same mass distribution over a large range in radius (from just below r-3 to the last measured data point). This remarkable finding likely implies much stronger constraints on the characteristics that subhalos extracted from cosmological simulations should have in order to host the dSph galaxies around the Milky Way.
Key words: galaxies: dwarf / galaxies: kinematics and dynamics
© ESO, 2013
1. Introduction
According to galaxy formation theories dwarf spheroidal galaxies are believed to inhabit massive dark matter halos, with maximum circular velocities somewhere in the range ~10–60 km s-1 (see e.g. Stoehr et al. 2002; Benson et al. 2002; Kravtsov et al. 2004; Strigari et al. 2010; Li et al. 2010, for various complementary studies on the masses of these systems). Because of their large mass to light ratio these galaxies are ideal to test fundamental predictions of the Lambda cold dark matter (ΛCDM) cosmological paradigm, since it is generally considered relatively safe to neglect baryons in the construction of dynamical models.
 |
Fig. 1 Radius versus line of sight velocity for Fornax, Sculptor Carina and Sextans. The horizontal lines show the borders of the bins, the vertical lines denote the mean systemic velocity of the galaxy together with the ±3σ region. |
One of the strongest predictions from ΛCDM concerns the dark matter density profile. Early simulations of dark matter halos assembled in a cosmological context showed that such a profile is accurately described by a two-sloped form, now known as NFW profile (Navarro et al. 1996, 1997). More recently Einasto profiles have been shown to provide a better fit (e.g. Springel et al. 2008; Navarro et al. 2010), in particular for satellite galaxies (Vera-Ciro et al. 2013). These predictions are made using dark matter only simulations and therefore neglect (by construction) the baryonic component. And although baryons are sub-dominant in the total potential of the system (Walker 2013), it has been suggested that they could play a role in the evolution of dwarf spheroidal galaxies, for instance, in modifying the internal orbital structure (Bryan et al. 2012) and the overall density profile (Governato et al. 2012). The complex evolution of baryons and its non-trivial interplay with the host halo are difficult to model and not yet completely understood (see Pontzen & Governato 2012).
Another effect driving the internal dynamics of satellite halos is the tidal interaction with the main host. It can change the density profile (Hayashi et al. 2003), the geometrical shape of the mass distribution (Kuhlen et al. 2007), and also influence the kinematics of the embedded stars (Łokas et al. 2010). Unfortunately these uncertainties imply that even when the observations of a Local Group dwarf spheroidal galaxy is not consistent with being embedded in the halos predicted from pure dark matter N-body simulations, this does not necessarily reflect a fundamental problem of ΛCDM.
Thanks to their relative proximity, information for individual stars in the dwarf galaxies satellites of the Milky Way are relatively easy to get. Sky positions are easily determined from photometry, and radial velocity measurements are possible to estimate within an error of ~2 km s-1. Some of the datasets compiled to the date include thousands of individual members with line-of-sight velocities (Helmi et al. 2006; Battaglia et al. 2006, 2008; Walker et al. 2009a; Battaglia et al. 2011) Proper motions of individual stars are currently still too difficult to measure. Despite the fact that only three of the total of six phase space coordinates are available from measurements, it is possible to create dynamical models of these systems that can be compared to these observables.
Following the method thoroughly described in Breddels et al. (2013) we set out to model Fornax, Sculptor, Carina and Sextans with orbit-based dynamical methods (Schwarzschild modeling) assuming they are embedded in spherical halos. As extensively shown in the literature (e.g. Richstone & Tremaine 1984; Rix et al. 1997; van der Marel et al. 1998; Cretton et al. 1999; Valluri et al. 2004; van den Bosch et al. 2008; Jardel & Gebhardt 2012) this method allows to construct a non-parametric estimator of the distribution function (although, in the work presented here, we use parametric forms for the gravitational potential). Among many, this method has one advantage over Jeans modeling, by not having to assume a particular velocity anisotropy profile, therefore being more general and thus less prone to biases associated to the assumptions. But even in this case there are other limitations in the modeling such as the mass-anisotropy degeneracy (e.g. Merrifield & Kent 1990; Dejonghe & Merritt 1992; Evans et al. 2009). In this work we use higher moments (fourth moment) of the line of sight velocity distribution to get a better handle on this degeneracy.
To compare how different shapes for the dark matter profiles fit the data, we first need to establish a statistical framework. In this paper we do this in a Bayesian way using the evidence (Mackay 2003). This method provides a natural way of comparing models in Bayesian inference and also makes it possible to combine the data of all the dwarf spheroidals to test for example, if all dwarf spheroidals could be embedded in a universal halo (Mateo et al. 1993; Walker et al. 2009b). Furthermore, the shape may give us hints to how the dwarf galaxy formed and the anisotropy profile may be used to distinguish between evolutionary scenarios (see e.g. Mayer 2010; Kazantzidis et al. 2011; Helmi et al. 2012).
This paper is organized as follows. We begin in Sect. 2 by presenting the data and all the ingredients needed to do the model comparison. In Sect. 3 we present our dynamical and statistical methods. We present the results of our Schwarzschild models for the four dSph in our sample in Sect. 4.1, while the Bayesian model comparison is done in Sect. 4.2. We discuss the implications of our results in Sect. 4.3 and conclude in Sect. 5.
2. Data
In this section we present the data that is used for fitting our dynamical models. The radial velocity measurements of the dwarf spheroidal galaxies come from Helmi et al. (2006), Battaglia et al. (2006, 2008), Walker et al. (2009a) and Battaglia et al. (2011). We plot radius versus heliocentric velocity in Fig. 1 for each galaxy separately.
Figure 1 shows that each dSph suffers from foreground (Milky Way) contamination. To remove this contamination and reliably identify member stars we have developed a simple analytic model for the positional and kinematic distribution of both foreground and the galaxy in question (along the lines of Battaglia et al. 2008; Breddels et al., in prep.). For each particular dataset1, we assume that the foreground has a constant surface density (see e.g. Irwin & Hatzidimitriou 1995; de Boer et al. 2011), and that the dSph follows a specific stellar density profile. We also assume that the velocity distribution at each radius may be modeled as sum of two Gaussians. The Gaussian describing the foreground has the same shape at all radii, while that of the stars associated with the dwarf can have a varying dispersion with radius. Their relative amplitude also changes as function of distance from the dwarf’s centre. This model results in a determination of the relative contribution of member-to-non-member stars as a function of velocity and radial distance R.
Based on this model we calculate the elliptical radius at which the ratio of dSph to foreground is 3:1 (without using any velocity information). We remove all stars outside of this radius from the dataset. A particular star included in more than one dataset is removed only when it it satisfies the condition for all sets, for instance a star outside Re,cut,Batt, but inside Re,cut,Walker will not be discarded. This simple clipping in elliptical radius cleans up part of the foreground contamination. For completeness, the radii for all datasets cleaned up in this way are presented in Table 2, as well as the fit to the foreground model. The number of stars and the sources are listed in Table 1.
For the resulting dataset, we compute the second and fourth moment of the radial velocity as a function of circular radius as follows2. We first define radial bins such that each bin has at least 250 stars in the velocity range vsys − 3σv,vsys + 3σv. If the last bin has less that 150 objects, the last two bins are merged. After this, we fit our parametric model for the galaxy plus foreground for each radial bin, to derive new velocity dispersions. Then for each bin we do a 3σ clipping on the velocity using the new velocity dispersion, and from this selection we calculate the second and fourth moments. The errors on the moments are computed using Eqs. (17) and (19) in Breddels et al. (2013). The second moment and the kurtosis3 are shown in Fig. 2 for each galaxy, where the black dot corresponds to the mean, and the error bars indicate the 1σ error bar. The blue region shows the confidence interval for the NFW model found in Sect. 4.1.
Number of stars in the kinematic samples used in this paper.
For the photometry we use analytic fits given by various literature sources as listed in Table 3. Although the stellar mass is sub-dominant in the potential, we do include its contribution in the dynamic models and fix M/LV = 1, as in Breddels et al. (2013).
3. Methods
3.1. Dynamical models
Our aim is to compare different models to establish what type of dark matter profile best matches the kinematical data of local dSph galaxies. Here we consider the following profiles to describe the dark matter halos of the dwarfs in our sample:  where x = r/rs and rs is the scale radius. Each model has at least two unknown parameters rs and ρ0. As we did in Breddels et al. (2013), we transform these two parameters to rs and M1 kpc (the mass within 1 kpc). As discussed in the Introduction, the NFW and Einasto models are known to fit the halo dark matter distributions extracted from cosmological N-body simulations. On the other hand, we explore the βγ models to test the possibility of a core in the dark halo. Note that, in comparison to the NFW profile, the Einasto model has one extra parameter (α′), but here we consider only two values for α′ = 0.2,0.4 to cover the range suggested by Vera-Ciro et al. (2013). On the other hand, the βγ profiles have two extra parameters, but we limit ourselves here to two different outer slopes (β = 3,4) and two different transition speeds between the inner and the outer slopes (γ = 1,2). Note that the βγ models have a true core only for γ > 1, however in all cases the central logarithmic slope vanishes, dlog ρ/dlog r = 0. However, we loosely refer to these models as cored in what follows. Note that, with these choices, all of our profiles ultimately have just two free parameters. The list of models explored and their parameters are summarized in Table 4.
where x = r/rs and rs is the scale radius. Each model has at least two unknown parameters rs and ρ0. As we did in Breddels et al. (2013), we transform these two parameters to rs and M1 kpc (the mass within 1 kpc). As discussed in the Introduction, the NFW and Einasto models are known to fit the halo dark matter distributions extracted from cosmological N-body simulations. On the other hand, we explore the βγ models to test the possibility of a core in the dark halo. Note that, in comparison to the NFW profile, the Einasto model has one extra parameter (α′), but here we consider only two values for α′ = 0.2,0.4 to cover the range suggested by Vera-Ciro et al. (2013). On the other hand, the βγ profiles have two extra parameters, but we limit ourselves here to two different outer slopes (β = 3,4) and two different transition speeds between the inner and the outer slopes (γ = 1,2). Note that the βγ models have a true core only for γ > 1, however in all cases the central logarithmic slope vanishes, dlog ρ/dlog r = 0. However, we loosely refer to these models as cored in what follows. Note that, with these choices, all of our profiles ultimately have just two free parameters. The list of models explored and their parameters are summarized in Table 4.
Parameters of the foreground plus dwarf galaxy model used for determining membership, as well as for deriving the radial profiles for the second and fourth velocity moments for each dSph.
 |
Fig. 2 Line of sight velocity moments for Fornax, Sculptor Carina and Sextans. For each galaxy we show the velocity dispersion and the kurtosis. The black dots show the mean, and the error bars the 1σ error. The blue regions show the confidence interval for the NFW fit, similar to Breddels et al. (2013). |
The orbit-based dynamical (Schwarzschild) models of each dwarf galaxy are obtained as follows (see Breddels et al. 2013, for a more detailed description). For each of the dark halo profiles, with its own set of parameters, we integrate a large number of orbits in the respective gravitational potential (including also the contribution of the stars). We then find a linear combination of these orbits that fits both the light and the kinematics. The orbital weights found in this way have a physical meaning and can be used to obtain the distribution function of the system. As data we have the line of sight velocity moments (second and fourth depicted in Fig. 2), and the light profile (Table 2). The best fit models (which give us the values of the parameters for a specific dark matter halo profile) are those that minimize the 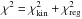 , under the condition that the orbital weights are positive, and that the observed light distribution is fit to better than 1% at each radius. Here
, under the condition that the orbital weights are positive, and that the observed light distribution is fit to better than 1% at each radius. Here 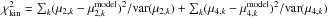 . The
. The  is a regularization term to make sure that the solution for the orbit weights leads to a relatively smooth distribution function. Breddels et al. (2013) calibrated the amplitude of this term for Sculptor. To have the regularization term for the other dwarfs of the same relative strength, we note that
is a regularization term to make sure that the solution for the orbit weights leads to a relatively smooth distribution function. Breddels et al. (2013) calibrated the amplitude of this term for Sculptor. To have the regularization term for the other dwarfs of the same relative strength, we note that 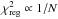 , where N is the number of members with radial velocities, since the
, where N is the number of members with radial velocities, since the 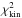 term also scales as 1/N. Therefore, normalizing its amplitude to that of Sculptor we get
term also scales as 1/N. Therefore, normalizing its amplitude to that of Sculptor we get 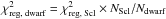 .
.
3.2. Bayesian model comparison
Background on Bayesian model comparison may be found in Mackay (2003). For completeness we discuss it here briefly, but we assume the reader is familiar with the basics of Bayesian inference.
Given the data 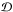 and assuming a model Mi, the posterior for the parameters θi of this model is:
and assuming a model Mi, the posterior for the parameters θi of this model is: 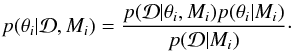 (4)The normalization constant
(4)The normalization constant 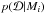 , also called the evidence, is of little interest in parameter inference, but is useful in Bayesian model comparison. To assess the probability of a particular model given the data, we find
, also called the evidence, is of little interest in parameter inference, but is useful in Bayesian model comparison. To assess the probability of a particular model given the data, we find 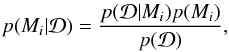 (5)where we see the evidence is needed. In this case
(5)where we see the evidence is needed. In this case 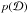 is the uninteresting normalization constant, as it cancels out if we compare two models:
is the uninteresting normalization constant, as it cancels out if we compare two models: 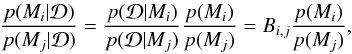 (6)where Bi,j is called the Bayes factor. If we take the priors on the different models to be equal (i.e. p(Mi) = p(Mj)), the ratio of the evidence (the Bayes factor Bi,j) gives the odds ratio of the two models given the data
(6)where Bi,j is called the Bayes factor. If we take the priors on the different models to be equal (i.e. p(Mi) = p(Mj)), the ratio of the evidence (the Bayes factor Bi,j) gives the odds ratio of the two models given the data 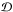 .
.
Using these results we can perform model comparison between dark matter density profiles, i.e. ℳ = { Mnfw,MEinasto,... }, and calculate for instance the odds that a given galaxy is embedded in an NFW profile compared to an Einasto model, BNFW,Einasto.
Not only can we do model comparison on a single object, but we may also test if our objects share a particular model (e.g. they are all embedded in NFW halos). If our dataset 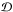 consists of the observations of two galaxies, i.e.
consists of the observations of two galaxies, i.e. 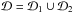 and assuming the datasets are uncorrelated and independent, we obtain:
and assuming the datasets are uncorrelated and independent, we obtain: 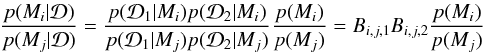 (7)where each factor
(7)where each factor 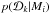 should be marginalized over its (own) characteristic parameters. From Eq. (7) we can see that the odds ratio of the models and Bayes factor from different measurements can be multiplied to give combined evidence for a particular model.
should be marginalized over its (own) characteristic parameters. From Eq. (7) we can see that the odds ratio of the models and Bayes factor from different measurements can be multiplied to give combined evidence for a particular model.
Distances, type of photometric profile used, scale radius and stellar luminosity used for the dynamic models.
Model names and their characteristic parameters of the various dark matter density profiles explored.
Behind each 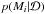 is a set of orbit based dynamical (Schwarzschild) models, obtained as described above. For each of the models we calculate the evidence. Later on we compare each model’s evidence to that of an NFW profile, i.e. we compute the Bayes factor Bi,NFW, where i can be e.g. Einasto. By definition BNFW,NFW = 1, and again assuming equal priors on the different models, the Bayes factor equals the odds ratio of the models, such that for Bi,NFW > 1, model i is favored over an NFW profile.
is a set of orbit based dynamical (Schwarzschild) models, obtained as described above. For each of the models we calculate the evidence. Later on we compare each model’s evidence to that of an NFW profile, i.e. we compute the Bayes factor Bi,NFW, where i can be e.g. Einasto. By definition BNFW,NFW = 1, and again assuming equal priors on the different models, the Bayes factor equals the odds ratio of the models, such that for Bi,NFW > 1, model i is favored over an NFW profile.
4. Results
4.1. Schwarzschild models
 |
Fig. 3 PDF for the two free parameters characterizing the dark halo profiles for each dSph galaxy obtained using Schwarzschild modeling. The top row shows the PDFs with NFW/Einasto models, the bottom panel those for all cored models explored. The contours show the 1 and 2σ confidence levels (the 3σ contour is not shown to avoid crowding the image). |
 |
Fig. 4 Similar to Fig. 2, except now we show the different best fit models for the various density profiles explored, which are indicated with different colors (the color scheme is the same as in Fig. 3). |
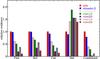 |
Fig. 5 Evidences for all models listed in Table 4, relative to the NFW case. The last column shows the combined evidence for all galaxies together, and shows that the core23 and core24 are strongly disfavored. |
As a result of our Schwarzschild modeling technique, we obtain a two dimensional probability density function (PDF) of the two parameters, M1 kpc and rs, for each galaxy and for each dark matter halo profile. In Fig. 3 we plot the PDF for the cored models and the NFW and Einasto models separately for each galaxy. The colored dots correspond to the maximum likelihood for each of the corresponding models as indicated by the legend. The contours show the 1 and 2σ equivalent confidence intervals (the 3σ contour is not shown for clarity). For both Fornax and Sculptor the parameters for all profiles are relatively well determined, while for Carina and Sextans this is less so. This can be attributed to the difference in sample size (and hence to the significantly smaller number of members) in these systems, which has translated into fewer bins where the moments can be computed (see Fig. 2). In general for all four galaxies the scale radius for the cored profiles is found to be smaller than that for the NFW/Einasto profiles. We come back to this point in Sect. 4.3.
Our model’s masses at r1/2, the 3D radius enclosing half of the stellar mass, are compatible with those of Wolf et al. (2010). However, our results for Fornax do not agree with those of Jardel & Gebhardt (2012). These authors prefer a cored profile with a much larger scale radius, and their enclosed mass is smaller in comparison to Wolf et al. (2010). We note that this might be partly related to the fact that the amplitude of their line of sight velocity dispersion profile (see their Fig. 2) is slightly lower than what we have determined here.
In Fig. 4 we overlay on the kinematic observables the predictions from the best fit Schwarzschild models. We note that all models provide very similar and virtually indistinguishable fits, especially for the 2nd moment. Some slight differences are apparent in the kurtosis, but in all cases, the differences are smaller than the error bars on the moments.
In general we find all anisotropy profiles to be roughly constant with radius and slightly tangentially biased on average. We do not find significant differences between the profiles for cored and NFW models (the reason for this will become clear in Sect. 4.3). Fornax’s anisotropy β ~ −0.2 ± 0.2, while Sculptor and Carina have on average β ~ − 0.5 ± 0.3. For Sextans the anisotropy cannot be determined reliably, β ~ −0.3 ± 0.5. These values are compatible with those of Walker et al. (2007), which were derived using the spherical Jeans equation assuming a constant velocity anisotropy profile.
4.2. Bayesian comparison of the models
We compute the evidence relative to the NFW using Eq. (6) by integrating over the parameters (in our case the scale radius and the mass) the PDFs shown in Fig. 3. We do this for each dwarf galaxy and for all the models listed in Table 4. The different Bayes factors are shown in Fig. 5. Each set of bars shows the Bayes factors for the given dSph galaxy (Bi,NFW,k), while the last set shows the combined result (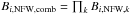 ). We note that an odds ratio between 1:2 till 1:3 is considered “Barely worth mentioning” (Jeffreys 1998), and only odds ratios above 1:10 are considered “strong” evidence.
). We note that an odds ratio between 1:2 till 1:3 is considered “Barely worth mentioning” (Jeffreys 1998), and only odds ratios above 1:10 are considered “strong” evidence.
For each galaxy there is hardly any evidence for or against an Einasto profile (with α′ = 0.2,0.4) compared to NFW. This is not unexpected since these profiles are quite similar over a large region (Vera-Ciro et al. 2013). Also in the case of the combined evidence the NFW and Einasto are hard to distinguish. Comparing the NFW or Einasto profiles for individual galaxies to the cored models, one cannot strongly rule out a particular model. For Fornax, Sculptor and Carina, the γ = 2 models (where the transition speed is fast) appear to be less likely, but this is not the case for Sextans. However, when we look at the combined evidence, i.e. we explore whether all dwarfs are embedded in the same halos, such γ = 2 models are clearly disfavored.
The results for Sculptor may be compared to those of Breddels et al. (2013). In that paper, the authors found that the maximum likelihood value for the central slope of the density profile corresponded to a cored model. Since the evidence is the integral of the PDF, and not directly related to the maximum likelihood (except for a Gaussian distribution), we should not be surprised to find a slightly stronger evidence for the NFW case here. In any case, the differences between the models are minor as shown graphically in Fig. 4, and the evidence and the maximum likelihood (marginally) favoring different models can be attributed simply to not being able to distinguish amongst these.
 |
Fig. 6 Top row: enclosed mass as a function of radius for the different dark matter density profiles, with the stellar component in black. Middle row: logarithmic density slope as a function or radius, where the black curve corresponds again to the stellar component. The red dashed line indicates r-3, the radius at which the light profile has a logarithmic slope of − 3, while the black line indicates r1/2, the radius at which half of the stellar mass in enclosed (in 3D). Bottom row: cumulative density distribution of the (2D) radial distribution of the data (black), and the light (red) showing the kinematic data is sampled more concentrated towards the center. |
4.3. A robust slope measurement
We now inspect in more detail the shape of the mass distributions found for the various best fitting models. We are interested in exploring why the differences between the various models as small as apparent in Fig. 4.
The top row of Fig. 6 shows the enclosed dark matter mass for the best fit models (indicated by the solid dots in Fig. 3) for each galaxy separately. We use the same color coding as in Fig. 3, and also include the stellar mass in black. The red-dashed vertical lines denote r-3, the radius at which the light density profile has a logarithmic slope of − 3, while the black line indicates r1/2. This remarkable figure shows that for each galaxy there is a region where the mass distributions are truly almost indistinguishable from one another. The different profiles, each characterized by its own functional form, scale radius rs and mass M1 kpc, conspire to produce a unique mass distribution. This region extends from slightly below r-3 to approximately the location of the outermost data point (see bottom panel). Here M(r) ∝ rx, where x ranges from 1.65 for Fnx, to 1.9 for Sextans.
In the middle row of Fig. 6 we plot the logarithmic slope of the dark halo density distribution, where the black line denotes the stellar density. Near the position where the logslope of the stellar density is − 3, all the best fit dark matter density profiles seem to reach a similar logslope, although the value of the slope varies from galaxy to galaxy. The radius where the logslopes coincide lies, as expected, inside the region where the mass distribution is well determined, since both quantities are related through derivatives.
To illustrate the distribution of the kinematic sample with respect to the light, we plot in the bottom row of Fig. 6 the cumulative 2D radial distribution of the kinematic data in black. The cumulative 2D radial distribution for the light is plotted as the red histogram. All kinematic datasets are more concentrated than the light, but no clear trend is visible between the distribution of the kinematic sample with respect to the light, and the exact location where the logslope of most accurately determined.
The existence of a finite region where the mass is more accurately determined has also been observed in the literature in works using MCMC in combination with Jeans modeling. For example, it is visible in e.g. the right panel of Fig. 1 in Wolf et al. (2010), Fig. 18 in Walker (2013), and Fig. 10 in Jardel et al. (2013) for Draco, in the case of a non-parametric density distribution with Schwarzschild models.
 |
Fig. 7 Similar to Fig. 3, except now using M-3 and r-3 as parameters. Note that the contours for the NFW cannot go beyond κ(r-3) ≥ − 1. |
The analysis of Wolf et al. (2010) used the light weighted average of the velocity dispersion to relate the radius at which the logslope of the light is −3, or the half light radius, to the point where the mass is accurately (being independent on the anisotropy) and precisely (showing the least uncertainty) determined. Our findings go beyond this result. They suggest that whatever dynamical model or method is explored, there is a better set of parameters to describe the mass distribution of dSph galaxies. Let r-3 be the radius at which the logslope of the (3D) light distribution is − 3. Since the mass is accurately determined in this region, a natural parameter would be M-3 = M(r-3). And since also the logslope at this radius is accurately determined, the next parameter should be 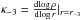 . For any general model, if the values of β and γ are fixed, this effectively makes rs a function of κ-3.
. For any general model, if the values of β and γ are fixed, this effectively makes rs a function of κ-3.
Figure 7 shows the PDF for the M-3 and κ-3 parameters for both the NFW and core13 models for each galaxy, assuming a flat prior on these parameters in the domain shown in this figure, except for the NFW profile which we limit to κ-3 = −1.05, since for κ-3 ≥ − 1 the scale radius is unphysical. As can be seen from the PDF while there is still uncertainty associated to the logslope at this radius, the value is nearly model independent and therefore we believe this value to be accurate, especially for Fornax and Sculptor (κ-3 = −1.4 ± 0.15 and κ-3 = −1.3 ± 0.12 respectively for the NFW model). Note also that some uncertainties might arise because the kinematics are not sampled exactly according to the light.
These results also help us understand why we found that the scale radii of the best fitting NFW profiles always to be larger than those of the cored models (see Fig. 3). For the NFW, we have 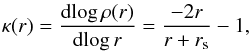 (8)which can be easily solved for rs:
(8)which can be easily solved for rs: 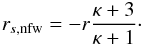 (9)A similar solution can be found for the other parametric models, for instance the γβ model gives:
(9)A similar solution can be found for the other parametric models, for instance the γβ model gives: 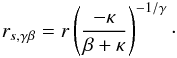 (10)If we now require that the slopes are the same at r-3 for the NFW and core13 models, we find
(10)If we now require that the slopes are the same at r-3 for the NFW and core13 models, we find 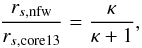 (11)which is >1 for κ < − 1, explaining why the cored profiles have smaller scale radii than the NFW profile, i.e. to get the same logslope at the same location for the cored models, their scale radius needs to be smaller than that of the NFW profile. A similar result holds for the other cored models.
(11)which is >1 for κ < − 1, explaining why the cored profiles have smaller scale radii than the NFW profile, i.e. to get the same logslope at the same location for the cored models, their scale radius needs to be smaller than that of the NFW profile. A similar result holds for the other cored models.
5. Conclusions
In this paper we have presented a comparison of dynamical models using different dark matter profiles for four dwarf spheroidal galaxies in the Local Group, namely Fornax, Sculptor, Carina and Sextans. The model comparison was done using Bayesian evidence. We have found that no particular model is significantly preferred, and that all four dwarf spheroidals are compatible with either NFW/Einasto or any of the explored cored profiles. Only Sextans shows a slight preference for cored models, but not with high odds. Nonetheless, we find that it is very unlikely that all four dwarf spheroidals are each embedded in a cored dark matter halo of the form ρDM ∝ 1/(1 + r2)β/2, with β = 3,4.
Our best fit models however, conspire to produce the same mass distribution over a relatively large range in radii, from r-3 up to the last measured data point (which is often close to the nominal tidal radius obtained from fitting the light profile). This M(r) ~ rx, with x = 1.65 − 1.9, is similar to that suggested by Walker et al. (2009b) albeit with a slightly steeper exponent. Another (related) quantity that is robustly determined and independent of the assumed dark matter density profile, is the logslope of the density distribution at r-3. We find for the dwarfs in our sample, that this slope ranges from κ-3 ~ − 1.4 at r-3 = 0.96 kpc for Fornax, to κ-3 ~ − 1.1 at r-3 = 0.98 kpc for Sextans.
Since the mass is accurately determined in a finite region around r-3 (of ~1 kpc in extent), this means that the velocity anisotropy has also been constrained in this region (Binney & Mamon 1982). Since the mass is known to a limited precision, this translates into an uncertainty on the anisotropy which can be reduced by acquiring larger kinematic datasets. The mass-anisotropy degeneracy (assuming spherical symmetry) has been limited thanks to the large coverage in radius of the dataset used.
These findings can be seen as an extension of the results of Wolf et al. (2010), who showed that the mass at r-3 can be determined very accurately in a model independent fashion. These authors demonstrated that this result might be understood from the Jeans equation. Although we do not have yet a solid mathematical explanation for our new findings, we suspect that this might be obtained using the virial theorem, which is effectively another, yet independent moment of the collisionless Boltzmann equation.
In the near future, we will apply Schwarzschild modeling to the same data but instead of the moments, we will use the discrete individual measurements directly. This approach should allows us to get the most out of the data, since no information is lost. When binning, one loses spatial resolution, but also the higher moments of the line-of-sight velocity distribution are not included in the fitting procedure because of their large and asymmetric errors. Furthermore, the use of the full line-of-sight velocity distribution should improve the precision of the anisotropy profile, which may be an interesting quantity to discriminate formation scenarios.
This moments-to-discrete modeling step must be carried out before deciding if and how much more data is needed to discriminate among various dark matter density profiles. Nonetheless, we have learned here that the functional form of the mass distribution may be determined over a large distance range, even when only a few hundred velocity measurements are available (as in the case of Sextans). However, the uncertainty on the value of the exact slope of the density profile at e.g. r-3 is driven by the sample size.
An obvious next step is to establish if the subhalos extracted from cosmological simulations have the right characteristics to host the dSph of the Milky Way, now that not only the mass, but also its functional form (1st and 2nd derivatives), of their dark halos have been determined reliably.
Acknowledgments
We are grateful to Giuseppina Battaglia, Glenn van de Ven and Remco van den Bosch for discussions that led to the work presented here. We acknowledge financial support from NOVA (the Netherlands Research School for Astronomy), and European Research Council under ERC-StG grant GALACTICA-240271.
References
- Battaglia, G., Tolstoy, E., Helmi, A., et al. 2006, A&A, 459, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, G., Helmi, A., Tolstoy, E., et al. 2008, ApJ, 681, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, G., Tolstoy, E., Helmi, A., et al. 2011, MNRAS, 411, 1013 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Benson, A. J., Frenk, C. S., Lacey, C. G., Baugh, C. M., & Cole, S. 2002, MNRAS, 333, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Mamon, G. A. 1982, MNRAS, 200, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Breddels, M. A., Helmi, A., van den Bosch, R. C. E., van de Ven, G., & Battaglia, G. 2013, MNRAS, 433, 3173 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, S. E., Kay, S. T., Duffy, A. R., et al. 2012 [arXiv:1207.4555] [Google Scholar]
- Cretton, N., de Zeeuw, P. T., van der Marel, R. P., & Rix, H. 1999, ApJS, 124, 383 [NASA ADS] [CrossRef] [Google Scholar]
- de Boer, T. J. L., Tolstoy, E., Saha, A., et al. 2011, A&A, 528, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dejonghe, H., & Merritt, D. 1992, ApJ, 391, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. W., An, J., & Walker, M. G. 2009, MNRAS, 393, L50 [NASA ADS] [Google Scholar]
- Governato, F., Zolotov, A., Pontzen, A., et al. 2012, MNRAS, 422, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, E., Navarro, J. F., Taylor, J. E., Stadel, J., & Quinn, T. 2003, ApJ, 584, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., Irwin, M. J., Tolstoy, E., et al. 2006, ApJ, 651, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., Sales, L. V., Starkenburg, E., et al. 2012, ApJ, 758, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, M., & Hatzidimitriou, D. 1995, MNRAS, 277, 1354 [NASA ADS] [CrossRef] [Google Scholar]
- Jardel, J. R., & Gebhardt, K. 2012, ApJ, 746, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Jardel, J. R., Gebhardt, K., Fabricius, M. H., Drory, N., & Williams, M. J. 2013, ApJ, 763, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffreys, H. 1998, Theory of Probability, Third Edition, International series of monographs on physics (Clarendon Press) [Google Scholar]
- Kazantzidis, S., Łokas, E. L., Callegari, S., Mayer, L., & Moustakas, L. A. 2011, ApJ, 726, 98 [Google Scholar]
- Koch, A., Grebel, E. K., Wyse, R. F. G., et al. 2006, AJ, 131, 895 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Gnedin, O. Y., & Klypin, A. A. 2004, ApJ, 609, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhlen, M., Diemand, J., & Madau, P. 2007, ApJ, 671, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y.-S., De Lucia, G., & Helmi, A. 2010, MNRAS, 401, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Łokas, E. L., Kazantzidis, S., Klimentowski, J., Mayer, L., & Callegari, S. 2010, ApJ, 708, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. J. C. 2003, Information Theory, Inference and Learning Algorithms, first edition edn. (Cambridge University Press) [Google Scholar]
- Mateo, M. L. 1998, ARA&A, 36, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Mateo, M., Olszewski, E. W., Pryor, C., Welch, D. L., & Fischer, P. 1993, AJ, 105, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, L. 2010, Adv. Astron. [arXiv:0909.4075] [Google Scholar]
- Merrifield, M. R., & Kent, S. M. 1990, AJ, 99, 1548 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Ludlow, A., Springel, V., et al. 2010, MNRAS, 402, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Pontzen, A., & Governato, F. 2012, MNRAS, 421, 3464 [NASA ADS] [CrossRef] [Google Scholar]
- Richstone, D. O., & Tremaine, S. 1984, ApJ, 286, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H., de Zeeuw, P. T., Cretton, N., van der Marel, R. P., & Carollo, C. M. 1997, ApJ, 488, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Wang, J., Vogelsberger, M., et al. 2008, MNRAS, 391, 1685 [NASA ADS] [CrossRef] [Google Scholar]
- Starkenburg, E., Hill, V., Tolstoy, E., et al. 2010, A&A, 513, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stoehr, F., White, S. D. M., Tormen, G., & Springel, V. 2002, MNRAS, 335, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Strigari, L. E., Frenk, C. S., & White, S. D. M. 2010, MNRAS, 408, 2364 [NASA ADS] [CrossRef] [Google Scholar]
- Valluri, M., Merritt, D., & Emsellem, E. 2004, ApJ, 602, 66 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, R. C. E., van de Ven, G., Verolme, E. K., Cappellari, M., & de Zeeuw, P. T. 2008, MNRAS, 385, 647 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., Cretton, N., de Zeeuw, P. T., & Rix, H.-W. 1998, ApJ, 493, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Vera-Ciro, C. A., Helmi, A., Starkenburg, E., & Breddels, M. A. 2013, MNRAS, 428, 1696 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G. 2013, in Planets, Stars and Stellar Systems, eds. T. D. Oswalt, & G. Gilmore (Dordrecht: Springer Science+Business Media) 5, 1039 [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2007, ApJ, 667, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., & Olszewski, E. W. 2009a, AJ, 137, 3100 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2009b, ApJ, 704, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, J., Martinez, G. D., Bullock, J. S., et al. 2010, MNRAS, 406, 1220 [NASA ADS] [Google Scholar]
All Tables
Parameters of the foreground plus dwarf galaxy model used for determining membership, as well as for deriving the radial profiles for the second and fourth velocity moments for each dSph.
Distances, type of photometric profile used, scale radius and stellar luminosity used for the dynamic models.
Model names and their characteristic parameters of the various dark matter density profiles explored.
All Figures
 |
Fig. 1 Radius versus line of sight velocity for Fornax, Sculptor Carina and Sextans. The horizontal lines show the borders of the bins, the vertical lines denote the mean systemic velocity of the galaxy together with the ±3σ region. |
| In the text | |
 |
Fig. 2 Line of sight velocity moments for Fornax, Sculptor Carina and Sextans. For each galaxy we show the velocity dispersion and the kurtosis. The black dots show the mean, and the error bars the 1σ error. The blue regions show the confidence interval for the NFW fit, similar to Breddels et al. (2013). |
| In the text | |
 |
Fig. 3 PDF for the two free parameters characterizing the dark halo profiles for each dSph galaxy obtained using Schwarzschild modeling. The top row shows the PDFs with NFW/Einasto models, the bottom panel those for all cored models explored. The contours show the 1 and 2σ confidence levels (the 3σ contour is not shown to avoid crowding the image). |
| In the text | |
 |
Fig. 4 Similar to Fig. 2, except now we show the different best fit models for the various density profiles explored, which are indicated with different colors (the color scheme is the same as in Fig. 3). |
| In the text | |
 |
Fig. 5 Evidences for all models listed in Table 4, relative to the NFW case. The last column shows the combined evidence for all galaxies together, and shows that the core23 and core24 are strongly disfavored. |
| In the text | |
 |
Fig. 6 Top row: enclosed mass as a function of radius for the different dark matter density profiles, with the stellar component in black. Middle row: logarithmic density slope as a function or radius, where the black curve corresponds again to the stellar component. The red dashed line indicates r-3, the radius at which the light profile has a logarithmic slope of − 3, while the black line indicates r1/2, the radius at which half of the stellar mass in enclosed (in 3D). Bottom row: cumulative density distribution of the (2D) radial distribution of the data (black), and the light (red) showing the kinematic data is sampled more concentrated towards the center. |
| In the text | |
 |
Fig. 7 Similar to Fig. 3, except now using M-3 and r-3 as parameters. Note that the contours for the NFW cannot go beyond κ(r-3) ≥ − 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.