| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321461 | |
| Published online | 15 October 2013 | |
Statistics of encounters in the trans-Neptunian region
1
INAF – Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi
5,
50125
Firenze,
Italy
e-mail:
delloro@arcetri.inaf.it
2
Departamento de Física, Ingeniería de Sistemas y Teoría de la
Señal, Universidad de Alicante, Carretera San Vicente del Raspeig S/N, 03690 San Vicente del Raspeig ( Alicante),
Spain
3
Instituto Universitario de Física Aplicada a las Ciencias y la
Tecnología, Universidad de Alicante, Carretera San Vicente del Raspeig S/N,
03690 San Vicente del Raspeig
( Alicante), Spain
e-mail:
acb@ua.es
Received:
13
March
2013
Accepted:
3
September
2013
The inventory of the populations of trans-Neptunian objects (TNO) has grown considerably over the last decade. As for other groups of small bodies in our solar system, TNOs are expected to have experienced a collisional evolution owing to their mutual impacts. The knowledge of the statistics of collisions, including determination of the rate of mutual collisions and the distribution of the impact velocity, is indeed a fundamental prerequisite for developing models of collisional evolution. We revised the evaluation of those statistical parameters for TNOs provided more than ten years ago on the basis of a much more limited sample of objects than currently available. We used the Canada-France Ecliptic Plane Survey (CFEPS) L7 model to extract an unbiased sample of orbits for TNOs, while the statistical parameters of impact are computed using a statistical tool. We investigated the statistics of impacts among TNOs for the whole population and for different dynamical subgroups. Moreover, we investigated the statistics of collisions between subgroups with crossing orbits. The peculiar dynamical behavior of objects in resonant orbits is taken into account. Our present computation of the probabilities of collision are 20% to 50% lower than previous estimates, while mean impact velocities turn out to be about 70% higher. For instance, the rate of collisions among Plutinos, expressed in terms of the so-called mean intrinsic probability of collision, results to be (3.90 ± 0.01) × 10-22 km-2 yr-1 and the mean impact velocity is 2.46 ± 0.01 km s-1. We also find that the distributions of impact velocities seem to be quite different from pure Maxwellian distributions. These results can be useful in developing models of the collisional evolution in the trans-Neptunian region.
Key words: Kuiper belt: general
© ESO, 2013
1. Introduction
Since the discovery of 1992 QB1, the first object found beyond Neptune with the exception of Pluto (and its largest moon Charon), many discoveries and follow up surveys of that region have been carried on by different teams of researchers. In most cases observational and selection biases were present. The Canadian-France Ecliptic Plane Survey (CFEPS) was set up at the beginning of the past decade (Kavelaars et al. 2009; Petit et al. 2011; Gladman et al. 2012), developing a discovery and follow-up strategy intended to minimize observational biases and to obtain a population of objects that can be considered representative of all dynamical classes of the trans-Neptunian region (also known as the Edgeworth-Kuiper belt, EKB). As a result of this observational effort involving researchers and facilities in many countries, we begin to understand the overall structure of the trans-Neptunian objects (TNO) populations in terms of dynamical features and absolute magnitude number distributions. Following the terminology introduced by the CFEPS, the TNOs can be roughly classified – from a dynamical point of view – as Resonant, Scattering and Classical or detached objects. This classification can be further divided into subclasses, as explained later.
A synthetic model was produced starting from the CFEPS observational data (CFEPS-L7), producing orbital and magnitude distributions corresponding to each dynamical class (Petit et al. 2011). In the analysis we present in this article, we have recovered the techniques explained in Dell’Oro & Paolicchi (1998a) and applied in Dell’Oro et al. (2001) to derive encounter probabilities and relative velocity distributions between objects belonging to the same classes and to different classes for which orbital crossing is possible.
2. The trans-Neptunian region
2.1. Dynamical structure of the trans-Neptunian region
We follow the convention stated in Gladman et al. (2008). Based on orbital elements and dynamical behavior, the EKB can be divided into three broad orbital classes.
-
1.
Resonant: objects currently in a mean motion resonance(MMR) with Neptune.
-
2.
Scattering: objects which over 10 Myr forward in time integrations experience encounters with Neptune resulting in a variation of their semimajor axes by more than 1.5 AU.
-
3.
Classical or detached belt: the rest of objects.
The classical belt can be further subdivided into:
-
3.a
inner classical belt (ICB): objects with semimajor axes inside3:2 MMR;
-
3.b
main classical belt (MCB): objects whose semimajor axes are between the 3:2 and 2:1 MMRs;
-
3.c
outer belt (OB): objects with semimajor axes outside to the 2:1 MMR, with eccentricites smaller than 0.24;
-
3.d
detached: objects with semimajor axes beyond the 2:1 MMR and eccentricities larger than 0.24.
The classical belt is also often divided into high-inclination and low-inclination objects. As described in Brown (2001), two distinct populations exist, one with a wide inclination distribution (the “hot” population) and another one with a narrow inclination distribution (the “cold”population), with both populations overlapping each other in inclination space. The CFEPS model has also found that the cold classical objects have two components, the stirred and kernel populations.
2.2. The CFEPS synthetic Edgeworth-Kuiper belt
The CFEPS model of the Kuiper belt (Petit et al. 2011) is an empirical parametric model that properly reproduces the observed orbital distribution of the trans-Neptunian region, once passed through the CFEPS survey simulator. The survey simulator takes a proposed EKB model, exposes it to the known detection biases of the CFEPS blocks, and produces simulated detections to be compared with the real detections. Starting from a simple parametrization of the intrinsic orbit and absolute magnitude distributions for the various components of the so-called classical belt, the CFEPS survey simulator determines which members of the population would have been detected by the survey. The orbital element distributions of the simulated detections are then compared to the CFEPS characterized sample. This process is iterated with models of increasing complexity until getting a model that provides a statistically acceptable match (no cosmogonic considerations are invoked). The result of this process is the CFEPS synthetic model1.
This model has allowed the identification of dynamical structures in the main classical belt. There is clear evidence of a population with a wide inclination distribution (the hot population) superposed on top of a population with a narrow inclination component with two semimajor axis/eccentricity distributions (the stirred and kernel populations). The hot population is defined as a band in perihelion distance q essentially confined within the range 35 to 40 AU, with a soft exponential decay outside this range. The cold population of the main classical belt can be then split into two subcomponents, being aware that there is mixing with the low-inclination tail of the hot component. The stirred population has orbits drawn from a narrow-inclination distribution with semimajor axes starting at a = 42.5 AU and extending to a ≃ 47 AU, with a range of eccentricities that increases going to larger a. The stirred component does not contain the sharp density change at ≃44.5 AU. There are more low-i and moderate-e TNOs per unit semimajor axis, in the interval between 44 AU and 44.5 AU, than at smaller and larger semimajor axes, indicating that a third component is required. This component is a dense low-inclination concentration, the kernel, near a = 44 AU.
The purpose of this parametric model is to provide absolutely calibrated population estimates of the various sub-populations of the EKB. The CFEPS synthetic model is also useful for observational modeling of the region (Stark & Kuchner 2010). The ability to provide a detailed quantitative comparison with a cosmogonic model is, however, the true power of the CFEPS survey. This is done by passing a proposed model of the current EKB distribution through the CFEPS survey simulator and then comparing this detection-biased model with the real CFEPS detections. Through this procedure one can choose between models in a statistically robust way. We consider that the CFEPS synthetic model is then the most complete and reliable model – at present – able to give estimates of the current transneptunian populations. For that reason, it is suitable to perform statistical analysis of close encounters of TNOs, deriving the probabilities and distributions of relative velocities for the corresponding populations. The goal of this work is not, however, to provide estimates of the number of encounters between any size bodies. In fact, that would need assumptions on the size distributions and boundary conditions of the evolution of populations that is beyond the scope of our calculations. Collisional evolution models – for which this work aims to provide intrinsic probabilities of encounters and relative velocities distributions – should do that. An example of application of past similar estimates is in Campo Bagatin & Benavidez (2012). An update of that model is in course according to the results of the present study.
3. The distributions of TNO orbital elements
Average values and 1-σ standard deviation for eccentricities (e) and inclinations (I) (in degrees) in the inner belt (ICB), hot main classical belt (HMCB), cold main classical belt (CMCB) and outer belt (OB).
 |
Fig. 1 Distribution (normalized frequency) of the orbital elements (semimajor axes a, eccentricities e, inclinations I and longitude of the ascending nodes Ω) of the CFEPS synthetic model for the Inner Classical Belt. |
 |
Fig. 2 Distribution (normalized frequency) of the orbital elements (semimajor axes a, eccentricities e, inclinations I and longitude of the ascending nodes Ω) of the CFEPS synthetic model for the Hot Main Classical Belt. |
 |
Fig. 3 Distribution (normalized frequency) of the orbital elements (semimajor axes a, eccentricities e, inclinations I and longitude of the ascending nodes Ω) of the CFEPS synthetic model for the Cold Main Classical Belt. |
 |
Fig. 4 Distribution (normalized frequency) of the orbital elements (semimajor axes a, eccentricities e, inclinations I and longitude of the ascending nodes Ω) of the CFEPS synthetic model for the Outer Belt. |
We have analyzed the distributions of the semimajor axes, eccentricities, inclinations and longitudes of the ascending nodes for all the dynamical populations identified by the CFEPS. Table 1 and Figs. 1 to 4 show such distributions. The most remarkable features of the orbital structure predicted by the CFEPS model are shortly summarized.
The inner belt is characterized by a lack of inclinations between 8 and 18 degrees, approximately. There are no inner classical belt objects in this inclination range due to the fact that the ν8 secular resonance is there and removes them all, as explained in Petit et al. (2011). Also, eccentricities have very small values, within 0.1.
It is interesting to notice the semimajor axes overall structure of the main belt, as described by the CFEPS synthetic model. Dynamical classes are clearly confined there. The cold component of the belt starts at some 42.5 AU, including both stirred and kernel populations. The kernel population is well confined within approximately 0.6 AU, starting around 43.8 AU. The bimodality in eccentricity and inclination distributions reflects the presence of the hot and cold components themselves. The distributions of eccentricities and inclinations of the cold component (the stirred and kernel populations together) show a Maxwellian-like profile that instead is not present in the distribution of eccentricities of the hot component of the main classical belt. This may be related to a relaxation in the collisional evolution of the cold component, that is also characterized by remarkably lower values of inclinations (and eccentricities) with respect to the hot component.
In the outer belt, the main feature is a clear lack of low eccentricity orbits, likely related to their scattered origin due to perturbations by giant planets in their early history (in agreement with Gomes et al. 2005). A nearly exponential decrease of the number of objects at increasing semimajor axes is also clearly shown (Fig. 1) down to some 500 AU.
The inhomogeneous distributions of the longitudes of the ascending nodes – in particular in the case of the cold main classical belt – is an effect due to the way data are handled in the synthetic model. In fact, elements are generated in the invariable plane reference frame, but the L7 model is given in ecliptic J2000 reference frame. The invariable plane has an inclination about 1.5 degrees with respect to J2000 ecliptic plane with direction of ascending node at about 107.5 deg. For this reason the distribution of the ascending nodes, uniformly generated in the invariable plane, is clustered in ecliptic coordinates. The effect is larger for the cold population due to its smaller mean inclination, while for the other components it is practically invisible.
4. Methods in TNO collisional statistics
4.1. Statistical parameters
Our goal is to investigate the statistics of collisions among objects regardless of their size belonging to any given dynamical group and for objects belonging to different groups. The main information about collisions among orbiting bodies around a common attracting mass the Sun, in our case is their mean intrinsic probability of collision (Wetherill 1967). In the simplified situation in which only two orbiting bodies with radii R1 and R2 (supposing them spherical) exist, the probability of collision is the average number per unit of time of the close approaches within a mutual distance that is less than the sum of their radii, R1 + R2. From the knowledge of such intrinsic probabilities, more practical quantities can be derived in specific environments (e.g, the transneptunian belt, the asteroid belt, the Jupiter Trojan asteroids). Namely, the probability of collision, or more properly, the mean frequency of collision, that is the number of close approaches within a distance less than R1 + R2 occurring during a sufficiently long time T, divided by T. For a sufficiently long time we mean an interval of time during which all possible geometrical configurations of the system can come about. The probability of collision, avoiding the effect of the mutual gravitational attraction, is proportional to the geometrical cross section, that is the square of the sum of the radii. For definition, the intrinsic probability of collision Pi is the probability of collision in the case R1 + R2 = 1 km, so that the probability of collision is simply (R1 + R2)2Pi. The intrinsic probability of collision is usually expressed in units of km-2 year-1, and depends only on the orbital configuration of the system, regardless the size distribution of the bodies.
When more than two orbits are taken into account, the mean intrinsic
probability of collisions ⟨ Pi ⟩ is computed.
We follow the convention that ⟨ Pi ⟩ for the
collisions between a given “target” orbit and a group of “projectile” orbits is defined as
the sum of the intrinsic probabilities of collision between the target orbit and each
projectile orbit, divided by the number of projectile orbits. In a statistical form, if
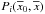 is the
intrinsic probability of collision between the target orbit
is the
intrinsic probability of collision between the target orbit
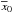 and the projectile
orbit
and the projectile
orbit 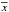 (obviously
(obviously
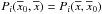 ), then:
), then:
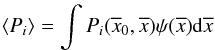
where 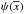 is the normalized
distribution of the projectile orbits. In the reasonable approximation (at least at first
order of the study of the collisional evolution of systems like the transneptunian region)
that the distribution of the orbits does not depend on the sizes of the objects, the total
number of collisions per unit of time suffered by a given target and due to a given
population of projectiles, in a given interval of sizes, is:
is the normalized
distribution of the projectile orbits. In the reasonable approximation (at least at first
order of the study of the collisional evolution of systems like the transneptunian region)
that the distribution of the orbits does not depend on the sizes of the objects, the total
number of collisions per unit of time suffered by a given target and due to a given
population of projectiles, in a given interval of sizes, is:
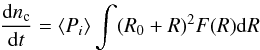
where R0 is the radius of the target, R is the radius of the projectile and F(R) is the distribution of the radii of the projectiles. The integral is performed on the size interval of interest of the projectiles. In this way the same value of the mean intrinsic probability of collision can be used with different size distributions, provided that the orbital distribution is the same. When the collisions among a group of targets and a group of projectiles are addressed, the mean intrinsic probability of collision is the average of the single mean probabilities of collision computed for each target. In this case the mean intrinsic probability of collision is a representative value for the whole ensemble of targets.
As far as the impact velocity U is concerned, we define it as the relative velocity of the projectile with respect to the target at the epoch of the close encounter, neglecting gravitational focusing effects. For a single orbit undergoing collisions with a population of background projectiles, we compute the distribution of U. In the case of a group of targets the statistical distribution of U is defined as the average of the single statistical distributions of U for each target weighted by the corresponding mean intrinsic collisional probability. From the distribution of the vector U, the distributions of the modulus U, of the radial (UR), transversal (UT) and normal (UN) components are extracted, together with the mean value of the modulus U and its standard deviation σ(U), and the mean values of the modulus of the three components | UR |, | UT | and | UN |. More precisely, if eR, eN, and eT are the unit vectors from the target at the time of the close approach respectively pointing to opposite direction respect to the Sun, parallel to the angular momentum of its orbit (normal to it), and equal to eN × eR, the impact velocity is U = UReR + UTeT + UNeN.
4.2. The dynamical/statistical model
A statistical model is required in order to compute all the above statistical information. For bodies whose orbits have no peculiar behavior, as not resonant orbits, the standard dynamical assumptions are:
-
(1)
semimajor axes a, eccentricities e and inclinations I are fixed and do not change in time;
-
(2)
mean longitude M, longitude of the node Ω and argument of the perihelion ω of a given orbit are uniformly distributed, meaning that their probability distributions are constant over the interval from 0 to 2π;
-
(3)
no correlation exists among the angular elements M, Ω and ω of the orbit of a body;
-
(4)
no correlation exists between any angular elements of the target and any angular element of the projectile.
Concerning hypothesis (1), orbital elements a, e and I are supposed not to have secular variations but only small periodic oscillations around mean values. Orbits are assumed to have semimajor axes, eccentricities and inclinations fixed and equal to their mean values. From a dynamical point of view, conditions (2)–(4) mean that the orbits circulate uniformly and independently of each other. The non uniformity of the distribution of the nodes shown in Fig. 3 can be ignored if the computation of the collision probability is performed using the orbital elements with respect to the invariable plane.
In the case of orbits in mean motion resonance with Neptune, the hypothesis (4) no longer
holds. It is well known that – for these kind of orbits – a critical angle can be defined
as the value that librates around a mean value, or in a more statistical sense, its value
is not distributed uniformly between 0 and 2π. For a
(j + k):j resonance, the critical
angle is defined as (Malhotra 1996):
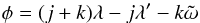
where λ = M + ω + Ω is the
mean longitude of the body, 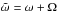 is its longitude of perihelion,
and λ′ is the mean longitude of the planet (Neptune, in our
case). The mean value of φ is generally (but not always) 0 or
π. Regardless the mean value of the critical angle of a single orbit,
the difference
σ = φt − φp
between the critical angle of the target and the critical angle of the projectile is not
uniformly distributed. This angle can be expressed clearly as a linear combination of the
angular elements of the target and the projectile:
is its longitude of perihelion,
and λ′ is the mean longitude of the planet (Neptune, in our
case). The mean value of φ is generally (but not always) 0 or
π. Regardless the mean value of the critical angle of a single orbit,
the difference
σ = φt − φp
between the critical angle of the target and the critical angle of the projectile is not
uniformly distributed. This angle can be expressed clearly as a linear combination of the
angular elements of the target and the projectile: 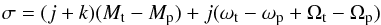 If
the probability distribution of σ is not uniform it entails that there is
some correlation among the angular elements of the target and the projectile, violating
condition (4). In this case we modify that hypothesis as:
If
the probability distribution of σ is not uniform it entails that there is
some correlation among the angular elements of the target and the projectile, violating
condition (4). In this case we modify that hypothesis as:
-
(4’)
the probability distribution of σ is a given function Ψ(σ).
The particular form of the function depends on the dynamics of the orbits and can be extracted from the CFEPS synthetic model data set. An example of distribution of the angle σ is shown in Fig. 5. The histogram in the figure has been obtained computing the differences of the critical angles φ for all possible pairs of orbits in mean motion resonance 3:2 with Neptune included in the CFEPS model data set. For orbits not in resonance the analogous distribution is flat.
 |
Fig. 5 Normalized distribution of the difference σ of the critical angles of the bodies included in our database that are in a 3:2 resonance with Neptune. |
4.3. The computational tool
In order to compute the mean intrinsic probabilities of collision and all the required
statistical distributions of the relative impact velocities and their components, we use
the approach by Dell’Oro & Paolicchi
(1998a), that is the evolution and improvement of the method by Dell’Oro & Paolicchi (1997). The approach has
been successfully used for the computation of the probabilities of impact among some
orbits in resonant conditions like the case Jupiter Trojans (Dell’Oro & Paolicchi 1998b) and the case of Plutinos (Dell’Oro et al. 2001). In the simple case of collisions
between two bodies, the computation of the intrinsic probability of collision is based on
the numerical evaluation of a surface integral in the space of the six angular orbital
elements of the target ft, ωt,
Ωt and the projectile fp,
ωp, Ωp, where f is true anomaly
(see Dell’Oro & Paolicchi 1998a, for
details). The integrand function contains, besides other factors, the probability
distribution of the six angular elements: 
In the canonical case in which the hypotheses (2)–(4) hold, the analytical form of Δ is:
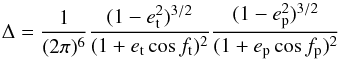 (1)expressing
in a statistical way the pure Keplerian motions of the two bodies. In the more general
situation in which the hypothesis (4’) holds, the form of Δ has to be modified as:
(1)expressing
in a statistical way the pure Keplerian motions of the two bodies. In the more general
situation in which the hypothesis (4’) holds, the form of Δ has to be modified as:
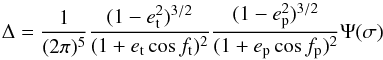 (2)provided that the
Ψ(σ) function is normalized between 0 and 2π. In any
case Δ has to be normalized over the six dimensional space
[0,2π] 6. The dependence on
ft and fp in function Ψ is
hidden inside the dependence of σ on Mt and
Mp respectively. The function Ψ(σ) is not
provided analytically but rather by means of numerical interpolation of the distribution
of σ, extracted from the specific sub-population.
(2)provided that the
Ψ(σ) function is normalized between 0 and 2π. In any
case Δ has to be normalized over the six dimensional space
[0,2π] 6. The dependence on
ft and fp in function Ψ is
hidden inside the dependence of σ on Mt and
Mp respectively. The function Ψ(σ) is not
provided analytically but rather by means of numerical interpolation of the distribution
of σ, extracted from the specific sub-population.
With a large number of targets and projectiles, the computation of many such integrals can be time consuming. In this case, a Monte Carlo technique can be used in order to obtain enough accurate results in a reasonable time (see Dell’Oro & Paolicchi 1998a, for details). The distribution of the impact velocity (and of any other kinematic parameter) is obtained as a by-product of the computation of the intrinsic probability of collision.
5. Results
Statistical impact parameters for the collisions between each group and the overall TNO population (ALL).
Statistical impact parameters for the collisions among pairs of the main TNO groups, and within each group.
 |
Fig. 6 Resonant groups (black dots) superimposed to the whole model population (gray dots) in the semimajor axis-eccentricity diagram. |
In order to provide a suitable sketch of the relevant features of the statistics of collisions among TNOs, we have divided our data set into different groups:
-
ALL: all objects (the combinations of following groups);
-
ICB: inner classical belt objects;
-
HMCB: objects belonging to the hot main classical belt;
-
CMCB: objects belonging to the kernel or stirred main classical belt;
-
OB: objects belonging to the outer region of the main belt or scattered objects;
-
N:M: objects in N:M mean motion resonance with Neptune (one group for each resonance).
We investigated the statistics of collisions (i) between the members of each group and the whole background population of potential projectiles (ALL), in order to evaluate the total intensity of the collisional evolution in each group; (ii) the collisions among the members of each group and (iii) the collisions between members belonging to different groups. The results are shown in Tables 2–3 and Fig. 7.
 |
Fig. 7 Distributions of the modulus U of the impact velocity between some groups and the overall TNO population (ALL). |
In Fig. 7 the distributions of the moduli of the
impact velocity between the members of some groups and the members of the whole population
are plotted. In each plot the real distribution is drawn as a bold line, while the
superimposed long-dashed line corresponds to the Maxwellian distribution that best fits the
real one. We used the following analytical expression for the Maxwellian distributions:
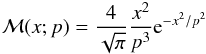
where parameter p is the abscissa for which the distribution has its
maximum value. In some cases (ALL vs. ALL, CMCB vs. ALL and 7:4 vs. ALL) a combination of
two Maxwellian distributions has been used: 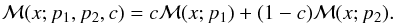
The parameter p, or p1, p2 and c, are reported in Table 2, with the most relevant parameters of the velocity distributions and, in particular, the mean value of the moduli of the impact velocities, their standard deviations and the mean values of the moduli of the three components.
In general, the distributions of the relative impact velocities are not exactly Maxwellian. The distributions that best seem to follow Maxwellian distributions are those for collisions between OB versus ALL, and 5:2 versus ALL. In three cases (ALL versus ALL, CMCB versus ALL, 7:4 versus ALL) the distributions can be interpreted as the combination of two unimodal distributions. In the case of the collisions ALL versus ALL, the distribution of the relative impact velocities shows a clear bimodality with two peaks at ~ 0.5 km s-1 and ~ 1.8 km s-1 corresponding respectively to the contributions of the overwhelming groups CMCB and OB plus HMCB. This does not mean that any object can be impacted with a relative velocity distributed as in the given upper left plot in Fig. 7. Instead, such distribution should be used only in the case of a collisional evolution model where the entire TNO population is treated as a whole, without following in detail the evolution of each single subgroup. For each subgroup, the corresponding velocity distribution must be used instead. The same holds for the values of the mean intrinsic collisional probabilities listed in Table 2.
The results regarding resonant groups reflect the position of each resonance in the space of orbital elements. In Table 2 resonant groups are listed from the very inner to the very outer ones. Intrinsic collisional probability is very low for 1:1, being those members well separated from the rest of the population. ⟨ Pi ⟩ grows up to the maximum value for the 7:4 group, that interacts with the core of the TNO population. ⟨ Pi ⟩ decreases for outer and outer resonances. On the contrary, the mean relative impact velocity has an opposite behavior. It is maximum for the 1:1 group, than it decreases for the closest groups to the core of the belt, and reaches its minimum value for the 7:4 group. For the groups outside the 7:4 mean motion resonance, the mean impact velocity grows because of the larger and larger values of the eccentricities of their members and of interacting projectiles (Fig. 6).
Table 3 reports the mean intrinsic collisional probabilities (in italics) and the mean impact velocity (in bold) for the intra-group and inter-group collisions for the main groups ICB, HMCB, CMCB and OB. It is worthwhile to note that the intrinsic collisional probability among CMCB members is much larger than the intrinsic collisional probability among ICB bodies, even if the former have smaller semimajor axes than the latter. This large difference is due to the different inclination distributions. In fact, the orbital inclinations of the ICB members reach 50 degrees, while the inclinations of CMCB members is generally below 10 degrees. For the same reason, ICB objects have a larger mean impact velocity than CMCB objects.
6. Discussion and conclusions
We have updated the computation of the probability of collisions among TNOs along with the determination of the distributions of the impact velocities. We computed such parameters for the different dynamical groups the TNO population is subdivided into. The aim of this work is to provide detailed information needed to implement or improve models of collisional evolution of the TNO population. We used as an input the orbital distribution provided by the CFEPS synthetic model, the most recent and updated model of the EKB dynamical structure.
A previous computation of the probability of collisions among TNOs has been done by Dell’Oro et al. (2001). At that time the number of known TNOs was much smaller than nowadays and no model nor extrapolation for the entire population was available. In that work the statistics of collisions were investigated on the basis of only 46 Plutinos and 140 non Plutinos objects with relatively low orbital reliability. The mean intrinsic probability of collision among Plutinos resulted to be equal to P = 4.44 × 10-22 km-2 yr-1 and mean velocity of impact 1.44 km s-1. Our current results are respectively ⟨ Pi ⟩ = 3.90 × 10-22 km-2 yr-1 and and ⟨ |U| ⟩ = 2.46 km s-1. The difference is due to the different distribution of the orbital elements of the two samples, in particular regarding inclinations. In the sample of 46 Plutinos the inclinations ranged from 0 to 40 deg, with a mean value around 10 deg, while in our present sample inclinations are between 0 and 60 deg and the mean value is about 20 deg.
Moreover, in Dell’Oro et al. (2001) the probability of collision between Plutinos and non Plutinos was reported to be 3.14 × 10-22 km-2 yr-1 and the mean impact velocity, 1.23 km s-1. Our present estimations are respectively 1.54 × 10-22 km-2 yr-1 and 2.10 km s-1 (3:2 versus ALL). Again, the lower value for ⟨ Pi ⟩ and the larger value for ⟨ |U| ⟩ is due to the larger extension of the orbital elements of the impactors.
As an example of the role of the peculiar dynamical behavior of resonant objects on their collisional statistics, we recomputed the probability of collisions among Plutinos without taking into account the factor Φ(σ) in the analytical expression of the function Δ (Eq. (2)). This is equivalent to assume that Plutinos have regularly circulating orbits. The result of this exercise provides a value for the mean intrinsic probability of collision 25% lower than the correct value (2.9 × 10-22 km-2 instead of 3.9 × 10-22 km-2), while ⟨ |U| ⟩ results to be more or less the same (about 2.4 km s-1 in both cases). The correction factor between canonical collisional probability (computed assuming circulating orbits) and non-canonical probability depends on the degree of polarization of the orientation of the orbits and in general increases more and more orbits are polarized (Dell’Oro & Paolicchi 1998a). Obviously, for collisions between resonant and non-resonant objects, the probability of collision is in any case the one provided by the canonical statistics because no correlation exists between the angular elements of the two kind of orbits.
The results presented in this paper may serve as a statistical tool of use in any situation in which the distribution of the relative encounter velocities and the collisional probabilities among TNO populations are needed. For example, these results may be useful for studies of the overall collisional evolution of TNOs, including the possible formation dynamical families and resurfacing processing due to collisions.
Acknowledgments
A.C.B. and P.G.B. acknowledge funding by the national program of the Spanish Ministerio de Ciencia e Innovación, project grant AYA2011-30106-C02-02.
References
- Benavidez, P. G., & Campo Bagatin, A. 2009, Planet. Space Sci., 57, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Nolan, M. C., Greenberg, R., & Kolvoord, R. A. 1994, Icarus, 107, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Campo Bagatin, A., & Benavidez, P. G. 2012, MNRAS, 423, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, D. R., & Farinella, P. 1997, Icarus, 125, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Oro, A., & Paolicchi, P. 1997, Planet. Space Sci., 45, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Oro, A., & Paolicchi, P. 1998, Icarus, 136, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Oro, A., Paolicchi, P., Marzari, F., Dotto, E., & Vanzani, V. 1998, A&A, 339, 272 [NASA ADS] [Google Scholar]
- Dell’Oro, A., Marzari, F., Paolicchi, P., & Vanzani, V. 2001, A&A, 366, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durda, D. D., & Stern, S. A. 2000, Icarus, 145, 220 [Google Scholar]
- Farinella, P., Davis, D. R., & Stern, S. A. 2000, Protostars and Planets IV, 1255 [Google Scholar]
- Gladman, B., Marsden, B. G., & Vanlaerhoven, C. 2008, The Solar System Beyond Neptune, eds. M. A. Barucci, H. Boehnhardt, D. P. Cruikshank, & A. Morbidelli (Univ. Arizona Press), 43 [Google Scholar]
- Gladman, B., Lawler, S. M., Petit, J.-M., et al. 2012, AJ, 144, 23 [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Greenberg, R. 1982, AJ, 87, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Kavelaars, J. J., Jones, R. L., Gladman, B. J., et al. 2009, AJ, 137, 4917 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, R. 1996, AJ, 111, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, A. H., & Kavelaars, J. J. 2010, ApJ, 722, L204 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, A. H., & Kavelaars, J. J. 2012, ApJ, 744, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, J.-M., Holman, M. J., Gladman, B. J., et al. 2006, MNRAS, 365, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, J.-M., Kavelaars, J. J., Gladman, B. J., et al. 2008, Science, 322, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, J.-M., Kavelaars, J. J., Gladman, B. J., et al. 2011, AJ, 142, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, C. C., & Kuchner, M. J. 2010, BAAS, 42, 527 [NASA ADS] [Google Scholar]
- Veillet, C., Parker, J. W., Griffin, I., et al. 2002, Nature, 416, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Wetherill, G. W. 1967, J. Geoph. Res., 72, 2429 [Google Scholar]
All Tables
Average values and 1-σ standard deviation for eccentricities (e) and inclinations (I) (in degrees) in the inner belt (ICB), hot main classical belt (HMCB), cold main classical belt (CMCB) and outer belt (OB).
Statistical impact parameters for the collisions between each group and the overall TNO population (ALL).
Statistical impact parameters for the collisions among pairs of the main TNO groups, and within each group.
All Figures
 |
Fig. 1 Distribution (normalized frequency) of the orbital elements (semimajor axes a, eccentricities e, inclinations I and longitude of the ascending nodes Ω) of the CFEPS synthetic model for the Inner Classical Belt. |
| In the text | |
 |
Fig. 2 Distribution (normalized frequency) of the orbital elements (semimajor axes a, eccentricities e, inclinations I and longitude of the ascending nodes Ω) of the CFEPS synthetic model for the Hot Main Classical Belt. |
| In the text | |
 |
Fig. 3 Distribution (normalized frequency) of the orbital elements (semimajor axes a, eccentricities e, inclinations I and longitude of the ascending nodes Ω) of the CFEPS synthetic model for the Cold Main Classical Belt. |
| In the text | |
 |
Fig. 4 Distribution (normalized frequency) of the orbital elements (semimajor axes a, eccentricities e, inclinations I and longitude of the ascending nodes Ω) of the CFEPS synthetic model for the Outer Belt. |
| In the text | |
 |
Fig. 5 Normalized distribution of the difference σ of the critical angles of the bodies included in our database that are in a 3:2 resonance with Neptune. |
| In the text | |
 |
Fig. 6 Resonant groups (black dots) superimposed to the whole model population (gray dots) in the semimajor axis-eccentricity diagram. |
| In the text | |
 |
Fig. 7 Distributions of the modulus U of the impact velocity between some groups and the overall TNO population (ALL). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


