| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 20 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201321396 | |
| Published online | 27 September 2013 | |
Cosmological model dependence of the galaxy luminosity function: far-infrared results in the Lemaître-Tolman-Bondi model
1
Observatório do Valongo, Universidade Federal do Rio de Janeiro,
Ladeira Pedro Antonio
43, 20080-090
Rio de Janeiro,
Brazil
e-mail:
iribarrem@astro.ufrj.br
2
European Southern Observatory (ESO), Karl-Schwarzschild-Straße 2, 85748
Garching,
Germany
3
INAF – Osservatorio Astronomico di Bologna, via Ranzani 1,
40127
Bologna,
Italy
4
Astrophysics, Cosmology and Gravitation Centre, and Department of
Mathematics and Applied Mathematics, University of Cape Town,
Rondebosch 7701, Cape Town, South
Africa
5
Instituto de Física, Universidade Federal do Rio de Janeiro,
CP 68532,
21941-972
Rio de Janeiro,
Brazil
6
Max-Planck-Institut für Extraterrestrische Physik (MPE),
Postfach 1312,
85741
Garching,
Germany
7
CEA-Saclay, Service d’Astrophysique, 91191
Gif-sur-Yvette,
France
8
Dipartimento di Astronomia, Università di Bologna,
via Ranzani 1, 40127
Bologna,
Italy
Received:
1
March
2013
Accepted:
24
July
2013
Aims. This is the first paper of a series aiming at investigating galaxy formation and evolution in the giant-void class of the Lemaître-Tolman-Bondi (LTB) models that best fits current cosmological observations. Here we investigate the luminosity function (LF) methodology, and how its estimates would be affected by a change on the cosmological model assumed in its computation. Are the current observational constraints on the allowed cosmology enough to yield robust LF results?
Methods. We used the far-infrared source catalogues built on the observations performed with the Herschel/PACS instrument and selected as part of the PACS evolutionary probe (PEP) survey. Schechter profiles were obtained in redshift bins up to z ≈ 4, assuming comoving volumes in both the standard model, that is, the Friedmann-Lemaître-Robertson-Walker metric with a perfect fluid energy-momentum tensor, and non-homogeneous LTB dust models, parametrized to fit the current combination of results stemming from the observations of supernovae Ia, the cosmic microwave background, and baryonic acoustic oscillations.
Results. We find that the luminosity functions computed assuming both the standard model and LTB void models show in general good agreement. However, the faint-end slope in the void models shows a significant departure from the standard model up to redshift 0.4. We demonstrate that this result is not artificially caused by the used LF estimator which turns out to be robust under the differences in matter-energy density profiles of the models.
Conclusions. The differences found in the LF slopes at the faint end are due to variation in the luminosities of the sources that depend on the geometrical part of the model. It follows that either the standard model is over-estimating the number density of faint sources or the void models are under-estimating it.
Key words: galaxies: luminosity function, mass function / galaxies: distances and redshifts / infrared: galaxies / cosmology: theory / galaxies: evolution
© ESO, 2013
1. Introduction
The luminosity function (LF) is an important observational tool for galaxy evolution studies because it encodes the observed distribution of galaxies in volumes and luminosities. However, a cosmological model must be assumed in its estimation, rendering it model dependent. On the other hand, the precision of the current constraints on the cosmological model might arguably be enough to yield an LF that has the same shape in all models allowed by the observations. To investigate this assertion, it is necessary to compute the LF considering one such alternative model, and perform a statistical comparison with the LF obtained assuming the standard model.
The currently favoured theory for explaining the shape and redshift evolution of the LF is that the dark matter haloes grow up hierarchically by merging, and that baryonic matter trapped by these haloes condense to form galaxies. Astrophysical processes (gas cooling, high redshift photoionization, feedbacks), are then responsible for reproducing the shape of the luminosity function of galaxies starting from the dark matter halo mass function (Benson et al. 2003). The usual approach in the context of the standard model is either to use semi-analytical models to parameterize these processes (e.g. Neistein & Weinmann 2010), or to use empirical models (e.g. Yang et al. 2003; Skibba & Sheth 2009; Zehavi et al. 2011) to allocate galaxies as a function of halo mass, both built on a dark matter hierarchical merger tree created by simulations, like the Millennium simulation (Springel et al. 2005; Boylan-Kolchin et al. 2009).
It has been well-established by observations made at many different wavelengths (some recent examples include van der Burg et al. 2010; Ramos et al. 2011; Cool et al. 2012; Simpson et al. 2012; Patel et al. 2013; Stefanon & Marchesini 2013), and particularly in the IR (Babbedge et al. 2006; Caputi et al. 2007; Rodighiero et al. 2010; Magnelli et al. 2011; Heinis et al. 2013), that the LF shows significant evolution with redshift. In practice the LF is traditionally computed using the comoving volume, which does not stem directly from the observations, but rather is derived from it assuming a cosmological model with a well-defined metric that translates redshifts into distances. The effects of the expanding space-like hypersurfaces can, therefore, be successfully factored out of the observations up to the limits where the assumed cosmological model holds. The last remark is of special importance, because Mustapha et al. (1997) proved that any spherically symmetric set of observations, like redshift surveys, can be fitted simply by spatial non-homogeneities in a more general cosmological model that assumes a Lemaître-Tolman-Bondi (LTB) line element and a dust-like energy-momentum tensor, regardless of any evolution of the sources. As a consequence, the reported redshift evolution of the LF could, in principle, be caused by a non-homogeneity on the cosmology at the scale of the observations. It is, therefore, crucial for galaxy evolution theories and past-lightcone studies (e.g. Ribeiro & Stoeger 2003; Albani et al. 2007; Rangel Lemos & Ribeiro 2008; Iribarrem et al. 2012; Helgason et al. 2012; Datta et al. 2012) that the underlying cosmological model be well-established by independent observations.
Results from many independent cosmological observations fit together in a coherent picture under the cold dark matter model with a cosmological constant (ΛCDM; e.g. Komatsu et al. 2009), which is now adopted as the main cosmological model.
One of the key observational results in selecting the ΛCDM parametrization for a Friedmann-Lemaître-Robertson-Walker (FLRW) perfect fluid model is the dimming in the redshift-distance relation of supernovae Ia, first obtained independently by Riess et al. (1998) and Perlmutter et al. (1999). This has led to the re-introduction of the cosmological constant Λ in Einstein’s field equations, and the further interpretation of it as an exotic fluid, dark energy, accelerating the expansion of the Universe.
Despite the many empirical successes of the standard model, understanding of the physical nature of dark energy is still lacking. This has encouraged many authors to investigate viable alternatives to it, like modified gravity (Tsujikawa 2010), the effect of small-scale spatial non-homogeneities of the matter content in the estimation of the cosmological model parameters (Busti & Lima 2012), often called the backreaction effect on cosmology (Clarkson et al. 2011; Clarkson & Umeh 2011; Clifton et al. 2012; Wiegand & Schwarz 2012), or non-homogeneous cosmological models (Célérier 2007; Bolejko et al. 2011a; Ellis 2011).
Many recent works have advanced our understanding of non-homogeneities and, particularly, of LTB models. From practical questions like those related to possible dimming or brightening of point-like sources due to the narrowness of their observed beams, compared to the typical smoothing scales in standard model simulations (Clarkson et al. 2012), or the possibility of accounting for the anomalous primordial Lithium abundances (Regis & Clarkson 2012), passing through the development of the models themselves (e.g. Hellaby & Alfedeel 2009; Alfedeel & Hellaby 2010; Meures & Bruni 2012; Humphreys et al. 2012; Nishikawa et al. 2012; Bull & Clifton 2012; Valkenburg et al. 2012; Wang & Zhang 2012; Hellaby 2012), to several tests and fits to different observations (e.g. February et al. 2010; Bolejko et al. 2011b; Hoyle et al. 2013; Bull et al. 2012; de Putter et al. 2012), much has been done to establish non-homogeneity as a well-grounded modification of the standard cosmology. Despite the recent interest in these models, to date no work has aimed at studying galaxy evolution on non-homogeneous cosmologies.
By restricting the available models to those which are well constrained by a wealth of observations, we focus on two questions: Given that the current observations still allow a certain degree of freedom for the cosmological model, are these constraining enough to yield a robust LF estimation, or are our statistical conclusions still dependent on the model? And how?
To address these questions, one needs at least two different cosmological models, in the sense of a set of equations that are a solution to the Einstein field equations, both parametrized to fit the whole set of available observations. Therefore, for the purpose stated above, the parametrization of Garcia-Bellido & Haugbølle (2008) for the LTB dust model is sufficient.
We started from the far-infrared (FIR) LF which has been recently established by (Gruppioni et al. 2013), using combined data obtained on the PACS (Poglitsch et al. 2010), and SPIRE (Griffin et al. 2010) instruments aboard the Herschel (Pilbratt et al. 2010) space telescope, as part of two surveys, the PACS Evolutionary Probe (PEP; Lutz et al. 2011), and the Herschel Multi-tiered Extragalactic Survey (HerMES; Oliver et al. 2012). We used this sample because of its wide range of observations spanning from UV to the FIR and because it is the most complete one in terms of wavelength coverage. In future works we intend to investigate the effect on LF when changing the underlying cosmology as a function of wavelength. The depth of the survey, or the relative depths at different wavelengths may also play a role.
Gruppioni et al. (2013) have used the PEP datasets to derive evolutionary properties of FIR sources in the standard cosmology. We aim at using the same catalogues and methodology used by Gruppioni et al. (2013) to assess them in alternative cosmologies. We computed the rest-frame monochromatic 100 μm and 160 μm, together with the total IR LFs in the void models described in Zumalacárregui et al. (2012). We then compared the redshift evolution of the luminosity functions in both standard and void models.
Although the present work uses both the standard and alternative cosmological models, it does not aim at model selection, that is, making a comparison of the models themselves. It is common to assume that works which deal with alternative cosmologies always have the goal of testing the models directly. However, this is not always the case.
This work is not about testing alternative cosmologies. Since the beginning of observational cosmology it has been clear that testing a cosmological model using galaxy surveys is extremely difficult because of the degeneracy between the intrinsic evolution of the sources and the relativistic effects caused by the underlying cosmology. Our understanding of galaxies is still far from allowing us to treat them as standard candles. Besides, the data used in this work come from a survey not nearly wide enough to compute meaningful angular correlation functions. The luminosity functions computed here depend, by definition, on the cosmological model assumed in its computation, and therefore cannot yield any independent conclusion about which model is the best fit. This is not the goal here.
Instead, by acknowledging that the computation of the luminosity functions depends on the cosmological model, we aim to assess how robust the luminosity function results are if the effective constraints on the cosmological model, like the Hubble diagram of a survey of standard candles like the Supernovae (SNe) Ia, or the power spectrum of the cosmic microwave background, are imposed. In other words, this work’s main interest is galaxy evolution models, and their possible dependency on the cosmological model but, not the cosmological models themselves.
Two recent papers have noteworthy similarities with the present work. Keenan et al. (2012) uses the near-infrared luminosity function of galaxies in the 0.1 < z < 0.3 redshift range to probe the central underdensity predicted by the void models. By assuming the standard model line element, the authors argue that the presence of a local underdensity would lead to an over-estimation of the normalization of their LFs. Marulli et al. (2012) discuss the effect of the cosmology dependence of the distance-redshift relation on the clustering of galaxies. Apart from having different goals, as stated above, the present work differs from the ones above in that it assumes the LTB void models in all the steps of the computation of its results.
The paper is divided as follows: in Sect. 2 we describe the dataset extracted from the PEP multi-wavelength catalogs, and discuss the method used for the estimation of the LFs in both cosmologies. In Sect. 3.1 we briefly describe the parameterization of the void models used, and obtain expressions for the luminosity and the comoving distances in those models. In Sect. 4 we present the LF computed in both cosmological models, as well as analytical fits to them. In Sect. 5 we perform quantitative comparisons of the LFs and their evolution in the different models. We present our conclusions in Sect. 6.
2. Luminosity functions
In this section we present and discuss the main results and equations in deriving the LFs that are susceptible to a change if the underlying cosmology is modified.
2.1. The PEP multi-wavelength samples
We started from the multi-wavelength catalogues described in Berta et al. (2011). The sources in these catalogues were blind selected in the following fields (effective areas): GOODS-N (300 arcmin2), GOODS-S (300 arcmin2), COSMOS (2.04 deg2), and ECDF-S (700 arcmin2), as part of the PEP survey in the 100 and 160 μm filters of Herschel/PACS. The number of sources detected and the 3-σ flux limits of this dataset are, in the 100 and 160 μm passbands, respectively: 291 sources down to 3.0 mJy, and 316 sources down to 5.7 mJy for GOODS-N; 717 down to 1.2 mJy, and 867 sources down to 2.4 mJy for GOODS-S; 5355 sources down to 5.0 mJy, and 5105 sources down to 10.2 mJy for COSMOS; and finally, 813 sources down to 4.5 mJy, and 688 sources down to 8.5 mJy for ECDF-S. For each of these fields, in each band individually, incompleteness corrections for the number counts were computed by the authors using simulations.
The semi-empirical spectral energy distribution (SED) models of Gruppioni et al. (2010) that expand on the models of Polletta et al. (2007) were used to fit the photometry
of the objects using the LePhare code (Arnouts et al.
1999; Ilbert et al. 2006). The code has an
output for each successfully fit source of a file with synthetic AB magnitudes
mν in the wavelength range of the combined
optical/NIR + FIR models. From this, we compute the spectral density of flux
f(ν) as 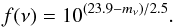 (1)Sources without a
redshift determination were removed from the catalogues, but no further redshift-based
selection rule have been applied. In the GOODS-N redshift completeness is 100% within the
ACS area (Berta et al. 2010), with 70% of the
redshifts there being spectroscopic. These figures are 100 (80)% for the GOODS-S, within
the MUSIC (Grazian et al. 2006; Santini et al. 2012) area; 93 (40)% for the COSMOS; and
88 (25)% for the ECDF-S fields. Non-detections in the 100 and 160 μm
filters were also removed. Our final combined samples have 5039 sources in the 100
μm band (183 in the GOODS-N, 468 in the GOODS-S, 3817 in the COSMOS,
and 578 in the ECDF-S fields); and 5074 sources in the 160 μm band (197
in the GOODS-N, 492 in the GOODS-S, 3849 in the COSMOS, and 547 in the ECDF-S fields).
Approximately 40% of these sources were best fit by typical spiral SED templates, 7% of
those were best fit by starburst templates, another 7% were found to be luminous IR
galaxies, and 46% were best fit by obscured, or low-luminosity AGN templates. For a more
complete description of the dataset used in this work, see Gruppioni et al. (2013).
(1)Sources without a
redshift determination were removed from the catalogues, but no further redshift-based
selection rule have been applied. In the GOODS-N redshift completeness is 100% within the
ACS area (Berta et al. 2010), with 70% of the
redshifts there being spectroscopic. These figures are 100 (80)% for the GOODS-S, within
the MUSIC (Grazian et al. 2006; Santini et al. 2012) area; 93 (40)% for the COSMOS; and
88 (25)% for the ECDF-S fields. Non-detections in the 100 and 160 μm
filters were also removed. Our final combined samples have 5039 sources in the 100
μm band (183 in the GOODS-N, 468 in the GOODS-S, 3817 in the COSMOS,
and 578 in the ECDF-S fields); and 5074 sources in the 160 μm band (197
in the GOODS-N, 492 in the GOODS-S, 3849 in the COSMOS, and 547 in the ECDF-S fields).
Approximately 40% of these sources were best fit by typical spiral SED templates, 7% of
those were best fit by starburst templates, another 7% were found to be luminous IR
galaxies, and 46% were best fit by obscured, or low-luminosity AGN templates. For a more
complete description of the dataset used in this work, see Gruppioni et al. (2013).
We computed the rest-frame total IR luminosity of each source using its best fit SED
f(ν) by means of
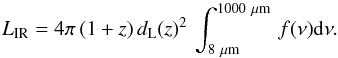 (2)While, the rest-frame
luminosity related to the observed flux fR at a given band
R can be obtained with
(2)While, the rest-frame
luminosity related to the observed flux fR at a given band
R can be obtained with 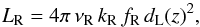 (3)where
dL is the luminosity distance in a particular cosmological
model, νR is the filter’s effective frequency at the
observer’s frame (corresponding to wavelengths approximately 100 and 160
μm for the PACS bands considered in the present work), and
kR is the k-correction between the observed frame flux
fR in the R band and its rest-frame flux,
at redshift z.
(3)where
dL is the luminosity distance in a particular cosmological
model, νR is the filter’s effective frequency at the
observer’s frame (corresponding to wavelengths approximately 100 and 160
μm for the PACS bands considered in the present work), and
kR is the k-correction between the observed frame flux
fR in the R band and its rest-frame flux,
at redshift z.
Because this paper deals with more than one underlying metric, it is important to note that, even though the relation between the cosmological redshift and the cosmological distances depend on the metric, thus affecting, for example, maximum redshift estimates, the redshift itself, and its effect on the SED of the sources, is directly measurable. Therefore, even though the rest-frame luminosities themselves depend on the cosmological model, the k-correction values depend only on the redshift measurements. It is when translating the measured redshift to an actual distance that a metric for the underlying spacetime is needed.
2.2. k-corrections
In the following discussion, all quantities are written in frequency units. Primes are used to mark quantities evaluated at the source’s rest frame. We follow closely the derivation in Hogg et al. (2002), but write the resulting k-correction in terms of fluxes instead of magnitudes.
The effect of the expansion of the metric over the frequencies of the light arriving from
each source is 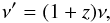 (4)where
ν′ are rest-frame frequencies measured by an observer in a
comoving frame with the source and ν are observed frequencies measured by
an observer that is receding in relation to the source at a redshift z.
(4)where
ν′ are rest-frame frequencies measured by an observer in a
comoving frame with the source and ν are observed frequencies measured by
an observer that is receding in relation to the source at a redshift z.
Fitting a SED template to the measured photometry for a given source yields a model for
its observed spectral density of flux f(ν) over a range
of observed-frame frequencies. With that in hand, one can then compute the spectral
density of flux fR as measured by a given filter
R(ν) in the observed-frame by means of the
dimensionless convolution (to ensure f(ν) and
fR are both written in the same units) 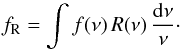 (5)To correctly
account for the expansion effects when computing the rest-frame spectral density of flux
(5)To correctly
account for the expansion effects when computing the rest-frame spectral density of flux
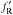 on the same
passband R, one must first redshift the filter function
R(ν) f(ν) in the
observed-frame back to the source’s rest-frame frequencies
f(ν′). Given the source’s measured redshift
z, this can be done by means of Eq. (4), which yields
R(ν′) = R [(1 + z)ν].
The rest frame R(ν′), can then be convolved
with the observed frame f(ν) to yield the spectral
density of flux measured by the passband R at the source’s rest frame as
on the same
passband R, one must first redshift the filter function
R(ν) f(ν) in the
observed-frame back to the source’s rest-frame frequencies
f(ν′). Given the source’s measured redshift
z, this can be done by means of Eq. (4), which yields
R(ν′) = R [(1 + z)ν].
The rest frame R(ν′), can then be convolved
with the observed frame f(ν) to yield the spectral
density of flux measured by the passband R at the source’s rest frame as
![\begin{equation} \label{zconv} f'_{\rm R} = \int f(\nu) \, R[(1+z)\nu] \, \frac{{\rm d}\nu}{\nu}\cdot \end{equation}](/articles/aa/full_html/2013/10/aa21396-13/aa21396-13-eq27.png) (6)Once
(6)Once
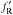 is obtained,
the k-correction expressed in terms of densities of fluxes is then
is obtained,
the k-correction expressed in terms of densities of fluxes is then 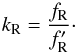 (7)We note that a
similar expression is used by Blanton & Roweis
(2007), based on the derivation for the k-correction expressed in terms of
magnitudes given in Hogg et al. (2002).
(7)We note that a
similar expression is used by Blanton & Roweis
(2007), based on the derivation for the k-correction expressed in terms of
magnitudes given in Hogg et al. (2002).
Next, we describe the use of the 1/Vmax estimator, (Schmidt 1968), in the computation of the LF of the samples.
2.3. 1/Vmax estimator
The 1/Vmax (Schmidt 1968; Johnston 2011) estimator for the LF has the advantage of not assuming a parametric form in its calculation. It also yields directly the comoving number density normalisation. Recent results from Smith (2012) show that large-scale density variations can introduce systematic errors in the subsequent fitting of the parameters. Since we are dealing with different cosmological models that predict different density parameter evolutions, it is important to check how dependent the method itself is on the cosmology. We report in Appendix A how we built mock catalogues to check the effects of density variation, similar to what is done in Takeuchi et al. (2000), and check that this methodology is adequate for the purpose of the paper.
To compute the LF values using this method, we started by dividing each sample in
redshift intervals Δz with centre values
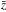 ,
and in luminosity bins ΔL with centre values
,
and in luminosity bins ΔL with centre values
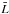 .
For each source in each (
.
For each source in each (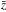 ,
,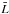 )
bin, we computed the maximum redshift at which it would still be included in the survey.
Given the corresponding flux limit for the field where the source was detected
(fR,lim; Berta et al. 2011), its measured flux at that filter R
(fR) and its redshift (z) the highest
redshift at which that source would still be included (ζ) can be obtained
by means of the following relation1,
)
bin, we computed the maximum redshift at which it would still be included in the survey.
Given the corresponding flux limit for the field where the source was detected
(fR,lim; Berta et al. 2011), its measured flux at that filter R
(fR) and its redshift (z) the highest
redshift at which that source would still be included (ζ) can be obtained
by means of the following relation1, ![\begin{equation} f_{\rm R, lim} = \left[ \frac{\dl(z)}{\dl(\zeta)} \right]^2 \, f_{\rm R}. \label{eq:kcorr} \end{equation}](/articles/aa/full_html/2013/10/aa21396-13/aa21396-13-eq37.png) (8)If the maximum
redshift for a given source is outside the redshift interval it originally belongs to, we
use the upper limit of this interval zh as the maximum
redshift instead. That is,
(8)If the maximum
redshift for a given source is outside the redshift interval it originally belongs to, we
use the upper limit of this interval zh as the maximum
redshift instead. That is, 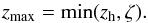 (9)The maximum comoving
volume Vmax enclosing each source is then
(9)The maximum comoving
volume Vmax enclosing each source is then  (10)where the sum is over
the k fields where the source would have been included;
Sk is the area of the field where the
source was detected, zl the lower limit of
the redshift interval at which the source is located, and
wk(z) the incompleteness
correction for effective area of the source, corresponding to its computed flux, as a
function of the redshift.
(10)where the sum is over
the k fields where the source would have been included;
Sk is the area of the field where the
source was detected, zl the lower limit of
the redshift interval at which the source is located, and
wk(z) the incompleteness
correction for effective area of the source, corresponding to its computed flux, as a
function of the redshift.
Although these corrections are computed from local simulations (z = 0), and, therefore, they do not assume any cosmological model, the computed flux of each source as a function of the redshift depends on its luminosity distance, which may change with the cosmological model assumed. In addition to this implicit effect, the radial comoving distance r and its redshift derivative dr/dz also depend explicitly on the cosmology.
For each luminosity bin centred around 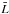 in each redshift interval centred around
in each redshift interval centred around 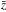 ,
we computed the 1/Vmax estimator for the
luminosity function in that bin
,
we computed the 1/Vmax estimator for the
luminosity function in that bin 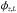 as
as 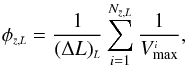 (11)where
(11)where
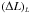 is the length of the luminosity bin centred on
is the length of the luminosity bin centred on 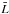 ,
and
,
and 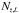 the number of sources inside that luminosity bin and redshift interval.
the number of sources inside that luminosity bin and redshift interval.
Assuming Poisson uncertainties, the error bars δφ can be estimated
simply by 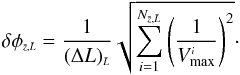 (12)Next, we briefly recall
the properties of the void models used in the computation of the LF, with a few key
results needed in the interpretation of the results.
(12)Next, we briefly recall
the properties of the void models used in the computation of the LF, with a few key
results needed in the interpretation of the results.
3. LTB/GBH dust models
Garcia-Bellido & Haugbølle (2008, henceforth GBH) have shown that an LTB dust model could be parametrized to fit successfully and simultaneously many independent observations without the inclusion of a cosmological constant. The extra dimming of distant SNe Ia, compared to their expected observed fluxes in a flat, spatially homogeneous Einstein-de Sitter (EdS) universe is then understood not as being caused by an acceleration of the expansion rate, but rather as an extra blueshift of the incoming light caused by a non-homogeneous matter distribution in the line of sight. This so-called void model is characterised by an effective under-dense region of Gpc scale around the Milky Way, as opposed to the average spatial homogeneity supposed to hold at that scale by the standard model. In this under-dense region, both the matter density profile ΩM and the transverse Hubble constant H0 are functions of the radial coordinate r. At high enough redshifts however, the model is made to converge to an EdS-like solution, making the non-homogeneity a localized property of the model and naturally reconciling it with the observed degree of isotropy in the cosmic microwave background radiation maps. The use of a pressure-less (dust) energy-momentum tensor, as opposed to the perfect fluid one allowed in the standard model, is required in order to obtain an exact solution for Einstein’s field equations assuming the LTB line element. At early ages (high redshifts), radiation dominated the Universe’s energy budget, and the pressure term was relevant, but as discussed before, at these scales, the LTB model is made to converge to the EdS solution by the GBH parameterization. At later ages (low redshifts), radiation pressure is negligible, and so the use of a dust energy-momentum tensor is well justified. Geometrically, the LTB dust model is an analytical solution for Einstein’s field equations, and arguably the simplest way to release the spatial homogeneity assumption present in the standard model of cosmology.
Spatial homogeneity is, nevertheless, a symmetry assumption that greatly simplifies the model. Removing it will unavoidably increase the degrees of freedom of the model. Because of this, even the most constrained parameterizations of the LTB models still show an increased number of free parameters compared to the standard model. Since the quality of the combined fits to the observations these alternative models can produce is similar to that produced by the standard model, any analysis that penalizes a greater degree of freedom of a model, like those used in Zumalacárregui et al. (2012) and de Putter et al. (2012), will disfavour such parameterization of the LTB model in comparison to ΛCDM.
3.1. Distances and comoving volume
Two quantities involved in the computation of the LF are affected by a change in the cosmology, the luminosity of the sources as computed in Eq. (3) through a change in the dL(z) relation, and their enclosing comoving volume as computed in Eq. (10) through a change in both r(z) and dr/dz relations. The aim is, therefore, to obtain these last three relations in the constrained GBH (hereafter CGBH, see below) model, that is the giant-void-GBH parameterization of the LTB dust model, with best-fit parameters from Zumalacárregui et al. (2012).
For comparison, we list the corresponding equations in the ΛCDM standard model. Throughout this work, where these comparisons are made we use the index Λ on the left-hand side to identify an equation computed in the standard model, and V to identify those obtained in the CGBH model.
 |
Fig. 1 Upper panel: present-time (t = t0) matter density parameters in the standard (ΛCDM, black line) and the void (GBH) cosmological models (red and cyan lines). Lower panel: redshift evolution of the dimensionless matter density parameters in the standard (ΛCDM) and the void (GBH) cosmological models. The dotted vertical lines delimit the lowest redshift interval considered in the computation of the LF at which the faint-end slopes are fit. |
We start by writing the Lemaître-Tolman-Bondi line element
dsV in geometrized units
(c = G = 1) as 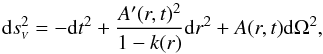 (13)where dΩ is the
spherical solid angle element, A(r,t) the angular
diameter distance, and k(r) an arbitrary function that
can be reduced to the Friedmann-Lemaître-Robertson-Walker line element
dsΛ,
(13)where dΩ is the
spherical solid angle element, A(r,t) the angular
diameter distance, and k(r) an arbitrary function that
can be reduced to the Friedmann-Lemaître-Robertson-Walker line element
dsΛ, 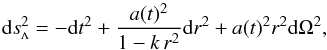 (14)by the suitable
choice of homogeneity conditions,
A(r,t) = a(t) r
and
k(r) = κ r2,
where κ is the spatial curvature parameter and
a(t) is the scale factor, both in the FLRW metric.
(14)by the suitable
choice of homogeneity conditions,
A(r,t) = a(t) r
and
k(r) = κ r2,
where κ is the spatial curvature parameter and
a(t) is the scale factor, both in the FLRW metric.
Because of the higher degree of freedom in the LTB metric Eq. (13), some extra constraining conditions must be imposed. One of these conditions is that the big-bang hypersurface be constant in time coordinate, or that the big-bang event occur simultaneously for all observers. This eliminates one degree of freedom of the model. The class of cosmological models with an LTB metric, a pressure-less (dust) content distributed according to an under-dense matter profile ΩM(r) around the Galaxy, and simultaneous big-bang time is known as CGBH, that is, a constrained case of the GBH void model.
The free parameters in the CGBH model are the expansion rate at the centre of the void Hin, and the parameters that characterize the matter density profile ΩM(r): the underdensity value at the centre of the void Ωin, the size of the underdense region R, and the width of the transition ΔR between the underdense interior and the assymptotic Einstein-de Sitter density Ωout at very large scales. Zumalacárregui et al. (2012) consider both the case of an assymptotically flat universe (Ωout = 1) and that of an open universe (Ωout ≤ 1; hereafter OCGBH), which they show to allow for a better fit to the cosmic microwave background radiation (CMB).
The matter density profile ΩM(r) is written in the GBH model
as a function of the fit parameters as ![\begin{equation} \label{GBHOM} \Omega_{\rm M}(r) = \Omega_{\rm out} + (\Omega_{\rm in}-\Omega_{\rm out}) \left( \frac{1-\tanh[(r-R)/2\Delta R]}{1+\tanh[R/2\Delta R]} \right), \end{equation}](/articles/aa/full_html/2013/10/aa21396-13/aa21396-13-eq79.png) (15)whereas the present-time
transverse Hubble parameter H0(r) is
(15)whereas the present-time
transverse Hubble parameter H0(r) is
![\begin{equation} \label{GBHH0} H_{\ssty 0}(r) = H_{\rm in} \left[ \frac{1}{\Omega_{\ssty k}(r)} - \frac{\Omega_{\rm M}(r)}{\Omega_{\ssty k}(r)^{3/2}}\sinh^{-1} \sqrt{\frac{\Omega_{\ssty k}(r)}{\Omega_{\rm M}(r)}} \right], \end{equation}](/articles/aa/full_html/2013/10/aa21396-13/aa21396-13-eq81.png) (16)with
Ωk(r) = 1−ΩM(r)
the curvature parameter inside the under-dense region needed to close the Universe. In the
standard model both the matter density parameter and the Hubble parameter do not depend on
the radial coordinate. In all the standard model computations done in this work we use
ΩM = 0.27, ΩΛ = 0.73, and H0 = 71 km
s-1 Mpc-1 as obtained in Komatsu
et al. (2011). Figure 1 shows the comparison
of the evolution of the matter density parameter in the standard and in the void
cosmologies.
(16)with
Ωk(r) = 1−ΩM(r)
the curvature parameter inside the under-dense region needed to close the Universe. In the
standard model both the matter density parameter and the Hubble parameter do not depend on
the radial coordinate. In all the standard model computations done in this work we use
ΩM = 0.27, ΩΛ = 0.73, and H0 = 71 km
s-1 Mpc-1 as obtained in Komatsu
et al. (2011). Figure 1 shows the comparison
of the evolution of the matter density parameter in the standard and in the void
cosmologies.
With these definitions, the angular diameter distance
A(r,t) can be computed in parametric form as
![\begin{equation} \label{GBHA} A(r,t) = \frac{\Omega_{\rm M}(r)}{2[1-\Omega_{\rm M}(r)]^{3/2}}[\cosh(\eta)-1] \, A_{\ssty 0}(r), \end{equation}](/articles/aa/full_html/2013/10/aa21396-13/aa21396-13-eq87.png) (17)where
A0(r) is the angular diameter distance at
t = t0, and the parameter
η advances the solution given r, t,
H0(r), and
ΩM(r) as follows:
(17)where
A0(r) is the angular diameter distance at
t = t0, and the parameter
η advances the solution given r, t,
H0(r), and
ΩM(r) as follows:
![\begin{equation} \sinh(\eta) - \eta = 2 \, \frac{[1 - \Omega_{\rm M}(r)]^{3/2}}{\Omega_{\rm M}(r)} \, H_{\ssty 0}(r) \, t. \end{equation}](/articles/aa/full_html/2013/10/aa21396-13/aa21396-13-eq92.png) (18)Once the angular diameter
distance
dA(z) = A [r(z),t(z)]
is computed, we can use the very general reciprocity theorem (Etherington 1933),
(18)Once the angular diameter
distance
dA(z) = A [r(z),t(z)]
is computed, we can use the very general reciprocity theorem (Etherington 1933), 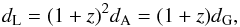 (19)to compute the luminosity
distance dL(z) in the void models considered
here. In the equation above, dG is the galaxy area distance
that reduces to the comoving distance in FLRW models. We still need to obtain the
r(z) and t(z)
relations in this cosmology. We start with the radial null-geodesic equation, which can be
written by making ds2 = dΩ2 = 0, yielding
(19)to compute the luminosity
distance dL(z) in the void models considered
here. In the equation above, dG is the galaxy area distance
that reduces to the comoving distance in FLRW models. We still need to obtain the
r(z) and t(z)
relations in this cosmology. We start with the radial null-geodesic equation, which can be
written by making ds2 = dΩ2 = 0, yielding
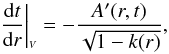 (20)where the minus sign is
set for incoming light. The corresponding standard model equation reads
(20)where the minus sign is
set for incoming light. The corresponding standard model equation reads
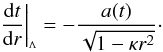 (21)In the LTB metric, the
time coordinate-redshift relation can be obtained to the first order in wavelength
starting from the redshift definition, (e.g. Enqvist
& Mattsson 2007)
(21)In the LTB metric, the
time coordinate-redshift relation can be obtained to the first order in wavelength
starting from the redshift definition, (e.g. Enqvist
& Mattsson 2007) 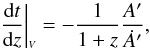 (22)whereas the
corresponding ΛCDM relation can be written as
(22)whereas the
corresponding ΛCDM relation can be written as
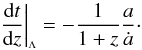 (23)The last two
equations allow us to write the radial coordinate r in terms of the
redshift z, by solving the expression
(23)The last two
equations allow us to write the radial coordinate r in terms of the
redshift z, by solving the expression 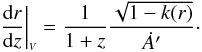 (24)where
k(r) can be written in terms of the formerly defined
quantities as
(24)where
k(r) can be written in terms of the formerly defined
quantities as 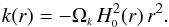 (25)Similarly, we can write,
again for comparison,
(25)Similarly, we can write,
again for comparison, 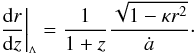 (26)It is worth noting that
the comoving distance r is not, in general, equal to the galaxy area
distance dG related to the luminosity distance through the
reciprocity theorem in Eq. (19).
(26)It is worth noting that
the comoving distance r is not, in general, equal to the galaxy area
distance dG related to the luminosity distance through the
reciprocity theorem in Eq. (19).
The usual comoving-to-luminosity distance relation,
dG = (1 + z) dA = r,
is only valid in the FLRW metric, for which the following relations holds,
 where
a(t) is the usual scale factor, and
a0 its value at present time (t = 0). The
last equation is valid only if we set a0 = 1. As a
consequence, an LTB model with its luminosity distance-redshift relation constrained to
fit the Hubble diagram for SNe Ia could still yield comoving distances, and therefore
volumes, significantly different from those obtained in the standard model.
where
a(t) is the usual scale factor, and
a0 its value at present time (t = 0). The
last equation is valid only if we set a0 = 1. As a
consequence, an LTB model with its luminosity distance-redshift relation constrained to
fit the Hubble diagram for SNe Ia could still yield comoving distances, and therefore
volumes, significantly different from those obtained in the standard model.
The additional constraint imposed by the measurements of the baryonic acoustic oscillations (BAO) (e.g. Percival et al. 2010; Reid et al. 2012) appears to pin down the comoving distance quite effectively up to intermediate redshifts, and it turns out that the difference in these distances computed in the ΛCDM and the GBH models is never larger than 10% at z = 1. However, r computed in the CGBH model at z = 5 is approximately 12% smaller, and ≈17% in the open CGBH model.
Rest-frame 100 μm 1/Vmax luminosity function assuming the ΛCDM cosmological model.
The non-linear nature of the equations relating distances to volumes and luminosities, in particular for high-redshift sources, must also be considered. At redshift z = 0.4, for example, the luminosity distances computed in the void models CGBH and OCGBH respectively, are 4.90% and 0.92% shorter then the standard model distances, whereas the comoving distances in the void models are 4.88% and 0.96% shorter when compared to the standard model value. Such differences correspond to an extra dimming in luminosities equal to 10.04% in the CGBH model and 1.85% in the OCGBH model. The corresponding reduction in volumes is 15.35% and 2.84% for the CGBH and OCGBH models.
 |
Fig. 2 Upper panel: luminosity (solid lines) and comoving distances (dotted lines) versus the redshift in the standard (ΛCDM) and the void (GBH) cosmological models. Up to redshift z ≈ 1 distances in the constrained, flat void model (CGBH) follow very closely their standard model counterparts, but even in the case of the best-fit parameters in Zumalacárregui et al. (2012) yield increasingly different distances with the redshift. Lower panel: comoving volume elements in the standard (ΛCDM) and the void (GBH) cosmological models. The quantities in the void models adopted here evolve with the redshift in a similar way to the standard model up to redshift approximately 0.6, then their values become consistently lower than in the ΛCDM model. |
When compared to the standard model, these non-linearities can make small discrepancies in luminosity and comoving distances caused by the central underdensity in GBH models and can result in non-negligible differences in the shape of the LF.
This can be understood by looking at Fig. 2, where the luminosity distance and the comoving distance are plotted against the redshift.
For any given redshift z′, consider the differences ΔdL(z′) and Δr(z′) between the distances computed in the standard model and those in the void models. Both differences depend on the redshift and do not, in general, cancel out or even yield a constant volume-to-luminosity ratio as a function of the redshift. As a result, the number of sources in each luminosity bin might change because of differences in the luminosities.
Additionally, the weight 1/Vmax that each source adds to the LF in that bin will not be the same, leading to a LF value in that luminosity bin in the void model that is different from the one in the standard model, even if the sources inside the bin are the same. Figure 2 shows the comoving volume element in the different cosmologies adopted here.
Such differences in the estimated value for the LF in each luminosity bin will not, in general, be the same. As a consequence, not only the normalization but also the shape of the LF might change from one cosmology to another.
4. Results
We computed the rest-frame monochromatic and total IR luminosity LF for sources in the combined fields, blind selected in the 100 μm and 160 μm bands, using the non-parametric 1/Vmax method, both in the standard model and the GBH void models. The LF values are listed in Tables 1−12, up to redshifts z ≈ 3 for the monochromatic LFs and up to z ≈ 4 for the total IR ones.
Rest-frame 100 μm 1/Vmax luminosity function assuming the CGBH cosmological model.
Rest-frame 100 μm 1/Vmax luminosity function assuming the OCGBH cosmological model.
Rest-frame 160 μm 1/Vmax luminosity function assuming the ΛCDM cosmological model.
Rest-frame 160 μm 1/Vmax luminosity function assuming the CGBH cosmological model.
Rest-frame 160 μm 1/Vmax luminosity function assuming the OCGBH cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 100 μm band, assuming the ΛCDM cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 160 μm band, assuming the ΛCDM cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 100 μm band, assuming the CGBH cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 160 μm band, assuming the CGBH cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 100 μm band, assuming the OCGBH cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 160 μm band, assuming the OCGBH cosmological model.
We use the same binning in luminosity and redshift as in Gruppioni et al. (2013). The average values for the redshift intervals are 0.2,
0.6, 1.0, 1.5, 2.1, and 3.0, for the monochromatic LFs, and 0.2, 0.4, 0.5, 0.7, 0.9, 1.1,
1.5, 1.9, 2.2, 2.8, and 3.6 for the total IR LFs. The effective wavelengths will be 60 and
90 μm in the rest-frame LF. Because of the lack of enough
1/Vmax LF points to fit a Schechter function in the higher
redshift bins, our analyses of the monochromatic luminosity functions are limited to
intervals 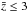 .
As a consistency check we compared our results for the standard model with those of
Gruppioni et al. and the agreement is excellent.
.
As a consistency check we compared our results for the standard model with those of
Gruppioni et al. and the agreement is excellent.
The monochromatic and the total luminosity LFs are shown in Figs. 3−6 for the three cosmologies considered in this paper. When comparing the values in each luminosity bin it is clear that in void cosmologies the density is lower at the lowest luminosities. While at redshift larger than 0.8 the incompleteness at low luminosities does not allow any firm conclusion to be drawn, in the two lowest redshift bins the void models show LF values up to an order of magnitude lower than their ΛCDM counterpart at L ≤ 1010 L⊙.
The resulting differences in the LF computed in the different models show up at the faint
luminosity end of the luminosity functions. We use the Schechter analytical profile (Schechter 1976), 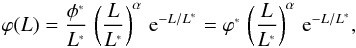 (29)and fit it to the
1/Vmax points over the
(
(29)and fit it to the
1/Vmax points over the
(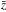 ,
,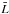 )
bins, where φ∗ is the comoving number density normalisation,
L∗ the characteristic luminosity and α the
faint-end slope, using the IDL routine MPFITFUN (Markwardt
2009) based on the Levenberg-Marquardt algorithm (Moré 1978). For each best-fit parameter, its formal 1-σ
uncertainty is obtained by taking the square root of its corresponding element in the
diagonal of the 3 × 3 covariance matrix of the fitting procedure (see also Richter 1995).
)
bins, where φ∗ is the comoving number density normalisation,
L∗ the characteristic luminosity and α the
faint-end slope, using the IDL routine MPFITFUN (Markwardt
2009) based on the Levenberg-Marquardt algorithm (Moré 1978). For each best-fit parameter, its formal 1-σ
uncertainty is obtained by taking the square root of its corresponding element in the
diagonal of the 3 × 3 covariance matrix of the fitting procedure (see also Richter 1995).
Since we are primarily interested in checking possible changes in the LF caused by the underlying cosmologies, we chose to use the classical Schechter function instead of the double exponential function (Saunders et al. 1990). The latter fits the FIR LF bright-end better, but the Schechter function has fewer free parameters that allows it to fit higher redshift intervals where the number of data points is small.
First we check for any variation of the α parameter with redshift, and
find that it is consistent with no evolution. We test the incompleteness using the
Ve/Va tests
(Avni & Bahcall 1980). A given
(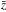 ,
,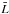 )
bin is considered complete by this test if its
Ve/Va value is
1/2. We find that the 1/Vmax LF points do not suffer from
significant incompleteness at
)
bin is considered complete by this test if its
Ve/Va value is
1/2. We find that the 1/Vmax LF points do not suffer from
significant incompleteness at 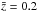 ,
where the Ve/Va
values in the lowest luminosity bins of the monochromatic luminosity functions are 0.6 ± 0.1
and 0.5 ± 0.1 for the rest-frame 100 and 160 μm, respectively. These values
become 0.15 ± 0.09 and 0.22 ± 0.03 at
,
where the Ve/Va
values in the lowest luminosity bins of the monochromatic luminosity functions are 0.6 ± 0.1
and 0.5 ± 0.1 for the rest-frame 100 and 160 μm, respectively. These values
become 0.15 ± 0.09 and 0.22 ± 0.03 at 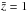 ,
and 0.12 ± 0.05 and 0.11 ± 0.04 at
,
and 0.12 ± 0.05 and 0.11 ± 0.04 at 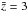 .
.
This is because at higher redshifts the flux limit of the observations corresponds to increasingly different luminosity limits, depending on the SED of the sources, leading to an incompleteness in the lower luminosity bins that is dependent on the galaxy type (Ilbert et al. 2004). Because of this we chose to fix the α parameter to its value in the lower redshift interval in the fits presented in Tables 13−16.
5. Discussion
In Figs. 3−6 we plot the 1/Vmax LF estimations in the three different cosmologies, together with the best-fit Schechter profiles for each of them. As can be seen in the four figures, the faint-end number densities in the void models are lower then the standard model ones.
If there was a direct correlation between the matter density parameter in the cosmology, and its estimated number density of sources selected in the FIR, then at the lowest redshift bin we should see higher number densities in the void models, since the ΩM(z) in those models are bigger in that redshift range than the standard model value (more on that in Appendix A, Fig. 1).
The difference in the number densities at the lower redshift interval for the different cosmologies does not follow the same relation as the matter density parameters ΩM(z). In addition, it shows a dependence on the luminosity, which is more pronounced at the fainter end in both the monochromatic and the total IR LFs.
This dependence produces significant differences in the faint-end slopes of the computed luminosity functions. This can only be attributed to the different geometrical parts of the cosmological models studied here, since the matter content, as discussed above, would only shift the normalization of the LF independently of the luminosity of the sources.
In Table 17 we present the best fit values of
α for each dataset/model combination. Simple error propagation allow us
to write the uncertainty of the difference Δα between the faint-end slopes
in the standard model (αΛ) and the void models
(αV) as
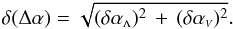 (30)The significance level of
this difference can then be obtained by computing
Δα/δ(Δα). For the
monochromatic 100 μm luminosity functions, the difference between the
α computed assuming the standard model and the α
computed in the GBH models studied here is 6.1-σ, as compared to its
propagated uncertainty. For the monochromatic 160 μm luminosity functions,
this value is 3.2-σ. For the total-IR 100-μ selected
luminosity functions, these values are 2.9-σ for the difference between
ΛCDM and CGBH models, and 3.1-σ, for the ΛCDM-OCGBH difference. Finally,
for the same differences in the total-IR 160 μm selected dataset, the
significances are 3.1-σ and 3.4-σ, respectively.
(30)The significance level of
this difference can then be obtained by computing
Δα/δ(Δα). For the
monochromatic 100 μm luminosity functions, the difference between the
α computed assuming the standard model and the α
computed in the GBH models studied here is 6.1-σ, as compared to its
propagated uncertainty. For the monochromatic 160 μm luminosity functions,
this value is 3.2-σ. For the total-IR 100-μ selected
luminosity functions, these values are 2.9-σ for the difference between
ΛCDM and CGBH models, and 3.1-σ, for the ΛCDM-OCGBH difference. Finally,
for the same differences in the total-IR 160 μm selected dataset, the
significances are 3.1-σ and 3.4-σ, respectively.
Could this difference be caused by a limitation of the 1/Vmax method used here? As we show in Appendix A, the matter density parameters in both the ΛCDM and GBH models do not affect the performance of this LF estimator significantly. When the same input LF and matter density are assumed, the 1/Vmax method obtains values within their error bars for all cosmological models considered. This indicates that the change in the slopes is caused by how the luminosities are computed from the redshifts in the different metrics.
To check this assertion, we investigate the effects of both luminosity and comoving volume separately on the shape of the LF. Starting from the 1/Vmax results for the LF in the interval 0 < z < 0.4, assuming the standard cosmological model, we compute alternative LFs using the same methodology, but assuming either the luminosity distance of one of the void models and keeping the comoving distance of the standard model, or the luminosity distance of the standard model and the comoving distance of one of the void models. This allows us to assess how each distance definition affect the LF individually. The results are plotted in Fig. 8 for the rest-frame 100 μm monochromatic luminosity dataset.
From these plots it is clear that the luminosity is the main cause of change in the shape of the LF. What remains to be investigated is whether the number density in a given luminosity bin is lower in the void models because of a re-arranging of the number counts in the luminosity bins, or because of a possible change in the maximum volume estimate of the sources in each bin. From this inspection, it turns out that the number counts in all three models are all within their Poisson errors, and therefore the number densities in the void models are lower because the maximum volumes in them are larger.
Looking at Eq. (10), we identify two parameters that can introduce a dependency of the maximum volume of a source on its luminosity, the incompleteness corrections wk(z) and the upper limit of the integral zmax.
The incompleteness correction wk(z) for each source depends on the observed flux that the source would have at that redshift, which is affected by the luminosity distance-redshift relation assumed.
More importantly however, at the higher luminosity bins, the zmax of most of the sources there assumes the zh value for that redshift interval, which does not depend on the luminosity of the source. This renders the Vmax of the high luminosity sources approximately the same, apart from small changes caused by the incompleteness corrections wk, as discussed above. At the lower luminosity bins, on the other hand, it happens more often that the zmax of a source assumes its ζ value, which in this case depends on its luminosity, as is clear from Eq. (8).
 |
Fig. 3 Luminosity functions derived in the standard (ΛCDM) (black dots) and the void (GBH) cosmological models (red and cyan dots). We also show the best-fit Schechter profiles to the rest-frame 100 μm 1/Vmax corresponding to effective wavelengths of 60 μm. |
 |
Fig. 4 As Fig. 3 for the rest-frame 160 μm 1/Vmax luminosity functions. Here the effective wavelength is 90 μm. |
 |
Fig. 5 Schechter profile fits to the rest-frame total IR luminosity functions computed from the PACS 100 μm 1/Vmax band, assuming the standard (ΛCDM) and the void (GBH) cosmological models. |
 |
Fig. 6 Schechter profile fits to the rest-frame total IR luminosity functions computed from the PACS 160 μm 1/Vmax band, assuming the standard (ΛCDM) and the void (GBH) cosmological models. |
Best-fitting Schechter parameters for the rest-frame 100 μm 1/Vmax luminosity functions.
Best-fitting Schechter parameters for the rest-frame 160 μm 1/Vmax luminosity functions.
Best-fitting Schechter parameters for the rest-frame total IR 1/Vmax luminosity functions in the PACS 100 μm band.
Best-fitting Schechter parameters for the rest-frame total IR 1/Vmax luminosity functions in the PACS 160 μm band.
In order for that equation to hold, given that fR and fR,lim are fixed, the dL(z)/dL(ζ) ratio must be the same for all cosmologies. Since the redshift z of each source is also fixed, then it follows that the ζ value that makes the dL(z)/dL(ζ) ratio hold in the void models must be higher then in the standard model (see Fig. 2). This, in turn, accounts for the larger maximum volumes and lower number densities at the low luminosity bins in the void models.
From the discussion above we conclude that a change in the luminosity distance – redshift relation changes the zmax of the low luminosity sources, which in turn changes the maximum volumes, and finally, the fitted faint-end slope. However, from Fig. 2, it is not obvious that such small differences in the dL(z) relation for the different cosmological models could cause such a significant change in the faint-end slopes, especially at low redshifts. It is useful to remember here that the LF is a non-linear combination of quantities that depend, from a geometrical point of view, on the luminosity distance (through the luminosities of the sources) and on the comoving distances (through their enclosing volumes). Even if the observational constraints on the luminosity-redshift relation, and the additional ones stemming from BAO results, yield both dL(z) and r(z) that are quite robust under changes of the underlying cosmological models, such small differences in the distances could pile up non-linearly and cause the observed discrepancies in the faint-end slope.
This appears to be the case here, at least in the low redshift interval where we can fit the faint-end slopes with confidence. Rather then following the trend of the matter density parameter, the number densities at those redshifts seem to be predominantly determined by their enclosing volumes (even if at low redshift the differences in the distance-redshift relations in the different cosmologies is quite small).
 |
Fig. 7 Upper panel: redshift evolution of the characteristic luminosity L∗ on the four datasets of the present work. Lower panel: redshift evolution of the characteristic luminosity φ∗ on the same datasets. |
 |
Fig. 8 Upper panel: effect of the luminosity distance − redshift relation on the shape of the LF. The black points were computed using the 1/Vmax method, assuming both dL(z) and r(z) relations stemming from the standard model, while the blue and red points kept the r(z) relation for the ΛCDM model, changing only the dL(z) relation for that in the listed void model. The effect of the dL(z) relation on the shape of the LF is clear, especially at the lower luminosity bins. Lower panel: effect of the comoving distance − redshift relation on the shape of the LF. The black points were computed using the 1/Vmax method, assuming both dL(z) and r(z) relations stemming from the standard model, while the blue and red points kept the dL(z) relation for the ΛCDM model, changing only the r(z) relation for that in the listed void model. The effect of the r(z) relation on the shape of the LF is found to be much less relevant than that of the dL(z) relation. |
Looking at how the distances in Fig. 2 have increasingly different values at higher redshifts, it would be interesting to check if the faint-end slopes in the different cosmologies at some point start following that trend. Unfortunately, at higher redshifts the incompleteness caused by different luminosity limits for different populations does not allow us to draw any meaningful conclusion about the faint-end slope of the derived LFs. As it is, all that can be concluded is that the standard model LF would be over-estimating the local density of lower luminosity galaxies if the Universe’s expansion rate and history followed that of the LTB/GBH models.
We proceed to investigate the robustness with respect to the underlying cosmology of the
redshift evolution of the other two Schechter parameters, the characteristic luminosity
L∗ and number density φ∗. Figure
7 presents the redshift evolution of these parameters
that we model by means of the simple relations  We
use a least-squares technique to fit such evolution functions to their corresponding
Schechter parameter results (Richter 1995). Table
18 lists the best-fit values for the evolution
parameters A and B in the different datasets/cosmologies.
We
use a least-squares technique to fit such evolution functions to their corresponding
Schechter parameter results (Richter 1995). Table
18 lists the best-fit values for the evolution
parameters A and B in the different datasets/cosmologies.
Faint-end slope values.
The listed uncertainties for the evolution parameters are the formal 1-σ values obtained from the square root of the corresponding diagonal element of the covariance matrix of the fit. We find no evidence of a significantly different evolution of either L∗ or φ∗ in the void models considered. The monochromatic luminosities, especially the number density of sources in the rest-frame 160 μm, show some mild evidence of being affected by the geometrical effect discussed above, but the evolution parameters in the total IR are remarkably similar. We also note that assuming an open or flat CGBH model makes no significant difference to such parameters. It seems that they are more strongly affected by the intrinsic evolution of the sources, and the secular processes and merging history of galaxy formation than by the expansion rate of the Universe.
Physically speaking, in terms of tracing the redshift evolution of different galaxy populations using the FIR data in the present work, the marginally significant difference in the faint-end slopes, together with the evolution parameters for the characteristic number densities and luminosities, can be understood as follows: assertions about the number density of FIR low-luminosity galaxies, broadly related to populations that are poor in dust content, are still systematically affected by model-dependent corrections due to survey flux limits in the construction of the LF. That is, there might be less of these galaxies in the local Universe (z ≈ 0.3) than what we expect based on the underlying standard model. On the other hand, evolution of the FIR high-luminosity end, broadly related to populations with high dust content, is well constrained by the flux limits of the PEP survey where the underlying cosmological model is concerned.
Comoving number density and characteristic luminosity evolution parameters.
6. Conclusions
In this work we have computed the FIR luminosity functions for sources in the PEP survey, observed at the Herschel/PACS 100 and 160 μm bands. We computed both monochromatic and total IR luminosities assuming both the ΛCDM standard and GBH void cosmological models, with the aim of assessing how robust the luminosity functions are under a change of observationally constrained cosmologies.
We conclude that the current observational constraints imposed on any cosmological model by the combined set of SNe + CMB + BAO results are enough to yield robust estimates for the evolution of FIR characteristic luminosities L∗ and number densities, φ∗.
We find, however, that estimations of the faint-end slope of the LF are still significantly dependent on the underlying cosmological model assumed, despite the above-mentioned observational constraints. In other words, if there is indeed an underdense region around the Milky Way, as predicted by the GBH models, causing the effective metric of the Universe at Gpc scale to be better fit by an LTB line element, then assuming the spatial homogeneous ΛCDM model in the computation of the LF would yield an over-estimated number density of faint galaxies, at least at lower redshifts (up to z ≈ 0.4).
To answer the original questions posed: the characteristic number density and the characteristic luminosity parameters of the FIR luminosity functions derived here are made robust by the present constraints on the cosmological model. The faint-end slope, however, still shows significant differences among the cosmologies studied here.
We show that these differences are caused mainly by slight discrepancies in the luminosity distance − redshift relation, still allowed by the observations. The 1/Vmax methodology studied here is a necessary way to compute the LF using a flux-limited survey like PEP. This methodology, as we show, is not biased by the kind of under-dense regions proposed by the alternative cosmologies studied here. On the other hand, the necessary volume corrections intrinsic to the method are still dependent enough on the underlying assumptions about the geometry and expansion rate of the Universe at Gpc scale to yield significant (≈3-σ) discrepancies in their results. In other words, the systematic dispersion in the values of the low luminosity LF points, caused by the (arguably still) remaining degree of freedom in the choice of the underlying cosmological model, combined with the current flux limits, is still significantly larger than the statistic uncertainty assumed in the computation of the error bars of those points, causing the differences in the LF values to be larger than the combination of their computed uncertainties.
Surveys with lower flux limits would allow lower FIR-luminosity sources to be fully accounted for, reducing the marginally significant dependency of the FIR LF on the cosmological model still detected here.
Since we are dealing with two observed-frame quantities, there is no need to include any k-corrections in the Eq. (8).
Acknowledgments
A.I. is grateful to Takamitsu Miyagi and Karina Caputi, for the helpful tips on the building of luminosity functions, and to Alan Heavens for the insightful discussions on Bayesian and Monte Carlo methods. Some Markov chain routines used at intermediate stages of this work were derived as a spin-off of a workshop at the Cape Town International Cosmology School, organized by the African Institute for Mathematical Sciences, between 15 and 28 January 2012. This work is jointly supported by Brazil’s CAPES and ESO studentships.
References
- Albani, V. V. L., Iribarrem, A. S., Ribeiro, M. B., & Stoeger, W. R. 2007, ApJ, 657, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Alfedeel, A. H. A., & Hellaby, C. 2010, General Relativity and Gravitation, 42, 1935 [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Avni, Y., & Bahcall, J. N. 1980, ApJ, 235, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Babbedge, T. S. R., Rowan-Robinson, M., Vaccari, M., et al. 2006, MNRAS, 370, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, A. J., Bower, R. G., Frenk, C. S., et al. 2003, ApJ, 599, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, S., Magnelli, B., Lutz, D., et al. 2010, A&A, 518, L30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berta, S., Magnelli, B., Nordon, R., et al. 2011, A&A, 532, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanton, M. R., & Roweis, S. 2007, AJ, 133, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Bolejko, K., Célérier, M.-N., & Krasiński, A. 2011a, Class. Quant. Grav., 28, 164002 [NASA ADS] [CrossRef] [Google Scholar]
- Bolejko, K., Hellaby, C., & Alfedeel, A. H. A. 2011b, J. Cosmol. Astropart. Phys., 9, 11 [Google Scholar]
- Boylan-Kolchin, M., Springel, V., White, S. D. M., Jenkins, A., & Lemson, G. 2009, MNRAS, 398, 1150 [NASA ADS] [CrossRef] [Google Scholar]
- Bull, P., & Clifton, T. 2012, Phys. Rev. D, 85, 103512 [NASA ADS] [CrossRef] [Google Scholar]
- Bull, P., Clifton, T., & Ferreira, P. G. 2012, Phys. Rev. D, 85, 024002 [NASA ADS] [CrossRef] [Google Scholar]
- Busti, V. C., & Lima, J. A. S. 2012, MNRAS, L504 [Google Scholar]
- Caputi, K. I., Lagache, G., Yan, L., et al. 2007, ApJ, 660, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Célérier, M.-N. 2007, New Adv. Phys., 1, 29 [Google Scholar]
- Clarkson, C., & Umeh, O. 2011, Class. Quant. Grav., 28, 164010 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, C., Ellis, G., Larena, J., & Umeh, O. 2011, Rept. Prog. Phys., 74, 112901 [CrossRef] [Google Scholar]
- Clarkson, C., Ellis, G. F. R., Faltenbacher, A., et al. 2012, MNRAS, 426, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Clifton, T., Rosquist, K., & Tavakol, R. 2012, Phys. Rev. D, 86, 043506 [NASA ADS] [CrossRef] [Google Scholar]
- Cool, R. J., Eisenstein, D. J., Kochanek, C. S., et al. 2012, ApJ, 748, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Datta, K. K., Mellema, G., Mao, Y., et al. 2012, MNRAS, 3286 [Google Scholar]
- de Putter, R., Verde, L., & Jimenez, R. 2012 [arXiv:1208.4534] [Google Scholar]
- Ellis, G. F. R. 2011, Class. Quant. Grav., 28, 164001 [NASA ADS] [CrossRef] [Google Scholar]
- Enqvist, K., & Mattsson, T. 2007, J. Cosmol. Astropart. Phys., 2, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Etherington, I. M. H. 1933, Philosophical Magazine, 15, 761; reprinted in Gen. Rel. Grav., 39, 1055, 2007 [Google Scholar]
- February, S., Larena, J., Smith, M., & Clarkson, C. 2010, MNRAS, 405, 2231 [NASA ADS] [Google Scholar]
- Garcia-Bellido, J., & Haugbølle, T. 2008, J. Cosmol. Astropart. Phys., 4, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Grazian, A., Fontana, A., de Santis, C., et al. 2006, A&A, 449, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Gruppioni, C., Pozzi, F., Andreani, P., et al. 2010, A&A, 518, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gruppioni, C., Pozzi, F., Rodighiero, G., et al. 2013, MNRAS [Google Scholar]
- Heinis, S., Buat, V., Béthermin, M., et al. 2013, MNRAS, 429, 1113 [Google Scholar]
- Helgason, K., Ricotti, M., & Kashlinsky, A. 2012, ApJ, 752, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Hellaby, C. 2012, J. Cosmol. Astropart. Phys., 1, 43 [Google Scholar]
- Hellaby, C., & Alfedeel, A. H. A. 2009, Phys. Rev. D, 79, 043501 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Baldry, I. K., Blanton, M. R., & Eisenstein, D. J. 2002 [arXiv:astro-ph/0210394] [Google Scholar]
- Hoyle, B., Tojeiro, R., Jimenez, R., et al. 2013, ApJ, 762, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, N. P., Maartens, R., & Matravers, D. R. 2012, General Relativity and Gravitation, 44, 3197 [Google Scholar]
- Ilbert, O., Tresse, L., Arnouts, S., et al. 2004, MNRAS, 351, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iribarrem, A. S., Lopes, A. R., Ribeiro, M. B., & Stoeger, W. R. 2012, A&A, 539, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnston, R. 2011, A&ARv, 19, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, R. C., Barger, A. J., Cowie, L. L., et al. 2012, ApJ, 754, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, D., Poglitsch, A., Altieri, B., et al. 2011, A&A, 532, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Elbaz, D., Chary, R. R., et al. 2011, A&A, 528, A35 [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Marulli, F., Bianchi, D., Branchini, E., et al. 2012, MNRAS, 426, 2566 [NASA ADS] [CrossRef] [Google Scholar]
- Meures, N., & Bruni, M. 2012, MNRAS, 419, 1937 [Google Scholar]
- Moré, S. 1978, in Lect. Notes Math. (Berlin: Springer Verlag), ed. G. A. Watson, 630, 105 [Google Scholar]
- Mustapha, N., Hellaby, C., & Ellis, G. F. R. 1997, MNRAS, 292, 817 [NASA ADS] [Google Scholar]
- Neistein, E., & Weinmann, S. M. 2010, MNRAS, 405, 2717 [NASA ADS] [Google Scholar]
- Nishikawa, R., Yoo, C.-M., & Nakao, K.-I. 2012, Phys. Rev. D, 85, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, S. J., Bock, J., Altieri, B., et al. 2012, MNRAS, 424, 1614 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patel, H., Clements, D. L., Vaccari, M., et al. 2013, MNRAS, 428, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos, B. H. F., Pellegrini, P. S., Benoist, C., et al. 2011, AJ, 142, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Rangel Lemos, L. J., & Ribeiro, M. B. 2008, A&A, 488, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Regis, M., & Clarkson, C. 2012, General Relativity and Gravitation, 44, 567 [Google Scholar]
- Reid, B. A., Samushia, L., White, M., et al. 2012, MNRAS, 426, 2719 [NASA ADS] [CrossRef] [Google Scholar]
- Ribeiro, M. B., & Stoeger, W. R. 2003, ApJ, 592, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Richter, P. H. 1995, Telecommunications and Data Acquisition Progress Report, 122, 107 [NASA ADS] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Vaccari, M., Franceschini, A., et al. 2010, A&A, 515, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santini, P., Rosario, D. J., Shao, L., et al. 2012, A&A, 540, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saunders, W., Rowan-Robinson, M., Lawrence, A., et al. 1990, MNRAS, 242, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, C., Rawlings, S., Ivison, R., et al. 2012, MNRAS, 421, 3060 [NASA ADS] [CrossRef] [Google Scholar]
- Skibba, R. A., & Sheth, R. K. 2009, MNRAS, 392, 1080 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. E. 2012, MNRAS, 426, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stefanon, M., & Marchesini, D. 2013, MNRAS, 429, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T. T., Yoshikawa, K., & Ishii, T. T. 2000, ApJS, 129, 1 [Google Scholar]
- Tsujikawa, S. 2010, in Lect. Notes Phys. 800 (Berlin: Springer Verlag), ed. G. Wolschin, 99 [Google Scholar]
- Valkenburg, W., Marra, V., & Clarkson, C. 2012 [arXiv:1209.4078] [Google Scholar]
- van der Burg, R. F. J., Hildebrandt, H., & Erben, T. 2010, A&A, 523, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, H., & Zhang, T.-J. 2012, ApJ, 748, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegand, A., & Schwarz, D. J. 2012, A&A, 538, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, X., Mo, H. J., & van den Bosch, F. C. 2003, MNRAS, 339, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2011, ApJ, 736, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Zumalacárregui, M., García-Bellido, J., & Ruiz-Lapuente, P. 2012, J. Cosmol. Astropart. Phys., 10, 9 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Mock catalogues
In this appendix we test whether the 1/Vmax LF estimator is reliable for studying Gpc scale voids like the ones proposed by the GBH models, embedded in an LTB dust model. We follow the general approach by Takeuchi et al. (2000) who made use of mock catalogues that were built assuming a non-central and small void with a radius of 1.6 Mpc at a distance of 0.8 Mpc, and at a limiting redshift of z = 0.1. Our mock catalogues are built using the matter density distributions in the GBH models, as shown in Fig. 1. In addition, the redshift range of our interest is four times larger since we want to test the validity of the estimator in the interval Δz = [0.01,0.4] where we fit the faint-end slope of the luminosity functions.
Mock catalogues were built by reproducing the detection limits and SED distributions in the GOODS-S and COSMOS fields in the PACS 100 and 160 μm filters, as listed in Gruppioni et al. (2013). We chose these two fields to better represent the whole of the data used in this work: GOODS-S is the field with the lowest flux limits in the PEP survey, while COSMOS is the one with the widest effective area.
Naively, one might decide to use the matter density distributions in Fig. 1 to randomly assign comoving distances to the sources in the mock catalogue. However, given the large redshift interval we aim to cover in our simulations, the redshift evolution of the density profiles must be fully considered.
For each of the present-time, rest-frame (z = 0) matter density profiles
ΩM(r), defined in a constant time coordinate hypersurface,
and fit by both the standard model and the void models (see Fig. 1), we compute the corresponding redshift evolution,
ΩM(z), defined in the past lightcone of the same
cosmological model. In the FLRW spacetime, the dimensionless density parameters
ΩM and ΩM(z) are related as follows:
![\appendix \setcounter{section}{1} \begin{equation} \label{FLRWomz} \Omega_{\rm M}(z) = \Omega_{\rm M} \left[ \frac{H_{\ssty 0}}{H(z)}\right]^2 a(z)^{-3}, \end{equation}](/articles/aa/full_html/2013/10/aa21396-13/aa21396-13-eq848.png) (A.1)where
H(z) is the Hubble parameter at redshift
z, carried over from the definition of the critical density
(A.1)where
H(z) is the Hubble parameter at redshift
z, carried over from the definition of the critical density
 , and
a(z) the scale factor, both as functions of the
redshift. Similarly, following the definition of ΩM(r) used in
GBH and Zumalacárregui et al. (2012), one may write
an analogue equation in the void-LTB models as
, and
a(z) the scale factor, both as functions of the
redshift. Similarly, following the definition of ΩM(r) used in
GBH and Zumalacárregui et al. (2012), one may write
an analogue equation in the void-LTB models as ![\appendix \setcounter{section}{1} \begin{equation} \label{LTBomz} \Omega_{\rm M}(z) = \Omega_{\rm M}[r(z)] \left\{\frac{H_{\ssty \perp 0}[r(z)]} {H_{\ssty \perp}[t(z),r(z)]}\right\}^2 a_{\ssty \perp}[t(z),r(z)]^{-3}, \end{equation}](/articles/aa/full_html/2013/10/aa21396-13/aa21396-13-eq852.png) (A.2)where
H⊥ [t(z),r(z)],
and
a⊥ [t(z),r(z)]
are now the transverse Hubble parameter and scale factor, respectively. Figure 1 shows the redshift evolution of the density parameters in
the three models considered in the present work. We note, however, that there is an
ambiguity in the definition of Eq. (A.2)
due to the fact that the LTB geometry possesses radial expansion rates and scale factors
that are in general different from their transverse counterparts. For the purpose of
building mock catalogues that are consistent with the void-LTB parametrizations used in
this work we chose to use the transverse quantities because those were the ones used in
Zumalacárregui et al. (2012), from where the
best-fit parameters used in this work were taken.
(A.2)where
H⊥ [t(z),r(z)],
and
a⊥ [t(z),r(z)]
are now the transverse Hubble parameter and scale factor, respectively. Figure 1 shows the redshift evolution of the density parameters in
the three models considered in the present work. We note, however, that there is an
ambiguity in the definition of Eq. (A.2)
due to the fact that the LTB geometry possesses radial expansion rates and scale factors
that are in general different from their transverse counterparts. For the purpose of
building mock catalogues that are consistent with the void-LTB parametrizations used in
this work we chose to use the transverse quantities because those were the ones used in
Zumalacárregui et al. (2012), from where the
best-fit parameters used in this work were taken.
Next, we randomly assign (a) redshifts using a probability distribution based on one of these ΩM(z) profiles; (b) rest-frame luminosities, based on an input Schechter LF with parameters L∗ = 1011 L⊙, φ∗ = 10-3 dex-1 Mpc-3, and α = −1/2; and (c) a representative empirical SED from the Poletta templates, drawn from the same distributions reported in Gruppioni et al. (2013). In this way we can test first the validity of the 1/Vmax estimator itself for the purposes of the present work, and then the possible effects of the different predicted density profiles on the values of the LF.
Having assigned a redshift, a luminosity and a SED for each Monte Carlo (MC) realisation, we proceed to compute k-corrections and fluxes, using the luminosity distance-redshift relation consistent with the cosmology assumed for the redshift assignment. We include the source in the mock catalogue if its observed flux is larger than the detection limit of the field. We repeat this process until we have a catalogue with a number of selected MC realisations equal to the number of sources in the redshift interval Δz = [0.01,0.4] for a given field.
We then compute the 1/Vmax LF following the same methodology described in Sect. 2.3, using 100 mock catalogues built as described above. To assess the goodness-of-fit of the 1/Vmax LF versus the input Schechter profile, we compute the one-sided Kolmogorov-Smirnov (KS) statistic of the normalised residuals against a Gaussian with zero mean and unit variance. We plot the 1/Vmax points computed using the mock catalogues against the input Schechter LF used in their build-up in Figs. A.1−A.3 The KS statistic for each mock/input comparison is given in parentheses in the plots. The smaller this value, the closer the normalised residuals are to a Gaussian with zero mean and unit variance.
We find that the matter density parameter profiles of interest do not change the LF results significantly, as can be seen by comparing different panels in a figure. We note what appears to be a general bias towards under-estimating the characteristic luminosity L∗ in agreement with the Smith (2012) results.
 |
Fig. A.1 Results for the 1/Vmax LF estimator, computed from mock catalogues assuming a constant density profile ΩM = 0.27 (ΛCDM), and the underdense profiles of Eq. (15) for the GBH void models (Fig. 1). Source luminosities in the mock catalogues are drawn from the Schechter LF (here shown by a green dashed line, with parameters L∗ = 1011 L⊙, ϕ∗ = 10-3 dex-1 Mpc-3, and α = −1/2). Flux limits and SED are taken from the results of Gruppioni et al. (2013) for the PEP survey dataset in the GOODS-S field. |
 |
Fig. A.2 Same as Fig. A.1, but assuming the redshift evolution of the matter density profiles in both the standard (ΛCDM) and the void-LTB models as in Fig. 1. |
Comparison between the 1/Vmax LF results for the GOODS-S mock catalogues built using either the present-time density profiles (Fig. A.1) or the appropriate redshift evolution (Fig. A.2), shows that the method successfully takes into consideration the redshift distortion in the matter distribution, yielding points in both cases that recover the input LF profile qualitatively close to each other, with respect to their KS statistics.
Comparison between the mock catalogues for the GOODS-S (Fig. A.2) and COSMOS (Fig. A.3) fields built using the redshift evolution of the density parameter in the different cosmological models shows that the 1/Vmax estimator fares slightly better in the deeper GOODS-S field than the wider COSMOS field.
Summing up, even if the method is not perfectly robust under a change in the cosmological model, the variations caused by a change in the underlying cosmology in the results obtained with the 1/Vmax estimator are not enough to explain the significant differences in the shape of the LF at the considered redshift interval, Δz = [0.01,0.4].
All Tables
Rest-frame 100 μm 1/Vmax luminosity function assuming the ΛCDM cosmological model.
Rest-frame 100 μm 1/Vmax luminosity function assuming the CGBH cosmological model.
Rest-frame 100 μm 1/Vmax luminosity function assuming the OCGBH cosmological model.
Rest-frame 160 μm 1/Vmax luminosity function assuming the ΛCDM cosmological model.
Rest-frame 160 μm 1/Vmax luminosity function assuming the CGBH cosmological model.
Rest-frame 160 μm 1/Vmax luminosity function assuming the OCGBH cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 100 μm band, assuming the ΛCDM cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 160 μm band, assuming the ΛCDM cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 100 μm band, assuming the CGBH cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 160 μm band, assuming the CGBH cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 100 μm band, assuming the OCGBH cosmological model.
Rest-frame total IR 1/Vmax luminosity function in the PACS 160 μm band, assuming the OCGBH cosmological model.
Best-fitting Schechter parameters for the rest-frame 100 μm 1/Vmax luminosity functions.
Best-fitting Schechter parameters for the rest-frame 160 μm 1/Vmax luminosity functions.
Best-fitting Schechter parameters for the rest-frame total IR 1/Vmax luminosity functions in the PACS 100 μm band.
Best-fitting Schechter parameters for the rest-frame total IR 1/Vmax luminosity functions in the PACS 160 μm band.
All Figures
 |
Fig. 1 Upper panel: present-time (t = t0) matter density parameters in the standard (ΛCDM, black line) and the void (GBH) cosmological models (red and cyan lines). Lower panel: redshift evolution of the dimensionless matter density parameters in the standard (ΛCDM) and the void (GBH) cosmological models. The dotted vertical lines delimit the lowest redshift interval considered in the computation of the LF at which the faint-end slopes are fit. |
| In the text | |
 |
Fig. 2 Upper panel: luminosity (solid lines) and comoving distances (dotted lines) versus the redshift in the standard (ΛCDM) and the void (GBH) cosmological models. Up to redshift z ≈ 1 distances in the constrained, flat void model (CGBH) follow very closely their standard model counterparts, but even in the case of the best-fit parameters in Zumalacárregui et al. (2012) yield increasingly different distances with the redshift. Lower panel: comoving volume elements in the standard (ΛCDM) and the void (GBH) cosmological models. The quantities in the void models adopted here evolve with the redshift in a similar way to the standard model up to redshift approximately 0.6, then their values become consistently lower than in the ΛCDM model. |
| In the text | |
 |
Fig. 3 Luminosity functions derived in the standard (ΛCDM) (black dots) and the void (GBH) cosmological models (red and cyan dots). We also show the best-fit Schechter profiles to the rest-frame 100 μm 1/Vmax corresponding to effective wavelengths of 60 μm. |
| In the text | |
 |
Fig. 4 As Fig. 3 for the rest-frame 160 μm 1/Vmax luminosity functions. Here the effective wavelength is 90 μm. |
| In the text | |
 |
Fig. 5 Schechter profile fits to the rest-frame total IR luminosity functions computed from the PACS 100 μm 1/Vmax band, assuming the standard (ΛCDM) and the void (GBH) cosmological models. |
| In the text | |
 |
Fig. 6 Schechter profile fits to the rest-frame total IR luminosity functions computed from the PACS 160 μm 1/Vmax band, assuming the standard (ΛCDM) and the void (GBH) cosmological models. |
| In the text | |
 |
Fig. 7 Upper panel: redshift evolution of the characteristic luminosity L∗ on the four datasets of the present work. Lower panel: redshift evolution of the characteristic luminosity φ∗ on the same datasets. |
| In the text | |
 |
Fig. 8 Upper panel: effect of the luminosity distance − redshift relation on the shape of the LF. The black points were computed using the 1/Vmax method, assuming both dL(z) and r(z) relations stemming from the standard model, while the blue and red points kept the r(z) relation for the ΛCDM model, changing only the dL(z) relation for that in the listed void model. The effect of the dL(z) relation on the shape of the LF is clear, especially at the lower luminosity bins. Lower panel: effect of the comoving distance − redshift relation on the shape of the LF. The black points were computed using the 1/Vmax method, assuming both dL(z) and r(z) relations stemming from the standard model, while the blue and red points kept the dL(z) relation for the ΛCDM model, changing only the r(z) relation for that in the listed void model. The effect of the r(z) relation on the shape of the LF is found to be much less relevant than that of the dL(z) relation. |
| In the text | |
 |
Fig. A.1 Results for the 1/Vmax LF estimator, computed from mock catalogues assuming a constant density profile ΩM = 0.27 (ΛCDM), and the underdense profiles of Eq. (15) for the GBH void models (Fig. 1). Source luminosities in the mock catalogues are drawn from the Schechter LF (here shown by a green dashed line, with parameters L∗ = 1011 L⊙, ϕ∗ = 10-3 dex-1 Mpc-3, and α = −1/2). Flux limits and SED are taken from the results of Gruppioni et al. (2013) for the PEP survey dataset in the GOODS-S field. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but assuming the redshift evolution of the matter density profiles in both the standard (ΛCDM) and the void-LTB models as in Fig. 1. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.2, but for the PEP survey dataset in the COSMOS field. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


