| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 3 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201321902 | |
| Published online | 27 August 2013 | |
Diagnosing transient ionization in dynamic events
1
Armagh Observatory, College Hill, BT61 9 DG Armagh UK
e-mail: madj@arm.ac.uk
2
Department of Physics, University of Strathclyde, 107 Rottenrow, G4 0 NG Glasgow, UK
3
Space Science and Technology Department, STFC Rutherford Appleton Laboratory, Chilton, Didcot, Oxfordshire, OX11 0QX, UK
4
Dept.of Physics and Electronics, Deen Dayal Upadhyaya College, University of Delhi, 110007 Delhi, India
Received:
16
May
2013
Accepted:
15
July
2013
Aims. The present study aims to provide a diagnostic line ratio that will enable the observer to determine whether a plasma is in a state of transient ionization.
Methods. We use the Atomic Data and Analysis Structure (ADAS) to calculate line contribution functions for two lines, Si iv 1394 Å and O iv 1401 Å, formed in the solar transition region. The generalized collisional-radiative theory is used. It includes all radiative and electron collisional processes, except for photon-induced processes. State-resolved direct ionization and recombination to and from the next ionization stage are also taken into account.
Results. For dynamic bursts with a decay time of a few seconds, the Si iv 1394 Å line can be enhanced by a factor of 2–4 in the first fraction of a second with the peak in the line contribution function occurring initially at a higher electron temperature due to transient ionization compared to ionization equilibrium conditions. On the other hand, the O iv 1401 Å does not show such any enhancement. Thus the ratio of these two lines, which can be observed with the Interface Region Imaging Spectrograph, can be used as a diagnostic of transient ionization.
Conclusions. We show that simultaneous high-cadence observations of two lines formed in the solar transition region may be used as a direct diagnostic of whether the observed plasma is in transient ionization. The ratio of these two lines can change by a factor of four in a few seconds owing to transient ionization alone.
Key words: Sun: corona / Sun: transition region / line: formation / atomic processes / line: profiles
© ESO, 2013
1. Introduction
All spectral lines have encoded information that allows the observer to diagnose important physical parameters of the underlying plasma. For example, forbidden or inter-system lines allow an evaluation of the plasma’s electron density, while resonance lines allow the observer to diagnose the electron temperature. With sufficient spectral resolution, all spectral lines can be used to give the observer information on plasma flows and/or turbulent motions. To diagnose a plasma’s state of ionization, however, requires both high-cadence data and suitable spectral lines.
Various authors have presented simulated spectra based on transient ionization (Mewe & Schrijver 1980; Reale & Orlando 2008) for comparison with observational data. In a recent paper, Doyle et al. (2012) discussed the diagnostic potential of high-cadence ultraviolet spectral data when transient ionization is considered. The above paper used high-cadence spectral line data from the Solar Maximum Mission (SMM) observed in O v 1371 Å which allowed the authors to measure electron densities and temperatures during the early stages of a feature’s evolution, something that is not currently possible. The high cadence UV spectrometer on SMM allowed observations of selected spectral lines with a subsecond cadence.
The forthcoming observations from the Interface Region Imaging Spectrograph1 will once again enable high quality observations of lines formed in the solar transition region. What we would like to have is a simple line ratio consisting of one line that shows a response to transient ionization and another line that is not responsive to transient ionization. Then, provided we can monitor these lines with sufficient cadence, any fast (≈0.5 s) increase in the ratio must be due to non-equilibrium conditions. Here, we look at the response of two such lines, Si iv 1394 Å and O iv 1401 Å. The Si iv 1394 Å line is in the ground spin system (3s 2S1/2–3p 2P3/2). The character of the excitation cross-sections (dipole and non-spin change) and access to higher n-shell/cascade will result in a line enhancement. However, the O iv 1401 line, by contrast, has an upper state in the quartet spin system (2s22p 2P3/2–2s2p24P5/2) which means that access to this spin system is driven by cross-sections that decrease with temperature, hence little or no line enhancement, therefore, transient ionization under-fills the population structure of the alternate spin systems from the ground. By contrast, the ground spin system population structure gets enhanced (due to the exponential factor in the rate coefficient) with increasing electron temperature.
2. Transient ionization
The atomic structure of atoms and ions is in principle an infinite assembly of levels with an infinite number of reactions between them, however, simplifying assumptions about the nature of the plasma, its dynamic character and the relative importance of the various reactions have to be made. As shown in the recent paper by Doyle et al. (2012), the generalized collisional-radiative theory (GCR) is the most appropriate approach. The above theory, plus ionization, recombination, excitation and radiative decay data are all as implemented in ADAS, the Atomic Data and Analysis Structure2. A good description of this is given in the Appendix of Lanza et al. (2001). Below we first discuss the various time constants and their relative importance.
2.1. Time constants
The lifetimes of the various states of ions and electrons in a plasma too radiative or collisional processes divide into two groups. The first is the intrinsic group, comprising purely of atomic parameters, and includes the metastable radiative decay time, τm, the ordinary excited-state radiative decay time τo, and auto-ionizing-state decay time, τa. These are generally ordered as τa ≪ τo ≪ τm.
The second is the extrinsic group, which depends on plasma conditions, especially density. It includes free particle thermalization including electron-electron τe−e, ion-ion τi−i, and ion-electron τi−e, charge-state change (ionization τion and recombination τrec) and redistribution of population amongst excited ion states (τred). Their order is τion,rec ≫ τi−e ≫ τi−i ≫ τe−e. More details on the above may be found in Summers et al. (2006).
From a dynamic point of view, the intrinsic and extrinsic groups are to be compared with each other and with timescales, τplasma, representing plasma ion diffusion across temperature or density scale lengths, the relaxation times of transient phenomena, and observation times. For astrophysics plasmas, τplasma ≈ τg ≈ τm ≫ τo ≫ τe−e, where τg represents the relaxation time of the ground-state populations of ions.
These time scales imply that the dominant population of impurities in the plasma are those of the ground and metastable states of the various ions. In a transient event, the dominant populations evolve on time scales similar to the plasma diffusion time scales and so should be modelled dynamically. From a theoretical point-of-view, non-equilibrium occurs when τplasma ≤ τion,rec = 1 / [Ne(S(z → z + 1) + α(z + 1 → z))] (McWhirter 1965), where Ne is the electron density, and S(z → z + 1) and α(z + 1 → z) are the effective ionization and recombination coefficients (see Sect. 2.2). This means that in a transient event, the plasma time scale (τplasma) is shorter than the atomic ionization/recombination time scale (τion,rec).
2.2. GCR
Here, we calculate the contribution functions for Si iv 1394 Å and O iv 1401 Å using the GCR theory. Each ion in an optically thin plasma is described by a complete set of levels with collisional and radiative couplings between them. All radiative and electron collisional processes are included, except for photon-induced processes. In addition, state-resolved direct ionization and recombination to and from the next ionization stage are also taken into account.
The emissivity of a spectral line is given by  (1)where Ael = N(Z) / NH
is the abundance of the element Z relative to hydrogen, NH / Ne, tabulated by McWhirter
et al. (1975), and
(1)where Ael = N(Z) / NH
is the abundance of the element Z relative to hydrogen, NH / Ne, tabulated by McWhirter
et al. (1975), and  is the time-dependent
contribution function defined as
is the time-dependent
contribution function defined as  (2)where
(2)where  is
the excitation photon emissivity coefficient, and
is
the excitation photon emissivity coefficient, and 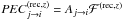 the
recombination photon emissivity coefficient.
the
recombination photon emissivity coefficient.
In the above, Aj → i is the radiative transition probability, N(z) and N(z + 1) are the population densities of the ground states of the ions of charge z and z + 1 and ℱ(exc,z), and ℱ(rec,z + 1) are the effective contributions to the population of the upper excited state i.
In a time-dependent plasma model, the line emissivity is no longer a unique function of
the local temperature and density conditions, but it depends on the past history of the
temperature, density, and state of ionization of the plasma. Therefore, the assumption of
ionization equilibrium in calculating the ionization balance is not appropriate and
time-dependent fractional abundances must be determined. The time dependence of ionization
stage populations, N(z), leads to the following equation: ![\begin{equation} { {\rm d}N^{(\it z)} \over {{\rm d}t}} = N_{\rm e} \left[S^{(\it z-1)}N^{\it (z-1)} + (S^{(\it z)}+\alpha^{\it (z)})N^{(\it z)} + \alpha^{(\it z+1)}N^{(\it z+1)}\right] \label{ion_time_evol} \end{equation}](/articles/aa/full_html/2013/09/aa21902-13/aa21902-13-eq43.png) (3)where S and α are the collisional-dielectronic ionization
and recombination coefficients. They give the contribution to the growth rates for the
ground state population due to the effective ionization, which includes direct and
excitation/auto-ionization contributions, and the effective recombination, which includes
radiative, dielectronic, and three-body contributions. The values of these coefficients,
currently within the ADAS database, have been obtained following the GCR approach as
described in Summers et al. (2006). The solution of
Eq. (3) is such that the number density of
the element of a nuclear charge Z, N(Z), is equal to
(3)where S and α are the collisional-dielectronic ionization
and recombination coefficients. They give the contribution to the growth rates for the
ground state population due to the effective ionization, which includes direct and
excitation/auto-ionization contributions, and the effective recombination, which includes
radiative, dielectronic, and three-body contributions. The values of these coefficients,
currently within the ADAS database, have been obtained following the GCR approach as
described in Summers et al. (2006). The solution of
Eq. (3) is such that the number density of
the element of a nuclear charge Z, N(Z), is equal to 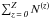 .
The time-dependent fractional abundances N(z)(t) / N(Z)
are calculated as follows: the code derives the solution for a range of fixed plasma
electron temperature and density pairs, starting from an initial population distribution N(z)(t = 0) / N(Z)
using an eigenvalue approach. At temperatures close to ionization equilibrium, the
contribution of recombination to the emissivity is small; however, this contribution
becomes large in non-equilibrium conditions. Further details on the above may be found in
Doyle et al. (2012) and references therein. Here we
use an initial starting temperature of 30 000 K and a fixed electron density of 1010 cm-3. We then calculate the ionization fraction and the
resulting line contribution function for different relaxation times, ranging from 0.2 s
after the initial start (i.e., in a highly transient state) to 10 s (close to ionization
balance) and finally when the plasma is in ionization equilibrium.
.
The time-dependent fractional abundances N(z)(t) / N(Z)
are calculated as follows: the code derives the solution for a range of fixed plasma
electron temperature and density pairs, starting from an initial population distribution N(z)(t = 0) / N(Z)
using an eigenvalue approach. At temperatures close to ionization equilibrium, the
contribution of recombination to the emissivity is small; however, this contribution
becomes large in non-equilibrium conditions. Further details on the above may be found in
Doyle et al. (2012) and references therein. Here we
use an initial starting temperature of 30 000 K and a fixed electron density of 1010 cm-3. We then calculate the ionization fraction and the
resulting line contribution function for different relaxation times, ranging from 0.2 s
after the initial start (i.e., in a highly transient state) to 10 s (close to ionization
balance) and finally when the plasma is in ionization equilibrium.
 |
Fig. 1 Line contribution function for Si iv 1394 Å and O iv 1401 Å in cm-3 s-1 at ionization equilibrium and for transient ionization. The electron density was fixed at 1010 cm-3, with an initial starting temperature of 30 000 K. |
3. Results and discussion
In Fig. 1, we give the line contribution function for different relaxation times, that are shorter than the time for the plasma to reach ionization equilibrium. This figure shows that the peak of the line contribution function for both lines occurs at a higher temperature for short relaxation times. However, for O iv 1401 Å, transient ionization does not produce a flux increase over the one for ionization equilibrium, while the Si iv 1394 Å line increases over a factor of three. The reason these two lines behave in a different manner under transient ionization is due to their formation process as outlined in Sect. 1.
For O iv 1401 Å at an electron density of 1010 cm-3, it takes ≈10 s for the line to reach ionization equilibrium, while Si iv 1394 Å takes ≈100 s to reach equilibrium.
Figure 1 shows that the ratio of Si iv 1394 to O iv 1401 ranges from ≈30 in ionization equilibrium to ≈120 for highly transient conditions (0.2 s). Multiplying by the relative elemental Si/O coronal abundance (Phillips et al. 2008) gives a ratio ranging from 3.3 to 12.9. The Curdt et al. (2001) SUMER spectral atlas gives the observed ratio for these lines as 4.6 in a sunspot and 6.9 in the quiet Sun. The above observational ratios are in general agreement (to within a factor of two) with the present Si iv 1394/O iv 1401 ratio when assuming ionization equilibrium. However, with a different DEM distribution, different abundances will change the ratio but the important point to note by the observer is not the absolute ratio but whether the observed ratio would change quickly. As a result, if observing these two lines simultaneously with, say, a 0.5 s cadence, then any sudden increase by a factor of 2−3 in the line ratio must be due to transient ionization. Such observations will therefore enable an evaluation of the plasma’s electron density as outlined in Doyle et al. (2012).
Acknowledgments
Research at the Armagh Observatory is grant-aided by the N. Ireland Dept. of Culture, Arts and Leisure. We thank UK STFC for support via ST/J001082/1 and the Leverhulme Trust.
References
- Curdt, W., Brekke, P., Feldman, U., et al. 2001, A&A, 375, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doyle, J. G., Giunta, A., Singh, A., et al. 2012, Sol. Phys., 280, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F., Spadaro, D., Lanzafame, A. C., et al. 2001, ApJ, 547, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- McWhirter, R. W. P. 1965, in Plasma diagnostic techniques, eds. R. H. Huddlestone, & S. L. Leonard (New York, London: Academic Press) [Google Scholar]
- McWhirter, R. W. P., Thonemann, P. C., & Wilson, R. 1975, A&A, 40, 63 [NASA ADS] [Google Scholar]
- Mewe, R., & Schrijver, J. 1980, A&A 87, 261 [NASA ADS] [Google Scholar]
- Phillips, K. J. H., Feldman, U., & Landi, E. 2008, Ultraviolet and X-ray spectroscopy of the solar atmosphere (Cambridge University Press) [Google Scholar]
- Reale, F., & Orlando, S. 2008, Sol. Phys., 684, 715 [Google Scholar]
- Spitzer, L. 1962, in Physics of Fully Ionized Gases (New York: Interscience), 120 [Google Scholar]
- Summers, H. P., Dickson, W. J., O’Mullane, M. G., et al. 2006, Plasma Phys. Controlled Fusion, 48, 263 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Line contribution function for Si iv 1394 Å and O iv 1401 Å in cm-3 s-1 at ionization equilibrium and for transient ionization. The electron density was fixed at 1010 cm-3, with an initial starting temperature of 30 000 K. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


