| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321886 | |
| Published online | 12 August 2013 | |
Time-resolved multicolour photometry of bright B-type variable stars in Scorpius⋆,⋆⋆
Copernicus Astronomical Center, Bartycka
18, 00-716 Warsaw, Poland
e-mail: gerald@camk.edu.pl
Received:
13
May
2013
Accepted:
8
July
2013
Context. The first two of a total of six nano-satellites that will constitute the BRITE-Constellation space photometry mission have recently been launched successfully.
Aims. In preparation for this project, we carried out time-resolved colour photometry in a field that is an excellent candidate for BRITE measurements from space.
Methods. We acquired 117 h of Strömgren uvy data during 19 nights. Our targets comprised the β Cephei stars κ and λ Sco, the eclipsing binary μ1 Sco, and the variable super/hypergiant ζ1 Sco.
Results. For κ Sco, a photometric mode identification in combination with results from the spectroscopic literature suggests a dominant (l,m) = (1, −1) β Cephei-type pulsation mode of the primary star. The longer period of the star may be a rotational variation or a g-mode pulsation. For λ Sco, we recover the known dominant β Cephei pulsation, a longer-period variation, and observed part of an eclipse. Lack of ultraviolet data precludes mode identification for this star. We noticed that the spectroscopic orbital ephemeris of the closer pair in this triple system is inconsistent with eclipse timings and propose a refined value for the orbital period of the closer pair of 5.95189 ± 0.00003 d. We also argue that the components of the λ Sco system are some 30% more massive than previously thought. The binary light curve solution of μ1 Sco requires inclusion of the irradiation effect to explain the u light curve, and the system could show additional low amplitude variations on top of the orbital light changes. ζ1 Sco shows long-term variability on a time scale of at least two weeks that we prefer to interpret in terms of a variable wind or strange mode pulsations.
Key words: stars: oscillations / binaries: eclipsing / stars: early-type / stars: variables: general / techniques: photometric
Reduced time series for all stars are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/557/A1
© ESO, 2013
1. Introduction
BRIght Target Explorer (BRITE)-Constellation is a space photometry mission consisting of six nano-satellites, two of each funded by the partner countries Austria, Canada, and Poland. The two Austrian satellites have been successfully launched on 25 February 2013, and the remaining four should sequentially follow until early 2014. The goal of the mission is to obtain high-quality time-resolved photometry of the brightest stars in the sky, in carefully selected fields with a diameter of 24◦. Subrasters of the CCD images of up to a dozen primary targets will be transmitted to Earth, and on-board reduced photometry can be obtained for up to a hundred further targets in the field. All satellites carry a 3-cm telescope each, but three of them will observe through a blue filter, and the other three through a red filter (approximating the Johnson B and R passbands). This setup will allow to obtain two-colour photometry, and the satellites can be operated either separately, or as an entity, depending on the science needs. We refer to Zwintz & Kaiser (2008) for more details.
Given the technical setup of the mission, it is expected to deliver the richest science return for OB stars. Being intrinsically luminous, such stars also feature prominently among the apparently brightest stars. OB stars naturally occur in groups, associations and clusters. Therefore sky fields rich in bright stars will also be rich in OB stars.
Variability is common among such stars, starting from the slowly pulsating B (SPB) and β Cephei pulsators on the main sequence, extending to pulsating supergiants, Luminous Blue Variables, Be stars, massive eclipsing binaries, etc. The prime observable that supplies astrophysical information of a variable star is the period of variability. The presence of multiperiodicity and the shape of the light curves are also revealing. However, time-resolved colour photometry provides valuable additional astrophysical information, namely on the presence and nature of temperature variations, that is essential for interpreting the observed variability. A prominent example is the ability to identify the spherical harmonics of pulsation modes (e.g., see Daszyńska-Daszkiewicz 2008 in the context of BRITE-Constellation).
In preparation for BRITE-Constellation, we carried out time-resolved multicolour photometry of bright early B-type stars in a field deemed to be likely observed by the mission. We chose a field in Scorpius, that contains the two β Cephei stars κ Sco (V = 2.4) and λ Sco (V = 1.6), the eclipsing binary μ1 Sco (V = 3.1), the variable ζ1 Sco (V = 4.7), and the two apparently constant stars υ Sco (V = 2.7) and μ2 Sco (V = 3.6) for comparison purposes. All these stars are located within 10◦ in the sky and their magnitude range is what can be expected within a typical BRITE-Constellation field.
2. Observations
 |
Fig. 1 Collected y-filter light curves of the low-amplitude and non-variables. Plus signs: ζ1 Sco. Diamonds: λ Sco. Filled circles: κ Sco. Open circles: μ2 Sco − υ Sco. The fits plotted over the κ Sco and λ Sco light curves are derived in Sects. 3.1 and 3.2. |
Time-resolved photometry was carried out at the 0.5-m telescope at the South African Astronomical Observatory. We were awarded two runs of two weeks each, separated by two weeks, in July and August 2011. The photoelectric Modular Photometer that is permanently mounted to this telescope was used in connection with Strömgren uvy and neutral density filters. For the five “fainter” stars, the 2.3 mag neutral density filter was sufficient, but for λ Sco, the 4.7 mag neutral density filter had to be used. Unfortunately, this filter has zero transmission in the ultraviolet, wherefore we could only obtain vy photometry for this star.
Because the two known β Cephei stars exhibit faster light variations than the other variables, the group κ/λ/υ Sco was observed twice as often as the μ1/μ2/ζ1 Sco ensemble. Sky background was measured at least once per group, depending on the position and brightness of the Moon. This resulted in an average cadence of 17 min per measurement for the first group, and about 33 min per measurement for the second. In total, we acquired 117 hours of measurement during 19 nights.
The data were reduced following standard photoelectric photometry schemes. First, the measurements were corrected for coincidence losses. Then, sky background was subtracted within each target/local comparison star group, and if found necessary, individually for each star. Extinction coefficients were determined on a nightly basis from the measurements of the two comparison stars via the Bouguer method (fitting a straight line to a magnitude vs. air mass plot). The same extinction correction was applied to each star. Differential magnitudes relative to the two comparison stars were computed by interpolation. The magnitude differences between the comparison stars themselves had standard deviations of 6.8, 6.5, and 5.3 mmag in u, v, and y, respectively, and no evidence for periodic variability of any of these two stars was found within the (rather unsatisfactory) limitations of our data. Finally, the timings were converted to heliocentric Julian date (HJD), and the data for the variable stars were subjected to analysis. Differential light curves in the y filter are displayed in Fig. 1, excluding μ1 Sco whose amplitude is much larger than that of the other variables.
3. Analysis, results, and discussion
The data were searched for periodicities using the program Period04 (Lenz & Breger 2005). This software package uses single frequency Fourier and multifrequency nonlinear least squares fitting algorithms. The analysis was started by computing the spectral window function and the amplitude spectrum of the data. If a signal was found to be present at a significant level and supposed intrinsic, it was fitted to the data, and its amplitude, frequency and phase were improved to obtain an optimal fit in each filter. Then, a signal-to-noise weighted mean frequency was computed for the data in each filter, adopted for all, and only the amplitudes and phases were optimized.
Consequently, this variation was subtracted from the measurements (we call this procedure “prewhitening”) and the residual amplitude spectrum was computed and examined. If more periodic signals were present, their parameters were optimized together with those of the ones previously detected. Once no significant variation was left in the residuals, the analysis was stopped. A signal was considered significant when it exceeded a signal-to-noise ratio (S/N) of four, following the empirical recommendation by Breger et al. (1993).
3.1. κ Sco
The spectral window, as well as original and prewhitened Fourier amplitude spectra of our κ Sco measurements are shown in Fig. 2. As the spectral window function of our light curves is for obvious reasons virtually the same, we only show it once in this paper. For the present example, we calculated it as the Fourier transform of a single noise-free sinusoid with a frequency of 5.003 d-1 and an amplitude of 5.2 mmag. This is the same as the strongest signal in our v filter data, that were also chosen to illustrate the prewhitening process.
 |
Fig. 2 Uppermost panel: spectral window of our v filter data of κ Sco. Second panel: amplitude spectrum of our data. Third panel: residual amplitude spectrum after prewhitening the dominant variation. Lower panel: residuals after prewhitening two frequencies. |
We were able to detect two statistically significant signals in our light curves and present the frequency solution in Table 1. It should be noted that there are some alias ambiguities concerning the second signal at low frequency. We decided to choose the frequency value that represented the variability in the combined uvy data best; competing frequencies were at 0.244, 1.245 and 1.276 d-1. The errors in the parameters listed in Table 1 were computed the analytical formulae by Montgomery & O’Donoghue (1999). These are known to underestimate the real accuracy of the frequency solution, but give an idea of the order of magnitude of the errors.
Frequencies present in the light curves of κ Sco.
κ Sco is known to be a spectroscopic binary system with two B-type components in a 195-d orbit, and the primary is responsible for the pulsational variability (Harmanec et al. 2004). Uytterhoeven et al. (2005) spectroscopically determined Teff = 25 000 ± 2000 K for the primary component, Teff = 20 000 ± 2000 K for the secondary, as well as log g = 3.8 ± 0.2 for both. As this large temperature difference is not possible assuming coeval evolution, we only take these values as starting points for placing the two components in the HR diagram.
Other available constraints comprise the Hipparcos parallax of the system (6.75 ± 0.17 mas, van Leeuwen 2007), translating into Mv = −3.48 ± 0.06 and a system luminosity log L = 4.23 ± 0.03 using the bolometric corrections by Flower (1996) and the uncertainties in Teff. The spectroscopic mass ratio is 1.1 (Harmanec et al. 2004), and the primary component oscillates with a frequency of 5.003 d-1 (Table 1).
We computed model evolutionary tracks with the Warsaw-New Jersey stellar evolution code (e.g., see Pamyatnykh et al. 1998 for a description) to bring all these constraints into agreement. The models were calculated using OP opacities and the Asplund et al. (2004) mixture. An overall metal abundance Z = 0.012 and a hydrogen abundance of X = 0.7 have been adopted for all models, and no convective core overshooting was used. Zero-age main sequence rotational velocities of 115 km s-1 and 195 km s-1, were adopted to match the observed vsini values of 100 and 170 km s-1 for the primary and secondary, respectively, during somewhat advanced main sequence evolutionary stages.
We found that model pairs in a rather narrow range of parameters (M1 = 10.2 ± 0.3 M⊙, M2 = 9.3 ± 0.3 M⊙, log g1 = 3.83 ± 0.06,log g2 − log g1 = 0.09 ± 0.02, log Teff,1 = 4.365 ± 0.015, log Teff,2 − log Teff,1 = −0.008 ± 0.005, log (age) = 7.18 ± 0.05) would fit all the observational constraints satisfactorily and within the errors. The orbital solution by Harmanec, Uytterhoeven & Aerts (2004) implied M1sin3i = 10.69 M⊙ and M2sin3i = 9.64 M⊙, which yields i < 77°.
To identify the spherical degree of the oscillation we have computed theoretical uvy amplitudes of models of M = 10.2 ± 0.3 M⊙ and log Teff,1 = 4.365 ± 0.015 following the approach by Balona & Evers (1999). We calculated theoretical uvy amplitudes for the modes whose frequencies were in the observed domain along this model sequence. The resulting theoretical amplitudes in the three passbands were normalized to that in the u filter, and the average amplitude ratios and their rms errors were calculated. Given the small temperature difference between the primary and secondary component, the falsification of the amplitude ratios due to the secondary flux is insignificant compared to the observational errors and hence was not taken into account. A comparison between the observed and theoretical amplitude ratios is shown in Fig. 3.
 |
Fig. 3 A comparison of the observed amplitudes of κ Sco in the different filters with theoretical predictions of pulsational uvy amplitude ratios, normalized to unity at u. The filled circles with error bars are the observed amplitude ratios. The full lines are theoretical predictions for radial modes, the dashed lines for dipole modes, the dashed-dotted lines for quadrupole modes, the dotted lines for ℓ = 3 modes, and the dashed-triple-dotted lines are for ℓ = 4. The thin error bars denote the uncertainties in the theoretical amplitude ratios. |
It is implied that the β Cephei oscillation is most consistent with a dipole mode. The dominant pulsation mode of the primary component has been spectroscopically identified as either (l,m) = (2, −1) or (1, −1) (Uytterhoeven et al. 2005). Our results point towards the latter possibility, which is also more favourable when considering the geometrical aspect of the mode (e.g., see Pesnell 1985) assuming the primary’s rotation axis is normal to the orbital plane.
We now turn to the 0.274 d-1 variation. A signal in this frequency domain has been observed before, both in space photometry (Cuypers et al. 2004) and in spectroscopy (Uytterhoeven et al. 2005). The spectroscopic observations were interpreted as a rotational modulation. However, its photometric amplitudes with respect to wavelength (Table 1) are also consistent with pulsation. On the other hand, the frequency reported by Uytterhoeven et al. (2005) is somewhat lower than the one detected in our and the space photometry. In fact, it corresponds to one of the aliases (0.244 d-1) mentioned before. With a radius of R = 6.45 ± 0.55 R⊙ resulting from the model computations described above and vrot = 110 km s-1, we obtain a rotation period of 2.97 ± 0.25 d for the primary component. This is somewhat shorter than the observed photometric and spectroscopic periods, but given the uncertainties in the preceding procedures, we cannot unambiguously distinguish between a rotational modulation or a g-mode oscillation with a period very close to the rotational one.
It is interesting to examine the photometric data of κ Sco for possible eclipses. Indeed, two nights (HJD 2 441 120 and 2 441 122) by Lomb & Shobbrook (1975) show magnitude zeropoints 0.024 mag fainter than the rest. However, data from the same authors from different seasons, but at the same orbital phase according to the spectroscopic 195.65-d orbital period (Uytterhoeven et al. 2001), do not show fainter mean magnitudes and therefore rather indicate an observational problem in those two nights. In addition, in one of these two nights λ Sco was also observed by these authors. This night shows a similar mean magnitude change in the λ Sco data. Consequently, there is no evidence for possible eclipses of κ Sco in the photometry available to us.
3.2. λ Sco
As can already be discerned in Fig. 1, in the night of HJD 2 455 760 (17/18 July 2011) λ Sco underwent part of a shallow eclipse. To determine the frequencies of its intrinsic light variations, we therefore discarded the data affected by the eclipse for the time being. Furthermore, after making sure that any variability had the same amplitude within the errors in both filters, we combined those data after setting their mean to zero. The frequency analysis of the remaining combined vy data is presented in Fig. 4, and the results, with the amplitudes individually determined for the different filters, in Table 2. The signals are in phase within the two filters within the observational errors. Given the lack of u data for λ Sco, we have no means to attempt a photometric identification of the dominant oscillation mode, despite its rather large amplitude.
 |
Fig. 4 Upper panel: amplitude spectrum of our data of λ Sco with the eclipse discarded. Second panel: residual amplitude spectrum after prewhitening the dominant variation. Lower panel: residuals after prewhitening two frequencies. A peak at the harmonic of the first variation is present. |
Frequencies present in the light curves of λ Sco.
The longer-period signal we found in the light variations has never been reported before. It appears convincingly present in our data, but we lack observational constraints to interpret it. However, one statement can be made: its frequency is close to, but significantly different from, the first harmonic of the orbital frequency of the close binary, which argues against a tidal origin.
λ Sco is a known triple system, consisting of a close double with an orbital period of 5.9525 d and of a tertiary star in a ≈ 3-yr orbit. The primary is the β Cephei star, the secondary has a mass of about 1/6 that of the primary, whereas the tertiary again is a B-type star with a mass of about 76% of the primary. We refer to Uytterhoeven et al. (2004, hereinafter U04) and Tango et al. (2006) for in-depth studies of the triple system. The masses and effective temperatures listed in Table 5 of Tango et al. (2006) lead to R = 5.2 ± 1.7 R⊙ for the primary and R = 5.3 ± 1.3 R⊙ for the tertiary, respectively. Hence, the pulsation constant for the β Cephei oscillation of the primary would be Q = 0.06 ± 0.02, implying a low-order g mode, which is rather unusual for β Cephei stars (cf. Stankov & Handler 2005). Additionally, Tango et al. (2006) reported a smaller distance of the λ Sco system obtained from their combined interferometric and spectroscopic analysis compared to that from the Hipparcos parallax. This raises the suspicion that the component masses, and hence the luminosities, of the components of the λ Sco system have previously been underestimated.
Consequently, we now apply the same methodology as for κ Sco, namely trying to find stellar model pairs of the same age in the effective temperature range implied by spectroscopy that are consistent with the system’s parallax. In this procedure, we neglect the luminosity of the secondary as it is insignificant within the errors. The luminosity ratio of the tertiary to the primary is 0.38 ± 0.08 (Tango et al. 2006). With the Hipparcos parallax of λ Sco (5.71 ± 0.75 mas, van Leeuwen 2007) and the bolometric corrections by Flower (1996), it follows that the primary component must have log L1 = 4.56 ± 0.13. At an effective temperature of Teff,1 = 25 000 ± 1000 K (U04) this corresponds to a mass of 14.5 ± 1.1 M⊙ according to our models, near the upper mass limit for the primary star inferred by Tango et al. (2006). We note that models with M > 14.5 M⊙ without overshooting are at the terminal-age main sequence at Teff = 25 000 K. The pulsation constant for the β Cephei mode of the primary component of λ Sco for models between 13.4−14.5 M⊙ lie in the range 0.026 d< Q < 0.031 d, in good agreement with common values for β Cephei stars (Stankov & Handler 2005). With the tertiary to primary mass ratio of 0.76 ± 0.04 (Tango et al. 2006), the tertiary star must have 9.6−11.6 M⊙. In this scenario, assuming coeval evolution and Teff,1 = 25 000 ± 1000 K, it would however need to be hotter than previously estimated (Teff,3 = 24 500 ± 1000 K).
The rotation periods of these models, assuming that the primary’s rotation axis is normal to the orbital plane, lie in the range of 3.4 ± 0.5 d, given vsini ≈ 150 km s-1 (see U04). This is in very good agreement with the low frequency detected in our photometry, which may therefore correspond to the rotation frequency or to a pulsational variation very close to it.
With the light curve fit from Table 2, we predicted the light curve for the night of the eclipse, subtracted it from the data, and show the rectified eclipse light curve in Fig. 5. The eclipse is a transit and about 0.03 mag deep. Eclipses of λ Sco have been seen before (Shobbrook & Lomb 1972, hereinafter SL72; Bruntt & Buzasi 2006) and are due to the closer pair in the λ Sco triple system (with an orbital period of 5.9525 d according to U04). Folding our data with this orbital period provides no evidence for the detection of a secondary eclipse; our data also do not cover the predicted times of further eclipses. From the primary’s and tertiary’s parameters inferred above, we thus obtain R1 = 8.8 ± 1.2 R⊙, R2 = 1.5 ± 0.2 R⊙, and R3 = 4.7 ± 1.0 R⊙. The secondary would then be a M2 = 2.0 ± 0.2 M⊙ star at the beginning of main sequence evolution.
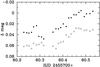 |
Fig. 5 Eclipse of λ Sco observed on the night of 17/18 July 2011. The filled circles are the v filter data, the open circles the measurements in y. |
The light curves by Bruntt & Buzasi (2006) allow to estimate that the eclipses of the primary of λ Sco by the secondary last about 8.5 h from mid-ingress to mid-egress. Unfortunately, the figures in this paper do not permit unambiguous eclipse timing determinations. We are therefore left with the partial eclipses in SL72’s and our data, as well as with two eclipses seen in the Hipparcos photometry of the star. The times of central eclipse determined from these data are listed in Table 3.
Times of central eclipse of the primary of λ Sco and comparison with the spectroscopic ephemeris of the close pair by U04.
Using the spectroscopic ephemeris of the close binary in λ Sco (U04), we can estimate an epoch zero of a potential eclipse of HJD 2 450 659.51 ± 0.06, and determine (O−C) values of the times of central eclipse for the 5.9525-d orbital period. These deviate considerably from the ephemeris (cf. Table 3). The light time effect caused by the tertiary component cannot be the cause of these (O−C) deviations because its maximum range can only be 0.03 d.
Consequently, we re-analysed the radial velocities by U04 with Period04. A fit with the two orbital periods, the first harmonic of the shorter orbital variation and with the dominant pulsation frequency resulted in an orbital period of the close system of 5.95242 ± 0.00004 d, within 3σ of U04. The formal error quoted here (cf. Montgomery & O’Donoghue 1999) is the same as given in U04. However, the data set is unevenly distributed: 74% of the radial velocities originate from only nine nights out of a total of 77, and the first two nights are separated by seven years from the remainder that also span seven years.
We therefore summed the data into bins separated by one pulsation period and repeated the frequency analysis (omitting the pulsation frequency). This resulted in an orbital period of the closer pair of 5.9522 ± 0.0002 d, and twice this uncertainty when not considering the first two nights. We therefore argue that the discrepancy between the spectroscopic orbital period of U04 and our eclipse timings is simply due to an earlier underestimate of the observational errors. Consequently we propose a refined value for the orbital period of the closer pair of 5.95189 ± 0.00003 d, to bring the photometric and spectroscopic measurements into agreement.
3.3. μ1 Sco
Given its brightness, its rather large light amplitude, and discovery as a spectroscopic binary already in the 19th century, there is rather little literature data for this eclipsing binary. On the other hand, a recent comprehensive study of this system was published by van Antwerpen & Moon (2010), wherefore it is of little point to repeat these authors’ work. However, we are interested in obtaining good binary light curve fits because the primary component is in the β Cephei instability strip and the secondary is in the domain of SPB stars.
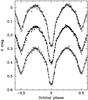 |
Fig. 6 Phased light curves of μ1 Sco according to the ephemeris by van Antwerpen & Moon (2010). The triangles are our u measurements, the filled circles are our v filter data, the open circles our measurements in y. The lines are fits to the data. |
We therefore applied the PHysics Of Eclipsing BinariEs (PHOEBE) code (Prša & Zwitter 2005) to our light curves, using the binary parameters from van Antwerpen & Moon (2010) as starting values. It is implied that the ephemeris given by these authors is still valid for our data (Fig. 6). However, according to our knowledge our measurements yielded the first photometric data of μ1 Sco in the ultraviolet. Indeed, irradiation of the cooler secondary (implemented in PHOEBE) had to be included to provide a fit our u data within the observational and analysis errors – as already predicted by Ruciński (1970).
Subtracting the light curve solution leaves non-white residuals with the two most interesting modulation frequencies around 0.123 and 8.07 c/d and about 3 mmag amplitude that are visible in all three filters’ data. These might correspond to intrinsic variability of at least one of the binary components, but do not reach the required S/N ≥ 4 to be considered as detected. Future BRITE data will enable us to investigate this possibility deeper.
3.4. ζ1 Sco
The light variations of this star are only discernible from night to night. Consequently, we show nightly averaged magnitude and colour variations of ζ1 Sco in Fig. 7. A period search in these data is (as to be expected from the light curves) not very revealing and implies a time scale of the variations of about two or four weeks. The latter is compatible with two of the variability periods of ζ1 Sco proposed by Sterken et al. (1997), but our data do not fold well with either of these two periods. There is also little colour variation associated with the light changes, in particular in (u − y), which can be taken as an argument against normal-mode pulsations.
 |
Fig. 7 Upper panel: our light curves of ζ1 Sco. The triangles are our u measurements, the filled circles are our v filter data, the open circles our measurements in y. Lower panel: the u − y (triangles) and v − y (filled circles) colour variations. |
ζ1 Sco is a very massive (M ≥ 36 M⊙) supergiant (Clark et al. 2012) and shows evidence for wind clumping (Prinja & Massa 2010). As a consequence of its high mass and luminosity, strange modes may be excited (Gautschy 2009). To us, these two possibilities appear to be more promising to explain the observed variability of the star, as opposed to normal mode pulsations.
4. Summary and conclusions
In anticipation of the BRITE-Constellation space mission, we have carried out time-resolved multicolour photometry of six diverse bright early-type stars in Scorpius, a sky region certainly interesting to be studied with BRITE. The magnitude range and temporal behaviour of those stars is also what is to be expected to be close to what a typical BRITE field will contain.
We have detected one long and one short period for each of the two known β Cephei stars κ and λ Sco. We observed part of an eclipse of the latter star and found a longer period in its light variation that has never been reported before. Due to the lack of ultraviolet data, we cannot provide a mode identification for λ Sco, but for κ Sco we were able to constrain l ≤ 1 for the dominant β Cephei pulsation mode. Together with spectroscopic results from the literature, this makes this mode most likely (l,m) = (1, −1). The uvy amplitudes of the longer period of κ Sco, are consistent with pulsation. However, a rotational origin can also not be ruled out, and a hypothesized longer-period pulsation would have a frequency very close to the rotational one.
A rotational modulation or g-mode pulsation may also be present in λ Sco on top of the known β Cephei oscillation. Previous analyses of this triple system are not in good agreement with its Hipparcos parallax and the pulsational behaviour of the primary. Therefore we argued that the components of this system are some 30% more massive than previously thought. We also noticed that the spectroscopic ephemeris of the close binary in the system does not predict observed eclipse timings correctly, and proposed a revised value for the orbital period.
We obtained full orbital coverage of the light curve of the known eclipsing binary μ1 Sco, and found its variability consistent with the latest ephemeris in the literature. We presented the first ultraviolet light curves of the system, which could only be satisfactorily modelled by including (long ago predicted) irradiation effects. There are hints of additional variability that may be pulsational in origin, which however remains to be revealed with BRITE-Constellation. Finally, our observations of the blue super/hypergiant ζ1 Sco showed variability on time scales of weeks, that we prefer to interpret in terms of wind variations or strange mode oscillations rather than normal mode pulsations.
Given the modest size of the present study, the number of new results on these bright stars is astounding. Part of the reason may be that ground based photometric studies of the brightest stars in the sky are technically difficult, wherefore comparatively less about them is known than for fainter stars. Consequently, we are eagerly looking forward to the new scientific results to be delivered by BRITE-Constellation.
Acknowledgments
This work was supported by the Polish NCN grant 2011/01/B/ST9/05448 and the BRITE PMN grant 2011/01/M/ST9/05914. We thank Bob Shobbrook for digitizing the archival observations of κ and λ Sco, Stefan Mochnacki for helpful discussions about binary star light curve modelling, and Katrien Uytterhoeven for providing her spectroscopic data of λ Sco.
References
- Asplund, M.,Grevesse, N.,Sauval, A. J., et al. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H., & Buzasi, D. 2006, Mem. Soc. Astron. It., 77, 278 [Google Scholar]
- Clark, J. S.,Najarro, F.,Negueruela, I., et al. 2012, A&A, 541, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuypers, J.,Buzasi, D., & Uytterhoeven, K. 2004, ASP Conf. Ser., 310, 251 [NASA ADS] [Google Scholar]
- Daszyńska-Daszkiewicz, J. 2008, Comm. Asteroseism., 152, 140 [Google Scholar]
- ESA 1997, The Hipparcos and Tycho catalogues, ESA SP, 1200 [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Gautschy, A. 2009, A&A, 498, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harmanec, P.,Uytterhoeven, K., & Aerts, C. 2004, A&A, 422, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lomb, N. R., & Shobbrook, R. R. 1975, MNRAS, 173, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Montgomery, M. H., & O’Donoghue, D. 1999, Delta Scuti Star Newsletter, 13, 28 (University of Vienna) [NASA ADS] [Google Scholar]
- Pamyatnykh, A. A.,Dziembowski, W. A.,Handler, G., & Pikall, H. 1998, A&A, 333, 141 [NASA ADS] [Google Scholar]
- Pesnell, W. D. 1985, ApJ, 292, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Prinja, R. K., & Massa, D. L. 2010, A&A, 521, L55 [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Ruciński, S. M. 1970, Acta Astr., 20, 327 [NASA ADS] [Google Scholar]
- Shobbrook, R. R., & Lomb, N. R. 1972, MNRAS, 156, 181 (SL72) [Google Scholar]
- Stankov, A., & Handler, G. 2005, ApJS, 158, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Sterken, C., de Groot, M., & van Genderen, A. M. 1997, A&A, 326, 640 [NASA ADS] [Google Scholar]
- Tango, W. J.,Davis, J.,Ireland, M. J., et al. 2006, MNRAS, 370, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Uytterhoeven, K.,Aerts, C., De Cat, P., et al. 2001, A&A, 422, 1013 [Google Scholar]
- Uytterhoeven, K.,Willems, B.,Lefever, K., et al. 2004, A&A, 427, 581 (U04) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uytterhoeven, K.,Briquet, M.,Aerts, C., et al. 2005, A&A, 432, 955 [Google Scholar]
- van Antwerpen, C., & Moon, T. T. 2010, MNRAS, 401, 2059 [NASA ADS] [CrossRef] [Google Scholar]
- Zwintz, K., & Kaiser, A. 2008, Commun. Asteroseismol, 152 [Google Scholar]
All Tables
Times of central eclipse of the primary of λ Sco and comparison with the spectroscopic ephemeris of the close pair by U04.
All Figures
 |
Fig. 1 Collected y-filter light curves of the low-amplitude and non-variables. Plus signs: ζ1 Sco. Diamonds: λ Sco. Filled circles: κ Sco. Open circles: μ2 Sco − υ Sco. The fits plotted over the κ Sco and λ Sco light curves are derived in Sects. 3.1 and 3.2. |
| In the text | |
 |
Fig. 2 Uppermost panel: spectral window of our v filter data of κ Sco. Second panel: amplitude spectrum of our data. Third panel: residual amplitude spectrum after prewhitening the dominant variation. Lower panel: residuals after prewhitening two frequencies. |
| In the text | |
 |
Fig. 3 A comparison of the observed amplitudes of κ Sco in the different filters with theoretical predictions of pulsational uvy amplitude ratios, normalized to unity at u. The filled circles with error bars are the observed amplitude ratios. The full lines are theoretical predictions for radial modes, the dashed lines for dipole modes, the dashed-dotted lines for quadrupole modes, the dotted lines for ℓ = 3 modes, and the dashed-triple-dotted lines are for ℓ = 4. The thin error bars denote the uncertainties in the theoretical amplitude ratios. |
| In the text | |
 |
Fig. 4 Upper panel: amplitude spectrum of our data of λ Sco with the eclipse discarded. Second panel: residual amplitude spectrum after prewhitening the dominant variation. Lower panel: residuals after prewhitening two frequencies. A peak at the harmonic of the first variation is present. |
| In the text | |
 |
Fig. 5 Eclipse of λ Sco observed on the night of 17/18 July 2011. The filled circles are the v filter data, the open circles the measurements in y. |
| In the text | |
 |
Fig. 6 Phased light curves of μ1 Sco according to the ephemeris by van Antwerpen & Moon (2010). The triangles are our u measurements, the filled circles are our v filter data, the open circles our measurements in y. The lines are fits to the data. |
| In the text | |
 |
Fig. 7 Upper panel: our light curves of ζ1 Sco. The triangles are our u measurements, the filled circles are our v filter data, the open circles our measurements in y. Lower panel: the u − y (triangles) and v − y (filled circles) colour variations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


