| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 6 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201321613 | |
| Published online | 03 September 2013 | |
Fluctuation dynamo amplified by intermittent shear bursts in convectively driven magnetohydrodynamic turbulence
1
Max-Planck-Institut für Plasmaphysik,
85748
Garching,
Germany
e-mail:
Jane.Pratt@ipp.mpg.de
2
Max-Planck-Institut für Sonnensystemforschung,
37191
Katlenburg-Lindau,
Germany
3 Faculty of Engineering and the Environment, University of
Southampton, UK
4
Center for Astronomy and Astrophysics, ER 3-2, TU Berlin,
Hardenbergstr. 36, 10623
Berlin,
Germany
Received:
31
March
2013
Accepted:
26
July
2013
Intermittent large-scale high-shear flows are found to occur frequently and spontaneously in direct numerical simulations of statistically stationary turbulent Boussinesq magnetohydrodynamic (MHD) convection. The energetic steady state of the system is sustained by convective driving of the velocity field and small-scale dynamo action. The intermittent emergence of flow structures with strong velocity and magnetic shearing generates magnetic energy at an elevated rate on time scales that are longer than the characteristic time of the large-scale convective motion. The resilience of magnetic energy amplification suggests that intermittent shear bursts are a significant driver of dynamo action in turbulent magnetoconvection.
Key words: convection / dynamo / magnetohydrodynamics (MHD) / turbulence / plasmas / Sun: dynamo
© ESO, 2013
1. Introduction
X-ray observations reveal that turbulent convection agitates the outer convection layer of stars (Güdel et al. 1997; Reiners & Basri 2007; Böhm-Vitense 2008; Simon et al. 2008). Measurements also show that planetary magnetic fields can change in magnitude and orientation (McFadden & Merrill 1995; Christensen et al. 2009; Stevenson 2010; Olson et al. 2011). Dynamo action driven by turbulent convection is accepted as the origin of solar and planetary magnetic fields. Key physical processes involved in turbulent convection and implicated in the amplification of magnetic fields remain to be identified and practically understood (Zeldovich et al. 1983; Biskamp 2003). Helicity, shear, and buoyancy remain intensely interesting to the dynamo problem (Tobias 2009; Wicht & Tilgner 2010; Weiss & Thompson 2009).
Because of the inherent nonlinearity of turbulent plasma flows, theoretical explanation of dynamo action is often approached by mean-field theory. Comparison with three-dimensional numerical simulations verifies and inspires theoretical models (Moll et al. 2011; Schrinner et al. 2005, 2007; Wilkin et al. 2007; Harder & Hansen 2005; Stanley & Glatzmaier 2010; Tobias et al. 2011). This work reports on a resilient and newly identified feature of characteristic dynamo action in three-dimensional, convectively driven, homogeneously turbulent, Boussinesq magnetoconvection based on pseudospectral direct numerical simulations using the magnetohydrodynamic (MHD) fluid approximation (Chandrasekhar 1961).
2. Simulation
Formulation of optimal boundary conditions for simulations of turbulent flows is delicate because boundaries strongly influence the structure and dynamics of the flow. The commonly used Rayleigh Bénard boundary conditions impose a temperature gradient to drive turbulent convection by fixing the temperature on impermeable top and bottom boundaries. For the Reynolds and Rayleigh numbers achievable with current numerical capabilities, the convection-cell pattern imposed on the flow by Rayleigh Bénard boundary conditions constrains the development of buoyantly driven turbulence.
The simulation volume considered in this work is confined by quasi-periodic rather than Rayleigh Bénard boundary conditions. The only deviation from full periodicity in the quasi-periodic boundary conditions is the explicit suppression of mean flows parallel to gravity, which are removed at each time step. Because our simulations are pseudospectral, the mean flow is straightforwardly isolated as the k = 0 mode in Fourier space, which corresponds to the volume-averaged velocity. The aim is to combine the conceptual simplicity of statistical homogeneity with a physically natural convective driving of the turbulent flow. In the flow allowed by the quasi-periodic boundary conditions we identify a process, the shear burst, in our simulation, which efficiently amplifies magnetic energy at all spatial scales in convective turbulence. This process can be relatively subtle, but arises in all cases considered in this work. The simulation model we employ is idealized, but can be viewed as a volume in an astrophysical or geophysical convective turbulent flow that is small in comparison to the pressure scale height.
Our system allows the study of a turbulent fluctuation dynamo (also known as a small-scale dynamo) in detail since the applied boundary conditions permit shear bursts on large spatial and temporal scales without enforcing a large-scale structuring of the turbulent flow. Hundreds of convective time scales prove necessary for the study of the shear bursts that arise spontaneously in simulations of steady-state convective MHD turbulence. Shear bursts are intermittent and spatially localized around high-shear flows. They are driven primarily at multiple large length scales that do not necessarily form a continuous band in wavenumber space, and that vary between bursts. A single isolated burst is not sufficient to maintain elevated magnetic energy; however, shear bursts can sometimes recur frequently, as shown in Fig. 1, providing an elevated growth of magnetic energy over significant periods of time. We address the properties of shear bursts and their importance for the understanding of the fluctuation-dynamo mechanism based on observations from high-resolution direct numerical simulations that span extended periods of time.
 |
Fig. 1 Magnetic energy, EB, is significantly amplified over long times due to repeated shear bursts in (above) simulation g1 and (below) simulation g11 (parameters described in Table 1). The signature of the shear burst, identified here with arrows, is clearly visible in the simultaneous peaks of the magnitude of the magnetic shear tensor ∇iBj, and magnetic stretching tensor Bi∇iuj, which have been normalized to their initial-time values for easy comparison. The magnitude of the velocity shear tensor ∇ivj closely follows the magnetic shear. The magnitude of these tensors is calculated as a sum of the squares of the elements. Shear, and therefore magnetic stretching, drive the intermittent growth of magnetic energy. |
The non-dimensional Boussinesq equations for MHD convection are 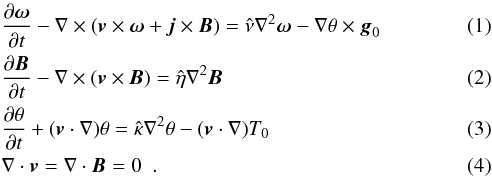 The
equations include the solenoidal velocity field v, vorticity
ω = ∇ × v, magnetic field
B, and current
j = ∇ × B. The quantity
θ denotes the temperature fluctuation about a linear mean temperature
profile T0(z) where z is the
direction of gravity. In Eq. (3) this mean
temperature provides the convective drive of the system. In Eq. (1), the term including the temperature
fluctuation θ is the buoyancy force. The vector
g0 is a unit vector in the direction of gravity.
These equations are solved using a pseudospectral method with an adaptive time integration
accomplished by a low-storage third-order Runge Kutta scheme (Williamson 1980).
The
equations include the solenoidal velocity field v, vorticity
ω = ∇ × v, magnetic field
B, and current
j = ∇ × B. The quantity
θ denotes the temperature fluctuation about a linear mean temperature
profile T0(z) where z is the
direction of gravity. In Eq. (3) this mean
temperature provides the convective drive of the system. In Eq. (1), the term including the temperature
fluctuation θ is the buoyancy force. The vector
g0 is a unit vector in the direction of gravity.
These equations are solved using a pseudospectral method with an adaptive time integration
accomplished by a low-storage third-order Runge Kutta scheme (Williamson 1980).
Turbulent convective motion defines the characteristic time and length scales of the
system: the large-scale buoyancy time,
tb = (αg|∇T0|)−1/2
and temperature gradient length scale
L = T∗/∇T0
where T∗ is defined as the root-mean-square of temperature
fluctuations θ. The volume thermal expansion coefficient at constant
pressure is α, and the gravitational acceleration is g
(Gibert et al. 2006; Škandera & Müller 2009). The magnetic field is given in Alfvénic
units, with Alfvén Mach number
v0/vA = 1,
v0 = L/tb.
Three dimensionless parameters appear in the equations:
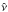 ,
,
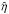 ,
and
,
and 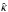 .
They derive from the kinematic viscosity ν, the magnetic diffusivity
η, and thermal diffusivity κ and can formally be
identified as the reciprocal value of classical Reynolds number, magnetic Reynolds number,
and Péclet numbers, respectively (see Table 1 for
definitions).
.
They derive from the kinematic viscosity ν, the magnetic diffusivity
η, and thermal diffusivity κ and can formally be
identified as the reciprocal value of classical Reynolds number, magnetic Reynolds number,
and Péclet numbers, respectively (see Table 1 for
definitions).
To investigate the influence of diffusivities on the shear burst phenomena, parameters
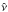 ,
,
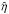 ,
and
,
and 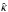 are varied; consequently the simulations probe values of the Prandtl
are varied; consequently the simulations probe values of the Prandtl
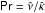 and the magnetic Prandtl number
and the magnetic Prandtl number 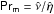 spread between 0.5 and 2. The magnetic Prandtl number has been shown to exhibit a
significant effect on small-scale dynamo action (Boldyrev
& Cattaneo 2004; Schekochihin et al.
2005); the dependence of the dynamo mechanism on Prandtl number has been the
subject of several wide-ranging investigations (Schmalzl et
al. 2002; Maron et al. 2004; Simitev & Busse 2005). Realistically small
Prandtl numbers cannot be reached with contemporary computer capabilities; in the solar
convection zone expected values are Prm ~ 10-4−10-7 and
in the earth’s core Prm ~ 10-6. Simultaneously, Reynolds numbers are
generally expected to be larger than can be computationally reached: Re ~ 1013 in
the solar convection zone and Re ~ 108 in the earth’s core (summarized in Busse 2009). Because of this discrepancy, the dynamical
ranges of fluctuations in modern simulations are smaller than those expected in real
systems. Our simulations thus present a first impression of the role of shear bursts for
astrophysical dynamos.
spread between 0.5 and 2. The magnetic Prandtl number has been shown to exhibit a
significant effect on small-scale dynamo action (Boldyrev
& Cattaneo 2004; Schekochihin et al.
2005); the dependence of the dynamo mechanism on Prandtl number has been the
subject of several wide-ranging investigations (Schmalzl et
al. 2002; Maron et al. 2004; Simitev & Busse 2005). Realistically small
Prandtl numbers cannot be reached with contemporary computer capabilities; in the solar
convection zone expected values are Prm ~ 10-4−10-7 and
in the earth’s core Prm ~ 10-6. Simultaneously, Reynolds numbers are
generally expected to be larger than can be computationally reached: Re ~ 1013 in
the solar convection zone and Re ~ 108 in the earth’s core (summarized in Busse 2009). Because of this discrepancy, the dynamical
ranges of fluctuations in modern simulations are smaller than those expected in real
systems. Our simulations thus present a first impression of the role of shear bursts for
astrophysical dynamos.
 |
Fig. 2 Total kinetic, magnetic and thermal energies during the initial growth phase of the dynamo in simulation g2. |
3. Results
The numerical turbulence data in this work results from a set of simulations conducted with
grid size 5123, which constitutes high resolution for the extremely long times
treated here. These simulations are performed in a quasi-periodic slab or cube; the cube has
a side of 2π, and the slab has slightly larger x- and
y-directions of (2π)3/2 to
allow for the well-defined initial onset of the convective instability driving the
turbulence (Chandrasekhar 1961). Our boundary
conditions inhibit the formation of viscous boundary layers, which appear when impermeable
boundary conditions are employed. The dissipative coefficients
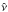 ,
,
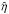 ,
and
,
and 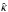 parametrize the extent of the turbulent inertial range of scales, and in each simulation are
chosen to be as small as possible so that the resolution constraint of
kmaxηkol > 1.5
is still satisfied (Pope 2000). Here,
kmax is the largest resolvable wavenumber allowed by numerical
resolution and ηkol is the Kolmogorov length scale. We performed
simulations for the wide range of parameters summarized in Table 1 in order to test for a possible dependence of the shear burst phenomenon
on the Reynolds numbers and Prandtl numbers. Shear bursts occurred in all of the simulations
listed. The Rayleigh number, characterizing the dynamical importance of buoyancy in
Rayleigh-Bènard configurations, is of limited informative value for the present
quasi-periodic system.
parametrize the extent of the turbulent inertial range of scales, and in each simulation are
chosen to be as small as possible so that the resolution constraint of
kmaxηkol > 1.5
is still satisfied (Pope 2000). Here,
kmax is the largest resolvable wavenumber allowed by numerical
resolution and ηkol is the Kolmogorov length scale. We performed
simulations for the wide range of parameters summarized in Table 1 in order to test for a possible dependence of the shear burst phenomenon
on the Reynolds numbers and Prandtl numbers. Shear bursts occurred in all of the simulations
listed. The Rayleigh number, characterizing the dynamical importance of buoyancy in
Rayleigh-Bènard configurations, is of limited informative value for the present
quasi-periodic system.
Dimensionless simulation parameters.
The initial state of the simulations contains fluctuations in a number of small k modes for the velocity, magnetic field, and temperature. The initial ratio of kinetic to magnetic energy of turbulent fluctuations is 106 with the kinetic energy of order unity. Figure 2 shows a typical example of the initial time-evolution of kinetic energy Ev = V-1∫VdVv2/2, magnetic energy EB = V-1∫VdVB2, and thermal energy ET = V-1∫VdVθ2 taken from simulation g2. The thermal energy should be understood as the variance of temperature fluctuations. Magnetic energy rises quickly due to small-scale dynamo action and saturates at Ev/EB ≈ O(1), characteristic of the quasi-stationary turbulent state of the MHD flow.
In Fig. 2 the global energies of the steady-state system evolve with fluctuations due to the convective motion. After a simulation reaches steady state, energies fluctuate on the order of 10%, with a period of a 1−2 buoyancy times (see also Fig. 5 of Cattaneo 1999a). During steady-state turbulent convection, we begin to observe a pattern of spontaneous longer periods (5−20 tb) of significant growth in the global magnetic, thermal and kinetic energies. During the kinematic stage of the dynamo, before steady-state convection is reached, we find no evidence of these physically interesting periods of energy growth. The net energy variation during one such period can differ greatly, but we observe the energy to reach 10 times the steady-state energy level during particularly strong instances. For example, these periods of unusually elevated energy growth occur 15 times, unevenly spaced over a time span of 225 tb, in the simulation g1. We associate the growth of energy during these periods with the shear burst phenomena. Shear bursts can occur in close sequence, but do not universally do so. The system can be regarded as statistically steady over periods of time significantly longer than the duration of a shear burst.
 |
Fig. 3 A hot (black) flow moves vigorously along a path upward from the bottom left corner, bending through the middle of the volume, and eventually turning downward again, shearing against a cold (light blue) flow. The shear along these opposing flow structures drives energy production during a shear burst. |
A shear burst centers around a period of increased growth of magnetic energy that is accompanied by growth of both magnetic shear and magnetic stretching. The growth rate of magnetic energy during a shear burst is uneven, and can vary wildly between shear bursts in the same simulation. Preceding the growth of magnetic energy, a coherent flow structure forms that has the appearance of high-velocity, hot or cold coherent streams, in contrast to the typical situation with many smoothly convecting plumes of hot and cold fluid. These high-energy streams become strongly aligned in space, producing regions of high and increasing velocity and magnetic shear. The nonlinear shape and orientation of the high-energy streams differ for each shear burst, displaying no preferred direction. The coherent flows that form in one instance of a shear burst are depicted in Fig. 3.
 |
Fig. 4 Global kinetic energy Ev, magnetic energy EB, and thermal energy ET scaled to run between 0 and 1, for the span of a typical shear burst in simulation g8. |
Shear causes magnetic field-line stretching, and thus amplification of magnetic energy (Childress & Gilbert 1995; Cattaneo 1999b). In Fig. 1 each shear burst can be defined by a peak in magnetic shear that correlates with an increase in magnetic energy. Figure 4 allows for closer inspection of the increase of magnetic, kinetic, and thermal energies for a typical isolated shear burst in simulation g8; between t = 225 and t = 235 the energies increase by a factor of three. Individual shear bursts can last from a couple buoyancy times to a couple tens of buoyancy times. At the peak of magnetic and kinetic energies, high energy hot and cold shearing is at its most vigorous. The flow structures lose their alignment, slow down, and ultimately break-up. The peak of global energy in Fig. 4 represents the beginning of the break-up of flow structures. The break-up of the fast streams spurs a slow decline in global energies. After the shear burst has dissipated, the energies dissipate until the steady-state level maintained by the fluctuation dynamo has been reached. Shear bursts can overlap in time, and also can occur closely in sequence, as shown in Fig. 1.
 |
Fig. 5 Characteristic double peak from two closely spaced shear bursts in simulation g11 is visible in magnetic helicity. The magnetic helicity HM at low-wavenumbers k is shown scaled to its initial time-value with sign preserved. Magnetic helicity quantities are shown scaled to their initial time values in a way that preserves sign. The magnitude of the magnetic stretching tensor is shown shifted and scaled to fit the scale of the magnetic helicity, to provide a time-reference for the shear bursts. |
 |
Fig. 6 (Above) probability distribution and (below) cumulative distribution of local magnetic helicity, i.e. dHM = A·B in the simulation volume before and during a shear burst event in simulation g1. During this shear burst, as the global magnetic helicity grows, the tail of negative magnetic helicity grows, and grows much higher than the positive tail. |
The lifetime and magnitude of the energy growth, in particular the peak in thermal energy, can vary greatly between simulations and even between shear bursts in the same simulation. This shows no apparent dependence on the Prandtl numbers. That the Prandtl numbers do not directly impact the shear burst phenomena is surprising because the Prandtl numbers express the ratio of turbulent intensities and dynamic ranges of the respective turbulent fields. This relationship between Prandtl numbers and the turbulence can be understood by relating the Prandtl numbers to the ratios of Reynolds numbers, Pr = Pe/Re and Prm = Rem/Re, where the Péclet number can be regarded as the same structure as a Reynolds number for thermal fluctuations.
The characteristic length-scale of Boussinesq convection is the Bolgiano-Obukhov length,
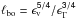 that separates convectively-driven scales of the flow
ℓ > ℓbo from the
range of scales where the temperature fluctuations behave as a passive scalar
ℓ < ℓbo. In this
definition ϵv and ϵT are the kinetic
and thermal energy dissipations respectively. Typically in our convection simulations
ℓbo is comparable to the system size so only the largest
scales in the flow are convectively driven. The shear bursts are large-scale phenomena by
this classification, but are not dominated by the convective motion. This suggests an
explanation for the apparent insensitivity to changes in the Prandtl numbers.
that separates convectively-driven scales of the flow
ℓ > ℓbo from the
range of scales where the temperature fluctuations behave as a passive scalar
ℓ < ℓbo. In this
definition ϵv and ϵT are the kinetic
and thermal energy dissipations respectively. Typically in our convection simulations
ℓbo is comparable to the system size so only the largest
scales in the flow are convectively driven. The shear bursts are large-scale phenomena by
this classification, but are not dominated by the convective motion. This suggests an
explanation for the apparent insensitivity to changes in the Prandtl numbers.
Although insensitive to the Prandtl numbers, the shear bursts interact nonlinearly with the turbulent environment, mainly via large-scale magnetic structures. This is reflected in the behavior of magnetic helicity, HM = V-1∫VdVA·B, which measures the linkage and knottiness of the magnetic field-lines (Biskamp 2000; Moffatt 1978). A signature of the shear burst is the growth of global magnetic helicity as the shear flows strengthen. Magnetic helicity is not conserved in the dissipative system we study, and this growth of magnetic helicity typically exceeds more than a standard deviation from the average magnetic helicity over the time-span of the simulation. A peak of global magnetic helicity frequently shortly precedes or coincides with a shear burst. Figure 5 shows the typical time-evolution of the magnetic stretching against the growth of global magnetic helicity and magnetic helicity at the largest scales. In the time pictured, two shear-busts occur within 5 tb, and a clear double-peak structure is also visible in the magnetic helicity.
The magnetic helicity grows particularly in low wavenumbers k, associated with the growth of an isolated structure with a strong helicity polarity; this low-k growth is a signature of an ongoing inverse spectral transfer of magnetic helicity common for 3D MHD systems (Müller et al. 2012; Biskamp 2003; Alexakis et al. 2008). The dramatic change in the bias of magnetic helicity in the system during one shear burst is shown in Fig. 6; in Fig. 5 the large-scale magnetic helicity of the structures spawned also has negative polarity for the two shear bursts pictured. Large-scale magnetic helicity structures persist longer than the high-energy shear streams, and longer than it takes for the global energies to taper off. Because the magnetic helicity experiences an inverse cascade and our system has small dissipation this is theoretically expected.
Shear bursts generate significant currents through magnetic shear, which change the global magnetic helicity. When no shear burst is present in the system small filaments of high current are common and likely indicate slow reconnection on small scales. However when a shear burst grows, large-scale high-current structures grow at the same time. A typical growth in current around a shear burst is shown in Fig. 7.
 |
Fig. 7 Current-squared in the lowest wavenumbers k = 1,2,3,4 scaled to its initial time-value during a shear burst in simulation g2. Global current-squared and magnetic shear are shown scaled and shifted to fit on the same scale for reference. |
In simulations similar to those discussed in this work, but performed with fully-periodic boundary conditions (sometimes called homogenous Rayleigh Bénard boundary conditions), the macroscopic elevator instability as it is presented by Calzavarini et al. (2006, 2005); Škandera (2007) can be readily identified. The elevator instability is an exact solution to the equations of motion in the homogeneous system. It is an extreme realization of the fact that the homogeneous, incompressible flow can gain vast amounts of energy by coherent large-scale vertical motions. The elevator instability creates parallel, vertical jets (kz = 0) of alternating direction throughout the volume that significantly degrade the quality of turbulence statistics. The flow pattern created by this elevator instability fully destroys the original, natural flow field. The instability can be eliminated in homogeneous Boussinesq systems by considering a horizontal mean temperature gradient (Škandera & Müller 2009).
In the quasi-periodic simulations presented in this work, we find no evidence of this instability although we follow the simulations for extremely long times. Mean flows parallel to gravity are manually suppressed in our quasi-periodic set-up. In contrast to the elevator instability, shear bursts are embedded into the turbulence and have limited coherence and lifetime with regard to the full flow-field. Shear bursts do not exhibit exponential growth of energy nor is their growth rate dependent on clear system parameters like the Prandtl number. The shear burst is superficially similar to the elevator instability because both involve coherent flows. However, the coherent flows associated with a shear burst do not display a preference for any fixed spatial direction, but follow a sometimes complicated, curved path in a localized section of the simulation volume. This flow path can change during the evolution of the shear burst, and is different for each shear burst. When the violent elevator instability is present, it is likely to mask finer-scale processes like the shear burst.
4. Conclusions
We have isolated a basic mechanism of dynamo action in MHD convection that operates through spontaneously developing, intermittent bursts of high shear during steady-state dynamo action. Because this process occurs in all simulations considered here, it is of potential importance for astrophysical small-scale dynamo action in turbulent convection scenarios. Shear bursts consist of the formation of coherent, highly-sheared flows along-side magnetic structures with a strong magnetic-helicity polarity bias. The slow growth and eventual decay of the magnetic helicity structure is key to the shear burst phenomenon. The increasing shear causes a gradual rise in energy on all spatial scales due to magnetic stretching in the system over several buoyancy times. After some time, the shear flows lose their alignment and decay. Once the shear flows are destroyed, the elevated energy dissipates over several buoyancy times. Closely spaced shear bursts can occur in a series, creating long periods of time where magnetic energy is elevated significantly above the steady state.
Acknowledgments
This work has been supported by the Max-Planck Society in the framework of the Inter-institutional Research Initiative Turbulent transport and ion heating, reconnection and electron acceleration in solar and fusion plasmas of the MPI for Solar System Research, Katlenburg-Lindau, and the Institute for Plasma Physics, Garching (project MIFIF- A-AERO8047). Simulations were performed on the VIP computer system at the Rechenzentrum Garching of the Max Planck Society.
References
- Alexakis, A., Mininni, P. D., & Pouquet, A. 2008, ApJ, 640, 335 [Google Scholar]
- Biskamp, D. 2000, Magnetic Reconnection in Plasmas (Cambridge: Cambridge University Press) [Google Scholar]
- Biskamp, D. 2003, Magnetohydrodynamic Turbulence (Cambridge: Cambridge University Press) [Google Scholar]
- Böhm-Vitense, E. 2008, ApJ, 657, 486 [Google Scholar]
- Boldyrev, S., & Cattaneo, F. 2004, Phys. Rev. Lett., 92, 144501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Busse, A. 2009, Ph.D. Thesis, Universität Bayreuth [Google Scholar]
- Calzavarini, E., Lohse, D., Toschi, F., & Tripiccione, R. 2005, Phys. Fluids, 17, 055107 [NASA ADS] [CrossRef] [Google Scholar]
- Calzavarini, E., Doering, C. R., Gibbon, J. D., et al. 2006, Phys. Rev. E, 73, 035301(R) [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, F. 1999a, in Motions in the solar atmosphere: Proc. of the summerschool and workshop held at the Solar Observatory Kanzelhöhe Kärnten, Austria, September 1−12, 1997, ed. M. M. Arnold Hanslmeier (Springer Verlag) [Google Scholar]
- Cattaneo, F. 1999b, ApJ, 515, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and hydromagnetic stability (Oxford: Oxford University Press) [Google Scholar]
- Childress, S., & Gilbert, A. D. 1995, Stretch, twist, fold: the fast dynamo (Springer Verlag), Lect. Notes Phys., 37 [Google Scholar]
- Christensen, U. R., Holzwarth, V., & Reiners, A. 2009, Nature, 457, 167 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gibert, M., Pabiou, H., Chillà, F., & Castaing, B. 2006, Phys. Rev. Lett., 96, 084501 [NASA ADS] [CrossRef] [Google Scholar]
- Güdel, M., Guinan, E. F., & Skinner, S. L. 1997, ApJ, 483, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Harder, H., & Hansen, U. 2005, Geophys. J. Int., 161, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Maron, J., Cowley, S., & McWilliams, J. 2004, ApJ, 603, 569 [NASA ADS] [CrossRef] [Google Scholar]
- McFadden, P., & Merrill, R. 1995, Phys. Earth Planet. Inter., 91, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Moffatt, H. 1978, Magnetic Field Generation in Electrically Conducting Fluids (Cambridge University Press) [Google Scholar]
- Moll, R., Graham, J. P., Pratt, J., et al. 2011, ApJ, 736, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, W.-C., Malapaka, S. K., & Busse, A. 2012, Phys. Rev. E, 85, 015302 [NASA ADS] [CrossRef] [Google Scholar]
- Olson, P. L., Glatzmaier, G. A., & Coe, R. S. 2011, Earth Planet. Sci. Lett., 304, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Pope, S. B. 2000, Turbulent Flows (Cambridge: Cambridge University Press) [Google Scholar]
- Reiners, A., & Basri, G. 2007, ApJ, 656, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Haugen, N. E. L., Brandenburg, A., et al. 2005, ApJ, 625, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Schmalzl, J., Breuer, M., & Hansen, U. 2002, Geophys. Astro. Fluid, 96, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M., & Christensen, U. 2005, AN, 326, 245 [Google Scholar]
- Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M., & Christensen, U. R. 2007, Geophys. Astro. Fluid, 101, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Simitev, R., & Busse, F. 2005, JFM, 532, 365 [Google Scholar]
- Simon, T., Ayres, T. R., Redfield, S., & Linsky, J. L. 2008, ApJ, 579, 800 [Google Scholar]
- Stanley, S., & Glatzmaier, G. A. 2010, Space Sci. Rev., 152, 617 [Google Scholar]
- Stevenson, D. J. 2010, Space Sci. Rev., 152, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Tobias, S. 2009, in The Origin and Dynamics of Solar Magnetism, eds. M. Thompson, A. Balogh, J. Culhane, et al. (New York: Springer), Space Sci. Ser. ISSI, 77, 32 [Google Scholar]
- Tobias, S. M., Cattaneo, F., & Brummell, N. H. 2011, ApJ, 728, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Škandera, D. 2007, Ph.D. Thesis, Technische Universität München [Google Scholar]
- Škandera, D., & Müller, W.-C. 2009, Phys. Rev. Lett., 102, 224501 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, N., & Thompson, M. 2009, Space Sci. Rev., 144, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Wicht, J., & Tilgner, A. 2010, Space Sci. Rev., 152, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkin, S. L., Barenghi, C. F., & Shukurov, A. 2007, Phys. Rev. Lett., 99, 134501 [NASA ADS] [CrossRef] [Google Scholar]
- Williamson, J. H. 1980, J. Comput. Phys., 35, 48 [Google Scholar]
- Zeldovich, Y. B., Ruzmaikin, A. A., & Sokoloff, D. D. 1983, Magnetic Fields In Astrophysics (New York: Gordon and Breach Science Publishers) [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Magnetic energy, EB, is significantly amplified over long times due to repeated shear bursts in (above) simulation g1 and (below) simulation g11 (parameters described in Table 1). The signature of the shear burst, identified here with arrows, is clearly visible in the simultaneous peaks of the magnitude of the magnetic shear tensor ∇iBj, and magnetic stretching tensor Bi∇iuj, which have been normalized to their initial-time values for easy comparison. The magnitude of the velocity shear tensor ∇ivj closely follows the magnetic shear. The magnitude of these tensors is calculated as a sum of the squares of the elements. Shear, and therefore magnetic stretching, drive the intermittent growth of magnetic energy. |
| In the text | |
 |
Fig. 2 Total kinetic, magnetic and thermal energies during the initial growth phase of the dynamo in simulation g2. |
| In the text | |
 |
Fig. 3 A hot (black) flow moves vigorously along a path upward from the bottom left corner, bending through the middle of the volume, and eventually turning downward again, shearing against a cold (light blue) flow. The shear along these opposing flow structures drives energy production during a shear burst. |
| In the text | |
 |
Fig. 4 Global kinetic energy Ev, magnetic energy EB, and thermal energy ET scaled to run between 0 and 1, for the span of a typical shear burst in simulation g8. |
| In the text | |
 |
Fig. 5 Characteristic double peak from two closely spaced shear bursts in simulation g11 is visible in magnetic helicity. The magnetic helicity HM at low-wavenumbers k is shown scaled to its initial time-value with sign preserved. Magnetic helicity quantities are shown scaled to their initial time values in a way that preserves sign. The magnitude of the magnetic stretching tensor is shown shifted and scaled to fit the scale of the magnetic helicity, to provide a time-reference for the shear bursts. |
| In the text | |
 |
Fig. 6 (Above) probability distribution and (below) cumulative distribution of local magnetic helicity, i.e. dHM = A·B in the simulation volume before and during a shear burst event in simulation g1. During this shear burst, as the global magnetic helicity grows, the tail of negative magnetic helicity grows, and grows much higher than the positive tail. |
| In the text | |
 |
Fig. 7 Current-squared in the lowest wavenumbers k = 1,2,3,4 scaled to its initial time-value during a shear burst in simulation g2. Global current-squared and magnetic shear are shown scaled and shifted to fit on the same scale for reference. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


