| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321420 | |
| Published online | 19 September 2013 | |
Evidence of direct detection of interstellar deuterium in the local interstellar medium by IBEX
1 Physics Institute, University of Bern, Sidlerstrasse 5, 3012 Bern, Switzerland
e-mail: diego.rodriguez@space.unibe.ch
2 Space Research Centre, Polish Academy of Sciences, Bartycka 18A, 00–716 Warsaw, Poland
3 Department of Astronomy and Astrophysics, University of Chicago, 5640 S. Ellis Avenue, Chicago, IL 60637, USA
4 Southwest Research Institute, San Antonio, TX 78228–0510, USA and University of Texas at San Antonio, San Antonio, TX 78249, USA
5 Space Science Center and Department of Physics, University of New Hampshire, 39 College Road, Durham, NH 03824, USA
Received: 6 March 2013
Accepted: 16 July 2013
We report the first in situ measurements of neutral deuterium originating in the local interstellar medium (LISM) in Earth’s orbit. These measurements were performed with the IBEX-Lo camera on NASA’s interstellar boundary explorer (IBEX) satellite. All data from the spring observation periods of 2009 through 2011 have been analysed. In the three years of the IBEX mission time, the observation geometry and orbit allowed for a total observation time of 115.3 days for the LISM. However, the effects of the spinning spacecraft and the stepping through 8 energy channels mean that we are only observing the interstellar wind for a total time of 1.44 days, in which 2 counts for interstellar deuterium were collected. We report here a conservative number, because a possibility of systematic error or additional noise, though eliminated in our analysis to the best of our knowledge, only supports detection at a 1-sigma level. From these observations, we derive a ratio D/H = (5.8 ± 4.4) × 10-4 at 1 AU. After modelling the transport and loss of D and H from the termination shock to Earth’s orbit, we find that our result of D/HLISM = (1.6 ± 1.2) × 10-5 agrees with D/HLIC = (1.6 ± 0.4) × 10-5 for the local interstellar cloud. This weak interstellar signal is extracted from a strong terrestrial background signal consisting of sputter products from the sensor’s conversion surface. As reference, we accurately measure the terrestrial D/H ratio in these sputtered products and then discriminate this terrestrial background source. Because of the diminishing D and H signal at Earth’s orbit during the rising solar activity due to photoionisation losses and increased photon pressure, our result demonstrates that in situ measurements of interstellar deuterium in the inner heliosphere are only possible during solar minimum conditions.
Key words: ISM: general / interplanetary medium / primordial nucleosynthesis / nuclear reactions, nucleosynthesis, abundances
© ESO, 2013
1. Introduction
In situ measurements of the interstellar D/H ratio by the interstellar boundary explorer satellite (McComas et al. 2009a) provide a new window on the chemical evolution of our galaxy. According to big bang cosmology, deuterium is produced in significant amounts only during primordial nucleosynthesis in the first 100–1000 s of the universe. Over time, baryonic matter is processed through stars where deuterium is destroyed by nuclear reactions (astration). Deuterium-poor and metal-rich material is returned to the interstellar medium in supernova explosions and stellar winds. Within our galaxy, deuterium is removed from the interstellar medium through astration and replenished by the accretion of pristine material onto the galaxy (Prodanović & Fields 2008; Yuan et al. 2012; Linsky 2003, 2007). With time, the D/H ratio in the galaxy should thus decreases and metal abundances should increase. As a result, measurements of the D abundance in different locations of the galaxy provide important tests for models of primordial nucleosynthesis and for the chemical evolution of the galaxy and intergalactic medium (IGM).
Local abundances of neutral deuterium in the interstellar gas are affected by photoionisation, deuterium depletion onto interstellar dust grains, and the evolutionary processing of dust grains in the interstellar medium (Linsky 2007). In the low density, warm, partially ionised LIC where fluxes of far ultraviolet radiation are high (Slavin & Frisch 2008; Frisch et al. 2009, 2011; McComas et al. 2012), the fractional abundance of deuterium in molecular form is expected to be insignificant. The mean deuterium abundance in the low density local bubble within 100 pc is D/H = 15.6 ± 0.4 ppm (Linsky et al. 2006). However, Linsky et al. (2006) have found that in the global interstellar medium the interstellar deuterium abundances vary within a factor four with a complex dependence on the hydrogen column densities. Before IBEX, the deuterium abundance in the local interstellar cloud (LIC) could only be investigated using spectroscopic measurements of the heavily blended deuterium and hydrogen Lyman-alpha lines towards nearby stars. The closest star showing representing the LIC is Sirius, where the D/H ratio of 16 ± 4 ppm is typical of the local bubble interior (Hébrard et al. 1999). The in situ D/H measurements should be consistent with the Sirius measurements, unless the chemical composition of the LIC gas is inhomogeneous or the LIC is not in an equilibrium state.
1.1. Interstellar wind at 1 AU
The local interstellar medium (LISM) is a warm, relatively dilute, partially ionised interstellar gas where the Sun resides and moves through (Slavin & Frisch 2008; Frisch et al. 2011; McComas et al. 2012). Because the Sun continuously ejects coronal plasma as the solar wind (mostly protons and electrons with frozen-in magnetic field), it inflates a bubble in the interstellar medium: the heliosphere, which effectively shields the LISM plasma from a region >100 AU around the Sun. That interaction determines the shape and structure of the heliosphere (e.g., Müller et al. 2006), which is one of the major scientific objectives of IBEX (McComas et al. 2009a). The behaviour of interstellar neutrals interacting with the heliosphere can be directly measured and thus provides the best paradigm for modelling and understanding the interplanetary environments of astrospheres (Fahr 1978).
Transport and survival of neutral interstellar atoms from the LISM to 1 AU is different for each species. While approaching the inner heliosphere, the interstellar wind is depleted of many neutral species by ionisation processes and affected by the Sun’s gravitational field (modified by radiation pressure for H and D). This forms a characteristic flow pattern and density structure with a cavity close to the Sun and with gravitational focusing on the downwind side (for all species except H, which forms a shadow; McComas et al. 2004; Möbius et al. 2012; Bzowski et al. 2012). Ionisation processes that affect the interstellar neutrals are: UV photon ionisation, charge exchange with solar wind ions, and electron impact ionisation (Ruciński et al. 1996; Möbius et al. 2004; Bzowski 2008; Bzowski et al. 2012).
The individual components of the interstellar wind have a different fate according to their interaction with the Sun and the solar wind. In the case of helium, the dominant ionisation process is UV ionisation, except within ~1 AU, where the steep radial dependence of electron impact ionisation produces high ionisation rates. Helium flows through the heliospheric boundary mostly unimpeded, because it has a high ionisation potential and low cross section for charge exchange with solar wind alpha particles and protons. A substantial fraction for hydrogen, in contrast to He, interacts with the plasma in the outer heliosheath by its principal ionisation process, which is charge exchange (CEX) with 1) the interstellar proton population that is compressed against the heliopause and 2) solar wind protons in the inner heliosheath. Charge exchange losses are much larger than losses by UV ionisation (Möbius et al. 2012) with both processes having a solar cycle dependence. Charge exchange results in the formation of the secondary population of neutral H, which are neutralised protons from the outer heliosheath. Both the primary and secondary populations enter the heliosphere, where they are subject to strong charge exchange and photoionisation losses. As a result, most of the neutral hydrogen becomes ionised and does not reach 1 AU, where IBEX resides. At 1 AU, the residual interstellar wind is composed mostly of helium (Saul et al. 2012) with a low fraction of hydrogen and other constituents, whose abundances decrease with increasing solar activity.
The cross sections for photoionisation, charge exchange, and electron impact ionisation of D are practically identical to that of H, thus leading to identical H and D ionisation rates (Tarnopolski & Bzowski 2008). However, some details do differ: the thermal speed of D in the LIC is lower with 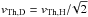 (Kubiak et al. 2013). Thus, the reaction rates are slightly different, and the dynamics of D are significantly different from H, because the radiation pressure does not counterbalance gravitational effects as it tends to do for H. The radiation pressure of D is affected by an isotope shift of Lyman-alpha wavelength of D relative to H of 0.3 Å. As mentioned above, He is not affected by radiation pressure. The pressure for D is expected to be in between the pressure for H and the (zero) pressure for He. During the IBEX observations along Earth’s orbit, the maximum D signal is thus expected after the maximum of He and O and before the maximum of H. Dynamics are complicated by the strong dependence of the effective force on radial velocity (Tarnopolski & Bzowski 2008; Kubiak et al. 2013).
(Kubiak et al. 2013). Thus, the reaction rates are slightly different, and the dynamics of D are significantly different from H, because the radiation pressure does not counterbalance gravitational effects as it tends to do for H. The radiation pressure of D is affected by an isotope shift of Lyman-alpha wavelength of D relative to H of 0.3 Å. As mentioned above, He is not affected by radiation pressure. The pressure for D is expected to be in between the pressure for H and the (zero) pressure for He. During the IBEX observations along Earth’s orbit, the maximum D signal is thus expected after the maximum of He and O and before the maximum of H. Dynamics are complicated by the strong dependence of the effective force on radial velocity (Tarnopolski & Bzowski 2008; Kubiak et al. 2013).
With the neutral atom detection technology available today (Wurz 2000), it becomes feasible to measure the D density in the interstellar wind by direct detection of neutral deuterium atoms in situ in the inner heliosphere. Interstellar boundary explorer (McComas et al. 2009a) is a state-of-the-art implementation of neutral atom detection that has the capability dedicated to the detection of interstellar neutral atoms. To date, IBEX has directly detected neutral interstellar H (Möbius et al. 2009a; Saul et al. 2012), He (Möbius et al. 2009a, 2012; Bzowski et al. 2012), Ne, and O (Möbius et al. 2009a; Bochsler et al. 2012). In the following, we show the detection of neutral interstellar D with the IBEX-Lo instrument.
1.2. Overview of the IBEX mission
NASA’s IBEX mission was designed to investigate the interaction of the heliosphere with the surrounding interstellar medium via the observation of energetic neutral atoms (ENAs) from a near Earth vantage point (McComas et al. 2004, 2009a). Interstellar boundary explorer avoids the interference from terrestrial and magnetospheric background as much as possible. The IBEX spacecraft was launched on 19 October 2008 into a highly elliptical, near-equatorial Earth orbit of ~3 × 50 RE (with RE the Earth radius). IBEX is a Sun-pointing, spinning satellite, whose spin axis is re-oriented toward the Sun after completion of each 7–8 day orbit, so that complete full-sky ENA maps are obtained with the 7° FWHM FoV of the sensors over a period of 6 months. As a consequence, IBEX samples the heliospheric and interstellar ENA distributions at 1 AU in a plane that is approximately perpendicular to the Earth-Sun line. This is equivalent to observing ENAs that arrive from the heliospheric boundary or beyond at the perihelia of their trajectories, which is independent of its flow direction at infinity.
The IBEX payload consists of two single-pixel ENA cameras with large geometric factors, IBEX-Lo (Fuselier et al. 2009a) and IBEX-Hi (Funsten et al. 2009b), whose fields-of-view (FoV) point radially outward into two opposite directions and whose combined energy range is 10–6000 eV with an overlap between 300 and 2000 eV. A single combined electronics unit (CEU) controls these sensors, stores data, and is the payload interface to the spacecraft bus (McComas et al. 2004, 2009a). IBEX recorded the first all-sky maps of ENAs produced by the interaction of the heliosphere with the LISM at heliocentric distances of about 100 AU (McComas et al. 2009b; Funsten et al. 2009a; Fuselier et al. 2009b; Schwadron et al. 2009).
1.3. Expected fluxes of interstellar deuterium at Earth’s orbit
As shown in this paper, it is challenging to identify neutral interstellar deuterium atoms at 1 AU. Estimates show that fluxes obtained in each IBEX orbit with IBEX-Lo at 1 AU are low, and the resulting signal remains at the level of individual counts (Tarnopolski & Bzowski 2008; Kubiak et al. 2013). Based on the modelling of the expected fluxes of H and D at Earth’s orbit, it is estimated that IBEX-Lo records a few D counts per year at most (Kubiak et al. 2013). Clearly, it is very challenging to identify these individual deuterium atoms, even with the advanced background suppression techniques used in IBEX-Lo (Wurz et al. 2009). The numerical ratio for interstellar deuterium to hydrogen is expected to have an approximate magnitude of about 10-4 at Earth’s orbit, possibly even lower. This is corroborated by astronomical measurements, simulations, and inspection of the data collected with the instrument during orbits in March and April of the three successive years.
Before the IBEX launch, the detectability of neutral interstellar deuterium was studied by Tarnopolski & Bzowski (2008) and more recently by Kubiak et al. (2013). The latter predicts that IBEX-Lo would be able to detect interstellar neutral deuterium for selected times of the year at specific energies.
1.4. IBEX-Lo sensor
The IBEX-Lo sensor is a single pixel, large geometric factor ENA camera (Fuselier et al. 2009b). It detects neutral atoms in the energy range 10–2000 eV from the heliosphere and from the interplanetary medium in eight broad energy bands. Interstellar neutrals are the brightest signal in the sky (apart from the Earth) observed in this energy range. The backgrounds present in the IBEX-Lo measurements from various sources are well below the signal of the main interstellar neutrals (Wurz et al. 2009).
The design of the entrance system is based on a cylindrical architecture with an annular collimator, which repels electrons and ions, and allows only neutral atoms to enter the sensor. It defines a field of view of 7° × 7° in three 90° angular sectors and 3.5° × 3.5° in the fourth angular sector. The ENAs (and ions >200 eV) that pass the collimator scatter off the charge conversion surface (carbon vapour deposited diamond on silicon) with some that obtain either a negative charge or sputter a negative ion from the surface (Wurz 2000), of which either can be subsequently analysed.
After leaving the conversion surface, the negative ions are pre-accelerated through a potential step into a toroidal electrostatic energy per charge analyser, which has been designed to accept a large angular range of backscattered and sputtered products from the conversion surface (Wieser et al. 2007). Serrations and blackening of the analyser surfaces also efficiently suppress photons. After passing the energy analyser, the negative ions are post-accelerated to +16 kV before they enter the time-of-flight section. Here, the ions are registered via coincidence detection (double and triple) in the two-section time-of-flight (TOF) spectrometer.
The spectrometer measures the TOF of an ion in three ways to verify the proper detection. These three times of flight (TOF0, TOF1, and TOF2) are measured independently from each other and are subsequently compared to efficiently eliminate background (Möbius et al. 2009b), which is very important because of the low fluxes of the LISM atoms to be detected. The TOF system is a carbon-foil time-of-flight instrument that contains two subsequent TOF paths: the second path, TOF1, is the time of flight of the ion between the second ultrathin carbon foil and the microchannel plate (MCP), where it is detected. The passage through the first path is measured as TOF2, which is the time of flight of the ion between the first and the second carbon foil. This TOF section has higher mass resolution than TOF1, because only the energy scattering from the first carbon foil affects the mass resolution. The third TOF measurement is TOF0, obtained between the first C-foil and the MCP. To detect the signals from the two foils, electrons are steered to two separate start portions on the MCP detector. We refer here to an ion measured in a single TOF section (TOF0, TOF1, or TOF2) as a double coincidence measurement. An ion that is measured in all three TOF channels satisfies triple coincidence (i.e., one start and two stop signals). For this paper, we only use triple coincidence counts that meet a rigorous set of criteria to minimise the background. The three TOFs are required to pass a checksum test (effectively requiring that TOF0 ≈ TOF2 + TOF1) to assure consistency for a real particle moving properly through the sensor. Details of this detection technique are given in earlier publications (Möbius et al. 2007; Fuselier et al. 2009b).
The triple coincidence TOF spectrometer of IBEX-Lo determines the mass of incoming neutral atoms directly for those species that are turned into negative ions at the conversion surface (e.g., H, D, and O). For our purpose, it is important to note that noble gases (e.g. He and Ne) do not produce enough negative ions for detection or none at all. However, they are detectable through sputtered negative ions H, C, and O, which are released from the conversion surface (Wurz et al. 2008; Möbius et al. 2009b). The IBEX-Lo sensor was also calibrated for its response to He and Ne at a variety of energies (Fuselier et al. 2009b; Möbius et al. 2009b). The observed ratios of sputtered H, C, and O are used to infer the identity of He or Ne in the flux of incoming neutral atoms (Möbius et al. 2012).
The sputtered H and O atoms are because of the conversion surface of the IBEX-Lo sensor is permanently covered with at least a monolayer of terrestrial water, originating from the outgassing of the sensor. The internal pressure of IBEX-Lo is estimated to be around 10-8 mbar even in space (Wurz et al. 2009). At this pressure, the water layer is replenished within ~10-3 s, if it were somehow removed, which cannot happen in a sensor always pointed about 90° away from the Sun.
Along with H and O, D is sputtered off the conversion surface according to its abundance in the terrestrial water layer. Since the terrestrial hydrogen contains 149 ± 3 ppm deuterium (Robin 2006), IBEX-Lo also detects D ions sputtered primarily by interstellar He atoms, thus producing a substantial D foreground that competes with interstellar D atoms (Kubiak et al. 2013). Thus, we speak about two types of deuterium collected by IBEX-Lo at 1 AU, depending on their sources: a terrestrial component, which is the product of sputtering by interstellar helium, and an interstellar component from the interstellar neutral wind, which is an external deuterium of interstellar origin. We pay careful attention in this analysis to correctly account for the terrestrial deuterium foreground from the instrument. The sputtered C can originate directly in the diamond-coated surface (Wurz et al. 2008).
Because IBEX is moving in solar orbit with the Earth and its observations are in a plane perpendicular to the Sun-Earth line, there are potentially two opportunities during each year to observe the interstellar wind: the first is between January and March (spring season), when the Earth travels into the gas flow of the interstellar neutral wind, and the second is between October and December (fall season), when the Earth recedes from the flow. In the spring season, the gas velocity is highest in the IBEX reference frame, which boosts the detection efficiency. In the fall season, the relative speed between the interstellar neutral flow and IBEX is low, thus leading to significantly lower efficiency. The energy range of the interstellar wind is covered solely by IBEX-Lo. The optimal time for detection of a faint signal, like D, is thus the spring passage of each year (Tarnopolski & Bzowski 2008). In particular, the expected total deuterium flux was assessed as 0.015 cm-2 s-1 (Tarnopolski & Bzowski 2008). During this interval, the energy of interstellar neutral deuterium falls into the IBEX-Lo energy bin 3 (centred at 55.5 eV).
The simulated position of the flux maximum as a function of ecliptic longitude of the Earth (or IBEX) shows that the absolute flux maxima for He, D, and H should be observed in sequence, because radiation pressure progresses from a negligible value for He to the strongest value for H (Tarnopolski & Bzowski 2008). This sequence was validated in the order of the observed He and H peaks with the IBEX data from the first two spring passes in 2009 and 2010 (Saul et al. 2012), as shown in Fig. 5. The interstellar neutral D maximum is expected to occur at two IBEX orbits after the peak of the He signal and approximately at one orbit before the peak of H (Kubiak et al. 2013). The position in the expected ecliptic longitude of the D peak provides a crucial consistency test in our measurement of interstellar neutral deuterium.
Expected TOF values in nanoseconds from simulations of the IBEX-Lo time of flight unit that are validated by pre-launch calibrations with neutral beams of H, He, C, and O.
2. Data analysis
2.1. Observation strategy and data selection
To derive the D/H ratio, we used IBEX-Lo data from all the orbits of the spring passage during the years of 2009, 2010, and 2011. During these years, the solar activity increased, appreciably reducing the H signal (and thus also the D signal) in 2011, producing an even stronger reduction of the H signal in 2012 (Saul et al. 2013). The data of the spring 2012 orbits, when IBEX-Lo was operated in a special mode for measuring interstellar O, could not be used for our investigation because of its low H signal.
 |
Fig. 1 Energy spectra of hydrogen raw counts taken shortly after the interstellar helium peak (orbit 18) and during the interstellar hydrogen peak (orbit 23) with the magnetospheric background removed. |
We use only triple coincident events (Möbius et al. 2007; Fuselier et al. 2009b) to guarantee a maximum background suppression, collected in the four lowest energy channels 1, 2, 3, and 4 of IBEX-Lo with central energies E1 = 14.5 eV, E2 = 28.5 eV, E3 = 55.5 eV, and E4 = 102.0 eV, respectively (Fuselier et al. 2009b). In energy bins 1 to 3, we find sputtered H from interstellar He, and we expect the sputtered D (i.e., the terrestrial D) in these same energy bins. Theory predicts that the interstellar deuterium signal is located in energy bin 3 (Tarnopolski & Bzowski 2008; Kubiak et al. 2013) to be observed late during the spring passage (see Fig. 5). The expected deuterium signal is at the level of individual counts (Kubiak et al. 2013). Figure 1 shows two energy spectra of H, in which one is from the interstellar He signal (Orbit 18) and one is from interstellar H (Orbit 23). The H spectrum from He sputtering has an almost flat behaviour for the first three energy steps, and then drops steeply by two orders of magnitude. The second peak at energy bins 5 and 6 results from sputtering by interstellar O and Ne (Bochsler et al. 2012). Hardly any sputtered H signal (and even less D) is expected in energy bin 4 (Fig. 1). Thus, energy bin 4 provides an additional test, where we expect no interstellar deuterium signal. The energy spectrum for interstellar H via direct ionisation on the conversion surface is clearly different from the sputtered H spectrum (Saul et al. 2012).
2.2. Determination of the deuterium location in the TOF spectra
Since the expected deuterium signal is at the level of individual counts (with no evident peak in the TOF histogram), its identification and subsequent measurement is a challenging task. An example of TOF spectra for the three TOF channels of IBEX-Lo for energy bin 1 is shown in Fig. 2, where data collected during orbit 65 (9–17 February 2010 near the maximum interstellar He flux) are presented. The shapes of the TOF peaks are typical of particles passing through thin carbon foils. For energies higher than the mean energy after transmission, the distribution can be described by a Gaussian profile, and for energies less than the mean energy, the distribution is much broader and features a tail to low energies. It can be described by a squared Lorentzian profile (Beiersdorfer et al. 1987; Mikheev et al. 1993; Wurz 2001). The TOF spectra show several peaks: H, C, and O, all from sputtering by interstellar He. The deuterium peak is expected on the flank of the H peak, but it is too small so that no identifiable peak is observed. To count D events and estimate the D/H ratio, we had to determine the exact D position in the three TOF spectra, which is identical for D of terrestrial and interstellar origin. We used three independent estimations.
 |
Fig. 2 Time-of-flight histograms with data recorded orbit 65 in energy bin 1. The principal interstellar wind component in this measurement is He, which sputters H, C, and O negative ions from the conversion surface of IBEX-Lo. The data points (circles) are overlaid by fits (lines) with the exponentially modified Gaussians (EMG) fit function. |
Expected TOF values in nanoseconds from simulations (Sim) of the IBEX-Lo time of flight unit, which are validated by pre-launch calibrations with neutral beams of H, He, C, and O.
The first estimation, which derives the deuterium time-of-flight, is given as an analytic expression for the TOF of a particle accelerated by the IBEX-Lo post-acceleration voltage before it enters the TOF unit according to 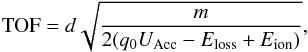 (1)where d is the distance travelled by the particle in the respective TOF section, q0 is the elementary charge, the acceleration voltage is UAcc = 16 kV, and Eloss describes the loss of kinetic energy during the passage of the foils, which is energy and species dependent (Wurz 2001). The ion energy is a combination of energy selected by the electrostatic analyser (ESA) EESA and that from post-acceleration. The energy loss was determined during sensor calibration (Möbius et al. 2009a) and from theory (Wurz 2001). The results are summarised in Table 2.
(1)where d is the distance travelled by the particle in the respective TOF section, q0 is the elementary charge, the acceleration voltage is UAcc = 16 kV, and Eloss describes the loss of kinetic energy during the passage of the foils, which is energy and species dependent (Wurz 2001). The ion energy is a combination of energy selected by the electrostatic analyser (ESA) EESA and that from post-acceleration. The energy loss was determined during sensor calibration (Möbius et al. 2009a) and from theory (Wurz 2001). The results are summarised in Table 2.
The second estimation derives the deuterium time-of-flight from simulations of ion and electron flight times within the IBEX-Lo TOF section using SimIon© software. For the energy loss of the ions in the carbon foil, the same value from Eq. (1) was used. This SimIon© simulation is validated with IBEX-Lo calibration results obtained at the MEFISTO calibration facility of the University of Bern (with neutral atom beams of H, He, C, and O). The simulation output also includes TOF values for the species that were not be calibrated with masses of 2 (deuterium), 3, 6, and 8 atomic mass units. The results of these simulations are given in Table 1.
To determine the most probable position of the deuterium peak in the TOF spectra, we used a third, empirical approach, deriving mathematical expressions that relate the masses of those species that are clearly identified in the TOF spectra during flight with their measured times of flight. The clearly identified peaks in the TOF histograms (H, C, and O – Fig. 2), allow us to derive mass equations which are separate for each TOF channel. The mass equations allow analytic interpolation to find the TOF position of uncalibrated species.
The process of establishing the mass equations begins by fitting the H, C, and O in each of the three TOF histograms for each of the first three energy channels of IBEX-Lo and five orbit grouping intervals. The function used for this task was an exponentially modified gaussian (EMG), which correctly describes the observed peak shape (Eq. (2)). The EMG is a mathematical function resulting from a convolution of a Gaussian with an exponential function. ![\begin{eqnarray} \label{eq:two} {\rm EMG}(t_{\rm i}) &= &\frac{a_{0}}{2 a_{3}} \exp\left(\frac{a_{2}^2}{2 a_{3}^2}+\frac{a_{1}-t_{\rm i}}{a_{3}}\right)\nonumber\\&&\quad\times\left[erf\left(\frac{t_{\rm i}-a_{1}}{\sqrt{2} a_{2}}+\frac{a_{2}}{\sqrt{2} a_{3}}\right)+\frac{a_{3}}{|a_{3}|}\right] , \end{eqnarray}](/articles/aa/full_html/2013/09/aa21420-13/aa21420-13-eq33.png) (2)where EMG(ti) describes the number of counts per TOF channel (with i = 0, 1, 2 for TOF0, TOF1, and TOF2). The parameter a0 describes the area under the peak, a1 is the peak position, a2 is the width, and a3 characterises the asymmetry. The averages of the peak positions for H, C, and O from the fit of the EMG function are summarised in Table 2.
(2)where EMG(ti) describes the number of counts per TOF channel (with i = 0, 1, 2 for TOF0, TOF1, and TOF2). The parameter a0 describes the area under the peak, a1 is the peak position, a2 is the width, and a3 characterises the asymmetry. The averages of the peak positions for H, C, and O from the fit of the EMG function are summarised in Table 2.
 |
Fig. 3 Histogram of triple-coincidence events in the TOF0-TOF2 plane (central panel). The data were collected for energy bin 1 for a time interval near the maximum He flux. Overlaid is a line (see text for details) that defines the centre for each species in this plane and that goes through the centres of the peaks of clearly identified species (designated by letters) and the expected position of the D peak. The leftmost and bottom panel are TOF histograms are products of collapse for TOF2 and TOF0, respectively. Red lines indicate the location and expected amplitude of the D peak. |
The average TOF peak values were used as independent variables in three equations listed in Eq. (3) with one set of three for each TOF channel (total of nine equations). The equation system that describes the relation between the atomic masses of H, C, and O are based on TOF0 measurements is shown: 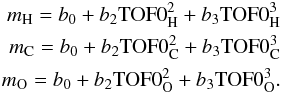 (3)Since b0, b2, and b3 are unknown coefficients, the equation system was used to obtain their values with the atomic weights of the three clearly identified species as input. The linear terms were dropped in this analysis, because they were inconsistent with the collected data. This system of equations was solved using the method of Gauss-Jordan. This procedure was repeated for TOF1 and TOF2. Finally, we define the characteristic TOF mass equation as follows:
(3)Since b0, b2, and b3 are unknown coefficients, the equation system was used to obtain their values with the atomic weights of the three clearly identified species as input. The linear terms were dropped in this analysis, because they were inconsistent with the collected data. This system of equations was solved using the method of Gauss-Jordan. This procedure was repeated for TOF1 and TOF2. Finally, we define the characteristic TOF mass equation as follows: 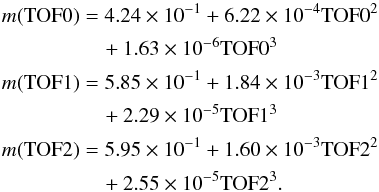 (4)Figure 3 shows the mass equations in two dimensions. The data were collected for energy bin 1 for a time interval near the maximum He flux. The letters designate the centres of the clearly observable species peaks. They are connected by a contiguous path in two-dimensional TOF space, which is described by the mass equations. For this, the mass equations were set to zero, and their real roots were found in a value range determined by the measured minimum and maximum TOF values [0, ~300 ns]. The curve depends on the TOF combination that is chosen for the plot (TOFi × TOFj, with i, j = 0, 1, 2; TOF0 and TOF2 in this example). As shown in Fig. 3, the model line clearly matches the centres of the peaks for the identified species. Thus, this line determines a solution that allows us to predict where the centre for a selected mass is located in the absence of a distinct peak. Table 2 shows the peak values found analytically for different observed species H, C, and O. These are very similar to the values found from simulation and fitting of the in-flight values. This similarity allows supports the conclusion that the derived TOF value for D is very close to its true value.
(4)Figure 3 shows the mass equations in two dimensions. The data were collected for energy bin 1 for a time interval near the maximum He flux. The letters designate the centres of the clearly observable species peaks. They are connected by a contiguous path in two-dimensional TOF space, which is described by the mass equations. For this, the mass equations were set to zero, and their real roots were found in a value range determined by the measured minimum and maximum TOF values [0, ~300 ns]. The curve depends on the TOF combination that is chosen for the plot (TOFi × TOFj, with i, j = 0, 1, 2; TOF0 and TOF2 in this example). As shown in Fig. 3, the model line clearly matches the centres of the peaks for the identified species. Thus, this line determines a solution that allows us to predict where the centre for a selected mass is located in the absence of a distinct peak. Table 2 shows the peak values found analytically for different observed species H, C, and O. These are very similar to the values found from simulation and fitting of the in-flight values. This similarity allows supports the conclusion that the derived TOF value for D is very close to its true value.
The TOF distribution displayed in Fig. 3 shows TOF data histogrammed in one and two dimensions. The central panel of Fig. 3, showing the 2D TOF histogram, also demonstrates why it is impossible to evaluate the deuterium peak with an analysis in just one dimension: notice the horizontal feature located in the area defined by [40–130 ns] in TOF0 and [12–18 ns] in TOF2, a tail of the H peak, which is a background for the D analysis and completely masks the D peak in the 1D-TOF0 and TOF2 histogram (red lines show a rough estimate of the D peak in the 1D histograms). The same situation occurs for the other two TOF pair combinations. To minimise the impact of background, the use of a combination of all three TOF dimensions for the analysis is absolutely necessary.
2.3. Totalling the deuterium events
With the values of the expected times-of-flight as listed above, we derive the most likely position for deuterium atoms in the TOF distributions. Owing to the use of triple coincidence events, we can define a 3-dimensional volume for the D-peak location in the coordinate system given by TOF0, TOF1, and TOF2. The size of this volume relates to the expected width of the D peak in 3-D TOF space. We start with one dimension (TOF histogram), where the range for event counting of hydrogen is determined statistically by relation between the FWHMH (full-width-half-maximum) and sigma σH (from the Gaussian distribution): 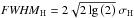 , wherein we know the FWHMH value from data analysis of each TOF channel when σH = 0.6609 ns, 1.2969 ns, and 1.1550 ns, because the interstellar H peak is very clearly identified. We also assume that the relation between FWHMH and FWHMD approximately complies with
, wherein we know the FWHMH value from data analysis of each TOF channel when σH = 0.6609 ns, 1.2969 ns, and 1.1550 ns, because the interstellar H peak is very clearly identified. We also assume that the relation between FWHMH and FWHMD approximately complies with 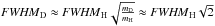 , so that we can compute an approximate value of the deuterium sigma σD as
, so that we can compute an approximate value of the deuterium sigma σD as 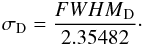 (5)This gives us σD = 0.9347 ns, 1.8341 ns, and 1.6335 ns for each TOF channel, respectively. For two dimensions (whichever possible linear combination between two TOFs), the counting range becomes an elliptical area, since the widths of the TOF peaks are different in each TOF channel. Both areas are determined by hydrogen and deuterium sigma, respectively, as was described above. In others words, we are working at the plus-minus one sigma level when collecting the events. In three dimensions, we have to simultaneously analyse all three TOFs. The volume allowing us to count the events is a constrained ellipsoid described by Eq. (6):
(5)This gives us σD = 0.9347 ns, 1.8341 ns, and 1.6335 ns for each TOF channel, respectively. For two dimensions (whichever possible linear combination between two TOFs), the counting range becomes an elliptical area, since the widths of the TOF peaks are different in each TOF channel. Both areas are determined by hydrogen and deuterium sigma, respectively, as was described above. In others words, we are working at the plus-minus one sigma level when collecting the events. In three dimensions, we have to simultaneously analyse all three TOFs. The volume allowing us to count the events is a constrained ellipsoid described by Eq. (6): 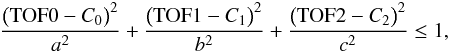 (6)where a, b, and c are semi-axes of the ellipsoid in the three coordinates determined by the sigma values, and the factors (TOF0 − C0), (TOF1 − C1), and (TOF2 − C2) define the ellipsoid centre. TOFi are the time-of-flight data, and the Ci’s are the peak centres for hydrogen (derived from the TOF histograms) or deuterium (from estimates, as discussed above). Sigmas, Ci, and TOFi are the values for hydrogen or deuterium, depending on the species under evaluation. The less than or equal to condition is used to include the events on and inside the surface. Equation (6) defines the volume in the 3D TOF space where the H and D events are counted (terrestrial, interstellar or of both origins). It was repeated for each time interval, in which the orbits were combined, and for the lowest four IBEX-Lo energy bins. The deuterium event ellipsoid centre in the 3D TOF space was at 42.72 ns, 19.53 ns, and 21.48 ns for TOF0, TOF1, and TOF2, respectively.
(6)where a, b, and c are semi-axes of the ellipsoid in the three coordinates determined by the sigma values, and the factors (TOF0 − C0), (TOF1 − C1), and (TOF2 − C2) define the ellipsoid centre. TOFi are the time-of-flight data, and the Ci’s are the peak centres for hydrogen (derived from the TOF histograms) or deuterium (from estimates, as discussed above). Sigmas, Ci, and TOFi are the values for hydrogen or deuterium, depending on the species under evaluation. The less than or equal to condition is used to include the events on and inside the surface. Equation (6) defines the volume in the 3D TOF space where the H and D events are counted (terrestrial, interstellar or of both origins). It was repeated for each time interval, in which the orbits were combined, and for the lowest four IBEX-Lo energy bins. The deuterium event ellipsoid centre in the 3D TOF space was at 42.72 ns, 19.53 ns, and 21.48 ns for TOF0, TOF1, and TOF2, respectively.
 |
Fig. 4 Summed spin phase-time histogram of data of energy bin 3 recorded by IBEX-Lo during orbit 65. The spin phase is the heliospheric latitude in spacecraft coordinates with the ecliptic plane being at spin phase of 0.75 (see text for details). The interstellar wind signal can be seen as a wide horizontal strip across the figure between 0.69 and 0.80 in spin phase, which is almost aligned with the ecliptic plane at spin phase 0.75. The right panel shows a histogram for the time period. |
Figure 4 shows, as an example, the data collected in orbit 65 in energy channel 3 of IBEX-Lo. The signal from the neutral interstellar wind is clearly observed as a band that crosses the figure from left to right (in day-of-year, DOY) and is located at spin phase values from 0.69 to 0.80. The spin phase is the heliospheric latitude in spacecraft coordinates with 1.0 being ecliptic north and with the ecliptic plane being at spin phase of 0.75. The red rectangle identified in Fig. 4 shows the selection of data in the spin phase that is applied for further analysis with the range in the spin phase being optimised for signal-to-noise. On the right side of Fig. 4, we show the histogram of these events against spin phase. The peak of the interstellar wind signal is located between the said values of spin phase with a maximum near 10-4 events. The red dashed lines over the histogram that bracket the rectangle exclude the base of the signal peak at a level of 1% of the peak value to optimise the signal/noise ratio.
Orbit numbers and their grouping in time intervals used in the analysis.
Orbits included in time interval 1.
2.4. Maxima of principal interstellar wind components
The origin of deuterium observed with IBEX-Lo at 1 AU varies with an ecliptic longitude, which depends on the main component helium or hydrogen of neutral interstellar wind observed at the time, it is very important to know its variation with ecliptic longitude, especially to identify their times of maximum flux. Saul et al. (2012) report measurements of interstellar H and He for the spring passages of 2009 and 2010. For this purpose, they had to subtract the hydrogen signal that arises from sputtering by the helium component, because the interstellar neutral signal at 1 AU is dominated by helium during most of the passage. After separating the two signals, a clear offset in ecliptic longitude of the interstellar hydrogen signal from the He signal is observed.
 |
Fig. 5 Normalised counts of He and H components of the interstellar wind are measured at different day-of-year (DOY) in Earth’s orbit. In the measurement panel, data from the first two spring passes of IBEX in 2009 and 2010 are shown (from Saul et al. 2012). In the lower part, predictions for the expected D signal are shown for the sputtered D (terrestrial D in energy bin 1 to 3) and interstellar D in energy bin 3. The time intervals are also indicated, which group the orbits (interval 1 to interval 5). |
The exact position in Earth’s orbit (day of year) in which IBEX observes the peak interstellar He and H flux depends not only on the direction of the interstellar wind but also on the ratio of radiation pressure to gravitational force, known as the μ-factor. The measured He and H fluxes are shown in the upper part of Fig. 5 labelled as measurements. The He and H components show a clear offset in ecliptic longitude of their respective flux maxima at about 35° between the respective peaks (Saul et al. 2012). This offset is caused by the different radiation pressure for He and H with μHe ≈ 0 and μH > 1. The parameter μH > 1 is consistent with the small temporal variation in the offset of the H peak flux, as the solar radiation has increased with the rising solar activity over 2010. The observed average offset in latitude is -2° ± 6.5°, which is also consistent with no latitudinal offset (Saul et al. 2012). In the lowest part of Fig. 5, which is labelled predictions, we show the expected D flux arising from sputtering by interstellar He, which is expected to have the same shape as the interstellar He signal, as scaled by the terrestrial D/H ratio. Also shown is the expected interstellar D signal, which is offset from the interstellar H signal to shorter longitudes and is scaled by using a D/H ratio predicted by Tarnopolski & Bzowski (2008) for this solar activity. In addition, a calculation for the D signal by Kubiak et al. (2013) is shown.
The orbits were grouped into five time intervals given in Table 3 and shown in Fig. 4, based on the conclusions found in the work of Saul et al. (2012) and the theoretical predictions for the interstellar D signal from Tarnopolski & Bzowski (2008) and Kubiak et al. (2013). The signal collected during these time intervals is optimised to the temporal behaviour of the interstellar D signal throughout the spring passage for both the sputtered and the interstellar component. The time intervals are sized to maximise statistics, yet they provide sufficient resolution in ecliptic longitude. All time intervals are defined as a combination of six orbits that share approximately the same detection times in each year. As an example, the first interval is composed of the sum of the orbits: Orbit 13 of the year 2009, orbits 60, 61 of the year 2010, and orbits 108, 109 of the year 2011. These orbits are successive in time and are taken at approximately on the same days of January (same ecliptic longitude), as can be seen in the columns, start and end, of IBEX high altitude science operations (HASO) in Table 4. The orbit number 12 (blank spaces in Tables 4 and 5) was still under an instrument commissioning phase, and IBEX-Lo was not yet run in its nominal science configuration. This combination of orbits is repeated for the time intervals 1 through 4. Owing to the low expected deuterium fluxes, we decided in time interval 5, to combine six orbits between March and April of each of the three years used (Table 3). In the lower part of Fig. 5, we show the different time intervals with their temporal coverage during the spring passage orbits. Because of this orbit grouping, the expected interstellar D signal is mostly of secondary population (Kubiak et al. 2013).
To summarise, Fig. 5 shows the comparison between the measurements of the He and H interstellar wind components and the predicted D signal. In addition, we show the five time intervals for which the data were combined. The figure provides a global picture of the variables involved in the analysis. The interstellar He peak is stable in longitude, latitude, width, and amplitude from year to year, while the hydrogen peak is observed to vary significantly from year to year (Saul et al. 2012, 2013). The maximum of interstellar He is found in time interval 3, as always, in the first and second week of February. Therefore, the maximum of the terrestrial deuterium from the conversion surface must also be located also in time interval 3. The interstellar hydrogen is measured first in time interval 4, overlapping with the hydrogen from sputtering by interstellar He, and in time interval 5 without this interference. The measurements show that the pure interstellar hydrogen can be measured directly only at the end of the spring passage, when the interstellar wind component is no longer helium (interstellar He is significantly lower). Then, the deuterium measurement would be almost completely free from additions of helium sputter products, which means that it is unambiguously of interstellar origin.
3. Results
We analyse the H and D events and calculate the D/H ratio for each time interval during the spring passage (Fig. 5). Figure 6 shows the collected hydrogen and deuterium counts (used for the D/H ratio) for energy bins 1–4 during the five time intervals. In the upper part of Fig. 6, we show the H measurements for these energy bins during each time interval. The spectral shape of the H measurements is the same as shown in Fig. 1 for the first four time intervals. Since this H signal is from H sputtered by the interstellar He flux, this spectral shape is as expected. In the last time interval, we used the known energy spectrum of sputtered H to derive the interstellar H contribution in this time interval (as in Saul et al. 2012), which is indicated by the grey bars in Fig. 6. The variation in time (i.e., time interval 1 to 5) reproduces the He flux variation as a function of ecliptic longitude, as shown in Fig. 5 (from Saul et al. 2012).
 |
Fig. 6 Total hydrogen (top panel) and deuterium counts (bottom panel) for the five time intervals and the four energy bins (indicated by colour code). In time interval 5, the fraction of hydrogen counts from interstellar hydrogen are identified by grey colour. |
In the lower part of Fig. 6, we show the measurements of deuterium for the four energy bins and five time intervals. The D data look similar to the H data but with much lower count rate. For each time interval, the energy bins show the expected spectral shape within statistics, which is similar to H and which repeats each time interval during the spring passage: the measurements of deuterium events in the three first energy bins have very similar values, and little or no D signal is found in energy bin 4. In time interval 5, the D counts in energy bins 1 and 2 follow the downward trend with ecliptic longitude as expected for the He sputtering (matching the shape of the interstellar He and H curves for the spring passage). Only energy bin 3 in time interval 5 appears to be outside the general pattern for D being sputtered by interstellar He.
Based on the time dependence of the sputtered H signal from interstellar He, which we also see in the sputtered D signal, we estimate that 1 of the 3 counts of the D signal in energy bin 3 of time interval 5 should be attributed to the sputtered component (terrestrial D) and 2 counts are the true interstellar D signal.
 |
Fig. 7 D/H ratios with different colour for the four energy bins, which are marked with the colours indicated in the legend. The solid black line represents the average of the D/H ratio from the measurements D/H = (1.72 ± 0.83) × 10-4 without the measurement of energy bin 3 in time interval 5. The dashed lines indicate the one-sigma interval from the average. On the right side, a frequency histogram is shown, where there is a clear difference of position between measurements along the spring passage and the measurement in energy bin 3 of the final time interval. |
To validate that the deuterium measurement in energy bin 3 of time interval 5 has a different origin than terrestrial, we first calculate the D/H ratio by taking a pessimistic assumption: the interstellar He sputtering product completely dominates the D and H signals during spring passage, including at time interval 5. Figure 7 shows the ratios of deuterium to hydrogen derived for all energy bins for each time interval, using that assumption. The ratio in this case is simply the fraction of deuterium and hydrogen counts collected in the each energy bin: D/H = 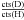 is represented by different coloured lines. As seen in Fig. 7, the D/H ratios are found to be at the same value (within uncertainty) for all but one measurement. Only the D/H measurement for energy bin 3 at time interval 5 significantly deviates from them, supporting that it is of different origin (see also the frequency histogram on the right-side of Fig. 7). We calculated the average ratio D/H = (1.72 ± 0.83) × 10-4 without the measurement of energy bin 3 in time interval 5 because this ratio is of a different origin than all the other measurements (with its position far away from the average, see Fig. 7, right panel). This average D/H ratio agrees with the terrestrial value of (1.49 ± 0.03) × 10-4 (Robert 2006) and strongly supports the sputter origin of those measurements, or the terrestrial origin. The solid black line in Fig. 7 represents the average measured D/H ratio without the measurement of energy bin 3 in time interval 5. If we attribute 1 of the 3 observed D counts in energy bin 3 to sputtering of D by interstellar He, then the resulting D/H value is (2.02 ± 2.02) × 10-4 for this measurement, which agrees within the 1-sigma interval with the average D/H value for the other 15 D/H measurements.
is represented by different coloured lines. As seen in Fig. 7, the D/H ratios are found to be at the same value (within uncertainty) for all but one measurement. Only the D/H measurement for energy bin 3 at time interval 5 significantly deviates from them, supporting that it is of different origin (see also the frequency histogram on the right-side of Fig. 7). We calculated the average ratio D/H = (1.72 ± 0.83) × 10-4 without the measurement of energy bin 3 in time interval 5 because this ratio is of a different origin than all the other measurements (with its position far away from the average, see Fig. 7, right panel). This average D/H ratio agrees with the terrestrial value of (1.49 ± 0.03) × 10-4 (Robert 2006) and strongly supports the sputter origin of those measurements, or the terrestrial origin. The solid black line in Fig. 7 represents the average measured D/H ratio without the measurement of energy bin 3 in time interval 5. If we attribute 1 of the 3 observed D counts in energy bin 3 to sputtering of D by interstellar He, then the resulting D/H value is (2.02 ± 2.02) × 10-4 for this measurement, which agrees within the 1-sigma interval with the average D/H value for the other 15 D/H measurements.
In the following, we assess the statistical significance of this measurement. If the 5 deuterium counts at time interval 5 are Poisson-distributed sputtered D, then the statistical probability for 3 counts in an energy bin for a μp = 5/3 is 15%, which means that the confidence for true detection of interstellar D is 85%. The probability for 0 counts in an energy bin in time interval 5 is 19%, and the probability is 37% to get zero counts in time interval 1. The significant excess in counts at energy step 3 in time interval 5 is strong evidence that these D atoms are of interstellar origin. We also can perform a similar counting statistics analysis for just energy bin 3 in time interval 5 (see the distribution in the right panel of Fig. 7). The probability for collecting 3 counts in energy channel 3 is 6% for an average sputtered terrestrial D of 1 count or less. This reasoning is based solely on Poisson statistics for this energy bin, and the time interval can be taken as evidence that we have detected interstellar D with a better than 94% confidence level. The right panel of Fig. 7 shows the histogram of all D/H measurements with uncertainties: the simple uncertainty gives the standard deviation of the D/H measurements, and the full uncertainty gives the uncertainty with consideration of the uncertainty of the individual measurement. By comparing the full uncertainty with the uncertainty of the measurement in energy bin 3 at time interval 5, we see that it is separated by 1-sigma.
Moreover, the D count rate in energy channel 3 at time interval 5 agrees with calculations based on the model by Kubiak et al. (2013) with the expected total counts for D atoms at 0.64 counts per mission year for IBEX observations, which are performed during orbits 68 through 74 (time interval during spring passage of year 2010) in energy bin 3. In the three years of the IBEX mission time, the observation geometry and orbit allowed for a total observation time in time interval 5 (see Fig. 5) of 115.3 days. However, the effects of the spinning spacecraft and the stepping through 8 energy channels mean that we are only observing the interstellar wind for a total time of 1.44 days, in which about ~2 counts for interstellar deuterium are expected in time interval 5. This corresponds to an average D flux at IBEX of (8.8 ± 6.7) × 10-3 cm-2 s-1. We report here a conservative number, because a possibility of systematic error or additional noise, though mostly eliminated with our analysis, does not support detection at a 2-sigma level, which a simple statistical argument might support (see error bars given in Fig. 7).
Values derived in the present work.
To obtain the interstellar D/H ratio, we need to convert the interstellar D and interstellar H counts into physical fluxes, because these species arrive at 1 AU at different energy and thus in different energy bins. To first order, we can assume the same detection efficiency for D and H in IBEX-Lo, since the ionisation during the scattering from the conversion surface is an electronic process and should not be affected by the heavier D nucleus (Wurz 2000). The agreement, within error bars, of the D/H ratio for the sputtered signal with the terrestrial value supports this assumption. For the interstellar H flux, we consider the counts in energy bin 1 and energy bin 2 (see Table 5), which are converted to the total H interstellar flux as described earlier (Rodríguez et al. 2012). We arrive at D/H = (2.69 ± 2.05) × 10-4 at 1 AU. Since we do not have a calibration for D, we can take the difference to second order between the terrestrial D/H and our measurement of the sputtered D/H as the difference in detection efficiency between D and H in IBEX-Lo. This difference in the detection efficiency can occur in the TOF spectrometer, since the registration of an ion relies on secondary electron production at two carbon foils and at the MCP (for triple coincidence detection). Thus, we have to correct our measurement of the interstellar D/H with the factor 1.49/1.72 = 0.866, which results in an interstellar D/H ratio of D/H = (2.33 ± 1.78) × 10-4 at 1 AU. We have to apply an additional correction because of the different viewing times of interstellar D and H in interval 5 (see Fig. 4). The viewing time for interstellar H is derived from the measurements (Saul et al. 2012) as 95.7%, and the viewing time for interstellar D is derived from model by Kubiak et al. (2013) as 38.6%. The resulting D/H of LISM at 1 AU is D/H = (5.8 ± 4.4) × 10-4.
4. Future IBEX-Lo deuterium measurements
Improving our knowledge of the local interstellar deuterium population bears our understanding of the past and future of the Sun in its environment, the evolution of the Galaxy, and its cosmological implications. The measurements reported here therefore represent only the tip of the iceberg as this work progresses. Our priority in this report is to best leverage the IBEX instruments for measurement of the local deuterium to hydrogen ratio in the VLISM and its variability in the inner heliosphere.
The interstellar neutral deuterium flux in the inner heliosphere is not only very small but is also expected to be variable in a similar way as the interstellar hydrogen flux (Kubiak et al. 2013; Saul et al. 2013). Therefore, these measurements require not only high sensitivity and long collection times but also a careful observation plan to optimise the measurement efficiency. During rising solar activity, the local neutral hydrogen density is vastly reduced (Saul et al. 2013), and the local deuterium flux is also reduced. Further, the observations made from IBEX are such that the deuterium count rate is at maximum during the spring passage, in which the Earth’s velocity and the interstellar wind component velocity are antiparallel. Therefore, we can predict that the best time for an interstellar deuterium viewing campaign would be in February through May of the years 2018 to 2021. While it is possible that the actual solar minimum is later or earlier than forecasted (Hathaway 2009), the calendar days are not that different, as the general direction of the interstellar wind at Earth’s orbit is unlikely to significantly change. With an observation programme optimised for D/H, we estimate that the counting statistics, which limit our currently reported observation, can be increased by at least a factor of 10.
4.1. Energy scan
The nominal heliospheric observation mode for IBEX-Lo scans through 8 logarithmically spaced energy bins with equal time allocated for each bin. The deuterium signal peaks in energy bin 3, while the interstellar hydrogen had been found to have a peak count rate in energy bin 1. An optimised deuterium viewing mode would not spend time in energy steps 5 and higher, as these bins are simply background and down time for the interstellar viewing campaign. One approach would be to simply leave the instrument in energy bin 3 for the duration of viewing during the peak deuterium times. This would provide a factor of eight more statistics in the observations. However, the co-measurement of interstellar hydrogen is also desirable, and some measurements in energy bins 1 and 2 or even 4 are necessary. These measurements do not require the observation time that the deuterium measurement requires, so their impact in the observation time of energy bin 3 in a deuterium search could be minimal.
In the past, the interstellar viewing mode was used to focus on oxygen observations and for using the high angular resolution mode of the IBEX-Lo camera, in which a segment with a more restrictive angular viewing of the collimator is used. Other implementations, such as a mode switching that changed the voltages at certain spin phases, have been attempted; however they are more complex and can fail to make the observations, if the spacecraft loses its spin pulse. We consider four other observations here that could compete with a deuterium measurement for this instrument time: a) heliospheric ENAs, b) interstellar hydrogen, c) interstellar oxygen, and d) interstellar helium.
Heliospheric ENA observations include the observation of the ribbon feature at ~1 keV (McComas et al. 2009a; Fuselier et al. 2009b) and other heliospheric ENAs, which are crucial to the IBEX goal of probing the heliospheric boundary and outer heliosphere. However, these regions are sampled every 6 months and can be sampled more at much lower observation times without great loss to the heliospheric science campaign. The IBEX-Hi instrument, which samples the bulk of the ribbon feature, would continue nominal operations during a deuterium observation campaign, while the IBEX-Lo nominal heliospheric mode could be run for several hours during the orbit depending on the observations of lower energy ENAs in the solar maximum and receding stage of the cycle.
Measuring interstellar hydrogen will also be of great interest during the solar minimum, as it is predicted to recover with the dropping ionisation rate. This variability is a probe of ionisation processes, which includes charge exchange in the outer heliosphere (Saul et al. 2012). The flux of interstellar hydrogen observed in IBEX-Lo energy bins 1 and 2 is a crucial component of this measurement. The normal heliospheric mode has provided a wealth of information on the neutral hydrogen component of the LISM that reaches Earth’s orbit. In this mode, these two bins received 1/8 of the total observation time, sharing the rest of the time with the other energy bins. Therefore, a deuterium mode, in which these two shares are left untouched and the remainder of the time filled with bin 3 observations, would be at least as good as current observations for the hydrogen, while increasing the deuterium statistics by a factor of 6. More reductions of viewing time in energy bin 1 and 2 could also be considered.
Measuring interstellar oxygen presents more of a problem: during a deuterium mode observation, the neutral oxygen, which normally arrives in energy bins 5 and 6 (Möbius et al. 2009a), would not be observed. A careful watch must be paid to the observations of interstellar oxygen leading up to solar minimum to see what other scientific campaigns could be pursued. Fortunately, peak time of oxygen measurements and those for helium along Earth’s orbit is before the expected peaks of the deuterium and the oxygen end, which is even before the helium peak (Kubiak et al. 2013). Therefore, the measurements of the primary and secondary oxygen flows could be performed earlier, giving time for a dedicated deuterium search.
With the advantage that the count rates for helium are already extremely high, the same applies for interstellar helium, which also appear in energy bins 1 to 3 as sputtered hydrogen that would continue to have some observation time during the deuterium mode. It is reasonable to expect that helium observations should not interfere with the deuterium campaign.
The high scientific interest in a measurement of the LISM deuterium ratio coupled with the extremely low count rate of deuterium during the first four years of IBEX measurements suggests that observational priority should go to a deuterium measurement during the observation window. The estimated increase in accumulated counts due to selective energy bin switching is 6.
4.2. IBEX spacecraft attitude
These measurements are made possible due to the highly elliptic orbit of the IBEX spacecraft, which enables long observation times outside the Earth’s magnetosphere. IBEX is a Sun-pointed spinning spacecraft, so there is relatively little one can do to alter the spacecraft attitude for optimising an observation campaign. However, we are aided in that a recent orbital adjustment has the spacecraft on a higher apogee and long-term stable orbit (McComas et al. 2011) and that there is one in which the deuterium peak signal will take place when the spacecraft is not in the Earth’s magnetotail. Observations thus far were made often from the Earth’s magnetotail, and during these times, there is a loss of data when encountering regions of enhanced high energy particles. The improved observation time due to an orbit outside the Earth’s magnetosphere is already a substantial increase in effective deuterium viewing time, in which approximately a factor of 1.5 can be gained.
There may be further room for improvement, because the spin axis of the spacecraft has some small freedom to be oriented: it could be a few degrees off from the Sun-pointing direction to the elevation angle of the deuterium flux above the ecliptic plane. A few degrees can be the difference in either mostly making the peak signal into the collimator or a peak signal just missing the entrance window. While this technique could be more useful for heavier species, the interstellar hydrogen and deuterium velocity distributions are however broader and would be less improved by this technique. More modelling of the adjustment of the elevation angle of the spacecraft is needed to assess how much of an improvement it could make.
4.3. Observation time
The first two years of IBEX measurements occurred as the Sun’s activity first started to show the rise from solar minimum. An observation campaign over an entire solar minimum would give the decreasing phase as well, which is about a factor of two in observation time. Combining these factors into a deuterium campaign, a factor of 6 from a dedicated energy deuterium mode, a factor of 1.5 from spacecraft attitude, and a factor of 2 from the viewing of an entire solar minimum, suggest that we could expect a factor of 18 or better in counting statistics in deuterium measurements. Because the current observation is near the 1 sigma level, this will represent a substantial improvement to our confidence in the deuterium ratio and enable some variation studies and energy spectral information of the deuterium. An extended operation of IBEX through the coming solar minimum with a deuterium viewing campaign is an extremely exciting possibility for isotopic composition science and will remain an exciting observation, even if all of these improvements can not be implemented.
5. Conclusions
In this paper, we demonstrated that deuterium from the local interstellar medium can be measured in the interstellar wind with IBEX-Lo at Earth’s orbit. We find a value of D/H = (5.8 ± 4.4) × 10-4 at 1 AU for the local interstellar deuterium. This value corresponds to D/HLISM = (1.6 ± 1.2) × 10-5 in the LISM, which is based on the modelling of the transport and losses of D and H from the heliosheath to Earth’s orbit (Kubiak et al. 2013). This value is consistent with the D/H ratio inferred by Hubble spectroscopy from a line of sight measurement of the LIC (1.6 ± 0.4) × 10-5 (Hébrard et al. 1999). The agreement between the LISM (by IBEX) and the LIC values provides additional support for the accuracy of the LIC value. The LIC value is typical of the ISM within 30 pc of the Sun. This value indicates that local deuterium is depleted compared to the pristine infalling D/H of the halo gas.
The estimate for D/HLISM presented in this paper is based on modelling by Kubiak et al. (2013), who used the current best available estimate of the relation between the primary and secondary population (Bzowski et al. 2008). This is based on a numerical multi-component model of the heliospheric interface by Izmodenov et al. (2003) and the best available ionisation and radiation pressure models (Sokół et al. 2013; Bzowski et al. 2013). The Kubiak et al. (2013) model accurately calculates the transmission of D through the heliosphere, including the radiation pressure, ionisation effects, the geometry of observations, and the geometric factor of the instrument.
The present analysis was made with all IBEX-Lo data available for this investigation, which date from the years 2009 through 2011. Although the deuterium signal is very weak, we are confident about this measurement, because the interstellar D signal was identified in the expected time interval (ecliptic longitude) and at the expected energy (energy bin 3, 55.5 eV centre energy). Moreover, the D signal that we measure for the sputtered signal from the interstellar He flux follows exactly the temporal evolution of the He signal and shows the characteristic energy spectra for a sputtered signal. The measured D/H ratio for this signal is in good agreement with the terrestrial D/H value, as expected, demonstrating the capability of IBEX-Lo to measure the D/H ratio with sufficient accuracy. However, our result for the interstellar deuterium of D/H = (5.8 ± 4.4) × 10-4 at 1 AU is statistically significant at only the 1-sigma level. The D/H ratio that we measure for the interstellar signal at Earth’s orbit (1 AU) is in good agreement with theoretical predictions by Tarnopolski & Bzowski (2008), assuming a D/H value of 1.6 × 10-5 in the LISM. For optimised IBEX-Lo observation conditions, the improved detection of interstellar D with IBEX-Lo by a factor of up to ~10 appears possible during the upcoming solar minimum period in about 2019 with a corresponding improvement in accuracy of the D/H ratio.
Acknowledgments
This work is supported by the Swiss National Science Foundation. M.B., M.A.K. and J.M.S. were supported by the Polish Ministry for Science and Higher Education grant N-N203-513-038, managed by the Polish National Science Center. The work by US authors was supported by the IBEX mission, which is funded as a part of NASA’s Explorer Program.
References
- Beiersdorfer, P., Roquemore, A. L., & Kaita, R. 1987, Rev. Sci. Instr., 58, 2092 [NASA ADS] [CrossRef] [Google Scholar]
- Bochsler, P., Petersen, L., Möbius, E., et al. 2012, ApJS, 198, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Bzowski, M. 2008, A&A, 488, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bzowski, M., Möbius, E., Tarnopolski, S., Izmodenov, V., & Gloeckler, G. 2008, A&A, 491, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bzowski, M., Izmodenov, V., McComas, D., et al. 2012, in COSPAR Meeting, 39, 39th COSPAR Scientific Assembly, 265 [Google Scholar]
- Bzowski, M., Sokól, J., Tokumaru, M., et al. 2013, in Cross-Calibration of Far UV Spectra of Solar System Objects and the Heliosphere, eds. E. Quémerais, M. Snow, & R.-M. Bonnet (New York: Springer), ISSI Sci. Rep. Ser., 13, 67 [Google Scholar]
- Fahr, H. J. 1978, A&A, 66, 103 [NASA ADS] [Google Scholar]
- Frisch, P. C., Bzowski, M., Grün, E., et al. 2009, Space Sci. Rev., 146, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, P. C., Redfield, S., & Slavin, J. D. 2011, ARA&A, 49, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Funsten, H. O., Allegrini, F., Bochsler, P., et al. 2009a, Space Sci. Rev., 146, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Funsten, H. O., Allegrini, F., Crew, G. B., et al. 2009b, Science, 326, 964 [Google Scholar]
- Fuselier, S. A., Allegrini, F., Funsten, H. O., et al. 2009a, Science, 326, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Fuselier, S. A., Bochsler, P., Chornay, D., et al. 2009b, Space Sci. Rev., 146, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H. 2009, Space Sci. Rev., 144, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, G., Mallouris, C., Ferlet, R., et al. 1999, A&A, 350, 643 [NASA ADS] [Google Scholar]
- Izmodenov, V., Gloeckler, G., & Malama, Y. 2003, Geophys. Res. Lett., 30, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Kubiak, M. A., Bzowski, M., Sokół, J. M., et al. 2013, A&A, 556, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linsky, J. L. 2003, Space Sci. Rev., 106, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Linsky, J. L. 2007, Space Sci. Rev., 130, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Linsky, J. L., Draine, B. T., Moos, H. W., et al. 2006, ApJ, 647, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D., Allegrini, F., Bochsler, P., et al. 2004, in Physics of the Outer Heliosphere, eds. V. Florinski, N. V. Pogorelov, & G. P. Zank, AIP Conf. Ser., 719, 162 [Google Scholar]
- McComas, D. J., Allegrini, F., Bochsler, P., et al. 2009a, Science, 326, 959 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McComas, D. J., Allegrini, F., Bochsler, P., et al. 2009b, Space Sci. Rev., 146, 11 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Carrico, J. P., Hautamaki, B., et al. 2011, Space Weather, 9, 11002 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Alexashov, D., Bzowski, M., et al. 2012, Science, 336, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Mikheev, S., Ryzhov, Y., Shkarban, I., & Yurasova, V. 1993, Nucl. Instrum. Methods Phys. Res. B, 78, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Möbius, E., Bzowski, M., Chalov, S., et al. 2004, A&A, 426, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Möbius, E., Kucharek, H., Granoff, M., et al. 2007, in Proc. 30th International Cosmic Ray Conference, COSPAR Meeting, 1, 841 [Google Scholar]
- Möbius, E., Bochsler, P., Bzowski, M., et al. 2009a, Science, 326, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Möbius, E., Kucharek, H., Clark, G., et al. 2009b, Space Sci. Rev., 146, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Möbius, E., Bochsler, P., Bzowski, M., et al. 2012, ApJS, 198, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H.-R., Frisch, P. C., Florinski, V., & Zank, G. P. 2006, ApJ, 647, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Prodanović, T., & Fields, B. D. 2008, J. Cosmology Astropart. Phys., 9, 3 [Google Scholar]
- Robert, F. 2006, Meteorites and the Early Solar System II, 1, 341 [NASA ADS] [Google Scholar]
- Robin, A. C. 2006, in IAU Joint Discussion, 13 [Google Scholar]
- Rodríguez, M. D. F., Saul, L., Wurz, P., et al. 2012, Planet. Space Sci., 60, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Ruciński, D., Cummings, A. C., Gloeckler, G., et al. 1996, Space Sci. Rev., 78, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Saul, L., Wurz, P., Rodriguez, D., et al. 2012, ApJS, 198, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Saul, L., Bzowski, M., Fuselier, S., et al. 2013, ApJ, 767, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Schwadron, N. A., Bzowski, M., Crew, G. B., et al. 2009, Science, 326, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Slavin, J. D., & Frisch, P. C. 2008, A&A, 491, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sokół, J. M., Bzowski, M., Tokumaru, M., Fujiki, K., & McComas, D. J. 2013, Sol. Phys., 285, 167 [Google Scholar]
- Tarnopolski, S., & Bzowski, M. 2008, A&A, 483, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wieser, M., Wurz, P., Moebius, E., et al. 2007, Rev. Sci. Instrum., 78, 124502 [NASA ADS] [CrossRef] [Google Scholar]
- Wurz, P. 2000, Detection of Energetic Neutral Atoms 265, eds. K. Scherer, H. Fichtner, & E. Marsch, Copernicus Gesellschaft e.V., Katlenburg-Lindau, Germany), 251 [Google Scholar]
- Wurz, P. 2001, Heavy Ions in the Solar Wind: Results from SOHO/CELIAS/ MTOF, 265 (Philosophisch-naturwissenschaftliche Fakultät, University of Bern), 1 [Google Scholar]
- Wurz, P., Saul, L., Scheer, J. A., et al. 2008, J. Appl. Phys., 103, 054904 [NASA ADS] [CrossRef] [Google Scholar]
- Wurz, P., Fuselier, S. A., Möbius, E., et al. 2009, Space Sci. Rev., 146, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Y., Neufeld, D. A., Sonnentrucker, P., Melnick, G. J., & Watson, D. M. 2012, ApJ, 753, 126 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Expected TOF values in nanoseconds from simulations of the IBEX-Lo time of flight unit that are validated by pre-launch calibrations with neutral beams of H, He, C, and O.
Expected TOF values in nanoseconds from simulations (Sim) of the IBEX-Lo time of flight unit, which are validated by pre-launch calibrations with neutral beams of H, He, C, and O.
All Figures
 |
Fig. 1 Energy spectra of hydrogen raw counts taken shortly after the interstellar helium peak (orbit 18) and during the interstellar hydrogen peak (orbit 23) with the magnetospheric background removed. |
| In the text | |
 |
Fig. 2 Time-of-flight histograms with data recorded orbit 65 in energy bin 1. The principal interstellar wind component in this measurement is He, which sputters H, C, and O negative ions from the conversion surface of IBEX-Lo. The data points (circles) are overlaid by fits (lines) with the exponentially modified Gaussians (EMG) fit function. |
| In the text | |
 |
Fig. 3 Histogram of triple-coincidence events in the TOF0-TOF2 plane (central panel). The data were collected for energy bin 1 for a time interval near the maximum He flux. Overlaid is a line (see text for details) that defines the centre for each species in this plane and that goes through the centres of the peaks of clearly identified species (designated by letters) and the expected position of the D peak. The leftmost and bottom panel are TOF histograms are products of collapse for TOF2 and TOF0, respectively. Red lines indicate the location and expected amplitude of the D peak. |
| In the text | |
 |
Fig. 4 Summed spin phase-time histogram of data of energy bin 3 recorded by IBEX-Lo during orbit 65. The spin phase is the heliospheric latitude in spacecraft coordinates with the ecliptic plane being at spin phase of 0.75 (see text for details). The interstellar wind signal can be seen as a wide horizontal strip across the figure between 0.69 and 0.80 in spin phase, which is almost aligned with the ecliptic plane at spin phase 0.75. The right panel shows a histogram for the time period. |
| In the text | |
 |
Fig. 5 Normalised counts of He and H components of the interstellar wind are measured at different day-of-year (DOY) in Earth’s orbit. In the measurement panel, data from the first two spring passes of IBEX in 2009 and 2010 are shown (from Saul et al. 2012). In the lower part, predictions for the expected D signal are shown for the sputtered D (terrestrial D in energy bin 1 to 3) and interstellar D in energy bin 3. The time intervals are also indicated, which group the orbits (interval 1 to interval 5). |
| In the text | |
 |
Fig. 6 Total hydrogen (top panel) and deuterium counts (bottom panel) for the five time intervals and the four energy bins (indicated by colour code). In time interval 5, the fraction of hydrogen counts from interstellar hydrogen are identified by grey colour. |
| In the text | |
 |
Fig. 7 D/H ratios with different colour for the four energy bins, which are marked with the colours indicated in the legend. The solid black line represents the average of the D/H ratio from the measurements D/H = (1.72 ± 0.83) × 10-4 without the measurement of energy bin 3 in time interval 5. The dashed lines indicate the one-sigma interval from the average. On the right side, a frequency histogram is shown, where there is a clear difference of position between measurements along the spring passage and the measurement in energy bin 3 of the final time interval. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


