| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 8 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201221021 | |
| Published online | 23 August 2013 | |
What X-ray source counts can tell about large-scale matter distribution
Nicolaus Copernicus Astronomical Center, Bartycka 18, 00-716 Warsaw, Poland
e-mail: soltan@camk.edu.pl; michal@camk.edu.pl
Received: 31 December 2012
Accepted: 13 July 2013
Context. Sources generating most of the X-ray background (XRB) are dispersed over a wide range of redshifts. Thus, statistical characteristics of the source distribution carry information on matter distribution on very large scales.
Aims. We test the possibility of detecting the variation in the X-ray source number counts over the celestial sphere.
Methods. A large number of Chandra pointings spread over both galactic hemispheres are investigated. We searched for all the point-like sources in the soft band of 0.5−2 keV and statistically assessed the population of sources below the detection threshold. A homogeneous sample of the number counts at fluxes above ~10-15 erg s-1 cm-2 was constructed for more than 300 ACIS fields. The sources were counted within a circular area of 15 arcmin diameter. The count correlations between overlapping fields were used to assess the accuracy of the computational methods used in the analysis.
Results. The average number of sources in the investigated sample amounts to 46 per field. It is shown that the source number counts vary between fields at a level exceeding the fluctuation amplitude expected for the random (Poissonian) distribution. The excess fluctuations are attributed to the cosmic variance generated by the large-scale structures. The rms variations of the source counts due to the cosmic variance within the 15 arcmin circle reach ~8% of the average number counts. An amplitude of the potential correlations of the source counts on angular scales larger than the size of a single pointing remains below the noise level.
Key words: X-rays: diffuse background / X-rays: galaxies / cosmology: observations
© ESO, 2013
1. Introduction
The largest structures identified in galaxy redshift surveys are located at distances comparable to the maximum distance at which structures can be effectively distinguished. In the CfA redshift survey beyond the Great Wall not much structure is recognizable at all (Geller & Huchra 1989). In the Sloan Digital Sky Survey (SDSS)1 the large galaxy filaments are discernible up to roughly 500 Mpc, and the most prominent feature is the Sloan Great Wall (Gott et al. 2005), found at a distance of ~300 Mpc.
Larger structures could potentially be isolated in the quasar part of the SDSS. Recently Clowes et al. (2013) report a group of 73 quasars that span redshifts 1.17−1.37. A total length of this twisted filament exceeds 1200 Mpc. Although Park et al. (2012) have shown that the largest structures found in the galaxy distribution are consistent with the canonical Λ cold dark matter (ΛCDM) model, it is plausible that the quasar alignment could be discordant with this model.
It appears that the question of the large structures could be addressed using the X-ray surveys. Most of extragalactic X-ray sources are asociated with various types of active galactic nuclei (AGN). Because of strong cosmic evolution and a wide luminosity function, the AGN observed in the selected flux range are distributed within a very wide range of redshifts. Equivalently, the observed source flux is only weakly correlated with the source distance. Roughly 90% of the X-ray background in the 0.5−2 keV energy band is generated by sources brighter than 3 × 10-16 erg s-1 cm-2 (e.g. Moretti et al. 2003; Lehmer et al. 2012). A majority of these sources are located at cosmological distances: 80% in the redshift range 0.3−2.2 (Sołtan 2008). The comoving radial distance2 between redshifts 0.3 and 2.2 exceeds 4200 Mpc, thus sources detected in a moderately deep Chandra observation are tracers of the matter distribution on Gpc scales. One can hardly expect fluctuations on this scale, but the present analysis would be capable also of detecting variations on smaller scales, although with decreasing sensitivity.
In the deepest Chandra exposures of 2 Ms CDF-N (Alexander et al. 2003) and 4 Ms CDF-S 3 (Xue et al 2011), several hundred sources are detected. This allows the source distribution to be investigated along the line of sight, provided the redshifts of objects are known. However, to investigate large-scale matter distribution, a transverse dimension of the survey should have a comparable size to the radial one. In the present paper we explore the possibility of analyzing the giant structures in the observable Universe using a large number of the Chandra medium depth observations scattered over the whole sky. Although a single pointing represents a pencil-like cut through space, a set of several hundred pointings to some extent act as a uniform all-sky survey. The main objective was to select all the pointings suitable for source detection from the Chandra Data Archive, and then to construct an efficient method of counting the sources in all the fields in a homogeneous way. A number of sources in each field was used to estimate the amplitude of the source counts, N(S), at a fixed flux range around 10-15 erg s-1 cm-2. A power law parametrization of the N(S) relationship was applied. Statistical characteristics of the N(S) amplitude variations are examined. Results, albeit preliminary, demonstrate the strong and weak points of the method. The volume of the archived Chandra observations is still too small for a comprehensive study. Nevertheless, the presently available data reveal the potential advantage of X-ray source counts in investigations of the large-scale matter distribution.
The organization of the paper is as follows. In the next section, selection and preparation of the observational data extracted from the Chandra archives is described. Section 3 gives procedures for estimating the amplitude of the number source counts, N(S). We apply two independent methods to determine the counts in two separate flux levels. Results of these calculations, as well as statistical and (possible) systematic errors are discussed in Sect. 4. In Sect. 5 we concentrate on the question of counts fluctuations that allowed us to estimate the amplitude of the cosmic variance. The main conclusions are summarized in Sect. 6.
2. Selection of observational material
Although the total number of the CXO observations now exceeds 10 000, only a small fraction of pointings is suitable for the present project. The number of pointings in ACIS-I configuration longer than 30 ks was equal to 963 (as for 2012−10−02). Of these 599 were located at |b| > 25 deg. Since we are mostly interested in the fields at high galactic latitudes, without the dominating extended source, the list of usable data was reduced substantially. In this step we rejected the pointings at: M87, M33, LMC, SMC, many Abell clusters (but not all), and the NGC galaxies. Additionally, it is desirable to have pointings scattered over the large area rather than superimposed one onto another or closely packed. Unfortunately, to some degree the pointings in the CXO Archive have been accumulated under the opposite criteria. The archive contains many observations of nearby galaxies and clusters of galaxies, as well as a large number of local sources close to the Galactic plane. Also, several pointings cover the same area (e.g. Chandra Deep Fields).
The Chandra Data Archive has been searched for all the ACIS-I observations at high galactic latitudes with the exposure time above 30 ks. Originally, a selection limit of | b | > 30° has been applied for both hemispheres. Then, only having a few adequate pointings, we searched for more observations in a belt of 25° < b < 30° in the southern galactic hemisphere. Eventually, within this extension just few pointings satisfied all the selection criteria and were included in the final set of data.
All the “interesting” observations were handled through the standard data processing pipelines at the Chandra X-ray Center4. Each observation was carefully inspected for its usefulness for the present investigation. In particular, pointings with an xtended source filling substantial fraction of the field were removed. If the extended source occupied a relatively small fraction of the field of view, a section with the source was cut off, and the remaining data unaffected by the extended emission were used. Fields with extremely strong point sources were treated in a similar way; i.e., only areas affected by linear smearing generated during a readout were removed. All the exposures were examined for the presence of the background flares and only “good time intervals” (GTI) were used. Because of a severe deterioration in the image quality with the increasing off-axis angle, the search for sources was limited to the circular area of 7.5 arcmin radius centered on chips 0 − 3.
Restrictive criteria of the field selection led to elimination of ~96% of pointings in the CXO Archive. The almost 400 observations that remain constitute a sample that is still numerous enough to make the data processing a painful and time-consuming operation. Since we are more interested in observations covering many different directions rather than a single spot in the sky, we removed some CDF-S and CDF-N pointings from our sample. However, we intentionally left several dozen observations in these areas to facilitate the error analysis (see below). Eventually, more than 300 individual pointings were qualified for the analysis. Their spatial distribution is highly nonrandom. Concentrations on various angular scales, as well as a strong asymmetry between galactic hemispheres is present.
 |
Fig. 1 Distribution of 190 pointings in the northern galactic hemisphere. Two circles represent galactic latitudes b = 30° and b = 60°. Each observation covers a circle of 15 arcmin in diameter. Labels close to some points in the map denote the actual number of pointings in the area. Symbol sizes are not to scale, and even in the crowded areas, the pointings do not necessarily overlap. |
The sky distribution of all the pointings is presented in the polar equal area projection in Figs. 1 and 2 for the northern and southern galactic hemispheres (NGH and SGH, respectively). Numerals close to some dots denote the numbers of pointings concentrated in the marked areas. In the NGH, 190 pointings were selected for further processing, and 112 in the SGH. Symbols in figures strongly exceed the actual extent in size of the individual observation. Thus, in some cases where several pointings are represented by a single dot, the pointings do not always overlap. A detailed discussion of the statistical properties of the selected material is presented in Sect. 4.
The data in a “canonical” soft energy band of 0.5 − 2 keV were used. For various reasons, both the exposure time and sensitivity are highly variable functions of the position within the field of view. To reduce the effects of sensitivity variations, low sensitivity areas have been delineated using the Chandra effective exposure map5. For each observation, the maximum amplitude of the exposure map was determined. Pixels with the exposure map below 75% of this maximum value have not been used. Although this constraint reduces the original area of 7.5 arcmin circle by roughly 13%, it secures for our purpose an acceptable uniformity of the exposure (Sołtan 2011).
3. “Bright” and “faint” source counts
Two independent methods have been applied to estimate the number of discrete point-like sources in a single observation. The first one was based on a standard procedure of finding prominent concentrations of counts within a detection cell. Sources isolated in this way are labeled here as “bright”. A second method, described in Sołtan (2011), estimates number of the “faint” sources. It calibrates deviations of the photon distribution from the Poissonian one using the nearest neighbor statistics. It is not able to isolate individual sources, but provides statistical information on the population of sources generating small numbers of photons.
 |
Fig. 2 Same as Fig. 1 for 112 pointings in the southern galactic hemisphere. A few pointings within − 30° < b < − 28° have been included to improve statistics. |
To count “bright” sources in a single observation, a circular cell was slid over the entire investigated area. The cell size was set to enclose 85% of counts generated by a point source. The radius of the detection cell varied as a function of the off axis angle according to the shape of the Chandra point spread function (PSF). All the information on the PSF shape required in the procedure of “bright” source selection as well as for the “faint” source assessment, was obtained from mkpsfmap - a standard tool of the Chandra data processing. The search for “bright” sources was performed in the same manner for all the pointings. The iterative procedure was applied. Using the sliding window technique, the strongest concentration of photons was localized, and it was recognized as the brightest source in the field of view. Then, the area surrounding this source was extracted from the data, and the search for the second brightest source was performed in the same way. The procedure was repeated for the consecutive sources until the number of counts selected as the next source dropped below the threshold adopted individually for each observation. The threshold counts were selected at a level high enough to prevent random fluctuation of counts to be approved as a real source. It was assumed in this step that the background counts were distributed randomly over the field of view. The search for sources was terminated when the probability of random accumulation of counts exceed 10-6. Owing to strong variations in the PSF width, the minimum counts recognized as a point-like source varies over the field of view, typically between 4 and 8. This range varied a little between observations because of different levels of the background counts.
Our data span a wide range of exposure times, from 30 ks through more than 170 ks. Because of that the pointings differ in the source detection threshold and in the number of detected sources. To use the observed number of sources as the estimator of the source counts per unit solid angle, which is independent of the exposure time, one needs to adopt an analytic model for the counts and to relate the observed number of sources in the individual field to the parameter(s) of the model.
A power law is the obvious choice for the source number counts per unit solid angle (hereafter per 1 sq. deg): 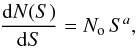 (1)with two a priori free parameters, normalization amplitude No, and the slope a. However, the limited number of sources, as well as a narrow dynamic range of fluxes populated by sources in a single pointing, prohibits any attempts to measure the slope a. Also the data on the source counts available in the literature for a couple of deep fields do not provide information on the potential field-to-field slope variations. In those few cases where the dynamic range within a single field allows tracking changes of the slope, it appears that the slope is constant below ~10-14 erg s-1 cm-2 down to at least 10-16 erg s-1 cm-2 (e.g. Georgakakis et al. 2008). Therefore, in the present investigation only the normalization is fitted for each field separately, while a single, universal value of the slope is assumed.
(1)with two a priori free parameters, normalization amplitude No, and the slope a. However, the limited number of sources, as well as a narrow dynamic range of fluxes populated by sources in a single pointing, prohibits any attempts to measure the slope a. Also the data on the source counts available in the literature for a couple of deep fields do not provide information on the potential field-to-field slope variations. In those few cases where the dynamic range within a single field allows tracking changes of the slope, it appears that the slope is constant below ~10-14 erg s-1 cm-2 down to at least 10-16 erg s-1 cm-2 (e.g. Georgakakis et al. 2008). Therefore, in the present investigation only the normalization is fitted for each field separately, while a single, universal value of the slope is assumed.
A several-step procedure was applied to find the best estimate of No using the observed number sources. Because the each enhancements of counts within the detection cell is considered a “source”, one should carefully evaluate a contribution of the background counts and apply the adequate statistical correction. Let ns(k) be the number of detected “sources” containing k counts, where k = ks + kb is a sum of the genuine X-ray photons emitted by a source, ks, and the background counts, kb. No is related to ns(k) in the following way: ![\begin{eqnarray} n_{\rm s}(k) = A \sum_{k_{\rm b}\,=\,0}^{k}\, \left[\, {P}_{\rm bkg}(k_{\rm b})\, \int {\rm d}S\,N_{\rm o}\, S^a\: {P}(k_{\rm s}\,|\,S)\, \right], \label{ns1} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21021-12/aa21021-12-eq59.png) (2)where A is the solid angle of the observation (in sq. deg), Pbkg(kb) denotes the probability that kb background counts would be found in the detection cell, and P(ks | S) is the probability that a source of flux S generates ks photons (it is elaborated below). The probability of finding kb counts within the detection cell is given by the Poissonian distribution:
(2)where A is the solid angle of the observation (in sq. deg), Pbkg(kb) denotes the probability that kb background counts would be found in the detection cell, and P(ks | S) is the probability that a source of flux S generates ks photons (it is elaborated below). The probability of finding kb counts within the detection cell is given by the Poissonian distribution: 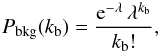 (3)where λ is the expected number of random counts within the detection cell. For clarity, in formulae 2 and 3, a fixed detection cell radius and λ have been assumed. In the actual calculations, the right-hand side of Eq. (2) was integrated over the solid angle A.
(3)where λ is the expected number of random counts within the detection cell. For clarity, in formulae 2 and 3, a fixed detection cell radius and λ have been assumed. In the actual calculations, the right-hand side of Eq. (2) was integrated over the solid angle A.
The sum over the background counts kb in Eq. (2) generally includes the ks = 0 and 1 components. However, the minimum value of k was set to warrant Pbkg(kb = k) < 10-6, and those components of the sum are effectively negligible.
It is convenient to use the instrumental count in each observation as a flux unit. The flux s in ACIS counts is related to S in physical units by a conversion factor η : s = S/η, with η in erg s-1 cm-2 count-1 is obtained from the exposure map. The source counts using the new flux unit are represented by 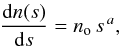 (4)where
(4)where 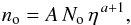 (5)and the probability P(ks | S) takes the form:
(5)and the probability P(ks | S) takes the form: 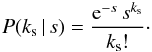 (6)Equations (1) and (4) with a fixed slope do not describe the actual counts over the entire flux range. Substantial fraction of sources is found above the count slope brake Sb ≈ 8 × 10-15 erg s-1 cm-2 (Sb is not very accurately determined, see Georgakakis et al. 2008). Above Sb the differential slope is close to ab = −2.5. Incorporating the broken power law into Eq. (2) and using the instrumental counts s, we finally get
(6)Equations (1) and (4) with a fixed slope do not describe the actual counts over the entire flux range. Substantial fraction of sources is found above the count slope brake Sb ≈ 8 × 10-15 erg s-1 cm-2 (Sb is not very accurately determined, see Georgakakis et al. 2008). Above Sb the differential slope is close to ab = −2.5. Incorporating the broken power law into Eq. (2) and using the instrumental counts s, we finally get ![\begin{eqnarray} n_{\rm s}(k) = n_{\rm o}\: A \nonumber \\ \times \;\sum_{k_{\rm b}\,=\,0}^{k\,-\,2}\, \left[\, {P}_{\rm bkg}(k_{\rm b})\, \frac{\gamma(k_{\rm s}\!+a\!+\!1,s_{\rm b}) + s_{\rm b}^{a-a_1}\,\Gamma(k_{\rm s}\!+\!a_{\rm b}\!+\!1,s_{\rm b})} {\Gamma(k_{\rm s})}\,\right] , \label{ns2} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21021-12/aa21021-12-eq78.png) (7)where γ(α,x) and Γ(α,x) are the lower and upper incomplete gamma functions, respectively.
(7)where γ(α,x) and Γ(α,x) are the lower and upper incomplete gamma functions, respectively.
Equation (7) summed over k gives the expected total number of “bright” sources. To evaluate no, the number of actually detected “bright” sources has been substituted on the left-hand side of Eq. (7). Then, the amplitude No was obtained using Eq. (5). Calculating the conversion factor, variations of soft energy absorption by the cold gas in the Galaxy were taken into account. We assumed that the intrinsic source spectra are represented by a power law with the photon spectral index Γ = −1.4. The detected fluxes were corrected for the galactic absorption using the appropriate NH data. We used the NASA HEASARC tool6 based on Kalberla et al. (2005). The lowest NH in the sample is 6 × 1019, and highest is 1.6 × 1022 cm-2. For the 0.5 − 2 keV energy band and the assumed spectrum, this NH range introduces variations of the average photon energy between 1.022 and 1.154, and a reduction of detected counts by a factor 0.984 through 0.695. The statistical properties of the No distribution in our sample are discussed in the next section in conjunction with the analogous distribution obtained for “faint” sources.
The population of sources below the formal source detection threshold, labeled as “faint”, is investigated using a statistical approach. Here only the basics of the method are presented. All the details and potential applications were discussed in a separate paper (Sołtan 2011).
After the removal of all the “bright” sources, the remaining counts are a mix of the non-X-ray events, truly diffuse X-ray background, and counts generated by a population of faint sources. Only this last constituent is responsible for fluctuations of the count distribution characteristic for point sources. One can express the total number of events, nt, within the investigated area in the following form: 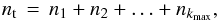 (8)where n1 represents counts that are distributed randomly, n2 – counts produced by sources contributing exactly two counts each (“2-photon sources”), n3 – counts by “3-photon sources”, and so on up to nkmax – counts due to the brightest sources left in the field (i.e., the brightest among the “faint” ones).
(8)where n1 represents counts that are distributed randomly, n2 – counts produced by sources contributing exactly two counts each (“2-photon sources”), n3 – counts by “3-photon sources”, and so on up to nkmax – counts due to the brightest sources left in the field (i.e., the brightest among the “faint” ones).
Counts distributed randomly constitute a composite collection of events that also includes the weakest discrete sources contributing single photons. Photons coming from sources producing 2 ≤ k ≤ kmax counts create local enhancement of a unique shape determined by the telescope PSF. Statistical characteristics of these variations are efficiently quantified using the nearest neighbor statistics (NNST) of the count distribution. The probability that a randomly chosen event has no neighbors within a distance r, is 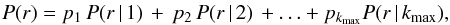 (9)where p1 is a probability that this event is not related to any source generating two or more counts, pk for k = 2,...,kmax is the probability that this event is produced by the k-photon source, and P(r | k) is the conditional probability that there are no other counts within r provided the selected event belongs to the k-photon source. Under the reasonable assumptions, for k ≥ 2
(9)where p1 is a probability that this event is not related to any source generating two or more counts, pk for k = 2,...,kmax is the probability that this event is produced by the k-photon source, and P(r | k) is the conditional probability that there are no other counts within r provided the selected event belongs to the k-photon source. Under the reasonable assumptions, for k ≥ 2 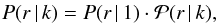 (10)where
(10)where 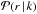 is the probability that within r there are no other counts from the same source. This quantity is uniquely defined by the PSF. Taking nk = k·ns(k) and pk = nk/nt and combining Eqs. (8)−(10), and (4) we get
is the probability that within r there are no other counts from the same source. This quantity is uniquely defined by the PSF. Taking nk = k·ns(k) and pk = nk/nt and combining Eqs. (8)−(10), and (4) we get ![\begin{eqnarray} \frac{n_{\rm o}}{n_{\rm t}}\, P(r\,|\,1) \sum_{k\,=\,2}^{k_{\rm max}} \frac{\Gamma(k+a+1)}{\Gamma(k)} [1 - {\cal P}(r\,|\,k)] = P(r\,|\,1) - P(r). \label{nnst} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21021-12/aa21021-12-eq108.png) (11)In the relevant flux range the source counts are adequately represented by a single power law. Since the maximum number of photons, kmax, is defined by the threshold for the “bright” sources, the actual value of kmax is a function of a position within the field of view; in most of the pointings 3 ≤ kmax ≤ 7.
(11)In the relevant flux range the source counts are adequately represented by a single power law. Since the maximum number of photons, kmax, is defined by the threshold for the “bright” sources, the actual value of kmax is a function of a position within the field of view; in most of the pointings 3 ≤ kmax ≤ 7.
Equation (11) allows us to determine no, provided the relevant probability distributions are known. One can estimate the probability P(r) for each observation by measuring the distance to the nearest neighbor for each photon in the field. Similarly, P(r | 1) is given by the distribution of distances of the randomly distributed points to the nearest photon. The PSF related probability distributions, 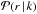 , were determined using the CIAO tool mkpsfmap. The distribution of photons produced by a large number of sources were generated by means of the Monte Carlo method, and the relevant probabilities were determined as a function of position and number of photons.
, were determined using the CIAO tool mkpsfmap. The distribution of photons produced by a large number of sources were generated by means of the Monte Carlo method, and the relevant probabilities were determined as a function of position and number of photons.
The efficiency of the NNST method depends strongly on the PSF width, and in the present investigation it provides interesting results only for small off-axis angles. Because statistical uncertainties increase rapidly at larger distances from the optical axis, we limited the NNST calculation to the central region of 5 arcmin diameter.
The best estimate of no was determined in the following way. All the probability distributions were calculated for several (usually more than 20) distances r, which uniformly covered the domains of distributions P(r | 1) and P(r). Then, the cumulative probability distributions in Eq. (11) were replaced by the corresponding probability densities; e.g., ΔP(r) = P(r) − P(r + Δr) for the consecutive distances r. In all the calculations, Δr = 0.246 arcsec (≡1/2 of the instrumental pixel) was used. Thus, a set of independent equations covering all the observed separations was constructed, and the best fit value of no was determined using the least square method. Finally, the count amplitude No was obtained using Eq. (5) as for the “bright” sources.
4. Count correlations
The amplitudes of the number source counts determined for “bright” and “faint” sources (hereafter denoted No [b] and No [f], respectively) define the number source counts over adjoining, but different flux levels. Therefore, the median flux of “bright” and “faint” sources in each observation is not widely separated, and the No [b] and No [f] averaged over the sky should be similar. Nevertheless, one can expect systematic differences between both estimates, if the count slope adapted in the calculations, a, did not match the slope actually observed in the data. The differential slope between 10-16 and 10-14 erg s-1cm-2 in the deep Chandra fields is well fitted with the slope of − 1.58 (Georgakakis et al. 2008; Sołtan 2011). Using a = −1.58 in the present calculations, the average amplitude of the “faint” source counts is larger by ~5% then that for the “bright” sources. Both amplitudes are practically identical for a = 1.60. To preserve internal consistency of the investigation, the latter slope was used in subsequent calculations. Although this is steeper by 0.02 than the best fit by Georgakakis et al. (2008), it stays within their 1σ limits. One should note that the present investigation is not suitable for assessing the count slope either within the individual field or the average over the sky. This is because most systematic errors involved in the estimates of the number of “bright” sources are independent of the errors affecting the “faint” source assessment. The source counts amplitudes, No [b] and No [f] are functionally dependent on the slope a. Therefore, a unique slope is required to balance both amplitudes. In fact, modification of the slope by just 0.02 demonstrates that the systematics do not play a significant role in the analysis. One should also stress that all the conclusions of the paper are not affected by a selection of the particular value of the slope.
An apparent consistency of the average No [b] and No [f] estimates does not exclude local inhomogeneities of the source distribution in the individual pointing. One should note that the amplitudes No for “bright” and “faint” sources are obtained using the disconnected classes of sources; i.e., none source was qualified as “bright” and “faint” at the same time. Thus, for the random source distribution, the source counts should be uncorrelated.
 |
Fig. 3 Amplitudes No of the source number counts for flux S in 10-15 erg s-1cm-2 (see Eq. (1)) for the “bright” and “faint” sources in the sample of 302 pointings; 293 pointings with the rms uncertainty of No [b] smaller than 160 per sq. deg are shown with dots, 9 pointings with larger rms – with crosses. |
Apart from the systematic errors, the No [b] and No [f] amplitudes are subject to large statistical uncertainties that generate substantial scatter. The average number of “bright” sources per field 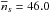 . Thus, the Poissonian scatter alone introduces ~15% rms fluctuations to the present estimate of No [b]. In reality, still larger variations of No [b] are expected due to cosmic variance (source clustering). The No estimates for the “faint” sources are afflicted by even larger errors, because the estimate of the count amplitudes is derived indirectly. Two factors contribute most to the final uncertainties. First, the amplitude estimate is proportional to the difference between two probability distributions (see Eq. (11)), and both distributions are subject to substantial statistical scatter. Second, the “faint” sources contribution to the total events is small, typically 2 − 6%, while all the remaining counts are distributed randomly. Therefore the net signal, represented by the right-hand side in Eq. (11), is also very modest in comparison to the noise that is dominated by the random scatter of the P(r | 1) distribution.
. Thus, the Poissonian scatter alone introduces ~15% rms fluctuations to the present estimate of No [b]. In reality, still larger variations of No [b] are expected due to cosmic variance (source clustering). The No estimates for the “faint” sources are afflicted by even larger errors, because the estimate of the count amplitudes is derived indirectly. Two factors contribute most to the final uncertainties. First, the amplitude estimate is proportional to the difference between two probability distributions (see Eq. (11)), and both distributions are subject to substantial statistical scatter. Second, the “faint” sources contribution to the total events is small, typically 2 − 6%, while all the remaining counts are distributed randomly. Therefore the net signal, represented by the right-hand side in Eq. (11), is also very modest in comparison to the noise that is dominated by the random scatter of the P(r | 1) distribution.
In Fig. 3 the “bright” and “faint” source amplitudes No as defined in Eq. (1)7, where S is in 10-15 erg s-1 cm-2, are plotted for the full sample of 302 pointings. The rms scatter of No [b] is slightly larger than what is expected from the Poissonian fluctuations of the “bright” source numbers (see below for the detailed discussion), while the amplitude of the No [f] variations is much higher, and it is clearly dominated by the statistical noise. The rms for “faint” sources amounts to 44% of the average amplitude of No [f]. Despite the scatter, the correlation of the “bright” and “faint” amplitudes is statistically significant. The correlation coefficient for 302 data points ρ = 0.2003. The non-directional probability that the data are drawn from the uncorrelated population amounts to 0.00046 (or 0.00023 for the directional case). To minimize statistical noise, the uncertainties of the individual No estimates are carefully examined (see below). Due to a wide range of exposure times in the processed observations, these uncertainties strongly differ. In order to check the influence of the poor quality estimates on the subsequent statistical analysis, pointings with the largest uncertainties of No [b] have been identified. A removal of pointings that suffer from the highest uncertainties does not strengthen the [b] − [f] correlation greatly. Nevertheless, if nine pointings with σo(No [b] ) > 160 per sq. deg are eliminated, the correlation coefficients in the sample of 293 pointings rises to ρ = 0.2205. The corresponding directional probability for the uncorrelated general population in this case drops to 7 × 10-5.
Although the No [f] estimates are strongly affected by the statistical noise at the level of the photon distribution within the each pointing, the correlation between No [f] and No [b] in the whole sample favors the calculations of a single amplitude No derived jointly from the “bright” and “faint” sources. To combine the No [b] and No [f] estimates into a single “best” estimate of the source number counts amplitude for each pointing, an adequate error estimate and data weighting for each measurement are essential. The errors for the “bright” source counts were calculated using the Poissonian noise, since this effect dominates. In the first step it was assumed that the underlying population of sources is the same for all the pointings; i.e., the cosmic variance effects were neglected. Next, the expected number of the observed “bright” sources was determined for each pointing separately, taking the exposure time into account. Finally, the Poissonian distribution around the expected number of sources was used to compute the corresponding dispersion σo(No [b]) individually for each pointing. The rms uncertainties are contained between 64 and 182 per sq. deg with the average in the whole sample of 112 per sq. deg. The rms scatter of No [b] amounts to 127, which exceeds the Poissonian estimate almost by 14%.
The No [f] uncertainties result from a complex combination of the Poisson-like fluctuations of the number of faint sources, contribution of background counts, and a stochastic character of the photon distribution on angular scales comparable to the width of the PSF. In effect, the variance of No [f] cannot be easily derived from theoretical considerations, but instead it is estimated directly from the observed distribution. It was evident that the cosmic variance contributed marginally to the observed No [f] scatter. Also, no clear correlation of the variance with the exposure time (or the total number of events) was found. Therefore, equal uncertainties were assigned to all the observations. As an error of the individual No [f] estimate, σo(No [f]), the rms scatter in the whole sample had been assumed: σ(No [f] ) = 337 per sq. deg.
Our final best estimate of Noi of the i-th observations is a weighted mean of No [b] i and No [f] i: ![\begin{eqnarray} N_{oi} = \alpha_i\cdot N_{\rm o}[b]_i + \beta\cdot N_{\rm o}[f]_i, \label{weighted_n_o} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21021-12/aa21021-12-eq153.png) (12)with weights αi and β inversely proportional to the squares of the corresponding rms uncertainties. The resulting uncertainties of No, σo(No), are spread between 63 and 161 per sq. deg.
(12)with weights αi and β inversely proportional to the squares of the corresponding rms uncertainties. The resulting uncertainties of No, σo(No), are spread between 63 and 161 per sq. deg.
The drastic unevenness of the pointing distribution in the celestial sphere presents a problem for our statistical analysis. Estimates of the average count amplitude, as well as the count correlation between different pointings, should take into account fact that a large number of pointings cover the same sky area. Obviously, the source counts based on pointings that cover the overlapping areas of the sky are related. For the detached (nonoverlapping) observations, the correlations would indicate structures in the source distribution on the corresponding angular scale. Since our sample contains a large number of overlapping pointings, the spurious count correlations are also present at larger angular scales than the field of view of a single pointing. This is because the overlapping observations are dominated by a few groups centered on Chandra deep fields. Some wide angular bins that happen to include the separation between these fields contain pairs predominantly drawn from those heavily observed areas. To account for this bias, we assign weights to all the pointings. As a result of the application of weights, cosmic signals from all the directions covered by the present observations contribute uniformly to the investigated correlations. The weight of the ith pointing is defined by the formula 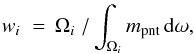 (13)where Ωi denotes the solid angle of the observation, and mpnt is the number of pointings that cover the area dω. Thus, for all the detached pointings, w = 1 since mpnt = 1 within the entire field of view, while for the coinciding pointings, the weights are reduced proportionally to the overlapped area and the number of the involved pointings. Unless otherwise stated, these weights are applied in the calculations below.
(13)where Ωi denotes the solid angle of the observation, and mpnt is the number of pointings that cover the area dω. Thus, for all the detached pointings, w = 1 since mpnt = 1 within the entire field of view, while for the coinciding pointings, the weights are reduced proportionally to the overlapped area and the number of the involved pointings. Unless otherwise stated, these weights are applied in the calculations below.
The average number counts amplitude 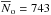 per sq. deg. with the rms scatter σ(No) = 125 per sq. deg. The flux limits that define “bright” and “faint” sources depend on the exposure time, but the flux separating both source classes is always close to 10-15 erg s-1 cm-2. Therefore the present
per sq. deg. with the rms scatter σ(No) = 125 per sq. deg. The flux limits that define “bright” and “faint” sources depend on the exposure time, but the flux separating both source classes is always close to 10-15 erg s-1 cm-2. Therefore the present 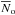 estimate characterizes the source counts just around this flux level.
estimate characterizes the source counts just around this flux level.
To compare the present result with the source number counts based on several deep Chandra fields, we adopt the count parametrization by Georgakakis et al. (2008). Their data converted to the units used here give dN/dS = 574 per sq. deg at S = 10-15 erg s-1 cm-2; i.e., our figure is 29% higher. Although this difference could partially be attributed to various systematic effects inherent in the present calculations, one should note that our amplitude is the average of a large number of pointings distributed over the whole sky, while the Chandra Deep Fields only cover a few selected areas. Applying the present method to the selection of 47 observations in the CDF-S we get the average amplitude No = 641 ± 8, per sq. deg, which exceeds the Georgakakis et al. (2008) result by 12%. The uncertainty of the average is based on the rms scatter of 56 per sq. deg in those 47 pointings. Although all these data are localized at CDF-S, the fields cover slightly different areas. Therefore variations of No not only represent the statistical noise generated by our procedures, but also include small contribution from the actual fluctuations in the number of sources.
In the CDF-N the present calculations give dN/dS = 797 ± 17 per sq. deg. This amplitude differs from the CDF-S one by 24% and it is consistent with results by Tozzi et al. (2001) for CDF-S, and CDF-N by Brandt et al. (2001).
 |
Fig. 4 Distribution of the “pair rms”, i.e. rms difference between the counts amplitudes in pairs of observations as a function of the pair separation. Results obtained with and without weights are shown with full and open circles, respectively (see text for detailed explanation). The dotted line separates the overlapping pointings from the detached ones. The lowest separation bin contains pairs closer than 0.1 arcmin. |
To assess the uncertainties proper to the method, and cleared of the contribution generated by the cosmic variance, all 302 observations (including overlapping) have been used in the following way. For all the possible pointing pairs, a difference between amplitudes No was obtained: Δij = No(i) − No(j), for i,j = 1,..., 302, and i ≠ j. The pairs were divided in several bins according to the pair angular separation Then, for the each separation bin the rms of Δij was calculated: 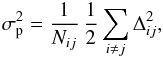 (14)where Nij denotes the number of pointing pairs in the given separation bin, and “2” in the denominator is introduced to normalize σp to the rms of No. For perfectly overlapping pointings, the “pair rms” σp represents the scatter intrinsic to the method, while for widely separated fields, σp is a quadratic sum of two components: noise produced by Poissonian scatter of the source counts detected in each pointing and the cosmic variance. If the observations partially overlap, intermediate amplitudes of σp are expected. In Fig. 4 the distribution of σp for several bins is shown. The abscissa positions give the average pair separation in the bin. One sigma error bars for detached pairs were calculated using the bootstrap Monte Carlo method. A large number (10 000) of simulated sets of observations were generated. In the simulated data the original sky coordinates were used, while the amplitudes No were drawn at random from the observed No distribution. Then, using Eq. (14) the pair rms σp were calculated for each simulated data set. The rms scatter of the σp was taken as the uncertainty of the actually observed signal.
(14)where Nij denotes the number of pointing pairs in the given separation bin, and “2” in the denominator is introduced to normalize σp to the rms of No. For perfectly overlapping pointings, the “pair rms” σp represents the scatter intrinsic to the method, while for widely separated fields, σp is a quadratic sum of two components: noise produced by Poissonian scatter of the source counts detected in each pointing and the cosmic variance. If the observations partially overlap, intermediate amplitudes of σp are expected. In Fig. 4 the distribution of σp for several bins is shown. The abscissa positions give the average pair separation in the bin. One sigma error bars for detached pairs were calculated using the bootstrap Monte Carlo method. A large number (10 000) of simulated sets of observations were generated. In the simulated data the original sky coordinates were used, while the amplitudes No were drawn at random from the observed No distribution. Then, using Eq. (14) the pair rms σp were calculated for each simulated data set. The rms scatter of the σp was taken as the uncertainty of the actually observed signal.
Weights are superfluous for almost completely overlapping pointings, since the rms mainly represents the method errors, while weights adequately measure the contribution due to the cosmic signal for the detached pairs. To calculate the pair rms in that latter case we use the formula: 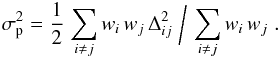 (15)At the smallest separations, the amplitude σp = 41.6 per sq. deg, and for the “bright” sources σp [b] = 37.5 per sq. deg. A substantial decline in the pair rms for overlapping pointings clearly indicates that the observed fluctuations are dominated by the actual variations of the cosmic signal while shortcomings of all the procedures and approximations engaged in the calculations do not play a significant role. One should also note that the rms scatter attributed here to the present method does not affect the Poissonian character of the distribution of the number of sources detected in a single observation. Thus, it is legitimate to assume that the statistical properties of the No distribution in the sample are described by the cosmic variance and the Poissonian scatter.
(15)At the smallest separations, the amplitude σp = 41.6 per sq. deg, and for the “bright” sources σp [b] = 37.5 per sq. deg. A substantial decline in the pair rms for overlapping pointings clearly indicates that the observed fluctuations are dominated by the actual variations of the cosmic signal while shortcomings of all the procedures and approximations engaged in the calculations do not play a significant role. One should also note that the rms scatter attributed here to the present method does not affect the Poissonian character of the distribution of the number of sources detected in a single observation. Thus, it is legitimate to assume that the statistical properties of the No distribution in the sample are described by the cosmic variance and the Poissonian scatter.
5. Cosmic variance
No obvious variations of the pair rms is present for the nonoverlapping pointings averaged over all the data. It indicates that any potential, strong fluctuations of the counts amplitude have angular scales that typically do not exceed a size of the individual pointing. However, on smaller angular scales, fluctuations exceeding the Poisson noise are present in our sample.
Assuming that the cosmic variance and the Poissonian noise add in squares to produce the observed scatter of No [b], the rms of the cosmic variance σCV ≈ 60, or 8.1% of the average No [b] signal. This figure represents the mean variance within a circle of 15 arcmin diameter. One should expect that the cosmic variance amplitude also depends on the source redshifts. However, over a wide range of X-ray fluxes, the average source redshift depends very weakly on the flux threshold (e.g. Sołtan 2008). Thus, even for a wide span of exposure times, the redshift distributions in the sample are statistically similar, and the σCV amplitude is representative of all our data.
The statistically significant correlation between the “bright” and “faint” source counts also affirms the role of the cosmic variance. The correlation alters the rms fluctuations of the combined counts amplitude No. To test this effect on the distribution of No, we generated a large number of simulated sets of count amplitudes using Eq. (12). In the simulated data we connected the actual “bright” source amplitude of the ith observation, No [b] i, with the No [f] randomly drawn from the sample. It was found that the rms fluctuations of the No in the simulated data are in 99% cases smaller than the fluctuations in the real data, which confirms the No [b] − No [f] correlation revealed using the Pearson test.
6. Discussion
Variations of the source number counts were analyzed using the Chandra observations distributed in both galactic hemispheres. We applied two independent methods determining the source counts in the two adjacent flux levels. Then, both amplitudes for each pointing were reduced to the standard flux of 10-15 erg s-1cm-2. The amplitudes represent separate species of sources. Thus, for the Poissonian distribution of sources both amplitudes are expected to be statistically uncorrelated.
The dominating contribution in the observed field-to-field variations comes from the Poissonian noise induced by the relatively small average number of sources per field. This effect seriously confused a search for the potential correlations in the No distribution on large angular scales. Scarce observational data, particularly in the south galactic hemisphere, prevent us from drawing conclusions at a high confidence level. The pointings are distributed very inhomogeneously in the celestial sphere on the large, as well as on small angular scales. Due to these deficiencies, the picture emerging from the present investigation is ambiguous to some extent.
On large angular scales, the fluctuations of the counts amplitude averaged over the whole sample of 302 observations do not exhibit distinct irregularities that could be symptomatic for the existence of the large angular scale structure of the XRB. However, the statistically significant correlation between “bright” and “faint” sources within individual pointings is clearly visible, implying a nonrandom source distribution on adequately small scales. The present data are insufficient to measure the angular range of these correlations precisely. A sharp rise of σp with increasing separation for the overlapping pointings (between 3 and 15 arcmin; see Fig. 4) indicates that the angular size of fluctuations is most likely smaller than the extent of a single pointing. A substantially larger collection of closely separated observations is needed to determine this question.
Despite the apparent absence of large angular scale features in the σp distribution, some differences between the data in both galactic hemispheres seem to be present. Unfortunately, the available observational material is inhomogeneous, which makes the comparison between N and S quite problematic. In particular, the number of pointings in the northern and southern hemispheres are 190 and 112, respectively. An asymmetry is even stronger in the total area covered by the pointings: in the north it is twice as big as in the south.
We notice that the fluctuations of No [b] in the north are noticeable larger than in the south. Since the average numbers of detected “bright” sources per field in both areas are very similar, the Poissonian contribution to the rms of No [b] are also equal and amount to 112 per sq. deg. In effect, the whole difference is attributed to the cosmic variance, which in the north exceeds 68 per sq. deg, while in the south σCV = 41 per sq. deg. Also the No [b] − No [f] correlations are substantially different in both hemispheres. In the north the correlation is statistically significant at the confidence level of 99.98% (using the directional probability), while the data in the south are consistent with no correlation. It is complicated to interpret these discrepancies. Although some statistical characteristics of count amplitudes in both hemispheres look essentially different at first glance, it is most likely that these “unusual” features are artifacts that should be attributed to the specific properties of this particular set of observations, rather than to the genuine large-scale variations of the source distribution.
A large number of the new pointings would improve statistical significance of the investigations. Unfortunately, one
cannot expect a rapid inflow of the new Chandra observations. Therefore, a more promising way to proceed would be to search for the correlation between the existing Chandra observations and the data in other available X-ray surveys. In particular, the relationship between the counts amplitude determined here and the RASS maps should be investigated.
See the Chandra Interactive Analysis of Observations (CIAO) at http://asc.harvard.edu/ciao
In the calculations broken power law and Eq. (7) have been used.
Acknowledgments
We are grateful to the anonymous referee for careful reading and for remarks and propositions for improving the paper that resulted in the substantial and – in some points – essential changes in our work. We thank all the people who created the Chandra Interactive Analysis of Observations software for producing a user-friendly environment. This work has been partially supported by the Polish NCN grant 2011/01/B/ST9/06023.
References
- Alexander, D. M., Bauer, F. E., Brandt, W. N., et al. 2003, AJ, 126, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, W. N., Alexander, D. M., Hornschemeier, A. E., et al. 2001, ApJ, 122, 2810 [Google Scholar]
- Clowes, R. G., Harris, K. A., Raghunathan, S., et al. 2013, MNRAS, 429, 2910 [NASA ADS] [CrossRef] [Google Scholar]
- Geller, M. J., & Huchra, J. P. 1989, Science, 246, 897 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Georgakakis, A., Nandra, K., Laird, E. S., Aird, J., & Trichas, M. 2008, MNRAS, 388, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Gott, J. R., Jurić, M., Schlegel, D., et al. 2005, ApJ, 624, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehmer, B. D., Xue, Y. Q., Brandt, W. D., et al. 2012, ApJ, 752, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Moretti, A., Campana, S., Lazzati, D., & Tagliaferri, G. 2003, ApJ, 588, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Park, C., Choi, Y., Kim, J., et al. 2012, ApJ, 759, 7 [Google Scholar]
- Sołtan, A. M. 2008, A&A, 490, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sołtan, A. M. 2011, A&A, 532, A19 [NASA ADS] [EDP Sciences] [Google Scholar]
- Tozzi, P., Rosati, P., Nonino, M., et al. 2001, ApJ, 562, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, Y. Q., Luo, B., Brandt, W. N., et al. 2011, ApJS, 195. 10 [Google Scholar]
All Figures
 |
Fig. 1 Distribution of 190 pointings in the northern galactic hemisphere. Two circles represent galactic latitudes b = 30° and b = 60°. Each observation covers a circle of 15 arcmin in diameter. Labels close to some points in the map denote the actual number of pointings in the area. Symbol sizes are not to scale, and even in the crowded areas, the pointings do not necessarily overlap. |
| In the text | |
 |
Fig. 2 Same as Fig. 1 for 112 pointings in the southern galactic hemisphere. A few pointings within − 30° < b < − 28° have been included to improve statistics. |
| In the text | |
 |
Fig. 3 Amplitudes No of the source number counts for flux S in 10-15 erg s-1cm-2 (see Eq. (1)) for the “bright” and “faint” sources in the sample of 302 pointings; 293 pointings with the rms uncertainty of No [b] smaller than 160 per sq. deg are shown with dots, 9 pointings with larger rms – with crosses. |
| In the text | |
 |
Fig. 4 Distribution of the “pair rms”, i.e. rms difference between the counts amplitudes in pairs of observations as a function of the pair separation. Results obtained with and without weights are shown with full and open circles, respectively (see text for detailed explanation). The dotted line separates the overlapping pointings from the detached ones. The lowest separation bin contains pairs closer than 0.1 arcmin. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


