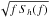EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A135 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A135
Number of page(s) 8
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/201219620
Published online 23 September 2013

© ESO, 2013

1. Motivation

Intermediate-mass black holes (IMBHs), with masses M ~ 102−5 M⊙ possibly exist at the centres of globular clusters (GCs) or small galaxies, if we assume that they follow the observed correlations between super-massive black holes (SMBHs) and their stellar surroundings (see Tremaine et al. 2002; Gültekin et al. 2009; Miller & Colbert 2004; Miller 2009, and references therein). Because of their mass, these objects cannot form via the formation scenarios of stellar-mass black holes (SBHs), which are the final results of the stellar evolution of massive stars (Fryer 1999; Fryer & Kalogera 2001; Belczynski et al. 2010) or SMBHs with masses M ~ 106 − 9 M⊙ that exist at the centres of galaxies (Rees 1978, 1984; Gillessen et al. 2009) and for which there is an emerging consensus about their formation (Volonteri & Rees 2005; Madau & Rees 2001).

Several scenarios have been proposed for the formation of IMBHs most of which require extremely dense environments similar to the centres of GCs for the IMBHs to form and grow in mass (van der Marel 2004; Miller & Colbert 2004). Miller & Hamilton (2002) suggest in their work that these massive black holes (BHs) can form from repeated mergers of a ~50 M⊙ BH, located at the centre of a GC, with other SBH of lower mass. The ~50 M⊙ threshold is required to ensure that the BH will not receive large recoil velocities after each merger and so will remain bound to the GC. According to (Miller & Hamilton 2002) the initial ~50 M⊙ BH could be formed either directly from the collapse of a massive star, or from a large number of SBH-SBH mergers, which would produce mostly escaping SBHs, but also a minority of large BHs bound to the GC.

An interesting scenario for the formation of IMBHs in the early evolution of GCs, has been studied by Quinlan & Shapiro (1990), Portegies Zwart & McMillan (2002, 2000), Gürkan et al. (2004), Portegies Zwart et al. (2004) and Freitag et al. (2006). According to this scenario, the most massive stars sink to the centre of a GC even before they become BHs and thus the cluster experiences an early core collapse during which the central density of stars becomes large enough, for massive stars to start rapidly and continuously merging with each other (see also Portegies Zwart et al. 2004; Goswami et al. 2012). This runaway process very soon leads to the formation of a very massive star (VMS), located close to the centre of the GC. It is unknown how stellar evolution proceeds in a VMS of this type (Glebbeek et al. 2009), but if it is assumed that the star directly collapses to a BH without significant mass-loss this could form an IMBH. Accretion of stars and gas during the next Myrs could increase its mass up to two orders of magnitude (Vesperini et al. 2010). Finally, as in SMBHs, Population III stars have been proposed as possible progenitors of IMBHs (see van der Marel 2004; Whalen & Fryer 2012,and references therein), but there are still many uncertainties in the evolution of such a star (Heger & Woosley 2002).

Although the formation of IMBHs has been studied extensively during the last decades and their existence was proposed in the early 1970s (Wyller 1970; Bahcall & Ostriker 1975; Frank & Rees 1976), there is still no direct proof of their existence. However, there is an increasing amount of favourable evidence that suggests that they should exist. The most well-known evidence is from the observations of ultra-luminous X-ray sources (ULXs, Feng & Soria 2011), which are usually associated to IMBHs. The brightest known ULX, known as HLX-1, is located in the outskirts of the edge-on S0a type galaxy ESO243-49 and is currently the strongest IMBH candidate. Based on the extreme luminosity of the X-ray source, which has a maximum of up to 1.1 × 1042 erg s-1 in the 0.2−10 keV band, Farrell et al. (2009) derive a conservative lower limit of 500 M⊙ for the potential IMBH (see also Godet et al. 2009; Farrell et al. 2010). More recent observations measured a peak luminosity of 1.3 × 1042 erg s-1 (Godet et al. 2011) and a possible period of variability of ~1 yr (Godet et al. 2012; Servillat et al. 2011). X-ray luminosities up to ~1041 erg s-1 can be explained by super-Eddington accretion to ~20 M⊙ SBHs (Begelman 2002) and/or beaming (King 2008). However, larger BH masses are needed to explain luminosities >1041 erg s-1. For HLX-1 the most recent estimate for the mass of the potential IMBH is ~3 × 103 − 105 M⊙ (Godet et al. 2012; Servillat et al. 2011; Davis et al. 2011), well within in the range of masses of IMBHs. Further investigations of HLX-1 confirmed its extraordinary luminosity by proving its association with galaxy ESO243-49 at a distance of 95 Mpc (Wiersema et al. 2010), and thus made the evidence of an IMBH even stronger. Interestingly, the X-ray source is not located at the centre of the host galaxy, but at a distance of ~3.3 kpc from its centre and ~0.8 kpc out of the galactic plane, possibly associated with a star cluster which appears to be in the same area. According to Farrell et al. (2012) this cluster has a mass of ~4 × 106 M⊙ and is either a massive young star cluster or an old GC. Optical observations of HLX-1 with VLT seem to rule out the case of a massive star cluster and favour the presence of a ~10 Gyr old GC with mass <106 M⊙ or a <10  Myr small star cluster with mass ~104 M⊙ (Soria et al. 2010, 2012).

Other recent interesting observational examples that point to the existence of these objects can be found in the work of Sutton et al. (2012), which evaluates a sample of eight extreme luminosity ultra-luminous X-ray source candidates and state that the observed luminosities can be explained in terms of IMBHs with masses in the range of 103 − 104 M⊙. Another X-ray source that might be associated with an IMBH is found at the centre of the nearby (d = 3.1 Mpc, Karachentsev et al. (2004)) dwarf lenticular galaxy NGC 404 (Binder et al. 2011). Using both stellar and gas dynamical mass estimates, Seth et al. (2010) estimated the mass of the potential IMBH to be ~ 105 M⊙, which agrees with recent estimates from Expanded Very Large Array observations (Nyland et al. 2012) and from X-ray observations (Binder et al. 2011). Finally, Nyland et al. (2012) confirmed the location of the source at the centre of the nuclear star cluster hosted by NGC 404 and ruled out other possible scenarios such as an X-ray binary, stellar formation, or a supernova remnant.

The above observational examples provide strong evidence of the existence of IMBHs, but do not indisputably prove that they exist. Direct proof would come from detailed kinematical observations of stars moving under the influence of the IMBH at the centres of GCs. Unfortunately, the radius of influence of an IMBH is only a few arc seconds (Peebles 1972; Chanamé et al. 2010; Miller & Colbert 2004), so it is very difficult, if not impossible, to accurately determine its mass by measuring the velocities of stars moving under its influence with the currently available instruments. This technique has been successfully used for determining the mass of the SMBH at the centre of the Milky Way Galaxy, where the stellar environment is less dense than the core of GCs and also there are a number of young and bright stars, moving under the gravitational influence of the SMBH which have been followed by observations for more than 15 years (Gillessen et al. 2009). The radius of influence R of an IMBH of mass M• can be defined as 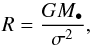R=GM•σ2,\begin{equation} R = \frac{G M_\bullet}{\sigma^2}, \end{equation}(1)where σ the velocity dispersion at the centre of the cluster. At a distance d this translates to an angular radius of influence (Bender 2005) α=1′′(M•103M⊙)(σ10kms-1)-2(d10kpc)-1.\begin{equation} \alpha = 1'' \Big( \frac{M_\bullet}{10^3 \ {M_\odot}} \Big) \left( \frac{\sigma}{10 \ {\rm km\ s^{-1}}} \right)^{-2} \left( \frac{d}{10 \ {\rm kpc}} \right)^{-1}. \end{equation}(2)For a 104 M⊙ IMBH the influence radius is of ~5′′, assuming a central velocity dispersion of σ = 20 km s-1 and a distance of ~5 kpc (see also Miller & Colbert 2004,for a similar example). Also, since GCs are old systems, this small sphere of influence contains mainly massive stellar remnants and old, dim stars that could not be easily observed and traced. For the above reasons, kinematical techniques can currently only give upper limits on the mass of the potential IMBHs at the centres of galactic GCs (Anderson & van der Marel 2010; van der Marel & Anderson 2010; Noyola et al. 2010; Lützgendorf et al. 2012; Kirsten & Vlemmings 2012; Strader et al. 2012). Since these limits are based on measurements of proper motions, velocity dispersion, or line of sight motions away of the sphere of influence of the potential IMBH, alternatives to IMBH explanations cannot be ruled out (Baumgardt et al. 2003a, 2005). Hence, we would need the Very Large Telescope Interferometer (VLTI) and one of the next-generation near-infrared instruments, the VSI or GRAVITY (Gillessen et al. 2006; Eisenhauer et al. 2008). In that case we could improve the astrometric accuracy by an order of magnitude and thus we would possibly be in a position to detect the innermost kinematics of a GC around a potential IMBH and thus accurately measure its mass.

An interesting avenue towards the direct detection of an IMBH, which would not require future optical or infrared telescopes and several years of observations, is GW astronomy. Additionally, IMBH-SBH binaries that might form in GCs represent an excellent test of GR, since they are similar to extreme mass-ratio inspirals (Amaro-Seoane et al. 2007). In particular, space-borne detectors such as the ESA-led eLISA (Amaro-Seoane et al. 2012) or Chinese mission study options (hereafter ALIA, see Bender et al. 2005; Crowder & Cornish 2005; Gong et al. 2011) will be able to catch these systems (which might also be referred to as intermediate mass-ratio inspirals, IMRIs) with good signal-to-noise ratios (SNR) if the GC is not farther than z ~ 0.7 (Amaro-Seoane et al. 2012; Miller & Hamilton 2002; Miller 2006). According to Miller & Hamilton (2002), LISA will be able to detect around ten IMBH-SBH binaries at any given time, while the merger of the BHs might be detectable by LIGO-II (and Advanced LIGO should see many of them Amaro-Seoane & Santamaria 2010; Fregeau et al. 2006).

If an IMRI forms in a GC, it is certain that sooner or later it will lead to an IMBH-SBH merger. Recent studies from numerical relativity (Koppitz et al. 2007; Pollney et al. 2007; Rezzolla et al. 2008; Rezzolla 2009; Lousto et al. 2010; Lousto & Zlochower 2011b,a) show that BH-BH mergers result in a gravitational wave recoil which, depending on the mass-ratio and spins of the merging BHs, might be as large as ~5000 km s-1 (Lousto & Zlochower 2011a). The mass-ratio of an IMRI in a GC is large enough to avoid such large recoils, but it is still possible for an IMBH of mass up to ~103 M⊙ to receive a kick greater than the escape velocity of the GC and therefore leave the system (Holley-Bockelmann et al. 2008).

In this work we use N-body simulations to study the interactions of an IMBH with SBHs in young star clusters and describe for the first time the production on an IMRI with our direct-summation code in one of our integrations. In Sect. 2 we describe the numerical tool and choice of the initial data used for the simulations. In Sect. 3 we describe the interactions of the IMBH with SBHs in the one simulation we observed an IMRI, and we discuss the possibility that the gravitational recoil velocity assigned to the IMBH after the merger kicks the IMBH out of the GC. In Sect. 4 we calculate the gravitational radiation from this IMRI in an approximate way. Finally, in Sect. 5 we conclude our work showing that an IMRI would be detectable by future space-based GW detectors such as LISA; we discuss the effects of the ejection of the IMBH on the GC and their possible connection with ULXs not associated with GCs; and we present our future plans for a statistical study of IMBH-SBH interactions in GCs.

Table 1

Description of the full set of initial data created for the investigation of the BH number and masses using different IMFs.

2. Numerical tool and initial conditions

We integrated the dynamical evolution of a GC containing a 500−1000 M⊙ IMBH with Myriad (Konstantinidis & Kokkotas 2010), a direct-summation N-body code that integrates all gravitational forces for all particles at every time step. The programme uses the Hermite integration scheme (Aarseth 1999, 2003). This requires computation not only of the accelerations, but also of their time derivatives. Particles that are tightly bound or with very small separation are integrated using the time-symmetric Hermite scheme (Kokubo et al. 1998), which is a symplectic integrator that makes the numerical errors oscillate between two limits that can be controlled by the choice of the time step. The code uses post-Newtonian correcting terms to the Newtonian forces, including 1, 2, and 2.5 order, as described for the first time in an N-body code by Kupi et al. (2006; their Eqs. (1)–(3)), and a recipe for gravitational recoil. The recoil velocity depends strongly on the mass ratio of the two holes, on the magnitude of their spins, and on their directions with respect to the plane of the orbit (see e.g. Rezzolla 2009,and references therein). The equation that we have implemented in the code is taken from Lousto et al. (2010), 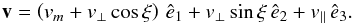v=(vm+v⊥cosξ) ê1+v⊥sinξ ê2+v∥ ê3.\begin{equation} \label{recoil} \vec{v} = \left(v_m + v_\bot \cos{\xi}\right)\, \hat{e}_1 + v_\bot \sin{\xi}\, \hat{e}_2 + v_{\parallel}\, \hat{e}_3. \end{equation}(3)In this equation, the indices ⊥ and ∥ stand for perpendicular and parallel directions with respect to the orbital angular momentum vector L of the binary; ê1 is a unit vector and lies on the plane of the orbit connecting the two MBHs, with direction from the heavier to the lighter one; ê2 is also on the plane of the orbit, but perpendicular to ê1, with direction such that ê1, ê2, and ê3 construct an orthonormal system, with ê3 defined such that it is the unit vector parallel to L; ξ is the angle between the unequal contributions of mass and spin to the recoil velocity. We assign random, maximal spins to the stars of the GC, and in particular we initially give the IMBH a spin a = S/M2 (see e.g. Lousto et al. 2010) of 0.998.

We assume that the IMBH forms at the centre of the cluster when the GC is 10 Myr old. This agrees with the formation scenario of runaway stellar mergers (Portegies Zwart & McMillan 2002) and also of the repeated SBH-SBH mergers (Miller & Hamilton 2002). For our study the number and masses of SBHs are of particular importance. Therefore, before creating the initial data for our simulations, we studied the number of SBHs and their masses assuming different initial mass functions (IMF) and metallicities. For the IMF we use Kroupa-like distributions (see Kroupa et al. 1993; Kroupa 2001) and also simple power-law distributions with different values for the slope α (see Salpeter 1955). We fix the total number of stars to N = 32768, the lower stellar mass limit to mlow = 0.2 M⊙, and the upper mass limit to mupper = 150 M⊙. Finally, we use values for the metallicity Z ranging from 0.0001 to 0.02. We investigate in total 15 models with different slopes of the IMF and metallicities and for each one of them we create a set of 100 random realisations. We evolve the stars of each realisation to 10 Myr using the stellar evolution code sse (Hurley et al. 2000) and we calculate averages for the number of SBH created and also for their higher and lower masses. The results are described in Table 1. Assuming no supernova kicks, the number of SBHs created depends strongly on the choice of the IMF slopes and ranges from ~20 to ~70 in our models. On the other hand the masses of the SBHs depend on the metallicity and range from ~3 M⊙ (for Z = 0.02) to ~27 M⊙ (for Z < 0.001).

For the initial data of our simulations, we picked four representative cases from our investigation that produce low and high numbers of SBHs. We also picked a value Z = 0.001 for the metallicity as typical for a GC which resulted in the formation of SBHs with masses between ~ 13 M⊙ and 27 M⊙. In these models all stars with masses above 20 M⊙ evolved off the main sequence at 10 Myr.

For our fiducial simulation A, we choose slopes α1 = 1.3 and α2 = 2.4 which, after stellar evolution until t = 10 Myr, result in 62 SBHs in the system, close to the highest number of SBHs created in our models. For the distribution of stars and BHs in the cluster, we use a King profile (King 1966) with concentration parameter W0 = 7. The initial escape velocity at the centre of the cluster is ~ 17 km s-1. At the centre of the cluster we introduce an IMBH of mass M• = 500 M⊙ and correct the velocities of all stars and BHs of the GC to reach dynamical equilibrium. We also created three additional initial data changing the IMF, the mass of the IMBH, and/or the initial concentration of the clusters. Case B is like A but with M• = 1000 M⊙ and α2 = 2.5, which results in 52 SBHs; case C is like B but with a King parameter of 6 and 48 SBHs. Finally, case D is like A but with a King parameter of 6 and α1 = 1.2 and α2 = 2.7, which results in only 17 SBHs, close to the lower number of SBHs created in our test models. The initial data for the four simulations are described in Table 2.

Table 2

Initial data for the 4 simulations.

We performed the dynamical evolution of each of the four models using Myriad, which treats the stars and stellar remnants as point particles, but takes into account their sizes in the case of collisions. No primordial mass segregation is taken into account, so the BHs are formed in all the distances from the centre of the cluster. The absence of initial mass-segregation leads to an underestimate of the initial frequency of IMBH-SBH interactions, but, as we will show below, most of the most massive SBHs sink to the centre and interact with the IMBH very soon. Stellar evolution is only used to create the initial data for our models. During the N-body simulations stellar evolution is turned off, so the masses of stars and the masses and the number of remnants remain constant in time. This is a simplification, which does dot have a significant impact on the dynamics of the IMBH and therefore on our results. Further stellar evolution (i.e. after the 10 Myr of the initial data) would create a number of SBHs with very low mass (<10 M⊙), which would have a negligible influence on the dynamics of the IMBH and on a possible binary that the IMBH would form with one of the higher-mass SBHs. Low-mass SBHs are expected not to be able to replace higher-mass SBH as companions of the IMBH. Instead, they are expected to be ejected easily through natal kicks and interactions with the IMBH and other higher-mass SBHs (Baumgardt et al. 2004).

thumbnail Fig. 1

Evolution of the semi-major axis and eccentricity of the three different binaries formed with the IMBH. Shortly after the beginning of the simulation, the IMBH builds a binary with the SBH with the 11th most massive mass, m•, 11. This corresponds to the first part of the curve (dashed blue curve). Later, there is an interaction which leads to a companion exchange for the binary, the SBH with the 18th most massive mass, m•, 18. This binary lives for about 40 Myr. We can see that the first two binaries have phases of very high eccentricity, ebin ~ 1, but not high enough to lead to a coalescence. The jumps in ebin indicate that the IMBH-SBH is still in a regime in which interactions with other stars play an important role. The system continues to shrink further and further until there is a three-body interaction. The binary is unbound and for a short period of time the IMBH has no companion, as indicated in the zoom-in subplots embedded in both the upper and lower panels. Then the final binary forms, with the second most massive SBH. This binary is very hard and quickly loses energy via GWs radiation, which very efficiently leads to circularization and the final merger.

From our set of simulations, only case A had an IMRI; we will therefore focus on this case in the remainder of the article. Myriad runs only with the assistance of the special-purpose GRAPE system (Makino et al. 2003), so we are restricted by the the availability and performance of GRAPE systems.

3. Dynamics of the system

Initially, the IMBH interacts strongly with a sub-group of stars and SBHs that contain approximately 20 members. As the system evolves, the members of this sub-group change. Soon, most of the SBHs of the system sink towards the centre and start to interact with the IMBH and its environment. During this process, some of them receive big kicks as a result of three-body interactions and are slingshot away from the centre of the cluster or the GC itself. After T ~ 3 Myr the first stable IMBH-SBH binary forms. The companion of the IMBH is a SBH with mass m•, 11 = 23.9 M⊙ and the initial semi-major axis of this binary is a ~ 88 AU. At T ~ 9.2 Myr this binary has a strong interaction with another SBH of the system. The interaction leads to a change of companion for the IMBH, which now builds a binary with a SBH of mass m•, 18 = 20.1 M⊙. The initial semi-major axis of the new binary is a ~ 17.6 AU. This binary survives for nearly 40 Myr, but its characteristics vary significantly. At T ~ 49 Myr the semi-major axis changes to a ~ 5 AU, while the eccentricity increases to e = 0.965. At this point in the simulation, this binary interacts strongly with the second most massive SBH, which leads to a companion exchange. The new binary has an initial semi-major axis of a ~ 6.55 AU and a very high eccentricity of e = 0.999. The mass of the new companion SBH is m•, 2 = 26.54 M⊙. In Fig. 1 we show the evolution of the semi-major axis and eccentricity for all of these binaries combined into a single curve. After T ~ 13 000 yr the binary merges and the resulting IMBH receives a random recoil velocity that depends on the mass ratio of the two members of the system and on the random spins that the code assigned to them. This gravitational rocket or recoil is such that the resulting velocity exceeds the escape velocity and the merged system leaves the GC. This is because we are using a low number of stars for the clusters; more realistic clusters will have larger escape velocities, so that the retained fraction of recoiling IMBH is larger and not well-represented by our case. We studied the distribution of recoil velocities for a merger of a binary similar to that of simulation A. We ran a two-body interaction 107 times and calculated the recoil using Eq. (3) with different spin orientations and magnitudes for the two black holes. We found that the most probable recoil velocity for a binary such as the one of case A peaks around 25 km s-1, with a probability of 21% that the merged system achieves velocities greater than 50 km s-1, of the order of realistic GC escape velocities.

In Fig. 2 we show the evolution of the distances of the ten most massive SBHs from the centre. The SBHs inspiral the centre very rapidly, as long as the IMBH exists in the cluster. Some of them escape the system, after passing very close to the central binary. After the IMBH merges with its binary companion SBH, the coalesced system leaves the GC and the trajectories of the remaining SBHs are not as steep, because they orbit the centre of density of the GC without sinking rapidly into it.

thumbnail Fig. 2

Distance R• to the density centre of the GC of the ten most massive SBHs and the IMBH (solid black line). Strong interactions of the SBHs lead to ejection of four of them before the IMBH merges. They are removed from the simulation when R• > 10 pc and they are unbound from the GC. At T ~ 47.7 Myr the IMRI leads to a coalescence that kicks the resulting merged system off the GC.

In Fig. 3 we show the Lagrange radii of the cluster during the simulation. We stop the simulation at ~10 Myr after the ejection of the IMBH. From t = 0 until the ejection of the IMBH, which happened at t ~ 49 Myr, the Lagrange radii increase constantly. This agrees with other results of other N-body (Baumgardt et al. 2004) and recent Monte Carlo (Umbreit et al. 2012) simulations of GCs containing IMBHs, and it happens because the central IMBH and the IMBH-SBH binary that forms almost instantly after the beginning of the simulation, act as a heating source for the cluster. Kinetic energy is transferred from the IMBH-SBH binary to the stars and SBHs that pass close from the density centre making the binary constantly harder and the stars more energetic and thus expanding the cluster. When the IMBH is removed from the cluster, the heating source is absent, so the cluster starts contracting slowly as is shown in the Lagrange radii. The shrinkage of the cluster would continue until the central number density of stars becomes high enough that another heating source (i.e. a new binary) is formed at the centre. Even though we integrated the system for another ~10 Myr after the ejection, no such source formed.

In all simulations the IMBH had as a companion a SBH, which was replaced several times with another SBH usually of greater mass. In the end, the companion of the IMBH was one of the most massive SBHs of the cluster. Most of the lower-mass SBHs, after sinking to the centre and interacting with the central IMBH-SBH binary, were kicked out of the GC. Also, we find a main-sequence or giant star tidally disrupted by the IMBH in none of the simulations. This is in agreement with the models of (Baumgardt et al. 2004) which contain a number of massive SBHs. In our models, SBHs are the most massive objects in the GC apart from the IMBH, and therefore sink to the centre faster than any other star. As a result an IMBH-SBH binary forms very soon with the companion of the IMBH because it is more massive than any other non-SBH object of the cluster. Thus, only interactions of the binary with another SBH of comparable or higher mass than the current companion of the IMBH may lead to a companion exchange, so it is almost impossible for a normal star to come too close to the IMBH and get tidally disrupted. Therefore, tidal disruptions of stars are not favoured in our models.

After the merger, the IMBH leaves the GC without any companion. This may be an artifact of the low number of stars used in the simulation. In real clusters a small number of stars or remnants are expected to be bound to the IMBH, so if the IMBH receives a large kick, these stars will follow it outside the GC. In this case, and if there are no massive SBHs among the IMBH companions, some stars might be tidally disrupted by the IMBH, and thus the system might become a ULX not associated with a GC.

thumbnail Fig. 3

Lagrangian radii showing the evolution of different mass fractions in the cluster: from top to bottom 90, 80 ... 20, 10, 5, 3, 2, 1, and 0.1% of the total mass. The green rectangle shows the interval of time before and after the kick of the IMBH off the cluster. All mass curves suffer a jump at the moment of ejection. After the removal of the heating source from the centre, the curves are flatter and their slopes start to decrease.

4. Gravitational waves from an IMRI

In this section we follow the binary IMBH-SBH from the standpoint of emission of GWs. In Fig.4 we can see the evolution of the IMRI in a semi-major axis and orbital period – eccentricity plane. The binary enters the plot from the top with a high eccentricity, which places it very close to the innermost stable circular orbit, but the loss of energy quickly circularises it and drives it to lower eccentricities. As we discussed in the previous section, the binary forms with a very small initial semi-major axis, so that it hardens very efficiently. Hence, the binary follows closely what we expect from the approach of Peters (1964), since the post-Newtonian terms lead the evolution of the system, which can be regarded as dynamically decoupled from the GC. It then enters the band of a LISA-like or ALIA detector with a significant eccentricity and the simulation is stopped when the semi-major axis is a = 5 RSchw, the Schwarzschild radius of the IMBH. That is the moment at which the code assigns a recoil velocity to the merged system based on the spins of the two compact objects.

thumbnail Fig. 4

Inspiral of the SBH into the IMBH from top to bottom and from left to right in the eccentricity-semi-major axis plane. The red solid curve starting at a very eccentric orbit shows the results of the Nbody simulation. The dashed green region corresponds to the band of a LISA-like mission. Dashed blue curves correspond to the trajectories due only to the emission of GWs in the Peters & Mathews (1963) approximation. We also plot the corresponding merger timescales in the same approximation in dashed blue lines starting at 1010 years, and in solid black lines the corresponding trajectories for evolution by GW emission Peters (1964) approximation. The black-shaded region on the right corresponds to the last stable circular orbit. Since the binary starts at a very high eccentricity, it basically follows one of the solid black lines, because it merges quickly and does not interact with other stars in the system.

In Fig. 5 we can see the same evolution from the perspective of the characteristic amplitude and frequency of the waves. We show the first harmonics in the approximation of Keplerian ellipses of Peters & Mathews (1963).

thumbnail Fig. 5

Characteristic amplitude hc of the first harmonics of the quadruple gravitational radiation emitted during the inspiral of the IMRI. The numbers show the first four of the harmonics. The orbital evolution is calculated in the Peters (1964) approximation and the amplitudes as in Peters & Mathews (1963). We assume the source is at a distance D = 1 Gpc. We indicate with a solid curve the noise curve f Sh(f)\hbox{$\sqrt{f\,S_h(f)}$} for the ALIA detector with an armlength of 3 × 109 m, a telescope diameter of 0.58 m, and a 1-way position noise of 8/Hz\hbox{$8/\!\!\sqrt{\rm Hz}$} pm, i.e. the 3H configuration of Gong et al. (2011). We also add the noise curve for a LISA-like detector (in grey, Larson et al. 2000), with the Galactic binary white dwarf confusion background (Bender & Hils 1997). Note that the SNR is not given by the height above the curve, but by the area below it. For each panel we show the ratio Rp0/Rs\hbox{$R_{\rm p}^0/R_{\rm s}$}, the initial periapsis distance over the Schwarzschild radius of the system. We indicate the moments in the evolution for which the time to coalescence is 5, 1 yr, 1 h, 10 min, and 1 s.

5. Conclusions

In this work we have investigated the evolution of GCs that harbour an IMBH in their centre with a direct-summation code. The code uses relativistic corrections and a prescription for gravitational recoil. For one of the cases we find that an IMRI forms with a SBH because of close interactions, which leads to the ejection of IMBH after coalescence. We follow the properties of the IMRI from the standpoint of the global evolution of the cluster and of GW.

Before the formation of the IMRI and the subsequent ejection of the IMBH, the cluster experiences strong expansion as a result of two-body relaxation in the presence of an IMBH. The IMBH-SBH binaries that are formed transfer kinetic energy to the stars that sink to the centre and as a result the GC expands significantly. Some of the inner Lagrange radii of the cluster almost double in size during the first ~ 50 Myr of dynamical evolution. Also, most of the massive SBHs sink to the centre very rapidly and after interacting with the IMBH, if they do not become its companions, they receive large kicks and get ejected violently from the GC. After the ejection of the IMBH, the GC slowly starts to contract as a result of the absence of the heating source at the centre. This might lead to another core collapse of the GC, something we do not observe in the simulation in the first 10 Myr after the ejection if the IMBH.

In our simulations, the IMBH forms a binary with a SBH very early and then exchanges its companion several times. In the simulation we observed an IMRI, the IMBH formed a binary with the second most massive SBH of the system. The initial high eccentricity of the IMBH-SBH binary leads to an IMRI and a subsequent merger. We showed that for 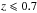\hbox{$z \leqslant 0.7$} the energy loss of the binary in GWs is easily detectable by space-borne missions such as a LISA-like observatory (Amaro-Seoane et al. 2012) or ALIA in its 8 pc configuration. Moreover, the IMRI enters the bandwidth of the detectors with a very high eccentricity, e = 0.9987, as with the EMRIs. One year before the final coalescence, the system still retains a residual eccentricity of e ~ 0.12, and ten minutes before merger of e ~ 10-3, which is detectable by data-analysis techniques (Amaro-Seoane et al. 2010; Porter & Sesana 2010; Key & Cornish 2011).

Intermediate mass-ratio inspirals represent a test of GR, as well as a probe of space and time around massive black holes and also of the innermost kinematics of GCs to very large distances, of the order of a few Gpc. Furthemore, a successful detection would represent very robust proof for the existence of IMBHs. The fact that the kick is making the merged system leave the GC is possibly an artifact of the low particle number we used in the simulations, though in principle recoiling velocities can be much higher than the escape velocity of a cluster, of the order of ~50 km s-1 (see e.g. Rezzolla 2009; Holley-Bockelmann et al. 2008). However, we have also demonstrated that there is a non-negligible statistical probability that a similar case leads to a kick of the IMBH off a realistic GC.

In our simulations we do not observe any tidal disruption of stars and in the simulation in which we had an IMRI, the IMBH also left the system without any companion. This is probably an artifact of the low number of stars used in the simulations. In real clusters there is normally a small number of stars bound to the IMBH, so after all the SBHs are ejected and probably after some IMBH-SBH mergers, the IMBH will be followed by a number of main-sequence or giant stars, even if it is ejected from the GC. Therefore, if after the IMBH-SBH merger the IMBH remains in the GC, it might soon become an X-ray source at the centre of the cluster, similar to the ULXs that are located at the centres of GCs (e.g. the ULX at NGC 404, Nyland et al. 2012; Binder et al. 2011). On the other hand, if it escapes the GC, followed by the stars bound to it, it might soon become a ULX outside of the GC. In this context, HLX-1 might be an escaping IMBH that originated at the centre of ESO243-49 and received a large recoil velocity after a merger with a massive SBH. The kick is responsible for the escape of the IMBH, which is followed by a number of stars gravitationally bound to it. This scenario supports one of the possible scenarios for HLX-1 suggested by Soria et al. (2012) according to which the HLX-1 is an IMBH embedded in a young population of stars with ages <10 Myr and total mass with upper bound of ~104 M⊙. A larger number of simulations of escaping IMBHs using a realistic number of stars would be appropriate for testing this scenario.

Even though the code was ported to run on a PC with the special-purpose hardware GRAPE, we cannot cover a broader parameter space, nor study cases with a larger number of stars, or study the global dynamical evolution of the GC after the kick for a longer time. We plan to perform a better parameter space exploration thanks to the availability of GPUs, which will allow us to address the limitations we described above. This will allow us to investigate the potential global structure of the GC after the kick, since the impact on the cluster could, in principle, be a signature for the process. This will also allow us to study the properties and detectability of the escaping IMBHs and their possible companions.

Acknowledgments

We thank Emma Robinson for comments on the manuscript and Nikolaos Stergioulas for suggesting that we also examine the possibility of kicks. S.K. and P.A.S. are indebted to Xuefei Gong, Shan Bai, and Yun Kau Lau for conversations, their hospitality in Beijing, and for sharing with us the data for the sensitivity curve of the ALIA detector. P.A.S. thanks the organizers of the 2011 summer workshop at the Aspen Center for Physics for inviting him to attend. S.K. and P.A.S. are thankful to Rainer Spurzem and Fukun Liu for the invitations to the meeting on black holes in Lijiang and to visit the KIAA and NAOC in Beijing in summer of 2011 where this work was finished. The work of S.K. was funded by the Deutsches Zentrum für Luft- und Raumfahrt (DLR; through the LISA Germany project), also by the German Science Foundation (DFG) via SFB/TR7 on Gravitational Waves, and by the FONDECYT Postdoctoral Fellowship number 3130570. S.K. would like to thank Kleomenis Tsiganis for the discussions.

References

  1. Aarseth, S. J. 1999, PASP, 111, 1333 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aarseth, S. J. 2003, Gravitational N-Body Simulations (Cambridge, UK: Cambridge University Press) [Google Scholar]
  3. Amaro-Seoane, P., & Santamaria, L. 2010, 722, 1197 [Google Scholar]
  4. Amaro-Seoane, P., Gair, J. R., Freitag, M., et al. 2007, Classical and Quantum Gravity, 24, 113 [Google Scholar]
  5. Amaro-Seoane, P., Eichhorn, C., Porter, E. K., & Spurzem, R. 2010, MNRAS, 401, 2268 [NASA ADS] [CrossRef] [Google Scholar]
  6. Amaro-Seoane, P., Aoudia, S., Babak, S., et al. 2012, GW Notes, accepted [Google Scholar]
  7. Anderson, J., & van der Marel, R. P. 2010, ApJ, 710, 1032 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bahcall, J. N., & Ostriker, J. P. 1975, Nature, 256, 23 [NASA ADS] [CrossRef] [Google Scholar]
  9. Baumgardt, H., Hut, P., Makino, J., McMillan, S., & Portegies Zwart, S. 2003a, ApJ, 582, L21 [NASA ADS] [CrossRef] [Google Scholar]
  10. Baumgardt, H., Makino, J., Hut, P., McMillan, S., & Portegies Zwart, S. 2003b, ApJ, 589, L25 [NASA ADS] [CrossRef] [Google Scholar]
  11. Baumgardt, H., Makino, J., & Ebisuzaki, T. 2004, ApJ, 613, 1143 [NASA ADS] [CrossRef] [Google Scholar]
  12. Baumgardt, H., Makino, J., & Hut, P. 2005, ApJ, 620, 238 [NASA ADS] [CrossRef] [Google Scholar]
  13. Begelman, M. C. 2002, ApJ, 568, L97 [NASA ADS] [CrossRef] [Google Scholar]
  14. Belczynski, K., Bulik, T., Fryer, C. L., et al. 2010, ApJ, 714, 1217 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bender, R. 2005, in Growing Black Holes: Accretion in a Cosmological Context Supermassive Black Holes in Nearby Galaxy Centers, eds. A. Merloni, S. Nayakshin, & R. A. Sunyaev, 147 [Google Scholar]
  16. Bender, P. L., & Hils, D. 1997, Classical and Quantum Gravity, 14, 1439 [NASA ADS] [CrossRef] [Google Scholar]
  17. Bender, P. L., Armitage, P. J., Begelman, M. C., & Pema, R. 2005, White Paper submitted to the NASA SEU Roadmap Committee [Google Scholar]
  18. Binder, B., Williams, B. F., Eracleous, M., et al. 2011, ApJ, 737, 77 [NASA ADS] [CrossRef] [Google Scholar]
  19. Chanamé, J., Bruursema, J., Chandar, R., et al. 2010, in HST’s hunt for intermediate-mass black holes in star clusters, eds. R. de Grijs, & J. R. D. Lépine, IAU Symp., 266, 231 [Google Scholar]
  20. Crowder, J., & Cornish, N. J. 2005, Phys. Rev. D, 72, 083005 [NASA ADS] [CrossRef] [Google Scholar]
  21. Davis, S. W., Narayan, R., Zhu, Y., et al. 2011, ApJ, 734, 111 [NASA ADS] [CrossRef] [Google Scholar]
  22. Eisenhauer, F., Perrin, G., Brandner, W., et al. 2008, in GRAVITY: getting to the event horizon of Sgr A*, SPIE Conf. Ser., 7013 [Google Scholar]
  23. Farrell, S. A., Webb, N. A., Barret, D., Godet, O., & Rodrigues, J. M. 2009, Nature, 460, 73 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  24. Farrell, S. A., Servillat, M., Oates, S. R., et al. 2010, X-ray Astronomy 2009; Present Status, Multi-Wavelength Approach and Future Perspectives, 1248, 93 [Google Scholar]
  25. Farrell, S. A., Servillat, M., Pforr, J., et al. 2012, ApJ, 747, L13 [NASA ADS] [CrossRef] [Google Scholar]
  26. Feng, H., & Soria, R. 2011, New A Rev., 55, 166 [NASA ADS] [CrossRef] [Google Scholar]
  27. Frank, J., & Rees, M. J. 1976, MNRAS, 176, 633 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fregeau, J. M., Larson, S. L., Miller, M. C., O’Shaughnessy, R., & Rasio, F. A. 2006, ApJ, 646, L135 [Google Scholar]
  29. Freitag, M., Gürkan, M. A., & Rasio, F. A. 2006, MNRAS, 368, 141 [NASA ADS] [Google Scholar]
  30. Fryer, C. L. 1999, ApJ, 522, 413 [NASA ADS] [CrossRef] [Google Scholar]
  31. Fryer, C. L., & Kalogera, V. 2001, ApJ, 554, 548 [NASA ADS] [CrossRef] [Google Scholar]
  32. Gürkan, M. A., Freitag, M., & Rasio, F. A. 2004, ApJ, 604, 632 [NASA ADS] [CrossRef] [Google Scholar]
  33. Gillessen, S., Perrin, G., Brandner, W., et al. 2006, in GRAVITY: the adaptive-optics-assisted two-object beam combiner instrument for the VLTI, SPIE Conf. Ser., 6268 [Google Scholar]
  34. Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
  35. Glebbeek, E., Gaburov, E., de Mink, S. E., Pols, O. R., & Portegies Zwart, S. F. 2009, A&A, 497, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Godet, O., Barret, D., Webb, N. A., Farrell, S. A., & Gehrels, N. 2009, ApJ, 705, L109 [NASA ADS] [CrossRef] [Google Scholar]
  37. Godet, O., Farrell, S., Barret, D., Webb, N., & Servillat, M. 2011, The Astronomer’s Telegram, 3569, 1 [NASA ADS] [Google Scholar]
  38. Godet, O., Plazolles, B., Kawaguchi, T., et al. 2012, ApJ, 752, 34 [NASA ADS] [CrossRef] [Google Scholar]
  39. Gong, X., Xu, S., Bai, S., et al. 2011, Classic. Quant. Grav., 28, 094012 [NASA ADS] [CrossRef] [Google Scholar]
  40. Goswami, S., Umbreit, S., Bierbaum, M., & Rasio, F. A. 2012, ApJ, 752, 43 [NASA ADS] [CrossRef] [Google Scholar]
  41. Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
  42. Heger, A., & Woosley, S. E. 2002, ApJ, 567, 532 [NASA ADS] [CrossRef] [Google Scholar]
  43. Holley-Bockelmann, K., Gültekin, K., Shoemaker, D., & Yunes, N. 2008, ApJ, 686, 829 [NASA ADS] [CrossRef] [Google Scholar]
  44. Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
  45. Karachentsev, I. D., Karachentseva, V. E., Huchtmeier, W. K., & Makarov, D. I. 2004, AJ, 127, 2031 [Google Scholar]
  46. Key, J. S., & Cornish, N. J. 2011, Phys. Rev. D, 83, 083001 [NASA ADS] [CrossRef] [Google Scholar]
  47. King, A. R. 2008, MNRAS, 385, L113 [Google Scholar]
  48. King, I. R. 1966, AJ, 71, 64 [Google Scholar]
  49. Kirsten, F., & Vlemmings, W. H. T. 2012, A&A, 542, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Kokubo, E., Yoshinaga, K., & Makino, J. 1998, MNRAS, 297, 1067 [NASA ADS] [CrossRef] [Google Scholar]
  51. Konstantinidis, S., & Kokkotas, K. D. 2010, A&A, 522, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Koppitz, M., Pollney, D., Reisswig, C., et al. 2007, Phys. Rev. Lett., 99, 041102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  53. Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
  54. Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
  55. Kupi, G., Amaro-Seoane, P., & Spurzem, R. 2006, MNRAS, L77 [Google Scholar]
  56. Larson, S. L., Hiscock, W. A., & Hellings, R. W. 2000, Phys. Rev. D, 62, 062001 [NASA ADS] [CrossRef] [Google Scholar]
  57. Lousto, C. O., & Zlochower, Y. 2011a, Phys. Rev. Lett., 107, 231102 [Google Scholar]
  58. Lousto, C. O., & Zlochower, Y. 2011b, Phys. Rev. D, 83, 024003 [NASA ADS] [CrossRef] [Google Scholar]
  59. Lousto, C. O., Campanelli, M., Zlochower, Y., & Nakano, H. 2010, Classical and Quantum Gravity, 27, 114006 [NASA ADS] [CrossRef] [Google Scholar]
  60. Lützgendorf, N., Kissler-Patig, M., Gebhardt, K., et al. 2012, A&A, 542, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Madau, P., & Rees, M. J. 2001, ApJ, 551, L27 [NASA ADS] [CrossRef] [Google Scholar]
  62. Makino, J., Fukushige, T., Koga, M., & Namura, K. 2003, PASJ, 55, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  63. Miller, C. 2006, in APS April Meeting Abstracts Gravitational Radiation from Intermediate-Mass Black Holes, 4003 [Google Scholar]
  64. Miller, M. C. 2009, Classic. Quant. Grav., 26, 094031 [NASA ADS] [CrossRef] [Google Scholar]
  65. Miller, M. C., & Colbert, E. J. M. 2004, Int. J. Mod. Phys. D, 13, 1 [NASA ADS] [CrossRef] [Google Scholar]
  66. Miller, M. C., & Hamilton, D. P. 2002, MNRAS, 330, 232 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  67. Noyola, E., Gebhardt, K., Kissler-Patig, M., et al. 2010, ApJ, 719, L60 [NASA ADS] [CrossRef] [Google Scholar]
  68. Nyland, K., Marvil, J., Wrobel, J., Young, L., & Zauderer, B. A. 2012, ApJ, 753, 103 [NASA ADS] [CrossRef] [Google Scholar]
  69. Peebles, P. J. E. 1972, ApJ, 178, 371 [NASA ADS] [CrossRef] [Google Scholar]
  70. Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
  71. Peters, P. C., & Mathews, J. 1963, Phys. Rev., 131, 435 [NASA ADS] [CrossRef] [Google Scholar]
  72. Pollney, D., Reisswig, C., Rezzolla, L., et al. 2007, Phys. Rev. D, 76, 124002 [NASA ADS] [CrossRef] [Google Scholar]
  73. Portegies Zwart, S. F., & McMillan, S. L. W. 2000, ApJ, 528, L17 [NASA ADS] [CrossRef] [Google Scholar]
  74. Portegies Zwart, S. F., & McMillan, S. L. W. 2002, ApJ, 576, 899 [NASA ADS] [CrossRef] [Google Scholar]
  75. Portegies Zwart, S. F., Baumgardt, H., Hut, P., Makino, J., & McMillan, S. L. W. 2004, Nature, 428, 724 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  76. Porter, E. K., & Sesana, A. 2010 [arXiv:1005.5296] [Google Scholar]
  77. Quinlan, G. D., & Shapiro, S. L. 1990, ApJ, 356, 483 [NASA ADS] [CrossRef] [Google Scholar]
  78. Rees, M. J. 1978, in Structure and Properties of Nearby Galaxies, Emission from the nuclei of nearby galaxies – Evidence for massive black holes, eds. E. M. Berkhuijsen, & R. Wielebinski, IAU Symp., 77, 237 [Google Scholar]
  79. Rees, M. J. 1984, ARA&A, 22, 471 [NASA ADS] [CrossRef] [Google Scholar]
  80. Rezzolla, L. 2009, Classical and Quantum Gravity, 26, 094023 [Google Scholar]
  81. Rezzolla, L., Dorband, E. N., Reisswig, C., et al. 2008, ApJ, 679, 1422 [NASA ADS] [CrossRef] [Google Scholar]
  82. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  83. Servillat, M., Farrell, S. A., Lin, D., et al. 2011, ApJ, 743, 6 [NASA ADS] [CrossRef] [Google Scholar]
  84. Seth, A. C., Cappellari, M., Neumayer, N., et al. 2010, ApJ, 714, 713 [NASA ADS] [CrossRef] [Google Scholar]
  85. Soria, R., Hau, G. K. T., Graham, A. W., et al. 2010, MNRAS, 405, 870 [NASA ADS] [Google Scholar]
  86. Soria, R., Hakala, P. J., Hau, G. K. T., Gladstone, J. C., & Kong, A. K. H. 2012, MNRAS, 420, 3599 [NASA ADS] [CrossRef] [Google Scholar]
  87. Strader, J., Chomiuk, L., Maccarone, T. J., Miller-Jones, J. C. A., & Seth, A. C. 2012, Nature, 490, 71 [NASA ADS] [CrossRef] [Google Scholar]
  88. Sutton, A. D., Roberts, T. P., Walton, D. J., Gladstone, J. C., & Scott, A. E. 2012, MNRAS, 423, 1154 [NASA ADS] [CrossRef] [Google Scholar]
  89. Tremaine, S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] [Google Scholar]
  90. Umbreit, S., Fregeau, J. M., Chatterjee, S., & Rasio, F. A. 2012, ApJ, 750, 31 [NASA ADS] [CrossRef] [Google Scholar]
  91. van der Marel, R. P. 2004, in Coevolution of Black Holes and Galaxies, Carnegie Obs. Centennial Symp. (CUP), 37 [Google Scholar]
  92. van der Marel, R. P., & Anderson, J. 2010, ApJ, 710, 1063 [NASA ADS] [CrossRef] [Google Scholar]
  93. Vesperini, E., McMillan, S. L. W., D’Ercole, A., & D’Antona, F. 2010, ApJ, 713, L41 [NASA ADS] [CrossRef] [Google Scholar]
  94. Volonteri, M., & Rees, M. J. 2005, ApJ, 633, 624 [NASA ADS] [CrossRef] [Google Scholar]
  95. Whalen, D. J., & Fryer, C. L. 2012, ApJ, 756, L19 [NASA ADS] [CrossRef] [Google Scholar]
  96. Wiersema, K., Farrell, S. A., Webb, N. A., et al. 2010, ApJ, 721, L102 [NASA ADS] [CrossRef] [Google Scholar]
  97. Wyller, A. A. 1970, ApJ, 160, 443 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Description of the full set of initial data created for the investigation of the BH number and masses using different IMFs.

In the text
Table 2

Initial data for the 4 simulations.

In the text

All Figures

thumbnail Fig. 1

Evolution of the semi-major axis and eccentricity of the three different binaries formed with the IMBH. Shortly after the beginning of the simulation, the IMBH builds a binary with the SBH with the 11th most massive mass, m•, 11. This corresponds to the first part of the curve (dashed blue curve). Later, there is an interaction which leads to a companion exchange for the binary, the SBH with the 18th most massive mass, m•, 18. This binary lives for about 40 Myr. We can see that the first two binaries have phases of very high eccentricity, ebin ~ 1, but not high enough to lead to a coalescence. The jumps in ebin indicate that the IMBH-SBH is still in a regime in which interactions with other stars play an important role. The system continues to shrink further and further until there is a three-body interaction. The binary is unbound and for a short period of time the IMBH has no companion, as indicated in the zoom-in subplots embedded in both the upper and lower panels. Then the final binary forms, with the second most massive SBH. This binary is very hard and quickly loses energy via GWs radiation, which very efficiently leads to circularization and the final merger.

In the text
thumbnail Fig. 2

Distance R• to the density centre of the GC of the ten most massive SBHs and the IMBH (solid black line). Strong interactions of the SBHs lead to ejection of four of them before the IMBH merges. They are removed from the simulation when R• > 10 pc and they are unbound from the GC. At T ~ 47.7 Myr the IMRI leads to a coalescence that kicks the resulting merged system off the GC.
In the text
thumbnail Fig. 3

Lagrangian radii showing the evolution of different mass fractions in the cluster: from top to bottom 90, 80 ... 20, 10, 5, 3, 2, 1, and 0.1% of the total mass. The green rectangle shows the interval of time before and after the kick of the IMBH off the cluster. All mass curves suffer a jump at the moment of ejection. After the removal of the heating source from the centre, the curves are flatter and their slopes start to decrease.

In the text
thumbnail Fig. 4

Inspiral of the SBH into the IMBH from top to bottom and from left to right in the eccentricity-semi-major axis plane. The red solid curve starting at a very eccentric orbit shows the results of the Nbody simulation. The dashed green region corresponds to the band of a LISA-like mission. Dashed blue curves correspond to the trajectories due only to the emission of GWs in the Peters & Mathews (1963) approximation. We also plot the corresponding merger timescales in the same approximation in dashed blue lines starting at 1010 years, and in solid black lines the corresponding trajectories for evolution by GW emission Peters (1964) approximation. The black-shaded region on the right corresponds to the last stable circular orbit. Since the binary starts at a very high eccentricity, it basically follows one of the solid black lines, because it merges quickly and does not interact with other stars in the system.

In the text
thumbnail Fig. 5

Characteristic amplitude hc of the first harmonics of the quadruple gravitational radiation emitted during the inspiral of the IMRI. The numbers show the first four of the harmonics. The orbital evolution is calculated in the Peters (1964) approximation and the amplitudes as in Peters & Mathews (1963). We assume the source is at a distance D = 1 Gpc. We indicate with a solid curve the noise curve f Sh(f)\hbox{$\sqrt{f\,S_h(f)}$} for the ALIA detector with an armlength of 3 × 109 m, a telescope diameter of 0.58 m, and a 1-way position noise of 8/Hz\hbox{$8/\!\!\sqrt{\rm Hz}$} pm, i.e. the 3H configuration of Gong et al. (2011). We also add the noise curve for a LISA-like detector (in grey, Larson et al. 2000), with the Galactic binary white dwarf confusion background (Bender & Hils 1997). Note that the SNR is not given by the height above the curve, but by the area below it. For each panel we show the ratio Rp0/Rs\hbox{$R_{\rm p}^0/R_{\rm s}$}, the initial periapsis distance over the Schwarzschild radius of the system. We indicate the moments in the evolution for which the time to coalescence is 5, 1 yr, 1 h, 10 min, and 1 s.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.