| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 20 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/20079306 | |
| Published online | 16 July 2013 | |
The 2.3 GHz continuum survey of the GEM project⋆
1
Divisão de Astrofísica, Instituto Nacional de Pesquisas Espaciais
(INPE), CP 515,
12201-970
São José dos Campos
SP
Brazil
2
Centro Internacional de Física, Bogotá, Colombia
3
Dipartimento di Fisica, Università degli Studi di
Milano, via Celoria
16, 20133
Milano,
Italy
4
Lawrence Berkeley National Laboratory, University of
California, 1 Cyclotron Road, Bldg.
50, MS 205, Berkeley, CA
94720,
USA
5
Physics Department, University of California,
Berkeley
CA
94720,
USA
6
Instituto de Física, Universidade de Brasília, Campus
Universitário Darcy Ribeiro − Asa Norte, 70919-970
Brasília, DF, Brazil
7
Physics Department, University of California,
Santa Barbara
CA
93106,
USA
8 Grupo de RadioAstronomia, Instituto
de Telecomunicações, Campus Universitário de Aveiro, Aveiro, Portugal
9
Departamento de Física, Facultad de Ciencias, Universidad Nacional
Autónoma de México, 04510
DF,
Mexico
10
INAF Osservatorio Astronomico di Padova,
Vicolo dell’Osservatorio 5,
35122
Padova,
Italy
11
Istituto di Fisica del Plasma, CNR-ENEA-EURATOM
Association, via R. Cozzi
53, 20125
Milano,
Italy
Received:
1
March
2013
Accepted:
19
April
2013
Context. Determining the spectral and spatial characteristics of the radio continuum of our Galaxy is an experimentally challenging endeavour for improving our understanding of the astrophysics of the interstellar medium. This knowledge has also become of paramount significance for cosmology, since Galactic emission is the main source of astrophysical contamination in measurements of the cosmic microwave background (CMB) radiation on large angular scales.
Aims. We present a partial-sky survey of the radio continuum at 2.3GHz within the scope of the Galactic Emission Mapping (GEM) project, an observational program conceived and developed to reveal the large-scale properties of Galactic synchrotron radiation through a set of self-consistent surveys of the radio continuum between 408MHz and 10GHz.
Methods. The GEM experiment uses a portable and double-shielded 5.5-m radiotelescope in altazimuthal configuration to map 60-degree-wide declination bands from different observational sites by circularly scanning the sky at zenithal angles of 30° from a constantly rotating platform. The observations were accomplished with a total power receiver, whose front-end high electron mobility transistor (HEMT) amplifier was matched directly to a cylindrical horn at the prime focus of the parabolic reflector. The Moon was used to calibrate the antenna temperature scale and the preparation of the map required direct subtraction and destriping algorithms to remove ground contamination as the most significant source of systematic error.
Results. We used 484 h of total intensity observations from two locations in Colombia and Brazil to yield 66% sky coverage from to . The observations in Colombia were obtained with a horizontal HPBW of and a vertical HPBW of . The pointing accuracy was and the RMS sensitivity was 11.42 mK. The observations in Brazil were obtained with a horizontal HPBW of and a vertical HPBW of . The pointing accuracy was and the RMS sensitivity was 8.24 mK. The zero-level uncertainty of the combined survey is 103mK with a temperature scale error of 5% after direct correlation with the Rhodes/HartRAO survey at 2326MHz on a T-T plot.
Conclusions. The sky brightness distribution into regions of low and high emission in the GEM survey is consistent with the appearance of a transition region as seen in the Haslam 408MHz and WMAP K-band surveys. Preliminary results also show that the temperature spectral index between 408MHz and the 2.3GHz band of the GEM survey has a weak spatial correlation with these regions; but it steepens significantly from high to low emission regions with respect to the WMAP K-band survey.
Key words: surveys / Galaxy: structure / radio continuum: general / radio continuum: ISM
The survey is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/556/A1
© ESO, 2013
1. Introduction
The large-scale distribution of non-thermal radiation from our Galaxy has been observed since the birth of radioastronomy at very low frequencies of a few tens of MHz (Jansky 1932, 1933, 1935) until the advent of the present era of precision cosmology at frequencies above 20GHz (e.g. Mather et al. 1990; Smoot et al. 1992; de Bernardis et al. 2000; Bennett et al. 2003; Meinhold et al. 2005). By the time its synchrotron nature was recognized to be due to relativistic electrons spiralling along interstellar magnetic field lines (Kiepenheuer 1950; Mayer et al. 1957; Mills 1959; Westerhout 1962; Wielebinski et al. 1962), free-free radiation from HII regions had already been identified as another Galactic emission component through the pioneering work of Reber (1940), who sketched the first radio maps of the Galaxy at 160MHz and 480MHz (Reber 1944, 1948). Excluding atmospheric emission and the 3K due to the cosmic microwave background (CMB), the sky signal on large angular scales is dominated by synchrotron radiation up to ~20GHz and by free-free and anomalous microwave emission (AME) up to ~70GHz, where the rising spectrum of thermal dust takes over the characterization of Galactic emission all the way into the infrared, including rotational line emission of CO molecules above 100GHz (Planck Collaboration 2013c,d). Given this association with distinct astrophysical sources, each Galactic emission component traces a unique spatial template. In the case of the non-thermal continuum, radioastronomers have always been actively pursuing the frequency dependance of the synchrotron template to understand the structure and composition of the interstellar medium. In cosmology, the nature of temperature anisotropies in the CMB and its polarization cannot be fully understood unless the contaminating role played by diffuse Galactic emission is accurately detailed.
In this article, we present the first survey of an observational program, the Galactic Emission Mapping (GEM) project, aimed at supplementing the frequency gap in radio-continuum surveys that map its large-scale distribution at centimeter wavelengths and the all-sky maps from the COBE, WMAP, and Planck satellite missions in the millimetric and submillimetric bands. We explore this deficiency in Sect. 2 as we review the present status of the GEM project toward the preparation of spatial templates of the synchrotron component between 408MHz and 10GHz. In Sect. 3 we describe our portable single-dish scanning experiment at 2.3GHz during three observing seasons in Colombia and Brazil. In Sect. 4 we outline the data reduction and preparation of a combined map with 66% of sky coverage in total intensity between and . Its baseline calibration and destriping techniques are treated in Sect. 5 together with the absolute temperature scale of the final map. We discuss our results in the light of the Rhodes/HartRAO survey at 2326MHz (Jonas et al. 1998) in Sect. 6 and, finally, we state our conclusions and future prospects in Sect. 7.
2. Large-scale Galactic emission and the GEM project
Unparalleled efforts have always been dedicated to delineate the complex morphology of the synchrotron-dominated Galactic emission at meter and centimeter wavelengths, which reveals the rich environment of supernova remnants with spurs and loops emanating from the Galactic plane and, in some cases, engulfing our location near the inner Perseus spiral arm of the Galaxy. The work of Jansky and Reber led naturally to the completion of the first all-sky radio surveys. The earliest of these was the 200MHz survey of Dröge & Priester (1956), which combined the observations of Allen & Gum (1950) in the southern hemisphere. The advent of the world’s largest radiotelescopes, together with an improvement in the performance of the receivers, prompted the realization of several partial surveys of better sensitivity and resolution at 178MHz (Turtle & Baldwin 1962), 30MHz (Mathewson et al. 1965), 38MHz (Milogradov-Turin & Smith 1973), 85MHz and 150MHz (Yates et al. 1967; Landecker & Wielebinski 1970), which were used to synthesize three additional low-frequency all-sky surveys: the 30MHz map of Cane (1978), the 85MHz map of Yates (1968), and the 150MHz map of Landecker & Wielebinski (1970). The integrity of these maps is, however, compromised by the need to assume spectral indices when combining different frequencies and by significant sidelobe level corrections due to differential ground and sky pick-up; let alone the differences in the mapping strategy of each radiotelescope.
A major improvement in the preparation of all-sky surveys was achieved by Haslam et al. (1981, 1982), whose 408MHz map of the whole sky reflects the choice of a single observing frequency and mapping strategy across four surveys to obtain a resolution under 1° with negligible sidelobe contamination using single-dish observations. More recently, another all-sky medium-resolution (~) survey was completed at 1420MHz through the observations of Reich & Reich (1982, 1986) in the northern hemisphere and those of Testori et al. (2001) in the southern hemisphere (Reich et al. 2001). Single-dish surveys of the radio continuum for mapping the large-scale Galactic emission have not been pursued at higher frequencies, with the exception of the Rhodes/HartRAO survey at 2326 MHz (Jonas et al. 1998) over 67% of the sky with a . Higher resolution surveys in this frequency range have been obtained with single-dish antennas at 1.4MHz (Reich et al. 1990a, 1997), 2.4MHz (Duncan et al. 1995), and 2.7MHz (Reich et al. 1984, 1990b; Fürst et al. 1990); but their sky coverage has been limited to within a few degrees of the Galactic plane. At lower frequencies, low-resolution antenna arrays have been used to conclude three other major surveys with 69% and 95% of total sky coverage, respectively, at 22MHz (Roger et al. 1999) and 45MHz (Alvarez et al. 1997; Maeda et al. 1999).
In astrophysics, medium- and low-resolution surveys complement high-resolution surveys in probing the full range of spatial scales that are necessary to explore the complexity of the ISM. In particular, toward the Galactic disk, where the majority of the Galactic radio sources and the 21-cm continuum emission of atomic hydrogen are concentrated. Combining dedicated single-dish observations and their sensitivity to diffuse emission with interferometric observations down to the resolution limit in the Galactic disk has resulted in the International Galactic Plane Survey of HI, which covers 90% of the Galactic disk extending across three surveys: the Canadian Galactic Plane Survey (CGPS, Taylor et al. 2003), the Southern Galactic Plane Survey (SGPS, McClure-Griffiths et al. 2005), and the VLA Galactic Plane Survey (VGPS, Stil et al. 2006).
2.1. CMB contamination
The detection of temperature anisotropies in the CMB radiation by the DMR experiment onboard the COBE satellite (Smoot et al. 1992) initiated a scientific breakthrough for cosmology; but it also showed, from the analysis of the COBE all-sky maps at 30GHz, 53GHz, and 90GHz (Bennett et al. 1992), the need to extend our knowledge of diffuse Galactic emission to higher frequencies. Experiments to measure the CMB with higher precision and resolution have since then been developed or are currently under way. These new generations of experiments are conducted from the ground (e.g. BEAST – Childers et al. 2005; Meinhold et al. 2005; O’Dwyer et al. 2005; QUIET – QUIET Collaboration 2011, 2012; SPT – Keisler at al. 2011; Reichardt et al. 2012; ACT – Das et al. 2011; Dünner et al. 2013), from balloon platforms (e.g. BOOMERanG – de Bernardis et al. 2000; EBEX – Reichborn-Kjennerud et al. 2010), or onboard satellites (WMAP – Bennett et al. 2003; Gold et al. 2011; Planck – Tauber et al. 2010; Planck Collaboration 2011a). All these efforts have established polarization measurements as one of the hottest topics in observational cosmology. The success of high-precision CMB observations imposes an even more reliable and accurate separation of the cosmological signal from the foreground emission of our own Galaxy, which cannot be removed by any improvement in the detectors, whether on the ground or in space. Several techniques have become available; from simple Galaxy masking of heavily contaminated regions and point sources (e.g. Mejía et al. 2005) to the novel approaches of component separation and foreground removal (Hobson et al. 1998; Maino et al. 2002; Delabrouille et al. 2003, 2009; Eriksen et al. 2004, 2006, 2008; Bonaldi et al. 2006; Cardoso et al. 2008; Leach et al. 2008; Stompor et al. 2009; Ricciardi et al. 2010; Fernández-Cobos et al. 2012; Planck Collaboration 2013c), which exploit the spectral and spatial diversity of the different astrophysical and cosmological components. The multi-frequency design of the WMAP mission had already revealed an impressive picture of unprecedented precision of the CMB at 23GHz, 33GHz, 41GHz, 61GHz and 94GHz (Hinshaw et al. 2007, 2012; Bennett et al. 2012); whereas the Planck mission, with its higher angular resolution and superb sensitivity at 30GHz, 44GHz, 70GHz, 100GHz, 143GHz, 217GHz, 353GHz, 545GHz, and 857GHz has, at the time of writing, made available an overwhelming set of results that push the standards of cosmological and astrophysical research to a state-of-the-art level (Planck Collaboration 2013b).
Yet, there remains a considerable gap in our knowledge of diffuse Galactic emission between the upper-frequency end of the large ground-based radio-telescopes and the lower end achievable from space or balloons, which confronts radioastronomers and cosmologists alike. In this frequency range, the increased resolution of single-dish observations imply that the time allocation at radio-astronomical facilities capable of surveying a sizable area of the sky, meaningful enough to address the large-scale properties of this diffuse component, becomes practically prohibitive. The few examples we find in the literature, where high-resolution surveys were undertaken in this frequency gap, default to efforts devoted to construct catalogues of radio sources against the high-intensity emission of the Galactic disk. Among them, we find arcminute-resolution surveys at 4.9GHz (Altenhoff et al. 1979), 5GHz (Haynes et al. 1978), and 10GHz (Handa et al. 1987). Without a dedicated instrument, free of time constraints in its observational schedule, diffuse Galactic emission will continue to lack the coverage it needs to map the sky away from the Galactic plane in this frequency gap. This is a crucial step in our understanding of the astrophysics of the ISM with a direct impact for the cosmological problem of foreground contamination. First of all, without a detailed morphological description of the variation of the synchrotron spectral index across the sky, the usefulness of a synchrotron spatial template looses its appeal in the study of CMB anisotropies. Second, the roll-off in the energy spectrum of relativistic electrons, as they leave their confinement volumes in the Galactic disk, is expected to introduce breaks in the spectrum of the non-thermal component up to a few GHz, with significant implications regarding (a) the elusive nature of anomalous microwave emission (AME) from spinning dust grains (Draine & Lazarian 1998, 1999; Lagache 2003; de Oliveira-Costa et al. 2004; Watson et al. 2005; Davies et al. 2006; Dobler & Finkbeiner 2008; Dickinson et al. 2009; Ysard et al. 2010; Planck Collaboration 2011b); (b) the identification of spectral distortions in the black body curve of the CMB signal (Burigana et al. 1991; Bartlett & Stebbins 1991); and more recently; (c) the residual radio signal in the ARCADE data (Seiffert et al. 2011; Kogut et al. 2011; Fixsen et al. 2011) and (d) the existence of the Galactic haze (Finkbeiner 2004; Dobler 2012; Planck Collaboration 2013a).
The lack of surveys in this frequency gap is even more critical for polarization surveys. Synchrotron radiation is intrinsically polarized and its contaminating role poses higher risks for polarization than for total intensity. In addition, the selection effect of Faraday depolarization is partial only toward the lower end of the gap. The first all-sky absolutely-calibrated polarization survey (Wolleben et al. 2006; Testori et al. 2004) was a rather recent achievement at 1.4GHz. Still, the gap extends up to the lowest of the WMAP frequency bands (Page et al. 2007; Hinshaw et al. 2009). From the point of view of cosmological implications, it becomes more urgent to bridge radio and microwave polarization surveys; whereas from the astrophysical point of view, the precise elucidation of the Galaxy as a Faraday screen is of key importance to the study of magnetic fields in the Galaxy (Beck 2007) via the synchrotron mechanism. Clearly, polarization surveys at frequencies higher than a few GHz (for example Leonardi et al. 2006) are needed to address the contamination of the CMB at higher frequencies, where the current Planck mission, with a wider frequency coverage and a better sensitivity, will undoubtedly deepen our cosmological understanding (Fauvet et al. 2012). Despite their lack of sensitivity to diffuse Galactic emission, Galactic plane surveys also produce a wealth of information regarding the magneto-ionic medium, which help us understand the complexity of the interplay between electron densities and magnetic field strengths in generating the pervading synchrotron radiation of the low-frequency sky (Gao et al. 2010). Below we outline the scope of a novel observational program aimed to bridge the mapping of diffuse Galactic emission in this frequency gap.
2.2. The Galactic Emission Mapping project
The concept of the GEM project dates back to 1992 when the first detections of CMB anisotropies called for an improved understanding of diffuse Galactic emission (Smoot et al. 1992; Bennett et al. 1992) to eliminate foreground contamination from genuine cosmic signals. The existing radio-continuum surveys suffered from two major shortcomings. First, they lacked mutual consistency in their baseline levels (Lawson et al. 1987; Banday & Wolfendale 1991) to be able to reliably predict the spectrum of Galactic synchrotron emission in the cosmologically interesting windows. Second, the spatial templates traced by the non-thermal component in the 408MHz and 1420MHz surveys were compromised by striping along the scanning direction of the radiotelescopes (Davies et al. 1996). Thus, given the frequency gap mentioned above, the initial goal of the GEM project became the production of an atlas of total sky brightness maps at 408MHz, 1465MHz, 2.3GHz, 5GHz and 10GHz, which would overcome these undesired radioastronomical shortcomings (De Amici et al. 1994; Smoot 1999) using a full-time dedicated experiment from different observational sites. Improved mapping of the spectral and large-scale properties of Galactic synchrotron radiation would result from an observational strategy aimed to minimize ground contamination and long-term systematics to guarantee baseline uniformity. In addition, the production of a self-consistent set of sky maps would allow the re-examination of the baseline and destriping in previous surveys to take advantage of their superior resolutions.
At the core of the GEM project stood the development of a portable 5.5-m double-shielded radiotelescope, which could be deployed at different geographic latitudes to maximize homogeneous sky coverage. Since ground contamination is one of the most common sources of systematic errors in this type of survey experiments, the two shields were built to minimize sidelobe pick-up of stray radiation and to level out the horizon profile at the site location. These shields are schematically drawn in Fig. 1 and consisted, respectively, of: (a) a 2.1-m-long rim-halo of aluminum panels extending tangentially from each of the 24 dish petals; and (b) a concentric network of inclined wire-mesh ground screens, which levels the horizon with a 10°-high azimuth profile. Under full illumination, the dish subtends an angle of 158° at the prime focus. Tello et al. (1999, 2000) modeled the diffraction and attenuation properties of this double-shielded radiotelescope to estimate the spillover and diffraction sidelobe contamination seen in elevation scans with back-fire helical feeds at 408MHz and 1465MHz.
 |
Fig. 1 Ray-tracing diagram (dotted lines) of the illumination properties of the double-shielded GEM dish. |
Diurnal and seasonal variations in the temperature of the ground also add low-frequency noise to survey measurements carried out continuously over extended periods of time. Similarly, the variability of atmospheric emission introduces, in addition to low-frequency noise, short-term contributions on the scale of minutes. To make individual scans insensitive to atmospheric fluctuations while still being able to map large areas of the sky, we adopted azimuthal scans of sufficiently high constant speed (1rpm for Z = 30° scans at 2.3GHz). Coupled to the rotation of the Earth, these zenith-centered circular scans achieve coverage of full declination bands with around-the-clock observations as shown schematically in Fig. 2, where sample circular scans, spaced at one-hour intervals, illustrate the coverage in declination for a site in the southern hemisphere.
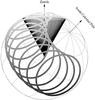 |
Fig. 2 Schematic representation of the mapping strategy with the GEM experiment. |
Total intensity observations with the GEM experiment.
Table 1 lists a summary of the main GEM observational campaigns since its first deployment in the Owens Valley desert near Bishop, CA, in 1993. In this period, the ground- and rim-halo shields have been continuously refurbished and upgraded to achieve satisfactory levels of ground rejection up to 10GHz. A new rim-halo was re-designed and installed in 2001, whereas the ground screen has gone through two major upgrades to incorporate a finer mesh along with a more robust support structure (two ground shields have been lost due to unusually gusty and strong winds). Another great impediment for radio astronomical surveys is the ever increasing usage of the spectrum by human-related activities, which plagues the radio environment with non-negligible levels of radio-frequency interference (RFI). 100% duty-cycle interferers have aborted GEM operations several times in the past (the 408MHz campaign in 1994, the 1465MHz runs in 1995, and follow-up observations at 2.3GHz in 2004).
Not included in Table 1 are the polarization measurements we have been conducting at 5GHz since 2006, which have already been used to prepare a preliminary version of our first polarization survey (Ferreira et al. 2008) from the southern hemisphere. The recent inclusion of Portugal in the GEM collaboration promises to extend our 5GHz and 10GHz polarization templates of Stokes I, Q and U parameters to the northern hemisphere, which can provide substantial ancilliary data for the Planck satellite mission and other future CMB polarization experiments. The GEM-P program will certainly benefit from a carefully chosen site (Fonseca et al. 2006).
3. The experiment at 2.3GHz
The portability of the GEM experiment reduces its operation to three main modules: (a) a dish pedestal with an altazimuthally rotating platform; (b) a radiometer; and (c) a control unit. These are graphically displayed in Fig. 3 with a slip-rings assembly aligned with the axis of rotation along the base column of the dish pedestal. Their task is to distribute power to the scanning dish and to establish a communication protocol with the radiometer. Two interface boxes, one inside a ground enclosure and another attached to the co-rotating base column, provide the connecting ports for the slip-rings. A 1-hp AC-motor, controlled by frequency inverters and coupled to the main gear of the pedestal by means of a speed reducer, provided the motion in azimuth. An optical shaft encoder was fixed to the bottom of the slip-rings assembly to measure the angular variations of the rotating platform. Similarly, an elevation encoder was installed on the dish horizontal axis. The analog signals of both encoders are also sent to connecting ports in their respective interface boxes, from where they are routed to the data acquisition box located on the elevation support arm beneath the dish. The data acquisition system (DAS) assembles the data frame by digitizing the analog inputs from the encoders, the radiometer and a noise source, before sending it seamlessly through the slip-rings up to the control panel for storage on a PC.
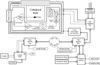 |
Fig. 3 Graphical layout of the GEM experiment at 2.3GHz. |
3.1. Data acquisition system
The data acquisition system (DAS) uses three single-width NIM modules to interface with the experiment and a data-logging PC. The control module has an EPROM with a 16-channel data frame burnt-in and an output connector for a serial output line. The analog multiplexer/ADC module receives 16 differential analog inputs of FSD ± 10V with a common-mode rejection of 86dB. The ADC limits hard at ±10V with no bleed-over between channels and overloads of ±30V. In addition to the EOF signal, the DAS also times the firing of a thermally stable noise source every 80 frames. The noise source is kept underneath the dish surface inside an insulated box and transmits an ≈140K reference signal from a small front-fire helix sitting at the junction of two of the dish petals. Two analog channels are dedicated to record the temperature and the voltage of the noise source. Finally, a serial-to-RS232 module takes the seamless serial data and synchronizes each frame with the hexadecimal EB90 word for decoding in the PC. LabView routines were used with Macintosh and Pentium PC to log the data. Proper time-stamping of the data followed by adding UT from a WWV digital receiver clock to the data frame for the observations in Colombia; whereas the WGS84 datum from a GPS receiver provided the time reference for the observations in Brazil.
3.2. Radiometric characterization
For the observations at 2.3GHz we used the three-legged support structure of the parabolic reflector to secure a direct-gain total-power radiometer at its focal plane by means of a latching mechanism. Its feed is built-in at the bottom of the radiometer enclosure, as shown in Fig. 4, and consists of a flanged cylindrical horn with 1/4-λ chokes and a measured voltage standing wave ratio (VSWR) of 1.023 at 2.3GHz (return loss of −39dB). Its circular aperture provides suitable illumination of the primary with a symmetric beam and a discrimination of −16dB at the edge of the reflector. Since the Moon is a reasonable approximation of a point source for our beam, horizontal and vertical beam patterns were obtained directly from the survey data by mapping the signal onto a Moon-centered coordinate system. With our circular scanning strategy, the horizontal pattern is derived from the antenna response when the Moon reaches the same elevation as the scanning circle, while the vertical pattern is established from the antenna response when the dish azimuth coincides with that of the Moon. These beam pattern profiles are shown in Fig. 5 for the data collected at the Colombian and Brazilian sites. Using Gaussian fits to these profiles, we obtained weighted average beam widths of for the horizontal and for the vertical planes of the pattern from the two experimental set-ups. Assuming that the secondary introduces no beam distortion, the 25% larger horizontal beam is an upper limit to the smearing of the beam due to the rotation of the antenna. Using internal errors only, this smearing of the beam is significant at the 4.5σ level.
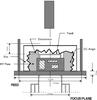 |
Fig. 4 Focal configuration at 2.3GHz with a direct-gain total power radiometer. |
The power fed by the reflector is captured at the throat of the horn by a waveguide probe, which sends it down a section of semi-rigid coax into a front-end high electron mobility transistor (HEMT) amplifier. As depicted in Fig. 3, the RF chain of the receiver section attains a nominal total amplification of ~70dB. The HEMT amplifier has a flat response across the entire 100MHz width of the bandpass-defining filter and a noise temperature of ≈30K at an operating temperature of 300K. After the filter, the signal is rectified by a square-law detector diode, and its DC voltage is amplified by a factor of 500 (low gain) or 1000 (high gain). The DC amplifier is housed with a thermo-regulating circuit and a timing board inside a detached electronics box. The timing board subdivides the pulses from an end-of-data frame (EOF) signal generated in the data acquisition box to sample the DC voltage with a time constant of τ = 0.56002s.
For the receiver to achieve an optimal performance, its gain variations were kept to a minimum by thermally stabilizing the interior of the RF-tight radiometer enclosure ≈10°C below the temperature set-point of the aluminum RF plate. To accomplish this functionality, we used a Peltier cooling unit on the side of the radiometer to continuously extract heat from its interior; while the thermo-regulating circuit maintained the RF plate (physical) temperature at its set-point by means of a sensing diode on the plate to actively control a set of power resistors. The rest of the RF enclosure was coated internally and externally with insulating styrofoam. Four calibrated temperature sensors constantly monitored the thermal state of the radiometer at the detector diode, the HEMT amplifier, the horn flange, and the electronics box.
The radiometric system was calibrated against the amplitude of the Gaussian fits to the
Moon-signal profiles shown in Fig. 5, which we
compared with the expression of Krotikov & Pelyushenko (1987) for the brightness temperature at the center of the lunar disk at
2.3GHz according to 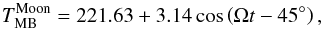 (1)where Ωt denotes the
dependance on the optical phase of the Moon and sets the full Moon at
Ωt = 0. This expression is equivalent to the one obtained by Mangum
(1993), except that the one above allows for the
averaging action of the antenna beam pattern. A summary of calibration constants and
antenna parameters obtained with this method is included in Table 2.
(1)where Ωt denotes the
dependance on the optical phase of the Moon and sets the full Moon at
Ωt = 0. This expression is equivalent to the one obtained by Mangum
(1993), except that the one above allows for the
averaging action of the antenna beam pattern. A summary of calibration constants and
antenna parameters obtained with this method is included in Table 2.
 |
Fig. 5 Beam pattern characterization at 2.3GHz from Moon measurements during routine survey scans away from the Galactic plane. |
There are some disadvantages with this method that impact the accuracy of our estimates,
but we have assessed the uncertainties in several ways to guarantee a reliable temperature
scale for our map. Independent estimates of the total and main beam solid angles are the
main source of uncertainty, since the ratio of the beam efficiency,
ϵM, and the aperture distribution factor,
κp, which scales the product of the horizontal and vertical
beam widths into the main beam solid angle, enter our gain calculation. Assuming a ratio
of ϵM/κp = 0.75/1.05 we have
tested the validity of the Moon calibration method by factoring out the total beam solid
angle from its relation to the effective aperture, such that 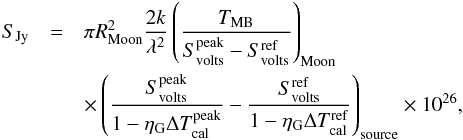 (2)where SJy is the
flux density of an observed known source in janskies, RMoon is
the angular radius of the lunar disk in radians, Svolts is the
signal output of the radiometer in volts, ηG is the thermal
gain susceptability in Table 2, and
ΔTcal is the temperature drift of the RF plate from its mean
temperature during the Moon
(2)where SJy is the
flux density of an observed known source in janskies, RMoon is
the angular radius of the lunar disk in radians, Svolts is the
signal output of the radiometer in volts, ηG is the thermal
gain susceptability in Table 2, and
ΔTcal is the temperature drift of the RF plate from its mean
temperature during the Moon 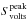 measurements. We chose Vir A and Cen A to
test the calibrating Moon amplitude in the Colombian and Brazilian data sets,
respectively. Vir A is sufficiently smaller than our beam size and we obtained 134Jy using
Eq. (2) compared to 140Jy using the Baars
et al. (1977) semi-absolute spectrum between 400MHz
and 25GHz as given by
measurements. We chose Vir A and Cen A to
test the calibrating Moon amplitude in the Colombian and Brazilian data sets,
respectively. Vir A is sufficiently smaller than our beam size and we obtained 134Jy using
Eq. (2) compared to 140Jy using the Baars
et al. (1977) semi-absolute spectrum between 400MHz
and 25GHz as given by ![\begin{eqnarray} \label{VirA} \log S_\mathrm{Vir A} [\mathrm{Jy}] = 5.023(\pm0.034) - 0.856(\pm0.010)\log\nu_\mathrm{MHz}. \end{eqnarray}](/articles/aa/full_html/2013/08/aa9306-07/aa9306-07-eq60.png) (3)The Baars scale was updated by Ott et al.
(1994) to assess source variability, and they
obtained new measurements at λ = 21, 11, 6, and 2.8cm for Vir A, which
allowed them to fit a second-order polynomial between 1408MHz and 10.55GHz, such that
(3)The Baars scale was updated by Ott et al.
(1994) to assess source variability, and they
obtained new measurements at λ = 21, 11, 6, and 2.8cm for Vir A, which
allowed them to fit a second-order polynomial between 1408MHz and 10.55GHz, such that
![\begin{eqnarray} \label{VirAA} \log S_\mathrm{Vir A}^\mathrm{Ott} [\mathrm{Jy}] = 4.484 - 0.603\log\nu_\mathrm{MHz} - 0.028\log^2\nu_\mathrm{MHz}. \end{eqnarray}](/articles/aa/full_html/2013/08/aa9306-07/aa9306-07-eq62.png) (4)However, at our frequency of 2.3GHz this
revised scale produces 138Jy, which does not differ significantly from the Baars scale.
Cen A, on the other hand, is an extended source covering some 4° × 10° in celestial
coordinates, so we targeted its brightest component, the northeast inner lobe, and
obtained 94Jy, compared to 99Jy using the Alvarez et al. (2000) integrated flux density relation between 80MHz and 43GHz as given by
(4)However, at our frequency of 2.3GHz this
revised scale produces 138Jy, which does not differ significantly from the Baars scale.
Cen A, on the other hand, is an extended source covering some 4° × 10° in celestial
coordinates, so we targeted its brightest component, the northeast inner lobe, and
obtained 94Jy, compared to 99Jy using the Alvarez et al. (2000) integrated flux density relation between 80MHz and 43GHz as given by
![\begin{eqnarray} \label{CenA} \log S_\mathrm{Cen A} [\mathrm{Jy}] = 4.35(\pm0.08) - 0.70(\pm0.02)\log\nu_\mathrm{MHz}. \end{eqnarray}](/articles/aa/full_html/2013/08/aa9306-07/aa9306-07-eq64.png) (5)The less than 5% discrepancy between our
estimates of both sources and the published values lends substantial support to the use of
the observed amplitude of the Moon signal to calibrate our antenna temperature scale. The
ratio ϵM/κp does not enter Eq.
(2) explicitly, but it is implied in the
calculation of the RF plate physical temperature drift. Given the good agreement between
observed and published fluxes, the assumed ratio restrains the beam efficiency to the
range defined by the uncertainty quoted in Table 2
on behalf of the expected range for κp alone
(1.00 ≤ κp ≤ 1.05).
(5)The less than 5% discrepancy between our
estimates of both sources and the published values lends substantial support to the use of
the observed amplitude of the Moon signal to calibrate our antenna temperature scale. The
ratio ϵM/κp does not enter Eq.
(2) explicitly, but it is implied in the
calculation of the RF plate physical temperature drift. Given the good agreement between
observed and published fluxes, the assumed ratio restrains the beam efficiency to the
range defined by the uncertainty quoted in Table 2
on behalf of the expected range for κp alone
(1.00 ≤ κp ≤ 1.05).
An additional source of uncertainty with the Moon calibration method is the need to estimate the temperature of the reference background level above which the Moon signal is superimposed. This level consists of two isotropic components, the CMB radiation and a small contribution of the diffuse background of extragalactic emission, but it also includes Galactic foreground radiation, atmospheric emission, and stray radiation from the ground through the sidelobes. The CMB contribution has been measured accurately to be 2.725 ± 0.002K (Mather et al. 1999), while we estimated the extragalactic background at 0.027K (Lawson et al. 1987). Likewise, we estimated the atmospheric emission at 1.64 ± 0.07K for the Colombian site and at 2.29 ± 0.13K for the Brazilian site according to the modeling prescription of Danese & Partridge (1989). As for the Galactic foreground component, the observations of the Moon took place in regions away from the Galactic plane, so that an estimate of 0.8 ± 0.4K was used in agreement with successive refinements of the calibration constants during the removal of the stray radiation component. The assessment of ground contamination proved to be the single most challenging aspect in the preparation of the GEM 2.3GHz map, as will be seen in the next section, and for this reason the system temperature estimate given in Table 2 includes the contribution of the ground.
GEM 2.3GHz survey.
4. Data description and processing
The data used in the preparation of the GEM 2.3GHz map were collected during three observational seasons at the Colombian and Brazilian sites listed in Table 1. A brief description of each observational site and their associated data sets is given in the first part of Table 2. We used Z = 30° scans for a total combined sky coverage of ≈66%. In Fig. 6 we have summarized the major steps in the preparation of the combined map.
 |
Fig. 6 Overview of the survey data processing. |
 |
Fig. 7 Images of the Moon before (left panel) and after (right panel) fine-tuning the pointing calibration constants. Contour levels are in antenna temperature units. |
4.1. Time stamping and pointing calibration
The Colombian data set had each frame tagged in seconds and we adjusted a simple linear progression with a step size of τ seconds to time-stamp each frame. For the Brazilian data, we relied on an iterative process to minimize the difference between the timing of the frames in the timeline of 1s updates of the GPS receiver and the expected cadence of the seamless data stream. We broke the latter into equal time slots of 2h and 34m to facilitate detection and correction of systematics during the data collection. Shorter time slots were inevitable whenever interruptions of the scanning process were encountered in lining up the TOD or when the data stream was found to be corrupted.
Readings from the azimuth angle encoder were first scaled to match rotations of 360° at constant speed. The ephemeris of the Sun was used to estimate the offset between the astronomical azimuth of the Sun and the encoder readout of the radiometer peak signal during scans with closest approach in the direction of the Sun. To guarantee a consistent mechanical configuration for all scans, we used a calibrated steel bar to lock the dish into pre-defined elevation angles. Fine-tuning of the actual azimuth and elevation angles was accomplished by re-projecting the polar coordinates, θ and φ, of the boresight onto a celestial grid centered on the ephemeris-specified position of the Moon, as shown in Fig. 7. We estimated the pointing accuracy of the surveys obtained from the Colombian and Brazilian data using the rms deviation of the centroid of the Gaussian fits in Fig. 5 from the origin of the Moon-centered coordinate system. We obtained rms values of from the Colombian data and from the Brazilian data.
4.2. Total power systematics
Once the time-ordered data were properly synchronized, we extracted the raw signal of the Moon and calibrated the radiometer constants as described in Sect. 3.2. Of these constants, the thermal gain susceptability ηG required extraction of the raw signal observed in pre-defined regions of low Galactic emission, or cold sky regions, as shown in the 408MHz survey of Haslam et al. (1982), to monitor the linear response of the radiometer signal output as a function of the RF plate physical temperature. Fortunately, these low-emission regions were scanned during routine day-time hours, when the drift in ΔTcal displayed its largest excursions and, thus, enabled accurate linear fits to the signal-RF plate temperature correlation. A set of three regions of 5° × 5° were chosen for each site as listed in Table 3 and the linear correlation coefficients of each set were averaged and scaled by the corresponding ratio of gain to system temperature to obtain ηG.
Low Galactic emission regions.
Total power systematics are both linear and non-linear in nature. Thermal gain
susceptability corrections address some of the systematics of the linear type. Non-linear
gain variations, on the other hand, cannot be corrected for without additional time-series
analysis of the data stream. Initially, we had intended to use the periodical firings of
the noise source to correct gain variations in general. However, after some careful
analysis of the noise source amplitude variations, we found that the noise source had
become unstable in the course of time and that its use as a transfer calibrator failed to
meet the accuracy we required. To filter oddly behaving data, we turned to an alternate
criterion, which relied on the distribution of the lowest observed antenna temperature
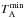 per time slot (154m max).
Non-linear excursions of the baseline were found to correspond to low values of
per time slot (154m max).
Non-linear excursions of the baseline were found to correspond to low values of
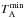 , so we fixed lower limits for its
distribution to improve the characterization of the systematics that affect the survey.
, so we fixed lower limits for its
distribution to improve the characterization of the systematics that affect the survey.
For this purpose, we split the Brazilian survey into three separate data sets, each
comprising about two weeks of data collection, whose characteristics reflect the
seasonality effect between summer and winter, but also the long-term performance of the
experiment over a month of winter observations. The first of the two Brazilian winter data
sets (winter I) coincided with the same period of the year as the single Colombian data
set. Figure 8 shows the distribution of
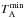 for the four data sets. All three
Brazilian data sets are seen to be well contained under a single-peaked distribution
centered around 4.5K, whereas the Colombia data are not as smoothly distributed with a
main peak below 3K, a secondary peak coinciding with the single peak of the Brazilian data
sets, and a likely third and smaller peak around 6K. Although a realistic lower limit at
3.5K could be chosen for the Brazilian data, as indicated by the vertical arrow in the
figure, a value of 2K had to be used for the Colombian data set to avoid excessive
decimation of the survey.
for the four data sets. All three
Brazilian data sets are seen to be well contained under a single-peaked distribution
centered around 4.5K, whereas the Colombia data are not as smoothly distributed with a
main peak below 3K, a secondary peak coinciding with the single peak of the Brazilian data
sets, and a likely third and smaller peak around 6K. Although a realistic lower limit at
3.5K could be chosen for the Brazilian data, as indicated by the vertical arrow in the
figure, a value of 2K had to be used for the Colombian data set to avoid excessive
decimation of the survey.
The clumpy distribution of 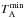 in the Colombian data set does have an
immediate effect in the mapping of its survey data. As Fig. 9 shows, there is clear evidence of an inhomogeneous baseline due to
scan-induced circular striping. On the other hand, mapping of the Brazilian survey shows a
smoother baseline contrast, but a rather different and disturbing systematic shows up in
the form of heavy striping in declination as a result of substantial ground pick-up in the
northern part of the Cachoeira Paulista sky.
in the Colombian data set does have an
immediate effect in the mapping of its survey data. As Fig. 9 shows, there is clear evidence of an inhomogeneous baseline due to
scan-induced circular striping. On the other hand, mapping of the Brazilian survey shows a
smoother baseline contrast, but a rather different and disturbing systematic shows up in
the form of heavy striping in declination as a result of substantial ground pick-up in the
northern part of the Cachoeira Paulista sky.
4.3. RFI and ground contamination removal
The two maps in Fig. 9 show several bright spots due to man-made interference (RFI), whose excision was accomplished by means of a low-pass filter during a four-step iteration process aimed at removing the ground striping. In the Colombia map there is also the sinusoidal streak left by an artificial satellite, whose transmissions highlight portions of the contaminating track. To remove this type of RFI, a tedious monitoring of the survey time slots was conducted and the affected time slots were cleaned of observations found within the perimeter of the satellite streak.
The cleaning of the ground striping proved, on the other hand, to be a homogeneous baseline-dependant process; so it was applied iteratively to the Colombian and Brazilian data sets in slightly different ways as indicated at the bottom of Fig. 6. For both data sets, the process started by flagging the presence of the Sun and Moon whenever their angular separation from the observing direction was less than 30° → 60° and 6°, respectively. Subsequently, a variance map of the antenna temperatures in the remainder of the survey was obtained; but the inhomogeneous baseline of the Colombian data set required its baseline to be calibrated as described in Sect. 5 before its variance map was obtained. In a second step, the observations were compared to the variance map on a per pixel basis and a new set of TOD was assembled from those observations that did not exceed three times the variance in the corresponding pixel. A pixel resolution of 360°/ was chosen to prevent undersampling for the size of our data sets. In the third iteration step, the new and RFI-cleaned TOD were averaged in azimuth to produce mean profiles of the ground contamination for each observed time slot, as long as the observations were distanced more than 30° from the Galactic plane to prevent real sky features from appearing as contaminating signatures in the mean azimuth profile. Finally, in the last and fourth step, an overall mean azimuth profile for each of the four data sets was secured by excluding any remaining isolated sky feature. This was accomplished with a low-pass filter, which looped over the azimuth profiles from all time slots in a given set, to exclude profile points with more than three times the variance per azimuth bin (0.5° wide). The loop was repeated until no more profile points were excluded. From here on, the four-step iteration process was repeated, but the subtraction of the normalized overall-mean azimuth profile from the previous iteration was subtracted in the first two steps. The normalization consisted in offsetting the profile down by the amplitude of its lowest profile point. In this way, the ground contamination was successively eliminated until the overall-mean aziumth profile of the last iteration was practically reduced to zero.
 |
Fig. 8 Histograms of observed antenna temperature minima in the Colombian and Brazilian data sets: Villa de Leyva (dotted line) and Cachoeira Paulista (gray line – summer; gray-filled – winter I; hatched – winter II). |
Figure 10 shows the cumulative overall-mean azimuth profiles of the four data sets after meeting the convergence criterion. The spiky Brazilian profiles reflect the nature of the striping in declination, but they also highlight the seasonality effect and the need to assess winter and summer data sets separately. As expected, the profile of the Colombian data set shows the contamination from the ground to be much lower and less variable. Still, residual horizontal striping remained visible in the final iterated map and additional destriping was applied in the final preparation of the map as described in the next section.
 |
Fig. 9 Maps of unprocessed survey data from selected time slots
( |
Surveyed data composition.
 |
Fig. 10 Cumulative overall-mean azimuth profiles of the ground contamination component of the antenna temperature: Villa de Leyva (cross-hatched)) and Cachoeira Paulista (thick line – summer; gray-filled – winter I; thin line – winter II). |
Table 4 summarizes all cuts applied to the data sets as a result of the selection and cleaning processes described so far. A more conservative minimum angular separation of 60° for the Sun was used with the Brazilian data sets to eliminate traces of scattering sidelobes from the three-legged feed support structure as well as to guarantee a safer margin of secondary sidelobe suppression. The angular separation for the Colombian data set at 30° reflects the lack of conclusive evidence for sidelobe contamination at larger angular separations due to the reduced sensitivity from a smaller data volume. Corrupted data and TOD mismatch did not apply to the Brazilian data sets, since an automatic data collection algorithm was implemented to keep the observational time slots of equal length. Finally, some 68 h of data associated with extreme weather conditions, severe cases of RFI and unusually large excursions in the readings of the temperature sensors and of the radiometer signal were flagged for exclusion during the observing runs in Colombia and did not enter the processing scheme outlined in Fig. 6. Consequently, they were not accounted for as part of the total survey time in Table 4 when compared with Table 1.
5. Final map preparation and calibration
The final preparation of the GEM 2.3GHz survey was divided into three major steps. First, the baseline of the ground-subtracted Brazilian data sets was calibrated and the resulting map was merged with the one from the cleaned Colombian data set. Second, the destriping technique developed by Platania et al. (2003) was applied to the merged map to clean residual striping due to ground contamination and baseline inhomogeneities. Third, a direct comparison with the Rhodes/HartRAO survey at 2326MHz (Jonas et al. 1998) was performed to absolutely calibrate the GEM survey.
5.1. Baseline calibration
To reduce the circular stripes introduced by the scanning technique in the TOD of the Brazilian data set, its baseline was calibrated following the same prescription as was applied to the Colombian data set (see Fig. 6). This calibration consisted in resolving the true sky temperature distribution at the level where its coldest contour would intersect, at least once, every survey scan (a 60° wide circular scan centered at the zenith with a HPBW). In other words, the coldest observation of every survey scan would be normalized to a uniform temperature, or apparent zero-point of our temperature scale, across the entire declination band. This assumption is, to a first-order approximation, sufficient to correct the 1/f-noise in the TOD as the dominant source of baseline inhomogeneity, but it also defines an effective full-beam brightness temperature scale for the survey.
 |
Fig. 11 Map of residual striping obtained with the FFT filtering technique of Platania et al. (2003) on the ground-corrected merged map. |
When applied to the Colombian data set, the precision of the baseline calibration was set by the level of the fluctuations in the ground profile of Fig. 10, or 62 ± 16mK. Without this a priori calibration, the ground profile fluctuations would have increased to 1357 ± 424mK and would have compromised any subsequent baseline calibration. For comparison, the ground profile fluctuations in the Brazilian data averaged to 355 ± 55mK in the winter I, 350 ± 56mK in the winter II and 362 ± 57mK in the summer data sets before their baseline was calibrated. This difference in implementing the baseline calibration did not allow the Colombian and Brazilian surveys to be merged along their entire region of overlap (−23° ≲ δ ≲ +6°). Instead, an offset of 148 ± 24mK was applied to the Colombian data according to the difference between the two surveys along the northern boundary (best signal-to-noise ratio) of the Brazilian survey for α ≲ 17h and around an overlapping rectangular region ~11° wide for α ≳ 17h. The merging of the two surveys in this overlap region allowed resiliant traces of ground striping in the Brazilian survey to be reduced. Ultimately, the baseline calibration relied on the uniformity in the sampling of the surveyed sky area. With our observational technique of zenith-centered circular scans, the sky is sampled preferentially toward the edges of the declination band. This intrinsic bias diminishes with the number of observations by statistical virtue alone and, thus, contributed to the baseline differences between the two maps. Of course, cuts in the TOD, such as those indicated in Table 4, also affected the sampling uniformity and introduced additional baseline inhomogeneities.
5.2. Cleaning of residual striping
The merged map showed traces of residual striping, whose RMS level could be estimated at 58mK after filtering the zero-frequency component of the map in Fourier space. The FFT destriping technique of Platania et al. (2003) was subsequently applied to produce a cleaner map. The technique was adapted from a method applied by Schlegel et al. (1998) to destripe the IRAS map and uses source extraction and stripe identification thresholds in 30 partially overlapping patches of 32 × 32 pixels for the GEM map. This small number of pixels per patch and the corresponding large angular dimension was suitable to address the variability of the striping pattern in the merged map and resulted in the stripe image shown in Fig. 11 with an RMS level of 22mK. The procedure was not applied to five patches (15.1% of the map) containing the Galactic plane because of steep signal gradients and a clean GEM map was obtained by subtracting the stripe image from the merged map.
The destriping procedure was applied in Platania et al. (2003) to the 408MHz full-sky map of Haslam et al. (1982) and to the 1420MHz (Reich 1982; Reich & Reich 1986) and 2326MHz (Jonas et al. 1998) surveys. Given the importance of the latter for the absolute calibration of the GEM map, we compare in Table 5 the effect of the destriping on the GEM and Rhodes maps in terms of the percentage temperature variations δT of the pixels. Nearly half of the destriped pixels in the GEM map did not exceed variations of more than 5%, whereas in the Rhodes map the corresponding percentage of pixels was higher (≈70%). Therefore, we examined the significance of the variations larger than 5% for the GEM map, and Table 5 also shows the distribution of the percentage variations in two separate temperature regimes, GEM-I of negative residuals (ΔT < 0K) and GEM-II of positive residuals (ΔT > 0K). Despite the higher contribution of pixels with positive residuals with variations δT > 10%, their average residual was only 27 ± 17mK, whereas the smaller fraction of pixels with negative residuals in the same range averaged to a significantly higher negative residual of −51 ± 44mK. For variations in the 5% <δT ≤ 10% range, the average residuals were 13 ± 11mK and −18 ± 13mK. Altogether, this tendency of the negative residuals to require larger corrections than the positive residuals could imply that the ground subtraction slightly overcorrected this type of contamination.
Distribution of percentage temperature variations δT in destriped pixels of the GEM and Rhodes/HartRAO surveys.
5.3. Absolute calibration
The absolute baseline calibration was obtained by means of a T-T plot between destriped versions of the GEM and Rhodes maps. The Rhodes survey, from which the isotropic components of the CMB and the diffuse extragalactic background had been subtracted, was convolved with a Gaussian profile with a FWHM of 140′ to match the GEM survey. The overlap between the two surveys covers the declination range −51° ≲ δ ≲ +30° after excluding boundary systematics. Using a celestial grid with a resolution of produced 13 132 paired pixels, whose T-T plot is shown in Fig. 12 along with a linear fit (98% correlation) for calibrating the true zero-point of the GEM survey baseline. Notwithstanding the spectral implications due to the small deviation of the linear coefficient from unity (+14.3 ± 1.6 mK K-1 is equivalent to a temperature ratio between two synchrotron components, had the GEM band been centered at 2314.05 ± 0.45MHz), we can alternatively estimate the zero-point correction from the straight mean of the pixel-by-pixel temperature differences at 3.125 ± 0.092K. Similarly, the distribution of these pixel differences is nearly normal, as shown in Fig. 13, with a Gaussian envelope centered at 3.1356 ± 0.0019K and standard deviation of 65.5 ± 1.9mK. An important feature of the destriping procedure is that it has only a negligible effect on the temperature scale of the map, and to illustrate this, we included in Fig. 13 the Gaussian envelope and its underlying distribution of pixel differences for the ground-corrected map before the destriping. We estimate the error in the zero-level of our survey at 103mK by combining in quadrature the standard deviation of the pixel differences with the error of 80mK in the absolute zero-level of the Rhodes survey, according to their calibration with the absolute sky temperature measurements of Bersanelli et al. (1994) at 2GHz from the South Pole.
 |
Fig. 12 T-T plot between the destriped GEM survey at 2300MHz and the Rhodes/HartRAO survey at 2326MHz. |
 |
Fig. 13 Distribution of pixel-by-pixel temperature differences between GEM and Rhodes maps before (ground-corrected) and after the destriping. |
Our estimate agrees with the expected accuracy of the Moon-calibrated temperature scale in Sect. 3.2, where we quoted an error <5% that the cold sky baseline calibration translates into <156mK. Similarly, the difference between the apparent Moon calibration-dependant zero-point and its true value is 108mK.
The clean and calibrated GEM survey at 2.3GHz is presented in Fig. 14. The brightness temperature scale of the survey is tied up to the resolution-limited approach of the cold sky baseline calibration and the full-beam definition of the Rhodes survey. We can obtain a conversion factor between the full-beam estimates of the two surveys by linearly correlating the GEM survey with the unconvolved version of the Rhodes survey. This gives a conversion factor 0.8151 ± 0.0031, which matches the 0.8641 for the emission ratio in the direction of the Galactic center reasonably well, given the 5% uncertainty of the Rhodes temperature scale and the compounded error in the zero-level accuracy of the GEM survey. In Figs. 15 and 16 a set of pre-defined contour levels shows a direct comparison between these two surveys, which enables some common features to be easily identified. In the next section we address some differences that emerge in the morphology of their large-scale structure of the radio continuum.
 |
Fig. 14 Mollweide projection of the 2.3GHz GEM survey in Galactic coordinates. |
 |
Fig. 15 Mollweide projection in Galactic coordinates of the large-scale structure of the radio continuum in the 2.3GHz GEM survey according to selected contours at the level of detection of well-known radio sources and Galactic features: (a) Virgo A and 3C273 contours between 0.23 and 0.43K; (b) Orion A, B and Rosette nebula contours between 0.43 and 0.63K; (c) Centaurus A and outer countours of the Cygnus region between 0.64 and 1.03K; (d) inner contours of the Cygnus region between 1.03 and 1.31K; and (e) innermost contours of the Gum nebula. |
 |
Fig. 16 Mollweide projection in Galactic coordinates of the large-scale structure of the radio continuum in the Rhodes/HartRAO survey at 2326MHz according to the same selected contours as in Fig. 15. |
6. Discussion
In Sect. 2.2 we introduced the GEM project as an experiment conceived to improve the mapping of the spectral and large-scale properties of Galactic synchrotron emission. This improvement would be centered on overcoming two major undesired radioastronomical shortcomings that affect existing ground-based surveys: the mutual consistency of their baselines and the observational bias of striping effects. In this section we discuss preliminary results based on the GEM 2.3GHz survey which, when compared to the already published HartRAO/Rhodes survey in the same frequency band, indicate a promising trend toward achieving these goals.
Our discussion will be developed in the framework of a concept introduced by Bennett et al. (2003) for defining foreground masks in studies of the CMB with the WMAP data products. Their basic assumption was that the asymmetry in a histogram of the sky temperature distribution is due to Galactic foreground emission. In their Fig. 1, they show how the sky temperature profile for the first-year results of the WMAP mission in the K-band may be decomposed into a symmetric distribution about the peak and a remainder. Even neglecting the effect of point sources, this remainder is recognized as a temperature excess caused by the intervening presence of our Galaxy.
6.1. All-sky surveys
Since the K-band survey of the WMAP mission has a significant synchrotron component of Galactic emission, we included in the present discussion the 408MHz all-sky survey of Haslam et al. (1982) with its notably dominant synchrotron character. We chose the one-degree smoothed version of the latest co-added total intensity map in the K-band1 as well as a destriped version of the 408MHz map (Platania et al. 2003). Their equal-area Mollweide projections in celestial coordinates are displayed in Fig. 17. This choice of coordinates enhances the declination-dependant nature of ground-based surveys and, to make the results comparable across all surveys, they were convolved to a resolution of for consistency with the GEM survey. Figure 18 shows the histograms of their corresponding temperature distributions. Their profiles are characterized by a similar two-component separation, which we applied to the color rendering of the maps, such that their shades of gray pixels represent the transition between the symmetric distribution of low-temperature pixels in black and the excess foreground emission within the bounds of the temperature scale of the maps. Conversely, pixels found in the range between the lower limit of the remainder and the upper limit of the symmetric distribution are displayed in gray.
 |
Fig. 17 Mollweide projection in celestial coordinates of the transition (gray pixels) between low- and high-emission regions in the all-sky surveys of the WMAP K-band at 23GHz and of the Haslam map at 408MHz. |
 |
Fig. 19 Mollweide projection in celestial coordinates of the transition regions for partial-sky coverage in the GEM strip: (upper left) WMAP K-band; (upper right) 408MHz; (lower left) Rhodes; and (lower right) GEM. |
The increasingly higher contrast of synchrotron radiation in Galactic emission toward the lower frequencies appears to be the determining factor of the appearance in the morphology of the transition region. At 408MHz, the transition beyond the Galactic ridge marks a well-defined boundary between the high-latitude areas of low Galactic emission and the excess foreground emission from the Galactic plane and bulge, as well as from structures like the north Galactic spur. At 23GHz, the transition region in the WMAP K-band survey breaks up into several patches of gray pixels that blend without any sharp boundary into the low-emission region of the symmetric component. From these considerations we accordingly expect that at intermediate frequencies the two-component scenario should be a constant feature of the large-scale structure of the radio continuum, and that the transition between high- and low-emission regions should disperse into the latter with increasing frequency.
6.2. Partial sky coverage
The Rhodes and GEM surveys, given their partial-sky coverage, are not readily comparable with the all-sky surveys. Ground-based experiments with their sky-scanning limitations are confined to bands of declination centered on the zenith of the observational site. A quick inspection of the surveys in Fig. 17 shows that any declination band will undoubtedly display the two-component separation, but their character may change with the range of Galactic Longitude that is intercepted. The Rhodes and GEM surveys were observed from observational sites with a privileged view of the central regions of the Galaxy. Consequently, we secured the common declination band in the range of −51° < δ < +9° for comparison with the WMAP K-band and 408MHz surveys. Below we refer to it as the GEM strip.
The upper panels in Fig. 19 show the effect of restricting the sky coverage of the WMAP K-band and 408MHz surveys to the GEM strip. Their histograms in the upper two panels of Fig. 20 show the expected two-component distribution. Moreover, since the lower limit of the remainder and the upper limit of the symmetric component are precisely the same as those found for the all-sky versions, the gray-shaded pixels representing the transition between the two components in Fig. 19 correspond to the exact same pixels in Fig. 17. We may therefore conclude that since the general properties of the morphology of the transition region in the WMAP K-band and 408MHz surveys are not affected by the particular choice of sky coverage in the GEM strip, the Rhodes and GEM surveys can be tested for these same general properties.
 |
Fig. 20 Histograms of the sky temperature distributions in the partial sky maps displayed in Fig. 19 showing their separation into symmetric and excess temperature components. |
The results are shown in the lower panels of Figs. 19 and 20. Because the Rhodes and GEM surveys are mapping the sky essentially at the same frequency, the morphology of their transition zones should not be significantly different from each other. Yet, these results tell a different story.
Spectral index in the 408MHz and WMAP K-band emission regions.
The main difference is the double-peaked distribution of the symmetric component in the temperature histogram of the Rhodes survey; whereas for the GEM survey, its low-emission region displays a single-peaked temperature profile similar to those in the histograms of the WMAP K-band and 408MHz surveys. In addition, the close proximity between the lower limit of the remainder and the upper limit of the symmetric component in the histogram of the Rhodes survey results in an exceptionally narrow transition region between the two components. This causes the considerable reduction in gray-shaded pixels that would otherwise mark the transition region. The GEM survey, on the other hand, shows an increase in the width of the transition region compared with 408MHz that suggests an intermediate stage toward the patchy distribution seen in the WMAP K-band morphology of the transition region. A deeper appreciation of these implications lies beyond the scope of the present discussion, but it certainly bears relevance to the distinction that synchrotron and free-free mechanisms can have in the characterization of Galactic emission. An improvement in the understanding of the morphology of the large-scale structure of the radio continuum in high-latitude regions is a major goal of the GEM project.
 |
Fig. 21 Mollweide projection in celestial coordinates of the temperature spectral index maps for the GEM (top) and Rhodes (bottom) surveys with respect to the 408MHz (left) and WMAP K-band (right) surveys in the GEM strip. |
6.3. Temperature spectral index
We close our discussion with a brief treatment of the temperature spectral index between the above set of surveys as a function of the two-component temperature distribution. In Table 6 we compare the mean spectral index between the surveys listed in the first and second columns over the emission regions of the 408MHz and WMAP K-band surveys. Between these two surveys the mean spectral index decreases from the high- to the low-emission regions, as expected from a Galactic latitude dependence, given the confinement of relativistic eletrons with lower energies, and therefore lower losses, to scale heights closer to the Galactic plane and their sources, but also due to the flatter spectral index of HII regions. The mean spectral index of the high-emission region is essentially insensitive to the survey used to determine it. However, for the transition and low-emission regions, the mean spectral index decreases more sharply in the regions defined for the WMAP K-band survey. The same behavior can be seen when the partial-sky coverage in the GEM strip is used instead.
The steepening of the synchrotron spectral index with frequency is also apparent for the GEM and Rhodes surveys. Their mean spectral index with respect to the 408MHz is practically constant across the two emission regions and their transition. For the GEM survey, this constant behavior is not readily verified unless the mean spectral indices are calculated with respect to the emission regions defined by the temperature distribution of the GEM survey itself. For this the estimates for the high-, transition-, and low-emission regions become −2.66 ± 0.24, −2.56 ± 0.17, and −2.62 ± 0.14, respectively. Thus the constancy of the mean spectral index between 408MHz and the 2300MHz can be given directly for the entire GEM strip, irrespective of emission region, and results in −2.64 ± 0.11 according to the Rhodes survey and −2.63 ± 0.21 according to the GEM survey. Guzman et al. (2011) have also recently reported a temperature spectral index of −2.5 to −2.6 over most of the sky between 45MHz and 408MHz. On the other hand, when the mean spectral index of the GEM and Rhodes surveys is obtained with respect to the WMAP K-band, the steepening of the spectral index increases toward the low-emission region, as expected for relativistic electrons of higher energies propagating to the larger scale heights that characterize these regions at high Galactic latitudes. This steepening is not entirely due to synchrotron losses and has been shown to have a dependance on the missing subtraction of a monopole component in the lower frequency data (Kogut et al. 2012).
Deriving the spectral and spatial distribution of the synchrotron spectral index fundamentally depends on the calibration of an homogeneous baseline in each of the compared surveys. This dependance is very sensitive to the scanning strategy of the observations. Despite significant improvements applying destriping techniques, it is apparent from the results in Table 6 that higher dispersions are associated with mean spectral indeces between surveys with different scanning strategy than between surveys with a similar one. The spatial distributions of the temperature spectral index shown in Fig. 21 have been rendered in false color shades to enhance the striping pattern of declination scans in the Rhodes and 408MHz surveys. Stripes in declination are mainly due to differential ground pick-up through the antenna sidelobes, a systematic effect that in the GEM survey was significantly reduced by the choice of zenith-centered circular scans and the double-shielded configuration of the experimental set-up.
The spectral index map between the GEM and the 408MHz surveys shows a systematic drop in a rather large region in an apparent southern extension of the Galactic bulge, however. A similar effect is seen in the corresponding map for the Rhodes survey over a rectangular region centered approximately on Cen A. Curiously, the apparent southern extension of the Galactic bulge does not show up as an unexpected symmetrical feature in the spectral index map between the GEM and WMAP K-band surveys, where its distribution follows similar patterns on both sides of the Galactic plane near the Galactic center. This kind of symmetry is absent from the Rhodes and 408MHz spectral index maps with respect to the WMAP K-band survey. For now, we can only expect that a more thorough revision of the method used to calibrate the baseline of the GEM survey can possibly ressolve discrepancies of this nature. As we noted in Sect. 5.2, the cleaning of residual destriping revealed a tendency of the negative residuals to require larger corrections than the positive residuals, which could imply that the ground subtraction slightly overcorrected this type of contamination.
7. Conclusions and future prospects
The preparation of low-frequency surveys of the radio continuum from the ground poses a considerable challenge to scientific endeavours, given the need to combine the stability of instrument performance with observational constraints over long periods of time. Any mismatch in this process introduces systematic effects, which radio-astronomers aim to keep under control by designing experiments that can address the desired balance between the proposed science and enduring logistics. The GEM project has evolved in this scenario for nearly two decades with the ultimate goal to improve our understanding of the large-scale structure of Galactic synchrotron emission in total intensity and polarization between 408MHz and 10GHz, signaling the ever-increasing impact that foreground contamination has on CMB studies and its implications for the astrophysics of the ISM.
We have presented our efforts at 2.3GHz by combining total intensity observations obtained with a portable 5.5-m radiotelescope in Colombia and Brazil to produce a synchrotron-dominated template of Galactic emission with 66% sky coverage from to with an average HPBW of . The main focus of our analysis has been a thorough assessment of the systematics that affected the observations; in particular, the ground contamination. The resulting survey shows that its sky temperature distribution into regions of low and high emission is consistent with the appearance of a transition region as seen in the Haslam 408MHz and the WMAP K-band surveys. The distribution of the temperature spectral index using the GEM survey does not show a spatial dependence on these regions when calculated against the Haslam 408MHz survey; but it steepens significantly from high- to low-emission regions with respect to the WMAP K-band survey in agreement with energy losses associated with relativistic electrons and their confinement volumes within the Galaxy. Proper accounting of the synchrotron spectral steepening between these surveys can help in establishing useful constraints on the fractional contribution of synchrotron and free-free components in the WMAP K-band survey and, therefore, place upper limits on residual emission components such as spinning dust (Tello et al., in prep.).
The results presented in this article summarize one of the main phases in the developing of the GEM project, which started with the total intensity 408MHz survey of Torres et al. (1996) and is currently dedicated to polarization and total intensity measurements of the Galactic foreground at 5GHz. The preparation of spectral index maps between the four working frequencies of the project (408MHz, 1465MHz, 2.3GHz, and 5GHz) promises yet to reveal an astrophysically interesting scenario for increasing our knowledge and understanding of the nature and composition of Galactic emission.
Acknowledgments
We are enormously grateful to several generations of students and technicians at LBNL and INPE, for whom GEM was a rich learning experience. We are particularly indebted to John Gibson, Alexandre M.R. Alves, Luiz Arantes, and Luiz Antonio Reitano for their dedicated commitment; to Jon Aymon, Tony Banday, Justin Jonas, and Andrew Jaffe for helpful advice and to SLB/INPE for logistics support in Cachoeira Paulista. The destriped version of the Rhodes/HartRAO map was reproduced courtesy of Tony Banday. The GEM project in Brazil was supported by FAPESP through grants 97/03861-2, 97/06794-4 and 00/06770-2. T.V. acknowledges support from CNPq through grants 305219/2004-9, 303637/2007-2, 484378/2007-4, 308113/2010-1, 506269/2010-8. M.B. acknowledges the support of the NATO Collaborative Grant CRG960175. S.T. acknowledges the support provided by Colciencias funding of the GEM project in Colombia through project 2228-05-103-96, contract No. 221-96. D.B. acknowledges support from FCT – Portugal and POCI through an SFRH/BPD grant and project grants POCTI/FNU/42263/2001 and POCI/CTE-AST/57209/2004. Last, but not least, we would like to acknowledge the referee’s comments, without which the significance of this article would not have been fully appreciated.
References
- Allen, C. W., & Gum, C. S. 1950, Austr. J. Sci. Res. A 3, 224 [Google Scholar]
- Altenhoff, W. J., Downes, D., Pauls, T., & Schraml, J., 1979, A&AS, 85, 691 [Google Scholar]
- Alvarez, H., Aparici, J., May, J., & Olmos, F., 1997, A&AS, 124, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez, H., Aparici, J., May, J., & Reich, P., 2000, A&A, 355, 863 [NASA ADS] [Google Scholar]
- Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A., 1977, A&A, 61, 99 [NASA ADS] [Google Scholar]
- Banday, A.J., & Wolfendale, A. W. 1991, MNRAS, 248, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Bartlett, J. G., & Stebbins, A. 1991, ApJ, 371, 8 [Google Scholar]
- Beck, R. 2007, in Sky Polarisation at Far-Infrared to Radio Wavelengths: The Galactic Screen before the Cosmic Microwave Background, eds. M.-A. Miville-Deschênes, & F. Boulanger, EAS Pub. Ser., 23, 19 [Google Scholar]
- Bennett, C. L., Smoot, G. F., Hinshaw, G., et al. 1992, ApJ, 396, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Hill, R. S., Hinshaw, G., et al. 2003, ApJS, 148, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., et al. 2012, ApJ, submitted [arXiv:1212.5225] [Google Scholar]
- Berkhuijsen, E. M. 1972, A&AS, 5, 263 [NASA ADS] [Google Scholar]
- Bersanelli, M., Bensadoun, M., De Amici, G., et al. 1994, ApJ, 424, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaldi, A., Bedini, L., Salerno, E., et al. 2006, MNRAS, 373, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Burigana, C., Danese, L., & De Zotti, G. F. 1991, A&A, 246, 49 [NASA ADS] [Google Scholar]
- Cane, H. V. 1978, Austr. J. Phys. 31, 561 [Google Scholar]
- Cardoso, J.-F., Martin, M., Delabrouille, J., et al. 2008, IEEE J. Selected Topics in Signal Processing, 2, 735 [CrossRef] [Google Scholar]
- Childers, J., Bersanelli, M., Figueiredo, N., et al. 2005, ApJS, 158, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Danese, L., & Partridge, R. B. 1989, ApJ, 342, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Das, S., Marriage, T. A., Ade, P. A. R., et al. 2011 ApJ, 729, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. D., Watson, R. A., & Gutiérrez, C. M. 1996, MNRAS, 278, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. D., Dickinson, C., Banday, A. J., et al. 2006, MNRAS, 370, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- De Amici, G., Torres, S., Bensadoun, M., et al. 1994, Ap&SS, 214, 151 [NASA ADS] [CrossRef] [Google Scholar]
- de Bernardis, P., Ade, P. A. R., Bock, J. J., et al. 2000, Nature, 404, 955 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- de Oliveira-Costa, A., Tegmark, M., Davies, R. D., et al. 2004, ApJ, 606, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Delabrouille, J., Cardoso, J.-F., & Patanchon, G. 2003, MNRAS, 346, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Delabrouille, J., Cardoso, J.-F., Le Jeune, M., et al. 2009, A&A, 493, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickinson, C., Davies, R. D., Allison, J. R., et al. 2009, ApJ, 690, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G. 2012, ApJ, 750, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., & Finkbeiner, D. P. 2008, ApJ, 680, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lazarian, A. 1998, ApJ, 494, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lazarian, A. 1999, ApJ, 512, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Dröge, F., & Priester, W. 1956, ZAp, 40, 236 [Google Scholar]
- Duncan, A. R., Stewart, R. T., Haynes, R. F., & Jones, K. L. 1995, MNRAS, 227, 36 [NASA ADS] [Google Scholar]
- Dünner, R., Hasselfield, M., Marriage, T. A., et al. 2013 ApJ, 762, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, H. K., Banday, A. J., Górski, K. M., & Lilje, P. B. 2004, ApJ, 612, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, H. K., Dickinson, C., Lawrence, C. R., et al. 2006, ApJ, 641, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, H. K., Jewel, J. B., Dickinson, C., et al. 2008, ApJ, 676, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fauvet, L., Macías-Pérez, J. F., Jaffe, T. R., et al. 2012, A&A, 540, 122 [Google Scholar]
- Fernández-Cobos, R., Vielva, P., Barreiro, R. B., & Martínez-González, E. 2012, MNRAS, 420, 2162 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, I. S. 2008, Ph.D. Thesis, Instituto Nacional de Pesquisas Espaciais, Brazil [Google Scholar]
- Finkbeiner, D. P. 2004, ApJ, 614, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Fixsen, D. J., Kogut, A., Levin, S., et al. 2011, ApJ, 734, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Fonseca, R., Barbosa, D., Cupido, L., et al. 2006, New, Astron., 11, 551 [Google Scholar]
- Fürst, E., Reich, W., Reich, P., & Reif, K. 1990b, A&AS, 85, 691 [NASA ADS] [Google Scholar]
- Gao, X. Y., Reich, W., Han, J. L., et al. 2010, A&A, 515, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gold, B., Odegard, N., Weiland, J. L., et al. 2011, ApJS, 192, 15 [Google Scholar]
- Guzman, A. E., May, J., Alvarez, H., & Maeda, K. 2011, A&A, 525, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Handa, T., Sofue, Y., Nakai, N., et al. 1987, PASJ, 39, 709 [NASA ADS] [Google Scholar]
- Haslam, C. G. T., Klein, U., Salter, C. J., et al. 1981, A&AS, 100, 209 [Google Scholar]
- Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
- Haynes, R. F., Caswell, J. L., & Simons, L. W. J. 1978, Austr. J. Phys. Supp. 45, 1 [Google Scholar]
- Hinshaw, G., Nolta, M. R., Bennett, C. L., et al. 2007, ApJS, 170, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Weiland, J., Hill, R. S., et al. 2009, ApJS, 180, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Larson, D., Komatsu, E., et al. 2012, ApJS, submitted [arXiv:1212.5226] [Google Scholar]
- Hobson, M. P., Jones, A. W., Lasenby, A. N., & Bouchet, F. R. 1998, MNRAS, 300, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jansky, K. G. 1932, Proc. I. R. E., 20, 1920 [Google Scholar]
- Jansky, K. G. 1933, Proc. I. R. E., 21, 1387 [CrossRef] [Google Scholar]
- Jansky, K. G. 1935, Proc. I. R. E., 23, 1157 [CrossRef] [Google Scholar]
- Jonas, J. L., Baart, E. E., & Nicolson, G. D. 1998, MNRAS, 297, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Keisler, R., Reichardt, C. L., Aird, K. A., et al. 2011, ApJ, 743, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Kiepenheuer, K. O. 1950, Phys. Rev. A, 79, 738 [NASA ADS] [Google Scholar]
- Kogut, A. 2012, ApJ, 753, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Kogut, A., Fixsen, D. J., Levin, S. M., et al. 2011, ApJ, 734, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Krotikov, V. D., & Pelyushenko, S. A. 1987, Soviet Ast., 31(2), 216 [NASA ADS] [Google Scholar]
- Lagache, G. 2003, A&A, 405, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landecker, T. L., & Wielebinsky, R. 1970, Austr. J. Phys. Supp. 16, 1 [Google Scholar]
- Lawson, K. D., Mayer, C. J., Osborne, J. L., & Parkinson, M. L. 1987, MNRAS, 225, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Leach, S. M., Cardoso, J.-F., Baccigalupi, C., et al. 2008, A&A, 491, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leonardi, R., Williams, B., Bersanelli, M., et al. 2006, New Astron. Rev. 50, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K., Alvarez, H., Aparici, J., et al. 2000, A&AS, 140, 145 [Google Scholar]
- Mangum, J. G. 1993, PASP, 105, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Maino, D., Farusi, A., Baccigalupi, C., et al. 2002, MNRAS, 334, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Mather, J. C., Fixsen, D. J., Shafer, R. A., et al. 1999, ApJ, 512, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathewson, D. S., Broten, N. W., & Cole, D. J. 1965, Austr. J. Phys. 18, 665 [Google Scholar]
- Mayer, C. H., McCullough, T. P., & Sloanaker, R. M. 1957, ApJ, 126, 468 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., et al. 2005, ApJS, 158, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Meinhold, P. R., Bersanelli, M., Childers, J., et al. 2005, ApJS, 158, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Mejía, J., Bersanelli, M., Burigana, C., et al. 2005, ApJS, 158, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Mills, B. Y. 1959, PASP, 71, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Milogradov-Turin, J., & Smith, F. G. 1973, MNRAS, 161, 269 [NASA ADS] [Google Scholar]
- O’Dwyer, I., Bersanelli, M., Childers, J., et al. 2005, ApJS, 158, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, M., Witzel, A., Quirrenbach, A., et al. 1994, A&A, 284, 331 [NASA ADS] [Google Scholar]
- Page, L., Hinshaw, G., Komatsu, E., et al. 2007, ApJS, 170, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2011a, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011b, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013a, A&A, 554, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013b, A&A, submitted [arXiv:1303.5062v1] [Google Scholar]
- Planck Collaboration 2013c, A&A, submitted [arXiv:1303.5072v1] [Google Scholar]
- Planck Collaboration 2013d, A&A, submitted [arXiv:1303.5073v2] [Google Scholar]
- Platania, P., Burigana, C., Maino, D., et al. 2003, A&A, 410, 847 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- QUIET Collaboration, Bischoff, C., Brizius, A., et al. 2011 ApJ, 741, 111 [NASA ADS] [CrossRef] [Google Scholar]
- QUIET Collaboration, Araujo, D., Bischoff, C., et al. 2012 ApJ, 760, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Reber, G. 1940, Proc. I. R. E. 28, 68 [Google Scholar]
- Reber, G. 1944, ApJ, 100, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Reber, G. 1948, Proc. I. R. E. 36, 1215 [Google Scholar]
- Reich, W. 1982, A&AS, 48, 219 [NASA ADS] [Google Scholar]
- Reich, P., & Reich, W. 1986, A&AS, 63, 205 [NASA ADS] [Google Scholar]
- Reich, W., Fürst, E., Haslam, C. G. T., et al. 1984, A&AS, 58, 197 [NASA ADS] [Google Scholar]
- Reich, W., Reich, P., & Fürst, E. 1990a, A&AS, 83, 539 [NASA ADS] [Google Scholar]
- Reich, W., Fürst, E., Reich, P., & Reif, K. 1990b, A&AS, 85, 633 [NASA ADS] [Google Scholar]
- Reich, P., Reich, W., & Fürst, E. 1997, A&AS, 126, 413 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reich, P., Testori, J. C., & Reich, W. 2001, A&A, 376, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reichardt, C. L., Shaw, L., Zahn, O., et al. 2012, ApJ, 755, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Reichborn-Kjennerud, B., Aboobaker, A. M., Ade, P., et al. 2010, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy V, eds. W. S. Holland, & J. Zmuidzinas, SPIE Conf. Ser. 7741 [Google Scholar]
- Ricciardi, S., Bonaldi, A., Natoli, P., et al. 2010, MNRAS, 406, 1644 [NASA ADS] [Google Scholar]
- Rodrigues, R. 2000, MSc Thesis, Instituto Nacional de Pesquisas Espaciais, Brazil [Google Scholar]
- Roger, R. S., Costain, C. H., Landecker, T. L., et al. 1999, A&AS, 137, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Seiffert, M., Fixsen, D. J., Kogut, A., et al. 2011, ApJ, 734, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Smoot, G. F. 1999, in Microwave Foregrounds, eds. A. de Oliveira-Costa, & M. Tegmark, ASP Conf. Ser. 181, 61 [Google Scholar]
- Smoot, G. F., Bennett, C. L., Kogut, A., et al. 1992, ApJ, 396, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Stil, J. M., Taylor, A. R., Dickey, J. M., et al. 2006, AJ, 132, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Stompor, R., Leach, S. M., Stivoli, F., & Baccilgalupi, C. 2009, MNRAS, 392, 216 [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, A. R., Gibson, S. J., Peracaula, M., et al. 2003, AJ, 125, 314 [CrossRef] [PubMed] [Google Scholar]
- Tello, C. 1997, Ph.D. Thesis, Instituto Nacional de Pesquisas Espaciais, Brazil [Google Scholar]
- Tello, C., Villela, T., Wuensche, C. A., et al. 1999, Rad. Sci. 34, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Tello, C., Villela, T., Smoot, G. F., et al. 2000, A&AS, 145, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tello, C., Villela, T., Smoot, G. F., et al. 2005, in New cosmological data and the values of the fundamental parameters, eds. A. Lasenby, & A. Wilkinson, ASP Conf. Ser., 201, 138 [Google Scholar]
- Testori, J. C., Reich, P., & Bava, J. A., et al. 2001, A&A, 368, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Testori, J. C., Reich, P., & Reich, W. 2004, in The Magnetized Interstellar Medium, eds. B. Uyaniker, W. Reich, & R. Wielebinski, 57 [Google Scholar]
- Torres, S., Cañon, V., Casas, R., et al. 1996, Ap&SS, 240, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Turtle, A. J., & Baldwin, J. E. 1962, MNRAS, 124, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, R. A., Rebolo, R., Rubiño-Martín, J. A., et al. 2005, ApJ, 624, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Westerhout, G., Seeder, C. L., Brouw, W. N., & Tinbergen, J. 1962, Bull. Astron. Inst. Netherlands, 16, 187 [NASA ADS] [Google Scholar]
- Wielebinski, R., Shakeshaft, J. R., & Pauliny-Toth, I. I. K. 1962, Observatory, 82, 158 [Google Scholar]
- Wolleben, M., Landecker, T. L., Reich, W., & Wielebinski, R. 2006, A&A, 448, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yates, K. W. 1968, Austr. J. Phys., 21, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Yates, K. W., Wielebinsky, R., & Landecker, T. L. 1967, Austr. J. Phys., 20, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Ysard, N., Miville-Deschênes, M. A., & Verstraete, L. 2010, A&A, 509, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Distribution of percentage temperature variations δT in destriped pixels of the GEM and Rhodes/HartRAO surveys.
All Figures
 |
Fig. 1 Ray-tracing diagram (dotted lines) of the illumination properties of the double-shielded GEM dish. |
| In the text | |
 |
Fig. 2 Schematic representation of the mapping strategy with the GEM experiment. |
| In the text | |
 |
Fig. 3 Graphical layout of the GEM experiment at 2.3GHz. |
| In the text | |
 |
Fig. 4 Focal configuration at 2.3GHz with a direct-gain total power radiometer. |
| In the text | |
 |
Fig. 5 Beam pattern characterization at 2.3GHz from Moon measurements during routine survey scans away from the Galactic plane. |
| In the text | |
 |
Fig. 6 Overview of the survey data processing. |
| In the text | |
 |
Fig. 7 Images of the Moon before (left panel) and after (right panel) fine-tuning the pointing calibration constants. Contour levels are in antenna temperature units. |
| In the text | |
 |
Fig. 8 Histograms of observed antenna temperature minima in the Colombian and Brazilian data sets: Villa de Leyva (dotted line) and Cachoeira Paulista (gray line – summer; gray-filled – winter I; hatched – winter II). |
| In the text | |
 |
Fig. 9 Maps of unprocessed survey data from selected time slots
( |
| In the text | |
 |
Fig. 10 Cumulative overall-mean azimuth profiles of the ground contamination component of the antenna temperature: Villa de Leyva (cross-hatched)) and Cachoeira Paulista (thick line – summer; gray-filled – winter I; thin line – winter II). |
| In the text | |
 |
Fig. 11 Map of residual striping obtained with the FFT filtering technique of Platania et al. (2003) on the ground-corrected merged map. |
| In the text | |
 |
Fig. 12 T-T plot between the destriped GEM survey at 2300MHz and the Rhodes/HartRAO survey at 2326MHz. |
| In the text | |
 |
Fig. 13 Distribution of pixel-by-pixel temperature differences between GEM and Rhodes maps before (ground-corrected) and after the destriping. |
| In the text | |
 |
Fig. 14 Mollweide projection of the 2.3GHz GEM survey in Galactic coordinates. |
| In the text | |
 |
Fig. 15 Mollweide projection in Galactic coordinates of the large-scale structure of the radio continuum in the 2.3GHz GEM survey according to selected contours at the level of detection of well-known radio sources and Galactic features: (a) Virgo A and 3C273 contours between 0.23 and 0.43K; (b) Orion A, B and Rosette nebula contours between 0.43 and 0.63K; (c) Centaurus A and outer countours of the Cygnus region between 0.64 and 1.03K; (d) inner contours of the Cygnus region between 1.03 and 1.31K; and (e) innermost contours of the Gum nebula. |
| In the text | |
 |
Fig. 16 Mollweide projection in Galactic coordinates of the large-scale structure of the radio continuum in the Rhodes/HartRAO survey at 2326MHz according to the same selected contours as in Fig. 15. |
| In the text | |
 |
Fig. 17 Mollweide projection in celestial coordinates of the transition (gray pixels) between low- and high-emission regions in the all-sky surveys of the WMAP K-band at 23GHz and of the Haslam map at 408MHz. |
| In the text | |
 |
Fig. 18 Histograms of the sky temperature distributions in the maps displayed in Fig. 17. |
| In the text | |
 |
Fig. 19 Mollweide projection in celestial coordinates of the transition regions for partial-sky coverage in the GEM strip: (upper left) WMAP K-band; (upper right) 408MHz; (lower left) Rhodes; and (lower right) GEM. |
| In the text | |
 |
Fig. 20 Histograms of the sky temperature distributions in the partial sky maps displayed in Fig. 19 showing their separation into symmetric and excess temperature components. |
| In the text | |
 |
Fig. 21 Mollweide projection in celestial coordinates of the temperature spectral index maps for the GEM (top) and Rhodes (bottom) surveys with respect to the 408MHz (left) and WMAP K-band (right) surveys in the GEM strip. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


