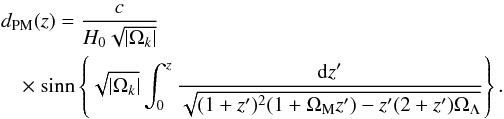| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 2 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201322088 | |
| Published online | 17 July 2013 | |
Research Note
A curious relation between the flat cosmological model and the elliptic integral of the first kind
1 Charles University in Prague, Faculty of Mathematics and Physics, Astronomical Institute, V Holešovičkách 2, 18000 Prague 8, Czech Republic
e-mail: meszaros@cesnet.cz
2 Institute of Basic Science, Natural Sciences Campus, Sungkyunkwan University, Engineering Building 2, 2066 Seobu-ro, Jangan-gu, Suwon, 440-746 Gyeonggi-do, Korea
e-mail: ripa.jakub@gmail.com
Received: 14 June 2013
Accepted: 16 June 2013
Context. The dependence of the luminosity distance on the redshift has a key importance in the cosmology. This dependence can well be given by standard functions for the zero cosmological constant.
Aims. The purpose of this article is to present a similar relation also for the non-zero cosmological constant, if the universe is spatially flat.
Methods. A definite integral was used.
Results. The integration ends in the elliptic integral of the first kind.
Conclusions. The result shows that no numerical integration is needed for the non-zero cosmological constant if the universe is spatially flat.
Key words: cosmology: theory
© ESO, 2013
1. Introduction
The dependence of the luminosity distance dL(z) on the redshift z is a key formula in cosmology (Carroll et al. 1992). It is given by three independent cosmological parameters: by two omega-parameters ΩM, ΩΛ, and by the Hubble constant H0. Its relation to the so-called proper-motion distance is given by dPM(z)(1 + z) = dL(z) (Weinberg 1972).
One has (Carroll et al. 1992)
In this equation c is the speed of light in vacuum, and it holds Ωk + ΩM + ΩΛ = 1. The notation “sinn” means the standard function sinh for Ωk > 0, and sin for Ωk < 0, respectively. If Ωk = 0, then one simply has an integration: 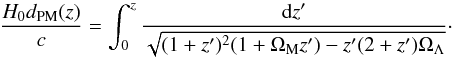 (2)In addition, from the physical point of view, in both equations it must be ΩM > 0. (The case ΩM = 0 can serve as a limit, but ΩM < 0 is fully unphysical.) On the other hand, ΩΛ can have both signs, but the observations of the past two decades strongly disfavour negative values (see, e.g., Perrett et al. 2012, and references therein).
(2)In addition, from the physical point of view, in both equations it must be ΩM > 0. (The case ΩM = 0 can serve as a limit, but ΩM < 0 is fully unphysical.) On the other hand, ΩΛ can have both signs, but the observations of the past two decades strongly disfavour negative values (see, e.g., Perrett et al. 2012, and references therein).
In the special case of ΩΛ = 0, the integral in Eq. (1) can be given by the so-called Mattig-formula (Mattig 1958) for any ΩM > 0. The formula can then easily be used in cosmological applications (see, e.g., Mészáros 2002). For ΩΛ ≠ 0 the integral in Eqs. (1), (2) is usually solved numerically1.
In this note we show that the integral on the right-hand side of Eq. (2) can be solved analytically also for ΩΛ ≠ 0.
2. Integration
We rewrite the right-hand side of Eq.(2) into the form 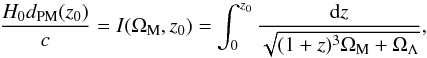 (3)where z ≥ 0, ΩM > 0 and ΩM + ΩΛ = 1. Introducing the substitution x = (1 + z)-1, we obtain
(3)where z ≥ 0, ΩM > 0 and ΩM + ΩΛ = 1. Introducing the substitution x = (1 + z)-1, we obtain 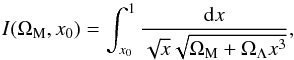 (4)where 0 < x0 = (1 + z0)-1 ≤ 1.
(4)where 0 < x0 = (1 + z0)-1 ≤ 1.
In this section we consider only the case ΩM < 1, i.e. ΩΛ = 1 − ΩM > 0. Introducing a further substitution y = (ΩΛ/ΩM)1/3x, we obtain 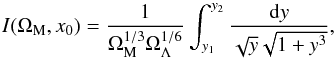 (5)where y1 = (ΩΛ/ΩM)1/3x0 and y2 = (ΩΛ/ΩM)1/3. The two limits are non-negative with y1 ≤ y2.
(5)where y1 = (ΩΛ/ΩM)1/3x0 and y2 = (ΩΛ/ΩM)1/3. The two limits are non-negative with y1 ≤ y2.
We aim to find the primitive function for 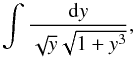 (6)where y ≥ 0. The following substitution helps:
(6)where y ≥ 0. The following substitution helps: 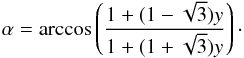 (7)There is a one-to-one correspondence between α and y. For y = 0 one has α = 0, and for y → ∞ one has
(7)There is a one-to-one correspondence between α and y. For y = 0 one has α = 0, and for y → ∞ one has 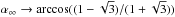 , i.e. α∞ = 105.54°. If y increases in the interval [0,∞), α is also increasing in the interval [0,α∞). Hence, this substitution is well-defined. Conversely, one obtains
, i.e. α∞ = 105.54°. If y increases in the interval [0,∞), α is also increasing in the interval [0,α∞). Hence, this substitution is well-defined. Conversely, one obtains 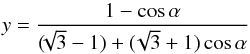 (8)and
(8)and ![\begin{equation} {\rm d} y = \frac{2\sqrt{3} \sin \alpha \; {\rm d}\alpha}{[\!\sqrt{3}(1+\cos \alpha) - (1-\cos \alpha)]^2}\cdot \end{equation}](/articles/aa/full_html/2013/08/aa22088-13/aa22088-13-eq47.png) (9)Using these two formulas, we curiously obtain
(9)Using these two formulas, we curiously obtain 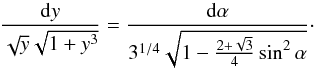 (10)The right-hand side of Eq. (10) is the function in the elliptic integral of the first kind (Gradshteyn et al. 2007) with
(10)The right-hand side of Eq. (10) is the function in the elliptic integral of the first kind (Gradshteyn et al. 2007) with 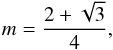 (11)where 0 < m < 1, as it should be in an elliptic integral.
(11)where 0 < m < 1, as it should be in an elliptic integral.
To calculate the definite integral 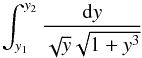 (12)in Eq. (5) for non-negative y1 ≤ y2, one can write
(12)in Eq. (5) for non-negative y1 ≤ y2, one can write 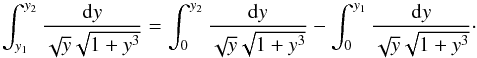 (13)After this one should use the formula with α from Eq. (10) and determine the integration limits in variable α. The substitution from Eq. (7) gives for y = 0 the value α = 0. This means
(13)After this one should use the formula with α from Eq. (10) and determine the integration limits in variable α. The substitution from Eq. (7) gives for y = 0 the value α = 0. This means
that – using α – the lower limits in both definite integrals are zeros. The upper limits from y1 and y2, respectively, are also calculable analytically and unambiguously from Eq. (7) via the arccos function. One obtains α1 and α2, respectively, as upper limits in the integrals. It must be α2 > α1. One should only clarify that, of course, if it were α2 from the interval (π/2,α∞), then the first elliptic integral itself should be given by a sum of two integrals: in one integral the limits should be 0 and π/2, and in the second one the limits should be (π − α2) and π/2. Both integrals must give positive values. If it were also α1 > π/2, then one should proceed similarly in the second integral, too. In any case, the integral I(ΩM,x0) is easily obtainable from standard elliptic integrals of the first kind.
3. Remarks
The integral in Eq. (5) is presented by Gradshteyn et al. (2007) (formula 3.166.22). Moreover, Carroll et al. (1992) reported that the integral of Eq. (2) can also be solved analytically. Paál et al. (1992) described similar efforts. But, on the other hand, we found nothing in the literature about the non-numerical integration of Eq. (2) using the elliptic integrals. Therefore, the substitution given by Eqs. (7), (8) is new and original.
For the sake of completeness it should still be added that integral of Eq. (4) can be solved also for ΩΛ < 0 and ΩM > 1. One obtains (up to a constant) the formula d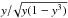 , which is also integrable (see the formula 3.166.23 of Gradshteyn et al. 2007).
, which is also integrable (see the formula 3.166.23 of Gradshteyn et al. 2007).
4. Conclusion
We have proven that the integral on the right-hand side of Eq. (2) can also be solved analytically using the elliptic integral of the first kind.
Acknowledgments
We wish to thank M. Křížek for the useful discussions and comments on the manuscript. This study was supported by the OTKA Grant K77795, by the Grant Agency of the Czech Republic Grant P209/10/0734, by the Research Program MSM0021620860 of the Ministry of Education of the Czech Republic, and by Creative Research Initiatives (RCMST) of MEST/NRF.
References
- Carroll, S. M., Press, W. H., & Turner, E. L. 1992, ARA&A, 30, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Gradshteyn, I. S., Ryzhik, I. M., Jeffrey, A., & Zwillinger, D. 2007, Table of Integrals, Series, and Products (Elsevier Academic Press) [Google Scholar]
- Mattig, W. 1958, Astron. Nachr., 284, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, A. 2002, ApJ, 580, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Paál, G., Horváth, I., & Lukács, B. 1992, Ap&SS, 191, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Perrett, K., Sullivan, M., Conley, A., et al. 2012, AJ, 144, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, S. 1972, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity (Wiley) [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.