| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321353 | |
| Published online | 05 August 2013 | |
Surface flux concentrations in a spherical α2 dynamo
1
Nordita, KTH Royal Institute of Technology and Stockholm
University,
Roslagstullsbacken 23,
10691
Stockholm,
Sweden
e-mail:
sarajab@kth.se
2
Department of Astronomy, AlbaNova University Center, Stockholm
University, 10691
Stockholm,
Sweden
3
Department of Mechanical Engineering, Ben-Gurion University of the
Negev, POB 653,
84105
Beer-Sheva,
Israel
4 Department of Radio Physics, N. I. Lobachevsky State
University of Nizhny Novgorod, Russia
Received:
23
February
2013
Accepted:
31
May
2013
Context. In the presence of strong density stratification, turbulence can lead to the large-scale instability of a horizontal magnetic field if its strength is in a suitable range (around a few percent of the turbulent equipartition value). This instability is related to a suppression of the turbulent pressure so that the turbulent contribution to the mean magnetic pressure becomes negative. This results in the excitation of a negative effective magnetic pressure instability (NEMPI). This instability has so far only been studied for an imposed magnetic field.
Aims. We want to know how NEMPI works when the mean magnetic field is generated self-consistently by an α2 dynamo, whether it is affected by global spherical geometry, and whether it can influence the properties of the dynamo itself.
Methods. We adopt the mean-field approach, which has previously been shown to provide a realistic description of NEMPI in direct numerical simulations. We assume axisymmetry and solve the mean-field equations with the Pencil Code for an adiabatic stratification at a total density contrast in the radial direction of ≈4 orders of magnitude.
Results. NEMPI is found to work when the dynamo-generated field is about 4% of the equipartition value, which is achieved through strong α quenching. This instability is excited in the top 5% of the outer radius, provided the density contrast across this top layer is at least 10. NEMPI is found to occur at lower latitudes when the mean magnetic field is stronger. For weaker fields, NEMPI can make the dynamo oscillatory with poleward migration.
Conclusions. NEMPI is a viable mechanism for producing magnetic flux concentrations in a strongly stratified spherical shell in which a magnetic field is generated by a strongly quenched α effect dynamo.
Key words: sunspots / Sun: dynamo / turbulence / magnetohydrodynamics (MHD) / hydrodynamics
© ESO, 2013
1. Introduction
The magnetic field of stars with outer convection zones, including that of the Sun, is believed to be generated by differential rotation and cyclonic convection (see, e.g., Moffatt 1978; Parker 1979; Zeldovich et al. 1983; Brandenburg & Subramanian 2005). The latter leads to an α effect, which refers to an important new term in the averaged (mean-field) induction equation, quantifying the component of the mean electromotive force that is aligned with the mean magnetic field (see, e.g., Steenbeck et al. 1966; Krause & Rädler 1980; Brandenburg et al. 2013). However, what is actually observed are sunspots and active regions, and the description of these phenomena is not part of conventional mean-field dynamo theory (see, e.g., Priest 1982; Stix 1989; Ossendrijver 2003; Cally et al. 2003; Stenflo & Kosovichev 2012).
Flux tube models (Parker 1955, 1982, 1984; Spiegel & Weiss 1980; Spruit 1981; Schüssler et al. 1994; Dikpati & Charbonneau 1999) have been used to explain the formation of active regions and sunspots in an ad hoc manner. It is then simply assumed that a sunspot emerges when the magnetic field of the dynamo exceeds a certain threshold just above the bottom of the convection zone for the duration of about a month (Chatterjee et al. 2004). Such models assume the existence of strong magnetic flux tubes at the base of the convection zone. They require magnetic fields with a strength of about 105 Gauss (D’Silva & Choudhuri 1993). However, such strong magnetic fields are highly unstable (Arlt et al. 2005) and are also difficult to produce by dynamo action in turbulent convection (Guerrero & Käpylä 2011).
Another possible mechanism for producing magnetic flux concentrations is the negative effective magnetic pressure instability (NEMPI), which can occur in the presence of strong density stratification, i.e., usually near the stellar surface, on scales encompassing those of many turbulent eddies. NEMPI is caused by the suppression of turbulent magnetohydrodynamic pressure (the isotropic part of combined Reynolds and Maxwell stresses) by the mean magnetic field. At large Reynolds numbers, the negative turbulent contribution can become so large that the effective mean magnetic pressure (the sum of turbulent and nonturbulent contributions) is negative. This results in the excitation of NEMPI that causes formation of large-scale inhomogeneous magnetic structures. The instability mechanism is as follows. A rising magnetic flux tube expands, the field becomes weaker, but because of negative magnetic pressure, its magnetic pressure increases, so the density decreases, and it becomes lighter still and rises further. Conversely, a sinking tube contracts, the magnetic field increases, but the magnetic pressure decreases, so the density increases, and it becomes heavier and sinks further. The energy for this instability is supplied by the small-scale turbulence. By contrast, the free energy in Parker’s magnetic buoyancy instability or in the interchange instability in plasma, is drawn from the gravitational field (Newcomb 1961; Parker 1966).
Direct numerical simulations (DNS; see Brandenburg et al. 2011; Kemel et al. 2012a), mean-field simulations (MFS; see Brandenburg et al. 2010, 2012; Kemel et al. 2012b; Käpylä et al. 2012), and earlier analytic studies (Kleeorin et al. 1989, 1990, 1996; Kleeorin & Rogachevskii 1994; Rogachevskii & Kleeorin 2007) now provide conclusive evidence for the physical reality of NEMPI. However, open questions still need to be answered before it can be applied to detailed models of active regions and sunspot formation.
In the present paper we take a first step toward combining NEMPI, which is described well using mean-field theory, with the α effect in mean-field dynamos. To study the dependence of NEMPI on the magnetic field strength, we assume that α is quenched. This allows us to change the magnetic field strength by changing the quenching parameter. We employ spherical coordinates (r,θ,φ), with radius r, colatitude θ, and azimuthal angle φ. We assume axisymmetry, i.e., ∂/∂φ = 0. Furthermore, α is a pseudo-scalar that changes sign at the equator, so we assume that α is proportional to cosθ, where θ is the colatitude (Roberts 1972). We arrange the quenching of α such that the resulting mean magnetic field is in the appropriate interval to allow NEMPI to work. This means that the effective (mean-field) magnetic pressure locally has a negative derivative with respect to increasing normalized field strength (Kemel et al. 2012b), so the mean toroidal magnetic field must be less than about 20% of the equipartition field strength.
The choice of using spherical geometry is taken because the dynamo-generated magnetic field depends critically on the geometry. Therefore, to have a more realistic field structure, we felt it profitable to carry out our investigations in spherical geometry. Guided by the insights obtained from such studies, it will in future be easier to design simpler Cartesian models to address specific questions regarding the interaction between NEMPI and the dynamo instability.
In the calculations presented below we use the Pencil Code1, which has been used in DNS of magneto-hydrodynamics in spherical coordinates (Mitra et al. 2009) and also in earlier DNS and MFS of NEMPI. Unlike most of the earlier calculations, we adopt an adiabatic equation of state. This results in a stratification such that the temperature declines approximately linearly toward the surface, so the scale height becomes shorter and the stratification stronger toward the top layers. This is done to have a clear segregation between the dynamo in the bulk and NEMPI near the surface, where the stratification is strong enough for NEMPI to operate. The gravitational potential is that of a point mass. This is justified because the mass in the convection zone is negligible compared to the one below. The goal of the present work is to produce reference cases in spherical geometry and to look for new effects of spherical geometry. We begin by describing the basic model.
2. The model
The evolution equations for mean vector potential  ,
mean velocity
,
mean velocity  ,
and mean density
,
and mean density  , are
, are
where  is the advective
derivative,
is the advective
derivative,  is the mean
density,
is the mean
density,  is the mean reduced enthalpy with
is the mean reduced enthalpy with
 the mean
enthalpy,
the mean
enthalpy,  the
mean temperature,
γ = cp/cv
is the ratio of specific heats at constant pressure and constant density, respectively, Φ is
the gravitational potential,
ηT = ηt + η and
νT = νt + ν are
the sums of turbulent and microphysical values of magnetic diffusivity and kinematic
viscosities, respectively, α is the aforementioned coefficient in the
α effect,
the
mean temperature,
γ = cp/cv
is the ratio of specific heats at constant pressure and constant density, respectively, Φ is
the gravitational potential,
ηT = ηt + η and
νT = νt + ν are
the sums of turbulent and microphysical values of magnetic diffusivity and kinematic
viscosities, respectively, α is the aforementioned coefficient in the
α effect,  is the mean current
density, μ0 is the vacuum permeability,
is the mean current
density, μ0 is the vacuum permeability,
 (4)is a
term appearing in the viscous force, where
(4)is a
term appearing in the viscous force, where  is the
traceless rate of strain tensor of the mean flow with components
is the
traceless rate of strain tensor of the mean flow with components
 ,
and finally
,
and finally  determines the turbulent
contribution to the mean Lorentz force. Here, qp depends on the
local field strength (see below). This term enters with a plus sign, so positive values of
qp correspond to a suppression of the total turbulent
pressure. The net effect of the mean field leads to an effective mean magnetic pressure
determines the turbulent
contribution to the mean Lorentz force. Here, qp depends on the
local field strength (see below). This term enters with a plus sign, so positive values of
qp correspond to a suppression of the total turbulent
pressure. The net effect of the mean field leads to an effective mean magnetic pressure
 , which becomes
negative for qp > 1, which can indeed be
the case for magnetic Reynolds numbers well above unity (Brandenburg et al. 2012).
, which becomes
negative for qp > 1, which can indeed be
the case for magnetic Reynolds numbers well above unity (Brandenburg et al. 2012).
Following Kemel et al. (2012c), the function
qp(β) is approximated by  (5)where
qp0, βp, and
(5)where
qp0, βp, and
 are
constants,
are
constants,  is the modulus of the
normalized mean magnetic field, and
is the modulus of the
normalized mean magnetic field, and  is the
equipartition field strength.
is the
equipartition field strength.
NEMPI can occur at a depth where the derivative,
dpeff/dβ2, is
negative. Since the spatial variation of β is caused mainly by the increase
in density with depth, the value of the mean horizontal magnetic field essentially
determines the location where NEMPI can occur. Therefore, the field strength has to be in a
suitable range such that NEMPI occurs within the computational domain. Unlike the Cartesian
cases investigated in earlier work (Brandenburg et al.
2010, 2012; Kemel et al. 2012c), where it is straightforward to impose a magnetic field, in a
sphere it is easier to generate a magnetic field by a mean-field dynamo. This is why we
include a term of the form  in
the expression for the mean electromotive force (second term on the righthand side of Eq.
(1)). When the mean magnetic field is
generated by a dynamo, the resulting magnetic field strength depends on the nonlinear
suppression of the dynamo. We assume here a simple quenching function for the
α effect, i.e.,
in
the expression for the mean electromotive force (second term on the righthand side of Eq.
(1)). When the mean magnetic field is
generated by a dynamo, the resulting magnetic field strength depends on the nonlinear
suppression of the dynamo. We assume here a simple quenching function for the
α effect, i.e.,  (6)where
Qα is a quenching parameter that determines
the typical field strength, which is expected to be on the order of
(6)where
Qα is a quenching parameter that determines
the typical field strength, which is expected to be on the order of
 . The value of
Qα must be chosen large enough so that the
nonlinear equilibration of the dynamo process results in a situation such that
. The value of
Qα must be chosen large enough so that the
nonlinear equilibration of the dynamo process results in a situation such that
 is indeed negative
within the computational domain. In analogy with the βp
parameter in Eq. (5), we can define a
parameter
is indeed negative
within the computational domain. In analogy with the βp
parameter in Eq. (5), we can define a
parameter  , which
will be quoted occasionally.
, which
will be quoted occasionally.
The strength of the dynamo is also determined by the dynamo number,
 (7)For our geometry
with 0.7 ≤ r/R ≤ 1, the critical value
of Cα for the onset of dynamo action is around
18. The excitation conditions for dipolar and quadrupolar parities are fairly close
together. This is because the magnetic field is strongest at high latitudes, so the
hemispheric coupling is weak. In the following we restrict ourselves to solutions with
dipolar parity. We adopt the value Cα = 30, so
the dynamo is nearly twice supercritical.
(7)For our geometry
with 0.7 ≤ r/R ≤ 1, the critical value
of Cα for the onset of dynamo action is around
18. The excitation conditions for dipolar and quadrupolar parities are fairly close
together. This is because the magnetic field is strongest at high latitudes, so the
hemispheric coupling is weak. In the following we restrict ourselves to solutions with
dipolar parity. We adopt the value Cα = 30, so
the dynamo is nearly twice supercritical.
As mentioned before, our gravitational potential Φ is that of a point mass. We define Φ
such that it vanishes at a radius r⋆, i.e.
 (8)where G is
Newton’s constant and M is the mass of the sphere. The radial component of
the gravitational acceleration is then
g = −GM/r2.
We adopt an initially adiabatic stratification with
(8)where G is
Newton’s constant and M is the mass of the sphere. The radial component of
the gravitational acceleration is then
g = −GM/r2.
We adopt an initially adiabatic stratification with  , so
, so
 vanishes at
r = r⋆. To avoid
singularities, the value of r⋆ has to be chosen
some distance above r = R. The radius
r⋆ is used to set the density contrast.
Table 1 gives the density contrast for different
values of r⋆. We vary
r⋆ between 1.001 R,
which corresponds to our reference model with a density contrast of 8900, and
1.1 R, where the density contrast is 14. The pressure scale height is
given by
vanishes at
r = r⋆. To avoid
singularities, the value of r⋆ has to be chosen
some distance above r = R. The radius
r⋆ is used to set the density contrast.
Table 1 gives the density contrast for different
values of r⋆. We vary
r⋆ between 1.001 R,
which corresponds to our reference model with a density contrast of 8900, and
1.1 R, where the density contrast is 14. The pressure scale height is
given by  (9)where
n = 1/(γ − 1) = 3/2
is the polytropic index for an adiabatic stratification with
γ = 5/3. The density scale height is
Hρ = r(1 − r/r⋆)/n.
The initial density profile is given by
(9)where
n = 1/(γ − 1) = 3/2
is the polytropic index for an adiabatic stratification with
γ = 5/3. The density scale height is
Hρ = r(1 − r/r⋆)/n.
The initial density profile is given by
 (10)Radial profiles of
(10)Radial profiles of
 and the inverse
pressure scale height
Hp0/Hp(r),
are shown in Fig. 1 for
r⋆/R
varying between 1.1 and 1.001. Here,
Hp0 = Hp(rref)
is the pressure scale height at the reference radius
rref = 0.95 R, corresponding to a depth of
35 Mm in the Sun.
and the inverse
pressure scale height
Hp0/Hp(r),
are shown in Fig. 1 for
r⋆/R
varying between 1.1 and 1.001. Here,
Hp0 = Hp(rref)
is the pressure scale height at the reference radius
rref = 0.95 R, corresponding to a depth of
35 Mm in the Sun.
Dependence of the density contrast on the value of r⋆.
 |
Fig. 1 Initial stratification of density and inverse scale height for r⋆/R = 1.001 (strongest stratification), 1.01, 1.05, and 1.1. The dashed lines mark the position of the reference radius rref = 0.95 R, where ρ/ρ0 ≈ 0.0068 for r⋆/R = 1.001 and Hp(r) = Hp0 by definition. The dotted line marks the value of ηt/β⋆urmsHp0. |
The analytic estimate of the growth rate of NEMPI, λ, based on an
isothermal layer with
Hp = Hρ = const.
is given by (Kemel et al. 2012b)
 (11)Assume that this equation
also applies to the current case where Hp depends on
r, and setting
(11)Assume that this equation
also applies to the current case where Hp depends on
r, and setting  ,
the normalized growth rate is
,
the normalized growth rate is  (12)In Fig. 1 we compare therefore
Hp0/Hp with
ηt/β⋆urmsHp0
and see that the former exceeds the latter in our reference model with
r⋆/R = 1.001.
This suggests that NEMPI should be excited in the outer layers.
(12)In Fig. 1 we compare therefore
Hp0/Hp with
ηt/β⋆urmsHp0
and see that the former exceeds the latter in our reference model with
r⋆/R = 1.001.
This suggests that NEMPI should be excited in the outer layers.
As nondimensional measures of ηt and
urms, we define
 (13)for which we take the
values
(13)for which we take the
values  and
and  , respectively. Using the
estimate
ηt = urms/3kf
(Sur et al. 2008), our choice of
ηt implies that the normalized wavenumber of the
energy-carrying eddies is
, respectively. Using the
estimate
ηt = urms/3kf
(Sur et al. 2008), our choice of
ηt implies that the normalized wavenumber of the
energy-carrying eddies is  and that
kfHp0 varies between 6.2 (for
r⋆/R = 1.1)
and 2.3 (for
r⋆/R = 1.001).
and that
kfHp0 varies between 6.2 (for
r⋆/R = 1.1)
and 2.3 (for
r⋆/R = 1.001).
For the magnetic field, we adopt perfect conductor boundary conditions on the inner and
outer radii, r0 = 0.7 R and
R, respectively, i.e.,
 (14)On the pole and the
equator, we assume
(14)On the pole and the
equator, we assume  (15)Since our simulations
are axisymmetric, the magnetic field is conveniently represented via
(15)Since our simulations
are axisymmetric, the magnetic field is conveniently represented via
 and
and
 . In particular,
contours of
. In particular,
contours of  give the magnetic
field lines of the poloidal magnetic field,
give the magnetic
field lines of the poloidal magnetic field,  .
.
In all cases presented in this paper, we adopt a numerical resolution of 256 × 1024 mesh points in the r and θ directions. This is significantly higher than what has been used previously, even in mean field calculations with stratification and hydrodynamical feedback included; see Brandenburg et al. (1992), where a resolution of just 41 × 81 meshpoints was used routinely. In principle, lower resolutions are possible, but in some cases we found certain properties of the solutions to be sensitive to the resolution.
 |
Fig. 2 Dependence of |
3. Results
In our model, the dynamo growth rate is about 170 ηT/R2. Although both dynamo and NEMPI are linear instabilities, this is no longer the case in our coupled system, because NEMPI depends on the magnetic field strength, and only in the nonlinear regime of the dynamo does the field reach values high enough for NEMPI to overcome turbulent magnetic diffusion. This is shown in Fig. 2 where we plot the growth of the magnetic field and compare with runs with different values of qp0. For qp0 = 100 we find a growth rate of about 270 ηT/R2. This value is significantly more than the dynamo growth rate, and the growth occurs at the time when structures form, so we associate this higher growth rate with that of NEMPI.
 |
Fig. 3 Meridional cross-sections of |
We now discuss the resulting magnetic field structure. We begin by discussing the effects
of varying the stratification. To see the effect of NEMPI more clearly, we consider a
somewhat optimistic set of parameters describing NEMPI, namely
qp0 = 100 and βp = 0.05, which
yields β⋆ = 0.5; see Eq. (5). This is higher than the values 0.23 and 0.33
found from numerical simulations with and without small-scale dynamo action, respectively
(Brandenburg et al. 2012). The effect of lowering
the value of qp0 can be seen in Fig. 2 and is also discussed below. We choose
Qα = 1000 for the α
quenching parameter so that the local value of 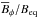 near the surface is
between 10 and 20 percent, which is suitable for exciting NEMPI (Kemel et al. 2012b). Meridional cross-sections of
near the surface is
between 10 and 20 percent, which is suitable for exciting NEMPI (Kemel et al. 2012b). Meridional cross-sections of
 together
with magnetic field lines of
together
with magnetic field lines of  are shown in
Fig. 3. Note that a magnetic flux concentration
develops near the surface at latitudes between 70° and 76° for weak and strong
stratification, respectively. Structure formation from NEMPI occurs in the top 5% by radius,
and the flux concentration is most pronounced when
r⋆ ≤ 1.01.
are shown in
Fig. 3. Note that a magnetic flux concentration
develops near the surface at latitudes between 70° and 76° for weak and strong
stratification, respectively. Structure formation from NEMPI occurs in the top 5% by radius,
and the flux concentration is most pronounced when
r⋆ ≤ 1.01.
 |
Fig. 4 Meridional cross-sections for different values of Qα, for r⋆ = 1.001. The dashed lines indicate the latitudes 49°, 61.5°, 75.6°, and 76.4°. |
 |
Fig. 5 Meridional cross-sections for different values of the parameter qp0 in the range 40 ≤ qp0 ≤ 100 for Qα = 103. The dashed lines indicate the latitudes 68°, 72.5°, 75.7°, and 76.3°. |
Next, if we increase the magnetic field strength by making
Qα smaller, we see that the magnetic flux
concentrations move toward lower latitudes down to about 49° for
Qα = 100; see Fig. 4. However, while this is potentially interesting for the Sun, where
sunspots are known to occur primarily at low latitudes, the magnetic flux concentrations
also become weaker at the same time, making this feature less interesting from an
astrophysical point of view. For comparison with the parameter
βp = 0.05 in Eq. (5) we note that  takes
the values 0.1, 0.07, 0.04, and 0.03 for
Qα = 100, 200, 500, and 1000, respectively.
Thus, for these models the quenchings of the nondiffusive turbulence effects in the momentum
and induction equations are similar.
takes
the values 0.1, 0.07, 0.04, and 0.03 for
Qα = 100, 200, 500, and 1000, respectively.
Thus, for these models the quenchings of the nondiffusive turbulence effects in the momentum
and induction equations are similar.
Also, if we decrease qp0 to more realistic values, we expect the magnetic flux concentrations to become weaker. This is indeed borne out by the simulations; see Fig. 5, where we show meridional cross-sections for qp0 in the range 40 ≤ qp0 ≤ 100 for Qα = 103. This corresponds to the range 0.32 ≤ β⋆ ≤ 0.5.
For weaker magnetic fields, i.e., for higher values of the quenching parameter
Qα, we find that NEMPI has a modifying effect
on the dynamo in that it can now become oscillatory. A butterfly diagram of
 and
and
 is shown in Fig.
6. Meridional cross-sections of the magnetic field at
different times covering half a magnetic cycle are shown in Fig. 7. It turns out that, at sufficiently weak magnetic field strengths, NEMPI
produces oscillatory solutions with poleward-migrating flux belts. The reason for this is
not understood very well, but it is reminiscent of the poleward migration observed in the
presence of weak rotation (Losada et al. 2012). Had
this migration been equatorward, it might have been tempting to associate it with the
equatorward migration of the sunspot belts in the Sun.
is shown in Fig.
6. Meridional cross-sections of the magnetic field at
different times covering half a magnetic cycle are shown in Fig. 7. It turns out that, at sufficiently weak magnetic field strengths, NEMPI
produces oscillatory solutions with poleward-migrating flux belts. The reason for this is
not understood very well, but it is reminiscent of the poleward migration observed in the
presence of weak rotation (Losada et al. 2012). Had
this migration been equatorward, it might have been tempting to associate it with the
equatorward migration of the sunspot belts in the Sun.
 |
Fig. 6 Butterfly diagram of |
 |
Fig. 7 Meridional cross-sections of |
 |
Fig. 8 The three inverse length scales kC, kM, and kK as a function of time. At time t0, the value of qp0 has been changed from 0 to 100. |
Finally, we discuss the change of kinetic, magnetic, and current helicities due to NEMPI.
We do this by using a model that is close to our reference model with
r⋆/R = 1.001
and Qα = 1000, except that
qp0 = 0 in the beginning, and then at time
t0 we change it to qp0 = 100. The
two inverse length scales based on magnetic and current helicities,
 (16)increase by 25%,
while the inverse length scale based on the kinetic helicity,
(16)increase by 25%,
while the inverse length scale based on the kinetic helicity,
 (17)drops to very low
values after introducing NEMPI, see e.g. Fig. 8. Here,
(17)drops to very low
values after introducing NEMPI, see e.g. Fig. 8. Here,
 is
the mean vorticity. This behavior of kK is surprising, but it
seems to be associated with an increase in kinetic energy. The reason for the increase in
the two inverse magnetic length scales, on the other hand, might be understandable as the
consequence of increasing gradients associated with the resulting flux concentrations.
is
the mean vorticity. This behavior of kK is surprising, but it
seems to be associated with an increase in kinetic energy. The reason for the increase in
the two inverse magnetic length scales, on the other hand, might be understandable as the
consequence of increasing gradients associated with the resulting flux concentrations.
4. Conclusions
The present investigations have shown that NEMPI can occur in conjunction with the dynamo; that is, both instabilities can work at the same time and can even modify each other. It was already clear from earlier work that NEMPI can only work in a limited range of magnetic field strengths. We therefore adopted a simple α quenching prescription to arrange the field strength to be in the desired range. Furthermore, unlike much of the earlier work on NEMPI, we used an adiabatic stratification here instead of an isothermal one; see Brandenburg et al. (2010) and Käpylä et al. (2012) for earlier examples with adiabatic stratification in Cartesian geometry. An adiabatic stratification implies that the pressure scale height is no longer constant and now much shorter in the upper layers than in the bulk of the domain. This favors the appearance of NEMPI in the upper layers, because the growth rate is inversely proportional to the pressure scale height.
There are two lines of future extensions of the present model. On the one hand, it is important to study the interplay between NEMPI and the dynamo instability in more detail. This is best done in the framework of a local Cartesian model, which is more easily amenable to analytic treatment. Another important extension would be to include differential rotation. At the level of a dynamically self-consistent model, where the flow speed is a solution of the momentum equation, differential rotation is best implemented by including the Λ effect (Rüdiger 1980, 1989). This is a parameterization of the Reynolds stress that is in some ways analogous to the parameterization of the electromotive force via the α effect.
Mean-field models with both α and Λ effects have been considered before (Brandenburg et al. 1992; Rempel 2006), so the main difference would be the additional parameterization of magnetic effects in the Reynolds stress that gives rise to NEMPI. In both cases, our models would be amenable to verification using DNS by driving turbulence through a helical forcing function. In the case of a spherical shell, this can easily be done in wedge geometry where the polar regions are excluded. In that case the mean-field dynamo solutions are oscillatory with equatorward migration (Mitra et al. 2010). At an earlier phase of the present investigations we studied NEMPI in the corresponding mean-field models and found that NEMPI can reverse the propagation of the dynamo wave from equatorward to poleward. However, owing to time dependence, the effects of NEMPI are then harder to study, which is why we have refrained from studying such models in further detail.
In the case of a Cartesian domain, helically forced DNS with an open upper layer have been considered by Warnecke & Brandenburg (2010). In this model, plasmoid ejections can occur and provide a more natural boundary. A more physical alternative is to use only nonhelical forcing, but to include rotation to produce helicity in conjunction with the stratification. Such models have recently been considered by Losada et al. (2013), who found that NEMPI begins to be suppressed by rotation at Coriolis numbers somewhat below those where α2-type dynamo action sets in. Furthermore, there is now evidence that the combined action of NEMPI and the dynamo instability has a lower threshold than the dynamo alone. Those models provide an ideal setup for future studies of the interaction between both instabilities.
Acknowledgments
This work was supported in part by the European Research Council under the AstroDyn Research Project No. 227952, by the National Science Foundation under Grant No. NSF PHY05-51164 (AB), by EU COST Action MP0806, by the European Research Council under the Atmospheric Research Project No. 227915, and by a grant from the Government of the Russian Federation under contract No. 11.G34.31.0048 (NK, IR). We acknowledge the allocation of computing resources provided by the Swedish National Allocations Committee at the Center for Parallel Computers at the Royal Institute of Technology in Stockholm and the Nordic Supercomputer Center in Reykjavik.
References
- Arlt, R., Sule, A., & Rüdiger, G. 2005, A&A 441, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A., & Subramanian, K., 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Moss, D., & Tuominen, I. 1992, A&A, 265, 328 [NASA ADS] [Google Scholar]
- Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2010, Astron. Nachr., 331, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Kemel, K., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2011, ApJ, 740, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Kemel, K., Kleeorin, N., & Rogachevskii, I. 2012, ApJ, 749, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Gressel, O.,Käpylä, P. J., et al. 2013, ApJ, 762, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Cally, P. S., Dikpati, M., & Gilman, P. A. 2003, ApJ, 582, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, P., Nandy, D., & Choudhuri, A. R. 2004, A&A, 427, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dikpati, M., & Charbonneau, P. 1999, ApJ, 518, 508 [NASA ADS] [CrossRef] [Google Scholar]
- D’Silva, S., & Choudhuri, A. R. 1993, A&A, 272, 621 [NASA ADS] [Google Scholar]
- Guerrero, G., & Käpylä, P. J. 2011, A&A, 533, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Brandenburg, A., Kleeorin, N., Mantere, M. J., & Rogachevskii, I. 2012, MNRAS, 422, 2465 [NASA ADS] [CrossRef] [Google Scholar]
- Kemel, K., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2012a, Sol. Phys., 280, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Kemel, K., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2012b, Sol. Phys., DOI:10.1007/s11207-012-0031-8 [Google Scholar]
- Kemel, K., Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2012c, Astron. Nachr., 333, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Kleeorin, N., & Rogachevskii, I. 1994, Phys. Rev. E, 50, 2716 [NASA ADS] [CrossRef] [Google Scholar]
- Kleeorin, N. I., Rogachevskii, I. V., & Ruzmaikin, A. A. 1989, Sov. Astron. Lett., 15, 274 [NASA ADS] [Google Scholar]
- Kleeorin, N. I., Rogachevskii, I. V., & Ruzmaikin, A. A. 1990, Sov. Phys. JETP, 70, 878 [Google Scholar]
- Kleeorin, N., Mond, M., & Rogachevskii, I. 1996, A&A, 307, 293 [NASA ADS] [Google Scholar]
- Krause, F., & Rädler, K.-H. 1980, Mean-field magnetohydrodynamics and dynamo theory (Oxford: Pergamon Press) [Google Scholar]
- Losada, I. R., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2012, A&A, 548, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Losada, I. R., Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2013, A&A, 556, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mitra, D., Tavakol, R., Brandenburg, A., & Moss, D. 2009, ApJ, 697, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Mitra, D., Tavakol, R., Käpylä, P. J., & Brandenburg, A. 2010, ApJ, 719, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Moffatt, H. K. 1978, Magnetic field generation in electrically conducting fluids (Cambridge: Cambridge University Press) [Google Scholar]
- Newcomb, W. A. 1961, Phys. Fluids, 4, 391 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ossendrijver, M. 2003, A&ARv, 11, 287 [Google Scholar]
- Parker, E. N. 1955, ApJ, 121, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E.N. 1966, ApJ, 145, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1979, Cosmical magnetic fields (New York: Oxford University Press) [Google Scholar]
- Parker, E. N. 1982, ApJ, 256, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1984, ApJ, 283, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R. 1982, Solar Magnetohydrodynamics (Dordrecht: D. Reidel Publ. Co.) [Google Scholar]
- Rempel, M. 2006, ApJ, 647, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, P. H. 1972, Phil. Trans. R. Soc., A272, 663 [Google Scholar]
- Rogachevskii, I., & Kleeorin, N. 2007, Phys. Rev. E, 76, 056307 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdiger, G. 1980, Geophys. Astrophys. Fluid Dyn., 16, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdiger, G. 1989, Differential rotation and stellar convection: Sun and solar-type stars (New York: Gordon & Breach) [Google Scholar]
- Schüssler, M., Caligari, P., Ferriz-Mas, A., & Moreno-Insertis, F., 1994, A&A, 281, L69 [Google Scholar]
- Spiegel, E. A., & Weiss, N. O. 1980, Nature, 287, 616 [CrossRef] [Google Scholar]
- Spruit, H. C. 1981, A&A, 98, 155 [NASA ADS] [Google Scholar]
- Sur, S., Brandenburg, A., & Subramanian, K. 2008, MNRAS, 385, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbeck, M., Krause, F., & Rädler, K.-H. 1966, Z. Naturforsch., 21, 369 [Google Scholar]
- Stenflo, J. O., & Kosovichev, A. G. 2012, ApJ, 745, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Stix, M. 1989, The Sun: An Introduction (Berlin and Heidelberg: Springer) [Google Scholar]
- Warnecke, J., & Brandenburg, A. 2010, A&A, 523, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeldovich, Ya. B., Ruzmaikin, A. A., & Sokoloff, D. D. 1983, Magnetic fields in astrophysics (New York: Gordon & Breach) [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Initial stratification of density and inverse scale height for r⋆/R = 1.001 (strongest stratification), 1.01, 1.05, and 1.1. The dashed lines mark the position of the reference radius rref = 0.95 R, where ρ/ρ0 ≈ 0.0068 for r⋆/R = 1.001 and Hp(r) = Hp0 by definition. The dotted line marks the value of ηt/β⋆urmsHp0. |
| In the text | |
 |
Fig. 2 Dependence of |
| In the text | |
 |
Fig. 3 Meridional cross-sections of |
| In the text | |
 |
Fig. 4 Meridional cross-sections for different values of Qα, for r⋆ = 1.001. The dashed lines indicate the latitudes 49°, 61.5°, 75.6°, and 76.4°. |
| In the text | |
 |
Fig. 5 Meridional cross-sections for different values of the parameter qp0 in the range 40 ≤ qp0 ≤ 100 for Qα = 103. The dashed lines indicate the latitudes 68°, 72.5°, 75.7°, and 76.3°. |
| In the text | |
 |
Fig. 6 Butterfly diagram of |
| In the text | |
 |
Fig. 7 Meridional cross-sections of |
| In the text | |
 |
Fig. 8 The three inverse length scales kC, kM, and kK as a function of time. At time t0, the value of qp0 has been changed from 0 to 100. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




![\begin{eqnarray} \nonumber\\[-4mm] \label{dUmean} &&{\DD\meanUU\over\DD t}={1\over\meanrho}\left[ \meanJJ\times\meanBB+\nab(q_{\rm p}\meanBB^2/2\mu_0)\right] -\nuT\meanQQQ-\nab\meanH,\\ &&{\DD\meanrho\over\DD t}=-\meanrho\nab\cdot\meanUU, \end{eqnarray}](/articles/aa/full_html/2013/08/aa21353-13/aa21353-13-eq16.png)



