| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A151 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220732 | |
| Published online | 09 August 2013 | |
The rotational motion of Vesta
1 Université Pierre et Marie Curie, UPMC – Paris 06, 4 place Jussieu, 75005 Paris, France
e-mail: Nicolas.Rambaux@imcce.fr
2 IMCCE, Observatoire de Paris, CNRS UMR 8028, 77 Avenue Denfert-Rochereau, 75014 Paris, France
Received: 13 November 2012
Accepted: 4 March 2013
Context. Vesta is the second largest body of the main asteroid belt, and it has been studied recently in great detail by the Dawn mission. It was the first time that this asteroid, or protoplanet, has been explored by a space mission, and it revealed a differentiated body. The knowledge of the rotational motion and, especially, its precession-nutation and length-of-day variations may add precious information on its interior.
Aims. The objective of this paper is to present the first rotational model of Vesta based on the data acquired by the Dawn mission. The Dawn mission determined the orientation of Vesta with 0.01 degree accuracy, as well as the second degree of the gravity coefficients with a few percent accuracy.
Methods. We built a semi-analytical model of the rotational motion of Vesta based on the orbital perturbations and the large triaxial shape of Vesta. The rotational motion is then described through the polar motion, precession, nutation, and length-of-day variations. The sensitivity of the precession-nutation is given as a function of the polar moment of inertia, which has not yet been determined.
Results. We find that the amplitude of the nutation is about 2000 milli-arcsec at the semi-annual period, whereas the amplitude of the length-of-day variation is about 3 mas/days, in the semi-diurnal period. Finally, we show that the signature of the polar moment of inertia, which is crucial for constraining geophysical model, is on the order of 200 milli-arcsec for the semi-annual nutations for two extrema of polar moment with inertia values of 0.38–0.42.
Key words: minor planets, asteroids: individual: Vesta / celestial mechanics
© ESO, 2013
1. Introduction
The protoplanet Vesta is the second largest asteroid of the main asteroid belt with a mean radius of 262.7 ± 0.1 km (Russell et al. 2012), and since July 2011, it has belonged to the short list of asteroids visited by a spacecraft. The Dawn mission orbited Vesta for almost one year and investigated the main characteristics of this body in great detail. Notably, the observational data allow assessing its origin as a remnant protoplanet from the formation of the early solar system (Russell et al. 2012). Therefore, it is crucial to determine its interior properties. One way to investigate the interior structure is to accurately determine the rotational motion, which is the objective of this paper.
The Dawn mission has mapped the surface of Vesta with an unprecedented resolution of 0.1 km that leads to determining the orientation of the spin axis at 0.01 degree accuracy (Russell et al. 2012). This accuracy improves the precision of the spin position upon the Hubble Space Telescope (HST) measurements by Thomas et al. (1997) and from the reanalysis of the combined HST/ground data by Li et al. (2011) collected from 1983 to 2006 by a factor of 500. In parallel to Vesta’s mapping, the radio-science experiment provides the gravity field of Vesta (Russell et al. 2012) and thereby leading to constraints on the mass distribution inside Vesta and proving that the interior is differentiated.
The objective of this paper is to present the first rotational model of Vesta based on the recent data obtained by Dawn and to predict the expected precession-nutation and length-of-day variations from various interior models. In return, the knowledge of the rotational motion can be used to infer the interior properties of this protoplanet. The article is divided into four parts. First, we present the input data coming from Dawn and from geophysical models used in this paper. Then, we explain the rotational theory, and in Sect. 5, we discuss the range of solutions. Finally, we conclude.
2. Input data
2.1. Orientation data
Estimation of the orientation of the spin axis of Vesta.
The Dawn mission has determined the orientation of the spin axis of Vesta during its mission from July 2011 to August 2012. The spin axis orientation is described in terms of the right ascension α and declination δ. That means that the spin axis is given in a reference frame defined by the ICRF (International Celestial Reference Frame). Table 1 presents the values of the right ascension and declination for Vesta obtained by Russell et al. (2012), Li et al. (2011), and Thomas et al. (1997). The data from Thomas et al. (1997) comes from images obtained during a campaign with the HST in December 1996, whereas Li et al. (2011) used combined ground data and HST data from 1986 to 2003.
Figure 1 shows the projection of Vesta’s spin axis on the ICRF XY plane reported by the different authors. We plot the ellipses of uncertainties related to each set of observations, including the five degrees uncertainties obtained by Thomas et al. (1997) and Li et al. (2011), whereas the uncertainty ellipse obtained by Dawn is 0.01 degree. The ellipse for the Dawn data is therefore too small to be visible on the scale of the figure. The figure also shows the projection of the orbital axis in the XY plane located at the coordinates 0.124, –0.375. The determination of the orbital axis comes from the Horizons ephemerides (Acton et al. 1996). In this figure, the position of the spin axis with respect to the orbital axis can be described by two spherical angles, the projected obliquity ρ and longitude angle λ represented in the figure. The values of ρ for each set of observation are in very good agreement, whereas the longitude angles present a larger error than the ellipse of uncertainties. The longitude angle uncertainty may be related to the angle of illumination at the surface of Vesta by the Sun. Thus, the uncertainty in the shape modeling could be the origin of the shift in the longitude angle.
 |
Fig. 1 Projection in the ICRF plane XY of the spin axis of Vesta from Thomas et al. (1997) (green curve), Li et al. (2011) (blue curve) and Russell et al. (2012) (red curve). The ellipses represent the measured uncertainties and in the case of Dawn the ellipse is not visible on the scale of the figure. The black point represents the orientation of the orbital axis of Vesta. The angles λ and ρ represent the longitude and projection of the obliquity of Vesta into the ICRF from the orbital axis. |
2.2. Gravity field and interior model
The gravity field of Vesta has been assessed by accurately tracking the Dawn spacecraft in orbit around Vesta (e.g. the method described in Konopliv et al. 2011). In addition to the mass, the two-degree coefficients of the gravity field of Vesta have been determined. They are in non-normalized form: C20 = −0.07106 and C22 = 0.00282 (Asmar et al. 2012; Russell et al. 2012). The large C22 indicates a complex history for Vesta involving possible giant impacts and reorientation (Matsuyama & Nimmo 2011). The non zero C22 implies that Vesta has not yet completely relaxed to reach its hydrostatic equilibrium figure. In addition, small S22 is given by Russell et al. (2012), because the system of reference for the gravity does not exactly match the principal axis orientation. The relations between the two-degree coefficients and the normalized moment of inertia A/MR2, B/MR2 are 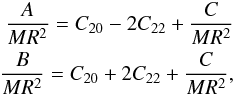 (1)where M and R are the mass and radius of Vesta, respectively. Because Vesta has a non zero C22, the values of A/MR2 and B/MR2 are different. In addition, C22 is large, around 0.4 of the C20, meaning that Vesta has a large triaxial shape. To obtain the set of the three moments of inertia, it is necessary to add an external constraint on the value of the polar moment of inertia C/MR2. According to Russell et al. (2012), Vesta is differentiated into two layers, a mantle and a core. In addition, they suggest that the core could still be in hydrostatic equilibrium. As a consequene, we compute the expected core’s flattening by using Clairaut equation for a two-layer Vesta. We obtain the core’s flattening equal to (ac − cc)/ac = 0.122, where ac and cc are the equatorial and polar axis of the oblate core. Then, the total polar moment of inertia of Vesta is expressed as
(1)where M and R are the mass and radius of Vesta, respectively. Because Vesta has a non zero C22, the values of A/MR2 and B/MR2 are different. In addition, C22 is large, around 0.4 of the C20, meaning that Vesta has a large triaxial shape. To obtain the set of the three moments of inertia, it is necessary to add an external constraint on the value of the polar moment of inertia C/MR2. According to Russell et al. (2012), Vesta is differentiated into two layers, a mantle and a core. In addition, they suggest that the core could still be in hydrostatic equilibrium. As a consequene, we compute the expected core’s flattening by using Clairaut equation for a two-layer Vesta. We obtain the core’s flattening equal to (ac − cc)/ac = 0.122, where ac and cc are the equatorial and polar axis of the oblate core. Then, the total polar moment of inertia of Vesta is expressed as 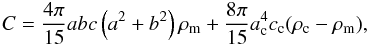 (2)where a,b, and c are the major, intermediate, and minor axes of the ellipsoidal shape of Vesta measured by the Dawn mission, and ρc and ρm are the density of the core and of the mantle. The mass of the ellipsoid is equal to M = 4π/3abcρmean with ρmean the mean density of the body. We compute the polar moment of inertia of Vesta for two sets of interior models: ρc = 7100 kg/m3, rc = 113 km and ρc = 7800 kg/m3, rc = 107 km (Russell et al. 2012). By conserving the mass, we obtain a density for the mantle of 3148.2 kg/m3 and 3148.4 kg/m3 that is in the range of mantle density determined in Zuber et al. (2011). The resulting polar moment of inertia is C/MR2 = 0.4168 and C/MR2 = 0.4161, which are very close. For the present study, we fix the value of the polar moment of inertia equal to 0.42. Therefore A/MR2 = 0.3433 and B/MR2 = 0.3546.
(2)where a,b, and c are the major, intermediate, and minor axes of the ellipsoidal shape of Vesta measured by the Dawn mission, and ρc and ρm are the density of the core and of the mantle. The mass of the ellipsoid is equal to M = 4π/3abcρmean with ρmean the mean density of the body. We compute the polar moment of inertia of Vesta for two sets of interior models: ρc = 7100 kg/m3, rc = 113 km and ρc = 7800 kg/m3, rc = 107 km (Russell et al. 2012). By conserving the mass, we obtain a density for the mantle of 3148.2 kg/m3 and 3148.4 kg/m3 that is in the range of mantle density determined in Zuber et al. (2011). The resulting polar moment of inertia is C/MR2 = 0.4168 and C/MR2 = 0.4161, which are very close. For the present study, we fix the value of the polar moment of inertia equal to 0.42. Therefore A/MR2 = 0.3433 and B/MR2 = 0.3546.
The polar moment of inertia is larger than the limit of 0.4. However, as explained in Yoder (1995), to conserve the limit of 0.4 for a homogeneous ellipsoid, it is necessary to use the equivalent radius 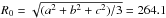 km and not the mean radius R. In this case, the mean moment of inertia
km and not the mean radius R. In this case, the mean moment of inertia 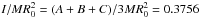 . This value is lower than the 0.4 value of a homogeneous body, so it indicates the presence of a central condensation. For the computation, either definition of R or R0 is valid because it is the relative moment of inertia that plays a role in the rotational motion (see Eq. (6)).
. This value is lower than the 0.4 value of a homogeneous body, so it indicates the presence of a central condensation. For the computation, either definition of R or R0 is valid because it is the relative moment of inertia that plays a role in the rotational motion (see Eq. (6)).
3. Rotational model of Vesta
3.1. Euler-Liouville equations for a triaxial body
The rotational motion of Vesta is analyzed with the Euler-Liouville equation that describes the variations in the angular momentum H due to external torques Γ. We use a reference frame attached to the body defined by the orientation of its principal axis. This reference frame is called the mean body reference frame (MBRF). This reference frame rotates at the mean angular velocity Ω and the Euler-Liouville equation is written as 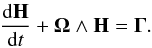 (3)The angular momentum H is composed of the inertia tensor [I] and the angular velocity Ω, such as H = [I] Ω. The main advantage of the MBRF is that, for a rigid body, the tensor of inertia is diagonal in that reference frame. The diagonal elements are the principal moments of inertia A,B,C introduced in Sect. 2.2.
(3)The angular momentum H is composed of the inertia tensor [I] and the angular velocity Ω, such as H = [I] Ω. The main advantage of the MBRF is that, for a rigid body, the tensor of inertia is diagonal in that reference frame. The diagonal elements are the principal moments of inertia A,B,C introduced in Sect. 2.2.
The angular rotation of Vesta Ω is composed of a fast rotation of 5.342128 h around the figure axis (Russell et al. 2012) and a slow precessional motion of the figure axis orientation of about 100 000 years (see the next section). Consequently, the rotational vector can be decomposed into a fast rotation velocity along the z-axis (proper rotation) and a precessional cone describing the orientation of the rotational vector or 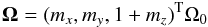 (4)with mx,my,mz small quantities, as for the Earth or Ceres (Dehant & Matthews 2007; Rambaux et al. 2011). We obtain the Euler-Liouville equations developed at first order in the small quantities mi
(4)with mx,my,mz small quantities, as for the Earth or Ceres (Dehant & Matthews 2007; Rambaux et al. 2011). We obtain the Euler-Liouville equations developed at first order in the small quantities mi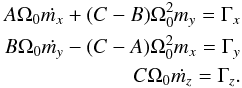 (5)Following Dehant and Mathews (2007), we introduce the polar e and equatorial e′ flattenings defined as
(5)Following Dehant and Mathews (2007), we introduce the polar e and equatorial e′ flattenings defined as 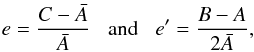 (6)where
(6)where 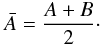 (7)We obtain the following set of equations
(7)We obtain the following set of equations 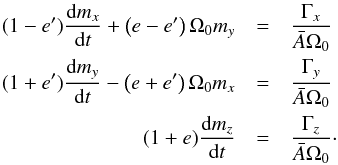 (8)The two first equations describe the equatorial motion of the rotational axis, whereas the third one describes the rotational velocity of the body. The equatorial part can be expressed in complex form by using the complex variable
(8)The two first equations describe the equatorial motion of the rotational axis, whereas the third one describes the rotational velocity of the body. The equatorial part can be expressed in complex form by using the complex variable 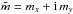 and its conjugate
and its conjugate 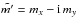 where i2 = −1. The combination of the two first Euler-Liouville Eqs. (8) gives
where i2 = −1. The combination of the two first Euler-Liouville Eqs. (8) gives 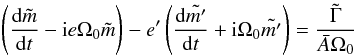 (9)where the gravitational torque is
(9)where the gravitational torque is 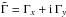 . The last equation describes the length of day (lod) variations of Vesta
. The last equation describes the length of day (lod) variations of Vesta 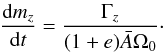 (10)
(10)
3.2. Gravitational torque
The gravitational torque exerted by the Sun on Vesta may be expressed as (Dehant & Mathews 2007) 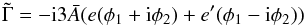 (11)where φ1 and φ2 are the potentials defined by Sasao et al. (1980) and are equal to
(11)where φ1 and φ2 are the potentials defined by Sasao et al. (1980) and are equal to  with G the gravitational constant, x,y,z the coordinates of the Sun in the mean body reference frame (MBRF), and d the relative distance between Vesta and the Sun. Finally, the torque Γz is equal to
with G the gravitational constant, x,y,z the coordinates of the Sun in the mean body reference frame (MBRF), and d the relative distance between Vesta and the Sun. Finally, the torque Γz is equal to 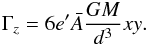 (14)
(14)
3.3. The tidal potentials
As for Ceres (see Rambaux et al. 2011), the gravitational tidal potential induced by the Sun may be expressed in a frame tied to Vesta, the MBRF, or the celestial frame (MCRF = Mean Celestial Reference Frame). Here, we compute the rotation with respect to the MBRF (see Eq. (3)) so the gravitational torque has to be expressed in this reference frame. Therefore, the orbital motion of Vesta that comes from the JPL Horizons ephemerides (Acton et al. 1996) is transformed into the MBRF through a rotation of the reference frame to the fixed orientation of the spin axis determined by Dawn and reported in Table 1. Then the gravitational torque is computed according to Eqs. (11) and (14) and expanded into Fourier series through a frequency analysis (Laskar 1988, 2005; Gastineau & Laskar 2008) into prograde (indices p) and retrograde components (indices r): 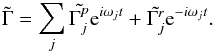 (15)We note that the quantities
(15)We note that the quantities 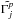 and
and 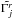 are complex quantities containing the amplitudes and phases of each frequency ωj. For an axisymmetric body, e′ = 0, so the amplitude of
are complex quantities containing the amplitudes and phases of each frequency ωj. For an axisymmetric body, e′ = 0, so the amplitude of 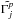 is equal to zero and the retrograde components are only present in the external torque (e.g. Dehant & Matthews 2007). Indeed, the retrograde torque comes from the retrograde motion of the Sun in the sky of Vesta. When the triaxiality (e′) is taken into account, the torque varies at 2Ω due to the orientation of the Sun with respect to the bulges (see Fig. 2). The combination of the varying amplitude with the retrograde motion leads to the retrograde and prograde components. The quantity
is equal to zero and the retrograde components are only present in the external torque (e.g. Dehant & Matthews 2007). Indeed, the retrograde torque comes from the retrograde motion of the Sun in the sky of Vesta. When the triaxiality (e′) is taken into account, the torque varies at 2Ω due to the orientation of the Sun with respect to the bulges (see Fig. 2). The combination of the varying amplitude with the retrograde motion leads to the retrograde and prograde components. The quantity 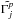 is proportional to the equatorial flattening e′, and so its amplitude is smaller than the retrograde components.
is proportional to the equatorial flattening e′, and so its amplitude is smaller than the retrograde components.
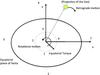 |
Fig. 2 Geometry of the torque acting on the triaxial Vesta. The x,y axes represent the orientation of the equatorial plane of Vesta: the long and intermediate axes, respectively. The triaxiality induces a semi-diurnal periodic variation in the equatorial torque where the torque is maximum at positions 2 and 4 and minimum at positions 1 and 3. The behavior of the amplitude of the torque is represented in the shaded line. The ellipsoidal shape of the equatorial plane of Vesta has been exaggerated for the cartoon. |
4. Description of the rigid rotational motion
4.1. Polar motion
We first solve the polar motion by introducing the torque expressed in prograde and retrograde components (Eq. (15)) into the equation of motion (Eq. (9)). The complex polar motion is then expressed as 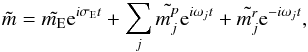 (16)which consists of a free mode (with amplitude
(16)which consists of a free mode (with amplitude 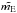 ) and a sum of forced modes that are prograde and retrograde. The solution is expressed in the MBRF.
) and a sum of forced modes that are prograde and retrograde. The solution is expressed in the MBRF.
The frequency of the free mode is called the Euler frequency σE by analogy to the rigid Earth rotation and it is written as 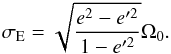 (17)Its period is about 1.0963 days with the interior parameters defined in Sect. 2.2. The presence of the e′ term shifts the Euler period by 0.0033 days or 0.3% of the Euler period value in the axisymmetric case (here simply without e′). This mode is a proper mode of rotation, and in the absence of excitation source, its amplitude is assumed to be zero due to damping. For the Earth the excitation of the corresponding proper mode (the Chandler period) comes from the fluid layers: the atmosphere and the ocean (e.g. Bizouard et al. 2011). For Vesta, there is no fluid layers, but this proper mode may be excited by impacts (e.g. see the discussion in Rambaux et al. 2011, for Ceres).
(17)Its period is about 1.0963 days with the interior parameters defined in Sect. 2.2. The presence of the e′ term shifts the Euler period by 0.0033 days or 0.3% of the Euler period value in the axisymmetric case (here simply without e′). This mode is a proper mode of rotation, and in the absence of excitation source, its amplitude is assumed to be zero due to damping. For the Earth the excitation of the corresponding proper mode (the Chandler period) comes from the fluid layers: the atmosphere and the ocean (e.g. Bizouard et al. 2011). For Vesta, there is no fluid layers, but this proper mode may be excited by impacts (e.g. see the discussion in Rambaux et al. 2011, for Ceres).
The forced polar motion coefficients are expressed as 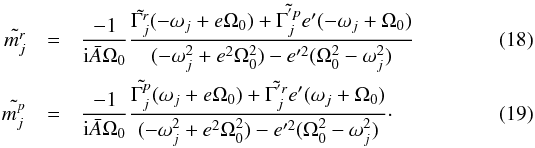 These relationships show that both the prograde and retrograde components of the gravitational torque affect the prograde and retrograde components. This is caused by the presence of the triaxiality introduced through the term in (e′). If e′ is zero, the prograde-retrograde coupling vanishes.
These relationships show that both the prograde and retrograde components of the gravitational torque affect the prograde and retrograde components. This is caused by the presence of the triaxiality introduced through the term in (e′). If e′ is zero, the prograde-retrograde coupling vanishes.
Vesta polar motion series.
The numerical value of the coefficients and frequencies are shown in Table 2. First, the frequencies of the polar motion are in the diurnal band of Vesta. The retrograde diurnal band of the polar motion results from the obliquity and polar flattening e, like it is classical for the axisymmetric Earth or Ceres (Dehant & Matthews 2007; Rambaux et al. 2011; and references therein). While the prograde diurnal band of the polar motion results from the equatorial flattening or triaxiality e′. Second, the amplitude of the retrograde band dominates the amplitudes of the prograde polar motion by a factor greater than twelve. This is because the prograde part is proportional to e′ and because the ratio e/e′ is about 12.6. Third, the second retrograde frequency in the diurnal band is equal to the rotational frequency of Vesta in the MBRF. Therefore, expressed in the MCRF, it will give rise to the precessional motion of the orientation axis of Vesta.
The polar motion of Vesta is projected onto the surface of Vesta in Fig. 3. The elliptical motion of the polar motion results from the triaxiality of Vesta where the amplitude of 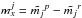 and
and 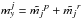 . The amplitude of the polar motion, multiplied by the mean radius of Vesta, is about 8.0 × 10-4 m and is thus very small.
. The amplitude of the polar motion, multiplied by the mean radius of Vesta, is about 8.0 × 10-4 m and is thus very small.
4.2. Precession-nutation of Vesta
Vesta’s figure axis describes, in the MCRF, a conic motion (the precession) that oscillates periodically (the nutations). The rotation angles (ψ the precession angle and θ the nutation angle) and their derivatives are computed by using the kinematic Euler equation, thereby allowing us to express the instantaneous rotation pole components in terms of the nutation angles as 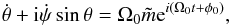 (20)where Ω0 accounts for the expression of the pole in space due to the rotation around the Z-axis, and φ0 is the initial value of the rotational angle (here fixed at J2000). After integrating Eq. (20), except for the case ωj = −Ω0 that leads to the precessional motion, we obtain the nutation series
(20)where Ω0 accounts for the expression of the pole in space due to the rotation around the Z-axis, and φ0 is the initial value of the rotational angle (here fixed at J2000). After integrating Eq. (20), except for the case ωj = −Ω0 that leads to the precessional motion, we obtain the nutation series ![\begin{eqnarray} \Delta \theta &+& {\rm i} \Delta {\psi}\sin{\theta} = -{\rm i} \frac{\Omega_0}{\Omega_0 + \sigma_{\rm E}} \tilde{m_{\rm E}} {\rm e}^{{\rm i} (\Omega_0 +\sigma_{\rm E})t} \nonumber \\ &-& {\rm i} \sum_{j \neq 0} \!\left[ \frac{\Omega_0}{(\omega_j\! +\! \Omega_0)} \tilde{m}_j^p {\rm e}^{{\rm i} ((\omega_j\! +\! \Omega_0) t)} \! +\! \frac{ \Omega_0}{(\!-\! \omega_j \!+\!\Omega_0)} \tilde{m}_j^r {\rm e}^{{\rm i} ((\!-\omega_j \!+\! \Omega_0) t)} \right]. \nonumber\\ \label{eq:nutprec} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20732-12/aa20732-12-eq101.png) (21)The nutation series is composed of three parts. First, a periodic part of frequency Ω0 + σE or 4.44 h, i.e. a decrease of 54 min with respect to the proper rotation of the body. Second, a semi-diurnal frequency from ωj + Ω0 that results from the triaxial components of the polar motion. Their amplitude is diminished by the ratio Ω0/(ωj + Ω0) and is around 0.02 milli-arcsec (mas). The third term is composed of long-period nutations in space and results from the retrograde polar motion, as for the axisymmetric Earth. In contrast for the semi-diurnal band, the ratio Ω0/( − ωj + Ω0) increases the amplitude of the long-period nutation at several hundred mas. Therefore, we focus on the long-period nutations, and we classified the frequencies as prograde and retrograde nutations ΔΩj in space, the MCRF, through
(21)The nutation series is composed of three parts. First, a periodic part of frequency Ω0 + σE or 4.44 h, i.e. a decrease of 54 min with respect to the proper rotation of the body. Second, a semi-diurnal frequency from ωj + Ω0 that results from the triaxial components of the polar motion. Their amplitude is diminished by the ratio Ω0/(ωj + Ω0) and is around 0.02 milli-arcsec (mas). The third term is composed of long-period nutations in space and results from the retrograde polar motion, as for the axisymmetric Earth. In contrast for the semi-diurnal band, the ratio Ω0/( − ωj + Ω0) increases the amplitude of the long-period nutation at several hundred mas. Therefore, we focus on the long-period nutations, and we classified the frequencies as prograde and retrograde nutations ΔΩj in space, the MCRF, through 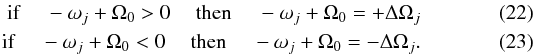 Table 3 lists the main nutations that have an amplitude larger than 1 mas. As shown in Eq. (21), the amplitudes of the long-period nutations are positively affected because the amplitude is inversely proportional to the forcing frequency. The main term is the semi-annual nutation 2λv related to the obliquity of Vesta. The following terms are sub harmonics of the annual period of Vesta around the Sun. The last nutation is not identified, and it might result from the perturbation by other large bodies in the solar system. The amplitude of the semi-annual nutation is around ~1850 mas, which represents a 2.4 m surface displacement, for a mean radius of 264.6 km (Russell et al. 2012).
Table 3 lists the main nutations that have an amplitude larger than 1 mas. As shown in Eq. (21), the amplitudes of the long-period nutations are positively affected because the amplitude is inversely proportional to the forcing frequency. The main term is the semi-annual nutation 2λv related to the obliquity of Vesta. The following terms are sub harmonics of the annual period of Vesta around the Sun. The last nutation is not identified, and it might result from the perturbation by other large bodies in the solar system. The amplitude of the semi-annual nutation is around ~1850 mas, which represents a 2.4 m surface displacement, for a mean radius of 264.6 km (Russell et al. 2012).
 |
Fig. 3 Polar motion of Vesta projected onto its surface. The motion is plotted for a period of 10 days. The elliptical motion results from the triaxiality of Vesta. |
Amplitude of the coefficients of nutations.
To complete the description of the nutations, we extract the real and imaginary part of Δθ + iΔψsinθ to obtain the nutation in obliquity Δθ and the nutation in longitude Δψsinθ. During the separation of the nutations, we take into account the in-phase and out-of-phase components explicitly as described in detail in (Defraigne et al. 1995). The respective amplitudes of these nutations are presented in Tables 4 and 5, and plotted in Fig. 4. In this plot, the gray part highlights the time spent for the rendez vous by Dawn around Vesta. During this time interval, the nutations in obliquity and in longitude were minimum at the beginning and then increased.
Nutations in obliquity Δθ.
Nutations in longitude Δψsinθ.
The precessional motion of the figure axis is represented by the oscillation at ωj = −Ω0 in the body reference frame that is purely imaginary. The amplitude of the second prograde polar motion in Table 2 that is equal to 0.6113 mas causes a precession period of 94 831 years that is slightly shorter than the 96 016 year period calculated with the classical formula 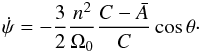 (24)The discrepancy between the two results (1.2%) is mainly due to the length of the ephemerides used in the frequency analysis of the potential.
(24)The discrepancy between the two results (1.2%) is mainly due to the length of the ephemerides used in the frequency analysis of the potential.
 |
Fig. 4 Evolution of the nutation in obliquity and in longitude for Vesta. The semi-annual nutation dominates, then the annual and finally the sub harmonics nutations. The gray box highlights the interval of time where Dawn was around Vesta. The initial time is J2000. |
4.3. Length-of-day variations
The length-of-day (lod) of Vesta varies over time owing to the torque acting on the non zero equatorial flattening of Vesta. The oscillations are computed by inserting the torque along z (Eqs. (14) into (10)): 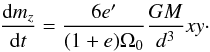 (25)The gravitational torque along z is proportional to e′; therefore, for axisymmetric bodies there is no lod variations due to the gravitational torque. Just as previously, we develop the varying part
(25)The gravitational torque along z is proportional to e′; therefore, for axisymmetric bodies there is no lod variations due to the gravitational torque. Just as previously, we develop the varying part 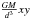 into Fourier series. Then, the resulting amplitude of the lod variations are computed from
into Fourier series. Then, the resulting amplitude of the lod variations are computed from 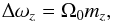 (26)and the oscillations are shown in Table 6. The variation in the lod of Vesta is dominated by a semi-diurnal 2Ω0 band that is split in orbital sub harmonics. We truncate the amplitude of the values in the table at 0.001 mas/day.
(26)and the oscillations are shown in Table 6. The variation in the lod of Vesta is dominated by a semi-diurnal 2Ω0 band that is split in orbital sub harmonics. We truncate the amplitude of the values in the table at 0.001 mas/day.
It is interesting to compare the lod variations with the present uncertainty in the determination of the spin rate. The maximum lod variations have an amplitude of 2.8 mas/days that is one third smaller than the accuracy of the spin rate equal to 10.8 mas/days (Russell et al. 2012). As a consequence, determining the lod variations in the Dawn observations is challenging.
We also compare our results with the determination coming from a Hamiltonian approach. We follow the approach developed in Cottereau et al. (2011) where the orbit is assumed to be circular. In this case, the lod variations appear in three terms that correspond to the first, third, and eighth terms of our Table 6. The first two terms are in good agreement, and the third one presents a variation of a factor 1.6. These differences may come from the eccentricity and orbital variations of Vesta that are not included in the simplified Hamiltonian.
 |
Fig. 5 Precession period of Vesta as a function of the assumed C/MR2 value. Here we plot the interval of C/MR2 between [0.38–0.42] and the dashed lines represent an accuracy of ±300 mas/year that is thirty times the accuracy obtained for the precession of Mars (Konopliv et al. 2006). |
5. Discussion
5.1. Introduction
In parallel to the semi-analytical model developed in this paper, we investigate two approaches: 1) a simplified model with a circular orbit and axisymmetric shape, in order to highlight the contributions of the equatorial flattening; and 2) a numerical model in order to quantify the different approximations done in the semi-analytical model.
5.2. Simple model: Vesta axisymetric and on circular orbit
The eccentricity of Vesta is low, about of 0.089. As a consequence, we can develop a first-order model where the orbit of Vesta is circular. In addition, we assume that Vesta is axisymmetric. By following the approach developed in Dehant & Mathews (2007) for the Earth, the angular momentum projection of Vesta is 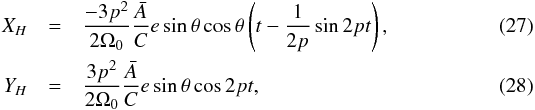 where p is the orbital period of Vesta. By using the relationship with the nutations
where p is the orbital period of Vesta. By using the relationship with the nutations  we obtain the variations in ψ and θ as
we obtain the variations in ψ and θ as 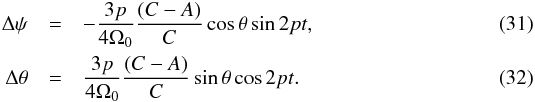 The amplitude of the nutation at the semi-annual period is 2026.49 mas for the nutation in obliquity Δθ and 1798.12 mas for the nutation in longitude Δψsinθ. The proximity of these values to the nutational amplitude in Tables 4 and 5 illustrates the small signature of the equatorial flattening on the nutations amplitude. Indeed, as shown in Eq. (19) the fast rotation of Vesta counteracts the effect of the equatorial shape for the amplitude of the long-period nutation. We recall, however, that the triaxiality is purely responsible for the semi-diurnal band nutations of Vesta.
The amplitude of the nutation at the semi-annual period is 2026.49 mas for the nutation in obliquity Δθ and 1798.12 mas for the nutation in longitude Δψsinθ. The proximity of these values to the nutational amplitude in Tables 4 and 5 illustrates the small signature of the equatorial flattening on the nutations amplitude. Indeed, as shown in Eq. (19) the fast rotation of Vesta counteracts the effect of the equatorial shape for the amplitude of the long-period nutation. We recall, however, that the triaxiality is purely responsible for the semi-diurnal band nutations of Vesta.
5.3. Numerical model of triaxial Vesta
In parallel to the semi-analytical theory, we integrate the rotational motion of Vesta numerically (Eq. (3)). The Euler angles (ψE,θE,ϕE) describe the transformation from an inertial reference frame (GXYZ) to the MBRF (Gxyz). Here, the inertial reference frame is the ICRF that corresponds to the reference frame of the orbital coordinates of Vesta (Acton et al. 1996). In this reference frame, we define (i) ψE, the precession angle between GX and the node N of the intersection of the inertial plane and the equator plane of Vesta (Gxy); (ii) the nutation angle θE, the angle between GZ and Gz; (iii) the proper rotation ϕE defined as the angle between GN and Gx.
Amplitude of the lod variations.
Series of the nutations in obliquity Δθ from the numerical integrations.
 |
Fig. 6 Evolution of the nutation in obliquity and in longitude for Vesta as a function of C/MR2. The red curve is obtained for a C/MR2 = 0.42 (used in previous sections), the green curve for C/MR2 = 0.40 and the blue curve for C/MR2 = 0.38. |
In this paper, we express the nutations with respect to the MCRF corresponding to the mean orbital motion of Vesta at J2000. The normal to the MCRF is expressed in the ICRF through a rotation of 288.17° in the right ascension and declination of 67.26°. After transforming the reference frame from ICRF to MCRF, we obtain the Euler angles (ψ,θ,ϕ) corresponding to the angles computed analytically.
The nutations in obliquity are the periodic variations in the θ angle and the nutations in longitude divided by the sinθ corresponding to the periodic variations of the ψ angle. We use the frequency analysis on the numerical solutions and the resulting periodic terms are listed in Tables 7 and 8. The comparison of these values with Tables 4 and 5 show very good agreement. The differences may be ascribed to the approximation in the analytical theory where the torque is expressed in the MBRF with no nutations. It is a second-order effect in the amplitude.
In addition to the periodic variations of ψ and θ, we extract the linear trend in ψ angle that corresponds to a precessional motion of 94 934.29 years, in agreement with Eq. (24).
5.4. Geophysical discussion
The rotational motion is sensitive to the moments of inertia of the body as shown by the presence of the polar flattening e and equatorial flatenning e′ in the gravitational torque and the polar motion (Eqs. (11) and (19)). Here, we quantify the relationship between the polar moment of inertia and the dynamical parameters: the precession rate and the semi-annual nutation. As discussed in Sect. 2.2 the determination of the three moments of inertia of Vesta (Eq. (1)) is underestimated from the two gravity coefficients C20 and C22 obtained by Dawn, and we develop a two-layer model as suggested by Zuber et al. (2011) and Russell et al. (2012) to fix the value of the polar moment of inertia C/MR2. The value of C/MR2 ranges between 0.38 and 0.42 (~10%) depending on the size of the core and the jump density between the core and the mantle. A C/MR2 = 0.38 corresponds to a higher concentration of mass in the interior of Vesta.
Series of the nutations in longitude Δψsinθ coming from the numerical integrations.
First, the precessional frequency (Eq. (24)) depends on the polar motion and its variation is linear in the 0.38–0.42 inversely proportional to C/MR2 (Fig. 5). The period of the precession is below 100 000 years, which is very long with respect to the one-year measurement period of the Dawn mission, so the determination of the precession rate requires very accurate measurement to detect this signature in the data.
Second, we explore the signature of C/MR2 on the nutation amplitude. The resulting behavior is illustrated in Fig. 6 where the nutations for C/MR2 = 0.42 (the value used in the previous part of the paper), 0.40, and 0.38 are represented. The variation of the amplitude of the semi-annual nutation is 209 mas for the nutation in obliquity and 181 mas for the nutation in longitude or a displacement of 0.3 m at the surface of Vesta. However, the signature of nutation can be obtained by analyzing the influence of the nutation rate on the gravity field (e.g. Konopliv et al. 2011) and by following the landmarks (e.g. Russell et al. 2012).
6. Conclusion
In this paper, we have developed a semi-analytical model of the precession-nutation of Vesta based on the Dawn data. The orbital motion of Vesta was expressed through a frequency analysis, and the solar gravitational torque acting on the triaxial figure of Vesta was decomposed in Fourier series. The problem was then solved analytically by keeping the triaxial shape explicit. The nutational motion of Vesta is dominated by a semi-annual nutation of amplitude around 2000 mas and then by the harmonics of the annual period. Some perturbations due to planets are also present but with very small amplitudes. The comparison of this model with gravity and cartographic data acquired during the Dawn mission may provide constraints on the polar moment of inertia C/MR2, hence on the knowledge of the interior structure of this unique remnant protoplanet.
Acknowledgments
The author wishes to thank J.C. Castillo-Rogez, A. Konopliv, and C. Raymond for fruitful discussions on Vesta and S. Lambert and C. Bizouard for discussions of the polar motion. This research benefits from the financial support of the Paris Observatory (2012).
References
- Acton, C. H. 1996 , Planet. Space Sci., 44, 1, 65 [Google Scholar]
- Asmar, S. W., Konopliv, A. S., Park, R. S., et al. 2012, Lunar and Planetary Institute Science Conf. Abstracts, 43, 2600 [NASA ADS] [Google Scholar]
- Bizouard, C., Remus, F., Lambert, S. B., Seoane, L., & Gambis, D. 2011, A&A, 526, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cottereau, L., Rambaux, N., Lebonnois, S., & Souchay, J. 2011, A&A, 531, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Defraigne, P., Dehant, V., & Pâquet, P. 1995, Celestial Mechanics and Dynamical Astronomy, 62, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Dehant, V., & Mathews, M. P. 2007, in Treatise of Geophysics, Elsevier Publ., Geodesy, eds. T. Herring, & J. Schubert, 3, 295 [Google Scholar]
- Gastineau, M., & Laskar, J. 2008, TRIP 0.99, Manuel de référence TRIP, Paris Observatory, http://www.imcce.fr/Equipes/ASD/trip/trip.html [Google Scholar]
- Konopliv, A. S., Asmar, S. W., Bills, B. G., et al. 2011, Space Sci. Rev., 163, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1988, A&A, 198, 341 [NASA ADS] [Google Scholar]
- Laskar, J. 2005, In Hamiltonian Systems and Fourier Analysis, eds. D. Benest, C. Froeschler, & E. Lega (Cambridge: Cambridge Scientific Publishers) [Google Scholar]
- Li, J.-Y., Thomas, P. C., Carcich, B., et al. 2011, Icarus, 211, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuyama, I., & Nimmo, F. 2011, Geophys. Res. Lett., 38, 14205 DOI: 10.1029/2011GL047967 [NASA ADS] [CrossRef] [Google Scholar]
- Rambaux, N., Castillo-Rogez, J., Dehant, V., & Kuchynka, P. 2011, A&A, 535, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russell, C. T., Raymond, C. A., Coradini, A., et al. 2012, Science, 336, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Sasao, T., Okubo, S., & Saito, M. 1980, IAU Symp., 78, 165 [Google Scholar]
- Thomas, P. C., Binzel, R. P., Gaffey, M. J., et al. 1997, Icarus, 128, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Yoder, C. F. 1995, In Global Earth Physics, A Handbook of Physical Constants, AGU Reference Shelf 1 [Google Scholar]
- Zuber, M. T., McSween, H. Y., Binzel, R. P., et al. 2011, Space Sci. Rev., 163, 77 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Series of the nutations in longitude Δψsinθ coming from the numerical integrations.
All Figures
 |
Fig. 1 Projection in the ICRF plane XY of the spin axis of Vesta from Thomas et al. (1997) (green curve), Li et al. (2011) (blue curve) and Russell et al. (2012) (red curve). The ellipses represent the measured uncertainties and in the case of Dawn the ellipse is not visible on the scale of the figure. The black point represents the orientation of the orbital axis of Vesta. The angles λ and ρ represent the longitude and projection of the obliquity of Vesta into the ICRF from the orbital axis. |
| In the text | |
 |
Fig. 2 Geometry of the torque acting on the triaxial Vesta. The x,y axes represent the orientation of the equatorial plane of Vesta: the long and intermediate axes, respectively. The triaxiality induces a semi-diurnal periodic variation in the equatorial torque where the torque is maximum at positions 2 and 4 and minimum at positions 1 and 3. The behavior of the amplitude of the torque is represented in the shaded line. The ellipsoidal shape of the equatorial plane of Vesta has been exaggerated for the cartoon. |
| In the text | |
 |
Fig. 3 Polar motion of Vesta projected onto its surface. The motion is plotted for a period of 10 days. The elliptical motion results from the triaxiality of Vesta. |
| In the text | |
 |
Fig. 4 Evolution of the nutation in obliquity and in longitude for Vesta. The semi-annual nutation dominates, then the annual and finally the sub harmonics nutations. The gray box highlights the interval of time where Dawn was around Vesta. The initial time is J2000. |
| In the text | |
 |
Fig. 5 Precession period of Vesta as a function of the assumed C/MR2 value. Here we plot the interval of C/MR2 between [0.38–0.42] and the dashed lines represent an accuracy of ±300 mas/year that is thirty times the accuracy obtained for the precession of Mars (Konopliv et al. 2006). |
| In the text | |
 |
Fig. 6 Evolution of the nutation in obliquity and in longitude for Vesta as a function of C/MR2. The red curve is obtained for a C/MR2 = 0.42 (used in previous sections), the green curve for C/MR2 = 0.40 and the blue curve for C/MR2 = 0.38. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


