| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A149 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321751 | |
| Published online | 17 July 2013 | |
Orbit, emission spectrum, and photometric analysis of two flickering sporadic fireballs
1
Facultad de Ciencias Experimentales, Universidad de Huelva,
21071
Huelva,
Spain
e-mail:
jmmadiedo@gmail.com
2
Departamento de Física Atómica, Molecular y Nuclear, Facultad de
Física, Universidad de Sevilla, 41012
Sevilla,
Spain
3
Institut de Ciències de l’Espai (CSIC-IEEC), Campus UAB, Facultat
de Ciències, Torre
C5-parell-2 a, 08193 Bellaterra,
Barcelona,
Spain
4
Institute of Astrophysics of the Academy of Sciences of the
Republic of Tajikistan, Bukhoro,
str. 22, 734042
Dushanbe,
Tajikistan
5
Instituto de Astrofísica de Andalucá, CSIC, Apt. 3004, 18080
Granada,
Spain
6
Universidad de Castilla-La Mancha, 45071
Toledo,
Spain
7
La Cañada Observatory (MPC J87), Ávila, Spain
Received:
22
April
2013
Accepted:
4
June
2013
We present the observations of two fireballs that exhibit fast and quasi-periodic brightness variations along their atmospheric path. This phenomenon, which is known as “flickering”, is associated to the entry of spinning non-spherical meteoroids into the atmosphere. Both bolides were imaged in the framework of the continuous fireball monitoring and meteor spectroscopy campaigns organized by the SPanish Meteor Network (SPMN) in 2012. Their atmospheric trajectory, radiant, and orbit were calculated. The preatmospheric mass and tensile strength of the parent meteoroids were also estimated, and the rotation of these bodies analyzed on the basis of the photometric behavior of the bolides. Although small (less than 80 grams), a non-zero terminal mass was determined for both events. The emission spectra produced during the ablation of the meteoroids in the atmosphere are also discussed.
Key words: meteorites, meteors, meteoroids
© ESO, 2013
1. Introduction
Classical meteor light curves have the basic shape of a parabola that is skewed about the point of maximum brightness (Hughes 1978). Most bright meteor light curves approximately fit this description, with events produced by compact meteoroids exhibiting their maximum luminosity during the second half of their trajectory (Murray et al. 1999; Campbell et al. 2000) and dustball meteoroids showing this maximum earlier (Hawkes & Jones 1975). However, about 5% of observed fireball events exhibit a distinct brightness modulation called flickering (Opik 1936; Beech & Brown 2000), so that they show fast quasi-periodic, small-amplitude brightness variations superimposed upon a classical light curve. This phenomenon is indicative of the parent meteoroid being both non-spherical and rotating and, so, the analysis of the light curve of flickering fireballs can provide information about the spin and shape of these particles (Beech 2001).
Here we present the results of the analysis of two flickering bolides recorded over the Iberian Peninsula in 2012 in the framework of our continuous fireball monitoring and meteor spectroscopy campaigns. These bright sporadic events, with absolute magnitudes of −16.5 ± 0.5 and −10.0 ± 0.5 were imaged on July 21 and December 29, respectively. For identification in our database they were assigned a SPanish Meteor Network (SPMN) code established after the recording date with format yymmdd. Besides this, the bolides were named according to the geographical location nearest to the projection on the ground of their atmospheric trajectory. Thus, bolide SPMN210712 was named “Fuencaliente” after this village located in Andalusia. On the other hand, the fireball SPMN2191212 was named “Sevilla”, because the meteoroid disintegrated over this city in the south of Spain.
2. Instrumentation and data reduction methods
The geographical coordinates of the meteor-observing stations that imaged the bolides analyzed here are shown in Table 1. From these we operate high-sensitivity CCD video devices (models 902H and 902H Ultimate from Watec Corporation, Japan) to monitor the night sky. These generate interlaced imagery according to the PAL video standard. Thus, they produce video files at a rate of 25 frames per second and with a resolution of 720 × 576 pixels. The operation of these video stations is given in Madiedo & Trigo-Rodríguez (2008, 2010), Trigo-Rodriguez et al. (2007, 2009), and Madiedo et al. (2010). For meteor spectroscopy, holographic diffraction gratings (500 or 1000 lines/mm, depending on the device) are attached to the objective lens of some of these CCD cameras.
Geographical coordinates of the meteor observing stations involved in this work.
Brightness, trajectory and radiant data (J2000) for the fireballs analyzed in this work.
Orbital elements (J2000) and Tisserand parameter with respect to Jupiter for the bolides discussed in the text.
For data reduction, we first deinterlaced the video sequences provided by our CCD cameras. Thus, even and odd fields were separated for each video frame, and a new video file containing these was generated. Since this operation implies duplicating the total number of frames in the original sequence, the frame rate in the resulting video was transformed from 25 to 50 fps. Then, an astrometric measurement was done by hand in order to obtain the plate (x, y) coordinates of the meteor along its apparent path from each station. The astrometric measurements were then introduced in our Amalthea software (Trigo-Rodríguez et al. 2009; Madiedo et al. 2011a), which transforms plate coordinates into equatorial coordinates by using the position of reference stars appearing in the images. This package employs the method of intersecting planes to determine the position of the apparent radiant and also to reconstruct the trajectory in the atmosphere of meteors recorded from at least two different observing stations (Ceplecha 1987). In this way, the beginning and terminal heights of the meteor are inferred. From the sequential measurements of the video frames and the trajectory length, the velocity of the meteor along its path is obtained. The preatmospheric velocity V∞ is found by measuring the velocities at the earliest part of the meteor trajectory. Once these data are known, the software computes the orbital parameters of the corresponding meteoroid by following the procedure described in Ceplecha (1987).
 |
Fig. 1 a) Composite image of the “Fuencaliente” fireball (code SPMN210712), imaged on July 21, 2012 at 22h21m56.7 ± 0.1s UTC from a) El Arenosillo and b) La Hita Astronomical Observatory. c) Apparent trajectory of the bolide as seen from La Hita. d) Heliocentric orbit of the meteoroid projected on the ecliptic plane. |
3. Observations: atmospheric trajectory and orbit
From calculation of the atmospheric trajectory of both fireballs, we obtained the beginning (Hb), ending (He), and maximum brightness (Hm) heights for each event. Their absolute magnitude (M) was obtained by comparing the brightness level of the pixels near the maximum luminosity of the meteor trail and those of stars appearing within the field of view. These characteristics of the fireball path are listed in Table 2. The planes intersection method also provided the location of the apparent radiant for each fireball and the preatmospheric velocity V∞ of the parent meteoroids. Once this information was known, we calculated the orbital elements in the solar system of these particles (Table 3). The characteristics and specific circumstances of both events are detailed below.
3.1. The “Fuencaliente” sporadic event (SPMN210712)
This deep-penetrating fireball was observed on July 21, 2012 at 22h21m56.7s ± 0.1s UTC (about 22 min after local midnight). It lasted over three seconds and was widely witnessed over Spain. Thus, because of the very high brightness of this bolide (its estimated absolute magnitude is −16.5 ± 0.5) and excellent weather conditions on the Iberian Peninsula, the fireball was imaged from most SPMN stations located in the south and center of Spain (Fig. 1). The best images, however, were obtained from our fireball monitoring systems operating from La Hita Astronomical Observatory, Toledo, El Arenosillo, Sevilla, Ávila, and Huelva. The emission spectrum produced during the ablation of the object that produced this event was also recorded by two video spectrographs operating from El Arenosillo and La Hita. Our calculations reveal that the meteoroid struck the atmosphere with an initial velocity V∞ = 19.4 ± 0.3 km s-1. The luminous phase began at a height of 81.8 ± 0.5 km and ended at 29.0 ± 0.5 km above the ground level. The angle of the atmospheric trajectory to the Earth’s surface was of about 74.3° and the apparent radiant was located at the position α = 292.0 ± 0.5°, β = 38.9 ± 0.4°. With this information, the heliocentric orbit of the parent meteoroid was obtained. The projection of this orbit on the ecliptic plane is plotted in Fig. 1c. The calculated orbital parameters (Table 3) confirmed the sporadic nature of the event, but also the likely asteroidal origin of the meteoroid (Tisserand parameter with respect to Jupiter TJ = 4.83 ± 0.06).
3.2. The “Sevilla” fireball (SPMN291212)
A slow-moving fireball was imaged on December 29, 2012, at 23h42m07.6 ± 0.1s UTC from stations #1 and #5 (Fig. 2). The event lasted about 4.7 s, and the photometric analysis of the video sequences recorded by our CCD cameras indicates that it reached an absolute magnitude of −10.0 ± 0.5 at its brightest phase. Its apparent trajectory in the sky as seen from both meteor observing stations is shown in Fig. 2c. The bolide began at 89.6 ± 0.5 km above the ground level, with the terminal point located at 30.7 ± 0.5 km. The angle of the atmospheric path to the Earth’s surface was of about 62.8°. The position of the apparent radiant was α = 44.3 ± 0.3°, β = 45.7 ± 0.3°. The analysis of the atmospheric trajectory also reveals that the parent meteoroid impacted the atmosphere with an initial velocity V∞ = 16.9 ± 0.3 km s-1. From the calculation of the orbital elements of this particle (Table 3) we infer that the meteoroid was following a Jupiter Family Comet orbit before impacting the atmosphere (TJ = 2.50 ± 0.08). This orbit is shown in Fig. 2d.
 |
Fig. 2 Composite image of the “Sevilla” sporadic fireball (code SPMN291212), imaged on Dec. 29, 2012 at 23h42m07.6 ± 0.1s UTC from a) Sevilla and b) El Arenosillo. c) Apparent trajectory of the bolide as seen (1) El Arenosillo and (2) Sevilla. d) Heliocentric orbit of the meteoroid projected on the ecliptic plane. |
4. Results and discussion
4.1. Photometric analysis
The photometric analysis of the video sequences recorded for each fireball provided the light curves shown in Figs. 3 and 4. As can be noticed, both events exhibit their maximum brightness during the second half of their trajectory, a behavior that is typical of fireballs produced by compact meteoroids (Murray et al. 1999; Campbell et al. 2000). The flickering effect is also obvious, as both light curves reveal rapid and quasi-periodic oscillations in luminosity.
One of the parameters that can be obtained from these light curves is the preatmospheric
mass of the meteoroids. Thus, this photometric mass mp can be obtained as the total mass
lost due to the ablation process between the beginning of the luminous phase and the
terminal point of the atmospheric trajectory,
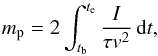 (1)where
tb and te are, respectively, the
times corresponding to the beginning and the end of the luminous phase, and I is the
measured luminosity of the fireball, which is related to the absolute magnitude M of the
event by means of the equation
(1)where
tb and te are, respectively, the
times corresponding to the beginning and the end of the luminous phase, and I is the
measured luminosity of the fireball, which is related to the absolute magnitude M of the
event by means of the equation 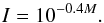 (2)The
velocity-dependent luminous efficiency (τ) was calculated according to
the relationships given by Ceplecha & McCrosky (1976). In this way, the calculation of the initial mass yields 212 ± 20 kg for
the “Fuencaliente” meteoroid and 4.1 ± 0.5 kg for the body producing the “Sevilla” event.
The diameter of these particles would be 55 ± 3 and 14.8 ± 1.5 cm, respectively, for a
bulk density ρm = 2.4 g cm-3. For a density
ρm = 3.7 g cm-3, the calculated diameter yields
47 ± 2 cm for the “Fuencaliente” meteoroid and 12.8 ± 1.5 cm for “Sevilla”.
(2)The
velocity-dependent luminous efficiency (τ) was calculated according to
the relationships given by Ceplecha & McCrosky (1976). In this way, the calculation of the initial mass yields 212 ± 20 kg for
the “Fuencaliente” meteoroid and 4.1 ± 0.5 kg for the body producing the “Sevilla” event.
The diameter of these particles would be 55 ± 3 and 14.8 ± 1.5 cm, respectively, for a
bulk density ρm = 2.4 g cm-3. For a density
ρm = 3.7 g cm-3, the calculated diameter yields
47 ± 2 cm for the “Fuencaliente” meteoroid and 12.8 ± 1.5 cm for “Sevilla”.
Observational data show that both, sporadic bright fireballs (Getman 1993; Brown et al. 1998; Beech 2001) but also bright bolides belonging to annual meteor showers such as the Geminids (Halliday 1963; Babadzhanov & Konovalova 2004) and the Taurids (Konovalova 2003) show quasi-periodic brightness variations during the flight in the Earth’s atmosphere. The flickering frequencies reported in the literature vary from a few Hz (low-frequency flickering) to about 500 Hz (high-frequency flickering). The flickering phenomenon is apparently associated with meteoroid ablation and can provide information about the spin and shape of the parent meteoroid, but also about its physical properties, mainly the density, strength, and structure. Some authors argued that this effect is a manifestation of the rotational modulation of surface mass loss during the ablation of non-spherical meteoroids (Kruchinenko 1995; Beech 2001). Undoubtedly, meteoroids can gain rotation before penetrating the Earth’s atmosphere by means of, for instance, collisions taking place in space. According to Olsson-Steel (1987), the angular frequency of these rotations decreases in inverse proportion to the second power of the radius of these bodies. Adolfsson (1994) proposed a method for calculating the initial rotation of large asymmetrical bodies. It must also be mentioned that, in the long term, the so-called Yarkovsky-O’Keefe-Radzievskii-Paddack (YORP) effect can also significantly change the rotational state of meteoroids and small asteroids (Čapek & Vokrouhlický 2004). On the other hand, other authors proposed that the flickering phenomenon can occur when the pressure of saturated vapors of meteor material and the outer pressure regulate each other automatically (Babadzhanov & Konovalova 2004). This is, in fact, one of the main possible mechanisms for meteor flickering listed in (Oleak 1964) and presented as responsible for the autofluctuating character of the evaporation process.
For the “Sevilla” fireball, the observed flickering modulation amplitude is
ΔM ≈ 1 and appears to be almost constant along the atmospheric
trajectory of the bolide (Fig. 4). We have analyzed
the flickering behavior exhibited by this event on the basis of the quasi-continuous
fragmentation (QCF) theory (Novikov et al. 1998).
According this model, the equation that provides the intensity
I(t) of the light emitted by the fireball can be
written as 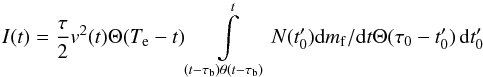 (3)with
(3)with
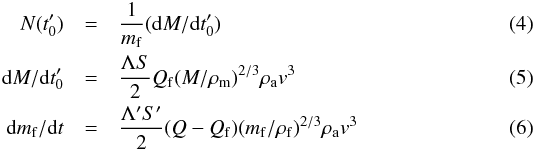 where
v is the velocity of meteoroid, M and
mf are the meteoroid mass and the initial masses of the
smaller fragments at the instant
where
v is the velocity of meteoroid, M and
mf are the meteoroid mass and the initial masses of the
smaller fragments at the instant 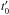 ,
respectively.
,
respectively.
 |
Fig. 3 Light curve of the SPMN210712 “Fuencaliente” fireball. |
 |
Fig. 4 Light curve of the SPMN291212 “Sevilla” fireball. The modeled light curve according to the QCF model is also included. |
In Eqs. (3)−(6) the velocity-dependent luminous efficiency τ is given by
Ceplecha & McCrosky (1976), and Λ,
S, and ρm are the heat transfer
coefficient, the shape factor, and the bulk density of meteoroid, respectively. On the
other hand, Λ′, S′, and
ρf represent these same physical quantities for fragments,
and Q and Qf are the energies of evaporation
and fragmentation, respectively, with ρa the atmospheric
density. The parameter Te is defined as
Te = τ0 + τe,
where τ0 is the lifetime of the meteoroid to complete
fragmentation, and τe is the lifetime of a fragment that was
detached at the end of fragmentation until its full evaporation. On the other hand,
τb is the lifetime of the fragment released at the instant
of beginning of fragmentation, and τf is the lifetime of the
individual fragment counted from 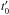 until its
full evaporation.
until its
full evaporation.
Aerodynamic pressure for flares and break-up processes discussed in the text.
Equations (3) to (6) have been solved numerically. We have considered the meteoroid as an
ellipsoid of rotation with semimajor axis a, semiminor axis
b and eccentricity
e2 = 1 − (b / a)2,
which is spinning about its minor axis during its flight in the atmosphere and,
consequently, has a time-varying cross-sectional area
A(t). We also assumed spherical symmetry for small
fragments, so that their shape factor is S′ = 1.21. For the
heat transfer coefficient of these fragments, we employed Λ′ = 1, while the
heat transfer coefficient was Λ = 0.05 for the meteoroid. In fact, this coefficient
depends on the flow regime, as it is conditioned by the thermal shielding of flying away
(jumping aside) air molecules and ablated material from the meteoroid. For large
meteoroids (with diameters >10 cm) this shielding is strong and
then Λ = 0.05 or even lower. For small particles, however, the shielding effect can be
neglected and then Λ = 1 (Bronshten 1981). In
addition, in our numerical model we have adopted the bulk density-dependent energy of
fragmentation Qf given by Lebedinets (1986). Besides, the shape factor S of the meteoroid
was expressed in terms of its volume and time-varying cross-section A(t) given by (Beech
2001):
![\begin{equation} A(t)=\pi b^2 \left[\cos^2 \omega + (a/b)\sin^2 \omega\right] \end{equation}](/articles/aa/full_html/2013/07/aa21751-13/aa21751-13-eq99.png) (7)where
ω = (2π/P) t + Φ,
with P being the rotation period of the meteoroid, Φ the rotation phase term, and
t the time since the beginning of the simulation.
(7)where
ω = (2π/P) t + Φ,
with P being the rotation period of the meteoroid, Φ the rotation phase term, and
t the time since the beginning of the simulation.
Figure 4 shows the observed and modeled light curves produced for a spinning meteoroid. The assumed axial ratio corresponds to b / a = 1 / 1.5, with a rotation period P = 0.58 s, phase Φ = 0, and bulk density of meteoroid material ρm = 3.2 ± 0.2 g cm-3. As can be noticed, both curves exhibit an almost synchronous amplitude brightness modulation. This correlation between the observed and modeled light curves is the evidence that the flickering effect exhibited by the “Sevilla” event is actually related to the instantaneous rotation rate of the parent meteoroid.
On the other hand, the light curve of the “Fuencaliente” fireball (Fig. 3) could not be modeled by means of the QCF or
single-body theory. Nevertheless, this light curve reveals a flickering frequency of about
10 Hz, with a maximum flickering modulation amplitude ΔM of around 2.0
mag. By assuming a homogeneous ellipsoidal profile for the meteoroid, the flickering
amplitude would vary according to (Beech et al. 2003) 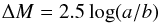 (8)with a
and b being, respectively, the semimajor and semiminor axes of the
meteoroid. Thus, an axis ratio
a / b = 6.3 is required to account for
the observed maximum amplitude, so, according to this, the meteoroid would be
significantly elongated. However as can be seen in Fig. 3, no significant flickering is exhibited in the beginning of the atmospheric
path, which suggests that the rotational state of the meteoroid before impacting the
atmosphere is not the main reason for the observed flickering behavior, and the calculated
a/b ratio would be unrealistic.
(8)with a
and b being, respectively, the semimajor and semiminor axes of the
meteoroid. Thus, an axis ratio
a / b = 6.3 is required to account for
the observed maximum amplitude, so, according to this, the meteoroid would be
significantly elongated. However as can be seen in Fig. 3, no significant flickering is exhibited in the beginning of the atmospheric
path, which suggests that the rotational state of the meteoroid before impacting the
atmosphere is not the main reason for the observed flickering behavior, and the calculated
a/b ratio would be unrealistic.
On the other hand, the observed flickering amplitude at times t > 0.7 seconds cannot be explained on the basis of an increase in the rotation rate in the atmosphere, since this mechanism is not effective for large meteoroids. Thus, for instance, Geminid meteoroids gain rotation in the atmosphere when their initial mass is below 6 × 10-7 g (Babadzhanov & Konovalova 2004). On the other hand, Fig. 3 also shows that the flickering effect practically disappears after the main fulguration. In this case, the most likely explanation for the flickering behavior observed for the “Fuencaliente” fireball would be a mechanism of successive detachment of fragments (wreckages) (Oleak 1964; Konovalova 2003).
4.2. Tensile strength
The compactness inferred for the meteoroids on the basis of the above-discussed
photometric behavior can be confirmed by the estimation of the tensile strength of these
particles. Thus, as can be noticed in the composite images shown in Figs. 1 and 2 and also in
the light curves plotted in Figs. 3 and 4, the fireballs exhibited at least one very bright flare
along their atmospheric path. These events are typically produced by the fragmentation of
the meteoroids when these particles penetrate denser atmospheric regions. Thus, once the
overloading pressure becomes higher than the particle strength, the particle breaks apart.
Quickly after that, a bright flare is produced as a consequence of the fast ablation of
tiny fragments delivered to the thermal wave in the fireball’s bow shock. The so-called
tensile (aerodynamic) strength S at which these breakups take place can
be calculated by means of the following equation (Bronshted 1981): 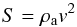 (9)where
v is the velocity of the meteoroid at the disruption point and
ρa the atmospheric density at the height where the fracture
takes place. The density can be calculated, for instance, by employing the US standard
atmosphere model (US Standard Atmosphere 1976).
This aerodynamic strength S can be used as an estimation of the tensile
strength of the meteoroid (Trigo-Rodríguez & Llorca 2006, 2007). The values obtained
for the fireballs analyzed in this work are summarized in Table 4, together with the corresponding heights and velocities.
(9)where
v is the velocity of the meteoroid at the disruption point and
ρa the atmospheric density at the height where the fracture
takes place. The density can be calculated, for instance, by employing the US standard
atmosphere model (US Standard Atmosphere 1976).
This aerodynamic strength S can be used as an estimation of the tensile
strength of the meteoroid (Trigo-Rodríguez & Llorca 2006, 2007). The values obtained
for the fireballs analyzed in this work are summarized in Table 4, together with the corresponding heights and velocities.
As Fig. 3 shows, the SPMN210712 “Fuencaliente” fireball experienced a big flare at the instant t1 = 1.7 s after the event started its luminous phase, followed by a second and more intense flare at the instant t2 = 2.3 s. These events are indicated in Fig. 3 with labels (1) and (2), respectively. The images reveal that the corresponding fragmentations were not catastrophic, as the remaining material continued penetrating the atmosphere. These break-ups took place, respectively, at a height of 55.8 ± 0.5 and 43.5 ± 0.5 km above the ground level. In this way, we infer that the meteoroid exhibited the first flare under a dynamic pressure of (1.2 ± 0.4) × 106 dyn cm-2, although the main flare took place at (5.4 ± 0.4) × 106 dyn cm-2. These values are higher than the typical strengths found for meteoroids from cometary streams (between ~4.0 × 103 and ~3.4 × 105 dyn cm-2 according to Trigo-Rodríguez & Llorca 2006, 2007), which is consistent with the likely asteroidal nature of the meteoroid inferred from the analysis of its orbital parameters.
The brightest phase of the “Sevilla” SPMN291212 fireball took place at a height of 44.5 ± 0.5 km above the ground level, when its velocity was 12.9 ± 0.3 km s-1. In this way, according to Eq. (9), the aerodynamic pressure at this point yields (3.3 ± 0.4) × 105 dyn cm-2. When this value is compared with the tensile strength found for meteoroids from cometary streams (Trigo-Rodríguez & Llorca 2006, 2007), we conclude that the “Sevilla” meteoroid is also tough, exhibiting a similar behavior to meteoroids from evolved cometary bodies such as the Taurids (S ~ 3.4 × 105 dyn cm-2), whose parent body is the Jupiter family comet 2P/Encke (Jenniskens 2006).
Derived elemental abundances relative to Si of the two fireballs discussed here compared with the inferred for other solar system undifferentiated materials.
4.3. Terminal mass and meteorite survival
By taking the calculated values of the ending height of their luminous trajectory into
account, the possibility that these deep-penetrating fireballs could produce meteorites
was considered. For this purpose the mass of the progenitor body at the terminal point of
the luminous atmospheric path was calculated. Thus, the meteoroid mass surviving the
ablation process was obtained from the following equation (Ceplecha et al. 1983):
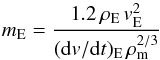 (10)where
mE, vE, and
(dv/dt)E are the mass, velocity and
deceleration at the terminal point, respectively. ρm is the
meteoroid density and ρE the air density at the terminal
height. The latter was again calculated by using the US standard atmosphere model (US
Standard Atmosphere 1976).
(10)where
mE, vE, and
(dv/dt)E are the mass, velocity and
deceleration at the terminal point, respectively. ρm is the
meteoroid density and ρE the air density at the terminal
height. The latter was again calculated by using the US standard atmosphere model (US
Standard Atmosphere 1976).
For the “Sevilla” fireball the calculation of the atmospheric trajectory yields vE = 8.3 km s-1 and (dv/dt)E = −23.8 km s-2, so the calculated terminal mass is mE = 14 ± 6 g for a meteor density ρm = 2.4 g cm-3 and 6 ± 3 g for ρm = 3.7 g cm-3. For the “Fuencaliente” event the analysis of the trajectory provided the values vE = 8.1 km s-1 and (dv/dt)E = −9.9 km s-2, and the terminal mass of the meteoroid yields mE = 78 ± 23 g for ρm = 2.4 g cm-3 and 33 ± 11 g for ρm = 3.7 g cm-3. Since these terminal masses are very low, no meteorite search was organized.
 |
Fig. 5 Calibrated emission spectrum recorded for the SPMN210712 “Fuencaliente” bolide. Intensity is expressed in arbitrary units. |
4.4. Emission spectra and inferred chemical abundances
Our video spectrographs recorded the emission spectrum for both fireballs. These were used to obtain insight into the chemical nature of the parent meteoroids. We employed our CHIMET software, which follows the technique described in Borovicka (1993) and Trigo-Rodriguez (2002), to reduce these spectra (Madiedo et al. 2011b, 2013a,b). Thus, we first deinterlaced the video sequences containing the emission spectrum. The frames in the resulting video files were then dark-frame substracted and flat-fielded. Next, the signal was calibrated in wavelengths by identifying typical lines appearing in meteor spectra and corrected by taking the efficiency of the recording instrument into account. The result can be seen in Figs. 5 and 6.
As can be seen in Fig. 5, the most prominent emission lines of the SPMN210712 “Fuencaliente” bolide spectrum correspond to multiplets Ca II-1 (at 393-397 nm), Fe I-42 (438 nm), and Mg I-2 (518 nm). Other Fe I lines are visible all along the spectrum. The Na I-1 line at 589 nm is almost missing, barely visible over the background. From this spectrum we suspect that the meteoroid was depleted in Na for some reason. Sometimes it has been found that fragile meteoroids suffer preferential ablation of Na in the highest parts of their luminous trajectories (Madiedo et al. 2013c). Another possibility could be heating experienced during close approaches to the Sun, but this seems unlikely due to the inferred meteoroid mass and relative high value of the perihelion distance (q = 0.929 ± 0.002). The rest of the spectrum looks quite normal for a meteoroid of chondritic nature but low geocentric velocity, as is also inferred from the comparison between the computed chemical abundance ratios relative to Si summarized in Table 5. On the other hand, the emission spectrum of the SPMN291212 “Sevilla” fireball is characteristic of a low geocentric velocity event (Trigo-Rodríguez 2002; Trigo-Rodríguez et al. 2003). In these particular cases, the abundance of elements forming part of refractory phases, like Ca and Al, are underestimated. This is because it is inefficient to bring all available Ca or Al to the vapor phase. Thus, we previously noted (Trigo-Rodríguez et al. 2003) that in chondritic meteoroids the elements Ca and Al are associated with refractory minerals that are not fully vaporized during atmospheric ablation (Trigo-Rodríguez 2002; Trigo-Rodríguez et al. 2003, 2004; Trigo-Rodríguez & Llorca 2007). Consequently, it is not surprising that the contribution of Ca II-1 (at 393−397 nm) is almost indistinguishable, since it is blended with the Fe I-4, Fe I-20 and Fe I-45 multiplets. In any case, the spectrum is dominated by the Fe I-42 (438 nm), Mg I-2 (518 nm), Fe I-15 (537 nm), and Na I-1 (589 nm) multiplets. In the red region of the spectrum we have identified atmospheric N2 bands around 626 nm. In general, the chemical ratios relative to Si for this meteoroid fall within the values expected for chondritic meteorites (Table 5).
 |
Fig. 6 Calibrated emission spectrum recorded for the SPMN291212 “Sevilla” fireball. Intensity is expressed in arbitrary units. |
5. Conclusions
We have analyzed two fireballs of sporadic origin observed over Spain in 2012. These were catalogued as SPMN210712 “Fuencaliente” and SPMN291212 “Sevilla”. Our main conclusions are as follows.
-
1.
Our analysis shows that the body that produced the“Fuencaliente” fireball had a preatmospheric mass of212 ± 20 kg. This mass was 4.1 ± 0.5 kg for the “Sevilla” event. The inferred orbital parameters reveal a likely asteroidal origin for the “Fuencaliente” meteoroid. On the other hand, the “Sevilla” meteoroid followed a JFC orbit before impacting the atmosphere. Their tensile strength was inferred from the aerodynamic pressure at which these particles fragmented in the atmosphere. The derived toughness of the “Sevilla” meteoroid suggests that this particle was produced by an evolved comet or that the meteoroid was ejected from that body long ago.
-
2.
Both bolides exhibited fast and quasi-periodic variations in brightness along their atmospheric path. These, however, were produced by different mechanisms. Thus, for the “Sevilla” fireball the observed flickering behavior was caused by the rotation of the non-spherical parent meteoroid. For the “Fuencaliente” event, a successive detachment of fragments would be responsible for the observed quasi-periodic variations of brightness.
-
3.
The calculation of the atmospheric trajectory reveals that these deep-penetrating fireballs ended their luminous phase at a height of 29.0 ± 0.5 and 30.7 ± 0.5 km above the ground level. A non-zero terminal mass was inferred for both events, which shows that these bolides were meteorite-droppers. However, since the inferred mass is low (below 100 grams), no meteorite search was organized.
-
4.
Both fireballs probably were chondritic in composition, but exhibiting some peculiarities. For example, the emission spectrum of the “Fuencaliente” fireball reveals Na depletion like the one predicted for a meteoroid suffering preferential ablation in the highest parts of the trajectory. Another possibility could be the heating experienced during close approaches to the Sun, but this seems unlikely due to the inferred meteoroid mass and relatively far perihelion distance. On the other hand, the “Sevilla” event has weaker emission lines probably due to its very low geocentric velocity that also participates in obtaining low chemical ratios for elements forming refractory minerals.
Acknowledgments
We acknowledge support from the Spanish Ministry of Science and Innovation (project AYA2011-26522) and Junta de Andalucía (project P09-FQM-4555). We also thank the AstroHita Foundation for its support in the establishment and operation of the automated meteor observing station located at La Hita Astronomical Observatory (La Puebla de Almoradiel, Toledo, Spain).
References
- Adolfsson, L. G., & Gustafson, B. A. S. 1994, P&SS, 42, 593 [Google Scholar]
- Babadzhanov, P. B., & Konovalova, N. A. 2004, A&A, 428, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beech, M. 2001, MNRAS, 326, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Beech, M., & Brown, P. 2000, Planet. Space Sci., 48, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Beech, M., Illingworth, A., & Murray, S. 2003, Meteor. Planet. Sci., 38, 1045 [Google Scholar]
- Borovička, J. 1993, A&A, 279, 627 [NASA ADS] [Google Scholar]
- Bronshten, V. A. 1981, Geophys. Astrophys. Monographs (Dordrecht: Reidel) [Google Scholar]
- Brown, P., et al. 1998, Nature, 37, 624 [Google Scholar]
- Campbell, M. D., Brown, P. G., Leblanc, A. G., et al. 2000, Meteor. Planet. Sci., 35, 1259 [Google Scholar]
- Čapek, D., & Vokrouhlický, D. 2004, Icarus, 172, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Ceplecha, Z. 1987, Bull. Astron. Inst. Cz., 38, 222 [Google Scholar]
- Ceplecha, Z., & McCrosky, R. E. 1976, J. Geophys. Res., 81, 6257 [NASA ADS] [CrossRef] [Google Scholar]
- Ceplecha, Z., Novakova-Jezkova, M., Porubcan, V., et al. 1983, Bull. Astron. Inst. Cz., 34, 195 [NASA ADS] [Google Scholar]
- Getman, V. S. 1993, in Meteoroids and their Parent Bodies. Astronomical Inst. Slovak. Acad. Sci., Bratislava, eds. I. Stohl, & I. P. Williams, 307 [Google Scholar]
- Halliday, I. 1963, Smithson. Contrib. Astrophys., 7, 161 [NASA ADS] [Google Scholar]
- Hawkes, R. L., & Jones, J. 1975, MNRAS, 173, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, D. W. 1978, in Cosmic Dust, ed. J. A. M. McDonnell (Chichester: Wiley and Sons), 167 [Google Scholar]
- Jenniskens P. 2006, Meteor Showers and their Parent Comets (Cambridge University Press) [Google Scholar]
- Jessberger, E. K., Christoforidis, A., & Kissel, J. 1988, Nature, 332, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Konovalova, N. A. 2003, A&A, 404, 1145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kruchinenko, V. G. 1995, Sol. Syst. Res., 29, 309 [NASA ADS] [Google Scholar]
- Lebedinets, V. N. 1986, Dokl. AN SSSR, 291, 313 [NASA ADS] [Google Scholar]
- Madiedo, J. M., & Trigo-Rodríguez, J. M. 2008, Earth Moon Planets, 102, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Madiedo, J. M., Trigo-Rodríguez, J. M., Ortiz, J. L., & Morales, N. 2010, Adv. Astron., 2010, 1 [CrossRef] [Google Scholar]
- Madiedo, J. M., Trigo-Rodríguez, J. M., & Lyytinen, E. 2011a, NASA/CP-2011-216469, 330 [Google Scholar]
- Madiedo, J. M., Toscano, F. M., & Trigo-Rodríguez, J. M. 2011b, EPSC-DPS Joint Meeting 2011, Abstract #Vol. 6, EPSC-DPS2011-72 [Google Scholar]
- Madiedo, J. M., Trigo-Rodríguez J. M., Lyyttinen, E., et al. 2013a, MNRAS, DOI: 10.1093/mnras/stt288 [Google Scholar]
- Madiedo, J. M., Trigo-Rodríguez, J. M., Williams, I. P., Ortiz, J. L., & Cabrera, J. 2013b, MNRAS, DOI: 10.1093/mnras/stt342 [Google Scholar]
- Madiedo J. M. et al. 2013c, MNRAS, submitted [Google Scholar]
- Murray, I. S., Hawkes, R. L., & Jenniskens, P. 1999, Meteorit., & Planet. Sci., 34, 949 [Google Scholar]
- Novikov, G. G., Pecina, P., & Konovalova, N. A. 1998, A&A, 329, 769 [NASA ADS] [Google Scholar]
- Oleak, N. 1964, Astron. Nachr., 228, 7 [NASA ADS] [Google Scholar]
- Olsson-Steel, D. I. 1987, MNRAS, 226, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Opik, E. 1936, Publ. Tartu Obs., 28, 13 [Google Scholar]
- Rietmeijer, F. 2002, Chemie der Erde, 62, 1 [Google Scholar]
- Rietmeijer, F., & Nuth, J. A. 2000, Earth, Moon Planets, 82, 325 [Google Scholar]
- Trigo-Rodríguez, J. M. 2002, Ph.D. Thesis, Universitat de Valencia [Google Scholar]
- Trigo-Rodríguez, J. M., & Llorca, J. 2006, MNRAS, 372, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Trigo-Rodríguez, J. M., & Llorca, J. 2007, MNRAS, 375, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Trigo-Rodríguez, J. M., Llorca, J., Borovička, J., & Fabregat, J. 2003, Meteorit. Planet. Sci., 38, 1283 [CrossRef] [Google Scholar]
- Trigo-Rodríguez, J. M., Llorca, J., Borovicka, J., & Fabregat, J. 2004, Earth Moon Planets, 95, 375 [Google Scholar]
- Trigo-Rodríguez, J. M., Madiedo, J. M., Llorca, J., et al. 2007, MNRAS, 380, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Trigo-Rodríguez, J. M., Madiedo, J. M., Williams, I. P., & Castro-Tirado, A. J. 2009, MNRAS, 392, 367 [NASA ADS] [CrossRef] [Google Scholar]
- US Standard Atmosphere 1976, NOA-NASA-USAF, Washington [Google Scholar]
All Tables
Brightness, trajectory and radiant data (J2000) for the fireballs analyzed in this work.
Orbital elements (J2000) and Tisserand parameter with respect to Jupiter for the bolides discussed in the text.
Derived elemental abundances relative to Si of the two fireballs discussed here compared with the inferred for other solar system undifferentiated materials.
All Figures
 |
Fig. 1 a) Composite image of the “Fuencaliente” fireball (code SPMN210712), imaged on July 21, 2012 at 22h21m56.7 ± 0.1s UTC from a) El Arenosillo and b) La Hita Astronomical Observatory. c) Apparent trajectory of the bolide as seen from La Hita. d) Heliocentric orbit of the meteoroid projected on the ecliptic plane. |
| In the text | |
 |
Fig. 2 Composite image of the “Sevilla” sporadic fireball (code SPMN291212), imaged on Dec. 29, 2012 at 23h42m07.6 ± 0.1s UTC from a) Sevilla and b) El Arenosillo. c) Apparent trajectory of the bolide as seen (1) El Arenosillo and (2) Sevilla. d) Heliocentric orbit of the meteoroid projected on the ecliptic plane. |
| In the text | |
 |
Fig. 3 Light curve of the SPMN210712 “Fuencaliente” fireball. |
| In the text | |
 |
Fig. 4 Light curve of the SPMN291212 “Sevilla” fireball. The modeled light curve according to the QCF model is also included. |
| In the text | |
 |
Fig. 5 Calibrated emission spectrum recorded for the SPMN210712 “Fuencaliente” bolide. Intensity is expressed in arbitrary units. |
| In the text | |
 |
Fig. 6 Calibrated emission spectrum recorded for the SPMN291212 “Sevilla” fireball. Intensity is expressed in arbitrary units. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


