| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 9 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201321377 | |
| Published online | 17 July 2013 | |
Electron-impact broadening parameters for Be II, Sr II, and Ba II spectral lines
1
Data Center for High Energy Density Physics, Institute of Applied Physics
and Computational Mathematics,
100088
Beijing,
PR China
e-mail:
alexduan1967@hotmail.com
2
National Astronomical Observatories, Chinese Academy of Sciences,
100012
Beijing, PR
China
3
Pakistan Atomic Energy Commission, PO Box 1114,
44000
Islamabad,
Pakistan
4
HEDPS, Center for Applied Physics and Technology, Peking
University, 100871
Beijing, PR
China
Received:
28
February
2013
Accepted:
8
May
2013
Aims. We present results of the electron-impact broadening parameters (i.e., widths and shifts) of spectral lines in singly ionized Be II, Sr II, and Ba II ions, calculated by using our relativistic quantum mechanical methods.
Methods. In these calculations, Dirac R-matrix methods were used to solve (N + 1)- electron colliding systems to obtain the required scattering matrices. The dimensionless collision strength Ω(ε) is calculated as a function of incident electron energies ε.
Results. The present line-broadening parameters are required for future spectral analysis by means of state-of-the-art nonlocal thermodynamic equilibrium atmospheres, which is now hampered largely by the paucity of reliable atomic and accurate line-broadening data tables. Our results for the spectral line-broadening parameters in the case of three ions obtained for a set of electron temperatures at an electron density 1017 cm-3 show very good agreement with other theoretical calculations, and are much closer to the available experimental measurements.
Key words: line: profiles / atomic processes / atomic data
© ESO, 2013
1. Introduction
The broadening of spectral lines by collisions with charged particles provide valuable insight into the behavior of atomic interactions, and serves as one of the most valuable diagnostic tools to map the interface between atomic and plasma physics. The electron-impact broadening mechanism plays a primordial role in stellar spectroscopy and is indispensable for spectral analysis of astrophysical and laboratory plasmas. In particular, collisional broadening is important for investigating and modeling A- and B-type stars, as well as for the white dwarf atmospheres (Dimitrijević et al. 2007). The atomic data of electron-impact broadening for line synthesis are needed to solve various problems in astrophysics, such as for determining the chemical abundance of elements and also for estimating radiative transfer through stellar plasmas, as well as for opacity calculations. The collisional broadening coefficients may also be important in the case of cooler stars, such as solar type stars, for transitions involving higher principal quantum numbers (Tankosić et al. 2003, and references therein).
For such investigations, accurate line-broadening parameters are required for a large number of lines for various elements and have frequently been missed in the literature (Konjević & Wiese 1976; Konjević et al. 1984). Presently, nonlocal thermodynamic equilibrium (NLTE) calculations for stellar spectroscopy have achieved a high level of precision and sophistication, but are restrained largely by the paucity of reliable atomic and line-broadening data. In NLTE techniques for elemental abundance determination, it has remained necessary that the existing line-broadening data be extrapolated for the required electron temperatures and electron densities. This procedure can cause inaccuracies in models of stellar interiors (Alecian et al. 1993), white dwarfs (Rauch et al. 2007), early type galaxies (Andrievsky et al. 2009), and extremely metal-poor stars (Andrievsky et al. 2011). The knowledge of NLTE line profiles having contributions from Stark broadening parameters of the three unblended Ba II lines (4554 Å, 5853 Å, 6496 Å) was used for Sr/Ba abundance determinations in very or extremely metal-poor stars (Andrievsky et al. 2009). Therefore, it is essential to validate line-broadening theories with the well-characterized experiments. It has also been emphasized by Rauch et al. (2007) that arduous efforts should be made to improve the scope of line-broadening parameters for spectral line forming regions in astrophysical plasmas. Simultaneously, there has been strong interest in providing more accurate line-broadening data to match observations for a large number of spectral lines of various emitters in the past ten years by developments in astronomy that have collected an extensive amount of spectroscopic information over large spectral regions for all kinds of celestial objects. Therefore, even though there are very successful semiclassical treatments (Sahal-Bréchot 1969a,b; Griem 1974) to deal with electron-impact broadening parameters, it is very useful to perform some more sophisticated quantum mechanical calculations.
Beryllium is an element of particular astrophysical importance due to its high cosmic abundance. Beryllium derives its abundance from high-energy reactions between heavy nuclei and cosmic rays or protons from interstellar medium. As an example, the cosmic abundance of beryllium is an important test bed for cosmological models (see Gilmore et al. 1991). A striking excess of beryllium as compared with lithium is found in our Sun, since beryllium is rapidly destroyed by thermonuclear reactions at temperatures above 3.6 × 106 K, and its abundance also constraints on mixing between photospheric and deeper regions of stars, which is of particular interest in the Sun (Balachandran & Bell 1998). The surface contents of light elements, especially beryllium, provide information on nucleogenesis, and it almost relies on the Be II resonance doublet at 3130 Å, which emphasizes the importance of these lines in our present work (Barklem & O’Mara 2000). Moreover, Be II line profiles are of interest for opacity calculations (Dimitrijević & Sahal-Bréchot 1992).
The Sr II resonance lines (4077.7 Å, 4215.5 Å) and its four other emission lines (4167.80 Å, 10 036.05 Å, 10 327.31 Å, 10 914.89 Å) have been regarded as extremely important for deriving precise strontium abundance in some astrophysical objects (see e.g. Barklem & O’Mara 2000; Zethson et al. 2001). Most recently, with the aid of these six Sr II lines, NLTE stellar strontium abundances have been derived by serval authors (Andrievsky et al. 2011; Bergemann et al. 2012). The widths and shifts of these Sr II spectral lines produced by electron impact have set up a basis for demonstrating NLTE calculations of stellar strontium abundances by fitting the synthetic line profiles to the observed spectrum. Therefore, the line-broadening parameters of the involved Sr II spectral lines must be known a priori for NLTE abundance calculations of strontium in stars, where Sr II lines are particularly strong.
In recent years, the interest in Ba II lines has been renewed by new observations for revising the barium abundance in solar and stellar atmospheres. Among numerous studies dedicated to Ba II lines in solar and stellar spectra, two Ba II multiplets, 6s 2S−6p 2P° and 5d 2D−6p 2P° transitions, are displayed in spectra of F-G stars (Mashonkina et al. 1999). The three Ba II lines (5853.69 Å, 6141.73 Å, 6496.91 Å) have been observed in red giants of NGC 6752 (Dobrovolskas et al. 2012). Andrievsky et al. (2013) have derived the barium atmospheric abundances for a large sample of Cepheids, comprising 270 stars with NLTE calculations by using these three Ba II lines. Komarov & Basak (1993) found Ba I and Ba II lines in the spectra of the Sun and of two Praesepe stars (for solar barium lines also see Anders & Grevesse 1989). Barium lines are also of immense interest for investigating laboratory plasmas. Although the Sr II and Ba II triplets are not particularly strong in the Sun, they are much stronger in other stars, such as BA- and S-type stars, and this is where the data presented in this paper are expected to be the most useful. For example, for quantitative spectroscopy of luminous BA-type supergiants with NLTE spectrum synthesis technique, Przybilla et al. (2006) utilized Stark broadening parameters of Ba II spectral lines published by Dimitrijević & Sahal-Bréchot (1997). The degree to which we can rely on quantitative studies of this class of stars as a whole depends on the quality of the atomic and line-broadening parameters. This indicates the importance of accurate electron-impact broadening widths and shifts for abundance determination studies.
The main aim of this paper is to provide new and more accurate electron-impact broadening data of singly ionized Be II, Sr II, and Ba II ions for a wide range of electron temperatures suitable for stellar spectroscopy. Our calculations were performed only for those plasma parameters for which the experimental electron-impact broadening data are available in the literature to provide uncertainty estimates. For evaluating widths and shifts of nonhydrogenic spectral lines of ionized atoms, various theoretical approaches have been used and discussed extensively in the literature (e.g. Griem 1974). Comprehensive calculations of the line-broadening parameters of spectral lines emitted by singly ionized atoms from lithium through calcium were performed by Jones et al. (1971), and the results are included in the book by Griem (1974). These calculations were based on the generalization of semiclassical methods, as previously employed for neutral helium lines. Our new quantum mechanical approach (Duan et al. 2012a, 2012b) was adopted to obtain the electron-impact broadening data. A similar approach is applied by Elabidi et al. (2008) for the electron-impact broadening widths of the 2s3s−2s3p transitions for the beryllium-like ions. These quantum mechanical calculations of electron-impact broadening widths for some isolated lines showed an excellent agreement between theory and experiments. Therefore, the other aim of this paper is to provide a quantitative check on the collisional broadening parameters by comparing them with the available experimental and theoretical results. These quantum results would be helpful in achieving more precision in the synthetic spectra of solar and stellar plasmas by means of NLTE techniques.
In this study, we perform quantum mechanical calculations of the electron-impact broadening parameters of Be II, Sr II, and Ba II ions within the framework of impact approximation theory. The key to these calculations is to choose the fully relativistic Dirac R-matrix methods to calculate electron-impact collision strength Ω(ε) of Be II, Sr II, and Ba II ions by using DARC codes (Norrington 2009). DARC is a fully relativistic package, considering relativistic effects both in the target states and the scattering study. The atomic structure parameters (i.e., the bound-electron orbitals, energy levels, etc.) of target states are computed with a General purpose Relativistic Atomic Structure Package (GRASP2, Dyall et al. 1989), partly improved by Duan et al. (2008). The rest of this paper is organized as follows. In Sect. 2, we outline the basic procedure before our calculations. In Sect. 3, we present results for the interesting lines in Be II, Sr II, and Ba II, and compare them with available experimental and theoretical results. The conclusions are summarized in Sect. 4.
2. Computational procedures
We present here an outline of our quantum mechanical formalism and the computational
procedure for linewidths and shifts of spectral lines for the sake of completeness. More
details have been offered in our previous electron-impact broadening works (2012a, b), so will not be repeated here. DARC is a fully
relativistic package that considers and calculates any atomic system in a
jj coupling scheme, and this leads us to write the dimensionless
collision strength Ω(ε) in the jj coupling scheme, which
is derived and obtained by Peach (1981):
![\begin{eqnarray} \Omega(\varepsilon) &=& \sum \limits_{J^{\tau}_{i} J^{\tau}_{f} jj^{\prime} \ell \ell\,^{\prime}} {1 \over 2}(-1)^{J_{i}+J_{i^{\prime}}+2{J^{\tau}_{f}}+ j+j^{\prime}} (2 J^{\tau}_{i}+1) \nonumber\\ &&\times (2 J^{\tau}_{f}+1) \left\{ \begin{array}{ccc } J^{\tau}_{f} & J^{\tau}_{i}& 1\\ J_{i} & J_{f}& j \end{array} \right\} \left\{ \begin{array}{ccc } J^{\tau}_{f} & J^{\tau}_{i}& 1\\ J_{i^{\prime}} & J_{f^{\prime}}& j^{\prime}\\ \end{array} \right\} \nonumber\\ &&\times\, \frac{1}{2} \left[ \delta _{\ell \ell{\prime}} \delta _{jj^{\prime}} \delta _{J_{i} J_{ i^{\prime}}} \delta_{J_{f} J_{f^{\prime}}}-S_{I} \left(J_{i^{\prime}} \ell^{\prime} j^{\prime}J^{\tau}_{i},J_{i} \ell j J^{\tau}_{i}\right)\right.\nonumber\\ &&\times \left. S^{*}_{F}\left(J_{f^{\prime}} \ell^{\prime} j^{\prime}J^{\tau}_{f},J_{f} \ell j J^{\tau}_{f}\right) \right] . \end{eqnarray}](/articles/aa/full_html/2013/07/aa21377-13/aa21377-13-eq19.png) (1)Where
the two coefficients of the type { ... } are the usual 6-j
symbols. The quantum numbers in a transition between lower and upper states of a target ion
(i.e., radiator) are Ji and
Jf, respectively, which
(Ji,
Jf) stand for the total angular momentum.
The quantum number of orbital angular momentum and total angular momentum of a colliding
electron are denoted by ℓ and j respectively, and all of
the quantum numbers of (N + 1)-electron colliding systems (colliding
electron+target ion) are denoted with the superscript “τ”.
SI and
SF (the superscript “*” represents the
complex conjugate matrix) are the scattering matrices of the upper and lower states,
respectively, and they are calculated under the same free energy ε of
colliding electrons. The expression for the quantum mechanical calculations of full width at
half maximum (FWHM) and shift of spectral lines by averaging over Maxwell distribution of
electron velocities is given below, which is similar to many authors (e.g., see Baranger
1958a–c; Bely & Griem 1970; Seaton 1988):
(1)Where
the two coefficients of the type { ... } are the usual 6-j
symbols. The quantum numbers in a transition between lower and upper states of a target ion
(i.e., radiator) are Ji and
Jf, respectively, which
(Ji,
Jf) stand for the total angular momentum.
The quantum number of orbital angular momentum and total angular momentum of a colliding
electron are denoted by ℓ and j respectively, and all of
the quantum numbers of (N + 1)-electron colliding systems (colliding
electron+target ion) are denoted with the superscript “τ”.
SI and
SF (the superscript “*” represents the
complex conjugate matrix) are the scattering matrices of the upper and lower states,
respectively, and they are calculated under the same free energy ε of
colliding electrons. The expression for the quantum mechanical calculations of full width at
half maximum (FWHM) and shift of spectral lines by averaging over Maxwell distribution of
electron velocities is given below, which is similar to many authors (e.g., see Baranger
1958a–c; Bely & Griem 1970; Seaton 1988):
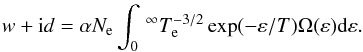 (2)Where
α = 2.8674 × 10-23 eV cm3,
Te (eV) is the electron temperature,
Ne(cm-3) the electron density, and
ε the energy of colliding electron in Rydbergs. In Eq. (2),
w corresponding to half half-width (i.e., a half of FWHM) and
d representing the shift of spectral lines, are expressed in eV units.
(2)Where
α = 2.8674 × 10-23 eV cm3,
Te (eV) is the electron temperature,
Ne(cm-3) the electron density, and
ε the energy of colliding electron in Rydbergs. In Eq. (2),
w corresponding to half half-width (i.e., a half of FWHM) and
d representing the shift of spectral lines, are expressed in eV units.
Our relativistic quantum mechanical calculations of width and shift of spectral lines in Be II, Sr II, and Ba II ions start with calculations of atomic structure data as a first ingredient. The atomic structure parameters of target ions are calculated with the nonrelativistic configurations 1s2nl(n ≤ 5,l ≤ 3), 1s22s22p63s23p63d104s24p6nl(n = 4,5,6,l ≤ 3 and n = 7,l ≤ 1), and 1s22s22p63s23p63d104s24p64d105s25p6nl(n = 4,5,l ≤ 3, n = 6,l ≤ 2 and n = 7,l ≤ 1), corresponding to Be II, Sr II, and Ba II ions, respectively. Their atomic structure parameters are read as part of the input of DARC package to construct the colliding system that consists of upper or lower states of the desired transition in target ion and a colliding electron.
In our present calculations, the colliding free electrons are constrained by two conditions. First, the quantum number of the orbital angular momentum is ℓ ≤ 21, and second, the total number of its continuum basis function for a given κ(κ = −ℓ − 1, if κ < 0, else κ = ℓ) is 30. To complete our numerical studies, we obtain K-matrices and their corresponding symmetry information of the colliding system by using DARC. Since the K-matrix is a function of incident electron energies, it is computed in an increasing energy sequence by repeating the same procedure for each considered ion. The energy increments for Be Ii, Sr II, and Ba II ions are, 0.008, 0.008, and 0.003 Rydberg, respectively. Thus the dimensionless collision strength as defined in Eq. (1) is obtained. The real (Re S) and imaginary (Im S) parts of the scattering S matrix are evaluated by using a new code developed by us, according to the expressions Re S = (1 − K2)/(1 + K2), Im S = 2 K/(1 + K2). Finally, the trapezoidal integration rule is taken to evaluate electron-impact broadening and shift parameters numerically.
3. Numerical results and discussion
3.1. Be II ion
Our relativistic quantum mechanical calculations in width and shift of spectral lines in Be II, Sr II, and Ba II ions start with calculations of their atomic structure data, which is performed through a fully relativistic GRASP2 code. The obtained relativistic atomic parameters are then read by the DARC package to construct the colliding system that consists of upper or lower states of the desired transition in the target ion and a colliding electron. In Be II ions, we calculated atomic structure data from the 13 nonrelativistic configurations 1s2nl (n ≤ 5,l ≤ 3) which give rise to 23 bound states. The lowest eight bound states are selected as the target states.
Comparison of electron-impact half half-widths w and shifts d of some transitions in Be II as a function of electron temperature Te at an electron density Ne = 1017 cm-3.
Our results of electron-impact widths and shifts in the eight Be II spectral lines at an electron density of 1017 cm-3 and for various electron temperatures are presented in Table 1, along with the available experimental and theoretical results. In Table 1, the experimental electron-impact widths and shifts in Be II lines are taken from the review article of Konjević & Wiese (1976) who critically reviewed the experimental results from Purić & Konjević (1972), Hadžiomerspahić et al. (1973), and Sanchez et al. (1973). Purić & Konjević (1972) compared their experimental results with the values from Griem’s semi-empirical formula (Griem 1968) and observed an apparent disagreement. Sanchez et al. (1973) measured and calculated the linewidth parameters for the Be II doublet transitions (3130.4219 Å, 3131.0667 Å) at Ne = 1017 cm-3 and Te = 1.9 × 104 K. The measured linewidths are 0.035 Å, which differs by less than 6%, while the calculated values obtained with the quantum mechanical and semiclassical calculations are 0.015 Å and 0.042 Å, respectively. The authors observed good agreement between the measured linewidths and the corresponding semiclassical calculations, whereas agreement with the quantum mechanical calculations is not better than a factor of 2. Hadžiomerspahić et al. (1973) measured the electron-impact linewidths and shifts of the same Be II doublet transitions, and found good agreement with the semiclassical calculations of Jones et al. (1972), as well as with predictions of semi-empirical formula of Griem et al. (1968). Hadžiomerspahić et al. (1973) also noted that Griem’s semi-empirical formula is useful and accurate for evaluation of isolated spectral lines of singly ionized earth alkaline metals. By adopting Eqs. (2.2), and (2.4) and Table 3 of Seaton’s works (1988), we derived the doublet linewidths to be 0.0143 Å for Te = 2.0 × 104 K. Thus, under an electron density of Ne = 1017 cm-3 and electron temperature of Te ≃ 2.0 × 104 K, it is obvious that our results for the doublet lines are about two times higher than the quantum mechanical calculations performed by both Sanchez et al. (1973) and Seaton (1988). Based on this analysis, one can see that our results for the doublet transitions are much closer to the available measurements of Sanchez et al. (1973), when compared with both the semiclassical calculations of Jones et al. (1972) and Sanchez et al. (1973).
Indeed, our present line widths of the resonance doublet of Be II show rather large differences from experimental values at all temperatures being considered, with the exception of the transition 3131.0667 Å at Te = 3.48 × 104 K, where the discrepancy amounts to 5%. If we compare our line widths with previous semiclassical and quantum calculations, our line widths seem much closer to the measured ones within 29% for all temperatures considered. Our calculated widths for the resonance doublet in Be II are smaller in magnitude than experimental values at three temperatures but 0.8 times higher for the component 3130.4219 Å at Te = 3.48 × 104 K. However, one can conclude that the agreement between current values and the measured line widths is quite good. We believe that new measurements of line widths of Be II spectral lines are required in order to update these experimental measurements and to address the worrying questions of disagreement between theory and experiment.
In Table 1, the measured shifts in resonance doublet components of Be II are compared with our results at Ne = 1017 cm-3. Regarding the comparison of line shifts, only two experimental measurements for the shift in resonance doublet lines of Be II were reported by Purić & Konjević (1972) and Hadžiomerspahić et al. (1973). Our line shifts for the resonance doublet at Te = 1.68 × 104 K are very similar to the experimental values within 7%, but show a large difference (46%) at Te = 3.48 × 104 K. Compared to our line shift of 2s 2S1/2 ← 2p 2Po1/2 at Te = 3.48 × 104 K, the semiclassical line shift obtained by Jones et al. (1972) is much closer to the experimental line shift of Hadžiomerspahić et al. (1973). On the other hand, our present line shift for the same line at Te = 1.68 × 104 K is much closer to the experimental value of Purić & Konjević (1972) than the line shift reported by Purić & Konjević (1972). More importantly, the present line shift values for Be II are of higher accuracies than the semi-empirical calculations by Purić & Konjević (1972) and semiclassical approach by Dimitrijević & Sahal-Bréchot (1993). Based on these comparisons, we can say that the present results of line widths and shift for spectral lines of Be II agree well with the available experimental and theoretical results, and are more reliable in typical astrophysical atmospheres.
3.2. Sr II ion
Four spectral lines (10 327.309, 10 036.654, 10 914.874, 4161.796 Å) of singly ionized strontium were employed for solar strontium abundance determinations by Lambert & Warner (1968). Therefore, the knowledge of electron-impact broadening of some Sr II spectral lines might be helpful in modeling and determining elemental abundances of hot stars, where electron-impact broadening is the dominant line-broadening mechanism. Moreover, for NLTE techniques and radiative transfer models in stellar plasmas, it is imperative that line-broadening parameters be determined accurately, but they are usually not known very well.
Some earlier interests in investigating the electron-impact widths and shifts of Sr II lines exist in the literature. A few experimental studies (Fleurier et al. 1977; Puric et al. 1972; Hadžiomerspahić et al. 1973) were devoted to determining these line-broadening parameters. Konjević & Wiese (1976) and Konjević et al. (1984) reviewed these experimental measurements of six Sr II lines (see Table 2). These results were obtained and compared with semiclassical theory (Fleurier et al. 1977 and references therein) at Ne = 1.3 × 1017 cm-3 and electron temperatures within the range 13 000–31 700 K. For the Sr II doublet resonance lines (4077.7 Å, 4215.5 Å), identical experimental results of Fleurier et al. (1977) have been listed in Table 2, because these doublet parameters do not differ by more than 5% according to Fleurier (private communication, see Konjevíc et al. 1984). In Table 2, we report electron-impact half half-widths w and shifts d for ten Sr II spectral lines at seven different electron temperatures and Ne = 1.0 × 1017 cm-3, along with the available experimental and theoretical results for the sake of comparison. From Table 2, we can see that our present widths of Sr II doublet resonance lines are in good agreement with the more accurate experimental results of Fleurier et al. (1977) within 13.6%. Our quantum line widths of the two principal resonance lines also show good agreement (1.3%) with the experimental widths of Hadžiomerspahić et al. (1973). Our results of line widths for Sr II lines are more closer to the experimental widths as compared to the semiclassical calculations of Fleurier et al. (1977). Unfortunately, comparison for other Sr II lines is impossible presently because no more experimental and other theoretical linewidth data exist in the literature.
For the shift in Sr II lines, there are large deviations from the experimental measurements except for the shift in two lines (4305.447 Å, 4161.796 Å), where the deviation does not exceed 20% and both the shifts agree well at 1.42 × 104 K. However, our results for line shifts are much closer to the experimental values when compared with semiclassical calculations of Fleurier et al. (1977). Nevertheless, we compared our result of line widths and shifts for Sr II spectral lines with other experimental data, and can conclude that our results for line widths and shifts in the case of most investigated Sr II resonance doublet are more accurate and much closer to the experimental values than the other theoretical results are. This comparison is highly satisfactory and in a way attests to the accuracy of our results. However, for the line shifts the disagreement is still large.
Comparison of electron-impact half half-widths w and shifts d of some transitions in Sr II as a function of electron temperature Te at an electron density Ne = 1017 cm-3.
Comparison of electron-impact half half-widths w and shifts d of some transitions in Ba II as a function of electron temperature Te at two different electron densities, i.e., Ne = 1017 cm-3 and 1.13 × 1017 cm-3.
3.3. Ba II ion
Dimitrijević & Sahal-Bréchot (1997) calculated the electron-impact line widths and shifts of 64 Ba II multiplets within the semiclassical perturbation approach for electron densities 1015−1018 cm-3 and electron temperatures within the ranges 5000–100 000 K. The linewidths of two Ba II lines (4554.033 Å, 4934.09 Å) calculated by Dimitrijević & Sahal-Bréchot (1997) show good agreement with high-precision experimental results of Fleurier et al. (1977). As for the comparison of line shifts for the same Ba II multiplets, line shifts obtained by Dimitrijević & Sahal-Bréchot (1997) agree with the experimental results of Purić & Konjević (1972). The experimental measurements of electron-impact widths of some Ba II lines reported by Platis˘a et al. (1971) agree with the experimental results of Jaeger (1969). On the theoretical side, Cooper & Oertel (1967) performed semiclassical calculations for Stark widths of Ba II lines by taking hyperbolic classical perturber trajectories and lower level broadening into account, but without specifying the electron temperature. The agreement between the theoretical calculations of Cooper & Oertel (1967) and experimental results of Jaeger (1969) is much better than the experimental widths of Platis˘a et al. (1971). The earlier calculations of electron-impact broadening widths and shifts for Ba II spectral lines within the semiclassical perturbation formalism were carried out by Sahal-Bréchot (1969b) and by Fleurier et al. (1977) within the same formalism but by taking the effects of Feshbach resonances into account. Purić et al. (1978) performed semiclassical calculations by using the semiclassical method described by Griem (1974). Newsemiclassical calculations with updated and optimized code performed by Dimitrijević & Sahal-Bréchot (1997) also agree well with semiclassical calculations by Cooper & Oertel (1967).
Table 3 presents our results of electron-impact
half half-widths w and shifts d for 10 Ba II spectral
lines at Ne = 1.0 × 1017 cm-3 and seven
different temperatures within the range 10 000–40 000 K. As described above, the available
measured and calculated half half-widths of Ba II spectral line are also given in Table
3 for comparison purposes. From Table 3, it is evident that a large disagreement exists
between our quantum calculations and experimentally measured (Fleurier et al. 1977; Hadžiomerspahić et al. 1973) half half-widths of Ba II lines. The situation is slightly better
with experimental results of Jaeger (1969), where
the ratio 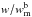 varies
between 0.52–0.82 and deviations does not exceed 44%. Our calculated half half-widths for
six Ba II lines are in better agreement with the results reported by Jaeger (1969) within 30%. There are only two lines
(4130.6491 Å, 4166.0014 Å) that show a maximum difference of 44% with the measured ones.
For Ba II multiplet 6141.713 Å, we found a large discrepancy between our present half
half-width and the experimental value reported by Fleurier et al. (1977). However, our half half-width for the other multiplet
(4554.033 Å) is 1.4 times larger (63%) than that of Fleurier et al. (1977). For these lines, the semiclassical half half-widths of
Dimitrijević & Sahal-Bréchot (1997) show
lower values than ours, and are much closer to Fleurier et al. (1977). If we now compare our widths with the semiclassical calculations
(wth), we find that the ratio
(w/wth) vary from
0.53–2.35. In other words, our quantum widths of Ba II lines are larger than the
predictions of semiclassical theory. We find good agreement for four lines (4524.926,
4899.927, 4166.0014, 4130.6491 Å) from Dimitrijević & Sahal-Bréchot (1997). According to this analysis, our half half-widths
of Ba II spectral lines agree with experimental results of Jaeger (1969) within a factor of two. We found that our half half-widths for
6141.713 Å and 4934.09 Å are about 2.6 and 1.6 times larger than those investigated by
Fleurier et al. (1977). It is perhaps not easy to
make a conclusion about the large discrepancy existing between our quantum theory and
experimental results since only two lines of Ba II were measured.
varies
between 0.52–0.82 and deviations does not exceed 44%. Our calculated half half-widths for
six Ba II lines are in better agreement with the results reported by Jaeger (1969) within 30%. There are only two lines
(4130.6491 Å, 4166.0014 Å) that show a maximum difference of 44% with the measured ones.
For Ba II multiplet 6141.713 Å, we found a large discrepancy between our present half
half-width and the experimental value reported by Fleurier et al. (1977). However, our half half-width for the other multiplet
(4554.033 Å) is 1.4 times larger (63%) than that of Fleurier et al. (1977). For these lines, the semiclassical half half-widths of
Dimitrijević & Sahal-Bréchot (1997) show
lower values than ours, and are much closer to Fleurier et al. (1977). If we now compare our widths with the semiclassical calculations
(wth), we find that the ratio
(w/wth) vary from
0.53–2.35. In other words, our quantum widths of Ba II lines are larger than the
predictions of semiclassical theory. We find good agreement for four lines (4524.926,
4899.927, 4166.0014, 4130.6491 Å) from Dimitrijević & Sahal-Bréchot (1997). According to this analysis, our half half-widths
of Ba II spectral lines agree with experimental results of Jaeger (1969) within a factor of two. We found that our half half-widths for
6141.713 Å and 4934.09 Å are about 2.6 and 1.6 times larger than those investigated by
Fleurier et al. (1977). It is perhaps not easy to
make a conclusion about the large discrepancy existing between our quantum theory and
experimental results since only two lines of Ba II were measured.
Our results of line shift for the three components (6141.713 Å, 5853.675 Å, 6496.89 Å) of
the multiplet (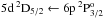 )
show good agreement with experimental measurements as compared to semiclassical
calculations (also see Table 3). Concerning
comparison of other line shifts, we find significant disagreement with the semiclassical
calculations of Dimitrijević & Sahal-Bréchot (1997) and with experimental results (Fleurier et al. 1977; Purić et al. 1978;
Hadžiomerspahić et al. 1973). Our calculated shift
for the line 4554.033 Å at Te = 1.30 × 104 K is
about three times higher than the high-precision line-shift measurement of Fleurier et al.
(1977). However, the agreement between the
measured line shifts and semiclassical calculations for the lines (4554.033 Å, 4934.09 Å,
and 3891.7790 Å) is much better than our quantum calculations. For Ba II line shifts, our
present quantum theory disagree significantly with the semiclassical approach, but agree
when only the signs are considered. Furthermore, the line shift calculations are less
accurate than the linewidth calculations due to mutual cancelation of positive and
negative contributions to the line shift values, especially if shift values are very small
as in our case of some Ba II lines. This is also true for experimental measurements, if
shift values are very small. Based on this analysis, we can say that agreement between our
calculated shifts for Ba II lines and the measured values as mentioned earlier is
satisfactory. We believe that new measurements for line broadening data of Ba II lines
will be used to update all these experimental results.
)
show good agreement with experimental measurements as compared to semiclassical
calculations (also see Table 3). Concerning
comparison of other line shifts, we find significant disagreement with the semiclassical
calculations of Dimitrijević & Sahal-Bréchot (1997) and with experimental results (Fleurier et al. 1977; Purić et al. 1978;
Hadžiomerspahić et al. 1973). Our calculated shift
for the line 4554.033 Å at Te = 1.30 × 104 K is
about three times higher than the high-precision line-shift measurement of Fleurier et al.
(1977). However, the agreement between the
measured line shifts and semiclassical calculations for the lines (4554.033 Å, 4934.09 Å,
and 3891.7790 Å) is much better than our quantum calculations. For Ba II line shifts, our
present quantum theory disagree significantly with the semiclassical approach, but agree
when only the signs are considered. Furthermore, the line shift calculations are less
accurate than the linewidth calculations due to mutual cancelation of positive and
negative contributions to the line shift values, especially if shift values are very small
as in our case of some Ba II lines. This is also true for experimental measurements, if
shift values are very small. Based on this analysis, we can say that agreement between our
calculated shifts for Ba II lines and the measured values as mentioned earlier is
satisfactory. We believe that new measurements for line broadening data of Ba II lines
will be used to update all these experimental results.
4. Conclusion
In this paper, we report electron-impact widths and shifts in spectral lines in singly ionized Be II, Sr II, and Ba II ions produced by electron impact within the framework of impact approximation theory. In our calculations, special attention was focused on experimental conditions (Ne = 1017 cm-3 and Te = 10 000−40 000 K), plasma diagnostics, and on an experimental data treatment. One aim of this work was to check some already existing electron-impact broadening parameters for singly ionized Be II, Sr II, and Ba II, and to provide new data by using our newly developed quantum technique. Under these plasma conditions, our results for line widths and shifts show very good agreement with other theoretical results and are much closer to the experimental measurements. From Table 3, it can be seen that there are some substantial differences between present line-broadening data and existing experimental results for Ba II lines. This is particularly significant in the case of line shifts of Ba II lines (4554.033 Å, 4934.09 Å, and 3891.7790 Å), where large differences exist. However, our line widths and shifts show good agreement with the most relevant previous experimental works and semiclassical predictions. The comprehensive analysis performed for the widths and shift for all the lines emerging from the three ions attests to the quality of the present calculations.
Nevertheless, the present line-broadening parameters certainly contribute to increasing the available theoretical information, which is imperative for NLTE elemental abundance analysis in solar and stellar atmospheres. Obviously, all the existing data for these ions does not represent a statistically significant data set that would allow us to test the agreement between experiment and various theories. More experiments with very different plasma conditions will be required to provide both this level of information and complete quantum mechanical calculations of heavy elements like Sr and Ba. Finally, we believe that our results are useful for new plasma diagnostics in laboratory astrophysical purposes, i.e., for the stellar spectroscopy and stellar synthesis, stellar plasma investigations, modeling, and the abundance studies of stellar atmospheres.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 11275029 and No. 11204017) and also supported by the Foundation for the Development of Science and Technology of Chinese Academy of Engineering Physics (Grant No. 2011A0102007). Dr. M. A. Bari acknowledges the support by the Chinese Academy of Sciences Fellowship for Young International Scientists.
References
- Alecian, G., Michaud, G., & Tully, J. 1993, ApJ, 411, 822 [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Andrievsky, S. M., Spite, F., Korotin, S. A., et al. 2009, A&A, 494, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Spite, F., Korotin, S. A., et al. 2011, A&A, 530, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Lépine, J. R. D., Korotin, S. A., et al. 2013, MNRAS, 428, 3252 [NASA ADS] [CrossRef] [Google Scholar]
- Balachandran, S. C., & Bell, R. A. 1998, Nature, 392, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Baranger, M. 1958a, Phys. Rev., 111, 481 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baranger, M. 1958b, Phys. Rev., 111, 494 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baranger, M. 1958c, Phys. Rev., 112, 855 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 2000, MNRAS, 311, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Bely, O., & Griem, H. R. 1970, Phys. Rev. A, 1, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., Hansen, C. J., Bautista, M., & Ruchti, G. 2012, A&A, 546, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cooper, J., & Oertel, G. K. 1967, Phys. Rev. Lett., 18, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Dimitrijević, M. S., & Sahal-Bréchot, S. 1992, J. Quant. Spectrosc. Radiat. Transfer, 48, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Dimitrijević, M. S., & Sahal-Bréchot, S. 1993, Pub. Obs. Astron. Belgrade, 44, 59D [NASA ADS] [Google Scholar]
- Dimitrijević, M. S., & Sahal-Bréchot, S. 1997, A&ASS, 122, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dimitrijević, M. S., Ryabchikova, T., Simić, Z., Popović, L. Č., & Dačić, M. 2007, A&A, 469, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobrovolskas, V., Kučinskas, A., Andrievsky, S. M., et al. 2012, A&A, 540, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duan, B., Bari, M. A., Zhong, J. Y., et al. 2008, A&A, 488, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duan, B., Bari, M. A., Wu, Z. Q., et al. 2012a, A&A, 547, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duan, B., Bari, M. A., Wu, Z. Q., Yan, J., & Li, Y. M. 2012b, Phys. Rev. A, 65, 052565 [Google Scholar]
- Dyall, K. G., Grant, I. P., Johnson, C. T., Parpia, F. A., & Plummer, E. P. 1989, Comput. Phys. Commun., 55, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Elabidi, H., Ben Nessib, N., Cornille, M., Dubau, J., & Sahal-Bréchot, S. 2008, J. Phys. B, 41, 5702 [NASA ADS] [CrossRef] [Google Scholar]
- Fleurier, C., Sahal-Bréchot, S., & Chapelle, J. 1977, J. Quant. Spectrosc. Radiat. Transfer, 17, 595 [Google Scholar]
- Gilmore, G., Edvardsson, B., & Nissen, P. E. 1991, ApJ, 378, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Goldberg, L., Müller, E. A., & Aller, L. H. 1960, ApJS, 5, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Griem, H. R. 1968, Phys. Rev., 165, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Griem, H. R. 1974, Spectral Line Broadening by Plasma (NewYork, USA: Academic press) [Google Scholar]
- Hadziomerspahic, D., Platisa, M., Konjević, N., & Popovic, M. 1973, Z. Phys., 262, 169 [Google Scholar]
- Jaeger, H. 1969, Z. Phys., 223, 19 [Google Scholar]
- Jones, W. W., Benett., S. M., & Griem., H. R. 1971, Tech. Rep. No. 71–128, Univ. of Maryland, College Park, Maryland [Google Scholar]
- Jones, W. W., Sanchez, A., Grieg, J. R., & Griem, H. R. 1972, Phys. Rev. A, 5, 2318 [NASA ADS] [CrossRef] [Google Scholar]
- Komarov, N. S., & Basak, N. Yu., 1993, Astron. Zh., 70, 111 [NASA ADS] [Google Scholar]
- Konjević, N., & Wiese, W. L. 1976, J. Phys. Chem. Ref. Data, 5, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Konjević, N., Dimitrijević, M. S., & Wiese, W. L. 1984, J. Phys. Chem. Ref. Data, 13, 649 [Google Scholar]
- Lambert, D. L., & Warner, B. 1968, MNRAS, 140, 197 [NASA ADS] [Google Scholar]
- Mashonkina, L., Gehren, T., & Bikmaev, I. 1999, A&A, 343, 519 [NASA ADS] [Google Scholar]
- Norrington, P. 2009, DARC manual, http://www.am.qub.ac.uk /users/p.norrington [Google Scholar]
- Peach, G. 1981, Adv. Phys. A, 30, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Platiša, M., Puric, J., Konjevic, N., & Labat, J. 1971, A&A, 15, 325 [NASA ADS] [Google Scholar]
- Przybilla, N., Butler, K., Becker, S. R., & Kudritzki, R. P. 2006, A&A, 445, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Purić, J., & Konjević, N. 1972, Z. Phys., 249, 440 [Google Scholar]
- Purić, J., Dimitrijević, M. S., & Lakićević, I. S. 1978, Phys. Lett. A, 67, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Rauch, T., Ziegler, M., Werner, K., et al. 2007, A&A, 470, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahal-Bréchot, S. 1969a, A&A, 1, 91 [Google Scholar]
- Sahal-Bréchot, S. 1969b, A&A, 2, 322 [Google Scholar]
- Sanchez, A., Blaha, M., & Jones, W. W. 1973, Phys. Rev. A, 8, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 1988, J. Phys. B, 21, 3033 [NASA ADS] [CrossRef] [Google Scholar]
- Tankosić, D., Popović, L. Č, & Dimitrijević, M. S. 2003, A&A, 399, 795 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zethson, T., Gull, T. R., Hartman, H., et al. 2001, ApJ, 122, 322 [Google Scholar]
All Tables
Comparison of electron-impact half half-widths w and shifts d of some transitions in Be II as a function of electron temperature Te at an electron density Ne = 1017 cm-3.
Comparison of electron-impact half half-widths w and shifts d of some transitions in Sr II as a function of electron temperature Te at an electron density Ne = 1017 cm-3.
Comparison of electron-impact half half-widths w and shifts d of some transitions in Ba II as a function of electron temperature Te at two different electron densities, i.e., Ne = 1017 cm-3 and 1.13 × 1017 cm-3.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


