| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321583 | |
| Published online | 10 June 2013 | |
Detectability of small-scale magnetic fields in early-type stars
1 Department of Physics and Astronomy, Uppsala University, Box 516, 75120 Uppsala, Sweden
e-mail: oleg.kochukhov@fysast.uu.se
2 Sobolev Astronomical Institute, Saint Petersburg State University, Universitetskij pr. 28, Staryj Peterhof, 198504 Saint Petersburg, Russia
Received: 27 March 2013
Accepted: 3 May 2013
Context. Strong, globally-organized magnetic fields are found for a small fraction of O, B, and A stars. At the same time, many theoretical and indirect observational studies have suggested the ubiquitous presence of weak localized magnetic fields at the surfaces of massive stars. However, no direct detections of such fields have been reported yet.
Aims. We have carried out the first comprehensive theoretical investigation of the spectropolarimetric observational signatures of the structured magnetic fields. These calculations are applied to interpret null results of the recent magnetic surveys of massive stars.
Methods. The intensity and circular polarization spectra of early-type stars were simulated using detailed polarized radiative transfer calculations with LTE model atmospheres. Similar to observational analyses, the mean Stokes I and V line profiles were obtained by applying a multiline averaging technique. Different spectropolarimetric observables were examined for multiple realizations of randomly distributed radial magnetic field spots on different spatial scales.
Results. We characterize the amplitude of the circular polarization profiles and the mean longitudinal magnetic field as a function of magnetic spot sizes. The dependence of these observables on the effective temperature, projected rotational velocity, and inclination angle is also investigated. Using results of the recently completed Magnetism in Massive Stars (MiMeS) survey, we derive upper limits on the small-scale magnetic fields compatible with the MiMeS nondetections.
Conclusions. According to our simulations, existing spectropolarimetric observations of sharp-lined massive stars rule out the presence of any small-scale fields stronger than 50–250 G, depending on the typical spot sizes. For broad-lined stars, the observations constrain such fields to being below approximately 1 kG.
Key words: stars: early-type / stars: magnetic field / starspots / polarization
© ESO, 2013
1. Introduction
There is a growing observational and theoretical support for a magnetic dichotomy among intermediate-mass and massive stars. A small fraction of the late-B and A stars possesses strong organized magnetic fields at their surfaces (see reviews by Donati & Landstreet 2009; Mathys 2009; Kochukhov 2011). These magnetic field topologies are approximately dipolar for the majority of stars and are often inclined relative to the stellar rotational axis, and have strengths of up to ~30 kG. The global magnetic fields of intermediate-mass stars are believed to be stable fossil remnants of the magnetic flux acquired at the stellar formation phase (Braithwaite & Nordlund 2006). These fields exhibit a lower threshold of ~300 G, below which the large-scale magnetic topologies are probably not able to withstand the shearing by the differential rotation (Aurière et al. 2007).
The incidence of fossil stellar magnetic fields is now understood to extend well into the mass range of early-B and O stars. The Magnetism in Massive Stars (MiMeS; Wade et al. 2011a) survey and other studies (Wade et al. 2006; Hubrig et al. 2011) have identified several examples of O stars with globally-organized, kG-strength magnetic fields. These discoveries are particularly frequent among the so-called Of?p stars (Martins et al. 2010; Wade et al. 2011b, 2012a), which appear to represent a massive-star extension of the Ap/Bp phenomenon. Remarkably, magnetic fields existing on the surface of some of these peculiar O stars exceed 20 kG (Wade et al. 2012c), rivaling the strongest fields found in much smaller Ap/Bp stars.
In addition to the strong, large-scale magnetic fields found for a handful of massive stars, there is a substantial indirect observational evidence and credible theoretical predictions of localized, and probably weak, magnetic fields in the majority of massive stars. Much of the indirect support for such fields is coming from various poorly understood wind and surface variability phenomena. For example, nearly all O-type stars and many B stars show unexplained cyclical variability in their winds (Kaper et al. 1996; Fullerton et al. 1996; Prinja et al. 2002). The most prominent feature of this variability is discrete absorption components (DACs), which are observed to accelerate through the UV-wind line profiles and maintain coherency over several stellar rotations. These features are probably caused by corotating interacting regions (CIRs) in the line-driven stellar wind, as proposed by Mullan (1984). In this model, a faster moving stream collides with a slow moving one, leading to the formation of curved large-scale structure in the stellar wind. The modeling by Cranmer & Owocki (1996) demonstrated that such wind structures give rise to DACs in the wind-sensitive UV line profiles. The velocity contrast required by this model arises from perturbations at the photospheric level, which may be connected to evolving small-scale magnetic spots.
An example of the compelling observational evidence of this connection between DACs and a magnetic field was provided by the long-term monitoring of the magnetic early-O star θ1 Ori C. Henrichs et al. (2005) show that 13 years of the C iv UV profile observations of this star, phase-folded with the 15.4 d rotational period, show a progressing absorption feature very similar to individual DACs observed in other early-type stars. The star θ1 Ori C is an oblique rotator with a stable dipolar magnetic field (Donati et al. 2002; Wade et al. 2006), so the feature in the UV wind lines reoccurs exactly at the same rotational phase, which is associated with one of the magnetic poles. Using this well-studied O-star as an example, one can suspect magnetic field to be the main culprit of the surface perturbations leading to DACs in other massive stars.
A considerable theoretical effort has been devoted to investigating various alternatives to the fossil magnetism of early-type stars. Massive stars generate strong magnetic fields in their convective cores (Brun et al. 2005), but these fields do not reach the stellar surface on observable time scales (MacGregor & Cassinelli 2003). A dynamo process operating in the differentially rotating radiative stellar interiors (Spruit 2002) can also produce magnetic fields emerging on the stellar surface (Mullan & MacDonald 2005). The reality of this particular magnetic-field generation mechanism, which has important implications for the evolution of massive stars (Maeder & Meynet 2005) and their descendants (Heger et al. 2005), however has been disputed by Zahn et al. (2007). Finally, recent stellar structure calculations of hot massive stars have suggested the presence of subsurface convectively unstable regions related to the iron opacity peak (Cantiello et al. 2009). By analogy with the turbulent magneto-convection operating in other astrophysical environments (e.g. Käpylä et al. 2008), these subsurface convection zones (SCZ) can produce magnetic fields in the presence of shear and stellar rotation and can provide an attractive framework for the explanation of other massive-star atmospheric phenomena, including excessive micro- and macroturbulent line broadening (Hunter et al. 2008) and stochastic nonradial oscillations (Degroote et al. 2010). Preliminary MHD simulations by Cantiello et al. (2011) confirm the ability of SCZ to generate localized magnetic fields visible at the stellar surface. The properties of such fields and associated brightness spots have been further investigated analytically by Cantiello & Braithwaite (2011).
Simultaneously with these developments for massive stars, the discovery of sub-G magnetic fields in the brightest intermediate-mass stars Vega (Lignières et al. 2009) and Sirius (Petit et al. 2011) hints at the hidden magnetism of normal A and late-B stars. In response to these findings, Braithwaite & Cantiello (2013) have developed a theoretical model of the dynamically evolving “failed” fossil magnetic fields, which are expected to be much weaker and structured on smaller scales than the well-known stable fossil fields of the magnetic Ap/Bp stars.
Despite an emerging interest in probing the small-scale magnetism of early-type stars and exploring the consequences for the stellar physics, the current theoretical models have not reached the level of sophistication and detail necessary for making meaningful predictions about the strengths and topologies of the localized magnetic fields in individual stars. Therefore, a gap currently exists between observational constraints, e.g., detections of the polarization signatures for Sirius and Vega and nondetections of the magnetic fields for most O- and B-type stars included in the MiMeS survey, and theoretical predictions. In particular, it is unknown which direct observational signatures of small-scale fields one can expect in the polarization spectra of the early-type stars and how the amplitude and variability of these features change with the characteristics of magnetic field and with the stellar parameters.
Even the very ability of modern spectropolarimetric methods to detect localized magnetic features on the stellar surfaces is a matter of debate. On the one hand, a contribution of the small-scale fields to the disk-integrated polarization spectra and to the resulting magnetic observables might be strongly reduced by the cancellation of different field polarities. On the other hand, high-resolution studies of polarization signatures inside spectral line profiles partly overcome this problem thanks to the rotational Doppler resolution of the stellar surface (Semel 1989). The interplay of the cancellation vs. Doppler resolution and its dependence on the stellar rotation and sizes of magnetic features has not been systematically investigated.
The goal of our study is to address several of these issues through a comprehensive and realistic numerical simulations of the circular polarization spectra corresponding to the small-scale magnetic fields of different degree of complexity. In the following, we describe the methodology of the magnetic spectrum synthesis and multiline analysis of the theoretical Stokes V spectra (Sect. 2), present a summary of the simulation results for a wide range of stellar and magnetic field parameters (Sect. 3), and then use these data to constrain the strength of possible small-scale stellar magnetic fields by comparing our predictions with the outcome of recent magnetic field surveys of massive stars (Sect. 4).
2. Methods
Two main spectropolarimetric observational techniques are currently being used in the context of large-scale magnetic field surveys of early-type stars. The low-resolution circular spectropolarimetry, using e.g. the FORS1/2 instrument at the ESO VLT, detects magnetic field by measuring the mean longitudinal magnetic field in the wings of the hydrogen Balmer lines or in the unresolved blends of metal lines (Bagnulo et al. 2002; Wade et al. 2007; Hubrig et al. 2011; Bagnulo et al. 2012). This technique is only sensitive to the line-of-sight magnetic field component integrated over the visible stellar hemisphere and is poorly suited to providing constraints on intermittent, small-scale magnetic structures. Furthermore, flexures and calibration problems of the Cassegrain-mounted polarimeters, such as FORS1/2, limit their usefulness for the search for a very weak magnetic field (see discussion in Bagnulo et al. 2012).
The second common magnetic field detection technique relies on obtaining high-resolution circular polarization spectra covering a wide wavelength range and applying a line-averaging technique to combine information from all suitable metal absorption features. This approach is adopted by the MiMeS survey for the analysis of circular polarization spectra obtained with ESPaDOnS, NARVAL, and HARPSpol spectropolarimeters (Grunhut et al. 2009; Alecian et al. 2011; Neiner et al. 2012). The mean Stokes V line profiles obtained with the least-squares deconvolution (LSD) method (Donati et al. 1997) are particularly useful for the magnetic field diagnostic since they behave similarly to real spectral lines (Kochukhov et al. 2010) and allow one to characterize and model spectrally resolved Zeeman signatures. The LSD profiles are therefore sensitive even to the field topologies that yield very low or null mean longitudinal fields (e.g. Shultz et al. 2012). The LSD method has been successfully used to detect and map complex dynamo-generated magnetic fields of cool active stars (Donati et al. 2003; Kochukhov et al. 2013).
The goal of our study is to characterize observational signatures of the magnetic fields that are at least as complex topologically as the surface magnetic structures found for cool active stars. As a result, the high-resolution spectropolarimetry combined with a multiline analysis appears to be the most suitable methodology for our investigation. More specifically, we have simulated the LSD Stokes I and V profiles for magnetic field geometries of varying degrees of complexity and have studied these polarization profiles as a function of the magnetic and stellar parameters. The following sections describe computation of the local LSD line profiles, explain how we generate random magnetic field maps, and perform surface integration. Finally, we discuss derivation of different spectropolarimetric observables from the resulting disk-integrated polarization profiles.
2.1. Local polarized line profiles
The analysis of the LSD profiles of early-type stars presented in previous spectropolarimetric studies relied on a simplified analytical description of the intensity and circular polarization profile shapes. The most common assumption is to describe Stokes I as a Gaussian and Stokes V as its scaled derivative (e.g. Petit & Wade 2012). Although straightforward to implement, this approach suffers from ambiguities in the choice of an analytical line profile model and its parameters, and is unable to properly describe the temperature dependence of the local line profile characteristics. Moreover, averaging over a small number of diagnostic lines available in the optical spectra of early-type stars does not necessarily yield a simple, symmetric Stokes I profile that could be described by an analytical function. Here we avoid these problems by numerically deriving the local LSD profiles from detailed polarized radiative transfer calculations of individual spectral lines.
The local Stokes I and V line profile tables were prepared by first computing the full local spectra covering the 4000–8000 Å wavelength range with the synmast polarized radiative transfer code and then applying the LSD line averaging procedure. A detailed description of the relevant computer codes and methodology required for this analysis can be found in our previous publications (Kochukhov et al. 2010).
The spectrum synthesis calculations were performed for five atlas9 LTE model atmospheres (Kurucz 1993) with Teff in the range from 10 000 to 30 000 K with a step of 5000 K. For all models we adopted the surface gravity of log g = 4.0 and microturbulent velocity of 2 km s-1. The atomic line data were extracted from the VALD database (Kupka et al. 1999), using the 1% line depth selection threshold and the same microturbulent velocity. The spectral regions containing the hydrogen and helium lines were subsequently excluded from the input line lists.
The local Stokes IV parameters and the unpolarized continuum intensity Ic were computed for a grid of 20 limb angles θ, distributed equidistantly with μ = cosθ, and for the two values of local magnetic field strength, B = 0 and 0.5 kG. For the radial magnetic field geometries considered below, the line-of-sight magnetic field component required for the polarized spectrum synthesis is given by Bz = Bμ, independently of the distribution of magnetic features over the stellar surface. For all spectrum synthesis calculations, we employed a microtubulence of 2 km s-1, consistently with the choice of model atmospheres and the VALD line list extractions.
 |
Fig. 1 Normalized disk-center LSD Stokes I and V profiles for different effective temperatures and a line-of-sight magnetic field of 0.5 kG. The Stokes V spectra are offset vertically by 1.05 and expanded by a factor of 5. |
In the next step, the local Stokes I(λ,μ,B) and V(λ,μ,B) spectra were normalized by the corresponding continuum intensity Ic(λ,μ) and convolved with the instrumental profile corresponding to the resolution of R = 65 000, appropriate for the ESPaDOnS and NARVAL spectropolarimeters. The resulting spectra were converted to the local LSD profiles, ILSD(v,μ,B) and VLSD(v,μ,B), by applying the least-squares deconvolution procedure to a subset of spectral lines deeper than 10% of the continuum. Simultaneously, the mean continuum intensity 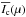 was established by averaging Ic(λ,μ) in the central wavelengths of the spectral lines included in the LSD masks. The LSD profiles were computed on a fine velocity grid with a step of 0.5 km s-1 covering the ± 500 km s-1 velocity range to ensure an accurate surface integration for vesini of up to 250 km s-1.
was established by averaging Ic(λ,μ) in the central wavelengths of the spectral lines included in the LSD masks. The LSD profiles were computed on a fine velocity grid with a step of 0.5 km s-1 covering the ± 500 km s-1 velocity range to ensure an accurate surface integration for vesini of up to 250 km s-1.
Table 1 summarizes statistics of the line lists used for the spectrum synthesis and LSD profile calculations. Depending on the temperature, we used 1500–2600 lines for the spectrum synthesis and up to ≈400 lines for LSD. The mean wavelength λ0, effective Landé factor 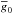 , and line depth d0 of the LSD masks are reported in the last three columns of Table 1. The same mean parameters were used to renormalize the LSD weights for each Teff as described by Kochukhov et al. (2010).
, and line depth d0 of the LSD masks are reported in the last three columns of Table 1. The same mean parameters were used to renormalize the LSD weights for each Teff as described by Kochukhov et al. (2010).
Examples of the local disk-center LSD Stokes I and V profiles for Teff = 10 000, 20 000, and 30 000 K are presented in Fig. 1. The strongest LSD profiles are obtained for low Teff. The line width systematically increases towards higher temperatures. The local Stokes parameter line shapes are not exactly symmetric and contain weak features outside the main profiles owing to blends unaccounted for in the LSD mask and to the limitations of the line-averaging procedure itself. These LSD profile distortions are, of course, also present in observations but cannot be described by an analytical line profile model.
Characteristics of the line lists used for synthetic LSD profile calculations.
 |
Fig. 2 Examples of random distributions of radial magnetic field spots with filling factor fsp = 0.5 and rsp = 10° (left panel) and 2° (right panel). In each case the star is shown at nine rotational phases and inclination angle i = 60°. The white and black regions correspond to the spots with positive and negative field polarity, respectively. The gray areas are field-free. |
2.2. Disk-integrated spectra for random magnetic fields
Many different mathematical models can be used to construct small-scale magnetic field distributions on the stellar surfaces. Here we employ a simple formulation that requires a few arbitrary parameters but still maintains sufficient physical realism. In the following we assume that the stellar magnetic field topology is given by a superposition of randomly distributed circular spots. The field inside the spots is purely radial, by analogy with sunspots, and is characterized by a single value of the magnetic field modulus. Outside the spots the photosphere is assumed not to be magnetic. An equal number of spots with the outward- and inward-directed radial field is used, thus maintaining the zero net magnetic flux over the stellar surface. The average properties of such magnetic field distributions are defined by three parameters: the spot angular radius rsp, the field strength Bsp inside the spots, and the fraction of the stellar surface fsp covered by the magnetic field (a filling factor).
 |
Fig. 3 Disk-integrated normalized LSD Stokes I and V profiles for vesini = 10 km s-1 and a random distribution magnetic spots with rsp = 10°. Other parameters are Teff = 20 000 K, i = 60°, and magnetic filling factor fsp = 0.5. The spectra corresponding to different rotational phases are offset vertically. |
 |
Fig. 4 LSD Stokes I and V profiles computed with the same magnetic map and setup as in Fig. 3, except for vesini = 100 km s-1. |
Once rsp is set, the area of each spot can be computed as 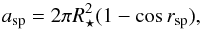 (1)and the total number of spots for a given fsp can be estimated by rounding
(1)and the total number of spots for a given fsp can be estimated by rounding 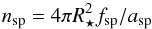 (2)to the nearest even integer. Then, the latitudes χ ∈ [ − π/2,π/2] and longitudes ϕ ∈ [0,2π] of the spot centers are obtained from
(2)to the nearest even integer. Then, the latitudes χ ∈ [ − π/2,π/2] and longitudes ϕ ∈ [0,2π] of the spot centers are obtained from 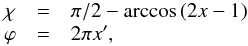 (3)where x and x′ represent two different sequences of uniformly distributed random numbers in the range between 0 and 1. This algorithm of the random spot position generation may produce overlapping spots. In practice, we allowed the spots to overlap by no more than 10% of their area, rejecting spot coordinates too close to the already existing spots.
(3)where x and x′ represent two different sequences of uniformly distributed random numbers in the range between 0 and 1. This algorithm of the random spot position generation may produce overlapping spots. In practice, we allowed the spots to overlap by no more than 10% of their area, rejecting spot coordinates too close to the already existing spots.
The local Stokes I line profiles in Fig. 1 have a full width at half maximum of δv = 8–14 km s-1. The corresponding approximate theoretical spatial resolution limit can be estimated as 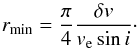 (4)Using δv = 10 km s-1, we can simplify this expression to rmin = 900/vesini. This indicates that an isolated surface feature with rsp = 4.5° is fully resolved for vesini = 200 km s-1. Using this estimate as guideline, we considered the spot sizes 2, 5, 10, 20, and 40°. An intermediate magnetic filling factor fsp = 0.5 was adopted for the majority of calculations. The corresponding total spot numbers varied from 4 (for rsp = 40°) to 1642 (for rsp = 2°).
(4)Using δv = 10 km s-1, we can simplify this expression to rmin = 900/vesini. This indicates that an isolated surface feature with rsp = 4.5° is fully resolved for vesini = 200 km s-1. Using this estimate as guideline, we considered the spot sizes 2, 5, 10, 20, and 40°. An intermediate magnetic filling factor fsp = 0.5 was adopted for the majority of calculations. The corresponding total spot numbers varied from 4 (for rsp = 40°) to 1642 (for rsp = 2°).
Numerically, magnetic maps were evaluated on the spherical surface grid containing 15130 zones of roughly equal areas (see Fig. 5 in Piskunov & Kochukhov 2002). This fine surface grid was required to properly resolve the spots on the smallest spatial scales. An example of the random magnetic spot distributions computed for rsp = 10 and 2° is illustrated in Fig. 2.
After establishing a surface magnetic field map, we computed the disk-integrated Stokes I and V LSD profiles, ⟨ ILSD ⟩ and ⟨ VLSD ⟩, by appropriate interpolation and weighted summation of the Doppler-shifted local LSD Stokes profiles for a specific inclination angle i and projected rotational velocity vesini. The line profiles were simulated for 20 equidistant rotational phases, using a velocity grid with 1.8 km s-1 step size. All calculations presented below were performed for the vesini values of 10, 20, 50, 100, and 200 km s-1.
An example of the phase variation of the circular polarization profiles for the random magnetic field distribution with rsp = 10° and fsp = 0.5 (the same as shown in the left panel of Fig. 2) is given in Figs. 3 and 4. These figures illustrate the line profiles computed for identical surface maps and the same set of viewing geometries, but for different projected rotational velocities. As expected, a higher projected rotational velocity (Fig. 4) reveals much more complex circular polarization profile shapes thanks to the Doppler resolution of the stellar surface. At the same time, the amplitude of the Stokes V signatures is also considerably reduced compared to the low vesini case (Fig. 3).
All our calculations were performed for the 0.5 kG field strength inside magnetic spots. Since here we deal with the magnetic line formation in the weak-field regime, it can be assumed that the Stokes V profiles and all resulting spectropolarimetric observables scale linearly with the magnetic field strength. Consequently, after verifying this behavior for the local Stokes V LSD profiles, we did not vary the field strength inside magnetic spots in any of the numerical experiments presented in this paper.
2.3. Magnetic observables
The main goal of our study is to assess the capability of recent high-resolution spectropolarimetric surveys of early-type stars to detect intermittent magnetic fields on their surfaces. Consequently, we consider the amplitude of the Stokes V signatures resulting from our numerical line profiles simulations as the primary magnetic field observable. For each set of circular polarization profiles we calculated the mean peak-to-peak Stokes V amplitude Vmean by averaging the instantaneous amplitude over 20 rotational phases. We also determined the maximum amplitude Vmax by finding the rotational phase with the largest circular polarization signature. To obtain statistically meaningful results with our random magnetic spot models, we averaged both Vmean and Vmax over 100 different random realizations of the magnetic field distributions for the same rsp and fsp. These calculations were repeated for a grid of five rsp and five vesini values (see above), yielding 50 000 individual synthetic line profiles for each Teff, fsp, i combination.
In addition to considering the amplitude of the Stokes V signatures, we introduced another parameter nz to characterize the complexity of the circular polarization profiles. This (integer) number was established by counting how many times a given Stokes V profile intersects the zero line. This parameter also roughly corresponds to the number of lobes in the Stokes V profile minus one. The final mean nz reported below for each rsp-vesini combination was obtained by computing the median over 20 rotational phases and 100 random map realizations. We found that this simple diagnostic exhibits a smooth variation with stellar parameters and readily distinguishes complex and simple polarization signatures. For example, for the magnetic spot distribution with rsp = 10° illustrated in Fig. 2, nz gradually increases from two for vesini = 10 km s-1 (line profiles in Fig. 3) to nine for vesini = 100 km s-1 (line profiles in Fig. 4).
 |
Fig. 5 Mean longitudinal magnetic field and the LSD Stokes V profile amplitude as a function of the magnetic spot radius and projected rotational velocity. These calculations were carried out for Teff = 20 000 K and magnetic filling factor fsp = 0.5. The top panels show maximum | ⟨ Bz ⟩ | for a sample of 20 rotational phases (top left) and | ⟨ Bz ⟩ | averaged over this set of rotational phases (top right). The bottom panels illustrate the corresponding maximum (bottom left) and mean (bottom right) circular polarization amplitude. Each point in this plot was computed by averaging over 100 different random realizations of the magnetic spot distributions. |
For completeness, we also determined the mean longitudinal magnetic field ⟨ Bz ⟩ from each pair of the disk-integrated Stokes I and V profiles. This was accomplished using the equation 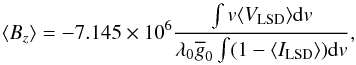 (5)where λ0 in Å and the resulting ⟨ Bz ⟩ is in G. The mean wavelength λ0 and effective Landé factor
(5)where λ0 in Å and the resulting ⟨ Bz ⟩ is in G. The mean wavelength λ0 and effective Landé factor 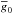 are the same parameters as applied above for normalizing the LSD line weights (see Table 1). Similar to the analysis of the Stokes V amplitude, the maximum and mean unsigned longitudinal magnetic fields, | ⟨ Bz ⟩ | max and | ⟨ Bz ⟩ | mean, were first obtained from a set of theoretical spectra computed for 20 rotational phases and then averaged over 100 different random realizations of the magnetic field maps with the same rsp and fsp.
are the same parameters as applied above for normalizing the LSD line weights (see Table 1). Similar to the analysis of the Stokes V amplitude, the maximum and mean unsigned longitudinal magnetic fields, | ⟨ Bz ⟩ | max and | ⟨ Bz ⟩ | mean, were first obtained from a set of theoretical spectra computed for 20 rotational phases and then averaged over 100 different random realizations of the magnetic field maps with the same rsp and fsp.
3. Results
Our main set of the line profile calculations for different rsp and vesini was generated by assuming Teff = 20 000 K, i = 60°, and fsp = 0.5. Here we present results obtained with this combination of parameters and then assess the impact of changing the effective temperature, inclination angle, and the filling factor. In all cases calculations were performed for Bsp = 500 G.
The mean longitudinal magnetic field and the amplitude of the Stokes V profiles are plotted as a function of the magnetic spot size and projected rotational velocity in Fig. 5. We illustrate the maximum | ⟨ Bz ⟩ | and the largest polarization amplitude that might be expected for the observations with a dense phase coverage (left column) and the phase-averaged values of these observables, representative of snapshot observations (right column).
 |
Fig. 6 Number of intersections of the zero line in the Stokes V profiles as a function of the magnetic spot radius and projected rotational velocity. Each point is a median computed over 20 rotational phases and 100 different random realizations of magnetic spot distributions. |
As one can see from the upper panels of Fig. 5, the maximum longitudinal magnetic field changes from ~10 G for rsp = 2° to 150–180 G for rsp = 40°. The corresponding | ⟨ Bz ⟩ | mean is approximately two times smaller. There is a small variation of | ⟨ Bz ⟩ | with vesini, which is not expected for the purely geometrical definition of this magnetic parameter. This vesini dependence is real and is explained by the presence of weak structures in the local LSD Stokes spectra outside main line profiles (see Fig. 1). These structures contribute differently to the disk-integrated profiles depending on the range of rotational Doppler shifts, which results in slightly different first-order moments of ⟨ VLSD ⟩ for different vesini. We have verified that the vesini dependence of | ⟨ Bz ⟩ | disappears if we substitute numerical local LSD profile tables with (less realistic) smooth analytical profiles.
The lower panels in Fig. 5 illustrate the mean and maximum Stokes V amplitude as a function of rsp and vesini. This figure reveals a nontrivial interplay between the Doppler resolution and cancellation of the opposite spot polarities. For sharp-lined stars there is a strong dependence of the polarization amplitude on rsp, with the largest spots yielding about a ten times higher amplitude of the Zeeman polarization signatures. As soon as vesini exceeds ~100 km s-1, the amplitude of polarization profiles becomes almost independent of rsp. The typical peak-to-peak line polarization amplitude obtained in our numerical experiments lies in the range from ~10-3 to ~10-4.
According to our results, the low-vesini stars show higher amplitude polarization features independently of the typical magnetic spot size. In other words, an increase in the polarization amplitude due to the rotational Doppler resolution does not compensate for the reduction of the signal due to weakening of spectral lines. This suggests that massive sharp-lined stars (intrinsically slow rotators or fast rotators visible pole-on) are the preferred targets for searching for signatures of complex magnetic fields. However, it should be remembered that an observational assessment of the typical sizes of magnetic features is only possible for fast rotators. To this end, Fig. 6 presents an analysis of the Stokes V profile complexity using the number of zero line intersections, nz, for the same range of vesini and rsp as shown in Fig. 5. Clearly, a high vesini is beneficial for ascertaining the field complexity and resolving the surface structures on the smallest spatial scales. At the same time, a moderate vesini of ~50 km s-1 is already sufficient for distinguishing, with a single high-quality spectropolarimetric observation, small-scale magnetic fields from the global fossil magnetic topologies.
All calculations presented here assumed 500 G field strength inside magnetic spots. Our results can be easily scaled to an arbitrary starspot field strength by multiplying the magnetic observables by Bsp/500 (for the field strength Bsp measured in G). For the logarithmic plots shown in Fig. 5 this rescaling corresponds to a vertical translation of all curves by lg(Bsp/500). For example, decreasing the spot field strength to 100 G will result in the downward shift in the Stokes V profile amplitude curves by a factor of ≈0.7. The morphology of the circular polarization profiles and Fig. 6 will remain unchanged.
In the following we describe the impact of variation in Teff, i, and fsp with respect to the default values of these parameters (Teff = 20 000 K, i = 60°, and fsp = 0.5). First, repeating the full set of calculations for i = 30° and 90°, we find no dependence of any of the considered Stokes V profile characteristics on the stellar inclination. Statistically, the observational signatures of localized magnetic fields turn out to be completely insensitive to this parameter.
The impact of using the local line profile tables corresponding to different Teff can be qualitatively assessed with the help of the local Stokes I and V profiles shown in Fig. 1. Compared to the full Teff range of 10 000–30 000 K, Teff = 20 000 K adopted for our main set of calculations represents the least favorable case owing to the smallest Stokes I line depth. Unsurprisingly, using Teff = 10 000 K increases the ⟨ VLSD ⟩ amplitude by 30% for rapidly rotating stars and up to 70% for sharp-lined stars. The change associated with increasing Teff from 20 000 to 30 000 K is less significant. In this case, an increase in the line depth is counteracted by an increase in the local profile width. As a result, we obtained ≈20% Stokes V signal enhancement for sharp-lined stars and no change or even a few per cent decrease in the polarization signal for rapid rotators.
Finally, we investigated the impact of reducing the filling factor of the magnetic spots from 0.5 to 0.2. As expected, this large decrease in the amount of unsigned magnetic flux on the stellar surface yields some reduction of both the Stokes V amplitude and the mean longitudinal magnetic field inferred from the circular polarization profiles. However, this reduction is not linear with fsp because having fewer magnetic spots on the visible hemisphere of the star also leads to a less efficient cancellation of the opposite magnetic field polarities. On average, we found about 50% decrease in Vmax, Vmean, as well as in | ⟨ Bz ⟩ | max and | ⟨ Bz ⟩ | mean for a factor of 2.5 reduction of the surface area covered with magnetic spots.
 |
Fig. 7 Upper limits for the small-scale magnetic field intensity corresponding to the null results of the MiMeS survey. Upper panel: Bsp corresponding to | ⟨ Bz ⟩ | = 30 G (solid lines) and 75 G (dashed lines). Lower panel: Bsp required for the magnetic field detection with the LSD Stokes V profiles at a confidence level of ≥99.9% for at least half of the rotational phases. The dotted horizontal lines show Bsp = 50, 100, 200, 500, and 1000 G. |
4. Discussion
In the previous section we calculated the amplitudes of the mean longitudinal magnetic field and the circular polarization inside spectral lines for a fixed magnetic field strength and for different magnetic spot sizes. These predictions cannot be directly compared to any observations because no detection of small-scale magnetic fields has been reported so far for early-B and O stars. Nevertheless, it is of interest to interpret our results in terms of the maximum strength of such fields compatible with the most sensitive of the existing observational nondetections.
The most comprehensive search of the magnetic fields in massive stars was carried out by the MiMeS survey using the ESPaDOnS, NARVAL, and HARPSpol spectropolarimeters. Several discoveries of the strong, large-scale magnetic fields have been made from these observations (e.g., Grunhut et al. 2009; Alecian et al. 2011; Wade et al. 2012c). In addition, the MiMeS survey component (SC) includes over 300 O and B stars for which no evidence of any magnetic field was found. According to Wade et al. (2012b), the resulting incidence of global magnetic fields is about 6% for both O and B stars.
A summary of the magnetic field nondetections for the MiMeS SC stars was kindly communicated to us by J. Grunhut. The median uncertainty of the ⟨ Bz ⟩ measurements is 25 G for all SC stars. Somewhat lower error bars of ~10 G were achieved for about two dozen stars with vesini ≤ 100 km s-1. The median signal-to-noise ratio of the LSD Stokes V profiles is 23 000. Using these observational constraints, we inferred the upper limits for the magnetic field strength using our line profile and | ⟨ Bz ⟩ | predictions for Teff = 20 000 K, fsp = 0.5, and i = 60°.
The upper panel of Fig. 7 shows the minimum Bsp necessary for a 3σ detection of the mean longitudinal magnetic field for σ = 25 G and 10 G. Evidently, ⟨ Bz ⟩ is not a particularly useful diagnostic when it comes to small-scale magnetic field topologies. The field detection using ⟨ Bz ⟩ requires Bsp ≥ 500 G for a subgroup of the MiMeS SC targets with the most accurate longitudinal magnetic field measurements. This limit is Bsp ≳ 1500 G for the entire SC sample.
Next, we assessed the ability of the MiMeS survey to detect small-scale magnetic fields with the LSD line profile analysis. We conducted a series of Monte-Carlo simulations by adding a random noise with different amplitude to the theoretical LSD Stokes V profiles corresponding to rsp = 10° and estimating the probability of polarization signal detection using the chi-square statistics (Donati et al. 1992). These calculations showed that, independently of the Stokes V profile morphology, the circular polarization signatures can be detected at a confidence level of ≥99.9% for at least half of the rotational phases if the noise is at least five times less than the peak-to-peak amplitude of the Stokes V profile. Combining this estimate with a typical precision of the Stokes V LSD profiles obtained by MiMeS, we could infer the maximum possible strength of the magnetic field inside small-scale spots. This Bsp limit is illustrated in the lower panel of Fig. 7 as a function of rsp and vesini. This figure confirms that the LSD Stokes V profile analysis is considerably more sensitive to the small-scale fields compared to ⟨ Bz ⟩. We find that for sharp-lined stars the detection of Bsp ≈ 50 G field is possible for rsp > 10°. The limiting field strength increases to 200–300 G for the smallest spatial scales we have considered (rsp = 2°). Fast-rotating stars show a less pronounced dependence of the maximum Bsp on rsp. Typically, one should be able to detect the signatures of 300–500 G magnetic fields for any rsp at vesini = 100 km s-1 and 800–1200 G fields at vesini = 200 km s-1. Interestingly, for fast-rotating stars the limit of 800 G corresponds to the field with rsp ≤ 5°, and it is comparatively more difficult to detect larger scale magnetic field structures.
How do these constraints compare with theoretical predictions? The only quantitative estimate of the strength of localized magnetic fields emerging on the surfaces of massive stars has been presented by Cantiello & Braithwaite (2011, hereafter CB11) in the context of their study of the effects of turbulence in the iron SCZ. Supposing that the dynamo action in the convection zone is in equipartition with the kinetic energy of the gas, the authors find magnetic fields of up to ~2 kG at the base of the surface radiative zone. Further assuming that the magnetic fields are brought up to the surface by the magnetic buoyancy, CB11 obtained the magnetic field strength of about 20 G to 150 G in the photospheric layers, depending on the magnetic flux tube geometry and stellar parameters. CB11 also did not rule out the photospheric fields reaching the equipartition limit of about 300 G.
Little is known about the typical sizes of the surface magnetic field structures generated by the SCZ. CB11 argue that the lower limit of the magnetic starspot size is given by the pressure scale height, which is about 0.2 R⊙ for a massive star with R⋆ = 10 R⊙. This corresponds to rsp ≈ 1°, i.e., close to the lower spatial limit investigated in our paper. At the same time, magneto-hydrodynamic simulations demonstrate formation of magnetic structures on scales that are significantly larger than the scale of convection (Käpylä et al. 2008; Cantiello et al. 2011). For the Sun, the observed active regions also have sizes that significantly exceed the pressure scale height (e.g. Zhang et al. 2010). Inhomogeneous wind models by Cranmer & Owocki (1996) considered surface spots with rsp ≈ 10°, so the magnetic concentrations with coherent field orientation should be similarly large for the magnetic interpretation of CIRs and DACs. Based on these arguments, we suggest that rsp = 5–10° might be a more realistic estimate of the typical size of the hypothetical surface magnetic field regions.
A remarkable result of our analysis is that the high-resolution Stokes V observations of massive sharp-lined stars have already reached the precision necessary for detecting rsp = 5–10° spots, filled with Bsp = 50–100 G radial magnetic field and occupying half of the stellar surface. However, no discovery of a corresponding population of narrow-line magnetic massive stars have been reported by MiMeS. This may indicate that the theoretical predictions by CB11 overestimate the surface field strength or that the fraction of the stellar surface covered by magnetic regions is much smaller than fsp = 0.5 adopted in our simulations. A more firm conclusion emerging from our work is the absence of equipartition fields with Bsp ≈ 300 G on the surfaces of massive stars.
The tentative comparison of the overall MiMeS survey results with the generic theoretical predictions for a wide range of stellar parameters can be put on more solid footing by considering fundamental parameters, observational constraints, and theoretical predictions for individual stars. On the one hand, such analysis would take the individual line lists, vesini, and circular polarization detection limits into account and, on the other hand, would allow choosing an appropriate maximum theoretical magnetic field strength according to the stellar luminosity and temperature (see Fig. 3 in CB11). In the future, it will be straightforward to perform this analysis of individual massive stars with the tools and methodology developed in our paper.
Acknowledgments
We thank Dr. Jason Grunhut for providing a summary of the MiMeS null results ahead of publication. O.K. is a Royal Swedish Academy of Sciences Research Fellow, supported by the grants from Knut and Alice Wallenberg Foundation and Swedish Research Council. N.S. is supported by the Saint-Petersburg State University through a research grant 6.38.73.2011.
References
- Alecian, E., Kochukhov, O., Neiner, C., et al. 2011, A&A, 536, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aurière, M., Wade, G. A., Silvester, J., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Szeifert, T., Wade, G. A., Landstreet, J. D., & Mathys, G. 2002, A&A, 389, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Landstreet, J. D., Fossati, L., & Kochukhov, O. 2012, A&A, 538, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braithwaite, J., & Cantiello, M. 2013, MNRAS, 428, 2789 [NASA ADS] [CrossRef] [Google Scholar]
- Braithwaite, J., & Nordlund, Å. 2006, A&A, 450, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brun, A. S., Browning, M. K., & Toomre, J. 2005, ApJ, 629, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., & Braithwaite, J. 2011, A&A, 534, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Langer, N., Brott, I., et al. 2009, A&A, 499, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Braithwaite, J., Brandenburg, A., et al. 2011, in IAU Symp. 272, eds. C. Neiner, G. Wade, G. Meynet, & G. Peters, 32 [Google Scholar]
- Cranmer, S. R., & Owocki, S. P. 1996, ApJ, 462, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Degroote, P., Briquet, M., Auvergne, M., et al. 2010, A&A, 519, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Semel, M., & Rees, D. E. 1992, A&A, 265, 669 [NASA ADS] [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Babel, J., Harries, T. J., et al. 2002, MNRAS, 333, 55 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Cameron, A. C., Semel, M., et al. 2003, MNRAS, 345, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Fullerton, A. W., Gies, D. R., & Bolton, C. T. 1996, ApJS, 103, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Grunhut, J. H., Wade, G. A., Marcolino, W. L. F., et al. 2009, MNRAS, 400, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Henrichs, H. F., Schnerr, R. S., & ten Kulve, E. 2005, in The Nature and Evolution of Disks Around Hot Stars, eds. R. Ignace, & K. G. Gayley, ASP Conf. Ser., 337, 114 [Google Scholar]
- Hubrig, S., Schöller, M., Kharchenko, N. V., et al. 2011, A&A, 528, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, I., Lennon, D. J., Dufton, P. L., et al. 2008, A&A, 479, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaper, L., Henrichs, H. F., Nichols, J. S., et al. 1996, A&AS, 116, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Korpi, M. J., & Brandenburg, A. 2008, A&A, 491, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kochukhov, O. 2011, in IAU Symp. 273, eds. D. Prasad Choudhary, & K. G. Strassmeier, 249 [Google Scholar]
- Kochukhov, O., Makaganiuk, V., & Piskunov, N. 2010, A&A, 524, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kochukhov, O., Mantere, M. J., Hackman, T., & Ilyin, I. 2013, A&A, 550, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid. Kurucz CD-ROM No. 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
- Lignières, F., Petit, P., Böhm, T., & Aurière, M. 2009, A&A, 500, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacGregor, K. B., & Cassinelli, J. P. 2003, ApJ, 586, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2005, A&A, 440, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Donati, J., Marcolino, W. L. F., et al. 2010, MNRAS, 407, 1423 [NASA ADS] [CrossRef] [Google Scholar]
- Mathys, G. 2009, in Solar Polarization 5: In Honor of Jan Stenflo, eds. S. V. Berdyugina, K. N. Nagendra, & R. Ramelli, ASP Conf. Ser., 405, 473 [Google Scholar]
- Mullan, D. J. 1984, ApJ, 283, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Mullan, D. J., & MacDonald, J. 2005, MNRAS, 356, 1139 [NASA ADS] [CrossRef] [Google Scholar]
- Neiner, C., Grunhut, J. H., Petit, V., et al. 2012, MNRAS, 426, 2738 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, V., & Wade, G. A. 2012, MNRAS, 420, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, P., Lignières, F., Aurière, M., et al. 2011, A&A, 532, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piskunov, N., & Kochukhov, O. 2002, A&A, 381, 736 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prinja, R. K., Massa, D., & Fullerton, A. W. 2002, A&A, 388, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]
- Shultz, M., Wade, G. A., Grunhut, J., et al. 2012, ApJ, 750, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Fullerton, A. W., Donati, J.-F., et al. 2006, A&A, 451, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Bagnulo, S., Drouin, D., Landstreet, J. D., & Monin, D. 2007, MNRAS, 376, 1145 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wade, G. A., Alecian, E., Bohlender, D. A., et al. 2011a, in IAU Symp. 272, eds. C. Neiner, G. Wade, G. Meynet, & G. Peters, 118 [Google Scholar]
- Wade, G. A., Howarth, I. D., Townsend, R. H. D., et al. 2011b, MNRAS, 416, 3160 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., Grunhut, J., Gräfener, G., et al. 2012a, MNRAS, 419, 2459 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., Grunhut, J. H., & MiMeS Collaboration 2012b, in Circumstellar Dynamics at High Resolution, eds. A. C. Carciofi, & T. Rivinius, ASP Conf. Ser., 464, 405 [Google Scholar]
- Wade, G. A., Maíz Apellániz, J., Martins, F., et al. 2012c, MNRAS, 425, 1278 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P., Brun, A. S., & Mathis, S. 2007, A&A, 474, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, J., Wang, Y., & Liu, Y. 2010, ApJ, 723, 1006 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Normalized disk-center LSD Stokes I and V profiles for different effective temperatures and a line-of-sight magnetic field of 0.5 kG. The Stokes V spectra are offset vertically by 1.05 and expanded by a factor of 5. |
| In the text | |
 |
Fig. 2 Examples of random distributions of radial magnetic field spots with filling factor fsp = 0.5 and rsp = 10° (left panel) and 2° (right panel). In each case the star is shown at nine rotational phases and inclination angle i = 60°. The white and black regions correspond to the spots with positive and negative field polarity, respectively. The gray areas are field-free. |
| In the text | |
 |
Fig. 3 Disk-integrated normalized LSD Stokes I and V profiles for vesini = 10 km s-1 and a random distribution magnetic spots with rsp = 10°. Other parameters are Teff = 20 000 K, i = 60°, and magnetic filling factor fsp = 0.5. The spectra corresponding to different rotational phases are offset vertically. |
| In the text | |
 |
Fig. 4 LSD Stokes I and V profiles computed with the same magnetic map and setup as in Fig. 3, except for vesini = 100 km s-1. |
| In the text | |
 |
Fig. 5 Mean longitudinal magnetic field and the LSD Stokes V profile amplitude as a function of the magnetic spot radius and projected rotational velocity. These calculations were carried out for Teff = 20 000 K and magnetic filling factor fsp = 0.5. The top panels show maximum | ⟨ Bz ⟩ | for a sample of 20 rotational phases (top left) and | ⟨ Bz ⟩ | averaged over this set of rotational phases (top right). The bottom panels illustrate the corresponding maximum (bottom left) and mean (bottom right) circular polarization amplitude. Each point in this plot was computed by averaging over 100 different random realizations of the magnetic spot distributions. |
| In the text | |
 |
Fig. 6 Number of intersections of the zero line in the Stokes V profiles as a function of the magnetic spot radius and projected rotational velocity. Each point is a median computed over 20 rotational phases and 100 different random realizations of magnetic spot distributions. |
| In the text | |
 |
Fig. 7 Upper limits for the small-scale magnetic field intensity corresponding to the null results of the MiMeS survey. Upper panel: Bsp corresponding to | ⟨ Bz ⟩ | = 30 G (solid lines) and 75 G (dashed lines). Lower panel: Bsp required for the magnetic field detection with the LSD Stokes V profiles at a confidence level of ≥99.9% for at least half of the rotational phases. The dotted horizontal lines show Bsp = 50, 100, 200, 500, and 1000 G. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


