EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 554 (June 2013) A&A, 554 (2013) A34 Full HTML
Free Access
Issue
A&A
Volume 554, June 2013
Article Number A34
Number of page(s) 12
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201321176
Published online 31 May 2013

© ESO, 2013

1. Introduction

Interstellar solid CO2 was first identified towards several protostars by the InfraRed Astronomical Satellite (IRAS) in the late 80s (d’Hendecourt & Jourdain de Muizon 1989). Since its detection, solid CO2 has been observed abundant (~10−30% with respect to H2O ice) towards different environments, such as quiescent dark clouds and star forming regions by the Infrared Space Observatory (ISO; e.g., Gerakines et al. 1999; Gibb et al. 2004; Nummelin et al. 2001) and more recently by the Spitzer Space Telescope (e.g., Boogert et al. 2004; Pontoppidan et al. 2005, 2008; Whittet et al. 2007; Öberg et al. 2008; Zasowski et al. 2009; Bottinelli et al. 2010; Cook et al. 2011). These observations have established that solid CO2, together with H2O, CO, and in some cases CH3OH, NH3, and CH4, represents the bulk of solid-state species in the interstellar and circumstellar medium (ISM/CSM) (e.g., Allamandola et al. 1992; Gibb et al. 2004; Öberg et al. 2011). In the past decades, several experimental studies have focused on the profile of the IR absorption bands of solid CO2 in different astrophysical relevant mixtures as a function of temperature and investigated the interaction of CO2 with neighbor molecules, such as H2O and CH3OH (e.g., Sandford & Allamandola 1990; Hudgins et al. 1993; Ehrenfreund et al. 1997; 1999; Dartois et al. 1999; Palumbo & Baratta 2000; Baragiola 2003; Gálvez et al. 2007; 2008; White et al. 2009). Recently, Pontoppidan et al. (2008) have compared selected laboratory spectra to Spitzer observations towards star forming regions, and found that roughly two thirds of the solid CO2 observed in quiescent molecular clouds and star forming regions is embedded in water-rich environment, suggesting that the formation routes of these two molecules are linked. The remaining CO2 ice is predominantly found in an H2O-poor, CO-rich environment.

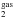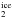Despite its ubiquity and abundance, the formation of interstellar CO2 ice remains uncertain. It is widely accepted that CO2 is not efficiently formed in the gas phase, with subsequent accretion onto interstellar grains (COgas2\hbox{$_2^{\rm{gas}}$}/COice2\hbox{$_2^{\rm{ice}}$}≪ 1; van Dishoeck et al. 1996; Boonman et al. 2003). Therefore, the observed CO2 most likely has to be formed in the solid phase through surface reactions with or without energetic input (e.g., UV photons with 6.9 ≤ E ≤ 13.6 eV, and cosmic rays with E ~ MeV). The problem is then further complicated by the fact that several reaction mechanisms have been proposed with often uncertain efficiency in the solid phase. The most cited surface reaction routes are CO+O→CO2HCO+O→CO2+HCO+OH→CO2+H.\begin{eqnarray} \label{CO+O}&&\rm CO + O \rightarrow CO_{2} \\ \label{HCO+O}&&\rm HCO + O \rightarrow CO_{2} + H \\ \label{CO+OH}&&\rm CO + OH \rightarrow CO_{2} + H . \end{eqnarray}The most straightforward surface reaction channel is the addition of an O atom to solid CO ice (Tielens & Hagen 1982). However, reaction 1 has a high reaction barrier (2970 K in the gas phase; Talbi et al. 2006; Grim & d’Hendecourt 1986), because the CO(1Σ) + O(3P) reactants do not correlate directly with the singlet ground state CO2(1Σ). Ruffle & Herbst (2001) were only able to reproduce the CO2 abundances observed towards cold clouds (e.g., Elias 16) if they artificially lowered the barrier to 130 K in their astrochemical model. Recently, Goumans & Andersson (2010) used harmonic quantum transition state theory to prove that, while quantum mechanical tunneling through the activation barrier increases the classical reaction rate for reaction 1 at low temperatures (10 − 20 K), the onset of tunneling is at temperatures that are too low for the reaction to efficiently contribute to CO2 formation in quiescent cold regions. Reaction 1 has been experimentally investigated by temperature-programed desorption experiments using thermal O atoms below 160 K (Roser et al. 2001) and by energetic O atoms (Madzunkov et al. 2006). In the first case, reaction 1 was found to proceed only in water pores under a water ice cap and upon heating, while in the second case the energetic O atoms allowed the reaction to proceed. More recently, Raut & Baragiola (2011) have shown by means of infrared (IR) spectroscopy and microgravimetry that CO2 forms in small quantities during codeposition of CO and cold (non-energetic) O and O2 into thin films at 20 K. They find that O atoms primarily react with O to form O2 and with O2 to form O3. Therefore, reaction 1 is most likely not an efficient surface CO2-formation route unless energetic processing is involved.

It has been further suggested that solid CO2 is formed through surface reaction 2 (Ruffle & Herbst 2001), which has never been experimentally investigated in the solid phase. Alternatively, solid CO2 can be formed through reaction 3, which yields an HO-CO intermediate. This complex can directly dissociate, forming solid CO2 and leaving an H atom, or can be stabilized by intramolecular energy transfer to the ice surface and eventually react with an incoming H atom in a barrierless manner to form CO2 and H2 or other products with a purely statistical branching ratio (Goumans et al. 2008). Recently, several independent experimental studies have shown that reaction 3 is an efficient surface CO2 formation channel without energetic input (i.e., Oba et al. 2010; Ioppolo et al. 2011; Noble et al. 2011). Moreover, reaction 3 can explain the observed formation link between CO2 and H2O ice under interstellar conditions, since OH radicals are involved in the reaction scheme, and water can be efficiently formed through reactions OH + H and OH + H2 (e.g., Romanzin et al. 2011; Oba et al. 2012). This is also recently confirmed by Garrod & Pauly (2011) in their three-phase (gas/surface/mantle) astrochemical model in which formation of solid CO2, as well as other species, is investigated. Thus, a combination of observations, models, and laboratory experiments indicates that CO2 can be formed through non-energetic induced surface reactions in a polar environment already in a quiescent molecular cloud phase.

Although dense molecular clouds are shielded from UV radiation to a great extent by dust particles, cosmic rays can still penetrate these regions and, therefore, they can efficiently process the ices (e.g., Prasad & Tarafdar 1983; Jenniskens et al. 1993; Mennella et al. 2003). Energetic processing becomes even more important at later stages of star forming regions, when ices are exposed to the irradiation of a new born star. In dense molecular clouds, cosmic rays generate UV photons and fast ions that can indeed release their energy to the target material. Owing to the interaction with fast ions molecular bonds are broken and, on timescales of picoseconds, the molecular fragments recombine giving rise to a rearrangement of the chemical structure that leads to forming new molecular species. In the case of UV photolysis, the energy is released to the target material through a single photo-dissociation or photo-excitation event. Therefore, energetic processing most likely contribute to the total CO2 abundance observed in polar and apolar interstellar ices. For instance, (i) photo-dissociation of H2O ice is a possible mechanism to form available OH radicals that can subsequently react with CO molecules to form solid CO2 through reaction 3; (ii) as mentioned before, CO2 can be formed through reaction 1 in apolar ices when the reaction is induced by energetic input.

Laboratory experiments have shown that CO2 is efficiently formed after energetic processing of pure CO ice and ice mixtures containing CO and H2O (e.g., d’Hendecourt et al. 1986; Moore et al. 1991; Bernstein et al. 1995; Gerakines et al. 1996; Ehrenfreund et al. 1997; Palumbo et al. 1998; Watanabe et al. 2002; Loeffler et al. 2005). Furthermore, CO2 ice can be formed upon irradiation of carbon grains covered by a water cap or an oxygen layer (Mennella et al. 2004, 2006; Gomis & Strazzulla 2005; Raut et al. 2012; Fulvio et al. 2012). Recently, Ioppolo et al. (2009) and Garozzo et al. (2011) quantitatively studied the formation of CO2 ice upon ion irradiation of interstellar relevant ice mixtures containing C- and O-bearing species at low (12−15 K) and high (40−60 K) temperatures, respectively. Ioppolo et al. (2009) used laboratory data of processed ice to fit the CO2 stretching and bending mode band profiles observed by ISO towards a few high-mass young stellar objects (YSOs). Here we compare new laboratory data, together with those presented in Ioppolo et al. (2009) and Garozzo et al. (2011), with a wider sample of sources in low-mass star forming regions with the intent of constraining the contribution of energetic processing to the formation of solid CO2 in space at different stages of star forming regions (see Tables 4, 5 and the discussion in Sect. 3.3). All the sources have been observed by the Spitzer Space Telescope and listed in Pontoppidan et al. (2008). In the next section the experimental method and data analysis are discussed.

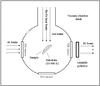thumbnail Fig. 1

A schematic top view of the high vacuum chamber.

2. Experimental and data analysis

2.1. Experimental

All the experiments discussed here were performed at the Laboratory for Experimental Astrophysics, INAF – Osservatorio Astrofisico di Catania. The experimental setup depicted in Fig. 1 comprises a stainless steel high-vacuum chamber (P < 10-7 mbar) and a 200 kV ions implanter (Danfysik 1080) that can produce, select, accelerate, and collimate ions covering an energy range between 30 and 200 keV (or 400 keV for double ionizations).

Placed in the center of the main chamber, a KBr or silicon inert substrate is in thermal contact with a closed-cycle helium cryostat. The substrate temperature can be controlled in a range between 10 and 300 K. Gas mixtures were admitted into the main chamber through a needle valve and subsequently deposited on the substrate kept at low temperature. The ice thickness is measured by means of a He-Ne laser as discussed in Baratta & Palumbo (1998) and Fulvio et al. (2009). The ion beam current density in the ion implanter is always kept below 1 μA cm-2 to avoid macroscopic heating of the target. For all the experiments the penetration depth of the impinging ions is greater than the sample thickness (s0.1 μm), so that the ice is always uniformly irradiated, as verified using the SRIM code (Ziegler et al. 2008). The substrate forms an angle of 45° with respect to the ion beam and the IR beam coming from a Fourier transform infrared (FTIR) spectrophotometer (Bruker Equinox 55 or Bruker Vertex 70) that works in the spectral range between 7500−400 cm-1 (1.33−25 μm). Transmittance spectra were then easily obtained in situ without tilting the sample. Infrared spectra were always acquired before and after irradiation at low temperatures (12−17 K) and after annealing (up to 90−100 K). A different procedure is used only in one experiment of pure CO ice (Ioppolo et al. 2009), as discussed in the next section. The selection of ice mixture components and ratios is based on observational data from astrophysical literature and includes the most abundant observed interstellar ice molecules, such as water, carbon dioxide, carbon monoxide, methanol, methane, and ammonia. A list of selected laboratory spectra used here to fit IR spectra of astronomical objects is shown in Tables 1 and 2. Spectra are also available in the Catania database1. Every label present in the aforementioned tables identifies a specific spectrum with a selected dose of ion irradiation (eV/16u) and temperature. The dose is derived from the knowledge of the stopping power (eV × cm2/molecule), calculated by SRIM software (Ziegler et al. 2008), and the ion fluence (ions cm-2).

Table 1

List of the database spectra relative to irradiation of CO-rich ice samples with 200 keV H+ and 30 keV He+.

A polarizer is placed in the path of the IR beam in front of the IR detector (Fig. 1). In this way, at each step of an experiment two IR spectra were recorded with a selected component of the electric vector parallel (P polarization) and perpendicular (S polarization) to the plane of incidence. For each experiment, background spectra in P and S were acquired before ice deposition and subtracted to all spectra with the same polarization (Baratta & Palumbo 1998). Baratta et al. (2000) and Palumbo et al. (2006) also show that when the band profiles obtained in P and S polarization are similar, the features seen in the transmittance spectra directly reflect the variation in the absorption coefficient of the solid sample. Under these circumstances a direct comparison between transmission laboratory spectra and astronomical observations is allowed. This is the case for all the band profiles presented here after ion irradiation. Thus, only P spectra will be considered since the signal-to-noise ratio is higher for this polarization. All P spectra shown in the following sections were taken with a resolution of 1 cm-1.

2.2. Data analysis

Laboratory spectra were acquired in transmittance units (If) and were converted into optical depth units τ(ν) = ln   (I0/If) where I0 is the normalization continuum. The column density (N, molecules cm-2) of species in the solid phase is then calculated using the equation 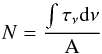N=∫τνdνA\begin{equation} N = \frac{ \int{\tau_{\mathrm{\nu}}{\rm d}\nu }}{\rm A} \end{equation}(4)where 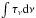τν∫dν\hbox{$\int{\tau_{\nu}}{\rm d}\nu$} (cm-1) is the area (in optical depth scale) of a selected band and A is the band strength (cm molecule-1). The A-values used in this work are listed in Table 3. The column density is corrected by a factor of 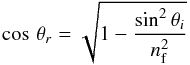cos θr=1−sin2θinf2\begin{equation} {\cos\,\theta_r}={\sqrt{1-\frac{\sin^2\theta_i}{n^2_{\rm f}}}} \label{corr} \end{equation}(5)where θr is the refractive angle and nf the refractive index of the film. This correction takes the increased path length of the IR beam at an angle of incidence θi = 45° into account (Fulvio et al. 2009; Modica & Palumbo 2010).

3. Results and discussion

3.1. Irradiation of ice mixtures

All the selected laboratory experiments presented here confirm the formation of CO2 ice upon energetic processing (i.e., ion irradiation) of C- and O-bearing ice mixtures. Ioppolo et al. (2009) calculated the column density of solid carbon dioxide (NCO2) produced in some of the experiments listed in Tables 1 and 2 with respect to the initial abundance of solid CO or CH3OH (NX) and as a function of the irradiation dose: 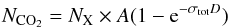NCO2=NX×A(1−e−σtotD)\begin{equation} N_{\rm CO_2}=N_{\rm X} \times A (1-{\rm e}^{- \sigma_{\rm tot} D}) \end{equation}(6)where A is the asymptotic value for the CO2 column density divided by the initial column density of CO or CH3OH, σtot is the total cross section in 16 u/eV, and D the dose in eV/16 u. For all these experiments the CO2 column density increases rapidly at low doses and then reaches a saturation level indicating that a steady state is always reached between the CO2 formation and destruction mechanisms.

Moreover, as discussed in Ioppolo et al. (2009), the band profile of solid CO2 bending mode is sensitive to mixture and temperature changes. Figure 2 shows the variations in CO2 bending mode band profile upon irradiation and thermal annealing of pure CO ice (top panels), binary mixtures containing CO mixed with H2O, N2, and NH3 (central panels), and pure CH3OH ice (right-bottom panel). The bending mode band profile of pure CO2 is also shown for comparison (left-bottom panel).

Table 2

List of the database spectra relative to irradiation of pure methanol ice with 30 keV He+.

Table 3

List of the band strength (A) values used here.

thumbnail Fig. 2

The bending mode band profile of the carbon dioxide in several ice mixtures irradiated with 200 keV H+ or 30 keV He+ and annealed. The spectra are acquired with a resolution of 1 cm-1 and the open symbols are only reported for clarity.

The CO2 bending mode band in pure CO2 ice in S polarization, as shown in Fig. 2, has two peaks at about 656 and 660 cm-1. When the spectrum is taken in P polarization an additional peak is present at 676 cm-1 due to the longitudinal optical (LO) mode (see Baratta & Palumbo 1998; Palumbo et al. 2006). The CO2 bending mode band present in the IR spectra after irradiation of a pure CO ice at 16 K appears as an asymmetric narrow sharp peak (660 cm-1) with a wider wing at lower wavenumbers (Fig. 2 top-left panel). The same peak then broadens upon heating to 40 K. Finally, at 80 K the CO2 bending mode band has a double peak, which is typical of a CO2-rich environment. This change in the band profile is due to the desorption of the unprocessed CO ice that starts already at 30 K. The broadening effect and the double peaks are indeed visible in all the panels of Fig. 2 in which a CO-bearing mixture is first irradiated and then annealed. As shown by Ioppolo et al. (2009), in these instances, the band profile in the spectra taken in P and S polarizations are the same. This is because CO2 is not in a pure ice but is mixed with other species, such as carbon chain oxides formed after ion irradiation (see e.g. Palumbo et al. 2008), and is trapped in a refractory residue also formed at low temperature after ion irradiation (Sicilia et al. 2012).

The experiment shown in the top-right panel of Fig. 2 was performed using a different procedure than in the other experiments. The aim in this case was to study changes in the CO2 bending mode band profile upon irradiation at high temperatures when CO is already desorbed. Therefore, a CO ice was grown at 16 K, irradiated with 200 keV H+ to form CO2 and subsequently heated to 70 K to then be irradiated further at the same temperature. After irradiation at 70 K the ice was cooled back to 16 K and further irradiated. The IR spectra plotted in the top right-hand panel of Fig. 2 show that the double peak is present at 70 K. Further irradiation of the ice slowly decreases the total amount of solid CO2 without changing the profile of the band significantly. Finally, there are no differences within experimental errors between the last spectrum at 70 K and the one after cooling the sample back to 16 K. When CO2 is formed after irradiation of methanol, the bending mode band profile shows two broad peaks at 650 and 660 cm-1 that shift towards lower wavenumbers when the sample is warmed up.

A general comparison among the IR spectra at the same temperature from all the panels of Fig. 2 confirms that the CO2 vibrational bending mode band profile is strongly sensitive to specific ice mixture (polar and non-polar environment) and ice temperature. Thus, the CO2 bending mode band profile is used here to fit the Spitzer observational data presented in the next sections.

thumbnail Fig. 3

The mid-IR spectra of water ice covering carbon grains before and after irradiation with 200 keV H+ at 17 K. The internal panel shows the newly formed solid CO2 bending mode band profile.

Table 4

List of selected low-mass young stellar objects and a field star observed by the Spitzer Space Telescope.

3.2. Irradiation of H2O ice on carbon grains

Carbon grains represent about 20% of the total interstellar dust grain abundance (Greenberg 1982). In the early stages of a quiescent cloud, water is formed onto these grains, creating a polar ice layer that is then processed by UV radiation and cosmic rays during the evolution of star forming regions. Recently, Mennella et al. (2004, 2006) and Raut et al. (2012) have experimentally proved that solid CO and CO2 can be formed in cold dark clouds after energetic processing of carbon grains with a water ice cap. Here we present new experimental results from the energetic proton exposure of a layer of water ice covering a carbon sample. The sample is prepared by coating a KBr substrate with fumes from combusted benzene. A microscopic exam of the sample highlights that carbon residuals aggregate upon deposition onto the KBr substrate and form irregular prominences that simulate the rough surface of interstellar carbon grains. The resulting amorphous carbon substrate has a surface area wider than the area of an optically flat substrate. The newly formed substrate is then placed in the vacuum chamber and cooled down to 17 K. A layer of 76 nm of water ice is then deposited onto the rough carbon surface at 17 K to reproduce interstellar ice mantles in cold dense clouds. Finally, the sample is irradiated with 200 keV protons, and IR transmittance spectra are acquired at different doses.

Figure 3 shows the spectra before and after irradiation of water ice on amorphous carbon at 17 K. For all the other experiments presented in this work the substrate is inert and, therefore, does not influence the investigated surface reactions induced by irradiation of interstellar ice analogs. Here, the irradiated carbon substrate interacts with the water ice and contributes to the formation of solid CO2 at the interface between carbon and ice. The characteristic bending mode feature of solid carbon dioxide in a water environment (small internal panel of Fig. 3) is indeed seen after a fluence of 8.36 × 1015 ions/cm2. The final CO2 column density is about 1.1 × 1016 mol/cm2.

The CO2 bending mode band profile shown in Fig. 3 is large and already quite symmetric at low temperatures. A similar profile is obtained by irradiating a CO:H2O = 10:1 ice sample and subsequently heating it to 40 K to induce CO thermal desorption (see Fig. 2). In the latter case, however, the broad CO2 bending mode band is asymmetric and the CO2 band broadens only above 30 K. The experiment presented in this section gives a CO2 bending mode broad component at low temperatures that is used to fit observational data as shown in the next sections. Moreover, this experiment simulates the formation of CO2 after energetic processing of water ice on carbon grains under cold molecular cloud conditions. This mechanism, together with the non-energetic routes, can contribute to the total CO2 observed in polar ices in dark clouds. The spectrum plotted in Fig. 3 also shows a downward feature at about 2900 cm-1 assigned to C-H bonds in the carbon substrate that are destroyed during irradiation. Other features are present at 2276 cm-1 (13CO2), 2136 cm-1 (CO), and 794 cm-1. This feature is tentatively assigned to the C-H out-of-plane bending mode of acetylene (C2H2) and/or of aromatic rings with three adjacent hydrogen atoms (Strazzulla & Baratta 1991). Further studies are, however, needed to confirm this identification.

3.3. Comparison with observations

All the selected sources are low-mass YSOs still embedded in their parent thick cloud, emitting in the IR spectral range and belonging to the Lada-Andre spectral classes 0, I, and II. A field star (CK2) is also included in the list. Their radiation was acquired by the Spitzer InfraRed Spectrometer (IRS), which operates into the 5−40 μm range. Pontoppidan et al. (2008) studied and compared the CO2 bending mode band profile from all these sources to laboratory spectra. They find that a five-component fit could reproduce the profile of the CO2 bending mode feature in most of the investigated cases. All their laboratory components correspond to interstellar relevant ice analogs and can be divided into polar and non-polar ices. Unlike our laboratory study in which CO2 is formed in the ice, in Pontoppidan et al. (2008) the CO2 is mixed with other species and subsequently deposited at low temperatures. Among all the available YSO sources in Pontoppidan et al. (2008), we selected those that have spectra with a good signal-to-noise ratio and an optical depth <1. Our selection of sources with some of their characteristics is reported in Tables 4 and 5.

Table 5

Column density values for CO2, CO, H2O, CH3OH and NH3 along the line of sight to selected young stellar objects and a field star.

In a previous study we compared the CO2 bending mode band profile from some high-mass YSOs observed by ISO satellite with laboratory spectra and proved that the observational CO2 band profile (i.e., band position, width, and shape) can be fitted with a linear combination of different laboratory spectral components (Ioppolo et al. 2009). Here we perform a more extensive and systematic comparison between recent Spitzer observations and laboratory spectra. The selection criteria in the choice of the laboratory components are based on the fact that the CO2 bending mode band profile observed towards several YSOs can present different characteristic features:

  • a double-peaked structure, in the660–655 cm-1 spectral range;

  • a narrow single-peak profile, at about 660 cm-1;

  • a shoulder at lower wavenumbers (at about 650 cm-1);

  • a broad component of the spectrum, peaked at about 655 cm-1.

Figures 2 and 3 show that these characteristic features correspond to certain chemical-physical conditions: a doubly peaked bending mode band profile is due to the segregation of carbon dioxide (e.g., Ehrenfreund et al. 1999; Palumbo & Baratta 2000), which can be induced by heating of the interstellar ices, hence desorption of volatile species; a narrow single peak suggests that CO2 is at low temperatures in a CO environment; a shoulder around lower wavenumbers can be caused by the interaction between solid CO2 and alcohols; a broad CO2 band is generally obtained when CO2 is formed by irradiation of water ice on carbon grains at low temperatures. A home-written software (Polyfit, realized by Spinella) is then used to compare observational spectra with laboratory data. The program gives a linear combination of up to five preselected laboratory spectra as a best fit. The best-fit results are presented in Figs. 4–5.

thumbnail Fig. 4

Comparison between the CO2 bending mode band profile towards several low-mass young stellar objects (open squares) and laboratory spectra. The spectra are acquired with a resolution of 1 cm-1 and the symbols are only reported for clarity. The fits are represented by solid thick lines.

thumbnail Fig. 4

continued.

thumbnail Fig. 5

As for Fig. 4. Here a field star is also compared to laboratory data.

Table 6

Expected solid CO2 (upper limits) formed after cosmic ion irradiation of water ice onto carbon grains (Ioppolo et al. 2009) for some selected sources for which AV is known compared to the column density of CO2 in water ice as obtained by the fit.

Table 7

Expected solid CO2 (upper limits) formed after cosmic ion irradiation of CH3OH ice based on laboratory data (Ioppolo et al. 2009) for some selected sources for which CH3OH column density is known compared to the column density of CO2 formed from methanol as obtained by the fit.

In all the panels of these figures the observational data are always represented by open squares and the fits by solid thick lines. Good agreement is always reached between observational data and a combination of a minimum of two laboratory spectra. Although the fits are not unique, all our fits can reproduce the observed CO2 bending mode band profile towards the selected YSOs.

3.4. Observational constraints

To verify that our fits are compatible with the observational data available for each source, we first considered the solid CO and H2O column density values (see Table 5), as reported by Pontoppidan et al. (2003, 2008) and Boogert et al. (2008), and calculated the CO/H2O column density ratio. In agreement with Cook et al. (2011), we noticed a correspondence between the CO/H2O ratio and the observed CO2 bending mode band profile. In particular, the band profile presents a double-peaked feature when the CO/H2O ratio is lower than about 0.4, while for higher values (as high as 1.44 in the case of IRS51), the band profile presents a single peak (see Figs. 4–5). The different CO/H2O ratio is expected to be related to the temperature of the icy grain mantles along the line of sight. In fact, high temperatures favor CO sublimation. Therefore, we used laboratory spectra at low temperature (T = 16−40 K) to fit the CO2 band profile for high CO/H2O values, and we considered laboratory spectra at higher temperature (T > 40 K), which show the double-peaked feature, to fit the CO2 band profile for low CO/H2O values. The column density of CH3OH observed towards the sources considered here is reported by Bottinelli et al. (2010) and Boogert et al. (2008), and is listed in Table 5. Although the CH3OH abundance is quite low with respect to water for all our sources, this component is an important ingredient for fitting the CO2 “shoulder” at the lower wavenumbers present in the observed spectra.

The next step is to extend laboratory results (i.e., laboratory column densities, formation and destruction rates) to the interstellar medium. Concerning the CO2 formed after irradiation of H2O ice on carbon grains, following Mennella et al. (2004, 2006) and Ioppolo et al. (2009), we assume that the CO2 column density produced in a cloud lifetime of t = 3 × 107 years is N(CO2) = 9.3 × 1015AV, where AV is the visual extinction of the cloud. The values of CO2 column density expected to be formed after irradiation of carbon grains covered by an ice mantle are reported in Table 6 for some selected sources whose AV is known. As extensively explained in Ioppolo et al. (2009), these values are to be considered as upper limits. The same table also lists the contribution to the fit given by CO2 formed after irradiation of H2O ice on carbon grains. Following Ioppolo et al. (2009), for the sources in which the methanol column density is known, we calculated the expected interstellar CO2 column density formed after cosmic irradiation of CH3OH ice (see Table 7) by using the following formula: N(CO2)=N(CH3OH)obs×[N(CO2)N(CH3OH)]lab\begin{equation} N({\rm CO}_2)=N({\rm CH_3OH})_{\rm obs} \times \left[\frac{N({\rm CO}_2)}{N({\rm CH_3OH})}\right]_{\rm lab} \end{equation}(7)where N(CH3OH) is the residual CH3OH column density after irradiation and the expression [N(CO2)N(CH3OH)]lab\hbox{$[\frac{N({\rm CO}_2)}{N({\rm CH_3OH})}]_{\rm lab}$} has a value of 2.36 according to the ratio between the laboratory band areas and the respective band strength (see Table 3), and assuming a cloud lifetime of t = 3 × 107 years. We point out that the ratio [N(CO2)N(CH3OH)]lab\hbox{$[\frac{N({\rm CO}_2)}{N({\rm CH_3OH})}]_{\rm lab}$} here defined is different from the ratio NCO2/NX defined in Eq. (6). As above, the expected column density derived from Eq. (7) is to be considered an upper limit. Tables 6 and 7 list the expected column density of CO2 formed after irradiation of carbon grains covered by an ice mantle and after irradiation of CH3OH, assuming a cloud lifetime of 3 × 107 years and the CO2 column density as given by the fit.

From a general analysis of all the fits shown in this work and the fit of the source Elias 16 (a field star) shown by Mennella et al. (2006), we notice that towards field stars: (i) 70−90% of the CO2 bending mode profile is due to CO2 formed after irradiation of carbon grains covered by water ice; (ii) the component due to irradiation of methanol is not required; and (iii) the component due to irradiation of CO-rich ice mantles is less than 20% of total CO2. On the other hand, towards embedded objects: (i) about 2−30% of the CO2 bending mode profile is due to CO2 formed after irradiation of carbon grains covered by water ice; (ii) the component due to irradiation of methanol is generally required; and (iii) the component due to irradiation of CO-rich ice mantles is as high as 20−70% with respect to total CO2. The last point (iii) is compatible with the high depletion of volatile gas phase species observed in starless cores (e.g. Caselli et al. 1999), which are the precursors of embedded objects.

The irradiation doses used in all our experiments correspond to an irradiation time for an interstellar cloud of 107–108 years (Ioppolo et al. 2009), which is compatible with the aforementioned cloud lifetimes. Moreover, as displayed in Tables 6 and 7, we found that our fits are also compatible with the known AV values and observed CH3OH column density. Therefore, the choice of these fits is constrained by laboratory results that indicate the irradiation of C- and O-bearing ices as an important and efficient mechanism to form interstellar CO2 ice in YSOs. Only in the case of a quiescent cloud, namely EC 118 (CK2), the expected CO2 column density formed upon energetic input cannot explain the observed abundances. A similar conclusion is obtained by applying the same calculations to the fit of the CO2 bending mode towards the field star Elias 16 shown by Mennella et al. (2006). Although these are only two sources, this result to be confirmed along the line of sight to different quiescent clouds gives an indirect indication that CO2 can also be formed in a early cloud stage through a different mechanism than for cosmic ray irradiation (e.g., surface reactions induced by non-energetic mechanisms; Oba et al. 2010; Ioppolo et al. 2011; Noble et al. 2011). In a later stage, when ices are exposed to higher UV and cosmic ray doses, the total abundance of CO2 is strongly affected by energetic formation mechanisms.

4. Conclusions

This laboratory work shows that the vibrational bending mode band profile of solid carbon dioxide is sensitive to ice composition and temperature, and in general, is asymmetric. This has been also observed along the line of sight towards several young stellar objects. These sources indeed suffer from a strong thermal gradient. As a consequence, volatile species can sublimate in the inner regions close to the protostar, UV photons are adsorbed by the envelope itself, while in the most external regions the temperature remains at 10−20 K.

It has been suggested (e.g. Palumbo et al. 1998; Teixeira et al. 1998) that low-energy (sMeV) cosmic rays can be responsible for the ion irradiation of C- and O-bearing interstellar ice mantles (10−70 K). Here we give experimental proof that the ion irradiation of ices is one of the most efficient mechanisms for forming new species on interstellar grains. This finding has been achieved by a qualitative and quantitative comparison between observational and laboratory data. A more extensive future work will shed light on the importance of surface reactions induced by non-energetic processes in the early stages of quiescent molecular clouds.

Acknowledgments

We thank F. Spinella for his technical support. This research is in part funded by the LASSIE Initial Training Network, which is supported by the European Community’s Seventh Framework Program (FP7/2007-2013) under Grant Agreement Number 238258. Support for S.I. from the Niels Stensen Fellowship and the Marie Curie Fellowship (FP7-PEOPLE-2011-IOP-300957) is gratefully acknowledged.

References

  1. Allamandola, L. J., Sandford, S. A., & Valero, G. J. 1988, Icarus, 76, 225 [NASA ADS] [CrossRef] [Google Scholar]
  2. Allamandola, L. J., Sandford, S. A., & Tielens, A. G. G. M. 1992, ApJ, 399, 134 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  3. Antonucci, S., Nisini, B., Giannini, T., & Lorenzetti, D. 2008, A&A, 479, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Baragiola, R. A. 2003, in Water in Confining Geometries, eds. V. Buch, & J. P. Devlin (Berlin, Heidelberg: Springer-Verlag), 359 [Google Scholar]
  5. Baratta, G. A., & Palumbo, M. E. 1998, J. Opt. Soc. Am. A, 15, 3076 [Google Scholar]
  6. Baratta, G. A., Palumbo, M. E., & Strazzulla, G. 2000, A&A, 357, 1045 [NASA ADS] [Google Scholar]
  7. Barsony, M., Greene, T. P., & Blake, G. A. 2002, ApJ, 572, L75 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bernstein, M. P., Sandford, S. A., Allamandola, L. J., Chang, S., & Scharberg, M. A. 1995, ApJ, 454, 327 [NASA ADS] [CrossRef] [Google Scholar]
  9. Boogert, A. C. A., Pontoppidan, K. M., Lahuis, F., et al. 2004, ApJS, 154, 359 [NASA ADS] [CrossRef] [Google Scholar]
  10. Boogert, A. C. A., Pontoppidan, K. M., Knez, C., et al. 2008, ApJ, 678, 985 [NASA ADS] [CrossRef] [Google Scholar]
  11. Boonman, A. M. S., van Dishoeck, E. F., Lahuis, F., & Doty, S. D. 2003, A&A, 399, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bottinelli, S., Boogert, A. C., Bouwman, J., et al. 2010, ApJ, 718, 1100 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bourke, T. L., Hyland, A. R., & Robinson, G. 1995, MNRAS, 276, 1052 [NASA ADS] [Google Scholar]
  14. Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
  15. Castelaz, M. W., & Hackwell, J. A. 1987, ApJ, 314, 317 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chiar, J. E., Adamson, A. J., Kerr, T. H., & Whittet, D. C. B. 1995, ApJ, 455, 234 [NASA ADS] [CrossRef] [Google Scholar]
  17. Chiar, J. E., Gerakines, P. A., & Whittet, D. C. B. 1998, ApJ, 498, 716 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  18. Cook, A. M., Whittet, D. C. B., Shenoy, S. S., et al. 2011, ApJ, 730, 124 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dartois, E., Demyk, K., d’Hendecourt, L., & Ehrenfreund, P. 1999, A&A, 351, 1066 [NASA ADS] [Google Scholar]
  20. Ehrenfreund, P., Boogert, A. C. A., Gerakines, P. A., Tielens, A. G. G. M., & van Dishoeck, E. F. 1997, A&A, 328, 649 [NASA ADS] [Google Scholar]
  21. Ehrenfreund, P., Kerkhof, O., Schutte, W. A., et al. 1999, A&A, 350, 240 [NASA ADS] [Google Scholar]
  22. Eiroa, C., & Hodapp, K.-W. 1989, A&A, 210, 345 [NASA ADS] [Google Scholar]
  23. Evans, N. J., Dunham, M. M., Jorgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
  24. Fulvio, D., Sivaraman, B., Baratta, G. A., et al. 2009, Spectrochimica Acta A, 72, 1007 [Google Scholar]
  25. Fulvio, D., Raut, U., & Baragiola, R. A. 2012, ApJ, 752, L33 [NASA ADS] [CrossRef] [Google Scholar]
  26. Gálvez, O., Ortega, I. K., Maté, B., et al. 2007, A&A, 472, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Gálvez, O., Maté, B., Herrero, V. J., & Escribano, R. 2008, Icarus, 197, 599 [NASA ADS] [CrossRef] [Google Scholar]
  28. Garozzo, M., La Rosa, L., Kanuchova, Z., et al. 2011, A&A, 528, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Garrod, R. T., & Pauly, T. 2011, ApJ, 735, 15 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gerakines, P. A., Schutte, W. A., Greenberg, J. M., & van Dishoeck, E. F. 1995, A&A, 296, 810 [NASA ADS] [Google Scholar]
  31. Gerakines, P. A., Schutte, W. A., & Ehrenfreund, P. 1996, A&A, 312, 289 [NASA ADS] [Google Scholar]
  32. Gerakines, P. A., Whittet, D. C. B., Ehrenfreud, P., et al. 1999, ApJ, 522, 357 [NASA ADS] [CrossRef] [Google Scholar]
  33. Gibb, E. L., Whittet, D. C. B., Boogert, A. C. A., & Tielens, A. G. G. M. 2004, ApJS, 151, 35 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  34. Gomis, O., & Strazzulla, G. 2005, Icarus, 177, 570 [NASA ADS] [CrossRef] [Google Scholar]
  35. Goumans, T. P. M., & Andersson, S. 2010, MNRAS, 406, 2213 [NASA ADS] [CrossRef] [Google Scholar]
  36. Goumans, T. P. M., Uppal, M. A., & Brown, W. A. 2008, MNRAS, 384, 1158 [NASA ADS] [CrossRef] [Google Scholar]
  37. Greenberg, J. M. 1982, in Comets, ed. L. L. Wilkening (Tucson: The University of Arizona Press), 131 [Google Scholar]
  38. Greene, T. P., Wilking, B. A., Andrè, P., Young, E. T., & Lada, C. J. 1994, ApJ, 434, 614 [NASA ADS] [CrossRef] [Google Scholar]
  39. Grim, R. J. A., & d’Hendecourt, L. B. 1986, A&A, 167, 161 [NASA ADS] [Google Scholar]
  40. Haikala, L. K., & Reipurth, B. 2010, A&A, 510, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. d’Hendecourt, L. B., & Allamandola, L. J. 1986, A&AS, 64, 453 [NASA ADS] [Google Scholar]
  42. d’Hendecourt, L. B., & Jourdain de Muizon, M. 1989, A&A, 223, L5 [NASA ADS] [Google Scholar]
  43. d’Hendecourt, L. B., Allamandola, L. J., Grim, R. J. A., & Greenberg, J. M. 1986, A&A, 158, 119 [NASA ADS] [Google Scholar]
  44. Henning, Th., Pfau, W., Zinnecker, H., & Prusti, T. 1993, A&A, 276, 129 [NASA ADS] [Google Scholar]
  45. Hudgins, D. M., Sandford, S. A., Allamandola, L. J., & Tielens, A. G. G. M. 1993, ApJS, 86, 713 [NASA ADS] [CrossRef] [Google Scholar]
  46. Ioppolo, S., Palumbo, M. E., Baratta, G. A., & Mennella, V. 2009, A&A, 493, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Ioppolo, S., Cuppen, H. M., van Dishoeck, E. F., & Linnartz, H. 2011, MNRAS, 413, 2281 [NASA ADS] [CrossRef] [Google Scholar]
  48. Jenniskens, P., Baratta, G. A., Kouchi, A., et al. 1993, A&A, 273, 583 [NASA ADS] [Google Scholar]
  49. Jiang, G. J., Person, W. B., & Brown, K. G. 1975, J. Chem. Phys., 62, 1201 [NASA ADS] [CrossRef] [Google Scholar]
  50. Knez, C., Moore, M., Travis, S., et al. 2008, Organic Matter in Space, eds. S. Kwok, & S. Sandford, Proc. IAU Symp., 251, [Google Scholar]
  51. Kruger, A. J., Richter, M. J., Carr, J. R., et al. 2011, ApJ, 729, 145 [NASA ADS] [CrossRef] [Google Scholar]
  52. Lacy, J. H., Faraji, H., Sandford, S. A., & Allamandola, L. J. 1998, ApJ, 501, L105 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  53. Loeffler, M. J., Baratta, G. A., Palumbo, M. E., Strazzulla, G., & Baragiola, R. A. 2005, A&A, 435, 587 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  54. Luhman, K. L. 2008, Handbook of Star Forming Regions Vol. II, ed. B. Reipurth (ASP) [Google Scholar]
  55. Madzunkov, S., Shortt, B. J., MacAskill, J. A., Darrach, M. R., & Chutjian, A. 2006, Phys. Rev. A, 73, 02091 [Google Scholar]
  56. Mennella, V., Baratta, G. A., Esposito, A., Ferini, G., & Pendleton, Y. J. 2003, ApJ, 587, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Mennella, V., Palumbo, M. E., & Baratta, G. A. 2004, ApJ, 615, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  58. Mennella, V., Baratta, G. A., Palumbo, M. E., & Bergin, E. A. 2006, ApJ, 643, 923 [NASA ADS] [CrossRef] [Google Scholar]
  59. Modica, P., & Palumbo, M. E. 2010, A&A, 519, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Moore, M. H., Khanna, R., & Donn, B. 1991, J. Geophys. Res., 96, 17541 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  61. Myers, P. C., Fuller, G. A., Mathieu, R. D., et al. 1987, ApJ, 319, 340 [NASA ADS] [CrossRef] [Google Scholar]
  62. Noble, J. A., Dulieu, F., Congiu, E., & Fraser, H. J. 2011, ApJ, 735, 121 [NASA ADS] [CrossRef] [Google Scholar]
  63. Nummelin, A., Whittet, D. C. B., Gibb, E. L., Gerakines, P. A., & Chiar, J. E. 2001, ApJ, 558, 185 [NASA ADS] [CrossRef] [Google Scholar]
  64. Oba, Y., Watanabe, N., Kouchi, A., Hama, T., & Pirronello, V. 2010, ApJ, 712, L174 [NASA ADS] [CrossRef] [Google Scholar]
  65. Oba, Y., Watanabe, N., Hama, T., et al. 2012, ApJ, 749, 67 [NASA ADS] [CrossRef] [Google Scholar]
  66. Öberg, K., Boogert, A. C. A., Pontoppidan, K. M., et al. 2008, ApJ, 678, 1032 [NASA ADS] [CrossRef] [Google Scholar]
  67. Öberg, K., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [NASA ADS] [CrossRef] [Google Scholar]
  68. Onishi, T., Mizuno, A., Kawamura, A., et al. 1998, ApJ, 502, 296 [NASA ADS] [CrossRef] [Google Scholar]
  69. Palumbo, M. E., & Baratta, G. A. 2000, A&A, 361, 298 [NASA ADS] [Google Scholar]
  70. Palumbo, M. E., Baratta, G. A., Brucato, J. R., et al. 1998, A&A, 334, 247 [NASA ADS] [Google Scholar]
  71. Palumbo, M. E., Castorina, A. C., & Strazzulla, G. 1999, A&A, 342, 551 [NASA ADS] [Google Scholar]
  72. Palumbo, M. E., Baratta, G. A., Collings, M. P., & McCoustra, M. R. S. 2006, Phys. Chem. Chem. Phys., 8, 279 [CrossRef] [PubMed] [Google Scholar]
  73. Palumbo, M. E., Leto, P., Siringo, C., & Trigilio, C. 2008, ApJ, 685, 1033 [NASA ADS] [CrossRef] [Google Scholar]
  74. Pontoppidan, K. M., Fraser, H. J., Dartois, E., et al. 2003, A&A, 408, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Pontoppidan, K. M., Dullemond, C. P., van Dishoeck, E. F., et al. 2005, ApJ, 622, 463 [NASA ADS] [CrossRef] [Google Scholar]
  76. Pontoppidan, K. M., Boogert, A. C. A., Fraser, H. J., et al. 2008, ApJ, 678, 1005 [NASA ADS] [CrossRef] [Google Scholar]
  77. Prasad, S. S., & Tarafdar, S. P. 1983, ApJ, 267, 603 [NASA ADS] [CrossRef] [Google Scholar]
  78. Raut, U., Fulvio, D., Loeffler, M. J., & Baragiola, R. A. 2012, ApJ, 752, 159 [NASA ADS] [CrossRef] [Google Scholar]
  79. Ressler, M. E., & Barsony, M. 2001, AJ, 121, 1098 [NASA ADS] [CrossRef] [Google Scholar]
  80. Romanzin, C., Ioppolo, S., Cuppen, H. M., van Dishoeck, E. F., & Linnartz, H. 2011, J. Chem. Phys., 134, 084504 [NASA ADS] [CrossRef] [Google Scholar]
  81. Roser, J. E., Vidali, G., Manicò, G., & Pirronello, V. 2001, ApJ, 555, L61 [NASA ADS] [CrossRef] [Google Scholar]
  82. Ruffle, D. P., & Herbst, E. 2001, MNRAS, 324, 1054 [NASA ADS] [CrossRef] [Google Scholar]
  83. Sandford, S. A., & Allamandola, L. J. 1990, ApJ, 355, 357 [NASA ADS] [CrossRef] [Google Scholar]
  84. Santos, N. C., Yun, J. L., Santos, C. A., & Marreiros, R. G. 1998, AJ, 116, 1376 [Google Scholar]
  85. Sicilia, D., Ioppolo, S., Vindigni, T., Baratta, G. A., & Palumbo, M. E. 2012, A&A, 543, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Strazzulla, G., & Baratta, G. A. 1991, A&A, 241, 310 [NASA ADS] [Google Scholar]
  87. Talbi, D., Chandler, G. S., & Rohl, A. L. 2006, Chem. Phys., 320, 214 [NASA ADS] [CrossRef] [Google Scholar]
  88. Taylor, K. N. R., & Storey, J. W. V. 1984, MNRAS, 209, 5 [Google Scholar]
  89. Teixeira, T. C., Emerson, J. P., & Palumbo, M. E. 1998, A&A, 330, 711 [NASA ADS] [Google Scholar]
  90. Tielens, A. G. G. M., & Hagen, W. 1982, A&A, 114, 245 [NASA ADS] [Google Scholar]
  91. van Dishoeck, E. F., Helmich, F. P., de Graauw, T., et al. 1996, A&A, 315, L349 [NASA ADS] [Google Scholar]
  92. Watanabe, N., & Kouchi, A. 2002, ApJ, 567, 651 [NASA ADS] [CrossRef] [Google Scholar]
  93. Watson, D. M., Kemper, F., Calvet, N., et al. 2004, ApJS, 154, 391 [NASA ADS] [CrossRef] [Google Scholar]
  94. White, D. W., Gerakines, P. A., Cook, A. M., & Whittet, D. C. B. 2009, ApJS, 180, 182 [NASA ADS] [CrossRef] [Google Scholar]
  95. Whittet, D. C. B., Shenoy, S. S., Bergin, E. A., et al. 2007, ApJ, 655, 332 [NASA ADS] [CrossRef] [Google Scholar]
  96. Wilking, B. A., & Lada, C. J. 1983 ApJ, 274, 698 [NASA ADS] [CrossRef] [Google Scholar]
  97. Wilking, B. A., Lada, C. J., & Young, E. T. 1989, ApJ, 340, 823 [NASA ADS] [CrossRef] [Google Scholar]
  98. Wilking, B. A., Greene, T. P., Lada, C. J., et al. 1992, ApJ, 397, 520 [NASA ADS] [CrossRef] [Google Scholar]
  99. Yamada, H., & Person, W. B. 1964, J. Chem. Phys., 41, 2478 [NASA ADS] [CrossRef] [Google Scholar]
  100. Zasowski, G., Kemper, F., Watson, D. M., et al. 2009, ApJ, 694, 459 [NASA ADS] [CrossRef] [Google Scholar]
  101. Ziegler, J. F., Biersack, J. P., & Ziegler, M. D. 2008, The stopping and range of ions in solids (New York: Pergamon Press), see also http://www.srim.org [Google Scholar]

All Tables

Table 1

List of the database spectra relative to irradiation of CO-rich ice samples with 200 keV H+ and 30 keV He+.

In the text
Table 2

List of the database spectra relative to irradiation of pure methanol ice with 30 keV He+.

In the text
Table 3

List of the band strength (A) values used here.

In the text
Table 4

List of selected low-mass young stellar objects and a field star observed by the Spitzer Space Telescope.

In the text
Table 5

Column density values for CO2, CO, H2O, CH3OH and NH3 along the line of sight to selected young stellar objects and a field star.

In the text
Table 6

Expected solid CO2 (upper limits) formed after cosmic ion irradiation of water ice onto carbon grains (Ioppolo et al. 2009) for some selected sources for which AV is known compared to the column density of CO2 in water ice as obtained by the fit.

In the text
Table 7

Expected solid CO2 (upper limits) formed after cosmic ion irradiation of CH3OH ice based on laboratory data (Ioppolo et al. 2009) for some selected sources for which CH3OH column density is known compared to the column density of CO2 formed from methanol as obtained by the fit.

In the text

All Figures

thumbnail Fig. 1

A schematic top view of the high vacuum chamber.
In the text
thumbnail Fig. 2

The bending mode band profile of the carbon dioxide in several ice mixtures irradiated with 200 keV H+ or 30 keV He+ and annealed. The spectra are acquired with a resolution of 1 cm-1 and the open symbols are only reported for clarity.
In the text
thumbnail Fig. 3

The mid-IR spectra of water ice covering carbon grains before and after irradiation with 200 keV H+ at 17 K. The internal panel shows the newly formed solid CO2 bending mode band profile.
In the text
thumbnail Fig. 4

Comparison between the CO2 bending mode band profile towards several low-mass young stellar objects (open squares) and laboratory spectra. The spectra are acquired with a resolution of 1 cm-1 and the symbols are only reported for clarity. The fits are represented by solid thick lines.
In the text
thumbnail Fig. 4

continued.
In the text
thumbnail Fig. 5

As for Fig. 4. Here a field star is also compared to laboratory data.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.