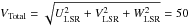| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 18 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321082 | |
| Published online | 07 June 2013 | |
The metallicity signature of evolved stars with planets⋆,⋆⋆
Universidad Autónoma de Madrid, Dpto. Física Teórica, Módulo 15, Facultad
de Ciencias,
Campus de Cantoblanco,
28049
Madrid,
Spain
e-mail:
jesus.maldonado@uam.es
Received: 11 January 2013
Accepted: 12 March 2013
Context. Currently, the core accretion model has its strongest observational evidence on the chemical signature of mostly main sequence stars with planets.
Aims. We aim to test whether the well-established correlation between the metallicity of the star and the presence of giant planets found for main sequence stars still holds for the evolved and generally more massive giant and subgiant stars. Although several attempts have been made so far, the results are not conclusive since they are based on small or inhomogeneous samples.
Methods. We determine in a homogeneous way the metallicity and individual abundances of a large sample of evolved stars, with and without known planetary companions, and discuss their metallicity distribution and trends. Our methodology is based on the analysis of high-resolution échelle spectra (R ≥ 67 000) from 2−3 m class telescopes. It includes the calculation of the fundamental stellar parameters (Teff, log g, microturbulent velocity, and metallicity) by applying iron ionisation and excitation equilibrium conditions to several isolated Fe i and Fe ii lines, as well as, calculating individual abundances of different elements such as Na, Mg, Si, Ca, Ti, Cr, Co, or Ni.
Results. The metallicity distributions show that giant stars hosting planets are not preferentially metal-rich because they have similar abundance patterns to giant stars without known planetary companions. We have found, however, a very strong relation between the metallicity distribution and the stellar mass within this sample. We show that while the less massive giant stars with planets (M⋆ ≤ 1.5 M⊙) are not metal rich, the metallicity of the sample of massive (M⋆ > 1.5 M⊙), young (age < 2 Gyr) giant stars with planets is higher than that of a similar sample of stars without planets. Regarding other chemical elements, giant stars with and without planets in the mass domain M⋆ ≤ 1.5 M⊙ show similar abundance patterns. However, planet and non-planet hosts with masses M⋆ > 1.5 M⊙ show differences in the abundances of some elements, specially Na, Co, and Ni. In addition, we find the sample of subgiant stars with planets to be metal rich, showing similar metallicities to main-sequence planet hosts.
Conclusions. While the metallicity distribution of planet-hosting subgiant stars and giant stars with stellar masses M⋆ > 1.5 M⊙ fits well in the predictions of current core-accretion models, the fact that giant planet hosts in the mass domain M⋆ ≤ 1.5 M⊙ do not show metal enrichment is difficult to explain. Given that these stars have similar stellar parameters to subgiants and main-sequence planet hosts, the lack of the metal-rich signature in low-mass giants could be explained by a pollution scenario in the main sequence that gets erased as the star becomes fully convective. However, there is no physical reason why it should play a role for giants with masses M⋆ ≤ 1.5 M⊙ yet not be observed for giants with M⋆ > 1.5 M⊙.
Key words: techniques: spectroscopic / stars: abundances / stars: late-type / planetary systems
Based on observations made with the Mercator Telescope, operated on the island of La Palma by the Flemish Community, and on observations made with the Nordic Optical Telescope, operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden.
Full Tables 2, 3, 5, and 7 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/554/A84
© ESO, 2013
1. Introduction
Understanding the origin and evolution of planets and planetary systems is one of the major goals of modern astrophysics. Twenty years after the discovery of the first exoplanets (Wolszczan & Frail 1992; Mayor & Queloz 1995), we are still far from understanding which stellar properties influence (and how) planet formation the most. Excluding the well-established correlation between stellar metallicity and the probability that the star hosts a gas-giant planet (e.g. Santos et al. 2004; Fischer & Valenti 2005), any other claim of a chemical trend in planet-hosting stars has been so far disputed. For instance, the evidence of a higher depletion of lithium in planet host stars has been the subject of an intense discussion (e.g. Israelian et al. 2009; Baumann et al. 2010; Ghezzi et al. 2010c; Sousa et al. 2010, and references therein), as well as whether stars with planets (specially solar analogs) show different trends on abundance-condensation temperature (see Ramírez et al. 2010; González Hernández et al. 2010, 2013; Gonzalez 2011; Schuler et al. 2011, and references therein).
The planet-metallicity correlation itself has been revealed to be more complex than initially thought, as stars with orbiting low-mass planets (Mpsini < 30 M⊕) do not seem to be preferentially metal rich (Ghezzi et al. 2010b; Mayor et al. 2011; Sousa et al. 2011, and references therein). This observational result, which is explained within the framework of core-accretion models (e.g. Pollack et al. 1996; Rice & Armitage 2003; Alibert et al. 2004; Mordasini et al. 2012), assumes that the timescale needed to form an icy/rocky core is largely dependent on the metal content of the protostellar cloud. In this way, in low-metal environments, the gas has already been depleted from the disk by the time the cores are massive enough to start a runaway accretion of gas. As a result, only low-mass planets can be formed. The metallicity patterns found in stars hosting dusty debris disks also agree with the predictions of this scenario of planet formation (see Maldonado et al. 2012, and references therein).
Observations of solar-type (FGK dwarfs) main sequence (MS) planet hosts point towards a metal-rich nature of the MS stars throughout their interiors and therefore to a primordial nature of the metallicity enhancement (e.g. Santos et al. 2004; Fischer & Valenti 2005). Alternative scenarios in which the metal enhancement results from the late-stage accretion of H and He-depleted material onto the convective zone of the star (Gonzalez 1997; Laughlin & Adams 1997) were rapidly ruled out. With our current understanding, and given its primordial nature, the observed correlation between the metallicity of the star and the presence of planets should also hold for red giants and subgiant stars that, having left the MS when they exhaust the hydrogen in the core, have larger radii, cooler photospheres, and are convective for the most part.
The opportunity of testing how well founded the planet-metallicity relation is with a statistically sound sample of evolved stars has become recently possible due to the large number of planets found by the different successful surveys. Some examples include the Lick K-giant Survey (Frink et al. 2002), the Okayama Planet Search (Sato et al. 2003), the Retired A stars and Their Companions (Johnson et al. 2007), and the Pennsylvania-Toruń Planet Search (Niedzielski et al. 2007).
The first conclusions regarding the metallicity of giant stars that host planets were based on the analysis of small or inhomogeneous samples obtained from the different surveys available: Sadakane et al. (2005, with 4 planet-hosting stars analysed), Schuler et al. (2005, 1 star), Pasquini et al. (2007, 10 stars). These studies suggested that, unlike their MS counterparts, G and K giants stars with planets do not have a tendency to show metal enrichment. An attempt to expand the sample size, setting stellar metallicities from the literature in a common spectroscopic scale, is made by Hekker & Meléndez (2007, with a total of 20 planet hosts analysed) where they find evidence that the giant planet metallicity correlation might also hold for giants stars. More recently, studies based on the analysis of high-resolution spectra, Takeda et al. (2008, ten stars), and Ghezzi et al. (2010a, 16 stars), point again towards a lack of a planet-metallicity relation for giant stars. This latter study also included 15 subgiants with planets which are found to have, on average, the same metallicity distribution as a sample of dwarf stars with planets.
Evidence that subgiant stars with planets might follow the planet-metallicity correlation was previously reported by Fischer & Valenti (2005), who analysed nine subgiant stars with planets from a total of 1040 stars observed as part of the California & Carnegie and the Anglo-Australian planet search projects. The metallicity distribution of the planet-host subgiant stars appeared to be consistent with that of MS stars with planets, being more metal-rich than their counterparts without detected planets. A recent analysis of the California Planet Survey targets is presented in Johnson et al. (2010), who analysed a sample of 1266 stars, including a broad range of stellar masses from late-K and M stars to subgiants with masses up to 1.9 M⊙. The authors found evidence of a planet-metallicity correlation for all stellar masses, even when the sample was restricted to subgiant stars with masses in the range M⋆ > 1.4 M⊙ (including 36 planet hosts). The occurrence of gas-giant planets was found to be not only dependent on the stellar metallicity, but it also scaled with the stellar mass (see also Johnson et al. 2011).
Several explanations have been put forward to explain the observed metallicity distribution of giant planet hosts, i.e. that planets around intermediate-mass stars are formed preferentially by instabilities and thus are not dependent on the metallicity of the primordial disk (see discussion in Pasquini et al. 2007), or that there was late-stage accretion of depleted material onto the convective zone of the star (Gonzalez 1997; Laughlin & Adams 1997). Moreover, recent simulations of planet population synthesis (Alibert et al. 2011; Mordasini et al. 2012), which are based on the core-accretion model of planet formation, have shown that stellar mass can play a role in planet formation by scaling the mass of the protoplanetary disk. In this scenario, a high-mass protoplanetary disk might compensate (at least up to certain point) for a low-metallicity environment, allowing the formation of giant planets even around low-metallicity stars. The positive correlation found between the presence of gas-giant planets with both stellar metallicity and stellar mass (e.g. Johnson et al. 2010) could be then explained by assuming that higher mass stars are likely to form with more massive protoplanetary disks.
We believe that the analysis of a homogeneous and large sample of evolved stars hosting planets is needed before an explanation about the apparent nature of the metallicity correlation for evolved stars is invoked. This is the goal of this paper, in which we present a homogeneous analysis of a large sample of evolved stars that is based on high resolution and high signal-to-noise ratio (S/N) échelle spectra.
The paper is organised as follows: Sect. 2 describes the stellar samples analysed in this work, the spectroscopic observations, and how stellar parameters and abundances are obtained. In order to explore the presence of any possible bias that could affect our analysis, the samples are compared in terms of age, distance, and kinematics, the parameters that most likely might affect the metallicity content of a star. Possible non-local thermodynamic equilibrium (non-LTE) effects are also discussed. The metallicity distributions are presented in Sect. 3, together with an exploration of the parameters that could explain the results and the properties of the planets orbiting around evolved stars. The results are discussed at length in Sect. 4. Our conclusions follow in Sect. 5.
2. Observations
2.1. The stellar sample
Our sample contains 142 evolved stars, of which 70 are known to host at least one planetary companion according to the available data at the Extrasolar Planets Encyclopaedia1. The selection criterion of the sample was very simple: from the list of evolved stars with confirmed planetary companions, we kept those stars for which a high S/N spectra (at least 100) could be taken with the combination of instruments and telescopes used. The control sample was drawn from the Massarotti et al. (2008) list of Hipparcos giants within 100 pc from the Sun to cover similar stellar parameters as the stars with detected planets.
Figure 1 shows the Hertzsprung-Russell (HR) diagram of the observed stars. They are classified as red giants (blue triangles, giants from now on), subgiants (red squares), and late MS (green asterisks). The classification among the different luminosity classes is somehow uncertain for those stars which are in the boundary between two classes. In order to distinguish between subgiants and red giants, a limit in Mbol = 2.82 mag (as in Ghezzi et al. 2010a) was set, although some stars brighter than 2.82 mag which had not yet started their ascent into the red giant branch (RGB) were kept as subgiants. In addition, 11 stars which are above the MS tracks on the HR diagram, but have not yet moved towards the red, have been denoted as late MS stars. According to their luminosity class and taking into account the presence (or absence) of planetary companions, our sample is divided into 43 giant stars with known planets (hereafter GWPs), 67 giant stars without planets (GWOPs), 16 subgiants hosting planets (SGWPs), 5 subgiants without planets (SGWOPs), and 11 late MS stars harbouring planets (LMSWPs). The sample of subgiant stars has been supplemented with data from the literature (see Sect. 2.6).
 |
Fig. 1 Luminosity versus Teff diagram for the observed stars. Giants are plotted with blue triangles, subgiants with red squares, and late MS stars with green asterisks. Filled symbols indicate planet hosts. Some evolutionary tracks ranging from 0.7 to 3.0 solar masses from Girardi et al. (2000) are overplotted. For each mass, three tracks are plotted, corresponding to Z = 0.008 ([Fe/H] = −0.4 dex, dotted lines), Z = 0.019 ([Fe/H] = + 0.0 dex, solid lines), and Z = 0.030 ([Fe/H] = + 0.20 dex, dashed lines). |
2.2. Spectroscopic observations
High-resolution spectra of the stars were obtained at La Palma observatory (Canary Islands, Spain) during four observing runs (two at the MERCATOR telescope and two at the Nordic Optical Telescope) between February and August 2011. At the MERCATOR telescope (1.2 m), 28 stars were observed with the HERMES spectrograph (Raskin et al. 2011). HERMES spectra have a resolution of R ~ 85 000 and cover the spectral range λλ 3800−9000 Å. They were automatically reduced by a detailed data reduction pipeline available at the telescope2. The rest of the data, 114 stars, was obtained with the FIES instrument (Frandsen & Lindberg 1999) at the Nordic Optical Telescope (2.56 m). FIES spectra cover a slightly shorter wavelength range, from 3640 to 7360 Å, with a resolution of R ≈ 67 000. They were reduced using the advanced option of the automatic data reduction tool FIEStool3. Both pipelines implement the typical corrections involved in échelle spectra reduction, i.e. bias level, flat-fielding, scattered light correction, removing of the blazeshape, order extraction, wavelength calibration, and merge of individual orders. HERMES spectra have S/N values between 90 and 340, with an average of ~150/160 in the spectral range around the Hα line. In the same spectral range, FIES spectra have a S/N of roughly 75 in the worst cases, but up to 480 in the best ones. The average value is around 225. The log of the observations is given in Table 1.
The spectra were corrected from radial velocity shifts by using the IRAF4 task dopcor. Radial velocities were previously measured by cross-correlating the spectra of our programme stars with spectra of radial velocity standard stars of similar spectral types obtained during the observations.
Observing runs performed on 2011.
Spectroscopic parameters with uncertainties for the stars measured in this work.
2.3. Analysis
The basic stellar parameters Teff, log g, microturbulent velocity (ξt), and [Fe/H] are determined using the code TGVIT5 (Takeda et al. 2005), which is based on iron ionization and excitation equilibrium conditions.
Iron abundances are computed for a well-defined set of 302 Fe I and 28 Fe II lines. Basically, the stellar parameters are adjusted until: i) no dependence is found between the abundances derived from Fe I lines and the lower excitation potential of the lines; ii) no dependence is found between the abundances derived from the Fe I lines and their equivalent widths; and iii) the derived mean Fe I and Fe II abundances are the same. The line list as well as the adopted parameters (excitation potential, log (gf) values, solar EWs) can be found on Y. Takeda’s web page. This code makes use of ATLAS9, plane-parallel, LTE atmosphere models (Kurucz 1993). The assumed solar Fe abundance is A⊙ = 7.50, as in Takeda et al. (2005). Uncertainties in the stellar parameters are computed by progressively changing each stellar parameter from the converged solution to a value in which any of the aforementioned conditions i), ii), iii) are no longer fulfilled. Uncertainties in the iron abundances are computed by propagating the errors in Teff, log g, and ξt. We are aware that this procedure only evaluates “statistical” errors. However, other systematic sources of uncertainties, such as the choice of atmosphere model, the adopted atomic parameters, or the list lines used, are difficult to estimate (see for details, Takeda et al. 2002a,b).
In order to avoid errors due to uncertainties in the damping parameters, only lines with EWs < 120 mÅ were considered (e.g. Takeda et al. 2008). Stellar EWs are measured using the automatic code ARES (Sousa et al. 2007). In order to test the quality of the EWs measured by ARES, we selected four representative stars of our sample that covered the whole space of parameters, namely HIP 118319 (5989 K), HIP 50887 (5001 K), HIP 42527 (4516 K), HIP 100587 (4259 K), and measured the EWs of iron lines “manually” by using the IRAF task splot. Median differences between the measured EWs are: ⟨ EWARES − EWIRAF ⟩ = −0.39 ± 2.1 mÅ, −0.34 ± 2.1 mÅ, −0.48 ± 2.6 mÅ, and −0.74 ± 4.1 mÅ for HIP 118319, HIP 50887, HIP 42527, HIP 118319, respectively. We do not find any significant difference between ARES equivalent widths and the manual measurements. The estimated stellar parameters and iron abundances are given in Table 2.
2.4. Photometric parameters and comparison with previous works
Photometric effective temperatures are derived from the Hipparcos (B − V) colours (Perryman & ESA 1997) by using the calibration provided by Casagrande et al. (2010, Table 4). Uncertainties in the photometric temperatures are estimated by taking into account the standard deviation of the calibration (~73 K), the uncertainty in the zero point of the temperature scale (which is, according to the authors, of the order of 15−20 K), and the propagation of the errors associated with colours and metallicities. These three sources of uncertainty have been added quadratically. Although this calibration was built using dwarfs and subgiant stars, we find that it also reproduces the spectroscopic temperatures obtained for our sample of giants.
Since our sample contains stars up to roughly 0.5 kpc, colours are de-reddened before we compute the photometric temperatures. Visual extinction, AV, and colour excesses, E(B − V)6, are computed as a function of the stellar distance and the galactic coordinates (l, b) by interpolating in the tables given by Arenou et al. (1992). Distances are obtained from the revised parallaxes provided by van Leeuwen (2007) from a new reduction of the Hipparcos’s raw data. For the five stars with planets that do not have Hipparcos’s data, the parallaxes were taken from the papers in which the discovery of the corresponding planets was announced. The comparison between the temperature values obtained by both procedures, spectroscopic and photometric, is illustrated in Fig. 2, where we do not find any sound systematic difference between them. The mean value of ΔTeff is ~−16 K, with a standard deviation of only 96 K. We also computed photometric temperatures using the calibration provided by González Hernández & Bonifacio (2009, Table 5), since this relationship was built using giant stars. We note that the temperatures obtained with this relationship tend to be slightly cooler than the ones obtained by using the relationship provided by Casagrande et al. (2010). They are therefore slightly cooler than our spectroscopic values. Nevertheless, the difference ΔTeff is small, ~71 K, with a standard deviation of 88 K. The small offset between both calibrations may be related to the different absolute calibration and zero points adopted for Vega (González Hernández & Bonifacio 2009; Casagrande et al. 2010).
Values of the stellar luminosities (log L⋆/L⊙) are estimated from the absolute magnitudes and bolometric corrections using the measurements by Flower (1996, Table 3). Uncertainties in the stellar luminosities were computed by propagating the errors associated with the V magnitudes, visual extinction, parallaxes, and effective temperatures. Estimates of the uncertainty in the visual extinction are already given in the tables by Arenou et al. (1992), while typical uncertainties in V are ±0.01 mag (Perryman & ESA 1997). Bolometric corrections were derived as a function of Teff. For the error computations, the uncertainty due to the propagation of the errors in Teff and the sigma of the calibration BC-Teff have been added quadratically. The values of visual extinction, photometric temperatures and luminosities, are shown in Table 3.
 |
Fig. 2 Comparison between our spectroscopically derived Teff and those obtained from (B − V) colours. The upper panel shows the differences between the spectroscopic and the photometric values. Mean uncertainties in the derived temperatures are also shown. |
Photometric and evolutionary parameters for the stars measured in this work (see text for details).
Evolutionary values of gravities are computed from Hipparcos V magnitudes and parallaxes using L. Girardi’s code PARAM7 (da Silva et al. 2006), which is based on the use of Bayesian methods. Our derived spectroscopic Teff and metallicities are used as inputs for PARAM. The code also estimates the stellar evolutionary parameters of age, mass, and radius. These quantities are also given in Table 3, while a comparison between the spectroscopic and evolutionary log g values is shown in Fig. 3. It is clear from the figure that spectroscopic log g values tend to be systematically larger than the evolutionary estimates. Specifically, spectroscopic values are ~0.09 larger (in median) than the evolutionary estimates with a standard deviation of 0.13. Such a trend of larger spectroscopic log g values has already been reported and discussed by several authors (e.g. da Silva et al. 2006, and references therein) pointing towards non-LTE effects on Fe I abundances or thermal inhomogeneities as possible causes. We note, however, that the standard deviation of the distribution log gspec − log gevol is 0.13, which is of the same order of magnitude of the uncertainties in the spectroscopically derived log g values. Therefore, we may state that our spectroscopic values are in agreement (within the uncertainties) with the evolutionary estimates, ruling out significant departures from LTE conditions (see discussion in Sect. 2.7).
There is one outlier, namely BD+20 2457 (left upper corner in Fig. 3); but this is due to its largely undetermined parallax, π = 5.0 ± 26.0 mas (Niedzielski et al. 2009).
 |
Fig. 3 Spectroscopically derived log g values versus log g estimates based on Hipparcos parallaxes. The upper panel shows the differences between the spectroscopic and the Hipparcos values. Mean uncertainties in log g values are also shown. |
We finally compare our metallicities with those already reported in the literature. Values for the comparison are taken from the Extrasolar Planets Encyclopaedia8 (and references therein) as well as from Hekker & Meléndez (2007), Luck & Heiter (2007), Takeda et al. (2008), and Ghezzi et al. (2010a), where we were able to find literature metallicities for roughly 70% of our programme stars. The comparison is shown in Fig. 4. The agreement is overall good, with ⟨[Fe/H]this work − [Fe/H]other works ⟩ = + 0.00 dex and a standard deviation of 0.08 dex.
2.5. Abundance computation
Chemical abundances of individual elements (Na, Mg, Al, Si, Ca, Sc, Ti i, Ti ii, Mn, Cr i, Cr ii, V, Co, Ni, Zn) are obtained using the WIDTH9 programme (Castelli 2005) together with ATLAS9 atmosphere models (Kurucz 1993), updated to work under Linux by Sbordone et al. (2004) and Sbordone (2005).
The measured equivalent widths of a list of narrow, non-blended lines for each of the aforementioned ions are used as inputs for WIDTH9. The selected lines are mainly taken from the list provided by Neves et al. (2009, Table 2), although we keep the parameters of the lines (excitation potential, oscillator strength) as given in Kurucz’s lists of lines. For Zn abundances, the lines at 4810.54 and 6362.34 Å were considered.
 |
Fig. 4 [Fe/H] values, this work, versus literature estimates. The upper panel shows the differences between the metallicities derived in this work and the values given in the literature. |
We have used the four representative stars mentioned in Sect. 2.3 in order to provide an estimate on how the uncertainties in the atmospheric parameters propagate into the abundance calculation. Abundances for each of these four stars were recomputed using Teff + ΔTeff, Teff − ΔTeff, and similarly for log g and ξt. Results are given in Table 4. As final uncertainties for the derived abundances, we give the quadratical sum of the uncertainties due to the propagation of the errors in the stellar parameters, plus the line-to-line scatter errors (computed as 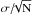 , where σ is the standard deviation of the derived individual abundances from the N lines). We would like to point out here that even these uncertainties should be considered as lower limits, given that the errors in the stellar parameters are only statistical (as explained in Sect. 2.3), and the abundance estimates are affected by systematics which are not taken into account in line-to-line errors (i.e. atomic data or uncertainties in the atmosphere models). The abundances obtained are given in Table 5. They are expressed relative to the solar values provided by Asplund et al. (2009).
, where σ is the standard deviation of the derived individual abundances from the N lines). We would like to point out here that even these uncertainties should be considered as lower limits, given that the errors in the stellar parameters are only statistical (as explained in Sect. 2.3), and the abundance estimates are affected by systematics which are not taken into account in line-to-line errors (i.e. atomic data or uncertainties in the atmosphere models). The abundances obtained are given in Table 5. They are expressed relative to the solar values provided by Asplund et al. (2009).
A comparison of our derived abundances with those previously reported in the literature is shown in Fig. 5. Derived abundances of Na, Al, Ti, and Ni agree reasonably well with previously reported values, with the σ of the distribution [X/H] (this work) – [X/H] (other work) ranging from ~0.03 to 0.08 dex, although our abundances seem to be slightly shifted towards higher values (maximum mean differences ≤~0.08 dex). In the cases of Si and Ca, our abundances are in median a bit larger (~0.1 dex) than those given in Gilli et al. (2006) and Valenti & Fischer (2005), but in agreement with Luck & Heiter (2007); Takeda (2007); Takeda et al. (2008). For Mg, our abundances are on average a bit lower (within 0.1 dex) than those given by Valenti & Fischer (2005) and Gilli et al. (2006), although in excellent agreement with Takeda (2007). Abundances of Cr and Co are slightly lower than those previously reported, especially in the case of Co, but mean differences are still within ±0.1 dex. The largest dispersions are found for Sc, V, and Mn, probably due to the small number of lines used for these elements or uncertainties in the atomic parameters. It is well known that some lines of Sc, V, Mn (and also Co) split into different subcomponents due to electron-nucleus interactions showing a significant hyperfine structure, (e.g. Schuler et al. 2011). A hyperfine structure (hfs) has not been considered in our analysis and, as a consequence, the abundances of these elements may be overestimated. We note, however, that the differences between hfs synthesis abundances and equivalent width-based abundances derived by Schuler et al. (2011) are small, ≤0.04 dex, in 8 out of the 10 late-F and G type analysed stars. In addition, we do not expect hfs effects to bias the results of the comparisons performed in this work (see Sect. 3.4) between samples of stars with and without planets, given that they have otherwise similar properties.
Finally, considering Zn, only Takeda et al. (2008) give abundances for this element. Despite the small number of stars in common, the agreement is quite clear, as shown in Fig. 5.
 |
Fig. 5 Comparison of our abundances to those of Beirão et al. (2005) (∗), Bensby et al. (2005) (open circles), Valenti & Fischer (2005) (+), Gilli et al. (2006) (×), Luck & Heiter (2007) (open triangles), Takeda (2007) (open squares), Takeda et al. (2008) (diamonds), and Neves et al. (2009) (filled triangles). |
Abundance sensitivities.
Derived abundances of Na, Mg, Al, Si, Ca, Sc, Ti i, Ti ii, V, Cr i, Cr ii, Mn, Co, Ni, and Zn.
2.6. Expanding the SGWOP sample
Given the small number of stars observed that are classified as SGWOPs, we expanded the sample with data from the literature in order to make a proper comparison between the properties of subgiants with and without planetary companions. We added to the SGWOP sample those stars given in Valenti & Fischer (2005, hereafter VF05) which fulfilled our criteria for being classified as subgiants (Sect. 2.1). These stars have been monitored for planets on the Keck, Lick, and Anglo-Australian Telescope planet search programmes, discarding the presence of planetary companions with radial velocity semiamplitudes K > 30 m s-1 and orbital periods shorter than 4 yr (Fischer & Valenti 2005). Stars already observed by us, as well as stars with recently discovered planets, were discarded. The final number of stars added to the SGWOP sample amounted to 50.
To keep the analysis as homogeneous as possible, VF05 metallicities were set into our own metallicity scale by using the stars in common. A linear fit was made, obtaining the following linear transformation: [Fe/H] (our scale) = (0.96 ± 0.11) × [Fe/H] (VF05) – (0.04 ± 0.03), (rms = 0.07, 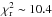 ). Effective temperatures provided by VF05 were also set into our own temperature scale by using the linear relationship Teff (our scale) = (1.02 ± 0.03) × Teff (VF05) – (140 ± 179), (rms = 42,
). Effective temperatures provided by VF05 were also set into our own temperature scale by using the linear relationship Teff (our scale) = (1.02 ± 0.03) × Teff (VF05) – (140 ± 179), (rms = 42, 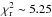 ). Considering log g values, we get the following transformation: log g (our scale) = (1.17 ± 0.06) × log g (VF05) – (0.79 ± 0.26), (rms = 0.009,
). Considering log g values, we get the following transformation: log g (our scale) = (1.17 ± 0.06) × log g (VF05) – (0.79 ± 0.26), (rms = 0.009, 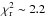 ).
).
Stellar ages, masses, and radius for these stars were recomputed, following the same procedure as the one used for the stars analysed in this work (Sect. 2.4), and are also listed in Table 3.
2.7. Possible biases
Before we proceed further in the comparison between the different samples, an exploration of the possible sources of bias that could mimic metallicity differences is called for. Metallicity reflects the enrichment history of the interstellar medium (see e.g. Timmes et al. 1995). It is, therefore, important to determine whether the different samples have randomly selected stellar hosts in terms of age, distance, and kinematics, which are the parameters most likely to reflect the original metal content of the molecular cloud where the stars were born. The properties of the stars obtained with the procedure explained in the previous subsections are summarised for the different samples in Table 6.
A comparison of the stellar properties among the different samples shows that planet hosts tend to be systematically at larger distances than stars without known planetary companions. This is not unexpected since we selected the control sample from stars within 100 pc, while the sample of stars with planets is not volume limited. To check whether there is a systematic trend in the metallicity due to the distance, the [Fe/H]-distance space is shown in Fig. 6. It can be seen from the figure that GWPs and GWOPs located within ~100 pc are well mixed in the [Fe/H]-distance plane showing a similar behaviour. At slightly larger distances and up to 200 pc, the GWP sample covers approximately the same range in [Fe/H] as the sample within ~100 pc. However, the four GWPs located beyond 200 pc have very small negative metallicities, especially BD+20 2457 (already mentioned in Sect. 2.4). We consider this figure (four stars, ~9% of the whole GWP sample) too low to bias the metallicity distribution of the GWP sample, so we do not expect any significant chemical difference between the GWP and GWOP samples introduced by their distances from the Sun. Nevertheless, we checked whether this is indeed the case in Sect. 3.2.
Comparison between the properties of the different samples studied in this work.
Thick-disk stars are expected to be relatively old (e.g. Bensby et al. 2005), metal poor, and to show α-enhancement (e.g. Fuhrmann 1998; Haywood 2008b; Adibekyan et al. 2011). We checked whether there are differences between the various samples in terms of membership to the thin/thick disk. The procedure involves measuring radial velocities by cross-correlating the spectra of the stars with spectra of radial velocity standard stars of similar spectral types. For the SGWOPs stars from the literature, the radial velocities values have been mainly taken from the compilation by Kharchenko et al. (2007).
Galactic spatial-velocity components (U,V,W) are computed from the radial velocities, together with Hipparcos parallaxes (van Leeuwen 2007) and Tycho-2 proper motions (Høg et al. 2000), following the procedure described in Montes et al. (2001), and Maldonado et al. (2010). The radial velocity of the centre of mass of the system is used for stars in known binary systems. Finally, stars were classified as belonging to the thin/thick disk applying the methodology described in Bensby et al. (2003, 2005).
Figure 7 shows the Toomre diagram for the observed stars, while the derived velocities are given in Table 7. This type of diagram constitutes a useful way to discriminate stellar populations in velocity space, since it plots the energy versus the angular momentum properties of the stars (e.g. Fuhrmann 2004). We find that ~80% of the stars belong to the thin disk and do not find any difference in the distribution of the different samples; in particular, there are no differences between planet host and stars without planets. While our classification of thin/thick disk stars is based only on kinematical criteria, a complete description of the thin/thick disk populations would require the combination of kinematics, metallicities, and stellar ages (e.g. Fuhrmann 1998). Nevertheless, the methodology used is sufficient to discard the presence of a significant fraction of thick-disk stars within our samples.
We note that the two GWP stars, which are possible members of the thick disk, have low metallicities ([Fe/H] < −0.3 dex) and ~43% of the GWPs, classified as transition stars, also have metallicities below − 0.3 dex. Haywood (2008a) argued that at metallicities [Fe/H] <−0.3 dex, giant planets seem to favour thick-disk stars. While statistics of thick-disk stars are small in our sample, they do not contradict Haywood’s idea.
 |
Fig. 7 Toomre diagram of the observed stars. Colours and symbols are as in Fig. 1. Dash-dot lines indicate constant total velocities, |
Radial velocities and Galactic spatial-velocity components for the observed stars.
Both samples of giant stars, with and without planets, cover a wider stellar mass range and represent on average a younger population of stars than the subgiant or late MS samples. The metallicity biases possibly hidden in the age and mass of the different samples are too complicated to discuss at length at this point; we refer their full examination to Sect. 3.
2.8. Non-LTE effects
If present, non-LTE effects should not constitute a bias in the comparison between groups of stars at the same evolutionary stage, provided that the samples are composed of a statistically significant number of stars showing similar properties (see previous section). Another issue, however, is whether non-LTE effects might bias the comparison of samples of stars at different stages in their evolution (dwarf/subigant/giant) by affecting in bulk the abundance determination within a group of stars.
The non-LTE corrections to the abundance determination increase with decreasing [Fe/H] and log g, showing a strong dependence on the effective temperature in dwarf stars (e.g. Bergemann et al. 2011). For the giant stars considered in this work, non-LTE corrections would be ≲0.1 dex, while for the hottest (i.e. the “worst” case) subgiants and late MS stars, non-LTE corrections could be up to ~0.1 dex (Bergemann et al. 2011, Fig. 3). Mashonkina et al. (2011) also analyse LTE and non-LTE iron abundances for five stars covering a wide range of stellar parameters (Teff: 4600−6400 K, log g: 1.60−4.5 dex, [Fe/H]: − 2.7 to +0.10 dex). The authors find that departures from LTE do not exceed 0.1 dex for stars with solar metallicity and mildly metal-deficient stars.
When significant departures from LTE populations in Fe I and Fe II are present, an LTE analysis produces systematically underestimated gravities and metallicities (e.g. Lind et al. 2012). Therefore, the comparison of log gspec and log gevol provides a mechanism to investigate whether non-LTE effects are significant or not. As discussed in Sect. 2.4, the standard deviation of the distribution log gspec − log gevol is of the same order of magnitude of the uncertainties in the spectroscopic log g values. In addition, a linear fit of (log gspec − log gevol) with Teff gives a slope consistent with zero (~10-7 dex/K). The dependence with the stellar metallicity is more evident, although the slope is still consistent with zero (~0.05 dex/dex)9. In other words, the good agreement between log gspec and log gevol values over the range of Teff and [Fe/H] analysed in this work suggests that there are not significant departures from LTE.
Considering other elements (Na, Mg, Si, etc.), the only comparisons performed in this paper are between GWPs and GWOPs (Sect. 3.4). Although abundances for individual stars may be affected by non-LTE effects, those effects, should not bias the comparison between GWPs and GWOPs.
 |
Fig. 8 Left: normalised metallicity distribution of the GWP sample (blue histogram) versus giant stars without known planets. Right: normalised metallicity distribution of the SGWP sample (red histogram) versus subgiant stars without known planets. Median values of the distributions are shown with vertical lines. |
3. Results
3.1. Analysis of the metallicity distributions of the different samples of stars
As mentioned before, our observations contain 67 giant stars without known planets and 43 giant stars with planets. Some statistical diagnostics for the GWOP and GWP samples are summarised in Table 8 and their normalised metallicity distributions are shown in Fig. 8 (left-hand side). We find that both samples show similar distributions and statistical diagnostics. However, to assess whether both distributions are equal from a statistical point of view, the standard two-sample Kolmogorov-Smirnov (K-S) test was performed. The maximum difference between the cumulative distribution functions of the GWOPs and GWPs is ~0.11, and the statistical probability of both distributions being drawn from the same parent distribution is significantly high, 87% (neff ~ 26). Therefore, we find that giant stars harbouring planets do not seem to follow the planet-metallicity correlation of MS stars. We find that giant stars with planets are not more metal rich than the giant stars without them. Other authors have reached the same conclusions based on smaller samples of stars, Sadakane et al. (2005), Pasquini et al. (2007), and Takeda et al. (2008).
[Fe/H] statistics of the stellar samples.
Figure 8, right-hand panel, shows the normalised metallicity distribution of the SGWP sample and of its corresponding comparison sample (SGWOPs). The data suggest that the metallicity distribution of the SGWP sample is significantly shifted towards higher metallicities with respect to the SGWOP sample, a behaviour which resembles the well-known giant-planet metallicity correlation found in MS stars (e.g. Santos et al. 2004; Fischer & Valenti 2005). A two-sample K-S test confirms that both distributions are different from a statistical point of view (p-value ~10-5, D ~ 0.66, neff ~ 12.4).
With the aim of completeness, a sample of main-sequence planet hosts (MSWPs) has been added to the discussion of the results that follows. We selected those stars hosting exclusively giant planets with available metallicities in VF05, where we removed stars with retracted or not confirmed exoplanets, as well as those stars already included in our SGWP or LMSWP samples. In order to keep the analysis as homogeneous as possible, we proceeded as in Sect. 2.6 to set the VF05 metallicities into our own metallicity scale.
The cumulative metallicity distributions of all samples, Fig. 9, allow us to get an overall picture of the metallicity trends. There are a few interesting facts to be taken from these distributions and their statistical tests: i) there is no difference in the metallicities of giant stars regarding the presence or absence of planets; ii) the distribution of subgiant stars with planets is clearly separated from that of subgiants without planets; iii) the distribution of subgiant stars without planets follows a trend similar to giant stars (with and without planets); and iv) more interestingly, the metallicity distribution of subgiant stars with planets is different from that of giant stars, but similar to the one of MS stars with planets.
We note that the metallicity distribution of SGWPs also seems to be slightly shifted towards lower metallicities with respect to the LMSWP sample. Nevertheless, their median metallicities are quite similar (see Table 8), and both are consistent with the known trends for MS stars hosting giant planets (see below).
The K-S test comparing the SGWP/GWP and LMSWP/GWP samples confirms that the distributions are different within a 98% confidence level10. The K-S test reveals that the probability of LMSWPs and SGWPs being drawn from the same parent distribution is low, around 0.12 (D = 0.44, neff ~ 6.5), although we cannot rule out this possibility. There is a clear outlier in the SGWP sample, namely HIP 36795, which is the only star in the SGWPs sample with a [Fe/H] below the solar value. We note that even if we do not take this star into account, the K-S probability is still low, of the order of 0.20. Therefore, we conclude that from a statistical point of view, we cannot establish a difference between the SGWP and LMSWP samples. However, with the data at hand, we can affirm that the metal distributions of subgiant stars with planets are similar to the ones of late and MS stars with planets and differ from those of giant stars with planets.
 |
Fig. 9 Histogram of cumulative frequencies for the different samples studied in this work. |
 |
Fig. 10 Stellar metallicity, [Fe/H], as a function of the stellar mass. A linear fit to the data is shown in GWPs with M⋆ > 1.5 M⊙ (continuous line). Typical uncertainties in metallicities and stellar masses are also shown. Colours and symbols are the same as in previous figures. |
3.2. Metallicity as a function of the stellar mass
The metallicity distribution of the different samples presented in Figure 9 suggests that the metal-rich nature of the planet-host stars tends to disappear as the star evolves. This could be a remarkable result that needs to be analysed very carefully as there are obvious differences between the samples in terms of mass and age. Therefore, the data have been examined for correlations between mass and metallicity, given that mass is the parameter which significantly varies between the giants (covering the mass range ~1−3.8 M⊙) and the SGWP and LMSWP samples (restricted to the mass range 1−1.5 M⊙) (see also Table 6) and the MS samples. Figure 10 shows the [Fe/H]-Mass diagram of the stars analysed in this work, where the mass has been determined as explained in Sect. 2.4. A similar plot covering the 0.8−1.2 M⊙ mass range was presented by Fischer & Valenti (2005). Our data allow us to extend the plot up to 3.8 M⊙. A hint of a possible dependency of metallicity on stellar mass seems to appear in Fig. 10, which could hinder the differences found for the giant stars with and without planets. We note that for stellar masses up to ~1.6 M⊙ giant stars with and without planets are mixed, showing a lot of scatter in the graph and covering the whole range of metallicities. However, a clear segregation in metallicity appears above the ~1.6 M⊙ stellar mass, the scatter in the metallicity axis is smaller, and the giant stars with planets are located systematically on the metal-rich part of the plot.
So, we find that for giant stars as a whole there is no correlation between the presence of giant planets and the metallicity of the star, but within the lack of correlation there seems to be hidden a dependency on the stellar mass. In the light of Fig. 10, we studied the metallicity distribution of the giant stars in the sample, which were separated according to their mass, those under 1.5 M⊙ and those with larger masses. The 1.5 M⊙ mass value was chosen so that a subsample of the giants covers the same mass range as the subgiant sample. The histograms of the distributions are shown in Fig. 11, while some statistic diagnostics are given in Table 9. We find that the GWPs and GWOPs samples are clearly separated in metallicity when only stars with M⋆ > 1.5 M⊙ are considered. A K-S test shows that the probability of GWPs and GWOPs being drawn from the same parent population is p-value ~0.70 when considering only stars with M⋆ ≤ 1.5 M⊙ (D ~ 0.19, neff ~ 12.3). However, when considering giants with masses larger than 1.5 M⊙, the K-S test probability diminishes significantly, p-value ~0.05 (D ~ 0.35, neff ~ 13.7).
[Fe/H] statistics of the sample of giant stars separated in two ranges of mass.
 |
Fig. 11 Left: normalised metallicity distribution of the GWP sample (blue histogram) versus giant stars without known planets for stars with M⋆ ≤ 1.5 M⊙. Right: normalised metallicity distribution of the GWP sample (blue histogram) versus giant stars without known planets for stars with M⋆ > 1.5 M⊙. Median values of the distributions are shown with vertical lines. |
As explained in Sect. 2.7, while there are four GWPs located further than 200 pc with significant negative metallicities, there are no similar comparison stars beyond this distance. We note that these four stars fall in the mass domain M⋆ ≤ 1.5 M⊙. It is important to check if these low-metallicity stars are biasing our GWP sample so that they are preventing us from reproducing a planet-metallicity correlation in giants with M⋆ ≤ 1.5 M⊙. If it is the case, removing these four stars should shift the GWP sample towards higher metallicities. If we repeat the K-S test for the GWPs/GWOPs samples within this mass domain and remove these four stars, the p-value increases up to roughly 80% (D ~ 0.19, neff ~ 11). So even excluding these four low-metallicity stars, GWPs and GWOPs in the mass domain M⋆ ≤ 1.5 M⊙ show a similar metallicity distribution. Therefore, the lack of a planet-metallicity correlation in this mass domain is not related to the inclusion of GWPs with low metallicitities located at larger distances.
A search for a correlation between [Fe/H] and stellar mass was performed for the GWP sample. For the giant hosts with M⋆ > 1.5 M⊙, a Spearman’s correlation test gives a probability of correlation of the order of 99%. A linear fit to the data was done and is shown in Fig. 10 (continuous line). For giant hosts with masses below 1.5 M⊙, there seems to be no correlation between metallicity and stellar mass; the probability of a non-correlation is around 0.24. In other words, the correlation is not significantly different from zero.
Fischer & Valenti (2005) found a correlation between metallicity and stellar mass in the 0.8−1.2 M⊙ mass domain. However, they note that such trend does not seem to be real (i.e. it is not related to the properties of the stars) but is instead “artificial”, i.e. a consequence of stellar evolution and the colour and magnitude cuts used in planet search programmes for target selection. Johnson et al. (2010) also notice an artificial mass-metallicity correlation in a sample of 246 subgiants with stellar masses between 1.4−2.0 M⊙. It is difficult to firmly establish if a similar effect could be the reason for the metallicity-mass relationship found for GWPs in the mass domain M⋆ > 1.5 M⊙, since the GWP sample is composed of stars selected in different planet search programmes with (probably) different criteria, sampling different regions of the HR diagram. The GWOP sample does not help since it is drawn from another source, the Massarotti et al. (2008) compilation. Nevertheless, most planet search programmes apply cuts in colours and magnitudes (see e.g. Johnson et al. 2006, Fig. 1), so we cannot rule out the possibility that the mass-metallicity relation in M⋆ > 1.5 M⊙ could be related to selection effects.
3.3. Metallicity as a function of the stellar radius
In subgiant stars, the envelope is still cooling and expanding, in part at the expense of the energy being supplied by the hydrogen-burning shell. These stars do not become fully convective until they reach the base of the red giant branch ascending track on the HR diagram. Giant stars, on the other hand, have fully convective envelopes. Therefore both subgiants and giants offer a unique opportunity to test the pollution hypothesis of planet formation. Within this scenario, high stellar metallicity of planet hosts is simply produced as a consequence of the accretion of gas-depleted material on the convective zone of the star (Gonzalez 1997; Laughlin & Adams 1997). Given that in this framework the metallicity would be confined to the convective zone in MS stars, only the external layers are affected. It is thus expected that the metallicity signature would be lost as the star evolves and the external metal-rich layers are gradually diluted when the convective zone penetrates the envelope. So late-stage accretion of material would produce several observables, and a tendency to systematically lower metallicities would be expected as the star evolves from the MS to the subgiant stage and finally to the red giant phase. A way to disentangle the metallicity signature with evolution is exploring whether there is any dependency on the radius of the star.
Stellar metallicity as a function of the stellar radius for the GWP and GWOP samples is shown in Fig. 12. The stellar radii have been computed as explained in Sect. 2.4. Different colours and symbols are used for stars with masses lower than 1.5 M⊙ and stars with masses greater than 1.5 M⊙. Besides the expected trend towards larger radius as the stellar sample considered is more evolved, no other obvious trend is apparent in Fig. 12. A very mild trend of decreasing metallicities with increasing stellar radius for GWPs with M⋆ ≤ 1.5 M⊙ is doubtful as it disappears if we remove the three stars with the largest radii (94% and 95% Pearson and Spearman tests respectively).
When considering the GWPs with masses greater than 1.5 M⊙ only, no correlation between metallicity and radius is found. The probabilities of non-correlation are ~0.26 (Pearson’s test), ~0.14 (Spearman’s test).
 |
Fig. 12 Stellar metallicity, [Fe/H], as a function of the stellar radius. Colours and symbols are the same as in previous figures for LMSWP, SGWP, and SGWOP samples. Giants with M⋆ ≤ 1.5 M⊙ are plotted in blue triangles, while giants with M⋆ > 1.5 M⊙ are shown with purple circles. In both cases, filled symbols indicate planet hosts. Typical uncertainties in metallicities and stellar radius are also shown. |
 |
Fig. 13 [X/Fe] cumulative fraction of GWPs and GWOPs. Left: stars with M⋆ ≤ 1.5 M⊙, GWPs (blue continuous line) against GWOPs (black dashed line). Right: stars with M⋆ > 1.5 M⊙, GWPs (purple continuous line) against GWOPs (black dashed line). |
Comparison between the elemental abundances of GWPs and GWOPs.
3.4. Other chemical signatures
To try to disclose differences in the abundances of other chemical elements besides iron, we show in Fig. 13 the cumulative distribution [X/Fe] comparing the abundances [X/Fe] (where X represents Na, Mg, Al, Si, Ca, Sc, Ti i, Ti ii, V, Cr i, Cr ii, Mn, Co, Ni, and Zn), between GWPs and GWOPs. In the left-hand panel the distributions for giants with masses M⋆ ≤ 1.5 M⊙ are shown, while in the right-hand panel we show the giants with masses M⋆ > 1.5 M⊙. Some statistic diagnostics are shown in Table 10, where the results of a K-S test for each ion are also listed.
Similar behaviour between planet hosts and stars without planets is found for giants in the mass domain M⋆ ≤ 1.5 M⊙. From the 15 chemical species analysed, the K-S probabilities in eight are considerably high (≥70%), especially when considering Na, Ni, and Ca. In the rest, although the probabilities are not high, they are not significantly low enough to state a difference between GWPs and GWOPs. The only remarkable exception is Si, for which the GWPs distribution seems to be slightly shifted towards higher abundances.
For stars with M⋆ > 1.5 M⊙, there are significant differences between planet hosts and stars without planets in three species, namely, Na (GWPs showing slightly lower abundances) and Co and Ni where abundances of GWPs seem to be higher than those of GWOPs. However, GWPs and GWOPs show very similar behaviours in Cr i and Al.
The question of whether MS planet hosts show overabundances of refractory elements11 is still open (see e.g. Adibekyan et al. 2012, and references therein). An overabundance of refractory elements with respect to volatiles in MS planet hosts is considered as a possible sign of late-stage accretion, a tendency that is expected to disappear during the star evolution towards the red-giant phase.
We find that GWPs show similar abundance patterns in all the elements analysed to those of GWOPs in the mass domain M⋆ ≤ 1.5 M⊙. We do not know whether this is due to i) mixing processes which diluted the refractory enrichment previously suffered by the stars’ progenitors; or because ii) pollution played a small role, so the GWPs progenitors never showed an overabundance of refractory elements. On the other hand, for masses larger than 1.5 M⊙, GWPs and GWOPs show differences in some elements, specially Na, Co, and Ni.
3.5. Age–metallicity relation
In the light of the metallicity trends with stellar mass found within the giant star sample, it is reasonable to explore a possible age−metallicity relation. In Fig. 14 we show the stellar age versus its metallicity of the different samples analysed in this work. For comparison, MS hosts from VF05 are overplotted with VF05 [Fe/H] values set into our metallicity scale, as explained in Sect. 2.6. In addition, the stellar ages of these stars have been recomputed using the methodology followed in this work (Sect. 2.4). Two clear trends can be identified in Fig. 14. To the left of the plot are located the giant stars with masses M⋆ > 1.5 M⊙ stars, and to the right of the plot all the other stars studied. The plot shows the expected trend in metallicity with stellar ages. As the population is older, the metallicity has a tendency to show a larger spread in values.
 |
Fig. 14 Age−metallicity relation for the different samples studied in this work. Open symbols indicate the corresponding comparison samples. |
3.6. Trends with the planetary properties
Studies around MS stars have revealed that the metal signature on the star seems to influence the maximum mass of the planet that can be formed (Mayor et al. 2011). It has been shown that the planet deficiency at small orbital distances found around red giant stars (see also Johnson et al. 2007; Sato et al. 2008; Wright et al. 2009) can be explained by tidal interactions in the star-planet system as the star evolves off the MS, which can lead to variations in the planetary orbits and to the engulfment of close-in planets (Villaver & Livio 2009). The planet accretion process can lead to a transfer of angular momentum to the stellar envelope, which ultimately can spin up the star and even indirectly modify its chemical abundances. Possible evidence of this process has been recently found (see e.g. Adamów et al. 2012). Furthermore, Carlberg et al. (2012) analysed a sample of slow and rapid RGB rotators and found lithium enrichment on the rapid rotators consistent with planet accretion onto the stellar envelope.
To disclose any possible trends on the planet properties among the stellar samples studied in this work, we show in the left-hand panel of Fig. 15 stellar metallicity versus orbital distance of the planet and in the right-hand panel stellar metallicity as a function of the mass of the more massive planet12. The planets in our sample follow the general trend mentioned above, that is, nearly all planets orbiting GWPs are cool, distant (a > 0.5 AU), gaseous jupiters, with the exception of HIP 57820 (which hosts a close-in Jupiter at a ~0.08 AU) and HIP 114855 (a = 0.3 AU). Regarding the planet-mass metallicity relation (right-hand panel), there seems to be a trend of decreasing metallicities as we move towards higher planetary masses. A Spearman correlation test provides a likelihood of correlation of 96%. This appears to be in contradiction with the known trends of MS FGK hosts in which a positive correlation between the metallicity of the host star and the mass of its most massive planet is found (Mayor et al. 2011; Sousa et al. 2011). A closer inspection of the metallicity-planetary mass plane reveals that this general tendency is due to the GWP stars in the mass domain M⋆ ≤ 1.5 M⊙. Considering only these stars, the likelihood of a correlation is ~99% (Spearman’s test). On the other hand, there is no obvious correlation when considering the other samples. The behaviour of LMSWPs and SGWPs is more or less flat, while for GWPs with M⋆ > 1.5 M⊙ there seems to be a hint of increasing metallicities with increasing planetary masses (a Spearman’s test gives a probability of correlation of ~91%). In other words, subgiants and high-mass giants reproduce the known trends for MS hosts, while giants in the low-mass domain show a behaviour which is hard to understand.
 |
Fig. 15 Left: stellar metallicity as a function of the semimajor axis of the innermost planet. Right: stellar metallicity as a function of the mass of the most massive planet. GWPs with M⋆ > 1.5 M⊙ are plotted with purple circles, GWPs less massive than 1.5 M⊙ in blue triangles, SGWPs as red squares, while LMSWPs are plotted as green asterisks. |
Next, we explore the planet properties among the different samples. It has been suggested that giant stars host more massive planets than MS hosts (e.g. Johnson et al. 2007; Lovis & Mayor 2007). A comparison of the cumulative frequency of planet mass13 between our sample of GWPs and MS stars from VF05 hosting exclusively giant planets reveals that the distribution of the former is clearly shifted towards higher masses. While MS hosts spread a planetary mass range from 0.1 to 18 MJup with a median value of 1.9 MJup, our sample of GWPs covers from 0.6 to 22 MJup with a median value of 3.3 MJup. A K-S test shows that both distributions are statistically different within a confidence level of 98% (p-value ~10-3). This result should be interpreted very carefully, since the larger levels of jitter in evolved stars might prevent the detection of lower mass planets shifting the planet mass distribution towards larger values. No obvious segregation in mass or in orbital distance is found among the planets orbiting giant stars with different masses.
Regarding multiplicity, we find a rate of multi-planet systems in GWPs of the order of 12%, which is in agreement with the 14% multiple confirmed planetary systems given by Wright et al. (2009). However, the authors note that it could be 28% or higher if those cases with significant evidence of being multiple are included. Finally, no correlation between the stellar metallicity and the planet’s eccentricity was found, although as pointed out by Johnson et al. (2008) we note that the eccentricity distribution of GWPs seems to be shifted towards lower values than the eccentricity distribution of MS hosts. While the median eccentricity in GWPs is 0.15, it is around 0.25 in MS hosts. A K-S test reveals both distributions to be different (p-value ~10-3).
Planets in the SGWP sample are predominantly cool, although around 30% of the stars host a hot Jupiter at a distance closer than 0.1 AU. In addition, two of our stars in the SGWP sample host low-mass planets (Mp < 30 M⊕), namely HIP 94256, and HIP 115100. Roughly 50% of the stars in the LMSWP sample harbour at least one hot Jupiter, while the other 50% only host cool distant planets. HIP 98767 hosts two planets, with the innermost one a low-mass planet.
4. Discussion
As pointed out in Sect. 3.1, we find that the metal distribution of subgiant stars with planets is clearly separated from that of subgiants without planets and that it is similar to the one of MS stars with planets. Considering the whole sample of giant stars (i.e. without mass segregation), we do not find a difference in the metal distribution of giant stars that host planets when compared with giant stars where no planetary systems have been detected. While the metallicity distribution of the subgiants fits well within the current paradigm of planet formation, the giant star results are harder to understand within this context.
One could argue that the metallicity signature of planet formation disappears at the moment the star evolves into the red giant branch. The Mbol criterion chosen to separate the subgiant from the giant sample physically reflects the time at which the star becomes fully convective. At this point, three lines of arguments could be followed: i) there was no metal difference between the stars bearing planets and stars with no planets in this sample of giant stars; ii) there was a different metallicity that has been lost; iii) the sample is biased so that we are prevented from seeing any metallicity difference.
Can massive proto-planetary disks explain the observed trends?
The first possibility is that the giant stars represent a different stellar population in which a metal-rich environment is not required for planet formation. The red giant stars that constitute our GWP sample are the result of the evolution of early-type MS dwarfs. If we go back in time on the evolutionary tracks, the stars in the GWP sample are the result of the evolution of MS dwarfs with effective temperatures in the range 5500−12 000 K (spectral types G5V-B8V and stellar masses between 0.9 and 4 M⊙). On the other hand, SGWPs come mainly from G5V-F0V (M⋆ between 0.9 and 1.6 M⊙), while stars in the LMSWP sample come from less massive stars with spectral types in the range K2V-F2V. It is therefore natural to ask whether the observed differences in the metallicity distribution of the different samples are related to the different mass distributions of the star’s progenitors in the MS (e.g. Ghezzi et al. 2010a). In principle, high-mass stars are likely to harbour more massive protoplanetary disks (e.g. Natta et al. 2000; see also Fig. 5 in Williams & Cieza 2011). Observations of Hα EWs in young, low-mass objects suggest that the mass-accretion rate scales approximately with the square of the stellar mass (Muzerolle et al. 2003; Natta et al. 2004; Mendigutía et al. 2011, 2012), a result which can be reproduced, assuming that a relationship between the disk mass and the central star mass of the form 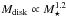 holds (Alibert et al. 2011).
holds (Alibert et al. 2011).
According to recent simulations of planet population synthesis (Alibert et al. 2011; Mordasini et al. 2012), protoplanetary disk masses play a significant role in planet formation. In particular, it is shown that giant planet formation can occur in low metallicity (low dust-to-gas ratio) but high-mass protoplanetary disks. The metallicity effect depends on the mass of the disk. The minimum metallicity required to form a massive planet is lower for massive stars than for low-mass stars. In this scenario, the fact that GWPs do not show the metal-rich signature could be explained by the more massive protoplanetary disks of their progenitors. However, several difficulties arise.
One of the consequences of the protoplanetary disk mass on planet formation is that planets orbiting massive giant stars should be more massive than planets around dwarf stars. However, as mentioned in Sect. 3.6, one should be careful in the comparison between planets around giant and MS stars, given that the detections are affected from biases introduced by the star. The samples of giant stars with different masses are, however, suitable for this comparison, and we find that there is no obvious difference in the minimum mass of the planet found between the low-mass and the high-mass giant stars.
Second, core-accretion models are not able to predict the presence of very massive companions around very low metallicity stars and stars that were not supposed to have a massive disk to begin with (giants with M⋆ ≤ 1.5 M⊙). Although those planets are rare, we note that there are some of them in our GWP sample, such as the two companions around BD+20 2457 ([Fe/H] = −0.79 dex, planets of 21.4 MJup at 1.5 AU, and 12.5 MJup at 2.0 AU), the planet around γ1 Leo ([Fe/H] = −0.44 dex, planet of ~8 MJup at 1.2 AU), and the one orbiting HD 13189 ([Fe/H] = −0.37 dex, planet of ~14 MJup at 2 AU). This is because the time needed to form a core big enough to start a runaway accretion of gas is so long that by that time the gas has already been significantly depleted.
But the most intriguing point is the mass segregation found for GWPs (Sect. 3.2). While the metallicity distribution of GWPs in the mass domain M⋆> 1.5 M⊙ is shifted towards higher metallicities with respect to a similar sample of giants without planets, GWPs in the mass range M⋆ ≤ 1.5 M⊙ do not show the metal signature of the presence of planets. This is a puzzling result, at least in two ways. First, if planet formation can occur in low-metal but high-protoplanetary disk mass environments, a population of massive giant stars with low metallicities hosting planets might be expected. Our observations somehow show the opposite: massive (M⋆ > 1.5 M⊙) giant stars with planets showing high metallicities.
Second, the sample of less massive (M⋆ ≤ 1.5 M⊙) giant stars with planets covers the same mass range as the MS progenitors and subgiant stars where the metal signature has been observed. In other words, the protoplanetary disks of GWPs and M⋆ ≤ 1.5 M⊙ are not massive, and thus, there is nothing to help planet formation at low metallicities. Furthermore, there is no age difference between this sample of stars and MS or subgiant stars. Thus, the fact that giant stars with M⋆ ≤ 1.5 M⊙ and planets are not more metal rich is hard to understand, as it is in apparent contradiction with the trademark of the core-accretion model.
Can the metallicity signature be erased as the star evolves?
If we accept the possibility that giant stars do not favour the existence of a metal-poor environment for planet formation, then we have to explore the option that the metallicity signature was present at the time the planet was formed but disappeared as a consequence of the evolution of the star. Gonzalez (1997; see also Lin et al. 1996) explain the metal content of planet-host stars as a consequence of the accretion of gas-depleted material on the stellar surface, the so-called pollution scenario. In this scenario, only the external layers of the stars are affected, and as the star evolves, the external metal-rich layers are gradually diluted as the convective zone of the star grows.
Our data do not support evidence of pollution. If the metal-rich signature was limited to the convective envelope of the stars, subgiants with planets should show lower metallicities than MS hosts. We find the opposite, with SGWP and MS planet host samples showing the same chemical signature (Sect. 3.1). Furthermore, the different metallicity behaviour of GWPs depending on their masses is again difficult to understand in the pollution scenario. There is no physical reason why the metal-rich nature of the star would be lost due to convection only for giant stars with M⋆ ≤ 1.5 M⊙, remaining for giants with M⋆ > 1.5 M⊙. The metallicity−stellar radius relation does not shed any light on this issue as M⋆ ≤ 1.5 M⊙ giant stars cover the same range of stellar radius as the M⋆ > 1.5 M⊙ stars.
Is our sample biased?
Other lines of arguments such as the one suggested by Haywood (2009), in which the observed correlation between the presence of gas-giant planets and enhanced stellar metallicity observed in MS planet hosts might be related to a possible inner-disk origin of these stars, does not fit the data either. In this scenario, the observed metallicity distribution of GWPs would be shifted towards lower metallicities with respect to the one of MS hosts, just because the GWP sample contains stars younger than the dwarf sample and, is therefore less contaminated by radial mixing. Nevertheless, according to this scenario, giant stars with planets and high masses (M⋆ > 1.5 M⊙) should not be metal rich.
The possible biases affecting our sample have been explored in the paper. We have found no biases in age, mass, population, or distance that could explain our results. However, an option that we cannot exclude is the risk of the sample size being small. To fix this issue, we will have to wait for more planet discoveries to take place.
4.1. Mass segregation and previous results
We should finally discuss how the mass segregation found for GWPs in this work compares with previous results on evolved stars with planets. It is worth noting that most of the stars included in previous works are in the mass-domain M⋆ ≤ 1.5 M⊙, where the metal-rich signature of planet hosts is lost. Specifically, the number of low-mass giants in each work are: 2 out the 4 stars analysed in Sadakane et al. (2005), 1/1 in Schuler et al. (2005), 7/10 in Pasquini et al. (2007), and 7/16 in Ghezzi et al. (2010a). However, among the 20 giants included in Hekker & Meléndez (2007), 11 are high-mass (M⋆ > 1.5 M⊙) giants. The fact that GWPs in the high-mass domain show metal enrichment, while less massive giants do not, could explain the disagreement between Hekker & Meléndez (2007) and other works. We note, however, that Takeda et al. (2008) did not found metal enrichment in GWPs, despite the fact that 7 out of the 10 stars analysed in that work are in the high-mass domain.
5. Conclusions
Evolved stars (subgiants and red giants) with planets are valuable tools to set constraints on our understanding of how planetary systems form and evolve. Nowadays, increasing efforts are being made to search for planetary companions around these kinds of stars. In addition, the properties of evolved stars with planets and the properties of the planets found around these stars seem to be different from what we already know about MS planet hosts. In this work, we performed an analysis of the stellar properties and elemental abundances of a large sample of evolved stars. Although data from the literature was used to expand the SGWOP sample, our analysis has, to our best knowledge, the best combination between homogeneity and sample size discussed so far. In addition, a detailed analysis of the stellar sample properties is performed to avoid any bias which could affect our results.
We find that, unlike the case of MS hosts, planets around giant stars are not preferentially found around metal-rich stars when the whole sample of giant stars is analysed. The metallicity distribution of GWPs is clearly shifted towards lower values in comparison with SGWPs and LMSWPs. Taking into account the homogeneous procedure followed in this work and the fact that we are dealing mainly with solar-type stars, we ascertain that the differences in the metallicity distributions are real and not due to non-LTE effects.
Subgiant stars show the same metal trends with planets as MS stars and also have a similar mass range. In an attempt to understand if the more massive stars within the giant sample are shifting the metal distribution of the GWP towards lower metallicities, we segregated the giant stars into two mass bins, M⋆ ≤ 1.5 M⊙ and M⋆ > 1.5 M⊙. We showed for the first time that the metallicity distribution of the more massive giant stars with planets is shifted towards higher metallicities. This behaviour is similar to the one of MS and subgiant stars with planets.
The metal signature of the presence of planets is lost, however, for stars in the M⋆ ≤ 1.5 M⊙ range, a fact which is difficult to understand with current models of planet formation. These stars show a range of stellar parameters that are similar to those of subgiant and main-sequence planet hosts but, do not show the metal-enrichment signature. In particular, giants with M⋆ ≤ 1.5 M⊙ show an age distribution that is similar to that of subgiants and MS hosts, thus ruling out radial mixing as a possible explanation of their metallicity distribution. Since they also show similar masses, a planet-formation scenario in which low-metallicity environments are compensated by higher mass protoplanetary disks can be also discarded. Considering that no bias that could affect the metallicity distribution of low-mass giant hosts has been identified, the only explanation points towards a non-primordial origin of the metallicity-gas giant planet relationship. We have not, however, found clear evidence of pollution. Furthermore, a more intriguing question is why convection should play a role in erasing the metal signature for giants in the mass domain M⋆ ≤ 1.5 M⊙, but not for giants with M⋆ > 1.5 M⊙.
Additional differences between giants with masses ≤1.5 M⊙ and more massive giants have been found when analysing the abundance patterns of different elements. In the case of the less-massive giants, planet hosts and non-planet hosts show similar abundance patters. However, with more massive stars there are differences in some elements between star-hosting planets and stars without known planets, especially in the cases of Na, Co, and Ni abundances.
Finally, we note that planets around evolved stars show some peculiarities with respect to the planets orbiting around MS stars, like a lack of close-in planets or higher masses and eccentricities. The data also suggest a decreasing trend between the stellar metallicity and the mass of the most massive planet.
See http://www.mercator.iac.es/instruments/hermes/ for details.
See http://www.not.iac.es/instruments/fies/fiestool/FIEStool.html for details
The usual relationship AV = 3.1 × E(B − V) is assumed (e.g. Savage & Mathis 1979).
Acknowledgments
This work was supported by the Spanish Ministerio de Ciencia e Innovación (MICINN), Plan Nacional de Astronomía y Astrofísica, under grant AYA2010-20630 and AYA2011-26202. J.M. acknowledges support from the Universidad Autónoma de Madrid (Department of Theoretical Physics). E.V. also acknowledges the support provided by the Marie Curie grant FP7-People-RG268111. The authors would like to thank Robert. L. Kurucz, Sergio Sousa, Yoichi Takeda, and Léo Girardi, for making their codes publicly available. Jean Schneider is also acknowledged for maintaining the Extrasolar Planets Encyclopedia. We sincerely appreciate the careful reading of the manuscript and the constructive comments of an anonymous referee.
References
- Adamów, M., Niedzielski, A., Villaver, E., Nowak, G., & Wolszczan, A. 2012, ApJ, 754, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., & Israelian, G. 2011, A&A, 535, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., et al. 2012, A&A, 543, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Mordasini, C., & Benz, W. 2004, A&A, 417, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Mordasini, C., & Benz, W. 2011, A&A, 526, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arenou, F., Grenon, M., & Gomez, A. 1992, A&A, 258, 104 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baumann, P., Ramírez, I., Meléndez, J., Asplund, M., & Lind, K. 2010, A&A, 519, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beirão, P., Santos, N. C., Israelian, G., & Mayor, M. 2005, A&A, 438, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2003, A&A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Lind, K., Collet, R., & Asplund, M. 2011, J. Phys. Conf. Ser., 328, 012002 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, J. K., Cunha, K., Smith, V. V., & Majewski, S. R. 2012, ApJ, 757, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F. 2005, Mem. Soc. Astron. It. Supp., 8, 44 [Google Scholar]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dehnen, W., & Binney, J. J. 1998, MNRAS, 298, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Frandsen, S., & Lindberg, B. 1999, in Astrophysics with the NOT, eds. H. Karttunen, & V. Piirola, 71 [Google Scholar]
- Frink, S., Mitchell, D. S., Quirrenbach, A., et al. 2002, ApJ, 576, 478 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fuhrmann, K. 1998, A&A, 338, 161 [NASA ADS] [Google Scholar]
- Fuhrmann, K. 2004, Astron. Nachr., 325, 3 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ghezzi, L., Cunha, K., Schuler, S. C., & Smith, V. V. 2010a, ApJ, 725, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Ghezzi, L., Cunha, K., Smith, V. V., et al. 2010b, ApJ, 720, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Ghezzi, L., Cunha, K., Smith, V. V., & de la Reza, R. 2010c, ApJ, 724, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, G., Israelian, G., Ecuvillon, A., Santos, N. C., & Mayor, M. 2006, A&A, 449, 723 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, G. 1997, MNRAS, 285, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G. 2011, MNRAS, 416, L80 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., & Bonifacio, P. 2009, A&A, 497, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González Hernández, J. I., Israelian, G., Santos, N. C., et al. 2010, ApJ, 720, 1592 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Delgado-Mena, E., Sousa, S. G., et al. 2013, A&A, 552, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M. 2008a, A&A, 482, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M. 2008b, MNRAS, 388, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2009, ApJ, 698, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Hekker, S., & Meléndez, J. 2007, A&A, 475, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Israelian, G., Delgado Mena, E., Santos, N. C., et al. 2009, Nature, 462, 189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Johnson, J. A., Marcy, G. W., Fischer, D. A., et al. 2006, ApJ, 652, 1724 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Fischer, D. A., Marcy, G. W., et al. 2007, ApJ, 665, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Marcy, G. W., Fischer, D. A., et al. 2008, ApJ, 675, 784 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Clanton, C., Howard, A. W., et al. 2011, ApJS, 197, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V., Scholz, R.-D., Piskunov, A. E., Röser, S., & Schilbach, E. 2007, Astron. Nachr., 328, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid, Kurucz CD-ROM No. 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory), 13 [Google Scholar]
- Laughlin, G., & Adams, F. C. 1997, ApJ, 491, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., Bodenheimer, P., & Richardson, D. C. 1996, Nature, 380, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Lind, K., Bergemann, M., & Asplund, M. 2012, MNRAS, 427, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., & Mayor, M. 2007, A&A, 472, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luck, R. E., & Heiter, U. 2007, AJ, 133, 2464 [NASA ADS] [CrossRef] [Google Scholar]
- Maldonado, J., Martínez-Arnáiz, R. M., Eiroa, C., Montes, D., & Montesinos, B. 2010, A&A, 521, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maldonado, J., Eiroa, C., Villaver, E., Montesinos, B., & Mora, A. 2012, A&A, 541, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massarotti, A., Latham, D. W., Stefanik, R. P., & Fogel, J. 2008, AJ, 135, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- Mendigutía, I., Calvet, N., Montesinos, B., et al. 2011, A&A, 535, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendigutía, I., Mora, A., Montesinos, B., et al. 2012, A&A, 543, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montes, D., López-Santiago, J., Gálvez, M. C., et al. 2001, MNRAS, 328, 45 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., Klahr, H., & Henning, T. 2012, A&A, 541, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzerolle, J., Hillenbrand, L., Calvet, N., Briceño, C., & Hartmann, L. 2003, ApJ, 592, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Grinin, V., & Mannings, V. 2000, Protostars and Planets IV, 559 [Google Scholar]
- Natta, A., Testi, L., Muzerolle, J., et al. 2004, A&A, 424, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neves, V., Santos, N. C., Sousa, S. G., Correia, A. C. M., & Israelian, G. 2009, A&A, 497, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Niedzielski, A., Konacki, M., Wolszczan, A., et al. 2007, ApJ, 669, 1354 [NASA ADS] [CrossRef] [Google Scholar]
- Niedzielski, A., Nowak, G., Adamów, M., & Wolszczan, A. 2009, ApJ, 707, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Döllinger, M. P., Weiss, A., et al. 2007, A&A, 473, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., & ESA 1997, The HIPPARCOS and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Asplund, M., Baumann, P., Meléndez, J., & Bensby, T. 2010, A&A, 521, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, W. K. M., & Armitage, P. J. 2003, ApJ, 598, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Sadakane, K., Ohnishi, T., Ohkubo, M., & Takeda, Y. 2005, PASJ, 57, 127 [NASA ADS] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sato, B., Ando, H., Kambe, E., et al. 2003, ApJ, 597, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, B., Toyota, E., Omiya, M., et al. 2008, PASJ, 60, 1317 [NASA ADS] [Google Scholar]
- Savage, B. D., & Mathis, J. S. 1979, ARA&A, 17, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Sbordone, L. 2005, Mem. Soc. Astron. It. Supp., 8, 61 [Google Scholar]
- Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. It. Supp., 5, 93 [Google Scholar]
- Schuler, S. C., Kim, J. H., Tinker, Jr., M. C., et al. 2005, ApJ, 632, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Schuler, S. C., Flateau, D., Cunha, K., et al. 2011, ApJ, 732, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Fernandes, J., Israelian, G., & Santos, N. C. 2010, A&A, 512, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Udry, S. 2011, A&A, 533, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeda, Y. 2007, PASJ, 59, 335 [NASA ADS] [Google Scholar]
- Takeda, Y., Ohkubo, M., & Sadakane, K. 2002a, PASJ, 54, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y., Sato, B., Kambe, E., Sadakane, K., & Ohkubo, M. 2002b, PASJ, 54, 1041 [NASA ADS] [Google Scholar]
- Takeda, Y., Ohkubo, M., Sato, B., Kambe, E., & Sadakane, K. 2005, PASJ, 57, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y., Sato, B., & Murata, D. 2008, PASJ, 60, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1995, ApJS, 98, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- van Leeuwen, F. V. 2007, Hipparcos, the New Reduction of the Raw Data, Astrophys. Space Sci. Lib., 350, 449 [Google Scholar]
- Villaver, E., & Livio, M. 2009, ApJ, 705, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Upadhyay, S., Marcy, G. W., et al. 2009, ApJ, 693, 1084 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Photometric and evolutionary parameters for the stars measured in this work (see text for details).
Derived abundances of Na, Mg, Al, Si, Ca, Sc, Ti i, Ti ii, V, Cr i, Cr ii, Mn, Co, Ni, and Zn.
Radial velocities and Galactic spatial-velocity components for the observed stars.
All Figures
 |
Fig. 1 Luminosity versus Teff diagram for the observed stars. Giants are plotted with blue triangles, subgiants with red squares, and late MS stars with green asterisks. Filled symbols indicate planet hosts. Some evolutionary tracks ranging from 0.7 to 3.0 solar masses from Girardi et al. (2000) are overplotted. For each mass, three tracks are plotted, corresponding to Z = 0.008 ([Fe/H] = −0.4 dex, dotted lines), Z = 0.019 ([Fe/H] = + 0.0 dex, solid lines), and Z = 0.030 ([Fe/H] = + 0.20 dex, dashed lines). |
| In the text | |
 |
Fig. 2 Comparison between our spectroscopically derived Teff and those obtained from (B − V) colours. The upper panel shows the differences between the spectroscopic and the photometric values. Mean uncertainties in the derived temperatures are also shown. |
| In the text | |
 |
Fig. 3 Spectroscopically derived log g values versus log g estimates based on Hipparcos parallaxes. The upper panel shows the differences between the spectroscopic and the Hipparcos values. Mean uncertainties in log g values are also shown. |
| In the text | |
 |
Fig. 4 [Fe/H] values, this work, versus literature estimates. The upper panel shows the differences between the metallicities derived in this work and the values given in the literature. |
| In the text | |
 |
Fig. 5 Comparison of our abundances to those of Beirão et al. (2005) (∗), Bensby et al. (2005) (open circles), Valenti & Fischer (2005) (+), Gilli et al. (2006) (×), Luck & Heiter (2007) (open triangles), Takeda (2007) (open squares), Takeda et al. (2008) (diamonds), and Neves et al. (2009) (filled triangles). |
| In the text | |
 |
Fig. 6 [Fe/H] as a function of the stellar distance. Colours and symbols are as in Fig. 1. |
| In the text | |
 |
Fig. 7 Toomre diagram of the observed stars. Colours and symbols are as in Fig. 1. Dash-dot lines indicate constant total velocities, |
| In the text | |
 |
Fig. 8 Left: normalised metallicity distribution of the GWP sample (blue histogram) versus giant stars without known planets. Right: normalised metallicity distribution of the SGWP sample (red histogram) versus subgiant stars without known planets. Median values of the distributions are shown with vertical lines. |
| In the text | |
 |
Fig. 9 Histogram of cumulative frequencies for the different samples studied in this work. |
| In the text | |
 |
Fig. 10 Stellar metallicity, [Fe/H], as a function of the stellar mass. A linear fit to the data is shown in GWPs with M⋆ > 1.5 M⊙ (continuous line). Typical uncertainties in metallicities and stellar masses are also shown. Colours and symbols are the same as in previous figures. |
| In the text | |
 |
Fig. 11 Left: normalised metallicity distribution of the GWP sample (blue histogram) versus giant stars without known planets for stars with M⋆ ≤ 1.5 M⊙. Right: normalised metallicity distribution of the GWP sample (blue histogram) versus giant stars without known planets for stars with M⋆ > 1.5 M⊙. Median values of the distributions are shown with vertical lines. |
| In the text | |
 |
Fig. 12 Stellar metallicity, [Fe/H], as a function of the stellar radius. Colours and symbols are the same as in previous figures for LMSWP, SGWP, and SGWOP samples. Giants with M⋆ ≤ 1.5 M⊙ are plotted in blue triangles, while giants with M⋆ > 1.5 M⊙ are shown with purple circles. In both cases, filled symbols indicate planet hosts. Typical uncertainties in metallicities and stellar radius are also shown. |
| In the text | |
 |
Fig. 13 [X/Fe] cumulative fraction of GWPs and GWOPs. Left: stars with M⋆ ≤ 1.5 M⊙, GWPs (blue continuous line) against GWOPs (black dashed line). Right: stars with M⋆ > 1.5 M⊙, GWPs (purple continuous line) against GWOPs (black dashed line). |
| In the text | |
 |
Fig. 14 Age−metallicity relation for the different samples studied in this work. Open symbols indicate the corresponding comparison samples. |
| In the text | |
 |
Fig. 15 Left: stellar metallicity as a function of the semimajor axis of the innermost planet. Right: stellar metallicity as a function of the mass of the most massive planet. GWPs with M⋆ > 1.5 M⊙ are plotted with purple circles, GWPs less massive than 1.5 M⊙ in blue triangles, SGWPs as red squares, while LMSWPs are plotted as green asterisks. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.