EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 553 (May 2013) A&A, 553 (2013) A122 Full HTML
Free Access
Issue
A&A
Volume 553, May 2013
Article Number A122
Number of page(s) 7
Section Celestial mechanics and astrometry
DOI https://doi.org/10.1051/0004-6361/201321320
Published online 22 May 2013

© ESO, 2013

1. Introduction

In 2009, the International Astronomical Union (IAU) adopted the second realization of the International Celestial Reference Frame (ICRF2), made up of precise coordinates of 3414 extragalactic radio sources observed with very long baseline radio interferometry (VLBI) at 2 and 8 GHz (Fey et al. 2010). This new fundamental catalog took advantage of recent improvements in the VLBI technique, both at the observational level (new antennas, better data acquisition systems) and at the analysis level (improved analysis methods). The noise floor of the ICRF2 was evaluated at the level of 40 μas. The frame axes are defined by the coordinates of 295 so-called defining sources and are stable at the level of 10 μas over the period running from 1979.6 to 2009.2.

The celestial reference frame plays an important role in geodetic VLBI analysis, especially for precise estimates of the Earth’s orientation with respect to a space-fixed reference frame: if not taken into account, any deformation of the ICRF axes could arise in either the nutation or the Earth rotation angles (IERS 1996, II–17). This is particularly critical since several studies have used VLBI nutation series to infer interesting physical parameters relevant to the Earth’s core and inner core (Mathews et al. 2002; Koot et al. 2008, 2010; Koot & Dumberry 2011).

Geodetic VLBI observations and analyses are mainly managed within the International VLBI Service for Geodesy and Astrometry (IVS, see Schuh & Behrend 2012), an international collaboration of laboratories and agencies for development, operation, and support of VLBI. Some IVS analysis centers have processed the geodetic VLBI observational database to obtain radio source coordinate time series. These time series represent the motion of the centroid of the radio source as seen by the network, and were intensively used in the past to build up a more stable reference frame (see, e.g., Feissel-Vernier 2003; Feissel-Vernier et al. 2005, 2006; Lambert & Gontier 2009). The selection of the ICRF2 defining sources was partly based on these series (Fey et al. 2010): the authors defined a stability criterion and ranked the sources from the most to the less stable. Then, they used the most recent computations of structure indices (e.g., Charlot 1990; Fey & Charlot 1997) in order to eliminate sources with significant structures. Finally, they loosened the selection threshold for lower declinations to allow sources in the southern hemisphere to be selected and to improve the homogeneity of the defining source distribution over the celestial sphere.

Can the ICRF2 defining sources still be considered as defining in the light of post-ICRF2 observations? Are the ICRF2 axes still undeformed? In this paper, I analyzed recent coordinate time series of the 295 ICRF2 defining sources, for which new observations have been accumulated since 2009.2. I investigated whether they can still be considered as stable in the astrometric sense, hence be conserved in the ICRF2 defining set. Section 2 explains how the coordinate time series are generated. In Sect. 3, I investigate the astrometric stability of the defining sources and the time stability of the ICRF2 axes. Section 4 presents some conclusions.

2. Generation of the coordinate time series

The Paris Observatory IVS analysis center (Lambert & Barache 2012) provided a set of coordinate time series for 3791 sources1. They were obtained by analyzing of 5441 diurnal sessions using single- and multi-baseline networks between August 1979 and January 2013. The full set of time series was obtained after four solutions. In each solution, one fourth of the sources’ coordinates were estimated as session parameters. Others were estimated as global parameters, including three fourths of the 295 ICRF2 defining sources that are constrained by a no-net rotation (NNR) condition with a priori coordinates taken in the ICRF2 catalog. In all solutions, the elevation cut-off was set to 5°. Station coordinates were estimated as global parameters with no-net rotation and no-net translation constraints with respect to the VTRF 2008A (Böckmann et al. 2010) on the coordinates and velocities of 24 stations. Nonlinear motions of antennas at Fort Davis (Texas), Pie Town (New Mexico), Fairbanks (Alaska), TIGO at Concepción (Chile), and Tsukuba (Japan) were modeled by splines. A priori zenith delays were determined from local pressure values (Saastamoinen 1972), which were then mapped to the elevation of the observation using the Vienna mapping functions (Böhm et al. 2006). Zenith wet delays were estimated as a continuous piecewise linear function at 20-min intervals. Troposphere gradients were estimated as 6-hr east and north piecewise functions at all stations. Station heights were corrected for atmospheric pressure and oceanic tidal loading. The relevant loading quantities were deduced from surface pressure grids from the NCEP/NCAR reanalysis project atmospheric, global circulation model (Kalnay et al. 1996; Petrov & Boy 2004) and from the FES 2004 ocean-tide model (Lyard et al. 2004). A priori precession and nutation comply with the IAU 2000/2006 resolutions, which include the nutation model of Mathews et al. (2002), the improved precession model of Capitaine et al. (2003b), and the nonrotating origin-based coordinate transformation between terrestrial and celestial coordinate systems (Capitaine et al. 2003a). The calculations used the Calc 10.0/Solve 2010.05.21 geodetic VLBI analysis software package, which was developed and is maintained at NASA Goddard Space Flight Center. To suppress large outliers in the time series, I removed points that are away from the mean by more than ten times their formal error. This rejection scheme was iterated a few times.

3. Analysis and results

3.1. Astrometric stability of the defining sources

Figure 1 displays the observational history of the ICRF2 defining sources. As mentioned in Fey et al. (2010), the southern hemisphere suffers from a lack of observations. The discrepancy between north and south still shows up over 2009.2–2013.1, particularly for declinations lower than 50°S. The overall stability of a time series, as defined by Eq. (8) of Fey et al. (2010), is 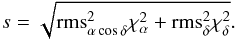(1)Comparing this quantity computed over the ICRF2 time span (1979.6–2009.2) and over the full time span (1979.6–2013.1) tells which sources underwent significant changes in their stability due to post-ICRF2 observations (Table 1). Results are displayed in Fig. 2, where one can see that the changes in the stability brought by the post-ICRF2 observations are never greater than 0.8 mas in absolute value, and become smaller when the number of post-ICRF2 observations increases. The averaged stability change is 0.007 mas. It is slightly larger for southern sources.

These changes in the stability can occur when the structure of the source changes with time, but also when a source that is poorly observed at the ICRF2 time is observed again. In the latter case, the accumulation of new observations allows more accurate conclusions about the astrometric suitability of the source. Indeed, if the number of sessions is small, the statistical quantities used during the selection process are less reliable than for well-observed sources. It basically tells us that the election of the source as defining could have been premature. This is especially true for the southern sources that were chosen, for some of them, not for reasons of stability but to balance out the source distribution between the two hemispheres.

thumbnail Fig. 1

Observational history of the 295 ICRF2 defining sources. The red vertical line indicates the end date of the ICRF2 data span.

thumbnail Fig. 2

Improvement in the stability brought by the observations after 2009.2 as a function of (top) the number of sessions and (bottom) the declination: a negative value means that the source becomes less stable.

3.2. Axis stability

From session coordinate time series, I computed annual points by applying a weighted moving average. (The averaging window is one year long and is displaced by steps of one year, so that there is no overlapping of data.) Doing so, I assumed that a year is representative of the time scale on which a significant radio center displacement can occur. Each annual point was affected by an uncertainty made up of the weighted standard deviation of the data within the averaging window.

thumbnail Fig. 3

Annual parameters obtained by fit to the annual frames using the three transformations.

I could therefore construct annual representations of the ICRF2 by taking the annual coordinates of the ICRF2 defining sources to check whether these annual frames deform from one year to the next. The radio source coordinate difference between two catalogs can be modeled by a coordinate transformation that takes the global rotation between the two catalogs into account, as well as the deformations. The coordinate transformation recommended by the IERS and in use at the ICRS-PC reads (IERS 1996, II–32) as 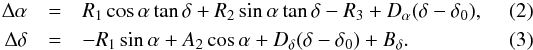wherein R1, R2, and R3 are rotation angles around the X, Y, and Z axes, respectively; Dα and Dδ are slopes in right ascension and declination as a function of the declination; and Bδ is a bias in declination. This transformation will be referred to as T1 in the following.

A simplified version of this transformation was used in several studies (e.g., Feissel-Vernier et al. 2006; Lambert & Gontier 2009; Fey et al. 2010). It neglects the slope parameters Dα and Dδ and keeps the bias Bδ (also known as equatorial tilt and designed by dz): 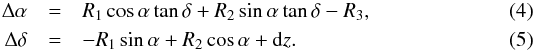This transformation will be referred to as T2.

Both transformations T1 and T2 imply, however, that a privileged direction exists, that is the Z-axis. A more general coordinate transformation is made up of three rotations, of angles noted Ri, plus another three parameters Di expressing a dipolar deformation of the coordinate field. It corresponds to the first-degree magnetic (toroidal) and electric (spheroidal) harmonics of the vector spherical harmonics development of a vector field (see, e.g., Mignard & Morando 1990; Oviedo 1996; Mignard & Klioner 2012): 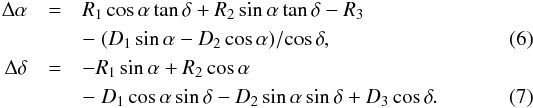In each of these equations, the first line corresponds to the rotation, and the second line expresses the dipolar deformation. This last transformation is referred to as T3. In both transformations T1 and T3, relatively high correlations arise between Dδ and Bδ (~0.5) for the former and between R1 and D2 or R2 and D1 (~0.4) for the latter.

For annual frames made up of more than four sources observed in more than ten sessions, parameters of the three transformations above were fitted to the annual coordinate differences of the defining sources by weighted least squares and reported in Fig. 3. The three transformations give consistent results. One can see that the axis stability does not change drastically after 2009.2. It remains around 20 μas for each axis. (In the ICRF2 work, the authors mention a stability of 10 μas, which does not contradict with this study, since they uses a different method to derive the axis stability: they compare the relative orientation of various subsets of sources.) Table 2 displays the rms of the annual transformation parameters for 1979.6–2009.2 and 1979.6–2013.1. It appears that there is no drastic degradation after 2009.2.

4. Concluding remarks

Using coordinate time series of the ICRF2 defining sources, I assessed the ICRF2 defining sources and axis stability. I showed that there is no noticeable deformation of the celestial reference frame axes after 2009.2, the date of the ICRF2 release. There is therefore no need to amend the definition of the frame axes by the list of 295 so-called defining sources.

Table 2

The rms of the annual transformation parameters for two time periods.

In the future, such a study should be undertaken regularly and source coordinate time series updated (e.g., on a yearly basis) so that the geodetic VLBI community can be informed of any problem due to the centroid displacement of some sources, and take it into account in the operational analysis by, e.g., removing the problematic sources from the constraint. This process of validating the ICRF2 axes is part of the tasks of the International Celestial Reference System Product Center (ICRS-PC) of the International Earth Rotation and Reference Systems Service (IERS). The monitoring of the sources through coordinate time series complements the regular VLBI imaging undertaken by the IVS in the RDV sessions. These observations

permit the computation of the source structure index, the other fundamental criterion used in the selection of the ICRF2 defining sources.

Online material

Table 1

Variation in the stability due to post-ICRF2 observations.

Acknowledgments

I thank the International VLBI Service for Geodesy and Astrometry (IVS) for their permanent efforts to schedule, observe, correlate, and analyze VLBI data, as well as an anonymous reviewer who helped in improving this manuscript.

References

  1. Böckmann, S., Artz, T., & Nothnagel, A. 2010, J. Geod., 84, 201 [NASA ADS] [CrossRef] [Google Scholar]
  2. Böhm, J., Werl, B., & Schuh, H. 2006, J. Geophys. Res., 111, 2406 [Google Scholar]
  3. Capitaine, N., Chapront, J., Lambert, S. B., & Wallace, P. T. 2003a, A&A, 400, 1145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Capitaine, N., Wallace, P. T., & Chapront, J. 2003b, A&A, 412, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Charlot, P. 1990, AJ, 99, 1309 [NASA ADS] [CrossRef] [Google Scholar]
  6. Feissel-Vernier, M. 2003, A&A, 403, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Feissel-Vernier, M., Ma., C., Gontier, A.-M., & Barache, C. 2005, A&A, 438, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Feissel-Vernier, M., Ma., C., Gontier, A.-M., & Barache, C. 2006, A&A, 452, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Fey, A. L., & Charlot, P. 1998, ApJS, 111, 95 [Google Scholar]
  10. Fey, A. L., Gordon, D. G., Jacobs, C. S., et al. 2010, International Earth Rotation and Reference Systems Service (IERS) Technical Note 35, Bundesamts für Kartographie und Geodäsie, Frankfurt am Main [Google Scholar]
  11. Gontier, A.-M., Le Bail, K., Feissel, M., & Eubanks, T. M. 2001, A&A, 375, 661 [Google Scholar]
  12. IERS 1996, International Earth Rotation Service Annual Report 1995 (Paris: Observatoire de Paris), II-19 [Google Scholar]
  13. Kalnay, E., Kanamitsu, M., Kistler, R., et al. 1996, Bull. Am. Met. Soc., 77, 437 [NASA ADS] [CrossRef] [Google Scholar]
  14. Koot, L., & Dumberry, M. 2011, Earth Plan. Sci. Lett., 308, 343 [Google Scholar]
  15. Koot, L., Rivoldini, A., de Viron, O., et al. 2008, J. Geophys. Res., 113, DOI: 10.1029/2007JB005409 [Google Scholar]
  16. Koot, L., Dumberry, M., Rivoldini, A., et al. 2010, Geophys. J. Int., 182, 1279 [NASA ADS] [CrossRef] [Google Scholar]
  17. Lambert, S. B., & Barache, C. 2012, in International VLBI Service for Geodesy and Astrometry (IVS) 2011 Annual Report, NASA/TP-2012-217505, eds. D. Behrend, & K. D. Baver, 245 [Google Scholar]
  18. Lambert, S. B., & Gontier, A.-M. 2009, A&A, 493, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Lyard, F., Lefèvre, F., Letellier, T., & Francis, O. 2006, Ocean Dyn., 56, 394 [NASA ADS] [CrossRef] [Google Scholar]
  20. Mathews, P. M., Herring, T. A., & Buffett, B. A. 2002, J. Geophys. Res., 107, DOI: 10.1029/2001JB000390 [Google Scholar]
  21. Mignard, F., & Klioner, S. 2012, A&A, 547, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Mignard, F., & Morando, B. 1990, in Proc. Journées 1990 Systèmes de Référence Spatio-Temporels (Observatoire de Paris), eds. N. Capitaine, & S. Débarbat, 151 [Google Scholar]
  23. Oviedo, X. 1996, Analyses de repères célestes VLBI au moyen d’harmoniques vectorielles (Observatoire de Paris) [Google Scholar]
  24. Petrov, L., & Boy, J.-P. 2004, J. Geophys. Res., 109, 3405 [Google Scholar]
  25. Saastamoinen, J. 1972, in The Use of Artificial Satellites for Geodesy, Geophysics Monograph Series (Washington, DC: American Geophysical Union), eds. W. Soren et al., 15, 247 [Google Scholar]
  26. Schuh, H., & Behrend, D. 2011, J. Geodyn., 61, 68 [Google Scholar]

All Tables

Table 2

The rms of the annual transformation parameters for two time periods.

In the text
Table 1

Variation in the stability due to post-ICRF2 observations.

In the text

All Figures

thumbnail Fig. 1

Observational history of the 295 ICRF2 defining sources. The red vertical line indicates the end date of the ICRF2 data span.
In the text
thumbnail Fig. 2

Improvement in the stability brought by the observations after 2009.2 as a function of (top) the number of sessions and (bottom) the declination: a negative value means that the source becomes less stable.
In the text
thumbnail Fig. 3

Annual parameters obtained by fit to the annual frames using the three transformations.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.