| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321175 | |
| Published online | 25 April 2013 | |
Nonlinear damped standing slow waves in hot coronal magnetic loops
1
Solar Physics and Space Plasma Research Centre
(SP 2RC), University of Sheffield,
Hicks Building, Hounsfield Road,
Sheffield
S3 7RH,
UK
2
Space Research Institute (IKI), Russian Academy of Sciences,
117997
Moscow,
Russia
e-mail: m.s.ruderman@sheffield.ac.uk
Received:
27
January
2013
Accepted:
19
March
2013
We study the nonlinear standing slow waves in coronal magnetic loops. We assume that the wave amplitude is sufficiently small and use it as a small parameter in the asymptotic expansions. In addition, we assume that the wave damping is sufficiently slow, which enables us to introduce the “slow” time related to the evolution of the wave amplitude and shape. We show that, in the leading-order approximation, the nonlinear standing wave is a superposition of two identical nonlinear waves propagating in the opposite directions. The two waves are governed by the Burgers equation. Using the Cole-Hopfe substitution, we obtain an analytical solution describing a standing wave that has the form of the linear fundamental eigenmode at the initial moment of time. This solution is used for the parametric study of nonlinear standing waves. In particular, the effect of nonlinearity on the oscillation damping time is investigated.
Key words: magnetohydrodynamics (MHD) / plasmas / waves / methods: analytical
© ESO, 2013
1. Introduction
Standing waves in hot (T ≳ 6 MK) coronal loops were observed by the Solar Ultraviolet Measurements of Emitted Radiation (SUMER) spectrometer onboard the SOHO spacecraft (Kliem et al. 2002; Wang et al. 2002, 2003a,b). Observations of 17 events revealed that the oscillation periods ranged from 11 to 31 min, and the decay time from 5.5 to 29 min. Ofman & Wang (2002) interpreted these oscillations as slow standing waves. The velocity amplitude in these oscillations was up to one quarter of the phase speed, so at least some of them were moderately nonlinear. Ofman & Wang (2002) modelled these oscillations numerically and found that the main damping mechanism causing their damping is thermal conduction. They also found that the damping prevents strong nonlinear steepening and shock formation. For a recent review of standing slow waves in coronal loops see Wang (2011).
In their modelling Ofman & Wang (2002) used the direct numerical solution of the one-dimensional non-stationary nonlinear equations describing the motion of compressible fluid with the account of viscosity and thermal conduction. They carried out the modelling only for a restricted range of parameters. More recently, a similar numerical modelling has been carried out by Mendoza-Briceño et al. (2004), Sigalotti et al. (2007), and Verwichte et al. (2008) for a wider range of coronal loop parameters and initial perturbation amplitude.
In this paper we aim to present a semi-analytical study of slow standing waves in hot coronal loops. Our analysis is based on the fact that the oscillation amplitude is quite moderate, so the dimensionless amplitude can be used as a small parameter in the asymptotic expansion. As a result we derive a simple differential equation describing the perturbation evolution with time. This enables us to carry out the parametric study of oscillations for a wide range of parameters.
The paper is organized as follows. In the next section we formulate the problem, discuss the main assumptions, and present the governing equations. In Sect. 3 we derive the nonlinear equation describing the time-evolution of the velocity in the slow standing wave. In Sect. 4 we obtain the analytic solution describing the evolution with time of the perturbation corresponding to the fundamental mode of slow standing waves. We then use this solution for the parametric study of the nonlinear damping of slow standing waves. Section 5 contains the summary of the obtained results and our conclusions.
2. Problem formulation and main assumptions
We study slow standing waves in hot coronal loops with the temperature
T ≳ 6 MK. The atmospheric scale height in these hot loops is larger
than 300 Mm. This implies that, in these loops, we can safely neglect the density variation
if the height of the loop apex point is smaller than or of the order of 100 Mm. The plasma
number density in hot loops usually does not exceed 1015 m-3. Then,
for T ≤ 10 MK, the plasma pressure does not exceed 0.3 Nm-2. The
magnetic pressure is equal
to B2/2μ0,
where B is the magnetic field magnitude and
μ0 ≈ 1.26 × 10-6 H m-1 is the magnetic
permeability of free space. Then we easily find that the plasma beta is smaller than 0.1
when B ≳ 10-3 Tesla = 10 G. Since this condition is usually
satisfied in the coronal loops, we can use the low-beta plasma approximation when studying
the slow waves in hot coronal loops. This implies that we can neglect the magnetic field
perturbation. If, in addition, we neglect the variation of the loop cross-section and the
equilibrium quantities in the directions perpendicular to the loop axis, and the loop
curvature, then we can describe the slow waves by one-dimensional hydrodynamic equations
(Priest 1982; Goedbloed & Poedts 2004) 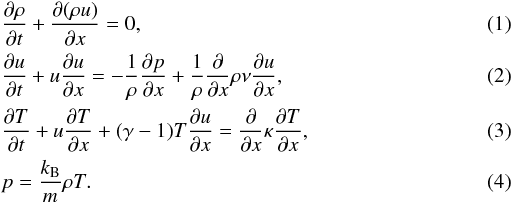 Here
u is the velocity, ρ the density, p the
pressure, T the temperature, γ the ratio of specific
heats, kB the Boltzmann constant, and m the
mean mass for a particle (m ≈ 0.6 mp in the
solar corona, where mp is the proton mass). The
coefficients ν and κ are defined by
Here
u is the velocity, ρ the density, p the
pressure, T the temperature, γ the ratio of specific
heats, kB the Boltzmann constant, and m the
mean mass for a particle (m ≈ 0.6 mp in the
solar corona, where mp is the proton mass). The
coefficients ν and κ are defined by 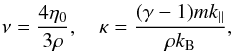 (5)where
kB is the Boltzmann constant,
η0 the first viscosity coefficient in the Braginskii’s
expression for the viscosity tensor, and k∥ the thermal
conductivity parallel to the magnetic field. These latter two quantities are given by (Braginskii 1965)
(5)where
kB is the Boltzmann constant,
η0 the first viscosity coefficient in the Braginskii’s
expression for the viscosity tensor, and k∥ the thermal
conductivity parallel to the magnetic field. These latter two quantities are given by (Braginskii 1965) 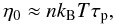 (6)and
(Spitzer 1962; Priest 1982)
(6)and
(Spitzer 1962; Priest 1982) 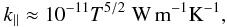 (7)where
n = ρ/mp
is the number density and τp the proton collision time. It is
given by the approximate expression
(7)where
n = ρ/mp
is the number density and τp the proton collision time. It is
given by the approximate expression 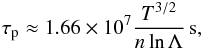 (8)where Λ is the Coulomb
logarithm and the number density n is measured in m-3. Fot
typical conditions in hot loops lnΛ ≈ 20, and τp is
approximately between 10 and 25 s.
(8)where Λ is the Coulomb
logarithm and the number density n is measured in m-3. Fot
typical conditions in hot loops lnΛ ≈ 20, and τp is
approximately between 10 and 25 s.
The system of Eqs. (1)–(4) is essentially the same as the one used by
Ofman & Wang (2002). The only difference is
that we neglected the term describing the viscous heating in the energy Eq. (4). The reason for this is that this term is
quadratic with respect to u, while, in what follows, we linearise the
dissipative terms. The system of Eqs. (1)–(4) has to be supplemented with
the boundary conditions. We assume that the magnetic loop is frozen in the dense
photosphere, so that 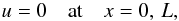 (9)where
L is the loop length.
(9)where
L is the loop length.
The system of Eqs. (1)–(4) with the boundary conditions (9) is used in the next section to derive the equation governing the evolution of the velocity with time in a slow standing wave.
3. Derivation of the governing equation for the oscillation velocity
In this section we derive the equation governing the evolution of the oscillation velocity with time. If we neglect the nonlinear and dissipative terms in Eqs. (1)–(4), this system of equations admits solutions describing periodic standing slow waves in the loop. We assume that the nonlinear and dissipative terms are small and only cause a slow evolution of perturbations. This assumption enables us to use the method of two scales with the “fast time” related to the quasi-periodic oscillations and “slow” time related to slow evolution of oscillations (e.g. Bender & Orszag 1978). Before starting the derivation we comment on the criterion of applicability of the two-scale method. When studying damped oscillations it is usually assumed that these oscillations can be considered as slowly evolving and the two-scale method can be applied if the characteristic damping time is much longer than the oscillation period. However, this is not completely correct. In the linear theory a typical function describing the damped oscillations is e−γtsinωt. The characteristic damping time is 1/γ. It is also clear that the characteristic time related to the oscillation is 1/ω rather than the oscillation period 2π/ω. This implies that the criterion for the applicability of the two-scale method is γ/ω ≪ 1. We see that even when the characteristic damping time is equal to the oscillation period, we have γ/ω < 0.2 and the use of the two-scale method is perfectly correct. Since, in accordance with observations, the characteristic damping time of the slow standing waves in hot coronal loops is longer than or of the order of the oscillation period, we can use the two-scale method to study these oscillations. Then we use the asymptotic method based on the expansions with respect to the small amplitude of oscillations. To complete this introductory discussion we mention that a similar method of asymptotic expansions was previously successfully applied by Gusev (1984b,a) to study the steady state of oscillation of driven standing nonlinear waves in a finite-length wave guide, and by Ruderman & Nocera (1998) to study the steady state of driven Alfvén oscillations in a magnetic cavity.
In what follows we assume that the dissipation is weak and introduce the scaled
coefficients at the dissipative terms, 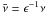 and
and 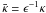 ,
where ϵ ≪ 1. We also assume that the oscillation amplitude is sufficiently
small and neglect the dependence of ν and κ
on T. Hence, in what follows, ν and κ
are constant. Finally we introduce the “slow” time
t1 = ϵt. Then Eqs. (1)–(3) are transformed to
,
where ϵ ≪ 1. We also assume that the oscillation amplitude is sufficiently
small and neglect the dependence of ν and κ
on T. Hence, in what follows, ν and κ
are constant. Finally we introduce the “slow” time
t1 = ϵt. Then Eqs. (1)–(3) are transformed to ![\begin{eqnarray} \label{eq:3.1} && \frac{\partial\rho}{\partial t} + \frac{\partial(\rho u)}{\partial x} = -\epsilon\frac{\partial\rho}{\partial t_1}, \\[3mm] \label{eq:3.2} && \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + \frac1\rho\frac{\partial p}{\partial x} = -\epsilon\frac{\partial u}{\partial t_1} + \epsilon\bar{\nu}\frac{\partial^2 u}{\partial x^2}, \\[3mm] \label{eq:3.3} && \frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + (\gamma-1)T\frac{\partial u}{\partial x} = -\epsilon\frac{\partial T}{\partial t_1} + \epsilon\bar{\kappa}\frac{\partial^2 T}{\partial x^2}\cdot \end{eqnarray}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq53.png) Equation (4) remains unchanged. We look for the solution to
the system of Eqs. (4) and (10)−(12) with the boundary conditions (9) in the form of expansions
Equation (4) remains unchanged. We look for the solution to
the system of Eqs. (4) and (10)−(12) with the boundary conditions (9) in the form of expansions 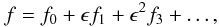 (13)where f
represents any of the quantities u, ρ, p
and T. The first term, f0, corresponds to the
unperturbed state, so f0 = const. Note
that u0 = 0.
(13)where f
represents any of the quantities u, ρ, p
and T. The first term, f0, corresponds to the
unperturbed state, so f0 = const. Note
that u0 = 0.
3.1. First-order approximation
In the first-order approximation we substitute the expansion (13) in Eqs. (4) and (10)−(12), and the boundary condition (9) and collect the terms proportional
to ϵ. As a result we obtain 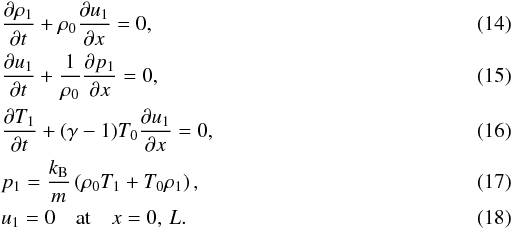 Eliminating
perturbations of all variables in favour of u1, we obtain
Eliminating
perturbations of all variables in favour of u1, we obtain
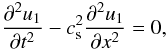 (19)where
cs = (γp0/ρ0)1/2
is the adiabatic sound speed. When deriving this equation we have used he relation
p0 = kBρ0T0/m
that follows from Eq. (4). The general
solution to Eq. (19) can be written as
(19)where
cs = (γp0/ρ0)1/2
is the adiabatic sound speed. When deriving this equation we have used he relation
p0 = kBρ0T0/m
that follows from Eq. (4). The general
solution to Eq. (19) can be written as
![\begin{equation} u_1 = c_{\rm s}[f(\xi) + g(\eta)], \quad \xi = \omega\left(t - \frac x{c_{\rm s}}\right), \;\; \eta = \omega\left(t + \frac x{c_{\rm s}}\right), \label{eq:3.11} \end{equation}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq66.png) (20)where, at present,
f and g are arbitrary functions, and
ω is an arbitrary constant with the dimension s-1. Note
that f and g also depend
on t1, however, at present, we do not write this argument
explicitly. Substituting Eq. (20) in
Eq. (18), we obtain
(20)where, at present,
f and g are arbitrary functions, and
ω is an arbitrary constant with the dimension s-1. Note
that f and g also depend
on t1, however, at present, we do not write this argument
explicitly. Substituting Eq. (20) in
Eq. (18), we obtain 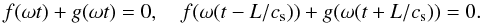 (21)It follows from these
equations that
g(y) = −f(y), and
f(y) is a function with the period equal to
2ωL/cs. It is convenient
to define ω such that the period of
function f(y) is equal to 2π. In this
case
ω = πcs/L.
Summarizing, we obtain that
(21)It follows from these
equations that
g(y) = −f(y), and
f(y) is a function with the period equal to
2ωL/cs. It is convenient
to define ω such that the period of
function f(y) is equal to 2π. In this
case
ω = πcs/L.
Summarizing, we obtain that ![\begin{equation} u_1 = c_{\rm s}[f(\xi) - f(\eta)], \label{eq:3.13} \end{equation}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq76.png) (22)where
f is a 2π-periodic function. Now it follows from
Eqs. (14), (15), and (17) that
(22)where
f is a 2π-periodic function. Now it follows from
Eqs. (14), (15), and (17) that
![\begin{equation} \rho_1 = \rho_0[f(\xi) + f(\eta)], \quad p_1 = \rho_0 c_{\rm s}^2[f(\xi) + f(\eta)], \label{eq:3.14} \end{equation}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq77.png) (23)
(23)![\begin{equation} T_1 = (\gamma-1)T_0 [f(\xi) + f(\eta)]. \label{eq:3.15} \end{equation}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq78.png) (24)
(24)
3.2. Second-order approximation
In the second-order approximation we collect the terms proportional
to ϵ2 in Eqs. (4) and (10)–(12), and the boundary condition (9). Then, using Eqs. (22)−(24), we obtain ![\begin{eqnarray} \label{eq:3.16} && \frac{\partial\rho_2}{\partial t} + \rho_0\frac{\partial u_2}{\partial x} = 2\omega\rho_0\left(f_- f'_- + f_+ f'_+\right) - \rho_0\left(\frac{\partial f_-}{\partial t_1} + \frac{\partial f_+}{\partial t_1}\right), \\ && \frac{\partial u_2}{\partial t} + \frac1{\rho_0}\frac{\partial p_2}{\partial x} = 2\omega c_{\rm s}\left(f_- f'_+ - f_+ f'_-\right) \nonumber\\ \label{eq:3.17} && \hspace*{2.4cm} - \, c_{\rm s}\left(\frac{\partial f_-}{\partial t_1} - \frac{\partial f_+}{\partial t_1}\right) + \frac{\bar{\nu}\omega^2}{c_{\rm s}}\left(f''_- - f''_+\right), \\ && \frac{\partial T_2}{\partial t} + (\gamma-1)T_0\frac{\partial u_2}{\partial x} = (\gamma-1)\omega T_0\left[\gamma\left(f_- f'_- + f_+ f'_+\right)\right. \nonumber\\ &&\hspace*{1.9cm} - \, \left. (2-\gamma)\left(f_- f'_+ + f_+ f'_-\right)\right] \nonumber\\ \label{eq:3.18} && \hspace*{1.9cm} - \, T_0\left(\frac{\partial f_-}{\partial t_1} + \frac{\partial f_+}{\partial t_1}\right) + \frac{(\gamma-1)\bar{\kappa}\omega^2 T_0}{c_{\rm s}^2}\left(f''_- + f''_+\right),\quad\quad\quad \\ \label{eq:3.19} && p_2 - \frac{k_{\rm B}}m\left(\rho_0 T_2 + T_0\rho_2\right) = p_0(\gamma-1)\left(f_- + f_+\right)^2, \\ \label{eq:3.20} && u_2 = 0 \quad \mbox{at} \quad x = 0,\,L, \end{eqnarray}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq80.png) where
f− = f(ξ,t1),
f + = f(η,t1),
and the prime denotes the partial derivative
of f(y,t1) with respect
to y. Eliminating ρ2,
p2, and T2 from Eqs. (25)−(28), we obtain the equation for u2:
where
f− = f(ξ,t1),
f + = f(η,t1),
and the prime denotes the partial derivative
of f(y,t1) with respect
to y. Eliminating ρ2,
p2, and T2 from Eqs. (25)−(28), we obtain the equation for u2:
![\begin{eqnarray} \frac{\partial^2 u_2}{\partial t^2} &-& c_{\rm s}^2\frac{\partial^2 u_2}{\partial x^2} = \frac{\omega^3[\gamma\bar{\nu} + (\gamma-1)\bar{\kappa} ]}{\gamma c_{\rm s}} \left(f'''_- - f'''_+\right) \nonumber\\ &-& 2\omega c_{\rm s}\left(\frac{\partial f'_-}{\partial t_1} - \frac{\partial f'_+}{\partial t_1}\right) + \omega^2 c_{\rm s} \Bigg[(\gamma+1)\Big({f'_-}^2 - {f'_+}^2 \nonumber\\ \label{eq:3.21} &+& f_- f''_- - f_+ f''_+\Big) + (3-\gamma)\left(f_- f''_+ - f_+ f''_-\right)\Bigg]. \end{eqnarray}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq89.png) (30)We
introduce the Fourier series
(30)We
introduce the Fourier series 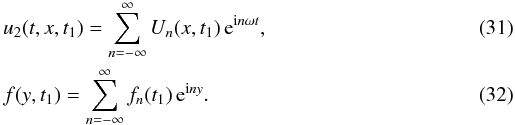 where
where
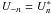 ,
,
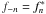 , and the
asterisk denotes the complex conjugate. Without loss of generality we can always assume
that f0 = 0. Substituting these expressions in Eq. (30), and using the identity
, and the
asterisk denotes the complex conjugate. Without loss of generality we can always assume
that f0 = 0. Substituting these expressions in Eq. (30), and using the identity 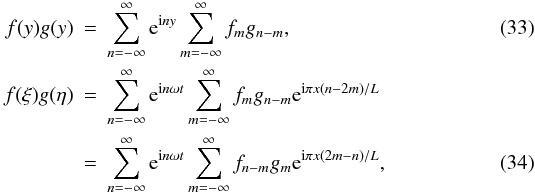 valid
for real functions f and g, we obtain
valid
for real functions f and g, we obtain ![\begin{eqnarray} \label{eq:3.26} \frac{\partial^2 U_n}{\partial x^2} &+& \frac{\pi^2 n^2}{L^2} U_n = \frac{2\omega^2}{c_{\rm s}}\Bigg[\Bigg(\frac{\omega n^3[\gamma\bar{\nu} + (\gamma-1)\bar{\kappa}]}{\gamma c_{\rm s}^2}f_n \nonumber\\ &+& \frac{2n}\omega\frac{\partial f_n}{\partial t_1} - {\rm i}n(\gamma+1) \sum_{m=-\infty}^\infty mf_m f_{n-m}\Bigg)\sin\frac{\pi nx}L \nonumber\\ &-& {\rm i}(3-\gamma)\gamma\sum_{m=-\infty}^\infty m^2 f_m f_{n-m} \sin\frac{\pi(n-2m)x}L\Bigg]\cdot \end{eqnarray}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq95.png) (35)It
follows from Eq. (9) that
Un satisfies the boundary conditions
(35)It
follows from Eq. (9) that
Un satisfies the boundary conditions
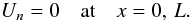 (36)The homogeneous
counterpart of Eq. (35) together with the
boundary conditions (36) constitute the
Sturm-Liouville problem. It has a non-trivial solution
Un = sin(πnx/L).
This implies that Eq. (35) has a solution
satisfying the boundary conditions (36)
only if the right-hand side of it satisfies the compatibility condition. This
compatibility condition is the condition that it is orthogonal to the
function sin(πnx/L), i.e. that the
integral of the product of the right-hand side and the
function sin(πnx/L) over the
interval [0,L] is equal to zero. In the last sum on the right-hand
side of Eq. (35) only two terms, one
proportional to sin(πnx/L) and the
other proportional to −sin(πnx/L)
can give non-zero contributions in this integral. However, due to the assumption that
f0 = 0, these two terms are identically zero. Hence, the
last sum on the right-hand side of Eq. (35) does not contribute in the integral. It is easy to show that this conclusion
remains correct even if we do not assume that f0 = 0. Then we
immediately obtain that the compatibility condition is
(36)The homogeneous
counterpart of Eq. (35) together with the
boundary conditions (36) constitute the
Sturm-Liouville problem. It has a non-trivial solution
Un = sin(πnx/L).
This implies that Eq. (35) has a solution
satisfying the boundary conditions (36)
only if the right-hand side of it satisfies the compatibility condition. This
compatibility condition is the condition that it is orthogonal to the
function sin(πnx/L), i.e. that the
integral of the product of the right-hand side and the
function sin(πnx/L) over the
interval [0,L] is equal to zero. In the last sum on the right-hand
side of Eq. (35) only two terms, one
proportional to sin(πnx/L) and the
other proportional to −sin(πnx/L)
can give non-zero contributions in this integral. However, due to the assumption that
f0 = 0, these two terms are identically zero. Hence, the
last sum on the right-hand side of Eq. (35) does not contribute in the integral. It is easy to show that this conclusion
remains correct even if we do not assume that f0 = 0. Then we
immediately obtain that the compatibility condition is ![\begin{equation} \frac{\partial f_n}{\partial t_1} - \frac{{\rm i}\omega(\gamma+1)}2\sum_{m=-\infty}^\infty mf_m f_{n-m} + \frac{\omega^2 n^2[\gamma\bar{\nu} + (\gamma-1)\bar{\kappa}]}{2\gamma c_{\rm s}^2}f_n = 0. \label{eq:3.28} \end{equation}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq102.png) (37)Multiplying this
equation by einy and taking the sum with respect
to n from −∞ to ∞ we obtain
(37)Multiplying this
equation by einy and taking the sum with respect
to n from −∞ to ∞ we obtain 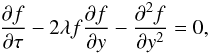 (38)where
τ = t/tdl,
(38)where
τ = t/tdl,
![\begin{equation} t_{\rm dl} = \frac{2\gamma L^2}{\pi^2[\gamma\nu + (\gamma-1)\kappa]}, \quad \lambda = \frac{\epsilon\gamma(\gamma+1)c_{\rm s} L}{2\pi[\gamma\nu + (\gamma-1)\kappa]}\cdot \label{eq:3.30} \end{equation}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq108.png) (39)Here
tdl is the damping time given by the linear theory. We see
that the function f satisfies the Burgers Eq. (38). The Burgers equation is one of the basic
equations in nonlinear acoustics (e.g. Burgers 1948;
Whitham 1974; Rudenko & Solujan 1977). In the leading-order approximation with respect
to the small parameter ϵ the plasma velocity, density, pressure, and
temperature are given by Eqs. (22)−(24). Hence, in the
leading-order approximation, the nonlinear standing wave is a superposition of two
identical nonlinear waves propagating in the opposite directions. The evolution of each of
these waves is governed by the Burgers Eq. (38).
(39)Here
tdl is the damping time given by the linear theory. We see
that the function f satisfies the Burgers Eq. (38). The Burgers equation is one of the basic
equations in nonlinear acoustics (e.g. Burgers 1948;
Whitham 1974; Rudenko & Solujan 1977). In the leading-order approximation with respect
to the small parameter ϵ the plasma velocity, density, pressure, and
temperature are given by Eqs. (22)−(24). Hence, in the
leading-order approximation, the nonlinear standing wave is a superposition of two
identical nonlinear waves propagating in the opposite directions. The evolution of each of
these waves is governed by the Burgers Eq. (38).
4. Nonlinear damping of slow waves
In this section we use the results obtained in the previous section to study the damping of
nonlinear standing waves. We assume that, at the initial moment of time, the
function f is given by 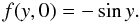 (40)This implies that in the
leading-order approximation
(40)This implies that in the
leading-order approximation 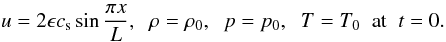 (41)We see that the initial
wave amplitude is 2ϵcs. Hence,
2ϵ is the perturbation Mach number at the initial moment of time.
To obtain the 2π-periodic solution of Eq. (38) satisfying the initial condition (40), we use the famous Cole-Hopf (Cole
1951; Hopf 1950) substitution
(41)We see that the initial
wave amplitude is 2ϵcs. Hence,
2ϵ is the perturbation Mach number at the initial moment of time.
To obtain the 2π-periodic solution of Eq. (38) satisfying the initial condition (40), we use the famous Cole-Hopf (Cole
1951; Hopf 1950) substitution 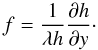 (42)Substituting this
expression in Eq. (38) yields
(42)Substituting this
expression in Eq. (38) yields 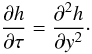 (43)The function
h has to be 2π-periodic. It follows from Eqs. (40) and (42) that h has to satisfy the initial condition
(43)The function
h has to be 2π-periodic. It follows from Eqs. (40) and (42) that h has to satisfy the initial condition
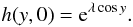 (44)The general
2π-periodic solution to Eq. (43) is
(44)The general
2π-periodic solution to Eq. (43) is ![\begin{equation} h(y,\tau) = a_0 + \sum_{n=1}^\infty {\rm e}^{-n^2\tau}\left[a_n\cos(ny) + b_n\sin(ny)\right]. \label{eq:4.6} \end{equation}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq118.png) (45)Using the formulae (e.g.
Abramowitz & Stegun 1964)
(45)Using the formulae (e.g.
Abramowitz & Stegun 1964) 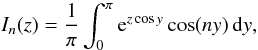 (46)where
n = 0,1,... and
In is the modified Bessel function of the
first kind and order n, we obtain the Fourier expansion
(46)where
n = 0,1,... and
In is the modified Bessel function of the
first kind and order n, we obtain the Fourier expansion 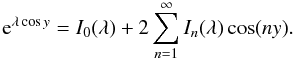 (47)It follows from
Eq. (44), and the comparison of the
Fourier expansion (45) calculated at
τ = 0 and the Fourier expansion (47) that
(47)It follows from
Eq. (44), and the comparison of the
Fourier expansion (45) calculated at
τ = 0 and the Fourier expansion (47) that 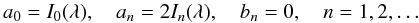 (48)Substituting
these expressions in Eq. (45), we eventually
arrive at
(48)Substituting
these expressions in Eq. (45), we eventually
arrive at 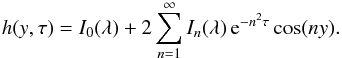 (49)This equation
together with Eq. (42) define the
2π-periodic solution to Eq. (38) satisfying the initial condition (40). We see that, in the dimensionless variables, the evolution of the initial
perturbation depends on one dimensionless parameter λ only. Using
Eqs. (4)−(8), we obtain the approximate expression
(49)This equation
together with Eq. (42) define the
2π-periodic solution to Eq. (38) satisfying the initial condition (40). We see that, in the dimensionless variables, the evolution of the initial
perturbation depends on one dimensionless parameter λ only. Using
Eqs. (4)−(8), we obtain the approximate expression 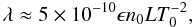 (50)n0
is in m-3, L is in m, and T0 is in
Kelvin, and we have taken the Coulomb logarithm lnΛ = 20.
(50)n0
is in m-3, L is in m, and T0 is in
Kelvin, and we have taken the Coulomb logarithm lnΛ = 20.
The parameter λ can vary in a quite large limits. For instance, in the
example considered by Ofman & Wang (2002) the
loop parameters are as follows: L ≈ 400 Mm, n = 5 ×
1014 m-3 and T = 6.3 MK. The initial perturbation
Mach number is about 0.2, so ϵ ≈ 0.1. Substituting these numbers in
Eq. (50), we obtain
λ ≈ 0.25. If we take higher values of ϵ
and/or n, we can obtain the value of λ exceeding unity.
However, for typical hot loop parameters and moderate Mach numbers of the initial amplitude
we can expect that λ is sufficiently smaller than unity. In that case we
can obtain the approximate solution using the expansion in the power series with respect
to λ. Using the expansions of the modified Bessel functions in the power
series (e.g. Abramowitz & Stegun 1964), we
obtain from Eq. (49) 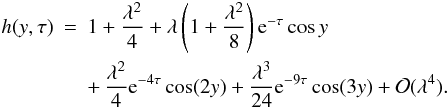 (51)Substituting
this expression in Eq. (42) yields
(51)Substituting
this expression in Eq. (42) yields
![\begin{eqnarray} \label{eq:4.13} f(y,\tau) &=& {\rm e}^{-\tau}\left[1 - \frac{\lambda^2}8 \left(1 - {\rm e}^{-2\tau}\right)^2\right]\sin y \nonumber\\ &&+ \, \frac\lambda2 {\rm e}^{-2\tau}\left(1 - {\rm e}^{-2\tau}\right)\sin(2y) \nonumber\\ &&+ \, \frac{\lambda^2}8 {\rm e}^{-3\tau}\left(1 - {\rm e}^{-2\tau}\right)^2 \left(2 + {\rm e}^{-2\tau}\right)\sin(3y) + {\cal O}(\lambda^3). \end{eqnarray}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq138.png) (52)In
order to study how nonlinearity affects the damping rate we calculate the average over
period energy of oscillations per unit area of the loop cross-section. In the leading-order
approximation with respect to ϵ it is given by
(52)In
order to study how nonlinearity affects the damping rate we calculate the average over
period energy of oscillations per unit area of the loop cross-section. In the leading-order
approximation with respect to ϵ it is given by 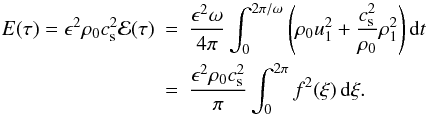 (53)We
define the dimensionless damping time τd by the equation
ℰ(τd) = e-2 (note that ℰ(0) = 1). Substituting
Eq. (52) in Eq. (53), we obtain
(53)We
define the dimensionless damping time τd by the equation
ℰ(τd) = e-2 (note that ℰ(0) = 1). Substituting
Eq. (52) in Eq. (53), we obtain ![\begin{equation} {\cal E}(\tau) = {\rm e}^{-2\tau}\left[1 - \frac{\lambda^2}4\left(1 - {\rm e}^{-2\tau}\right)^3\right] + {\cal O}\big(\lambda^3\big). \label{eq:4.15} \end{equation}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq143.png) (54)Using this result we easily
find
(54)Using this result we easily
find 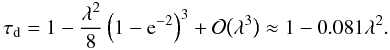 (55)We see that
nonlinearity reduces the damping time. This is an expected result because the nonlinearity
transfers a part of the wave energy from the fundamental mode to the overtones that damp
faster than the fundamental mode. As we have already pointed out, in the example considered
by Ofman & Wang
(2002)λ ≈ 0.4. Then, using Eq. (55), we find that the nonlinear damping time is by about 1.3% shoter
than that given by the linear theory. We see that even for a moderately high value
of λ the correction to the damping time given by the nonlinear theory is
very small.
(55)We see that
nonlinearity reduces the damping time. This is an expected result because the nonlinearity
transfers a part of the wave energy from the fundamental mode to the overtones that damp
faster than the fundamental mode. As we have already pointed out, in the example considered
by Ofman & Wang
(2002)λ ≈ 0.4. Then, using Eq. (55), we find that the nonlinear damping time is by about 1.3% shoter
than that given by the linear theory. We see that even for a moderately high value
of λ the correction to the damping time given by the nonlinear theory is
very small.
We introduce the oscillation period
P = 2π/ω = 2L/cs
and the damping time ![\begin{equation} t_{\rm d} = \frac{2\gamma L^2\tau_{\rm d}}{\pi^2[\gamma\nu + (\gamma-1)\kappa]}\cdot \label{eq:4.17} \end{equation}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq147.png) (56)Then we obtain for
the ratio of damping time to the wave period
td/P = τdtdl/P,
where
(56)Then we obtain for
the ratio of damping time to the wave period
td/P = τdtdl/P,
where ![\begin{equation} \frac{t_{\rm dl}}P = \frac{\gamma c_{\rm s} L}{\pi^2[\gamma\nu + (\gamma-1)\kappa]} \approx 1.3\times10^{-10}\frac{n_0 L}{T_0^2}, \label{eq:4.18} \end{equation}](/articles/aa/full_html/2013/05/aa21175-13/aa21175-13-eq149.png) (57)where
tdl is the damping time given by linear theory,
and n0, L and T0
are measured in SI units. When deriving this formula we have used the relation
m = 0.6 mp. Using Eqs. (50) and (57) we obtain one more useful formula,
(57)where
tdl is the damping time given by linear theory,
and n0, L and T0
are measured in SI units. When deriving this formula we have used the relation
m = 0.6 mp. Using Eqs. (50) and (57) we obtain one more useful formula, 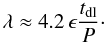 (58)In Fig. 1 the evolution of the velocity profile during one
oscillation period is shown for tdl = 5P and
ϵ = 0.1, which corresponds to λ ≈ 2.1. We can clearly
see the wave steepening related to the generation of higher harmonics due do nonlinearity.
(58)In Fig. 1 the evolution of the velocity profile during one
oscillation period is shown for tdl = 5P and
ϵ = 0.1, which corresponds to λ ≈ 2.1. We can clearly
see the wave steepening related to the generation of higher harmonics due do nonlinearity.
 |
Fig. 1 Evolution of the velocity profile with time for tdl = 5P and ϵ = 0.1. The upper, middle, and lower panel correspond to t = 0, P/2, and P respectively. |
 |
Fig. 2 Dependence of the dimensionless damping time τd on the nonlinearity parameter λ. The solid line shows the dependence calculated numerically using the full Fourier expansion (49), while the dashed line shows the approximate dependence for small λ given by Eq. (55). |
Figure 2 shows the dependence of the dimensionless damping time, τd, on the nonlinearity parameter λ. Once again we see that nonlinearity reduces the damping time. It is interesting to note that, although Eq. (55) was derived under the assumption that λ ≪ 1, in fact it approximates τd for λ ≲ 1 fairly well.
We can see from Fig. 2 that the nonlinearity effect can be neglected for λ ≲ 1. Then it follows from Eq. (58) that the nonlinear correction to the damping time must be taken into account only when ϵtdl/P ≳ 0.3. Once again using Fig. 2 we conclude that, for realistic values of λ ≲ 3, nonlinearity can reduce the damping time by no more than about one third, so tdl ≲ 1.5td. Hence, eventually, the criterion for the importance of nonlinearity effect on the damping time is ϵtd/P ≳ 0.2. Since, in accordance with observations, td ≲ 2P, we conclude that the nonlinearity effect is important only when ϵ ≳ 0.1, i.e. when the Much number of the initial perturbation is of the order of or larger than 0.2.
It is expedient to compare the results obtained in this paper with those presented by Verwichte et al. (2008). Unfortunately, we cannot carry out a quantitative comparison. The reason for this is that, for the loop parameters considered by Verwichte et al. (2008) Eq. (57) gives tdl/P ≈ 0.43, so, for this set of loop parameters, the condition tdl/P ≳ 1 is not satisfied, i.e. one of the main assumptions made in this paper is violated. It follows from Fig. 5 of Verwichte et al. (2008) that the correct value is tdl/P ≈ 1.4. This discrepancy is not surprising at all. It is well known that tdl/P is inversely proportional to k∥ only when k∥ is not too large. When k∥ increases, tdl/P takes its minimum value, and then starts to grow (e.g. De Moortel & Hood 2003). However, we can still make a qualitative comparison. First of all, similar to Verwichte et al. (2008), we found that nonlinearity reduces the damping time, which is a result expected on physical grounds. If, in accordance with the results obtain by Verwichte et al. (2008), we take tdl/P ≈ 1.4, then, using Eq. (58), we have λ ≈ 6ϵ = 3V0/cs, where V0 is the initial perturbation amplitude. Then it follows from Fig. 2 that the nonlinear correction to the damping time becomes important for V0/cs ≳ 0.3, and for this values of V0/cs the nonlinear correction to the damping time is an almost linear function of V0/cs. Taking into account that this correction is sufficiently small, we can conclude that the nonlinear correction to P/td, which is proportional to 1/τd, is also an approximately linear function of V0/cs. The inspection of Fig. 5 of Verwichte et al. (2008) reveals that P/td is also a linear function of V0/cs when V0/cs is approximately between 0.3 and 0.6, i.e. for values of V0/cs that can be considered as moderate. Our analytical results are not applicable for higher values of V0/cs. It is also worth noting that, for low values of V0/cs, the dependence of P/td on V0/cs given by both Fig. 2 of this paper and by Fig. 5 of Verwichte et al. (2008) is approximately quadratic.
We now compare the results obtained in this paper with the dependence of the damping time
on the initial perturbation amplitude obtained from the observations. This dependence is
presented in Fig. 6 of Verwichte et al. (2008). If we
approximate the solid curve in Fig. 2 by a linear
curve, then we obtain τd ≈ 1−0.215λ,
so 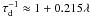 . Using
this result yields
. Using
this result yields 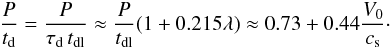 We
see that the slope of the curve showing the dependence of
P/td on
V0/cs is
about 0.44, which is much smaller than the slope 1.8 found by Verwichte et al. (2008) from observations. Hence, similar to Verwichte et al. (2008), we conclude that our theory
cannot explain the strong dependence of the damping time on the initial perturbation
amplitude.
We
see that the slope of the curve showing the dependence of
P/td on
V0/cs is
about 0.44, which is much smaller than the slope 1.8 found by Verwichte et al. (2008) from observations. Hence, similar to Verwichte et al. (2008), we conclude that our theory
cannot explain the strong dependence of the damping time on the initial perturbation
amplitude.
5. Summary and conclusions
We have studied the nonlinear damping of slow standing waves in hot coronal loops. We assumed that the wave amplitude is small and used it as a small parameter in the asymptotic expansions. In addition, we assumed that the wave damping is sufficiently slow and introduced the “slow” time related to the evolution of the wave amplitude and shape. We showed that, in the leading-order approximation, the nonlinear standing wave is a superposition of two identical nonlinear waves propagating in the opposite directions. The evolution of the two waves is governed by the Burgers equation.
When written in the dimensionless variables, the Burgers equation contains only one dimensionless parameter λ that defines the ratio of the nonlinear and dissipative term. Using the Cole-Hopfe substitution, we obtained an analytical solution
describing the evolution of a standing wave that has the form of the linear fundamental eigenmode at the initial moment of time. Then we used this solution for the parametric study of the nonlinear damping of standing waves. In particular, we studied the dependence of td/tdl on λ, where td and tdl are the damping time given by linear and nonlinear theory, respectively. We showed that, for λ ≤ 3, nonlinearity can reduce the damping time by no more than about one third. Moreover, for realistic coronal loop parameters and observed periods and damping times, the nonlinearity effect on the damping time must be taken into account only when the Mach number of the initial velocity perturbation is sufficiently large, of the order of or larger than 0.2.
We compared the results obtained in this paper with those obtained from observations. Similar to Verwichte et al. (2008), we found that out theory cannot explain strong dependence of the damping time on the initial perturbation amplitude.
Finally, we note that the analysis presented in this paper can be modified to study the effect of loop cooling on the nonlinear damping of slow standing waves in hot coronal loops. Recently, this effect has been studied in the linear approximation by Al-Ghafri & Erdélyi (2013).
Acknowledgments
M.S.R. acknowledges the support by the STFC grant, and thanks the unknown referee for very useful comments.
References
- Abramowitz, M., & Stegun, I. 1964, Handbook of Mathematical Functions (National Bureau of Standards) [Google Scholar]
- Al-Ghafri, K. S., & Erdélyi, R. 2013, Sol. Phys., 283, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, C. M., & Orszag, S. A. 1978, Advanced Mathematical Methods for Scientists and Engineers (New York: McGraw-Hill) [Google Scholar]
- Braginskii, S. I. 1965, Rev. Plasma Phys., 1, 205 [NASA ADS] [Google Scholar]
- Burgers, J. M. 1948, in Advances in Applied Mechanics, eds. R. von Mises, & T. von Karman (New York, N. Y.: Academic Press Inc.), 171 [Google Scholar]
- Cole, J. D. 1951, Quart. Appl. Math., 9, 225 [Google Scholar]
- De Moortel, I., & Hood, A. W. 2003, A&A, 408, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goedbloed, J. P. H., & Poedts, S. 2004, Principles of Magnetohydrodynamics (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Gusev, V. E. 1984a, Soviet Physics Acoustics-USSR, 30, 121 [Google Scholar]
- Gusev, V. E. 1984b, Vestnik Moskovskogo Universiteta Seriya 3 Fisika Astronomiya, 25, 29 [Google Scholar]
- Hopf, E. 1950, Comm. Pure and Appl. Math., 3, 201 [Google Scholar]
- Kliem, B., Dammasch, I. E., Curdt, W., & Wilhelm, K. 2002, ApJ, 568, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Mendoza-Briceño, C. A., Erdélyi, R., & Sigalotti, L. D. G. 2004, ApJ, 605, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., & Wang, T. 2002, ApJ, 580, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. 1982, Solar Magneto-Hydrodynamics, Geophysics and Astrophysics Monographs (Kluwer Academic Publishers) [Google Scholar]
- Rudenko, O. V., & Solujan, S. I. 1977, Theoretical Foundations of Nonlinear Acoustics (New York and London: Plenum Publishing Corporation, Consultants Bureau) [Google Scholar]
- Ruderman, M. S., & Nocera, L. 1998, A&A, 340, 287 [NASA ADS] [Google Scholar]
- Sigalotti, L. D. G., Mendoza-Briceño, C. A., & Luna-Cardozo, M. 2007, Sol. Phys., 247, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. J. 1962, Physics of Fully Ionized Gases (New York: Wiley Interscience) [Google Scholar]
- Verwichte, E., Haynes, M., Arber, T. D., & Brady, C. S. 2008, ApJ, 685, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J. 2011, Space Sci. Rev., 158, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J., Solanki, S. K., Curdt, W., Innes, D. E., & Dammasch, I. E. 2002, ApJ, 574, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J., Solanki, S. K., Curdt, W., et al. 2003a, A&A, 406, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., Solanki, S. K., Innes, D. E., Curdt, W., & Marsch, E. 2003b, A&A, 402, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitham, G. B. 1974, Linear and Nonlinear Waves (John Wiley & Sons) [Google Scholar]
All Figures
 |
Fig. 1 Evolution of the velocity profile with time for tdl = 5P and ϵ = 0.1. The upper, middle, and lower panel correspond to t = 0, P/2, and P respectively. |
| In the text | |
 |
Fig. 2 Dependence of the dimensionless damping time τd on the nonlinearity parameter λ. The solid line shows the dependence calculated numerically using the full Fourier expansion (49), while the dashed line shows the approximate dependence for small λ given by Eq. (55). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


